1 Introduction

Modern design solutions of gear transmissions assume that the ratio of the effective value of power transmitted by gears to their mass is as small as possible. In addition, there is a tendency to minimize the load on the teeth by increasing the speed of the rotating wheels. From an operational point of view, the rotational speed of the transmission input cannot be increased indefinitely, being limited by the dynamic properties of the drive motors. In addition, an increase in the rotational speed of the rotating elements in the drive system causes an increase in the amplitude of the excited mechanical vibrations [1]. High load values adversely affect the exploitation of the machine and its operator [2, 3]. Increased vibroacoustic activity adversely affects the durability and reliability of the gear transmission. Failures caused by material fatigue are very often caused by cyclically varying loads, which most often occur at low excitation frequencies. From the theoretical point of view, the cheapest method of testing the dynamic properties of machines and their subassemblies is via computer simulation. They are carried out on the basis of phenomenological models, attempting to take into account the most important features of the physical system and omitting those which are of minor importance.

For the assessment of the forces arising from the meshing of gears, discrete models consisting of two discs coupled with a parallel connection of elastic and dissipative element are most often used [4]. The proper meshing of the gears ensures the presence of gear backlash, which is one of the main factors introducing nonlinearity. In most studies, this nonlinearity is reproduced by a discontinuous function containing a so-called dead zone [5], or a straight broken line [6, 7]. When designing gearboxes, the value of backlash is assumed to be 0.04 of the tooth module. However, according to DIN 3967, its value should be in the range from 100 to \(400\,\upmu \hbox {m}\) [8]. Increasing its value causes transmission impact loads, and the cooperation of the gear wheels runs chaotically [9]. For this reason, the modification of the backlash is possible only to a limited extent. Due to the simplifications related to numerical calculations, the discontinuous characteristics of the gear backlash are sometimes approximated by polynomial functions of degree three [10, 11]. An alternative approach to the numerical mapping of the backlash is the approximation with a continuous function, with the equation proposed in the paper [12]. The use of this type of simplification is mainly related to the strong nonlinearity of gear backlash, which causes computational problems, in particular manifested by inaccurate mapping of time series and derivatives of higher orders in generalized coordinates [13]. Meshing stiffness is variable and is directly related to the number of intermeshing teeth. In the case of only one pair, the meshing teeth are subject to the greatest deflection, because the cooperating pair of teeth is affected by the highest load. The easiest way to identify the stiffness of the teeth is to treat them as a fixed beam. Although this simplification provides approximate information, it is, nevertheless, sufficient to carry out initial quantitative and qualitative model tests. Much more accurate results are obtained using models based on the finite element method [14]. In model tests, the periodic stiffness of the intermittent teeth is usually mapped using a periodic function [15] and less frequently with a rectangular [16] or trapezoidal [17] profile. The source of the excited mechanical vibrations of meshing gear teeth is the so-called performance and location errors. They are mainly caused by radial beating and geometric deviations of the tooth profile. This parameter depends on the accuracy of the production and assembly of the cooperating wheels. In mathematical models, this quantity is described by a single harmonic function or a superposition of harmonics [18]. An additional adverse phenomenon affecting the increase in dynamic loads is the wear of the tooth surface and possible damage occurring as the time of machine operation increases [19,20,21,22]. The entire mentioned factors mean that the phenomenon of energy dissipation in cooperating toothed wheels is a complex issue. Admittedly, works are undertaken in the field of its mathematical description [23, 24]. However, due to the complexity of the energy dissipation phenomenon in meshing, the energy losses are usually modelled with a viscous damper [25]. Taking into account these factors leads to a nonlinear mathematical model of a gear transmission in which chaotic phenomena may occur.

Fig. 1
figure 1

A phenomenological model of a single-stage gear transmission

Full size image

The subject of this paper is the evaluation of the function modelling gear backlash influence on the effectiveness of computer simulations. Numerical experiments were carried out for three methods of mapping the backlash. For each characteristic, multi-coloured maps of the largest Lyapunov exponent were generated, and on this basis the ranges of variability of the mathematical model parameters, in which the chaotic movement takes place, were identified. The obtained results enabled the rejection of the backlash models approximated by functions based on the polynomials of the third degree, due to significant differences in the distribution of chaotic motion zones. For further research, the model of backlash described by the logarithmic function was adopted, for which the coefficient responsible for the nature of its variability was optimized.

2 Formulation of the mathematical model of the gear transmission

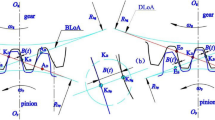
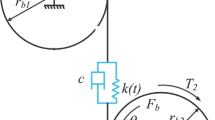
The object of the model tests is a single-stage gear with total transmission ratio \(i = 36.85\), which is an integral component of a hoisting mechanism with a load capacity \(Q=12.5t\) and hoisting speed \(v_{p}=9.7\,\hbox {m}/\hbox {min}\). The dynamics of the gearbox have been modelled by a vibrational mechanical system with two degrees of freedom. The model consists of two non-deformable discs with radii \(R_{1}\) and \(R_{2}\), whose inertial properties are given by mass moments of inertia \(J_{1}\) and \(J_{2}\). The discs rotate rigidly supported with respect to the axes \(O_{1}\) and \(O_{2}\). The gears are coupled by a parallel connection of the spring element \(c_{Z}\) and dissipative element \(b_{Z}\). Due to the complexity of the phenomena caused by the friction between cooperating teeth, the dissipative properties were approximated using a linear viscous damper. The formulated model also includes an element modelling the error of gear wheels cooperation e(t), which is connected in series with the spring element \(c_{Z}\) and dissipative element \(b_{Z}\). The transmission movement is caused by the external drive torque \(M_{N}\), acting on gear wheel with radius \(R_{1}\). In contrast, to the wheel \(R_{2}\) the load moment \(M_{O}\) has been applied. The \(L_{Z}\) value is a constant equal to half the backlash value. The schematic diagram of the phenomenological model is shown in Fig. 1.

On the basis of such a formulated phenomenological model of single-stage gear transmission, differential equations of motion were derived:

$$\begin{aligned} \left\{ {\begin{array}{l} {J_1}{{\ddot{\varphi }}_1} + {R_1}{b_Z}\left( {{R_1}{{\dot{\varphi } }_1} - {R_2}{{\dot{\varphi } }_2} - \dot{e}\left( t \right) } \right) \\ \quad +\, {R_1}{c_Z}\left( {{R_1}{\varphi _1} - {R_2}{\varphi _2} - e\left( t \right) } \right) f\left( u \right) = {M_N},\\ {J_2}{{\ddot{\varphi }}_2} - {R_2}{b_Z}\left( {{R_1}{{\dot{\varphi } }_1} - {R_2}{{\dot{\varphi } }_2} - \dot{e}\left( t \right) } \right) \\ \quad -\,{R_2}{c_Z}\left( {{R_1}{\varphi _1} - {R_2}{\varphi _2} - e\left( t \right) } \right) f\left( u \right) = -\,{M_O}. \end{array}} \right. \end{aligned}$$
(1)

Differential equations of motion (1) can be derived using the classic formalism of Lagrange equations of the second order or using non-classical methods such as graphs [26, 27].

Fig. 2
figure 2

Graphical visualization of the gear backlash characteristics and their approximation: a the polynomial of the third degree, b the modified polynomial of the third degree, c the logarithmic function

Full size image

2.1 A reduced mathematical model of gear transmission

The quantitative and qualitative assessment of the phenomena occurring during intermeshing of cooperating wheels is most efficiently analysed using a reduced model with one degree of freedom. The starting point for its derivation is the system of differential equations (1). After several transformations and the introduction of a new coordinate \(q=R_1 \varphi _1 -R_2 \varphi _2 \), the mathematical model is reduced to the form:

$$\begin{aligned}&{m_\mathrm{red}}\ddot{q} + {b_Z}\left( {\dot{q} - \dot{e}\left( t \right) } \right) + {c_Z}\left( {q - e\left( t \right) } \right) f(u) \nonumber \\&\quad = {m_\mathrm{red}}\delta , \end{aligned}$$
(2)

where

$$\begin{aligned} m_\mathrm{red}= & {} \frac{J_1 J_2 }{J_2 R_1^2 +J_1 R_2^2 },\,\mu =\frac{M_0 }{M_N },\\ \delta= & {} \left( {\frac{R_1 }{J_1 }+\frac{R_2 \mu }{J_2 }} \right) M_1 ,\, e\left( t \right) =e_1 \cos ({\omega _z t}). \end{aligned}$$

Furthermore, \(\omega _{z} = z_{1}\cdot \omega _{S}\) is the frequency of meshing, where \(\omega _{S}\) is the angular velocity of the rotor of the drive motor and \(z_{1}\) is the number of teeth on the gear. Taking into account the characteristics of periodically variable meshing stiffness \(c_Z \left( t \right) =c_0 +c_1 \cos \left( {\omega _z t} \right) \) and using the substitution \(q=u+e\left( t \right) \), Eq. (2) takes the form:

$$\begin{aligned}&{m_\mathrm{red}}\ddot{u} + {b_Z}\dot{u} + \left( {{c_0} + {c_1}\cos \left( {{\omega _z}t} \right) } \right) f(u) \nonumber \\&\quad = {m_\mathrm{red}}\delta + {m_\mathrm{red}}\omega _z^2{e_1}\cos ( {{\omega _z}t}). \end{aligned}$$
(3)

Until now, gear has been treated as a system in which there is no backlash. From a mathematical point of view, its inclusion consists in replacing the displacement u with an adequate function f(u) which maps the displacement properties, but in the so-called dead zone takes values equal to zero. It is worth noting that the physical interpretation of the function f(u) is the same as the displacement:

$$\begin{aligned}&{m_\mathrm{red}}\ddot{u} + {b_Z}\dot{u} + \left( {{c_0} + {c_1}\cos \left( {{\omega _z}t} \right) } \right) f(u) \nonumber \\&\quad = {m_\mathrm{red}}\delta + {m_\mathrm{red}}\omega _z^2{e_1}\cos ( {{\omega _z}t}). \end{aligned}$$
(4)

The mathematical model (4) can be further reduced to dimensionless form:

$$\begin{aligned}&\ddot{x} + 2h\dot{x} + \left[ {1 + \alpha \cos \left( {\omega \tau } \right) } \right] f(x)\nonumber \\&\quad = {F_\mathrm{av}} + {F_e}{\omega ^2}\cos ({\omega \tau }). \end{aligned}$$
(5)

where

$$\begin{aligned}&\omega _0^2 =\frac{c_0 }{m_\mathrm{red}},\,\, h=\frac{b_Z }{2\sqrt{m_\mathrm{red} c_0}},\,\,\alpha =\frac{c_1 }{c_0},\,\,\omega =\frac{\omega _z }{\omega _0 },\\&\quad F_\mathrm{av} =\frac{m_\mathrm{red} \delta }{L_Z c_0},\,\,F_e =\frac{e_1 }{L_Z},\,\,x=\frac{u}{L_Z }. \end{aligned}$$

The introduction of a new variable x, dependent on the dimensionless time \(\tau =\omega _0 t\), affects the width of the dead zone of the tooth gap, now falling within the range limited by the values \(-\,1\) and 1.

Table 1 Numerical values of approximating functions
Full size table
Table 2 Parameters characterizing the tested gear model
Full size table

2.2 Mathematical models of gear backlash

The subject of the research presented in this work is the assessment of the approximation of the gear backlash characteristics impact on the dynamic properties of the gear. The results of numerical calculations were computed using a discontinuous function describing backlash:

$$\begin{aligned}&{f{\begin{array}{ll} {(u)=\left\{ {{\begin{array}{ll} {u+L_Z ,}&{}\quad {u<-\,L_Z ,} \\ {0,}&{}\quad {-\,L_Z \le u\le L_Z ,} \\ {u-L_Z ,}&{}\quad {u>L_Z ,} \\ \end{array} }} \right. } &{} {\mathop \Rightarrow \limits ^{x=\frac{u}{L_Z }} } \\ \end{array} }}\nonumber \\&\quad {L_Z f(x)=\left\{ {{\begin{array}{ll} {x+1,}&{}\quad {x<-\,1,} \\ {0,}&{}\quad {-\,1\le x\le 1,} \\ {x-1,}&{}\quad {x>1.} \\ \end{array} }} \right. } \end{aligned}$$
(6)

When conducting computer simulations, instead of using the conditional function (6), it is more convenient to use the function given by the equation:

$$\begin{aligned} f(x)=x+\frac{\left| {a_2 x-1} \right| -\left| {a_2 x+1} \right| }{2}. \end{aligned}$$
(7)

Bearing in mind the reduction in the numerical calculations time, simplifications are applied, streamlining model tests. The most often discontinuous characteristic of the backlash is represented by the third-degree polynomial [7]:

$$\begin{aligned} f(x)=a_1 x+a_2 x^{3}. \end{aligned}$$
(8)

For the approximation of the discontinuous function (6), the characteristics proposed in paper [28] can also be used:

$$\begin{aligned} f(x)=a_1 \left( {\left| {a_2 x-1} \right| -\left| {a_2 x+1} \right| } \right) +a_3 x^{3}. \end{aligned}$$
(9)

From the mathematical point of view, the best results are achieved using the logarithmic function proposed in the paper [12]:

$$\begin{aligned} f(x)=\frac{1}{a_1 }\hbox {ln}\left( {\frac{1+e^{a_1 \left( {x-1} \right) }}{1+e^{-a_1 \left( {x+1} \right) }}} \right) . \end{aligned}$$
(10)

The accuracy of the approximation of the backlash characteristics with continuous functions is illustrated graphically in Fig. 2. With a view to highlighting the differences between the discontinuous backlash function and its logarithmic approximation (Fig. 2c), the relationship (10) is plotted for the coefficient \(a_{1} = 10\). This was because the value adopted in further research meant that the characteristics were practically overlapping.

The numerical values of the coefficients of the smooth approximations describing the characteristics of the gear backlash are summarized in Table 1.

Numerical experiments were carried out in the paper, in which the effect of the mathematical model of the backlash on the dynamics of the gear was compared.

3 Model studies of gear transmission

Model tests were carried out on the basis of the numerical data (Table 2), characterizing a single-stage gear. The source of motion of the tested mechanical system is a 4-pole induction electric motor with rated power \(P=7.5\,\hbox {kW}\) and speed \(n_\mathrm{S} = 1450\,\hbox {min}^{-1}\). During numerical experiments, perfectly rigid shafts connecting gears with the engine and massless element, which is affected by the load moment, were adopted. In addition, it was assumed that the value of the moment of load applied to the gear with a radius \(R_{2}\) is 80% of the torque value. The substitute damping factor b captures the total energy losses caused by the movement resistance in the bearings and the friction of the cooperating gear teeth.

3.1 Identification of chaotic motion zones of backlash various models

On the basis of the numerical data characterizing the mathematical model, numerical calculations showing the effect of normalized frequency \(\omega \) and the dimensionless error of gear wheel cooperation \(F_{e}\) on the location of chaotic motion zones were carried out. Both analytical methods and numerical algorithms find applications [29,30,31] to estimate the so-called largest Lyapunov exponent \(\uplambda \). This indicator is one of the key concepts of chaos theory through which it is possible to distinguish where unpredictable chaotic behaviour.

$$\begin{aligned} \lambda =\mathop {\lim }\limits _{\varepsilon \left( 0 \right) \rightarrow 0,n\rightarrow \infty } \frac{1}{n \tau }\mathop \sum \limits _{i=1}^n \hbox {ln}\left( {\frac{\varepsilon _i \left( t \right) }{\varepsilon \left( 0 \right) }} \right) . \end{aligned}$$
(11)

In the above equation, \(\varepsilon _{i}(t)\) represent the vectors connecting, at the same instant of time, the trajectory of the studied motion with a reference trajectory, with the origins of both trajectories being located in the close vicinity determined by \(\varepsilon (0)\). In practical applications, this method of estimating the largest Lyapunov exponent is reduced to averaging values over many iterations, in an adequate suppression space. In our case, we assume a phase space containing the displacement and speed of the transmission model \((x,\dot{x})\). Positive values of \(\uplambda \) indicate chaotic behaviour; otherwise, the trajectories tend towards either stable points or periodic orbits. In the case of discontinuous slack characteristics, the Lyapunov exponent can be incorrectly estimated on the basis of the Jacobian algorithm; therefore, in this work we use the concept of its identification based on Eq. (11). The results of model tests illustrating the influence of the function approximating backlash are presented in the form of multi-coloured maps of the maximum Lyapunov exponent. The procedure for generating these kinds of multi-coloured maps is not fundamentally different from the calculations made with respect to a single control parameter.

In order to obtain a satisfactory resolution, the range of variability of control parameters defining the abscissa and ordinates is divided into 500 intervals. The calculated values of the largest Lyapunov exponent depend to a large extent on the assumed distance of the initial conditions \(\varepsilon (0)\), of the two trajectories. In this study, the distance was assumed to be equal \(\varepsilon (0)=10^{-5}\). On the generated two-dimensional maps of the largest Lyapunov exponent (Fig. 3), in the rainbow scale one can notice areas of chaotic solutions, which are marked in orange and red.

It is worth mentioning that the calculation time of the multi-coloured map of the largest Lyapunov exponent, when the characteristics of backlash was mapped with the discontinuous function (6), was about 41,000 s. In the case of modelling with functions based on polynomials (7) and (8), the calculation times were on a similar level and amounted to approx. 5000 s. On the other hand, in the case of approximation of the characteristics with a logarithmic function (9), the calculation of the multi-coloured map of the largest Lyapunov exponent lasted approx. 10,000 s.

During the verification of the obtained results of the model tests, a priori static characteristics of the backlash for the most reliable gear model were assumed, modelled by the so-called dead zone. This model was considered a template, because the results of model tests obtained through it show convergence with the results of experimental research [22, 32]. The direct comparison of multi-coloured maps of the largest Lyapunov exponent shows no correlation with respect to backlash models based on polynomial functions (Fig. 3b, c). This premise constitutes a formal basis for omitting them in further model studies. The dynamics of the toothed gear significantly depend on the parameter \(F_e \), representing the accuracy of the execution and cooperation of gears. The mathematical model in which the characteristics of the backlash are approximated by the logarithmic function (Fig. 3d) is the only approximation, which shows an acceptable correspondence with the solution based on the discontinuous backlash function (Fig. 3a). In order to verify the thesis formulated for a given parameter value \(F_e =0.1\), bifurcation diagrams of steady states are plotted. On their basis, conclusions can still be drawn regarding the nature of the mechanical vibrations excited in the areas where the doubling period takes place [33, 34].

Fig. 3
figure 3

Maps of the Lyapunov exponent generated at zero initial conditions (\(x_0 =0,\dot{x}_{0}=0)\) models of backlash represented by the function: a discontinuous with a dead zone, b polynomial of the third degree, c modified polynomial, d logarithmic approximation

Full size image

Bifurcation diagrams are constructed on the basis of time responses or trajectories recorded on the phase plane. In our case, they were plotted on the basis of local maxima (Fig. 4 points in navy blue) and minima (Fig. 4 points in red) of numerical solutions of data in the form of time series. To determine the periodicity of solutions, diagrams of the number of phase stream intersections with the axis of the abscissa were used (NPSI—number of phase stream intersection), which correspond with the bifurcation diagrams of steady states (Fig. 4).

Fig. 4
figure 4

Bifurcation diagrams and corresponding diagrams of the number of phase stream intersections (NPSI), for the characteristics of the backlash modelled by: a a discontinuous function, b a logarithmic function

Full size image

In general terms, the essence of generating NPSI diagrams is to determine the number of intersections between trajectories and the axis of phase plane displacements from \(\dot{x} =0\). At the same time, only the intersection points are taken into account, in which the coordinate representing the speed changes sign, for example, from negative to positive. In this place, it should be clearly indicated that the precise assessment of the number of intersections of the phase trajectory, in the areas of variability of the control parameter where the motion of the system is irregular, depends on the width of the time window. This is due to the fact that in chaotic motion zones, recorded trajectories are characterized by very long vibration periods.

Irrespective of the characteristics of the backlash used in the simulation, the obtained results show the presence of two zones where the irregular movement of the gearbox takes place. Despite the visual agreement between multi-coloured maps of the largest Lyapunov exponent (Figs. 2a, 3b), graphical images of the bifurcation diagrams of steady states show differences. These differences are observed mainly in the vicinity of areas of chaotic motion. It is also worth noting that in terms of frequency \(\omega \in \langle 0.35\), \(0.45\rangle \), the solution (Fig. 4b) suggests the presence of the period doubling phenomenon. With regard to the discontinuous model (Fig. 4a), the first zone is estimated to be within limits \(\omega \in \langle 0.9\), \(1.1\rangle \) and second within \(\omega \in \langle 1.2\), \(1.6\rangle \). However, on the bifurcation diagram, the zones in which the transmission behaves chaotically are limited by the values of the control parameter, respectively, the first \(\omega \in \langle 0.9\), \(1.15\rangle \) and second \(\omega \in \langle 1.25\), \(1.645\rangle \). Direct comparison of the diagrams of the number of phase stream intersections (lower graphs of Fig. 4) shows that, apart from the areas of chaotic solutions, periodic vibrations dominate. However, the 2T-periodic movement takes place in the vicinity of the bifurcation zones. On the basis of the bifurcation diagrams and the NPSI, it is difficult to assess the dimensionless excitation frequency \(\omega \) on the nature of the solution. Adequate model test results are depicted in the form of time courses, amplitude and frequency spectra, and Poincaré cross sections (Fig. 5). When conducting computer simulations, zero initial conditions were assumed \(x_0=0,\dot{x}_{0}=0\). Exemplary results showing the system response in the time domain plotted in navy blue represent a solution in which the backlash characteristics are approximated by a logarithmic function (9). However, the time sequence marked in red corresponds to the backlash modelled with the discontinuous function (5). The width of the time window in which the system response was observed was determined to be equal to 20 periods of excitation. The same colour assignment was applied to the generated frequency–amplitude spectra. To obtain satisfactory spectral resolution, numerical calculations were carried out on the basis of data taken from a time window with a width equal to 350 periods of excitation. Direct visual comparison of frequency–amplitude spectra (Fig. 5b) does not show any noticeable differences in the distribution of the excited harmonics. These differences become important in the case of time responses (Fig. 5a) and Poincaré cross sections (Fig. 5c).

Fig. 5
figure 5

Influence of mapping characteristics of backlash for \(\omega = 1.05\) on: a time histories of solutions, b frequency–amplitude spectra, c Poincaré cross sections

Full size image

The numerical simulations indicate that the classic Fourier’s spectrum is not an appropriate indicator on the basis of which the reliability of the formulated model can be assessed.

3.2 The influence of parameter \(a_{1}\) on the amplitude–frequency spectrum distribution

Much more information about the dynamics of the system is provided by spectrograms STFT [35] or wavelet scales [36, 37]. In our research, for the evaluation of the activity of individual harmonic components, a transform based on a Gaussian wavelet was used in selected moments of time. In Fig. 6, multi-coloured maps of the activity of the harmonic components of the backlash models are provided. Bearing in mind the insight into the dynamics of the evolution of harmonic components, spectrograms were calculated on the basis of fixed time series with the number of samples \(n = 2^{11}\), observed in time windows \(\tau _{W}\) with a width of 400 periods of external excitation.

The time sequence spectrogram, based on the discontinuous backlash model (Fig. 6a), shows the highest activity of the harmonic components located in the range \(\omega \in \langle 0.082\), \(0.657\rangle \). The dominant subharmonics, represented in red, are excited irregularly over time. In the low frequency range \(\omega \in \langle 0\), \(0.041\rangle \), individual harmonics are activated cyclically. The largest activity of spectrogram harmonics, where the backlash was modelled with a smooth logarithmic function (Fig. 6b), is located in the area of variability \(\omega \in \langle 0.167\), \(0.669\rangle \). Increasing the parameter \(a_{1}\) of logarithmic function, approximating the discontinuous backlash characteristics, results in a range change \(\omega \in \langle 0.084\), \(0.669\rangle \), in which the dominant harmonic components are located (Fig. 6b, c). Differences in graphic images of time series, Fourier spectra, and in particular bifurcation diagrams and Poincaré cross sections, can be minimized by adjusting the parameter \(a_{1}\) of Eq. (9). Decreasing its value means that below \(\omega = 0.5\) frequency, the width of the 2T-periodic vibration zone (Fig. 4) increases; this is not found with the discontinuous model. It is also worth mentioning that limiting the value of \(a_{1}\) causes overlapping of the first \(\omega \in \langle 0.9\), \(1.1\rangle \) and second zones \(\omega \in \langle 1.2\), \(1.6\rangle \) of chaotic movement (Fig. 4a).

Fig. 6
figure 6

Spectrometry of wavelet transformations of backlash models mapped by function (\(x_0 =0,\dot{x}_{0}=0)\): a discontinuous \(\omega = 1.05\), b logarithmic \(\omega = 1.05\), \(a_{1} = 60\), c logarithmic \(\omega = 1.05\), \(a_{1} = 370\), d logarithmic \(\omega = 1.05\), \(a_{1} = 685\)

Full size image

3.3 Optimization of parameter \(a_{1}\)

The influence of the value of the logarithmic coefficient of the function approximating the backlash and the associated evolution of the bifurcation diagrams is presented in Fig. 7. The value of parameter \(a_{1} = 420\), at which 2T-periodic vibrations in the frequency range from \(\omega \) 0.4 to 0.5 disappear, is not optimal. In order to determine the optimal \(a_1 \), from the point of view of the numerical experiment, the parameter of the logarithmic function was identified on the basis of the equation, approximating the increment of frequency \(\omega _{1}\). Frequencies \(\omega _{1}\) were defined as points of bifurcation diagrams in which a 2T-periodic solution does not appear (Fig. 4a). When the factor \(a_{1}\) reaches values around 450, 2T-periodic vibrations disappear. On this basis, the horizontal asymptote to which the approximated function is aimed, along with the increase in the \(a_{1}\) parameter, has been established:

$$\begin{aligned} \omega _1 \left( {a_1 } \right) =\left( {\frac{0.17a_1 }{0.364a_1 +5.451}} \right) . \end{aligned}$$
(12)
Fig. 7
figure 7

Influence of the logarithmic coefficient \(a_{1}\) of the function approximating the backlash, on the evolution of the bifurcation diagram

Full size image

When calculating the limit of the approximation function (12), it was found that the position of the asymptote is set at 0.467. This number approximately corresponds to the frequency of external load when there is a hopping of the amplitude of periodic vibrations. Assuming a 1% horizontal mapping error, the value of the parameter \(a_{1}\) equals 685; this value makes it possible to approximate the section with acceptable accuracy. This is confirmed by the calculated correlation dimensions included in the diagrams (Fig. 8a, b). The relative errors of the correlation dimensions of the calculated Poincare cross sections, for discontinuous and approximated backlash characteristics, amount to 0.4% for an excitation frequency \(\omega _{1} = 1.05\) and 0.9% in case of \(\omega _{1} = 1.4\). Referring to the Poincaré cross sections, which are shown in Fig. 5c, where the approximation function was generated for \(a_{1} = 60\), the estimated relative error is about 3.5%. However, this error value does not guarantee compliance of solutions in the field of time and frequency. Assuming the error row at the level of 0.1% of the horizontal asymptote mapping, the value of parameter \(a_{1}\) increases more than 10 times reaching the value of 6980, in relation to \(a_{1} = 685\). For this value, the estimated correlation dimension of the Poincaré cross section is 1.237, which is approx. 0.08% of the mapping error of the trajectory points with the control plane.

Fig. 8
figure 8

Poincaré cross section: a\(\omega = 1.05\), b\(\omega = 1.4\)

Full size image
Fig. 9
figure 9

Influence of the value of the parameter \(a_{1}\) on the chaotic solution of the system: a\(a_{1} = 685\), b\(a_{1} = 6980\)

Full size image

Time sequences of solutions obtained on the basis of a discontinuous gear model are marked in red, while navy blue corresponds to solutions based on the approximation of the backlash characteristics by a logarithmic function (Fig. 9). By increasing the value of the parameter \(a_1 \) by more than tenfold, the solution much better reflects the solution of the discontinuous model. However, as time passes, the solutions start to vary more and more (Fig. 9b chart at the top). The accuracy of the approximation of the backlash characteristics becomes even more evident when the excitation frequency assumes values corresponding to the second chaotic movement zone (Fig. 9b central chart). This behaviour is therefore dependent on whether the transmission’s operating point is in the chaotic or predictable motion zone. Accuracy of the approximation between the characteristics of the backlash, when the frequency of the external load is located in the chaotic movement zone, shows similarity in the behaviour that is observed during the study of the sensitivity of initial conditions to a negligible small displacement. Striving to obtain acceptable compatibility of solutions in the frequency domain implies the use of very large values of parameter \(a_{1}\). Excessive values significantly extend the time of numerical calculations, as a result of which the model based on the approximation of the backlash characteristics becomes ineffective, as the computer simulation times do not differ much.

In the case when the system is affected by excitation with a value that lies outside the chaotic motion zones, the solution’s compatibility is in principle perfect. Convergence of results is already achieved with \(a_{1} = 685\); therefore, there are no solutions for larger values of \(a_{1}\) (Fig. 9a bottom charts), where time responses are presented in the zones of the control parameter \(\omega \), in which the doubling period takes place.

4 Conclusions

Based on the model tests carried out on the nonlinear dynamics of a single-stage gear transmission, the following conclusions can be made:

  • The use of functions based on third-degree polynomials in numerical experiments, which approximate the characteristics of the backlash, causes incorrect and inaccurate results in the computation of the time dynamics of the system. These errors are mainly caused by imprecise mapping of functions at the discontinuity points of the backlash.

  • The use of logarithmic functions in model studies is an alternative approach, providing comparable information about dynamic phenomena occurring in the system, which is obtained through a discontinuous model.

  • Additionally, the undoubted advantage of the logarithmic function, which approximates the characteristics of the backlash, is the reduction in nearly four times the calculation time, when the coefficient \(a_{1} = 685\). Adoption of large values for \(a_{1}\) improves the convergence of solutions in relation to the discontinuous model, but this is achieved at the expense of extending the time of numerical calculations.

Our analysis was carried out for the same zero initial conditions (\({x}_0 =0,\dot{x}_{0}=0\)) which allowed for parallel calculations for all considered values of the system parameters. This strategy has allowed to significantly shorten the time of calculations in comparison with testing basins of attraction for individual solutions. The cost of this omission is to narrow our analysis to one solution for each set of system parameters. The calculations were carried out using the proprietary program in the MATHEMATICA environment.