Skip to main content
SpringerLink
Log in

Series solutions and bifurcation of traveling waves in the Benney–Kawahara–Lin equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

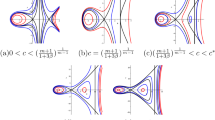
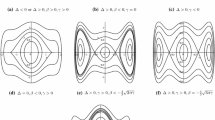
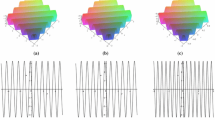
In this paper, the Lie group method is performed on the BKL equation. By reducing the BKL equation to four classes of ODEs, we obtain new power series solutions of it. Furthermore, as an important reduced equation, the traveling wave equation is investigated in detail. Treating it as a singular perturbation system in \({\mathbb {R}}^4\), we apply the geometric singular perturbation theory and dynamical system methods to study its phase space geometry. By using some techniques, such as tracking the unstable manifold of the saddle, discussing transversality of the stable and unstable manifolds and investigating some complicated nonlocal bifurcation, we obtain wave speed conditions to guarantee the existence of various bounded traveling waves of the BKL equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Xie, Y.X.: New explicit and exact solutions of the Benney–Kawahara–Lin equation. Chin. Phys. B 18, 4094–4099 (2009)

    Article  Google Scholar 

  2. Benney, D.J.: Long waves on liquid films. J. Math. Phys. 45, 150–155 (1966)

    Article  MathSciNet  MATH  Google Scholar 

  3. Lin, S.P.: Finite amplitude side-band stability of a viscous film. J. Fluid Mech. 63, 417–429 (1974)

    Article  MATH  Google Scholar 

  4. Hunter, J.K., Scheurle, J.: Existence of perturbed solitary wave solutions to a model equation for water waves. Physica D 32, 253–268 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  5. Kawahara, T., Takaoka, M.: Chaotic behaviour of soliton lattice in an unstable dissipative-dispersive nonlinear system. Physica D 39, 43–58 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  6. Kuramoto, Y., Tsuzuki, T.: On the formation of dissipative structures in reaction–diffusion systems. Prog. Theor. Phys. 54, 687–699 (1975)

    Article  Google Scholar 

  7. Kuramoto, Y., Tsuzuki, T.: Persistent propagation of concentration waves in dissipative media far from thermal equilibrium. Prog. Theor. Phys. 55, 356–369 (1976)

    Article  Google Scholar 

  8. Sivashinsky, G.I.: Nonlinear analysis of hydrodynamic instability in laminar flames—I. Derivation of basic equations. Acta. Astronaut. 4, 1177–1206 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  9. Sivashinsky, G.I.: On irregular wavy flow of a liquid film down a vertical plane. Prog. Theor. Phys. 63, 2112–2114 (1980)

    Article  Google Scholar 

  10. Babchin, A.J., Frenkel, A.L., Levich, B.G., Sivashinsky, G.I.: Nonlinear saturation of Rayleigh–Taylor instability in thin films. Phys. Fluids 26, 3159–3161 (1983)

    Article  MATH  Google Scholar 

  11. Kawahara, T.: Formation of saturated solitons in a nonlinear dispersive system with instability and dissipation. Phys. Rev. Lett. 51, 381–383 (1983)

    Article  Google Scholar 

  12. Sivashinsky, G.I.: Large cells in nonlinear marangoni convection. Physica D 4, 227–235 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kudryashov, N.A.: Exact solutions of the generalized Kuramoto–Sivashinsky equation. Phys. Lett. A 147, 287–291 (1990)

    Article  MathSciNet  Google Scholar 

  14. Kudryashov, N.A., Zargaryan, E.D.: Solitary waves in active–dissipative dispersive media. J. Phys. A 29, 8067–8077 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  15. Ruan, S.G., Xiao, D.M.: Stability of steady states and existence of travelling waves in a vector-disease model. Proc. R. Soc. Edinb. A 134, 991–1011 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  16. Bates, P.W., Chen, F.X.: Spectral analysis of traveling waves for nonlocal evolution equations. SIAM J. Math. Anal. 38, 116–126 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  17. Constantin, A.: The trajectories of particles in Stokes waves. Invent. Math. 166, 523–535 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  18. Li, J.B., Dai, H.H.: On the Study of Singular Nonlinear Traveling Wave Equation: Dynamical System Approach. Science Press, Beijing (2007)

    Google Scholar 

  19. Hsu, S.B., Zhao, X.Q.: Spreading speeds and traveling waves for nonmonotone integrodifference equations. SIAM J. Math. Anal. 40, 776–789 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  20. Shatah, J., Walsh, S., Zeng, C.C.: Travelling water waves with compactly supported vorticity. Nonlinearity 26, 1529–1564 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  21. Ovsiannikov, L.V.: Group Analysis of Differential Equations. Academic, New York (1982)

    MATH  Google Scholar 

  22. Olver, P.J.: Application of Lie Groups to Differential Equations. Springer, New York (1986)

    Book  MATH  Google Scholar 

  23. Bluman, G.W., Kumei, S.: Symmetries and Differential Equations. Springer, New York (1989)

    Book  MATH  Google Scholar 

  24. Katzengruber, B., Krupa, M., Szmolyan, P.: Bifurcation of traveling waves in extrinsic semiconductors. Physica D 144, 1–19 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  25. Li, J.B., Qiao, Z.J.: Bifurcations of traveling wave solutions for an integrable equation. J. Math. Phys. 51, 042703 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  26. Li, J.B., Zhang, Y.: Homoclinic manifolds, center manifolds and exact solutions of four-dimensional traveling wave systems for two classes of nonlinear wave equations. Int. J. Bifurc. Chaos 21, 527–543 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  27. Li, J.B., Chen, G.R.: Exact traveling wave solutions and their bifurcations for the Kudryashov–Sinelshchikov equation. Int. J. Bifurc. Chaos 22, 1250118 (2012)

    Article  MATH  Google Scholar 

  28. Li, J.B., Qiao, Z.J.: Peakon, pseudo-peakon, and cuspon solutions for two generalized Camassa–Holm equations. J. Math. Phys. 54, 123501 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  29. Li, J.B.: Bifurcations and exact travelling wave solutions of the generalized two-component hunter-saxton system. Discrete Cont. Dyn. B 19, 1719–1729 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  30. Zhang, Y., Li, J.B.: Comment on superposition of elliptic functions as solutions for a large number of nonlinear equations. J. Math. Phys. 56, 084101 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  31. Leta, T.D., Li, J.B.: Exact traveling wave solutions and bifurcations of the generalized derivative nonlinear Schrödinger equation. Nonlinear Dyn. 85, 1031–1037 (2016)

    Article  MATH  Google Scholar 

  32. Zhang, T.H., Li, J.B.: Exact solitons, periodic peakons and compactons in an optical soliton model. Nonlinear Dyn. 91, 1371–1381 (2018)

    Article  MATH  Google Scholar 

  33. Fenichel, N.: Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equ. 31, 53–98 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  34. Li, C.Z., Zhang, Z.F.: A criterion for determining the monotonicity of the ratio of two Abelian integrals. J. Differ. Equ. 24, 407–424 (1990)

    MathSciNet  MATH  Google Scholar 

  35. Zhang, Z.F., Ding, T.R., Huang, W.Z., Dong, Z.X.: Qualitative Theory of Differential Equations. American Mathematical Society, Providence (1992)

    Google Scholar 

  36. Chow, S.N., Hale, J.K.: Method of Bifurcation Theory. Springer, New York (1982)

    Book  MATH  Google Scholar 

  37. Rottschäfer, V., Wayne, C.E.: Existence and stability of traveling fronts in the extended Fisher–Kolmogorov equation. J. Differ. Equ. 176, 532–560 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  38. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems and Bifurcation of Vector Fields. Springer, New York (1983)

    Book  MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by the Natural Science Foundation of China (Nos. 11301043 and 11701480), China Postdoctoral Science Foundation (No. 2016 M602663), Innovative Research Team of the Education Department of Sichuan Province (No. 15TD0050).

Author information

Authors and Affiliations

  1. College of Applied Mathematics, Chengdu University of Information Technology, Chengdu, 610225, Sichuan, People’s Republic of China

    Yuqian Zhou

  2. School of Computer Science and Technology, Southwest Minzu University, Chengdu, 610041, Sichuan, People’s Republic of China

    Qian Liu

Authors
  1. Yuqian Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qian Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qian Liu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, Y., Liu, Q. Series solutions and bifurcation of traveling waves in the Benney–Kawahara–Lin equation. Nonlinear Dyn 96, 2055–2067 (2019). https://doi.org/10.1007/s11071-019-04905-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-04905-x

Keywords

Search

Navigation