Quasiperiodic waves, solitary waves and asymptotic properties for a generalized (3 + 1)-dimensional variable-coefficient B-type Kadomtsev–Petviashvili equation

Abstract

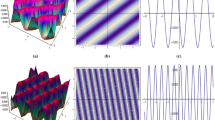
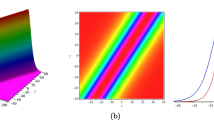
Under investigation in this paper is a generalized (3 + 1)-dimensional variable-coefficient BKP equation, which can be used to describe the propagation of nonlinear waves in fluid mechanics and other fields. With the aid of binary Bell’s polynomials, an effective and straightforward method is presented to explicitly construct its bilinear representation with an auxiliary variable. Based on the bilinear formalism, the soliton solutions and multi-periodic wave solutions are well constructed. Furthermore, the tanh method and the tan method are employed to construct more traveling wave solutions of the equation. Finally, the asymptotic properties of the multi-periodic wave solutions are systematically analyzed to reveal the connection between periodic wave solutions and soliton solutions. It is interesting that the periodic waves tend to solitary waves under a limiting procedure. Our results can be used to enrich the dynamical behavior of higher-dimensional nonlinear wave fields.

Appendix: Riemann theta function periodic waves

In order to consider three-periodic wave solutions of Eq. (1). By taking $N=3$, Riemann theta function takes the following form

$$\begin{aligned}&\vartheta (\xi ,\tau )= \vartheta (\xi _{1},\xi _{2},\xi _{3},\tau )=\sum _{n\in Z^{3}}\exp (\pi i\langle \tau n,n\rangle \nonumber \\&\qquad +\,2\pi i\langle \xi ,n\rangle ), \end{aligned}$$

(59)

in which $n=(n_{1},n_{2},n_{3})^{T}\in Z^{3}$, $\xi =(\xi _{1},\xi _{2},\xi _{3})\in C^{3}$, $\xi _{i}=k_{i} x+l_{i}y+r_{i}z+{\mathcal {M}}_{i} t +\varepsilon _{i},(i=1,2,3)$. $-i\tau$ is a positive-define and real-valued symmetric $2\times 2$ matrix, which is of explicit form

$$\begin{aligned} \tau =\left( \begin{array}{ccc} \tau _{11} &{} \quad \tau _{12} &{}\quad \tau _{13} \\ \tau _{21} &{}\quad \tau _{22} &{} \quad \tau _{23} \\ \tau _{31} &{} \quad \tau _{321} &{} \quad \tau _{33} \\ \end{array} \right) , \end{aligned}$$

(60)

in which ${\text {Im}}(\tau _{ij})>0$, $i=j=1,2,3$.

Theorem 6.1

[43,44,45,46,47] Supposing that $\vartheta (\xi _{1},\xi _{2},\xi _{3},\tau )$ is a multi-dimensional Riemann theta function as $N=3$ and $\xi _{i}=k_{i}x+l_{i}y+r_{i}z+{\mathcal {M}}_{i}t+\varepsilon _{i}$, then $k_{i},l_{i},r_{i},{\mathcal {M}}_{i}(i=1,2,3)$ hold the following expressions

$$\begin{aligned}&\sum _{n\in Z^{3}}H\left( 2\pi i\langle 2n-\theta _{i},k_{i}\rangle ,\ldots ,2\pi i\langle 2n-\theta _{i},{\mathcal {M}}_{i}\rangle \right) \nonumber \\&\quad \exp \left[ \pi i(\langle \tau (n-\theta _{i}),n-\theta _{i}\rangle +\langle \tau n,n\rangle \right] =0, \end{aligned}$$

(61)

in which $\theta _{i}=\left( \begin{array}{c} \theta _{i}^{1} \\ \theta _{i}^{2} \\ \theta _{i}^{3} \\ \end{array} \right)$ and $\theta _{1}=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right)$, $\theta _{2}=\left( \begin{array}{c} 0 \\ 0 \\ 1 \\ \end{array} \right)$, $\theta _{3}=\left( \begin{array}{c} 0 \\ 1 \\ 0 \\ \end{array} \right)$, $\theta _{4}=\left( \begin{array}{c} 0 \\ 1 \\ 1 \\ \end{array} \right)$, $\theta _{5}=\left( \begin{array}{c} 1 \\ 0 \\ 0 \\ \end{array} \right)$, $\theta _{6}=\left( \begin{array}{c} 1 \\ 0 \\ 1 \\ \end{array} \right)$, $\theta _{7}=\left( \begin{array}{c} 1 \\ 1 \\ 0 \\ \end{array} \right)$, $\theta _{8}=\left( \begin{array}{c} 1 \\ 1 \\ 1 \\ \end{array} \right)$, $i=1,2,3,\dots ,8$.

According to the above Theorem 6.1 and Eq. (18), the parameters $k_{i},l_{i},r_{i},{\mathcal {M}}_{i}$ should provide the following expressions

$$\begin{aligned}&\sum _{(n_{1},n_{2},n_{3})\in Z^{3}}\left[ -4\pi ^{2}\left( \langle 2n-\theta _{i},k\rangle +\langle 2n -\theta _{i},l\rangle \right. \right. \nonumber \\&\left. \left. \quad +\,\langle 2n-\theta _{i},r\rangle \right) \langle 2n-\theta _{i},{\mathcal {M}}\rangle \right. \nonumber \\&\left. \quad +\,16\alpha \pi ^{4}\langle 2n-\theta _{i},k\rangle ^{3}\langle 2n-\theta _{i},l\rangle \right. \nonumber \\&\quad -\,12\alpha u_{0}\pi ^{2}\langle 2n-\theta _{i},k\rangle ^{2}\nonumber \\&\left. \quad -\, 4\gamma \pi ^{2}\left( \langle 2n-\theta _{i},k\rangle ^{2} +\langle 2n-\theta _{i},r\rangle ^{2}\right) +{\mathcal {C}}\right] \nonumber \\&\quad \exp \left[ \pi i(\langle \tau (n-\theta _{i}),n-\theta _{i}\rangle +\langle \tau n,n\rangle \right] =0. \end{aligned}$$

(62)

The above equation can be written in a new form

$$\begin{aligned} \left( \begin{array}{ccccc} h_{11} &{} \quad h_{12} &{}\quad h_{13} &{}\quad h_{14} &{} \quad h_{15} \\ h_{21} &{}\quad h_{22} &{} \quad h_{23} &{}\quad h_{24} &{}\quad h_{25} \\ h_{31} &{}\quad h_{32} &{}\quad h_{33} &{}\quad h_{34} &{}\quad h_{35} \\ h_{41} &{}\quad h_{42} &{}\quad h_{43} &{}\quad h_{44} &{}\quad h_{45} \\ h_{51} &{}\quad h_{52} &{}\quad h_{53} &{}\quad h_{54} &{}\quad h_{55} \\ \end{array} \right) \left( \begin{array}{c} {\mathcal {M}}_{1} \\ {\mathcal {M}}_{2} \\ {\mathcal {M}}_{3} \\ u_{0} \\ {\mathcal {C}} \\ \end{array} \right) = \left( \begin{array}{c} b_{1} \\ b_{2} \\ b_{3} \\ b_{4} \\ b_{5} \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$

(63)

where

$$\begin{aligned}&h_{i1}=\sum _{n\in Z^{3}}-4\pi ^{2}\left( \langle 2n-\theta _{i},k\rangle +\langle 2n-\theta _{i},l\rangle \right. \nonumber \\&\left. \qquad +\,\langle 2n-\theta _{i},r\rangle \right) \left( 2n_{1}-\theta _{i}^{1}\right) {\mathscr {U}}_{i},\nonumber \\&h_{i2}=\sum _{n\in Z^{3}}-4\pi ^{2}\left( \langle 2n-\theta _{i},k\rangle +\langle 2n-\theta _{i},l\rangle \right. \nonumber \\&\left. \quad \qquad +\,\langle 2n-\theta _{i},r\rangle \right) \left( 2n_{2}-\theta _{i}^{2}\right) {\mathscr {U}}_{i},\nonumber \\&h_{i3}=\sum _{n\in Z^{3}}-4\pi ^{2}\left( \langle 2n-\theta _{i},k\rangle +\langle 2n-\theta _{i},l\rangle \right. \nonumber \\&\left. \quad \qquad +\,\langle 2n-\theta _{i},r\rangle \right) \left( 2n_{3}-\theta _{i}^{3}\right) {\mathscr {U}}_{i},\nonumber \\&h_{i4}=\sum _{n\in Z^{3}}-12\alpha \pi ^{2}\langle 2n-\theta _{i}\rangle ^{2}{\mathscr {U}}_{i},\nonumber \\&h_{i5}=\sum _{n\in Z^{3}}{\mathscr {U}}_{i},\nonumber \\&b_{i}=\sum _{n\in Z^{3}}-16\alpha \pi ^{4}\langle 2n-\theta _{i},k\rangle ^{3}\langle 2n-\theta _{i},l\rangle \nonumber \\&\qquad \quad +4\gamma \pi ^{2}\left( \langle 2n-\theta _{i},k\rangle ^{2}+\langle 2n-\theta _{i},r\rangle ^{2}\right) ,\nonumber \\&{\mathscr {U}}_{i}={\mathscr {A}}_{1}^{n_{1}^{2}+(n_{1}-\theta _{i}^{1})^{2}}{\mathscr {A}}_{2}^{n_{2}^{2}+(n_{1}-\theta _{i}^{2})^{2}} {\mathscr {A}}_{3}^{n_{3}^{2}+(n_{3}-\theta _{i}^{3})^{2}}\nonumber \\&\qquad \quad {\mathscr {A}}_{12}^{n_{1}n_{2}+(n_{1}-\theta _{i}^{1})(n_{2}-\theta _{i}^{2})} {\mathscr {A}}_{13}^{n_{1}n_{3}+(n_{1}-\theta _{i}^{1})(n_{3}-\theta _{i}^{3})} \nonumber \\&\qquad \quad {\mathscr {A}}_{23}^{n_{2}n_{3}+(n_{2}-\theta _{i}^{2})(n_{3}-\theta _{i}^{3})},\nonumber \\&{\mathscr {A}}_{1}=e^{\pi i\tau _{11}},\quad {\mathscr {A}}_{2}=e^{\pi i\tau _{22}},\quad {\mathscr {A}}_{3}=e^{\pi i\tau _{12}}, \nonumber \\&{\mathscr {A}}_{12}=e^{2\pi i\tau _{12}},\quad {\mathscr {A}}_{13}=e^{2\pi i\tau _{13}},\nonumber \\&{\mathscr {A}}_{23}=e^{2\pi i\tau _{23}}, \end{aligned}$$

(64)

We solve the above system and we can obtain the three-periodic wave solution as

$$\begin{aligned} u=u_{0}y+\frac{6\alpha }{\beta }\partial _{x} \ln \vartheta (\xi _{1},\xi _{2},\xi _{3},\tau ), \end{aligned}$$

(65)

in which $\vartheta (\xi _{1},\xi _{2},\xi _{3},\tau )$ and $({\mathcal {M}}_{1},{\mathcal {M}}_{2},{\mathcal {M}}_{3},u_{0},{\mathcal {C}})^{T}$ are known by (59). The other parameters $k_{i},l_{i},r_{i},\varepsilon _{i},\tau _{ij}(i,j=1,2,3)$ are free.

Summing up the above analysis for the three-periodic wave solution, the following assertion is constructed.

Theorem 6.2

Supposing that $\vartheta (\xi _{1},\xi _{2},\xi _{3},\tau )$ is a Riemann theta function with $N=3$ and $\xi _{i}=k_{i}x+l_{i}y+r_{i}z+{\mathcal {M}}_{i}t+\varepsilon _{i}(i=1,2,3)$. The VC-BKP equation (i.e., Eq. (1)) admits a three-periodic wave solution as follows

$$\begin{aligned} u=u_{0}y+\frac{6\alpha }{\beta }\partial _{x} \ln \vartheta (\xi _{1},\xi _{2},\xi _{3},\tau ), \end{aligned}$$

(66)

where $u_{0}$ and $\vartheta (\xi _{1},\xi _{2},\xi _{3},\tau )$ fulfill the expression (63) and (63). In addition, $\theta _{i}=\left( \begin{array}{c} \theta _{i}^{1} \\ \theta _{i}^{2} \\ \theta _{i}^{3} \\ \end{array} \right)$ and, $\theta _{i_{1}}^{1}=0$, $\theta _{j_{1}}^{1}=1$, with $i_{1}=1,2,3,4,j_{1}=5,6,7,8$, $\theta _{i_{2}}^{2}=0$, $\theta _{j_{2}}^{2}=1$, with $i_{2}=1,2,5,6,j_{2}=3,4,7,8$, $\theta _{i_{3}}^{3}=0$, $\theta _{j_{3}}^{3}=1$, with $i_{3}=1,3,5,7,j_{2}=2,4,6,8$. The other parameters $k_{i},l_{i},r_{i},\varepsilon _{i},\tau _{ij}(i,j=1,2,3)$ are arbitrary parameters.