Skip to main content
SpringerLink
Log in

Traveling Wave Solutions of a Generalized Burgers-\(\alpha \beta \) Equation

  • Published:
Qualitative Theory of Dynamical Systems Aims and scope Submit manuscript

Abstract

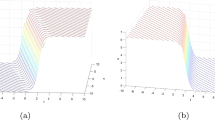
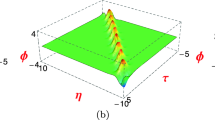
In this paper, we investigate the bifurcations and exact traveling wave solutions of a generalized Burgers-\(\alpha \beta \) equation. Employing the bifurcation theory of planar dynamical system, we obtain the phase portraits of the corresponding traveling wave system. The existence of the singular straight line \(\phi =c\) leads to the dynamical behavior of solutions with two scales. Corresponding to some special level curves, we give the exact explicit parametric representations of smooth and non-smooth solutions under different parameter conditions, including solitary wave solutions and peakon solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

References

  1. Byrd, P.F., Fridman, M.D.: Handbook of elliptic integrals for engineers and sciensists. Springer, Berlin (1971)

    Book  Google Scholar 

  2. Chen, A., Tian, C., Huang, W.: Periodic solutions with equal period for the Friedmann-Robertson-Walker model. Appl. Math. Lett. 77(01), 101–107 (2018)

    Article  MathSciNet  Google Scholar 

  3. Chen, L., Guan, C.: Global solutions for the generalized Camassa-Holm equation. Nonlin. Anal. Real World Appl. 58, 103227 (2021)

    Article  MathSciNet  Google Scholar 

  4. Chen, R.M., Walsh, S., Wheeler, M.H.: Center manifolds without a phase space for quasilinear problems in elasticity, biology, and hydrodynamics. arXiv: 1907.04370 (2019)

  5. Chu, J., Meng, G., Zhang, Z.: Continuous dependence and estimates of eigenvalues for periodic generalized Camassa-Holm equations. J. Differ. Equ. 269, 6343–6358 (2020)

    Article  MathSciNet  Google Scholar 

  6. Chu, J., Wang, L.: Analyticity of rotational travelling gravity two layer waves. Stud. Appl. Math. 146(3), 605–634 (2021)

    Article  MathSciNet  Google Scholar 

  7. Constantin, A., Lannes, D.: The Hydrodynamical Relevance of the Camassa-Holm and Degasperis-Procesi Equations. Arch. Ration. Mech. Anal. 192(1), 165–186 (2008)

    Article  MathSciNet  Google Scholar 

  8. Constantin, A.: On the scattering problem for the Camassa-Holm equation. Proc. R Soc. Lond. Ser. A Math. Phys. Eng. Sci. 457, 953–970 (2008)

    Article  MathSciNet  Google Scholar 

  9. Du, Z., Li, J., Li, X.: The existence of solitary wave solutions of delayed Camassa-Holm equation via a geometric approach. J. Funct. Anal. 275, 988–1007 (2018)

    Article  MathSciNet  Google Scholar 

  10. Ge, J., Du, Z.: The solitary wave solutions of the nonlinear perturbed shallow water wave model. Appl. Math. Lett. 103, 106202 (2020)

    Article  MathSciNet  Google Scholar 

  11. Groves, M.D., Wahlén, E.: Spatial dynamics methods for solitary gravity-capillary water waves with an arbitrary distribution of vorticity. SIAM. J. Math. Anal. 39, 932–964 (2007)

    Article  MathSciNet  Google Scholar 

  12. Gui, G., Liu, Y., Luo, T.: Model equations and traveling wave solutions for shallow-water waves with the coriolis effect. J. Nonlin. Sci. 29, 993–1039 (2019)

    Article  MathSciNet  Google Scholar 

  13. Gui, G., Liu, Y., Sun, J.: A nonlocal shallow-water model arising from the full water waves with the coriolis effect. J. Math. Fluid Mech. 21, 27 (2019)

    Article  MathSciNet  Google Scholar 

  14. Holm, D.D., Staley, M.F.: Nonlinear balance and exchange of stability in dynamics of solitons, peakons, ramps/cliffs and leftons in a 1+1 nonlinear evolutionary PDE. Phy. Lett. A 308, 437–444 (2003)

    Article  MathSciNet  Google Scholar 

  15. Kirchgässner, K.: Nonlinearly resonant surface waves and homoclinic bifurcation. Adv. Appl. Mech. 26, 135–181 (1988)

    Article  MathSciNet  Google Scholar 

  16. Lenells, J.: Traveling wave solutions of the Camassa-Holm equation. J. Differ. Equ. 217, 393–430 (2005)

    Article  MathSciNet  Google Scholar 

  17. Lenells, J.: Traveling wave solutions of the Degasperis-Procesi equation. J. Math. Anal. Appl. 306, 72–82 (2005)

    Article  MathSciNet  Google Scholar 

  18. Lenells, J.: Classification of traveling waves for a class of nonlinear wave equations. J. Dyn. Differ. Equ. 18, 381–391 (2005)

    Article  MathSciNet  Google Scholar 

  19. Lenells, J.: Classification of all travelling-wave solutions for some nonlinear dispersive equations. Phil. Trans. R. Soc. A 365, 2291–2298 (2005)

    Article  MathSciNet  Google Scholar 

  20. Li, J.: Singular nonlinear traveling wave equations: bifurcation and exact solutions, Science, Beijing (2013)

  21. Li, J., Chen, G.: On a class of singular nonlinear traveling wave equations, Internat. J. Bifur. Chaos Appl. Sci. Engrg. 17, 4049–4065 (2007)

    Article  MathSciNet  Google Scholar 

  22. Liu, H., Yue, C.: Lie symmetries, integrable properties and exact solutions to the variable-coefficient nonlinear evolution equations. Nonlin. Dyn. 89(3), 1989–2000 (2017)

    Article  MathSciNet  Google Scholar 

  23. Ji, S., Zhou, Y.: Wave breaking and global solutions of the weakly dissipative periodic Camassa-Holm type equation. J. Differ. Equ. 306, 439–455 (2022)

    Article  MathSciNet  Google Scholar 

  24. Moon, B.: Traveling wave solutions to the Burgers-\(\alpha \beta \) equation. Adv. Nonlin. Stud. 16, 147–157 (2016)

    Article  MathSciNet  Google Scholar 

  25. da Silva, P., Freire, I.L.: Well-posedness, traveling waves and geometrical aspects of some generalizations of the Camassa-Holm equation. J. Differ. Equ. 267(2), 5318–5369 (2019)

    Article  Google Scholar 

  26. Song, Y., Tang, X.: Stability, steady-state bifurcations, and turing patterns in a predator-prey model with herd behavior and prey-taxis. Stud. Appl. Math. 139(3), 371–404 (2017)

    Article  MathSciNet  Google Scholar 

  27. Sun, X., Yu, P.: Periodic traveling waves in a generalized BBM equation with weak backward diffusion and dissipation terms. Discrete Contin. Dyn. Syst. 24(2), 965–987 (2019)

    MathSciNet  MATH  Google Scholar 

  28. Sun, X., Huang, W., Cai, J.: Coexistence of the solitary and periodic waves in convecting shallow water fluid. Nonlin. Anal. Real World Appl. 53, 103067 (2020)

    Article  MathSciNet  Google Scholar 

  29. Tang, S., Huang, W.: Bifurcations of travelling wave solutions for the generalized double Sinh-Gordon equation. Appl. Math. Comput. 189, 1774–1781 (2007)

    MathSciNet  MATH  Google Scholar 

  30. Wang, L.: Small-amplitude solitary and generalized solitary traveling waves in a gravity two-layer fluid with vorticity. Nonlin. Anal. 150, 159–193 (2017)

    Article  MathSciNet  Google Scholar 

  31. Zhang, B., Zhu, W., Xia, Y., Bai, Y.: A unified analysis of exact traveling wave solutions for the fractional-order and integer-order Biswas-Milovic equation: via bifurcation theory of dynamical system. Qual. Theory Dyn. Syst. 19(1), 11 (2020)

    Article  MathSciNet  Google Scholar 

  32. Zhu, W., Li, J.: Exact traveling wave solutions and bifurcations of the Burgers-\(\alpha \beta \) equation. Internat. J. Bifur. Chaos 26(10), 1650175 (2016)

    Article  MathSciNet  Google Scholar 

  33. Zhu, K., Shen, J.: Smooth travelling wave solutions in a generalized Degasperis-Procesi equation. Commun. Nonl. Sci. Numer. Simulat. 98, 105763 (2021)

    Article  MathSciNet  Google Scholar 

  34. Zhu, W., Xia, Y., Zhang, B., Bai, Y.: Exact traveling wave solutions and bifurcations of the time fractional differential equations with applications. Internat. J. Bifur. Chaos 29(3), 1950041 (2019)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mathematics and Computer Science, Zhejiang Normal University, Jinhua, 321004, Zhejiang, People’s Republic of China

    Wenjing Zhu & Yonghui Xia

  2. Department of Mathematics, China Jiliang University, Hangzhou, 310018, Zhejiang, People’s Republic of China

    Wenjing Zhu

Authors
  1. Wenjing Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yonghui Xia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yonghui Xia.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was jointly supported by the National Natural Science Foundation of China under Grant (No. 11901547, No. 11931016, No. 11671176), Natural Science Foundation of Zhejiang Province under Grant (No. LY20A010016).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhu, W., Xia, Y. Traveling Wave Solutions of a Generalized Burgers-\(\alpha \beta \) Equation. Qual. Theory Dyn. Syst. 21, 23 (2022). https://doi.org/10.1007/s12346-021-00558-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12346-021-00558-7

Keywords

Search

Navigation