Study on the dynamics of a lock-up mass damper: asymptotic analysis and application limits

Abstract

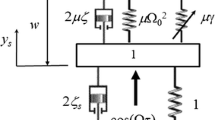
Tuned mass dampers are useful devices for limiting vibrations in various machines. Their main advantage is that they can be used as add-on elements and do not require integration into the main structure. However, conventional tuned mass dampers that use viscous or material damping are not attractive from the energetic point of view because they also dissipate energy in the case of unobjectionable small vibrations. Dry friction used as a lock-up element for the tuned mass damper could aid in overcoming this disadvantage. The dynamics of such a system are investigated in this paper. A special analytic technique based on variables’ rescaling is applied to obtain approximate analytical predictions of the steady-state amplitudes for both the main system and the mass damper. The results show that the lock-up mass damper can efficiently limit the amplitudes at resonance for a wide range of parameters but cannot supply perfect vibration suppression at any tuned frequency. Additionally, the efficiency of the system is limited to a certain excitation range. Excitation that increases over a certain threshold leads to notably high vibration amplitudes that cannot be handled by the described simple approach. All analytical results are confirmed by numerical simulations of the full system.

Appendix A: Formal averaging procedure

Equations (13) and (14) can be written in the following compact form:

$$\begin{aligned} {x}'= & {} \varepsilon X_1 \left( {x,{\tilde{A}},\psi } \right) +\varepsilon ^{2}X_2 \left( {x,{\tilde{A}},\psi } \right) \nonumber \\ {\psi }'= & {} p+\varepsilon \Psi _1 \left( {x,{\tilde{A}},\psi } \right) +\varepsilon ^{2}\Psi _2 \left( {x,{\tilde{A}},\psi } \right) \nonumber \\ x= & {} \left[ {A,\gamma ,B,\theta } \right] ^{\mathrm{T}} \end{aligned}$$

(A.1)

It is useful for further analysis to convert to $\psi$ as the independent variable:

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}\psi }=\frac{\varepsilon X_1 \left( {x,{\tilde{A}},\psi } \right) +\varepsilon ^{2}X_2 \left( {x,{\tilde{A}},\psi } \right) }{p+\varepsilon \Psi _1 \left( {x,{\tilde{A}},\psi } \right) +\varepsilon ^{2}\Psi _2 \left( {x,{\tilde{A}},\psi } \right) } \end{aligned}$$

(A.2)

Retaining the terms of $O\left( {\varepsilon ^{2}} \right)$, the following equation can be obtained:

$$\begin{aligned}&\frac{\hbox {d}x}{\hbox {d}\psi }=\varepsilon \frac{X_1 \left( {x,{\tilde{A}},\psi } \right) }{p}\nonumber \\&\qquad +\varepsilon ^{2}\left( \frac{X_2 \left( {x,{\tilde{A}},\psi } \right) }{p}-\frac{X_1 \left( {x,{\tilde{A}},\psi } \right) \Psi _1 \left( {x,{\tilde{A}},\psi } \right) }{p^{2}} \right) \nonumber \\ \end{aligned}$$

(A.3)

Second-order averaging means applying the following nearly identical variable transformation:

(A.4)

It is common within the averaging procedure to require that the new variables $\xi$ fulfill the following autonomous equations (functions $\varXi$ must be determined within the procedure later):

$$\begin{aligned}&\frac{\hbox {d}\xi }{\hbox {d}\psi }=\varepsilon \varXi _1 \left( {\xi ,\tilde{\bar{{A}}}} \right) +\varepsilon ^{2}\varXi _2 \left( {\xi ,\tilde{\bar{{A}}}} \right) +O(\varepsilon ^{3}) \nonumber \\&\frac{\hbox {d}\tilde{\bar{{A}}}}{\hbox {d}\psi }=\varepsilon \varXi _{1,{\tilde{A}}} \left( {\xi ,\tilde{\bar{{A}}}} \right) +\varepsilon ^{2}\varXi _{2,{\tilde{A}}} \left( {\xi ,\tilde{\bar{{A}}}} \right) +O(\varepsilon ^{3})\nonumber \\ \end{aligned}$$

(A.5)

Substituting (A.4) into Eq. (A.3), applying Taylor series expansion, considering (A.5) and balancing terms with the same powers of $\varepsilon$ leads to the following equations:

$$\begin{aligned}&\frac{{X_{1} \left( {\xi ,\tilde{\bar{A}},\psi } \right) }}{p} = \varXi _{1} \left( {\xi ,\tilde{\bar{A}}} \right) + \frac{{\partial u_{1} \left( {\xi ,\tilde{\bar{A}},\psi } \right) }}{{\partial \psi }} \end{aligned}$$

(A.6)

$$\begin{aligned}&\frac{{X_{2} \left( {\xi ,\tilde{\bar{A}},\psi } \right) }}{p} - \frac{{X_{1} \left( {\xi ,\tilde{\bar{A}},\psi } \right) \Psi _{1} \left( {\xi ,\tilde{\bar{A}},\psi } \right) }}{{p^{2} }} \nonumber \\&\quad \quad + \frac{1}{p}\left. {\frac{{\partial X_{1} \left( {x,\tilde{A},\psi } \right) }}{{\partial x}}} \right| {\mathop {\mathop {}\limits _{x = \xi }}\limits _{\tilde{A} = \tilde{\bar{A}}}} u_{1} (\xi ,\tilde{\bar{A}},\psi )\nonumber \\&\quad \quad + \frac{1}{p}\left. {\frac{{\partial X_{1} \left( {x,\tilde{A},\psi } \right) }}{{\partial \tilde{A}}}} \right| {\mathop {\mathop {}\limits _{x = \xi }}\limits _{\tilde{A} = \tilde{\bar{A}}}} u_{{1,\tilde{A}}} \left( {\xi ,\tilde{\bar{A}},\psi } \right) \nonumber \\&\quad = \varXi _{2} \left( {\xi ,\tilde{\bar{A}}} \right) + \frac{{\partial u_{1} \left( {\xi ,\tilde{\bar{A}},\psi } \right) }}{{\partial \xi }}\varXi _{1} \left( {\xi ,\tilde{\bar{A}}} \right) \nonumber \\&\qquad + \frac{{\partial u_{1} \left( {\xi ,\tilde{\bar{A}},\psi } \right) }}{{\partial \tilde{\bar{A}}}}\varXi _{{1,\tilde{A}}} \left( {\xi ,\tilde{\bar{A}}} \right) + \frac{{u_{2} \left( {\xi ,\tilde{\bar{A}},\psi } \right) }}{{\partial \psi }}\nonumber \\ \end{aligned}$$

(A.7)

The function $u_1 \left( {\xi ,\tilde{\bar{{A}}},\psi } \right)$ must be limited in the fast variable $\psi$. This requirement enables us to determine the function $\varXi _1$:

$$\begin{aligned}&\varXi _1 \left( {\xi ,\tilde{\bar{{A}}}} \right) =\frac{1}{2\pi }\int _0^{2\pi } {\frac{X_1 \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) }{p}d\psi } \nonumber \\&\quad =\frac{1}{p}\left\langle {X_1 \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) } \right\rangle _\psi \nonumber \\&u_1 \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) =u_{01} \left( {\xi ,\tilde{\bar{{A}}}} \right) \nonumber \\&\qquad +\int _{\psi _0 }^\psi {\frac{X_1 \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) }{p}d\psi } -\varXi _1 \left( {\xi ,\tilde{\bar{{A}}}} \right) \left( {\psi -\psi _0 } \right) \nonumber \\ \end{aligned}$$

(A.8)

In this work, $\left\langle \ldots \right\rangle _\psi$ means periodic averaging with respect to the variable $\psi$. Note that the scaling of the variable A according to (8) is also valid for the corresponding u-terms:

$$\begin{aligned} u_{1,A} \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) =\varepsilon u_{1,{\tilde{A}}} \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) \end{aligned}$$

(A.9)

The function $\varXi _2$ is determined similarly from Eq. (A.7) combined with the requirement that the function $u_2$ must be limited in $\psi$:

$$\begin{aligned}&\varXi _2 \left( {\xi ,\tilde{\bar{{A}}}} \right) =\left\langle {\frac{X_2 \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) }{p}} \right\rangle _\psi \nonumber \\&\quad -\left\langle {\frac{X_1 \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) \Psi _1 \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) }{p^{2}}} \right\rangle _\psi \nonumber \\&\quad +\left\langle {\frac{1}{p}\left. {\frac{\partial X_1 \left( {x,{\tilde{A}},\psi } \right) }{\partial x}} \right| {\mathop {\mathop {}\limits _{x=\xi }}\limits _{{\tilde{A}}=\tilde{\bar{{A}}}}} u_1 \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) } \right\rangle _\psi \nonumber \\&\quad +\left\langle {\frac{1}{p}\left. {\frac{\partial X_1 \left( {x,{\tilde{A}},\psi } \right) }{\partial {\tilde{A}}}} \right| {\mathop {\mathop {}\limits _{x=\xi }}\limits _{{\tilde{A}}=\tilde{\bar{{A}}}}} u_{1,{\tilde{A}}} \left( {\xi ,\tilde{\bar{{A}}},\psi } \right) } \right\rangle _\psi \nonumber \\ \end{aligned}$$

(A.10)

It is not necessary to calculate $u_2$ explicitly if the analysis is limited to the second-order approximation.

Substituting expressions (A.8) and (A.10) into Eq. (A.5) and setting the right-hand side to zero give the algebraic equations that determine the steady-state solutions of the averaged equations:

$$\begin{aligned} 0= & {} \varepsilon \varXi _1 \left( {\xi ,\tilde{\bar{{A}}}} \right) +\varepsilon ^{2}\varXi _2 \left( {\xi ,\tilde{\bar{{A}}}} \right) =\Gamma \left( {\xi ,\tilde{\bar{{A}}},\varepsilon } \right) \nonumber \\ \xi= & {} \left[ {\bar{{A}},\bar{{\gamma }},\bar{{B}},\bar{{\theta }}} \right] ^{\mathrm{T}} =\xi _1 +\varepsilon \xi _2 =\left[ {A_1 ,\gamma _1 ,B_1 ,\theta _1 } \right] ^{\mathrm{T}} \nonumber \\&+\,\varepsilon \left[ {A_2 ,\gamma _2 ,B_2 ,\theta _2 } \right] ^{\mathrm{T}}\nonumber \\ \tilde{\bar{{A}}}= & {} {\tilde{A}}_1 +\varepsilon {\tilde{A}}_2 \end{aligned}$$

(A.11)

These equations have been solved in an asymptotic manner by balancing the terms with the same powers of $\varepsilon$. This approach delivers the following two sets of four algebraic equations each, thus determining the required approximations:

$$\begin{aligned}&\varXi _1 (\xi _1 ,{\tilde{A}}_1 )=0 \end{aligned}$$

(A.12)

$$\begin{aligned}&\varXi _2 \left( {\xi _1 ,{\tilde{A}}_1 } \right) +\left. {\frac{\partial \varXi _1 \left( {\xi ,\tilde{\bar{{A}}}} \right) }{\partial \xi }} \right| _{\varepsilon =0} \xi _2 \nonumber \\&\quad +\left. {\frac{\partial \varXi _1 \left( {\xi ,\tilde{\bar{{A}}}} \right) }{\partial \tilde{\bar{{A}}}}} \right| _{\varepsilon =0} {\tilde{A}}_2 =0 \end{aligned}$$

(A.13)

The first set leads directly to the stationary solutions (15). The second set delivers the solutions used to calculate the black solid lines in Fig. 2.