1 Introduction

Geometrically nonlinear beam models are popular due to their suitability for modeling frame-like structures undergoing arbitrary large displacements and rotations but small strains with sufficient accuracy and relatively low computational costs. Despite the simplified kinematics, the governing equations remain challenging from the perspective of numerical solution methods. Computationally efficient, accurate, robust and stable numerical formulations demand firm understanding of the model, relationships between the quantities describing the beam and their dependence with respect to both space and time. Modern techniques in numerical analysis allow many possible approaches in handling the problem of such complexity. It is thus not a surprise that after more than three decades of intensive research this field is still a subject of interest for many researchers, as reflected by recent publications, see, e.g., [1,2,3,4,5,6,7,8,9,10,11,12].

Many challenges in beam formulations reported in the literature stem from the use of spatial rotations as members of the configuration space of the beam. Spatial rotations form a multiplicative group with interesting properties that are not easily preserved in numerical solution methods. Since the pioneering work of Simo and Vu-Quoc [13], beam finite elements have often been based on the interpolation of rotational degrees of freedom. In [13], a rotational vector is used for the parametrization of rotations, but this is only one among a variety of choices, see [14]. The chosen parametrization of rotations has an important impact on their discretization and the behavior of solution methods. Thorough discussions and comparisons can be found, e.g., in [15,16,17,18,19]. Crisfield and Jelenić [20, 21] pointed out that standard additive-type interpolation of rotational vectors could lead to nonobjective strain measures in many rotation-based approaches. Different interpolation strategies for rotational degrees of freedom were studied by Romero [22] and Bauchau and Han [23]. The use of only three parameters for the description of rotations results in lower storage demands for the primary unknown quantities. However, we can not easily avoid the calculation of rotation matrices and computationally more sensitive extraction of rotational parameters from rotation matrices [24]. This concept can be completely avoided by the introduction of rotational quaternions as a four-parameter representation of rotations. Not only that such parametrization is free from singularities, but also it is computationally more efficient regarding the number of calculations needed to rotate a vector. The use of quaternions seems to be standard for the efficient implementation of algorithms involving rotation matrices, see [54, p. 281] and the references therein. In beam formulations, quaternions were first employed by Bottasso [25] and Kehrbaum and Maddocks [26], while McRobie and Lasenby [27] used theoretically equivalent Clifford algebra. The interest in quaternion algebra as a suitable tool for beam formulations has increased in the last decade, see [2, 28,29,30,31,32,33]. Another alternative is the interpolation of all nine components of the rotation matrix by Betsch and Steinmann [34] and recently by Sonneville et al. [35].

The description of the relationship between the deformed configuration of the beam and the strain measures is an important aspect of beam theories. In the “geometrically exact” approach, see Reissner [36, 37], strain resultants of the cross section are introduced and related to configuration variables in such a way that the kinematic equations are consistent with the virtual work principle. Several alternatives to this approach can be found, such as co-rotational method [38] and absolute nodal coordinate method [39]. In the present paper, we will stem from geometrically exact model as a suitable basis for the proposed numerical formulation.

In dynamics, a proper treatment of the configuration space with three-dimensional rotations might still result in a loss of numerical stability in the case of long-term calculations [40]. Several energy-preserving and energy-decaying algorithms were proposed as the answer to this phenomenon, e.g., [40,41,42,43,44,45,46]. These algorithms use similar strategy within different frameworks. For a more general approach, the reader is referred to the paper by Bauchau and Bottasso [47]. A common characteristic of these formulations is the special approximation of the kinematic equations imposed by preservation constraints. These approximations can be in contradiction with other properties of continuous systems, i.e., the orthogonality of rotation at the midtime is often violated. Despite this shortcoming, increased stability of long-term calculations using such methods was confirmed numerous times. Another important property of a continuous dynamic system, surprisingly rarely considered in beam formulations, is the direct relation between the strains and the velocities without any configuration variables being present, called the compatibility equations [48] or, alternatively, the intrinsic kinematic equations [49].

In the present paper, we will employ the rotational quaternions for the description of three-dimensional rotations. However, in contrast to our quaternion-based approach presented in [32], we will avoid the interpolation of rotational quaternions due to the above-mentioned problems. The crucial idea exploited here assumes the spatial and temporal derivatives of configuration variables to be the natural quantities for the description of total mechanical energy of the system. The previously developed strain-based beam formulation by Zupan and Saje [50] for static analysis of three-dimensional beams was motivated by this idea. In dynamics, angular velocities have a similar role as the rotational strains in statics, which was exploited in the paper by Zupan and Zupan [51], where velocities and angular velocities were taken as the primary unknowns of both spatial and temporal discretization. The time discretization employed in [51] can be interpreted as a modification of the implicit Newmark scheme. Unfortunately, a more suitable choice of the primary variables does not automatically assure the energy preservation. For sparse meshes and larger time steps, we can observe in some cases a loss of convergence accompanied with unrealistic increase in the total mechanical energy [51]. To avoid this phenomenon, we here propose a novel energy-conserving method based on a more suitable form of discrete governing equations while preserving the advantages of the velocity-based approach. Three important computational benefits of our approach are: (i) the additivity of the primary unknowns enables the use of standard interpolation techniques in space and simplifies the iteration procedure; (ii) the kinematic compatibility equations are satisfied with the same level of accuracy as the governing equations; and (iii) the energy of conservative systems is preserved without the need to introduce any special approximation of rotation or strain field. The computational advantages of the quaternion representation of rotations are preserved; moreover, proper treatment of the primary unknowns and the governing equations provides us with a relatively simple, numerically stable and robust method. The accuracy and excellent numerical performance of the present approach will be demonstrated by several benchmark examples.

2 Governing equations

Among several possible approaches in modeling deformable bodies with one dimension more significant than the other two, we base our numerical formulation on Cosserat geometrically exact theory of rods [52]. The Cosserat rod model describes the beam with a reference curve (often, but not necessarily, the line of centroids), and rigid cross sections attached to each point of this curve. Such description is capable of representing an arbitrary deformation of a beam including bending, extension, shear and torsion. We introduce two coordinate systems: One is fixed in space and time, the other rigidly attached to the cross section. The corresponding base vectors will be denoted by \(\{ \overset{\rightharpoonup }{g}_{1},\overset{\rightharpoonup }{g}_{2},\overset{ \rightharpoonup }{g}_{3}\} \) for the fixed and \(\{ \overset{ \rightharpoonup }{G}_{1}\left( x,t\right) ,\overset{\rightharpoonup }{G} _{2}\left( x,t\right) ,\overset{\rightharpoonup }{G}_{3}\left( x,t\right) \} \) for the local frame of reference, see Fig. 1. In the following, t denotes the time and \(x\in \left[ 0,L\right] \) the arc-length parameter of the reference curve at the initial state of the beam with L being its initial length. An arbitrary configuration of such a beam can be described by the position vectors \(\overset{\rightharpoonup }{r}\left( x,t\right) \) and the rotations between fixed and local bases. We will use the rotational quaternions as a suitable representation of rotations. Taking \(\vartheta \) to be the angle of rotation and \(\overset{\rightharpoonup }{e}\) denoting the unit vector on the axis of rotation, a rotational quaternion \(\widehat{q}\) is expressed as

$$\begin{aligned} \widehat{q}=\cos \frac{\vartheta }{2}+\sin \frac{\vartheta }{2}\,\overset{ \rightharpoonup }{e}=\mathrm {exp}\left( \frac{\vartheta }{2}\overset{ \rightharpoonup }{e}\right) ,\qquad \left| \overset{\rightharpoonup }{e} \right| =1. \end{aligned}$$
(1)

The first part of (1) is written in the polar form while the second part employs the quaternion exponential to get the same result. After introducing the conjugated quaternion \(\widehat{q}\,^{*}=\cos \frac{ \vartheta }{2}-\sin \frac{\vartheta }{2}\,\overset{\rightharpoonup }{e}\) and the quaternion multiplication \(\left( \circ \right) \), we have

Fig. 1
figure 1

Description of a three-dimensional beam

Full size image
$$\begin{aligned} \overset{\rightharpoonup }{G}_{i}\left( x,t\right) =\widehat{q}\left( x,t\right) \circ \overset{\rightharpoonup }{g}_{i}\circ \widehat{q}\,^{*}\left( x,t\right) ,\qquad i=1,2,3. \end{aligned}$$
(2)

From (2), it follows that rotational quaternions can be used for describing rotations in \({\mathbb {R}}^{3}\). This is admissible since \({\mathbb {R}}^{3}\) is a linear subspace of the space of quaternions. While an arbitrary quaternion is usually represented as

$$\begin{aligned} \widehat{x}=s+\overset{\rightharpoonup }{v}, \end{aligned}$$

(\(s\in {\mathbb {R}}\) is the scalar part and \(\overset{\rightharpoonup }{v}\in {\mathbb {R}}^{3}\) is the vector part), the quaternions with zero scalar part can be identified with vectors:

$$\begin{aligned} \widehat{v}\equiv 0+\overset{\rightharpoonup }{v}. \end{aligned}$$

Quaternions with zero scalar part are called pure quaternions. In what follows, abstract vectors and abstract quaternions will be replaced by one-column representations and denoted by bold face symbols. The hat over the symbol will be omitted when the first component equals zero since the appropriate size of one-column representation will be evident from the context. Such notation will enable a clear distinction between pure and arbitrary quaternions. In component description, the rotational quaternion also serves for transformation between the fixed and local basis representation and vice versa:

$$\begin{aligned} \mathbf {X}=\widehat{\mathbf {q}}^{*}\circ \mathbf {x}\circ \widehat{ \mathbf {q}},\qquad \mathbf {x}=\widehat{\mathbf {q}}\circ \mathbf {X}\circ \widehat{\mathbf {q}}^{*}. \end{aligned}$$
(3)

Here and henceforth, we use lowercase letters for the component representations with respect to the fixed basis and uppercase letters for the local basis representations. All equations in the sequel will be written in terms of quaternion algebra without presenting all the details. A more detailed derivation of equations of a three-dimensional beam in terms of quaternion algebra can be found in [2, 25, 29, 31].

It should be noted that all vector quantities in the sequel take values on the current configuration of the beam. The initial length of the line of centroids is used only as a suitable parameter for computational purposes. The transformation between the spatial and material form of equations is straightforward since the pull-back and push-forward are performed by the quaternion rotation (3). For further details, see the discussion in [37, 53].

2.1 Kinematic equations

In a geometrically exact beam theory, the resultant strains of the cross section are introduced and related to the configuration variables—positions of the reference curve and rotations of the cross sections. A thorough introduction, derivation and interpretation of these equations, crucial for the model was given by Reissner [36] and Simo [37]. We will only briefly present the kinematic equations expressed in terms of quaternion algebra. The translational strain vector, \(\varvec{\Gamma }\), consists of an extensional strain and two shear strain components. It is defined by the following equation

$$\begin{aligned} {\varvec{\Gamma }}=\widehat{\mathbf {q}}^{*}\circ \mathbf {r}^{\prime }\circ \widehat{\mathbf {q}}+{\varvec{\Gamma }}_{0}, \end{aligned}$$
(4)

where \({\varvec{\Gamma }}_{0}\) is determined from known strains, position vectors and rotations at the initial configuration of the beam. When we have no initial strains and the cross sections are initially orthogonal to the axis of the beam, we get \({\varvec{\Gamma }}_{0}=\left[ -1,0,0 \right] ^\text {T}\). The prime \(\left( ^{\prime }\right) \) denotes the derivative with respect to x and the coordinate transformation is carried out using rotational quaternions. Thus, translational strain describes the rate of change of the position vector along the length of the beam. The rotational strain, \({\mathbf {K}}\), consists of a torsional and two bending strain components. In terms of quaternions, it is determined by

$$\begin{aligned} {\mathbf {K}}=2\widehat{\mathbf {q}}^{*}\circ \widehat{\mathbf {q}}^{\prime }. \end{aligned}$$
(5)

Vector \({\mathbf {K}}\) describes the rate of change of the local basis with respect to x and is expressed with respect to the local basis. The analogy of the above formula to the standard definition using rotation matrices is evident, while the factor 2 that additionally appears arises from the definitions (1)–(2).

In dynamics, the measures for the rate of change of configuration variables with respect to time are also needed. For the reference curve, we simply have

$$\begin{aligned} {\mathbf {v}}=\dot{{\mathbf {r}}}, \end{aligned}$$
(6)

describing its velocity with respect to the fixed basis, while the angular velocity of the cross sections is defined as

$$\begin{aligned} {\varvec{\Omega }}=2\widehat{\mathbf {q}}^{*}\circ \dot{\overset{\vspace{-50pt}}{\widehat{\mathbf {q}}}}. \end{aligned}$$
(7)

The dot above a symbol \(\left( \overset{{\cdot }}{}\right) \) denotes the time derivative. For the angular velocities, the description in local basis is more convenient, as we will show later. From the above definitions, it is evident that the strain measures and the velocities are mutually dependent. By comparing mixed partial derivatives of (4)–(7), we get

$$\begin{aligned} \dot{\varvec{\Gamma }}&=\widehat{\mathbf {q}}^{*}\circ {\mathbf {v}} ^{\prime }\circ \widehat{\mathbf {q}}+\left( \varvec{\Gamma }-\varvec{{\Gamma }}_{0}\right) \times \varvec{\Omega } \end{aligned}$$
(8)
$$\begin{aligned} \dot{{\mathbf {K}}}&={\varvec{\Omega }}^{\prime }+ {\mathbf {K}}\times \varvec{\Omega }. \end{aligned}$$
(9)

The significance of equations (8)–(9) was pointed out by Antman [48] and Hodges [49]. They are called compatibility equations and will play an important role in our numerical formulation.

2.2 Equations of motion

When expressed in terms of quaternion algebra, the balance equations of a three-dimensional beam read

$$\begin{aligned}&\mathbf {n}^{\prime }+\tilde{\mathbf {n}}-\frac{\text{ d }}{{\text{ d }}t }\left( \rho A{\mathbf {v}}\right) =\mathbf {0} \end{aligned}$$
(10)
$$\begin{aligned}&\mathbf {m}^{\prime }+\mathbf {r}^{\prime }\times \mathbf {n}+ \tilde{\mathbf {m}}-\frac{\text{ d }}{{\text{ d }}t}\left( \widehat{\mathbf {q}}\circ \left( \mathbf {J}_{\rho }{\varvec{\Omega }}\right) \circ \widehat{\mathbf {q}} ^{\,*}\right) =\mathbf {0} \end{aligned}$$
(11)

and the boundary conditions are:

$$\begin{aligned}&\mathbf {n}^{0}+\mathbf {f}^{0}=\mathbf {0} \end{aligned}$$
(12)
$$\begin{aligned}&\mathbf {m}^{0}+\mathbf {h}^{0}=\mathbf {0} \end{aligned}$$
(13)
$$\begin{aligned}&\mathbf {n}^{L}-\mathbf {f}^{L}=\mathbf {0} \end{aligned}$$
(14)
$$\begin{aligned}&\mathbf {m}^{L}-\mathbf {h}^{L}=\mathbf {0}. \end{aligned}$$
(15)

Here, \(\mathbf {n}\) and \(\mathbf {m}\) represent the stress-resultant force and moment vectors of the cross section with respect to the fixed basis; \( \tilde{\mathbf {n}}\) and \(\tilde{\mathbf {m}}\) are the external distributed force and moment vectors; \(\mathbf {f}^{0}\), \(\mathbf {h}^{0}\), \(\mathbf {f} ^{L}\) and \(\mathbf {h}^{L}\) are the external point forces and moments at the two boundaries, \(x=0\) and \(x=L\). \(\rho \) is mass per unit of the initial volume; A is the area of the cross section; \(\mathbf {J}_{\rho }\) is the mass-inertia matrix of the cross section.

The kinetic energy of a beam consists of the translational part representing the inertia of motion of the reference axis and the rotational part representing the inertia of motion of cross sections:

$$\begin{aligned} W_{K}=\frac{1}{2}\int \limits _{0}^{L}\biggl [{\mathbf {v}}\cdot \rho A{\mathbf {v}}+ \varvec{\Omega }\cdot \mathbf {J}_{\rho }{\varvec{\Omega }}\biggr ]\mathrm{d}x. \end{aligned}$$
(16)

Note that the second term is written with respect to the local frame.

2.3 Constitutive equations

The stress resultants depend on the strain vectors \({\varvec{\Gamma }}\) and \({\mathbf {K}}\). We will assume here that the stress–strain relationship is linear in the strain measures, leading to

$$\begin{aligned}&\mathbf {N} =\mathbb {C}_{\Gamma \Gamma }{\varvec{\Gamma }}+\mathbb {C} _{\Gamma \mathrm {K}}{\mathbf {K}} \end{aligned}$$
(17)
$$\begin{aligned}&\mathbf {M} =\mathbb {C}_{\mathrm {K}\Gamma }{\varvec{\Gamma }}+\mathbb {C}_{ \mathrm {KK}}\mathbf {K.} \end{aligned}$$
(18)

The matrix \(\mathbb {C}=\left[ \begin{array}{cc} \mathbb {C}_{\Gamma \Gamma }\quad &{} \mathbb {C}_{\Gamma \mathrm {K}} \\ \mathbb {C}_{\mathrm {K}\Gamma }\quad &{} \mathbb {C}_{\mathrm {KK}} \end{array} \right] \) is called the cross-sectional constitutive tangent matrix. It can be fully populated, but we will assume it is symmetric. \(\mathbf {N}\) and \( \mathbf {M}\) represent the stress-resultant force and moment vectors of the cross section in the local basis. For the sake of completeness, let us express the stress resultants in both frames using the coordinate transformation (3):

$$\begin{aligned}&\mathbf {n} =\widehat{\mathbf {q}}\circ \mathbf {N}\circ \widehat{\mathbf {q}} ^{\,*} \end{aligned}$$
(19)
$$\begin{aligned}&\mathbf {m} =\widehat{\mathbf {q}}\circ \mathbf {M}\circ \widehat{\mathbf {q}} ^{\,*}. \end{aligned}$$
(20)

Now, we define the strain energy of a linear elastic beam as

$$\begin{aligned} W_{D}=\frac{1}{2}\int \limits _{0}^{L}\left[ \begin{array}{c} {\varvec{\Gamma }} \\ {\mathbf {K}} \end{array} \right] \cdot \mathbb {C}\left[ \begin{array}{c} {\varvec{\Gamma }} \\ {\mathbf {K}} \end{array} \right] \mathrm{d}x. \end{aligned}$$
(21)

An important property of the continuous system of equations is the conservation of the total mechanical energy, defined as \(W=W_{K}+W_{D}\), for conservative external loads. As pointed out by many authors, this property is not automatically preserved after the discretization of equations, in spite of that being a highly desirable goal due its direct correlation to the increased long-term stability of calculations.

3 Numerical formulation

We are dealing with a system of nonlinear partial differential equations. The governing equations will thus be discretized with respect to time and space. In contrast to the widely used beam models where the configuration variables are usually interpolated, the velocities in fixed basis and the angular velocities in local basis are here employed as the primary unknowns. Despite its nonstandard nature, such an approach has firm theoretical grounding. Note that velocities and angular velocities directly appear in the description of kinetic energy (16) and are thus crucial for its evaluation. Another reason stems from noncommutativity and multiplicative nature of spatial rotations, which restrict and complicate the admissible treatment of rotational degrees of freedom. A multiplicative update or a special transformation of rotational increments that are (locally) additive is therefore often used in beam formulations. To avoid this, we here exploit the well-known property of additivity of the components of angular velocity vectors, when expressed in the local basis. We can then use standard interpolation functions in Euclidean vector spaces without any inconsistency introduced and the increments can be simply added to the current values in the iteration procedure. Instead of working on manifolds, most of the computational effort is done in vector spaces, which considerably reduces the complexity of calculations. Due to our choice of primary variables, it is convenient to express the angular momentum balance equation (11) in the local basis:

$$\begin{aligned} \widehat{\mathbf {q}}^{\,*}\circ \left( \mathbf {m}^{\prime }+ \mathbf {r}^{\prime }\times \mathbf {n}+\tilde{\mathbf {m}}\right) \circ \widehat{\mathbf {q}}-{\varvec{\Omega }} \times \mathbf {J}_{\rho } {\varvec{\Omega }}-\frac{\text{ d }}{{\text{ d }}t}\left( \mathbf {J}_{\rho }{\varvec{\Omega }}\right)= & {} \mathbf {0.}\nonumber \\ \end{aligned}$$
(22)

After considering (4)–(5) and (20), we get its final form:

$$\begin{aligned}&\mathbf {M}^{\prime }+{\mathbf {K}}\times \mathbf {M}+\left( {\varvec{\Gamma }}- {\varvec{\Gamma }}_{0}\right) \times \widehat{\mathbf {q}}^{\,*}\circ \mathbf {n}\circ \widehat{\mathbf {q}}+\widehat{\mathbf {q}}^{\,*}\circ \tilde{\mathbf {m}}\circ \widehat{\mathbf {q}}\nonumber \\&\quad -{\varvec{\Omega }}\times \mathbf {J}_{\rho }{\varvec{\Omega }}-\frac{\text{ d }}{{\text{ d }}t}\left( \mathbf {J}_{\rho } \varvec{\Omega }\right) =\mathbf {0.} \end{aligned}$$
(23)

The boundary conditions for internal moments need to be expressed in the local basis as well. By direct use of coordinate transformation, we have

$$\begin{aligned}&\mathbf {M}^{0}+\widehat{\mathbf {q}}^{\,*}\left( 0\right) \circ \mathbf {h} ^{0}\circ \widehat{\mathbf {q}}\left( 0\right) =\mathbf {0} \end{aligned}$$
(24)
$$\begin{aligned}&\mathbf {M}^{L}+\widehat{\mathbf {q}}^{\,*}\left( L\right) \circ \mathbf {h} ^{L}\circ \widehat{\mathbf {q}}\left( L\right) =\mathbf {0}. \end{aligned}$$
(25)

3.1 Time discretization

After employing the midpoint rule [54], equations (10) and (23) are replaced by the following time-discrete set of equations:

$$\begin{aligned}&\rho A{\mathbf {v}}^{\left[ n+1\right] }-\rho A{\mathbf {v}}^{\left[ n\right] } =h\left( \bar{\mathbf {n}}^{\prime }+\tilde{\mathbf {n}}^{\left[ n+1/2\right] }\right) \end{aligned}$$
(26)
$$\begin{aligned}&\mathbf {J}_{\rho }\left( \varvec{\Omega }^{\left[ n+1\right] }- {\varvec{\Omega }}^{\left[ n\right] }\right) \nonumber \\&=h\biggl [\overline{\mathbf {M }}^{\prime }+{\mathbf {K}}^{\left[ n+1/2\right] }\times \overline{\mathbf {M}}- {\varvec{\Omega }}^{\left[ n+1/2\right] }\times \mathbf {J}_{\rho } {\varvec{\Omega }}^{\left[ n+1/2\right] } \nonumber \\&\,\, \quad \mathbf {+}\,\left( \varvec{\Gamma }^{\left[ n+1/2\right] }- {\varvec{\Gamma }}_{0}\right) \times \widehat{\mathbf {q}}^{*\left[ n+1/2\right] }\circ \overline{\mathbf {n}}\circ \widehat{\mathbf {q}}^{\left[ n+1/2\right] } \nonumber \\&\,\quad +\,\widehat{\mathbf {q}}^{*\left[ n+1/2\right] }\circ \tilde{\mathbf { m}}^{\left[ n+1/2\right] }\circ \widehat{\mathbf {q}}^{\left[ n+1/2 \right] }\biggr ]. \end{aligned}$$
(27)

The superscript denotes the time at which a particular quantity is evaluated, \(h=t_{n+1}-t_{n}\) is the time step, and time \(t_{n+1/2}=t_{n}+h/2\) denotes the midtime between \(t_{n}\) and \(t_{n+1}\). The right-hand side of (26)–(27) consists of the values of the quantities of the beam at the midtime. The way they are evaluated is not yet fixed (in contrast to standard midpoint rule), leaving us enough freedom to satisfy additional constraints. We will especially focus on the newly introduced quantities \(\overline{\mathbf {n}}\) and \(\overline{\mathbf {M}}\), which represent the approximations of stress resultants at the midtime. They will be introduced in Sect. 3.3. The kinematic compatibility equations (8)–(9) are discretized in a similar manner to obtain

$$\begin{aligned} {\varvec{\Gamma }}^{\left[ n+1\right] }-{\varvec{\Gamma }}^{\left[ n \right] } =&\,h\biggl [\widehat{\mathbf {q}}^{*\left[ n+1/2\right] }\circ {\mathbf {v}}^{\prime \left[ n+1/2\right] }\circ \widehat{\mathbf {q}}^{\left[ n+1/2\right] } \nonumber \\&+\left( \varvec{\Gamma }^{\left[ n+1/2\right] }- {\varvec{\Gamma }}_{0}\right) \times \varvec{\Omega }^{\left[ n+1/2 \right] }\biggr ] \end{aligned}$$
(28)
$$\begin{aligned} {\mathbf {K}}^{\left[ n+1\right] }-{\mathbf {K}}^{\left[ n\right] } =&\,h\biggl [{ {\varvec{\Omega }}}^{\prime \left[ n+1/2\right] }-{\varvec{\Omega }}^{ \left[ n+1/2\right] }\times {\mathbf {K}}^{\left[ n+1/2\right] }\biggr ] \end{aligned}$$
(29)

and are therefore satisfied with the same accuracy as the equations of motion. Observe that no accelerations appear in our discrete governing equations (26)–(29), which is an important computational advantage.

In accord with equations (26)–(27) and (28)–(29), we need to express all the quantities of the beam at the middle of the time step. Velocities and angular velocities at \(t_{n+1/2}\) are determined by averaging the values at the boundaries of time interval \(\left[ t_{n},t_{n+1}\right] \):

$$\begin{aligned} {\mathbf {v}}^{\left[ n+1/2\right] }&=\overline{{\mathbf {v}}}=\frac{1}{2}\left( {\mathbf {v}}^{\left[ n\right] }+{\mathbf {v}}^{\left[ n+1\right] }\right) \\ {\varvec{\Omega }}^{\left[ n+1/2\right] }&=\overline{{\varvec{\Omega }}} =\frac{1}{2}\left( \varvec{\Omega }^{[n]}+{\varvec{\Omega }} ^{[n+1]}\right) . \end{aligned}$$

For the configuration variables, we assume

$$\begin{aligned} \mathbf {r}^{[n+1/2]}&=\mathbf {r}^{[n]}+\frac{h}{2}\overline{{\mathbf {v}}} \end{aligned}$$
(30)
$$\begin{aligned} \widehat{\mathbf {q}}^{[n+1/2]}&=\widehat{\mathbf {q}}^{[n]}\circ \exp \left( \frac{h}{4}\overline{{\varvec{\Omega }}}\right) , \end{aligned}$$
(31)

which is again a second-order approximation of exact relations (6)–(7). Additionally, multiplicative formula (31) is kinematically consistent as it preserves the unit norm of rotational quaternions. After applying (30)–(31) in (4)–(5) at times \(t_{n}\) and \( t_{n+1/2}\), we get

$$\begin{aligned} {\varvec{\Gamma }}^{[n+1/2]} =&\exp ^{*}\left( \frac{h}{4}\overline{ {\varvec{\Omega }}}\right) \circ \left( \varvec{\Gamma }^{[n]}- {\varvec{\Gamma }}_{0}\right) \circ \exp \left( \frac{h}{4}\overline{ {\varvec{\Omega }}}\right) \nonumber \\&+\,h\widehat{\mathbf {q}}^{*[n+1/2]}\circ \overline{{\mathbf {v}}}^{\prime }\circ \widehat{\mathbf {q}} ^{[n+1/2]}+{\varvec{\Gamma }}_{0} \end{aligned}$$
(32)
$$\begin{aligned} {\mathbf {K}}^{[n+1/2]} =&\exp ^{*}\left( \frac{h}{4}\overline{\varvec{ \Omega }}\right) \circ {\mathbf {K}}^{[n]}\circ \exp \left( \frac{h}{4} \overline{{\varvec{\Omega }}}\right) \nonumber \\&+\,2\exp ^{*}\left( \frac{h}{4} \overline{{\varvec{\Omega }}}\right) \circ \exp ^{\prime }\left( \frac{h}{4 }\overline{{\varvec{\Omega }}}\right) . \end{aligned}$$
(33)

Assuming that all the quantities of a beam are known at \(t_{n}\), equations can be expressed with average velocities and angular velocities, \(\overline{{\mathbf {v}}}\) and \(\overline{ \varvec{\Omega }}\) as the only unknown functions along the length of the beam.

3.2 Spatial discretization

Functions \({\mathbf {v}}(x,t)\) and \({\varvec{\Omega }}(x,t)\) are at each time t replaced by a set of their space-discrete values \({\mathbf {v}}^{p}\left( t\right) \) and \({\varvec{\Omega }}^{p}\left( t\right) \) and interpolated by a set of N interpolation functions \(I_{p}\left( x\right) \)

$$\begin{aligned}&{\mathbf {v}}(x,t)=\sum _{p=1}^{N}I_{p}\left( x\right) {\mathbf {v}}^{p}\left( t\right) \end{aligned}$$
(34)
$$\begin{aligned}&{\varvec{\Omega }}(x,t)=\sum _{p=1}^{N}I_{p}\left( x\right) {\varvec{\Omega }}^{p}\left( t\right) . \end{aligned}$$
(35)

The points \(x_{p};\ p=1\), \(\ldots \), N, are chosen from the interval \( \left[ 0,L\right] \) with \(x_{1}=0\) and \(x_{N}=L\). Thus, the sets of discrete vectors \({\mathbf {v}}^{p}\) and \({\varvec{\Omega }}^{p}\) become the unknowns of the problem. In accord with the time discretization presented above, the only unknowns of the present formulation at each time step are the average velocities and angular velocities \(\overline{{\mathbf {v}}}^{p}\) and \(\overline{{\varvec{\Omega }}} ^{p}\) at interpolation points.

Equations (26)–(27) are, in accord with the method of weighted residuals, multiplied by test functions \( I_{p}(x) \), \(p=1,\dots ,N\), and integrated along the length of the beam. Some terms are integrated by parts and the boundary conditions are considered to get the final discrete set of governing equations:

$$\begin{aligned}&\int \limits _{0}^{L}\biggl [\left( \rho A{\mathbf {v}}^{\left[ n+1\right] }-\rho A{\mathbf {v}}^{\left[ n\right] }-h\tilde{\mathbf {n}}^{\left[ n+1/2 \right] }\right) I_{p}+h\overline{\mathbf {n}}I_{p}^{\prime }\biggr ]\mathbf {\, }\mathrm{d}x \nonumber \\&\quad -\,\delta _{p}\varvec{f}=\mathbf {0} \end{aligned}$$
(36)
$$\begin{aligned}&\int \limits _{0}^{L}\biggl [\left( \mathbf {J}_{\rho }{\varvec{\Omega }}^{ \left[ n+1\right] }-\mathbf {J}_{\rho }{\varvec{\Omega }}^{\left[ n\right] }-h{\mathbf {K}}^{\left[ n+1/2\right] }\times \overline{\mathbf {M}} \right) I_{p} \nonumber \\&\quad +\,h\overline{{\varvec{\Omega }}}\times \mathbf {J}_{\rho }\overline{{\varvec{\Omega }}}I_{p} +h\overline{\mathbf {M}}I_{p}^{\prime } \nonumber \\&\quad -\,h\left( \varvec{ \Gamma }^{\left[ n+1/2\right] }-{\varvec{\Gamma }}_{0}\right) \times \widehat{\mathbf {q}}^{*\left[ n+1/2\right] }\circ \overline{\mathbf {n}} \circ \widehat{\mathbf {q}}^{\,\left[ n+1/2\right] }I_{p} \nonumber \\&\quad -\,h\widehat{\mathbf {q}}^{*\left[ n+1/2\right] }\circ \tilde{\mathbf {m}}^{\left[ n+1/2\right] }\circ \widehat{\mathbf {q}}^{\left[ n+1/2\right] }I_{p}\biggr ]\mathbf {\,}\mathrm{d}x \nonumber \\&\quad -\,\delta _{p}{} \mathbf{H}=\mathbf {0}, \end{aligned}$$
(37)

where

$$\begin{aligned}&\delta _{p}\mathbf {f} = \left\{ \begin{array}{cc} \mathbf {f}^{0}, &{} p=1 \\ \mathbf {f}^{L}, &{} p=N \\ 0, &{} \mathrm {otherwise} \end{array} \right. \\&\delta _{p}\mathbf {H} = \left\{ \begin{array}{cc} \widehat{\mathbf {q}}^{\,*\left[ n+1/2\right] }\circ \mathbf {h}^{0}\circ \widehat{\mathbf {q}}^{\left[ n+1/2\right] }, &{} p=1 \\ \widehat{\mathbf {q}}^{\,*\left[ n+1/2\right] }\circ \mathbf {h}^{L}\circ \widehat{\mathbf {q}}^{\left[ n+1/2\right] }, &{} p=N \\ 0, &{} \mathrm {otherwise} \end{array} \right. . \end{aligned}$$

It is evident that the governing equations are nonlinear and will be therefore solved iteratively. Before we present the solution procedure, we still need to find suitable formulae for \(\overline{\mathbf {n}}\) and \( \overline{\mathbf {M}}\). They will be derived from the energy preservation constraint.

3.3 Energy conservation

The proposed method is general regarding the load conditions, but for the special case of conservative system the total mechanical energy can be algorithmically preserved. Let us start from the difference of kinetic energy between two successive times of the scheme

$$\begin{aligned} \Delta W_{K} =&\,\frac{1}{2}\int \limits _{0}^{L}\biggl [{\mathbf {v}}^{\left[ n+1 \right] }\cdot \rho A{\mathbf {v}}^{\left[ n+1\right] }+{\varvec{\Omega }}^{ \left[ n+1\right] }\cdot \mathbf {J}_{\rho }{\varvec{\Omega }}^{\left[ n+1 \right] } \\&-{\mathbf {v}}^{\left[ n\right] }\cdot \rho A{\mathbf {v}}^{\left[ n\right] }+{\varvec{\Omega }}^{\left[ n\right] } \cdot \mathbf {J}_{\rho }{\varvec{\Omega }}^{\left[ n\right] }\biggr ]\mathrm{d}x\\ =&\,\int \limits _{0}^{L}\biggl [\frac{1}{2}\left( {\mathbf {v}}^{\left[ n\right] }+ {\mathbf {v}}^{\left[ n+1\right] }\right) \cdot \rho A\left( {\mathbf {v}}^{\left[ n+1\right] }-{\mathbf {v}}^{\left[ n\right] }\right) \\&+\frac{1}{2}\left( \varvec{\Omega }^{[n]}+ {\varvec{\Omega }}^{[n+1]}\right) \cdot \mathbf {J}_{\rho }\left( {\varvec{\Omega }}^{\left[ n+1\right] }-{\varvec{\Omega }}^{\left[ n \right] }\right) \biggr ]\mathrm{d}x \\ =&\,\int \limits _{0}^{L}\biggl [\overline{{\mathbf {v}}}\cdot \rho A\left( \mathbf { v}^{\left[ n+1\right] }-{\mathbf {v}}^{\left[ n\right] }\right) \\&+\overline{ {\varvec{\Omega }}}\cdot \mathbf {J}_{\rho }\left( \varvec{\Omega }^{ \left[ n+1\right] }-{\varvec{\Omega }}^{\left[ n\right] }\right) \biggr ]\mathrm{d}x. \end{aligned}$$

Considering the chosen interpolation (34)–(35), we have

$$\begin{aligned} \Delta W_{K}=&\sum _{p=1}^{N}\int \limits _{0}^{L}\biggl [\overline{{\mathbf {v}}} ^{p}I_{p}\cdot \rho A\left( {\mathbf {v}}^{\left[ n+1\right] }-{\mathbf {v}}^{ \left[ n\right] }\right) \\&+\overline{{\varvec{\Omega }}}^{p}I_{p}\cdot \mathbf {J}_{\rho }\left( \varvec{\Omega }^{\left[ n+1\right] }- {\varvec{\Omega }}^{\left[ n\right] }\right) \biggr ]\mathrm{d}x. \end{aligned}$$

When there are no external forces acting on a beam, the discrete equations (36)–(37) are simplified accordingly, leading to

$$\begin{aligned} \Delta W_{K}=&-\,\sum _{p=1}^{N}h\int \limits _{0}^{L}\biggl [\overline{{\mathbf {v}} }^{p}\cdot \overline{\mathbf {n}}I_{p}^{\prime }+\overline{{\varvec{\Omega }}}^{p}\cdot \overline{\mathbf {M}}I_{p}^{\prime }\\&+\overline{{\varvec{\Omega }}}^{p}\cdot \left( -{\mathbf {K}}^{\left[ n+1/2\right] }\right. \\&\times \left. \overline{\mathbf {M}}I_{p} +\overline{{\varvec{\Omega }}}\times \mathbf {J}_{\rho }\overline{{\varvec{\Omega }}}I_{p} \right) -\overline{{\varvec{\Omega }}}^{p}\cdot \left( \varvec{ \Gamma }^{\left[ n+1/2\right] }-{\varvec{\Gamma }}_{0}\right) \\&\times \widehat{\mathbf {q}}^{*\left[ n+1/2\right] }\circ \overline{\mathbf {n}} \circ \widehat{\mathbf {q}}^{\,\left[ n+1/2\right] }I_{p}\biggr ]\mathrm{d}x \\ =&-\,h\int \limits _{0}^{L}\biggl [\overline{{\mathbf {v}}}^{\prime }\cdot \mathbf { \overline{n}}+\overline{{\varvec{\Omega }}}^{\prime }\cdot \overline{ \mathbf {M}}-\overline{{\varvec{\Omega }}}\cdot {\mathbf {K}}^{\left[ n+1/2 \right] }\times \overline{\mathbf {M}} \\&-\overline{{\varvec{\Omega }}}\cdot \left( \varvec{ \Gamma }^{\left[ n+1/2\right] }-{\varvec{\Gamma }}_{0}\right) \widehat{\mathbf {q}}^{*\left[ n+1/2\right] }\circ \overline{\mathbf {n}} \circ \widehat{\mathbf {q}}^{\,\left[ n+1/2\right] }\biggr ]\mathrm{d}x. \end{aligned}$$

A rearrangement of terms gives

$$\begin{aligned} \Delta W_{K} =&-\,h\int \limits _{0}^{L}\biggl [\biggl (\widehat{\mathbf {q}}^{*\left[ n+1/2\right] }\circ \overline{{\mathbf {v}}}^{\prime }\circ \widehat{ \mathbf {q}}^{\left[ n+1/2\right] } \\&+\left( \varvec{\Gamma }^{\left[ n+1/2\right] }-{\varvec{\Gamma }} _{0}\right) \times \overline{{\varvec{\Omega }}}\biggr )\cdot \widehat{ \mathbf {q}}^{*\left[ n+1/2\right] }\circ \overline{\mathbf {n}}\circ \widehat{\mathbf {q}}^{\left[ n+1/2\right] }\\&+\left( \overline{\varvec{\Omega }}^{\prime }-\overline{{\varvec{\Omega }}}\times {\mathbf {K}}^{\left[ n+1/2\right] }\right) \cdot \overline{\mathbf {M}}\biggr ]\mathrm{d}x \end{aligned}$$

and after considering the discrete kinematic compatibility equations (28)–(29), we get

$$\begin{aligned} \Delta W_{K}=&-\,\int \limits _{0}^{L}\biggl [\left( \varvec{\Gamma }^{\left[ n+1\right] }-{\varvec{\Gamma }}^{\left[ n\right] }\right) \cdot \widehat{ \mathbf {q}}^{*\left[ n+1/2\right] }\circ \overline{\mathbf {n}}\circ \widehat{\mathbf {q}}^{\left[ n+1/2\right] }\nonumber \\&+\left( {\mathbf {K}}^{\left[ n+1 \right] }-{\mathbf {K}}^{\left[ n\right] }\right) \cdot \overline{\mathbf {M}} \biggr ]\mathrm{d}x. \end{aligned}$$
(38)

To preserve the energy of a conservative system within the time step, we should have \(\Delta W_{K}=-\Delta W_{D}\), where

$$\begin{aligned} \Delta W_{D}=\frac{1}{2}\int \limits _{0}^{L}\left[ \begin{array}{c} {\varvec{\Gamma }}^{\left[ n+1\right] }-{\varvec{\Gamma }}^{\left[ n \right] } \\ {\mathbf {K}}^{\left[ n+1\right] }-{\mathbf {K}}^{\left[ n\right] } \end{array} \right] \cdot \mathbb {C}\left[ \begin{array}{c} {\varvec{\Gamma }}^{\left[ n\right] }+{\varvec{\Gamma }}^{\left[ n+1 \right] } \\ {\mathbf {K}}^{\left[ n\right] }+{\mathbf {K}}^{\left[ n+1\right] } \end{array} \right] \mathrm{d}x. \end{aligned}$$
(39)

Comparison of (38) and (39) leads to the admissible stress resultants. To preserve the total mechanical energy in conservative problems, the approximative stress-resultant vectors need to be evaluated by the following formulae:

$$\begin{aligned} \overline{\mathbf {n}} =&\,\widehat{\mathbf {q}}^{\left[ n+1/2\right] }\circ \Biggl ( \mathbb {C}_{\Gamma \Gamma }\left( \frac{{\varvec{\Gamma }}^{ \left[ n\right] }+{\varvec{\Gamma }}^{\left[ n+1\right] }}{2}\right) \nonumber \\&+ \mathbb {C}_{\Gamma \mathrm {K}}\left( \frac{{\mathbf {K}}^{\left[ n\right] }+ {\mathbf {K}}^{\left[ n+1\right] }}{2} \right) \Biggr ) \circ \widehat{\mathbf {q}} ^{*\left[ n+1/2\right] } \end{aligned}$$
(40)
$$\begin{aligned} \overline{\mathbf {M}} =&\,\mathbb {C}_{\mathrm {K}\Gamma }\left( \frac{ {\varvec{\Gamma }}^{\left[ n\right] }+{\varvec{\Gamma }}^{\left[ n+1 \right] }}{2}\right) +\mathbb {C}_{\mathrm {KK}}\left( \frac{{\mathbf {K}}^{\left[ n\right] }+{\mathbf {K}}^{\left[ n+1\right] }}{2}\right) . \end{aligned}$$
(41)

For the simplest case where \(\mathbb {C}\) is block-diagonal, we have

$$\begin{aligned} \overline{\mathbf {n}}&=\widehat{\mathbf {q}}^{\left[ n+1/2\right] }\circ \mathbb {C}_{\Gamma \Gamma }\left( \frac{{\varvec{\Gamma }}^{\left[ n\right] }+{\varvec{\Gamma }}^{\left[ n+1\right] }}{2}\right) \circ \widehat{ \mathbf {q}}^{*\left[ n+1/2\right] } \\ \overline{\mathbf {M}}&=\mathbb {C}_{\mathrm {KK}}\left( \frac{{\mathbf {K}}^{ \left[ n\right] }+{\mathbf {K}}^{\left[ n+1\right] }}{2}\right) . \end{aligned}$$

In order to preserve the energy of conservative systems we only need to evaluate the internal stresses from the average strains. This concludes the derivation of the present model.

It is obvious that the use of above formulas for the evaluation of midtime stress resultants does not restrict the applicability of our approach for nonconservative problems. Let us stress that no special approximation of rotations or strains was needed in the present approach. Due to a suitable choice of primary variables and governing equations, we get the desired properties of the formulation, while the kinematic compatibility is satisfied with the same accuracy as the governing equations.

4 Computational aspects

At each discrete time, the nonlinear discrete governing equations (36)–(37) are solved for the nodal values of average velocities and angular velocities using the Newton–Raphson method. This requires the construction of the Jacobian matrix, which is in our case expressed analytically. The analytical Jacobian is advantageous compared to the approximative one due to the presence of rotational degrees of freedom. Its derivation is relatively simple as the primary variables were conveniently chosen.

4.1 Linearization of equations

The linearization of rotational quaternions demands the consideration of their multiplicative and noncommutative nature. In order to linearize \(\widehat{\mathbf {q}}^{\, \left[ n+1/2\right] }\) with respect to \(\overline{{\varvec{\Omega }}}\) the following directional derivative is expressed:

$$\begin{aligned} \delta \widehat{\mathbf {q}}^{\left[ n+1/2\right] }=\frac{\text{ d }}{{\text{ d }}\epsilon } \bigg \vert _{\epsilon =0}\widehat{\mathbf {q}}^{\left[ n\right] }\circ \exp \left( \frac{h}{4}\left( \overline{{\varvec{\Omega }}}+\epsilon \delta \overline{{\varvec{\Omega }}}\right) \right) . \end{aligned}$$

After a straightforward derivation, we get

$$\begin{aligned} \delta \exp \left( \frac{h}{4}\overline{{\varvec{\Omega }}}\right) = \mathbf {T\,}\delta \overline{{\varvec{\Omega }}}, \end{aligned}$$
(42)

where

$$\begin{aligned} \mathbf {T}=a_{0}\mathbf {T}_{0}+a_{1}\mathbf {T}_{1}. \end{aligned}$$
(43)

\(\mathbf {T}_{0}\) and \(\mathbf {T}_{1}\) are the \(4\times 3\) matrices

$$\begin{aligned} \mathbf {T}_{0}=\left[ \begin{array}{ccc} -\frac{h}{4}\Omega _{1} &{} -\frac{h}{4}\Omega _{2} &{} -\frac{h}{4}\Omega _{3} \\ 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] \end{aligned}$$
$$\begin{aligned} \mathbf {T}_{1}=\left[ \begin{array}{ccc} 0 &{} 0 &{} 0 \\ \Omega _{1}\Omega _{1} &{} \Omega _{1}\Omega _{2} &{} \Omega _{1}\Omega _{3} \\ \Omega _{2}\Omega _{1} &{} \Omega _{2}\Omega _{2} &{} \Omega _{2}\Omega _{3} \\ \Omega _{3}\Omega _{1} &{} \Omega _{3}\Omega _{2} &{} \Omega _{3}\Omega _{3} \end{array} \right] , \end{aligned}$$

composed from the components \(\Omega _{1}\), \(\Omega _{2}\), \(\Omega _{3}\) of vector \(\overline{{\varvec{\Omega }}}\). The scalar coefficients \(a_{0}\) and \(a_{1}\) are

$$\begin{aligned} a_{0}&=\frac{1}{\overline{\Omega }}\sin \frac{h\overline{\Omega }}{4} \\ a_{1}&=\frac{h}{4\overline{\Omega }^{2}}\cos \frac{h\overline{ \Omega }}{4}-\frac{1}{\overline{\Omega }^{3}}\sin \frac{h\overline{\Omega }}{ 4}, \end{aligned}$$

where \(\overline{\Omega }\) denotes the Euclidean norm of \(\overline{ {\varvec{\Omega }}}\).

In a similar manner, we get the variations of \(\exp ^{*}\left( \frac{h}{4} \overline{{\varvec{\Omega }}}\right) \) and \(\exp ^{\prime }\left( \frac{h}{ 4}\overline{{\varvec{\Omega }}}\right) \). The remaining terms are varied in a standard manner. The details are therefore omitted. At each step of the iteration procedure, we solve a linear set of equations

$$\begin{aligned} \mathbf {{J}}^{\left( i\right) }\delta \mathbf {y}=-\mathbf {f}^{\left( i\right) }, \end{aligned}$$
(44)

where \(\mathbf {{J}}^{\left( i\right) }\) is the Jacobian tangent matrix, \( \mathbf {f}^{\left( i\right) }\) the residual vector of discretized equations (36)–(37), both in iteration i, and \(\delta \mathbf {y}\) a vector of corrections of all nodal unknowns

$$\begin{aligned} \delta \mathbf {y}=\left[ \begin{array}{ccccc} \delta \overline{{\mathbf {v}}}_{1}&\delta \overline{{\varvec{\Omega }}}_{1}&\cdots&\delta \overline{{\mathbf {v}}}_{N_k}&\delta \overline{\varvec{\Omega }}_{N_k} \end{array} \right] ^\mathrm{T}. \end{aligned}$$

Our choice of variables allows the iterative corrections to be directly added to the current values:

$$\begin{aligned} \overline{{\mathbf {v}}}^{\left( i+1\right) }=\overline{{\mathbf {v}}}^{\left( i\right) }+\delta \overline{{\mathbf {v}}},\qquad \overline{{\varvec{\Omega }} }^{\left( i+1\right) }=\overline{{\varvec{\Omega }}}^{\left( i\right) }+\delta \overline{{\varvec{\Omega }}} \end{aligned}$$
(45)

at each nodal point of the structure.

Fig. 2
figure 2

A rigid joint of two elements with different initial orientations

Full size image

4.2 Prediction of initial values

To begin the iteration procedure, we need to predict the initial values. A natural assumption that initial velocities are equal to the converged values of the previous time:

$$\begin{aligned} \overline{{\mathbf {v}}}^{\left( 0\right) }={\mathbf {v}}^{\left[ n+1\right] ,\left( 0\right) }={\mathbf {v}}^{\left[ n\right] }\quad \quad \overline{ {\varvec{\Omega }}}^{\left( 0\right) }={\varvec{\Omega }}^{\left[ n+1 \right] ,\left( 0\right) }={\varvec{\Omega }}^{\left[ n\right] } \end{aligned}$$

is applied. The midtime configuration and strains are then evaluated in accord with this assumption and approximations (30)–(33).

4.3 Compatibility of boundary conditions

We wish to assemble at the structural level elements with different initial rotations that are connected at rigid joints as simple as possible. Let two elements have different initial orientations at a joint, described by rotational quaternions \(\widehat{\mathbf {q}}_{0}^{\mathrm {I}}\) and \(\widehat{\mathbf {q}} _{0}^{\mathrm {II}}\), see Fig. 2. The total rotation is then a composition of initial and superimposed rotation

$$\begin{aligned} \widehat{\mathbf {q}}^{\mathrm {I}}=\widehat{\mathbf {q}}_{0}^{\mathrm {I}}\circ \widehat{\mathbf {k}}^{\mathrm {I}}\qquad \mathrm {and}\qquad \widehat{\mathbf {q }}^{\mathrm {II}}=\widehat{\mathbf {q}}_{0}^{\mathrm {II}}\circ \widehat{ \mathbf {k}}^{\mathrm {II}}, \end{aligned}$$
(46)

where the superimposed rotations at the node must be equal:

$$\begin{aligned} \widehat{\mathbf {k}}^{\mathrm {I}}=\widehat{\mathbf {k}}^{\mathrm {II}}. \end{aligned}$$
(47)

For the present approach, this yields

$$\begin{aligned} \overline{{\mathbf {v}}}^{\mathrm {I}}=\overline{{\mathbf {v}}}^{\mathrm {II}}\qquad \mathrm {and}\qquad \overline{{\varvec{\Omega }}}^{\mathrm {I}}\ne \overline{{\varvec{\Omega }}}^{\mathrm {II}}, \end{aligned}$$

as the angular velocities are expressed in different local frames:

$$\begin{aligned} \overline{{\varvec{\Omega }}}^{{\mathrm {I}}}=2\widehat{\mathbf {q}}^{\mathrm {I }*}\circ \dot{\overset{}{\widehat{\mathbf {q}}}}^{{ \mathrm{I}}} \qquad \mathrm {and}\qquad \overline{{\varvec{\Omega }}}^{\mathrm {II}}=2 \widehat{\mathbf {q}}^{\mathrm {II}*}\circ \dot{\overset{}{\widehat{\mathbf {q}}}}^{{ \mathrm{II}}} . \end{aligned}$$

After considering (46) and (47), we have

$$\begin{aligned} \widehat{\mathbf {q}}_{0}^{\mathrm {I}}\circ \overline{{\varvec{\Omega }}}^{ \mathrm {I}}\circ \widehat{\mathbf {q}}_{0}^{\mathrm {I}*}=\widehat{\mathbf { q}}_{0}^{\mathrm {II}}\circ \overline{{\varvec{\Omega }}}^{\mathrm {II} }\circ \widehat{\mathbf {q}}_{0}^{\mathrm {II}*}. \end{aligned}$$
(48)

We can enforce the condition (48) using the method of Lagrangian multiplies, but it is computationally more efficient to recognize that the angular velocities can be expressed as

$$\begin{aligned} \overline{{\varvec{\Omega }}}_{R}=\widehat{\mathbf {q}}_{0}\circ \overline{ {\varvec{\Omega }}}\circ \widehat{\mathbf {q}}_{0}^{*}. \end{aligned}$$
(49)

By choosing an appropriate basis for the description of quantities and equations in the local coordinate system, we can thus simply use a standard Boolean identification of unknowns at the structural level.

4.4 Energy dissipation

It is often desired that a numerical scheme allows dissipation of the high-frequency response. The present scheme can be easily extended to have dissipative properties. Starting from the energy-preserving stress-resultant approximations (40)–(41) dissipative terms can be added in the following manner

$$\begin{aligned} \overline{\mathbf {n}} =&\,\widehat{\mathbf {q}}^{\left[ n+1/2\right] }\circ \Biggl ( \mathbb {C}_{\Gamma \Gamma }\left( \frac{{\varvec{\Gamma }}^{ \left[ n\right] }+{\varvec{\Gamma }}^{\left[ n+1\right] }}{2}\right) \\&+ \mathbb {C}_{\Gamma \mathrm {K}}\left( \frac{{\mathbf {K}}^{\left[ n\right] }+ {\mathbf {K}}^{\left[ n+1\right] }}{2}\right) \Biggr ) \circ \widehat{\mathbf {q}} ^{*\left[ n+1/2\right] } \\&+\beta \widehat{\mathbf {q}}^{\left[ n+1/2\right] }\circ \Biggl ( \mathbb {C}_{\Gamma \Gamma }\left( \varvec{\Gamma }^{\left[ n+1\right] }- {\varvec{\Gamma }}^{\left[ n\right] }\right) \\&+\mathbb {C}_{\Gamma \mathrm {K} }\left( {\mathbf {K}}^{\left[ n+1\right] }-{\mathbf {K}}^{\left[ n\right] }\right) \Biggr ) \circ \widehat{\mathbf {q}}^{*\left[ n+1/2\right] } \\ \overline{\mathbf {M}} \,=&\,\mathbb {C}_{\mathrm {K}\Gamma }\left( \frac{ {\varvec{\Gamma }}^{\left[ n\right] }+{\varvec{\Gamma }}^{\left[ n+1 \right] }}{2}\right) +\mathbb {C}_{\mathrm {KK}}\left( \frac{{\mathbf {K}}^{\left[ n\right] }+{\mathbf {K}}^{\left[ n+1\right] }}{2}\right) \\&+\beta \left( \mathbb {C}_{\mathrm {K}\Gamma }\left( {\varvec{\Gamma }}^{ \left[ n+1\right] }-{\varvec{\Gamma }}^{\left[ n\right] }\right) +\mathbb {C }_{\mathrm {KK}}\left( {\mathbf {K}}^{\left[ n+1\right] }-{\mathbf {K}}^{\left[ n \right] }\right) \right) . \end{aligned}$$

We can interpret the above approximation as the decomposition of stress resultants to conservative and dissipative part. The dissipative part is proportional to the increment of strain measures and \(\beta \in [0,0.5] \) is a parameter related to the magnitude of dissipation. For conservative problems, we now have

$$\begin{aligned}&\Delta W_{K}+\Delta W_{D}=\\&\qquad =-\beta \int \limits _{0}^{L}\left[ \begin{array}{c} {\varvec{\Gamma }}^{\left[ n+1\right] }-{\varvec{\Gamma }}^{\left[ n \right] } \\ {\mathbf {K}}^{\left[ n+1\right] }-{\mathbf {K}}^{\left[ n\right] } \end{array} \right] \cdot \mathbb {C}\left[ \begin{array}{c} {\varvec{\Gamma }}^{\left[ n+1\right] }-{\varvec{\Gamma }}^{\left[ n \right] } \\ {\mathbf {K}}^{\left[ n+1\right] }-{\mathbf {K}}^{\left[ n\right] } \end{array} \right] \mathrm{d}x, \end{aligned}$$

which confirms that the contribution of additional terms to the total mechanical energy is always negative.

5 Numerical simulations

Several numerical examples will be presented to demonstrate the ability of proposed formulation to solve problems with large displacements and rotations on long time intervals. We will focus on well-documented and widely studied problems from the literature with the main focus on computational performance of the formulation. The problems under consideration are classical benchmark examples with \(\mathbb {C}_{\Gamma \mathrm {K}}=\mathbb {C }_{\mathrm {K}\Gamma }=\mathbf {0,}\)

$$\begin{aligned} \mathbb {C}_{\Gamma \Gamma }=\left[ \begin{array}{ccc} EA_{1} &{} 0 &{} 0 \\ 0 &{} GA_{2} &{} 0 \\ 0 &{} 0 &{} GA_{3}\ \end{array} \right] , \, \mathbb {C}_{\mathrm {KK}}=\left[ \begin{array}{ccc} GJ_{1} &{} 0 &{} 0 \\ 0 &{} EJ_{2} &{} 0 \\ 0 &{} 0 &{} EJ_{3}\ \end{array} \right] . \end{aligned}$$

E and G are the elastic and shear moduli of material. The remaining quantities represent the geometric properties of the cross section expressed with respect to its centroid: \(A_{1}\) is the area; \(J_{1}\) is the torsional inertial moment; \(A_{2}\) and \(A_{3}\) are the effective shear areas; \(J_{2}\) and \(J_{3}\) are the bending inertial moments. All problems involve deformable beam members. In first three examples, a part of the motion is conservative, while the last one is a nonconservative problem.

The interpolation points in all of the examples were taken to be equidistant and standard Lagrange polynomials were used as shape functions. Integrals were evaluated numerically using the Gaussian quadrature rule. The number of integration points was taken to be equal to the number of interpolation points, N, for full integration and \(N-1\) for the reduced integration. Newton–Raphson iteration was terminated when the Euclidean norm of the vector of all unknowns at the structural level, \( \left\| \delta \mathbf {y}\right\| _{2}\), was less than \(10^{-8}\). A quadratic convergence of iteration procedure has been observed in all test problems at all time steps.

5.1 Free flight of a beam

This example, introduced by Simo and Vu-Quoc [13], shows the ability of formulation to consider very large displacements and rotations. This is also an excellent test for the long-term stability of time integrator. Simo et al. [40] shown a rapid growth of total mechanical energy causing a failure of the iteration process when using classical time-integration schemes.

Fig. 3
figure 3

Free flight of a flexible beam

Full size image

Initially inclined beam is subjected at the lower end to triangular pulse load, consisting of force \(f_{X}\) and moments \(h_{Y}\) and \(h_{Z}\), see Fig. 3. The load vanishes at \(t=5\) leaving the beam to fly in free motion. The remaining data of the beam are:

$$\begin{aligned} EA&=GA_{2}=GA_{3}=10000, \\ GI_{1}&=EI_{2}=EI_{3}=500, \\ \rho A&=1,\quad \mathbf {J}_{\rho }=\mathrm {diag}\left[ \begin{array}{ccc} 10&10&10 \end{array} \right] . \end{aligned}$$
Fig. 4
figure 4

Free flight of a flexible beam: projections of the deformed shapes on the coordinate plane XY

Full size image
Fig. 5
figure 5

Free flight of a flexible beam: projections of the deformed shapes on the coordinate plane XZ

Full size image

In our simulation, the finite-element mesh consisted of 10 quadratic elements, \(N=3\). To demonstrate the performance of the proposed approach, we study the long-term behavior of the beam. We show the results for constant time step \(h=0.1\) until the time \(t=1000\), but need to stress that our solver experienced no difficulties and we could continue with calculation.

In Figs. 4 and 5, projection of the deformed shapes on the coordinate planes XY and XZ, respectively, is depicted at the beginning and at the end of the calculation period. The problem is nonlinear and nonperiodic. Still, we can observe a paddling-like pattern, which is preserved during the whole analysis. The energy remains constant after the load is removed as illustrated in Fig. 6.

Fig. 6
figure 6

Free flight of a flexible beam: time history of the total mechanical energy

Full size image

5.2 Right-angle cantilever

This example, also presented by Simo and Vu-Quoc [13], studies a right-angle cantilever beam under triangular pulse load in the direction out of the plane of the beam, see Fig. 7.

Other geometrical and material properties are taken to be:

$$\begin{aligned} EA&=GA_{2}=GA_{3}=10^{6}, \\ GI_{1}&=EI_{2}=EI_{3}=10^{3}, \\ \rho A&=1,\quad \mathbf {J}_{\rho }=\mathrm {diag}\left[ \begin{array}{ccc} 20&10&10 \end{array} \right] . \end{aligned}$$
Fig. 7
figure 7

The right-angle cantilever subjected to out-of-plane loading

Full size image

Both parts of the structure are modeled with only four cubic elements, \(N=4\). It has been reported by several authors, see, e.g., [21], that for this example numerical problems appear at approximately \(t=50\). We therefore used longer time interval \(\left[ 0,100\right] \) and relatively large time step \(h=0.2\). For comparison reasons, we also present the results for a smaller time step \( h=0.02\). We can observe from Fig. 8 that the results for longer time step agree well with the ones obtained by smaller time increments. Moreover, the calculations remain stable during the whole time interval.

Fig. 8
figure 8

Right-angle cantilever: out-of-plane displacements at the elbow and at the free-end

Full size image

In Fig. 9, we compare our results with the ones presented by Simo and Vu-Quoc [13]. A good agreement between the results can be observed. Moreover, we can see that the present approach gives excellent results even if a mesh of only two elements is used (one per each leg of the cantilever).

Fig. 9
figure 9

Right-angle cantilever: comparison with the literature and illustration of the mesh size sensitivity

Full size image

5.3 Circular beam

Another problem that reveals the energy growth when using classical trapezoidal or midpoint rule is a closed circular beam, [40]. This problem is interesting as such structures appear in many engineering problems. A ring of radius 5 is free in space and set in motion by two forces of equal magnitude in opposite directions at points A and B, see Fig. 10. Other data are as follows:

$$\begin{aligned} EA&=GA_{2}=GA_{3}=10^{6}, \\ GI_{1}&=EI_{2}=EI_{3}=10^{3}, \\ \rho A&=1,\quad \varvec{J}_{\rho }=\mathrm {diag}\left[ 10,10,10\right] . \end{aligned}$$
Fig. 10
figure 10

The geometry and loading of the circular beam

Full size image

We used a mesh of sixteen straight elements of third order, \(N=4\). A solution was sought on a long time interval \(\left[ 0,500\right] \) with time step \(h=0.1\). The calculations remain stable for the whole simulation. Besides the constant energy after the load was removed, the long-term stability of the proposed formulation is evident from time histories of displacements at point A, see Fig. 11. Figure 11 also reveals large magnitudes of displacements and a complicated response of structure without any evident pattern of movement.

Fig. 11
figure 11

The displacement of the node initially at the top of the circular beam

Full size image

5.4 Four-bar mechanism

The four-bar mechanism with misaligned joint introduced by Bauchau [55] belongs to the well-documented benchmark examples [56, 57], suitable for testing new formulations. The mechanism consists of three bars connected by revolute joints, as shown in Fig. 12. The axes of rotation of revolute joints A, B and D are orthogonal to the plane of mechanism. The revolute joint at point C is inclined with respect to the normal axis by the angle \(\varphi =5^{\circ }\) simulating initial imperfection. Bars AB and BC share equal properties:

$$\begin{aligned} EA&=52.99\times 10^{6},\quad GA_{2}=GA_{3}=16.88\times 10^{6}, \\ GI_{1}&=733.5,\quad EI_{2}=EI_{3}=1131, \\ \rho A&=1.996,\quad \varvec{J}_{\rho }=10^{-5}\times \mathrm {diag}\left[ 7.186,4.262,4.262\right] , \end{aligned}$$

while the data of the bar CD are:

$$\begin{aligned} EA&=13.25\times 10^{6},\quad GA_{2}=GA_{3}=4.22\times 10^{6}, \\ GI_{1}&=45.84,\quad EI_{2}=EI_{3}=70.66, \\ \rho A&=0.499,\quad \varvec{J}_{\rho }=10^{-6}\cdot \mathrm {diag}\left[ 4.491,2.663,2.663\right] , \end{aligned}$$

A constant angular velocity \(\Omega =0.6\) is applied at support A. Initial imperfection results in three-dimensional motion of the system.

Fig. 12
figure 12

Four-bar mechanism with misaligned revolute joint

Full size image

We modeled each beam with four elements of third order, \(N=4\). For the perfect joint, Boolean identification of degrees of freedom was used, while for the inclined joint the method of Lagrange multipliers was applied. In accord with the present model, we enforced the constraints at the level of angular velocities by satisfying the equations

$$\begin{aligned} \left( \widehat{\mathbf {q}}_{e}^{*}\circ \left( \overline{{\varvec{\Omega }}} ^{\mathrm {I}}-\overline{{\varvec{\Omega }}}^{\mathrm {II}}\right) \circ \widehat{\mathbf {q}}_{e}\right) \cdot \left[ \begin{array}{ccc} 1&0&0 \end{array} \right] ^{T}&=0 \\ \left( \widehat{\mathbf {q}}_{e}^{*}\circ \left( \overline{{\varvec{\Omega }}} ^{\mathrm {I}}-\overline{{\varvec{\Omega }}}^{\mathrm {II}}\right) \circ \widehat{\mathbf {q}}_{e}\right) \cdot \left[ \begin{array}{ccc} 0&1&0 \end{array} \right] ^{T}&=0, \end{aligned}$$

where \(\overline{{\varvec{\Omega }}}^{\mathrm {I}}\) and \(\overline{ {\varvec{\Omega }}}^{\mathrm {II}}\) denote the angular velocities of the beams BC and CD at point C and \(\widehat{\mathbf {q}}_{e}\) is the rotational quaternion describing the initial imperfection of the joint. The simulation was carried out until \(t=12\). Following [57], we obtained the results presented here using numerical dumping and constant time step \(h=0.004\).

Fig. 13
figure 13

Displacements at point C of the four-bar mechanism

Full size image

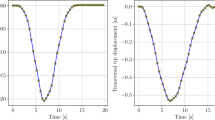
The results for the displacements of joint C are presented in Fig. 13, while Fig. 14 shows the first Euler angle of the bar BC at point C and the relative rotations at the revolute joint D. The present results are in excellent agreement with other authors, see [56, 57].

Fig. 14
figure 14

Rotations at points C and D of the four-bar mechanism

Full size image

6 Conclusions

We have presented a novel energy-preserving scheme based on velocities and angular velocities, where we satisfy the kinematic compatibility equations with the same accuracy as the governing equations. The discrete kinematic compatibility equations enforce the admissible update of strain vectors. This update is in our approach completely harmonized with the energy conservation demands, which additionally provides the consistent approximation of stress resultants. The finite element proposed is based on the interpolation of velocities in a fixed basis and angular velocities in the local basis. The use of standard shape functions is therefore completely consistent with properties of the configuration space. The main advantage of the proposed solution method is in its simplicity, robustness and long-term stability. Its favorable behavior was demonstrated by several numerical examples.