An inclined cable excited by a non-ideal massive moving deck: an asymptotic formulation

Abstract

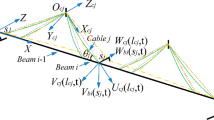
A moving deck is an important (kinematic) excitation source for the inclined cable in cable-stayed bridges. In ideal cases, the deck motion is assumed to be harmonic oscillation and cable’s dynamic effects on the deck are neglected. As a refined version, an inclined cable excited by a massive non-ideal moving deck, i.e., the deck’s oscillation, is slowly modulated by the cable and thus not exactly harmonic is investigated in an asymptotically coupled formulation for understanding cable–deck dynamic interactions. More explicitly, by ordering the deck/cable mass ratio as a large parameter, the coupled system is reduced using asymptotic approximations and multi-scale expansions. After neglecting the reduced model’s nonlinear terms, firstly, cable–deck linear coupled modes are obtained, leading to two different kinds of linear modal dynamics, i.e., the cable-dominated one and the deck-dominated one, whose asymptotic characteristics are also revealed. Then cable’s forced nonlinear vibrations, excited by the deck’s modulated oscillation (i.e., non-ideal moving deck), are fully investigated. Nonlinear frequency responses of the cable–deck coupled system are found, and the dynamic effects on the cable’s periodic and quasi-periodic behaviors, due to cable–deck coupling (characterized by the deck/cable mass ratio), cable’s inclinations, and boundary damping, are also presented.

Appendices

Appendix A

Cable’s linear modal analysis can be found in reference [1]. We restrict our attention to cable’s in-plane symmetric modes in this paper, and these modes are given by

$$\begin{aligned} \phi _i \left( x \right)= & {} c_i \left[ {1-\tan \left( {{\omega _i }/2} \right) \sin \omega _i x-\cos \omega _i x} \right] ,\nonumber \\&i=1,3,5\ldots \end{aligned}$$

(59)

where $c_{\mathrm{i}}$ is the normalization constants. And the associated eigen-frequencies are determined by

$$\begin{aligned} \frac{1}{2}\omega _i -\tan \left( {\frac{1}{2}\omega _i } \right) -\frac{1}{2\lambda ^{2}}\omega _i^3 =0,\;i=1,3,5\ldots \end{aligned}$$

(60)

where $\lambda ^{2}={ EA}/{ mgl}(8b/l)^{3}$ is the elasto-geometric parameter. The above nonlinear transcendental equations can be solved by the Newton- Raphson method.

$$\begin{aligned} L\left[ w \right]= & {} -{w}''-\alpha {y}''\int _0^1 {\left( {{y}'{w}'} \right) } \hbox {d}x,\quad \nonumber \\ N_2 \left[ w \right]= & {} \alpha {w}''\int _0^1 {\left( {{y}'{w}'} \right) } \hbox {d}x+\alpha {y}''\int _0^1 {\left( {{{w}'^{2}}/2} \right) } \hbox {d}x,\nonumber \\ N_3 [ w ]= & {} \alpha {w}''\int _0^1 {\left( {{{w}'^{2}}/2} \right) } \hbox {d}x \end{aligned}$$

(61)

$$\begin{aligned} N_3 \left[ {w_1 } \right]= & {} \alpha {w}''_1 \int _0^1 {\left( {{{w'}_1^{2}}/2} \right) } \hbox {d}x \nonumber \\ N_3 \left[ {w_1,w_2 } \right]= & {} \alpha {w}''_1 \int _0^1 {\left( {{y}'{w}'_2 } \right) } \hbox {d}x+\alpha {y}''\int _0^1 {\left( {{w}'_1 {w}'_2 } \right) } \hbox {d}x\nonumber \\&+\,\alpha {w}''_2 \int _0^1 {\left( {{y}'{w}'_1 } \right) } dx \end{aligned}$$

(62)

Appendix B

The shape functions $\varPsi _1 \left( x \right) ,\;\varPsi _2 \left( x \right)$ are governed by the following linear boundary value problems (BVPs)

$$\begin{aligned}&4\omega _n^2 \varPsi _1 \left( x \right) +\varPsi _1 ^{\prime \prime }+\alpha {y}''\int _0^1 {{y}' \varPsi _1 ^{\prime }} \hbox {d}x=-\varPi _1 \left( x \right) \end{aligned}$$

(63)

$$\begin{aligned}&\varPsi _2 ^{\prime \prime }+\alpha {y}''\int _0^1 {{y}' \varPsi _2 ^{\prime }} \hbox {d}x=-\varPi _2 \left( x \right) \end{aligned}$$

(64)

with boundary conditions $\varPsi _k \left( 0 \right) =\varPsi _k \left( 1 \right) =0$. Here $\varPi _1 \left( x \right)$ and $\varPi _2 \left( x \right)$ are

$$\begin{aligned} \varPi _1 \left( x \right)= & {} \alpha /2\left\langle {{\phi }'_1,{\phi }'_1 \;} \right\rangle {y}''+\alpha \left\langle {{y}',{\phi }'_1 \;} \right\rangle {\phi }''_1 \end{aligned}$$

(65)

$$\begin{aligned} \varPi _2 \left( x \right)= & {} \alpha /2\left\langle {{\phi }'_1,{\phi }'_1 \;} \right\rangle {y}''+\alpha \left\langle {{y}',{\phi }'_1 \;} \right\rangle {\phi }''_1 \end{aligned}$$

(66)

$$\begin{aligned} \chi _n \left( x \right)= & {} \alpha \left[ \frac{3}{2}\phi _n ^{\prime \prime }\left\langle {\phi _n ^{\prime },\phi _n ^{\prime }} \right\rangle +\phi _n ^{\prime \prime }\left\langle {{y}',\varPsi _1 ^{\prime }} \right\rangle +{y}''\left\langle {\phi _n ^{\prime },\varPsi _1 ^{\prime }} \right\rangle \right. \nonumber \\&+\varPsi _1 ^{\prime \prime }\left\langle {{y}',\phi _n ^{\prime }} \right\rangle +2\phi _n ^{\prime \prime }\left\langle {{y}',\varPsi _2 ^{\prime }} \right\rangle +2{y}''\left\langle {\phi _n ^{\prime },\varPsi _2 ^{\prime }} \right\rangle \nonumber \\&\left. +2\varPsi _2 ^{\prime \prime }\left\langle {{y}',\phi _n ^{\prime }} \right\rangle \right] \end{aligned}$$

(67)