1 Introduction

The nonlinear energy sinks (NESs), which are usually light-weighted devices coupled to the primary vibrating systems through essentially nonlinear elements, have been studied extensively in recent years, as they have better performances for broadband vibration suppression than the tuned mass dampers (TMDs). In NESs, the vibration energy can transfer from the primary system to the nonlinear local attachment irreversible through targeted energy transfer (TET) mechanism [1]. In case of transient excitations, the systems will experience nonlinear normal modes; for forced systems, the responses will be periodic or quasi-periodic and the quasi-periodic response refers to strongly modulated response (SMR) [2].

Fig. 1
figure 1

Structure of the NES. a Nonlinear spring, b assemble of linear springs, c reaction forces comparison

Full size image

Based on the type of nonlinearities of the nonlinear elements, the NESs are largely divided into 4 types [3]: translational NESs with springs of polynomial stiffness (mainly cubic stiffness) [4], vibro-impact NESs [5], bi-stable NESs [6], rotating NESs [7].

The nonlinear elements between the NES masses and the primary systems are very important, as they are the tunnels through which the TET mechanism happens. The traditional nonlinear element is coil springs, but the coil spring will produce a large linear stiffness, and it is difficult to eliminate the linear part. Although some approaches such as adding negative linear stiffness to balance the linear part are effective [8], it will increase the size or complexity of the NES.

To overcome the shortcoming of coil springs, various nonlinear elements are proposed, the most common are the cubic stiffness nonlinear elements made up of two transverse springs [9,10,11,12,13] or strings [14,15,16], and the cubic restoring forces can be achieved by self-geometric nonlinearity when the springs stretch in tension. Besides, some NESs are formed by permanent magnets or electromagnet, as the magnetic forces are strongly nonlinearity [17,18,19,20,21].

Fig. 2
figure 2

Parameters of the leaf spring. a Combination of leaf spring, b dimensions of the leaf spring

Full size image
Fig. 3
figure 3

Structure of the NES. a 3D map of the NES, b sectioning map

Full size image
Fig. 4
figure 4

Dynamic model of the rotor–NES system. a Primary vibration system, b primary system with NES

Full size image

Besides the cubic nonlinearity, it has been proved that NESs with non-polynomial nonlinearity can also have good performance in vibration suppression [22] and many NESs with non-polynomial nonlinearity, especially piecewise linear nonlinearity, have been developed [23,24,25,26,27]. For practical investigations in industry, using piecewise linear energy sink is more realistic and more easy to be implemented [23].

Although many types of nonlinear elastic elements are proposed, new types of nonlinear elastic elements, especially those with simple and compact structures, are still needed in the designing of new type of NESs. Leaf springs are simple and compact structures and are often used to produce bending stiffnesses [28]. As there is no study of NES formed by leaf springs, a new NES with leaf springs is presented in this paper. The structures of the piecewise linear stiffness spring and the NES are proposed, the dynamics of the primary system with the nonlinear energy sink is studied, and the effectiveness of the NES is proved by experiment.

2 NES with piecewise linear stiffness

2.1 Spring with piecewise linear stiffness

The nonlinear stiffness of a spring can be fitted by combination of linear springs, in which each spring has different stiffnesses. For example, a spring with cubic nonlinear stiffness is shown in Fig. 1a, in which the relationship of the dimensionless force with the dimensionless displacement is

$$\begin{aligned} y=kx^{3}\hbox { }\left( {-3\le x\le 3} \right) \end{aligned}$$
(1)

The combination of springs is shown in Fig. 1b, and the relation between the dimensionless reaction force with the dimensionless displacement can be written as

$$\begin{aligned} y=\left\{ \begin{array}{l} {kx\,\left( {\left| x \right| \le 1} \right) } \\ {kx+6k\left( {\left| x \right| -1} \right) \hbox {sgn}\left( x \right) \,\left( {1\le \left| x \right| \le 2} \right) } \\ kx+6k\left( {\left| x \right| -1} \right) \hbox {sgn}\left( x \right) \\ \quad +\, 12k\left( {\left| x \right| -2} \right) \hbox {sgn}\left( x \right) \,\left( {2\le \left| x \right| \le 3} \right) \\ \end{array} \right. \end{aligned}$$
(2)

The comparison of reaction forces of the nonlinear spring and the spring with piecewise linear stiffness is shown in Fig. 1c, from which it can seen that the fitting effect is very good.

2.2 Structure of the NES with piecewise linear stiffness

So in this paper, the spring with piecewise linear stiffness is formed by combination of leaf springs, as shown in Fig. 2a. The bending stiffness \(k_{ni} \), which is the rigidity of the leaf spring \(lf_{i}\), can be calculated as

$$\begin{aligned} k_{ni} ={3EI_i }/{l_i^3 }={Eb_i h_i^3 }/{\left( {4l_i^3 } \right) } \end{aligned}$$
(3)

where E is the elasticity modulus of the material and \(I_{i}\) is the section moment. The other parameters are shown in Fig. 2a, b.

The structure of the NES with piecewise linear stiffness is formed by NES mass and the combination of leaf springs, as shown in Fig. 3a. The NES mass only connects with the leaf spring \(lf_{1}\) and has clearances with the other leaf springs, as shown in Fig. 3b. The leaf spring \(lf_{i}\) produces reaction force when the vibration amplitude of the NES mass exceeds clearance \(e_{i-1}\). So the whole reaction force of the leaf springs is

$$\begin{aligned} F_n \left( x \right) =\left\{ \begin{array}{l} {2k_{n1} x\,\left( {\left| x \right| \le e_1 } \right) } \\ {2k_{n1} x+2k_{n2} \left( {\left| x \right| -e_1 } \right) \hbox {sgn}\left( x \right) \,\left( {e_1 {\le } \left| x \right| {\le } e_2 } \right) } \\ 2k_{n1} x+2k_{n2} \left( {\left| x \right| -e_1 } \right) \hbox {sgn}\left( x \right) \\ \quad +\,2k_{n3} \left( {\left| x \right| -e_2 } \right) \hbox {sgn}\left( x \right) \,\left( {e_2 \le \left| x \right| \le e_3 } \right) \\ 2k_{n1} x+2k_{n2} \left( {\left| x \right| -e_1 } \right) \hbox {sgn}\left( x \right) \\ \quad +\,2k_{n3} \left( {\left| x \right| -e_2 } \right) \hbox {sgn}\left( x \right) \\ \quad +\,2k_{n4} \left( {\left| x \right| -e_3 } \right) \hbox {sgn}\left( x \right) \,\left( {\left| x \right| \ge e_3 } \right) \\ \end{array} \right. \end{aligned}$$
(4)

2.3 Dynamic model of the vibration system with the NES

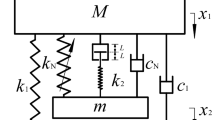
Assuming the NES is installed on a one-degree-of-freedom vibration system (shown in Fig. 4a), then the dynamic model of the primary vibration system with the NES is shown in Fig. 4b; the dynamic equations are

$$\begin{aligned}&m_1 \ddot{x}_1 +c_1 \dot{x}_1 +k_1 x_1 \nonumber \\&\quad +\, F_c \left( {\dot{x}_1 -\dot{x}_2 } \right) +F_n \left( {x_1 -x_2 } \right) =F\hbox {cos}\left( {\omega t} \right) \nonumber \\&m_2 \ddot{x}_2 -F_c \left( {\dot{x}_1 -\dot{x}_2 } \right) -F_n \left( {x_1 -x_2 } \right) =0 \end{aligned}$$
(5)

where ‘\(\cdot \)’ denotes d/dt. \(F_n \left( {x_1 -x_2 } \right) \) is the piecewise linear reaction force. \(F_c \left( {\dot{x}_1 -\dot{x}_2 } \right) \) is the damping force between primary system and the NES.

Table 1 Parameters of the leaf springs for numerical simulation
Full size table

The damping coefficient \(c_{1}\) can be calculated as

$$\begin{aligned} c_1 =2\xi _1 \sqrt{k_1 m_1 } \end{aligned}$$
(6)

where \(\xi _1 \) is the damping ratio of the primary system.

The damping force \(F_c \left( {\dot{x}_1 -\dot{x}_2 } \right) \) can be calculated as

$$\begin{aligned} F_c \left( {\dot{x}_1 -\dot{x}_2 } \right) \left\{ {{\begin{array}{l} {2\xi _2 \sqrt{2k_{n1} m_2 }\left( {\dot{x}_1 -\dot{x}_2 } \right) \,\left( {\left| x \right| \le e_1 } \right) } \\ {2\xi _2 \sqrt{2\left( {k_{n1} +k_{n2} } \right) m_2 }\left( {\dot{x}_1 -\dot{x}_2 } \right) \,\left( {e_1 \le \left| x \right| \le e_2 } \right) } \\ {2\xi _2 \sqrt{2\left( {k_{n1} +k_{n2} +k_{n3} } \right) m_2 }\left( {\dot{x}_1 -\dot{x}_2 } \right) \,\left( {e_2 \le \left| x \right| \le e_3 } \right) } \\ {2\xi _2 \sqrt{2\left( {k_{n1} +k_{n2} +k_{n3} +k_{n4} } \right) m_2 }\left( {\dot{x}_1 -\dot{x}_2 } \right) \,\left( {\left| x \right| \ge e_3 } \right) } \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(7)

where \(\xi _2 \) is the damping ratio of the NES system.

3 Numerical simulations and verifications

3.1 Parameters definition

Assuming \(m_1 =1\,\hbox {kg}\), \(m_2 =0.06\,\hbox {kg}\) and \(k_1 =1\times 10^{5}\,\hbox {N/m}\). The damping ratio of the primary system is \(\xi _1 =0.005\). The damping ratio of the NES system is \(\xi _2 =0.02\), as the leaf springs will contact with the NES mass and can produce contact damping in the contacting course.

The parameters of the leaf springs are shown in Table 1. Assuming the material is 60Si2Mn and the modulus of elasticity is \(2.06\times 10^{11}\,\hbox {Pa}\), then the stiffness of the leaf springs can be calculated using Eqs. (3) and (4).

Three types of clearances are used in the numerical simulation, the first type is \(e_1 =0.75\,\hbox {mm}\), \(e_2 =1.5\,\hbox {mm}\) and \(e_3 =2.25\,\hbox {mm}\); the second type is \(e_1 =0.5\,\hbox {mm}\), \(e_2 =1.0\,\hbox {mm}\) and \(e_3 =1.5\,\hbox { mm}\); third type is \(e_1 =0.25\,\hbox {mm}\), \(e_2 =0.5\,\hbox {mm}\) and \(e_3 =0.75\,\hbox {mm}\). With the different clearances, the nonlinearity of the leaf springs will change.

3.2 Responses analysis

3.2.1 Responses of the primary system without NES

Firstly, the responses of the system without NES are studied using Runge–Kutta method. Time step is 0.0001 s; relative error tolerance, absolute error tolerance and absolute error tolerance are all \(1\times 10^{-12}\). The acceleration vibration transmission of primary vibration system is obtained, so as to compare the results with the experimental results in the next section. The transfer function is

$$\begin{aligned} H( \omega )=\frac{\ddot{x}_1 ( \omega )}{F( \omega )} \end{aligned}$$
(8)

The acceleration vibration transmission of primary vibration system is shown in Fig. 5. It can be seen that the resonant frequency is about 50 Hz and the largest acceleration transmissibility is about \(100\,\hbox { ms}^{-2}/\hbox {N}\).

Fig. 5
figure 5

Acceleration vibration transmission of primary vibration system without NES

Full size image
Fig. 6
figure 6

Piecewise linear restoring force and polynomial fitting in the case of clearances type 1

Full size image

3.2.2 Responses of the primary–NES system with clearances type 1

Then, the responses of the system when the clearances of the leaf springs are \(e_1 =0.75\,\hbox {mm}\), \(e_2 =1.5\,\hbox {mm}\) and \(e_3 =2.25\,\hbox {mm}\) are analyzed. With these clearances, the relationship between the reaction force and the displacement is shown in Fig. 6.

The results of the responses when amplitudes of exciting force are 0.8, 1.0 and 2.0 N are shown in Fig. 7a, b, c, respectively.

Fig. 7
figure 7

Acceleration vibration transmission of primary–NES system with clearances type 1. a \(F=0.8\,\hbox { N}\), b \(F=1.0\,\hbox {N}\). c \(F=2.0\,\hbox {N}\)

Full size image
Fig. 8
figure 8

Acceleration vibration responses of the primary system in different exciting forces. a \(F=1.0\,\hbox { N}\), b \(F=2.0\,\hbox {N}\)

Full size image

It can be seen from Fig. 7 that the vibrations of the primary system decline as the NES is installed on the primary system. The largest transmissibility in the three cases is about 53, 44 and \(25\,\hbox { ms}^{-2}/\hbox {N}\), respectively. Compared with Fig. 5, it can be seen that the vibration suppression rates are 47, 56 and 75%, respectively. In these three cases, only in case three (\(F=2.0\,\hbox {N}\)) the SMR behavior occurs. This can be proved by the time responses of the primary system, which are shown in Fig. 8a, b with the exciting frequency of 50 Hz and exciting force amplitude of \(F=1.0\,\hbox {N}\) and \(F=2.0\,\hbox {N}\), respectively. It can be seen that when \(F=1.0\,\hbox {N}\), the response is periodic, while when \(F=2.0\,\hbox {N}\), the response is quasi-periodic, which is an obvious sign of SMR behavior.

3.2.3 Responses of the primary–NES system with clearances type 2

Then, the responses of the system when the clearances of the leaf springs are \(e_1 =0.5\,\hbox {mm}\), \(e_2 =1.0\,\hbox {mm}\) and \(e_3 =1.5\,\hbox {mm}\) are analyzed. With these clearances, the relationship between the reaction force and the displacement is shown in Fig. 9.

Fig. 9
figure 9

Piecewise linear restoring force and polynomial fitting in the case of clearances type 2

Full size image

In these three cases, the largest transmissibility in the three cases is about 37, 31 and \(19\,\hbox { ms}^{-2}/\hbox {N}\), respectively. The vibration suppression rates are 63, 69 and 81%, respectively. In these three cases, SMR behavior happens when \(F=1.0\,\hbox {N}\) and \(F=2.0\,\hbox {N}\), as can be seen from the steady-state time responses of the primary in Fig. 11.

The results of the responses when amplitude of exciting force is 0.8, 1.0 and 2.0 N are shown in Fig. 10a, b, c, respectively.

Fig. 10
figure 10

Acceleration vibration transmission of primary–NES system with clearances type 2. a \(F=0.8\,\hbox {N}\), b \(F=1.0\,\hbox {N}\), c \(F=2.0\,\hbox {N}\)

Full size image
Fig. 11
figure 11

Acceleration vibration responses of the primary system in different exciting forces. a \(F=0.8\,\hbox {N}\), b \(F=1.0\,\hbox {N}\), c \(F=2.0\,\hbox {N}\)

Full size image

3.2.4 Responses of the primary–NES system with clearances type 3

Finally, the responses of the system when the clearances of the leaf springs are \(e_1 =0.25\,\hbox {mm}\), \(e_2 =0.5\,\hbox {mm}\) and \(e_3 =0.75\,\hbox {mm}\) are analyzed. With these clearances, the relationship between the reaction force and the displacement is shown in Fig. 12.

Fig. 12
figure 12

Piecewise linear restoring force and polynomial fitting in the case of clearances type 3

Full size image
Fig. 13
figure 13

Acceleration vibration transmission of primary–NES system with clearances type 3. a \(F=0.8\,\hbox {N}\), b \(F=1.0\,\hbox {N}\), c \(F=2.0\,\hbox {N}\)

Full size image

The results of the responses when amplitude of exciting force is 0.8, 1.0 and 2.0 N are shown in Fig. 13a, b, c, respectively.

It can be seen from Fig. 13 that the vibrations suppression effects are very good when \(F=0.8\,\hbox {N}\) and \(F=1.0\,\hbox {N}\), but becomes bad when \(F=2.0\), which is because the exciting force is too large in this case.

Three conclusions can be obtained from the above analyses

  1. (a)

    The NES with piecewise linear stiffness can have good vibration suppression effect. In the case of middle clearances, the best vibration effect is 81%.

  2. (b)

    The vibration suppression becomes better when the clearances become smaller and the exciting force becomes larger.

  3. (c)

    The NES will lost its efficacy when the exciting force is too large, as can be seen from the case of \(F=2.0\) N with small clearances.

3.2.5 Comparison of the present stiffness with cubic stiffness

A comparison between the present stiffness with cubic stiffness is made, assuming the dimensions of the leaf springs are same to Table 1.

Fig. 14
figure 14

Comparison of the piecewise linear force and the polynomial force

Full size image

The clearances used in numerical simulation is type 2, which is \(e_1 =0.5\,\hbox {mm}\), \(e_2 =1.0\,\hbox {mm}\) and \(e_3 =1.5\,\hbox {mm}\). The relationship between the reaction force and the displacement is shown in Fig. 14. Polynomial fitting of the reaction force and the relationship between the reaction force and the displacement can be written as

$$\begin{aligned} F=p_1 x^{3}+p_2 x^{2}+p_3 x+p_4 \end{aligned}$$

where \(p_1 =2.35\times 10^{9}\), \(p_2 =-8.38\times 10^{2}\), \(p_3 =1.69\times 10^{3}\) and \(p_4 =1.68\times 10^{-4}\).

The comparison of the two kinds of reaction forces is shown in Fig. 14.

The results of the responses under the two kinds of nonlinear stiffness when amplitude of exciting force is 0.8, 1.0 and 2.0 N are shown in Fig. 15a, b, c, respectively. It can be seen that the two results are very alike, which proves the effectiveness of the present spring.

4 Experimental results

4.1 Parameters definition

Experiments are carried out on a test rig, the photograph of which is shown in Fig. 16. The primary system is a beam with a lamped mass, and the NES is mounted on the beam. The system is excited by an electromagnetic vibration exciter, and the vibration signals are collected by acceleration transducers. The beam is made up of stainless steel with elastic modulus of \(2.1\times 10^{11 }\,\hbox {Pa}\). The dimension of the beam is \(35\,\hbox {mm}\times 5\,\hbox {mm}\times 125\,\hbox {mm}\). The first step modal mass is 1.1 kg, so the first natural frequency of the primary system is about 50 Hz. The mass of the NES is about 0.06 kg. The dimensions of the spring with piecewise linear stiffness (Fig. 16b) are the same as in Table 1.

Fig. 15
figure 15

Comparison of the response under piecewise linear stiffness and the polynomial stiffness. a \(F=0.8\,\hbox {N}\), b \(F=1.0\,\hbox {N}\), c \(F=2.0\,\hbox {N}\)

Full size image
Fig. 16
figure 16

Picture of the test rig and the spring. a Photograph of test rig, b photograph of the spring with piecewise linear stiffness

Full size image
Fig. 17
figure 17

Test results: acceleration vibration transmission and time response of primary system. a Acceleration vibration transmission, b time response

Full size image
Fig. 18
figure 18

Test results: acceleration vibration transmission of primary system when NES with clearances type 2 is installed. a \(F=0.8\,\hbox {N}\), b \(F=1.0\,\hbox {N}\), c \(F=2.0\,\hbox {N}\)

Full size image
Fig. 19
figure 19

Test results: acceleration vibration transmission of the NES with clearances type 2. a \(F=0.8\,\hbox {N}\), b \(F=1.0\,\hbox {N}\), c \(F=2.0\,\hbox { N}\)

Full size image
Fig. 20
figure 20

Time response of the primary with NES in case of clearances type 3. a Primary system, b NES

Full size image

4.2 Experimental results

4.2.1 Responses of the system without NES

Firstly, the experiment of frequency sweeping is carried out and the acceleration vibration transmission of the primary vibration system without NES is obtained and shown in Fig. 17a. It can be seen that the natural frequency of the primary rotor system is about 49 Hz. The time response of the primary system in the peak resonance is shown in Fig. 17b; it can be seen that the maximum of the acceleration is about \(54\,\hbox { m}/\hbox {s}^{2}\).

4.2.2 Responses of the system with NES of clearances type 2

Then, the acceleration vibration transmission curves of the primary system with NES are obtained. The clearances of the leaf springs are 0.5, 1.0 and 1.5 mm. Figure 18a, b, c shows the acceleration vibration transmission curves of primary system with different exciting forces. It can be seen from Fig. 18 that SMR behavior occurs in the 2 latter cases. The best vibration suppression effect is 83%.

Figure 19a, b, c shows the acceleration vibration transmission curves of NES with different exciting forces. It can be seen from Fig. 19 that the vibrations of NES increase with the increase in exciting force magnitudes.

Figure 20a, b shows the time responses of primary system and NES in the case of middle force and 50 Hz. It can be seen from Fig. 20 that the responses of the system are in quasi-periodic state.

4.2.3 Responses of the system with NES of clearances type 3

The amplitude–frequency response curves of the primary system with NES are obtained when the clearances of the leaf springs are 0.25, 0.5 and 0.75 mm. Figure 21 is the acceleration vibration transmission curves of primary system with large exciting force. The responses of the primary are very large in the frequency range of 43–46 Hz. This is because the clearances are too small, so the nonlinearity is too large.

Fig. 21
figure 21

Amplitude–frequency response of the primary with NES in case of clearances type 3. a Primary system, b NES system

Full size image

5 Discussions

5.1 The verification of the effectiveness of the piecewise linear spring

The effectiveness of the piecewise linear spring is verified by the numerical and experimental results. It can be seen that the nonlinearity of the spring can be adjusted by changing the clearances. And also, the nonlinearity can be changed by adjusting the lengths of the leaf springs. Another advantage is the compact structure: Compared with the NESs made up of two transverse springs or strings, this structure is simple and compact.

5.2 Experimental results that verify the numerical results

Although there is some difference between the numerical results and experimental results, the main characters and fundamental principles of the numerical results are verified by experimental results. It can be seen from the experimental results in the case that the NES with middle clearances, the NES has good vibration suppression effects. And also, the vibration suppression becomes better when the clearances become smaller and the exciting force becomes larger. The NES lost its efficacy when the exciting force is too large in the case of NES with small clearances.

The difference between the experiment and numerical simulation maybe comes from the simple modeling of the main structure and the NES. They are beam structures in reality, but are modeled as single degree of freedoms so as to simplify the numerical simulation. Another main reason is the damping assignment, as the damping can affect the numerical results seriously.

5.3 The verification of the vibration suppression effect

It can be seen from the numerical and experimental results that the NES has good vibration suppression effect. The best vibration suppression effect is 81% in numerical simulation and 83% in experiment. In all the cases, the suppression effects are obvious, no matter SMR behavior happens or not. The vibration descends even when the nonlinearity is large, and the clearances are very small.

5.4 The comparison of the present spring with other springs.

The traditional nonlinear element is coil spring, but the coil spring will produce a large linear stiffness; also it is the transverse linear spring. To eliminate the linear part of the coil spring or the transverse linear spring, additional mechanical parts must be added, which will increase the size and weight of the NES.

On the contrary, the present nonlinear spring can work without additional parts and the nonlinearity can be changed by simply changing the length of the leaf spring, so the present spring is compact and simple.

6 Conclusions

A piecewise linear stiffness spring is proposed and the principles and fundamental characteristics of the NES formed by the proposed spring are studied numerically and experimentally, and some conclusions are as follows:

  1. (1)

    The proposed piecewise linear spring is effective, and its structure is simple and compact. The nonlinearity of the spring can be adjusted by changing the clearances or the length of the leaf springs.

  2. (2)

    The vibration suppression of the NES is proved by both the numerical simulation and the experimental results.

  3. (3)

    The vibration suppression is effective only in moderate exciting force, and the SMR behavior will not happen under too large or too small exciting.