1 Introduction

One of the common features of nonlinear systems is multistability [1]; that is, two or more attractors can coexist at a fixed parameter combination. Multistability appears in almost any field of science; for instance in biological systems [2, 3], hydrodynamics [4], mechanical engineering [5], chemical reactions [6, 7], neuron dynamics [8], climate dynamics [9] or social systems [10] to name a few. Multistability is also found in bubble dynamics and acoustic cavitation [11], the topic of the present study. In applications, a major challenge in nonlinear dynamics is how to control multistability and switch between coexisting states representing different system behaviour.

The mechanism of the emergence of multiple attractors can be rather different. In conservative systems, for example, one can obtain an arbitrarily large number of coexisting attractors by introducing small dissipation [12] (see also the Kolmogorov–Arnold–Moser (KAM) theory [13]). The number of attractors is roughly inversely proportional to the damping factor [14]. The appearance of homoclinic tangencies or the coupling of systems with a large number of unstable invariant manifolds can also lead to a high level of multistability. In these cases, even an infinite number of attracting periodic orbits called Gavrilov–Shilnikov–Newhouse sinks can coexist [15, 16]. Another important mechanism leading to multistability is the coupling of a large number of identical systems, where the number of the attractors scales with the number of oscillators [17]. This results in a so-called attractor crowding that makes the system extremely sensitive to external noise leading to random hopping between many coexisting states. Several other mechanisms such as delayed feedback [18], parametric forcing [19] or external noise [20] can also induce multistability.

The importance of the control of multistability can be explained with the fact that different stable states represent different system performances. A good example is the large subject of chaos control [21,22,23,24,25], where the main aim is to eliminate unpredictable behaviour. Furthermore, there are various fields where the control of multistability is of paramount importance: laser technology [26], optical communication [27], cardiology [28], genetics [29] or ecology [30]. If multistability is undesired, then basically two approaches are possible: make the system monostable or preselect and stabilize an attractor against external noise. In case of a desirable multistability, where the control between different states (operations) on demand is important, the task is to properly select an attractor the system should approach and/or exclude certain undesired attractors from the dynamics. In these cases, the stabilization against external noise can also be crucial.

There are three main control strategies known in the literature, namely non-feedback, feedback and stochastic control [1]. Each has its own advantages and disadvantages. The non-feedback techniques are simple and easy to use, where the main aim is to kick the system to another stable state [31] or annihilate attractors by periodic perturbation (modulation) of a parameter or a state variable [32]. Unfortunately, it cannot be guaranteed that the system settles down onto the desired attractor. The kick introduces randomness to the control, and extremely long transients are also possible in the presence of transient chaos. In case of periodic modulation, there is no direct control over which attractors are annihilated, since usually the attractor with the smallest basin is destructed first. With increasing perturbation magnitude, the annihilation process continues with attractors having successively the next smaller basin. Applying a feedback control strategy, the desired attractor can be targeted directly; moreover, it is a reliable technique to control attractors against external noise. However, details are necessary about the state space [33] or even the solution of the attractor itself [34] or its Jacobian. This makes the feedback control technique unusable in certain problems. For instance, in an acoustically trapped bubble, it is hard to obtain state space information about the oscillating bubble and feed this information back to the resonator. The third kind of control (stochastic) also performs attractor annihilation, this time with the addition of external noise [35]. The drawback is similar as in case of the non-feedback technique: the attractors are destructed in the order of the size of their basin of attraction [1]. That is, the direct control is again lost. Attractors with very small basins are usually buried by the noise immediately, without the need of increasing the magnitude of the noise to some higher level.

The main aim of the present study is to propose a possible non-feedback control technique capable of driving a sinusoidally excited system to a pre-selected periodic attractor directly. It is based on the observation that a period-2 and a period-3 attractor can be continuously transformed into each other by adding a second, sinusoidal component to the excitation. The proper tuning of the excitation amplitudes is necessary; moreover, the fixed commensurate frequency combination must be adjusted according to the periods of the attractors being transformed. The advantages and disadvantages over other, already existing control techniques, the limitations and possible extensions to transformation of a period-n to a period-m attractor in general, and the application to other nonlinear oscillators are also discussed.

The test model is the Keller–Miksis equation well known in the bubble dynamics community. It is a second-order nonlinear ordinary differential equation describing the oscillation of a bubble in a liquid [11]. The parameter space of the present study is relatively large due to the dual-frequency driving (amplitudes and frequencies). The approach to obtain a global picture about the bifurcation structure in the four-dimensional driving parameter space within reasonable time is to exploit the high arithmetic processing power of professional graphics cards (GPUs) using an in-house initial-value problem (IVP) solver written in C++/CUDA C. The parameter scans are supplemented with results obtained by the boundary-value problem solver AUTO [36], which is suitable to compute periodic orbits directly regardless of their stability, and follow their paths with the pseudo-arclength continuation technique.

2 Mathematical model

The test model studied (Keller–Miksis equation [11]) describing the evolution of the bubble radius reads

$$\begin{aligned}&\left( 1-\frac{\dot{R}}{c_\mathrm{L}} \right) R\ddot{R} + \left( 1-\frac{\dot{R}}{3c_\mathrm{L}} \right) \frac{3}{2} \dot{R}^2 \nonumber \\&\quad = \left( 1+\frac{\dot{R}}{c_\mathrm{L}} + \frac{R}{c_\mathrm{L}}\frac{\mathrm{d}}{\mathrm{d}t} \right) \frac{\left( p_\mathrm{L} - p_{\infty }(t) \right) }{\rho _\mathrm{L}}, \end{aligned}$$
(1)

where R(t) is the time dependent bubble radius; \(c_\mathrm{L}=1497.3\,\mathrm {m/s}\) and \(\rho _\mathrm{L}=997.1\,\mathrm {kg/m^3}\) are the sound speed and density of the liquid domain, respectively. According to the general, dual-frequency treatment, the pressure far away from the bubble

$$\begin{aligned} p_{\infty }(t) = P_{\infty } + P_{A1} \sin (\omega _1 t) + P_{A2} \sin (\omega _2 t + \theta ) \end{aligned}$$
(2)

consists of a static component, \(P_{\infty }\), and periodic components with pressure amplitudes \(P_{A1}\) and \(P_{A2}\), angular frequencies \(\omega _1\) and \(\omega _2\), and with a phase shift \(\theta \). The connection between the pressures inside and outside the bubble at its interface can be written as

$$\begin{aligned} p_\mathrm{G} + p_\mathrm{V} = p_\mathrm{L} + \frac{2 \sigma }{R} + 4 \mu _\mathrm{L} \frac{\dot{R}}{R}, \end{aligned}$$
(3)

where the total pressure inside the bubble is the sum of the partial pressures of the non-condensable gas, \(p_\mathrm{G}\), and the vapour, \(p_\mathrm{V}=3166.8\,\mathrm {Pa}\). \(p_{\mathrm{L}}\) denotes the pressure in the liquid at the bubble-liquid interface. The surface tension is \(\sigma =0.072\,\mathrm {N/m}\), and the liquid kinematic viscosity is \(\mu _\mathrm{L}=8.902^{-4}\,\mathrm {Pa\,s}\). The gas inside the bubble obeys a simple polytropic relationship

$$\begin{aligned} p_\mathrm{G} = \left( P_{\infty } - p_\mathrm{V} + \frac{2 \sigma }{R_\mathrm{E}} \right) \left( \frac{R_\mathrm{E}}{R}\right) ^{3 \gamma }, \end{aligned}$$
(4)

where the polytropic exponent is \(\gamma =1.4\) (adiabatic behaviour), the equilibrium bubble radius is \(R_\mathrm{E}=10\,\mu \mathrm {m}\) and the static pressure is \(P_{\infty }=1\,\mathrm {bar}\).

For numerical purposes, system (1)–(4) is rewritten into a dimensionless form by introducing the dimensionless variables

$$\begin{aligned}&\tau = \frac{\omega _1}{2 \pi } t, \end{aligned}$$
(5)
$$\begin{aligned}&y_1 = \frac{R}{R_\mathrm{E}}, \end{aligned}$$
(6)
$$\begin{aligned}&y_2 = \dot{R} \frac{2\pi }{R_\mathrm{E} \omega _1}, \end{aligned}$$
(7)

and the equations are rearranged to minimize the number of coefficients. The final form of the numerical model is

$$\begin{aligned} \dot{y}_1&= y_2, \end{aligned}$$
(8)
$$\begin{aligned} \dot{y}_2&= \frac{N_\mathrm{KM}}{D_\mathrm{KM}}, \end{aligned}$$
(9)

where the numerator, \(N_\mathrm{KM}\), and the denominator, \(D_\mathrm{KM}\), are

$$\begin{aligned} N_\mathrm{KM}= & {} \left( C_0 + C_1 y_2 \right) \left( \frac{1}{y_1} \right) ^{C_{10}} - C_2 \left( 1 + C_9 y_2 \right) \nonumber \\&- C_3 \frac{1}{y_1} - C_4 \frac{y_2}{y_1} - \left( 1 - C_9 \frac{y_2}{3} \right) \frac{3}{2} y_2^2 \nonumber \\&-\,\left( C_5 \sin (2 \pi \tau ) + C_6 \sin (2 \pi C_{11} \tau + C_{12}) \right) \nonumber \\&\left( 1 + C_9 y_2 \right) -y_1 \left( C_7 \cos (2 \pi \tau ) \right. \nonumber \\&\left. +\, C_8 \cos (2 \pi C_{11} \tau + C_{12}) \right) , \end{aligned}$$
(10)

and

$$\begin{aligned} D_\mathrm{KM} = y_1 - C_9 y_1 y_2 + C_4 C_9. \end{aligned}$$
(11)

The coefficients are summarized as follows:

$$\begin{aligned} C_0&= \frac{1}{\rho _\mathrm{L}} \left( P_{\infty } - p_\mathrm{V} + \frac{2 \sigma }{R_\mathrm{E}} \right) \left( \frac{2 \pi }{R_\mathrm{E} \omega _1} \right) ^2, \end{aligned}$$
(12)
$$\begin{aligned} C_1&= \frac{1-3\gamma }{\rho _\mathrm{L} c_\mathrm{L}} \left( P_{\infty } - p_\mathrm{V} + \frac{2 \sigma }{R_\mathrm{E}} \right) \frac{2 \pi }{R_\mathrm{E} \omega _1},\end{aligned}$$
(13)
$$\begin{aligned} C_2&= \frac{P_{\infty } - p_\mathrm{V}}{\rho _\mathrm{L}} \left( \frac{2 \pi }{R_\mathrm{E} \omega _1} \right) ^2,\end{aligned}$$
(14)
$$\begin{aligned} C_3&= \frac{2 \sigma }{\rho _\mathrm{L} R_\mathrm{E}} \left( \frac{2 \pi }{R_\mathrm{E} \omega _1} \right) ^2,\end{aligned}$$
(15)
$$\begin{aligned} C_4&= \frac{4 \mu _\mathrm{L}}{\rho _\mathrm{L} R_\mathrm{E}^2} \frac{2 \pi }{\omega _1},\end{aligned}$$
(16)
$$\begin{aligned} C_5&= \frac{P_{A1}}{\rho _\mathrm{L}} \left( \frac{2 \pi }{R_\mathrm{E} \omega _1} \right) ^2,\end{aligned}$$
(17)
$$\begin{aligned} C_6&= \frac{P_{A2}}{\rho _\mathrm{L}} \left( \frac{2 \pi }{R_\mathrm{E} \omega _1} \right) ^2,\end{aligned}$$
(18)
$$\begin{aligned} C_7&= R_\mathrm{E} \frac{\omega _1 P_{A1}}{\rho _\mathrm{L} c_\mathrm{L}} \left( \frac{2 \pi }{R_\mathrm{E} \omega _1} \right) ^2,\end{aligned}$$
(19)
$$\begin{aligned} C_8&= R_\mathrm{E} \frac{\omega _1 P_{A2}}{\rho _\mathrm{L} c_\mathrm{L}} \left( \frac{2 \pi }{R_\mathrm{E} \omega _1} \right) ^2,\end{aligned}$$
(20)
$$\begin{aligned} C_9&= \frac{R_\mathrm{E} \omega _1}{2 \pi c_\mathrm{L}},\end{aligned}$$
(21)
$$\begin{aligned} C_{10}&= 3\gamma ,\end{aligned}$$
(22)
$$\begin{aligned} C_{11}&= \frac{\omega _2}{\omega _1},\end{aligned}$$
(23)
$$\begin{aligned} C_{12}&= \theta . \end{aligned}$$
(24)

The angular frequencies \(\omega _1\) and \(\omega _2\) are normalized by the linear, undamped angular eigenfrequency [37]

$$\begin{aligned} \omega _0 = \sqrt{ \frac{3\gamma (P_{\infty }-p_\mathrm{V})}{\rho _\mathrm{L} R_\mathrm{E}^2} - \frac{2(3\gamma -1)\sigma }{\rho _\mathrm{L} R_\mathrm{E}^3} } \end{aligned}$$
(25)

of the unexcited system that defines the relative frequencies as

$$\begin{aligned} \omega _{R1}&= \frac{\omega _1}{\omega _0},\end{aligned}$$
(26)
$$\begin{aligned} \omega _{R2}&= \frac{\omega _2}{\omega _0}. \end{aligned}$$
(27)

With \(R_\mathrm{E}=10\,\upmu \mathrm {m}\) and with the other constants in (25) given before in this section, the eigenfrequency is \(f_0 =\omega _0 / 2 \pi = 340 \text { kHz}\).

3 Numerical implementation and parameter choice

The simplest technique to solve the system (8)–(9) is to take an initial-value problem solver, integrate the equations forward in time and, after the convergence of the transient trajectory, record and save the important properties of the solutions found. Thereby, our main interest is in periodic solutions and their organization in the reduced driving parameter space discussed below. The first part (\(2048\,T\)) of the integration is regarded as initial transient and dropped followed by integration of the system further by \(8192\,T\) for the proper convergence of average quantities like Lyapunov exponent or winding number, where T is the period of the dual-frequency excitation function. The scheme employed is the explicit and adaptive Runge–Kutta–Cash–Karp method with embedded error estimation of orders 4 and 5 (the algorithm is adapted from [38]). The quantities stored are the points of the (global) Poincaré section (see the choice in Sect. 4 below), which are standard ingredients for bifurcation diagrams; furthermore, the maximum bubble radius and the maximum absolute value of the bubble wall velocity, which are important for applications; finally, the period, the Lyapunov exponent and the winding number of the attractors found, quantities that are essential for a detailed analysis of bifurcation structures.

A strategy to represent the results of parametric studies involving high-dimensional parameter spaces consists in creating high-resolution bi-parametric plots, a rapidly spreading technique in the investigation of nonlinear systems with a high-dimensional parameter space [39,40,41,42,43,44,45,46,47,48,49]. The system studied here, a bubble in water with dual-frequency acoustic excitation, has a four-dimensional driving parameter space (\(P_{A1}, P_{A2}, \omega _{R1}, \omega _{R2}\)). For simplicity, the phase shift is set to \(\theta =0\). It is restricted in the present study by the requirement that the relative-frequency pairs obtained from \(\omega _{R1}\) and \(\omega _{R2}\) are rational. The pressure amplitudes \(P_{A1}\) and \(P_{A2}\) are taken as the main control parameters at fixed relative-frequency pairs. The range of each pressure amplitude is 0–5 \(\mathrm {bar}\), investigated at first with a resolution of 501 steps for an overview. The relative-frequency values \(\omega _{R1}\) and \(\omega _{R2}\) are chosen from the following set:

$$\begin{aligned} \frac{1}{10}, \frac{1}{5}, \frac{1}{3}, \frac{1}{2}, \frac{1}{1}, \frac{2}{1}, \frac{3}{1}, \frac{5}{1}, \frac{10}{1}. \end{aligned}$$
(28)

Exploiting symmetries in the driving parameter space, this gives \(\sum _{i=1}^8 i = 36\) combinations of two frequencies. Observe that two orders of magnitude difference in the frequency range are covered and that, for instance, \(\omega _{R1} = 1/5\) and \(\omega _{R2} = 1/1\) means that in an experiment, the bubble is driven by \(0.2\,\omega _0\) and by the resonance frequency \(\omega _0\). Computations are performed at every possible frequency combination of the above set, which means altogether 36 two-dimensional plots for every quantity to be studied (period, Lyapunov exponent, etc). Moreover, owing to the fine details in the diagrams, high-resolution surveys are necessary. In order to reveal possible coexisting attractors, 10 randomized initial conditions are used at each parameter set. Indeed, the 10 different trajectories can converge to different attractors with distinct properties (e.g. period). Altogether, a single plot contains \(501\times 501\times 10\approx 2.5\,\mathrm {million}\) initial-value problems.

Even a single bi-parametric plot requires large computational capacities; thus, the high processing power of professional videocards (GPGPUs) is exploited. During the parameter studies, millions of simple (only second order) and independent ordinary differential equations are to be solved. Moreover, the algorithm employed needs only function evaluations. Therefore, our problem is well suited for parallelization on GPUs. The program code is written in a C++ and CUDA C software environment. The available GPUs are a Titan Black card (Kepler architecture, 1707 GFLOPS double-precision processing power), two Tesla K20 cards (Kepler architecture, 1175 GFLOPS) and eight Tesla M2050 cards (Fermi architecture, 515 GFLOPS). The application of double-precision floating-point arithmetic is mandatory in bubble dynamics due to the possibly large-amplitude, collapse-like response of the system [11]. The final, optimized code is approximately about 50 times faster on the Titan Black, about 30 times faster on the Tesla M2050 and about 120 times faster on the Tesla K20 than on a four-core Intel Core i7-4790 CPU. Surprisingly, the professional Tesla K20 card was more than two times faster than the gamer Titan Black card even though the theoretical peak processing power is higher for the Titan Black GPU. A thorough performance analysis between GPUs and CPUs solving large numbers of ordinary differential equations is beyond the scope of the present study. The interested reader is referred to the publications [38, 50,51,52] for more details.

4 Global Poincaré section and the period-reducing phenomenon

The parameters investigated in the present study are the pressure amplitudes (\(P_{A1}, P_{A2}\)) and the relative frequencies (\(\omega _{R1}, \omega _{R2}\)) of the dual-frequency excitation with phase shift \(\theta =0\), i.e. \(C_{12}=0\). The main control parameters are the pressure amplitudes at several fixed frequency combinations. The ratio of each frequency pair is rational; therefore, periodicity of the dual-frequency driving is guaranteed (quasiperiodic forcing is excluded).

As an example, a dual-frequency excitation is presented in Fig. 1 as a function of time together with its two periodic components at \(\omega _{R1}=3\) and \(\omega _{R2}=2\). For definiteness, the pressure amplitudes are set to \(P_{A1}=P_{A2}=1\,\mathrm {bar}\). The black and blue curves are the high- and low-frequency components, respectively. Since the dimensionless time \(\tau \) is defined by means of the first frequency component, see Eq. (5), the normalized period corresponding to the relative frequency \(\omega _{R1}\) is \(T_1=1\), indicated by the vertical black line in Fig. 1. The normalized period of the second component (relative frequency \(\omega _{R2}\)) can be calculated with the frequency ratio; that is, \(T_2 = 1/C_{11} = \omega _{R1} / \omega _{R2} = 3/2 = 1.5\) (blue vertical line). Compare these periods with the arguments of the harmonic functions in equation (10) and keep in mind that the phase shift is zero (\(\theta = C_{12} = 0\)). As only normalized periods will be used throughout the article, this very often occurring quantity will be simply called “period”.

Fig. 1
figure 1

Example for graphs of a dual-frequency excitation (red) and its two harmonic components as mainly used in the study (\(\omega _{R1}=3\), black; \(\omega _{R2}=2\), blue) with pressure amplitudes \(P_{A1}=P_{A2}=1\,\mathrm {bar}\). The vertical lines marked by \(T_1\) (black solid), \(T_2\) (blue solid) and T (red dashed) designate the periods of the high-frequency component, the low-frequency component and the dual-frequency driving, respectively. \(T = 3 \times T_1 = 2 \times T_2 = 3\). (Color figure online)

Full size image

The sum of the two harmonic components results in a still periodic, but non-harmonic forcing function presented by the red curve in Fig. 1. The period of this function is \(T=3T_1=2T_2=3\), which is used as a global Poincaré section for the system (8)–(9). Consequently, during the numerical integration of the system with an initial-value problem solver, the continuous trajectories are sampled at time instants \(\tau _n=n \cdot T\) (\(n=0,1,2,\ldots \)). Accordingly, the period, \(T_N\), of a periodic orbit is defined as \(T_N=N \cdot T, N \in \mathrm{I} \! \mathrm{N}\), and the solution is called period-N orbit. Observe, however, that in the special cases of \(P_{A1}=0\,\mathrm {bar}\) or \(P_{A2}=0\,\mathrm {bar}\), the period T, which defines the global Poincaré section, does not coincide with the period of the actual driving \(T_2\) or \(T_1\). For \(P_{A1}=0\,\mathrm {bar}\), the dual-frequency forcing becomes a purely harmonic function shown by the blue curve in Fig. 1, and the continuous trajectories are sampled only after every second period of excitation, \(2T_2\). Therefore, an originally period-2k solution is observed only as a period-k orbit. Similarly, when \(P_{A2}=0\,\mathrm {bar}\), the trajectories are sampled only after every third period of the excitation, \(3T_1\) (compare the black and red vertical lines in Fig. 1), and the period of an originally period-3k orbit is reduced from 3k to k. This period-reducing phenomenon, occurring when one of the two components of the forcing function is vanishing and only a purely harmonic excitation is left, plays an important role in the bifurcation structure of the system, discussed in more detail in Sect. 5; furthermore, period reduction necessarily takes place for other frequency pairs as long as the ratio of a pair is rational.

5 Results from a global scan

Throughout the following subsections, the fundamental mechanism capable of controlling multistability in harmonically driven nonlinear oscillators is presented. The basis is the period-reducing phenomenon discussed above, by which the dual-frequency treatment can generate “bridges” between different periodic attractors. First, a global picture is shown via a series of high-resolution bi-parametric plots of Lyapunov-exponent and periodicity diagrams at different frequency combinations (the control parameters are the excitation amplitudes). Next, the details are demonstrated through a specific example with frequencies \(\omega _{R1}=3\) and \(\omega _{R2}=2\) (see again Fig. 1 for the driving signals). It must be emphasized that the amplitudes for both frequencies of the driving can be arbitrary; that is, there is no restriction to small-amplitude perturbations corresponding to the second sinusoidal component.

Fig. 2
figure 2

List of high-resolution bi-parametric plots as a function of the pressure amplitudes at different relative-frequency pairs organized in rows. Left column: Lyapunov-exponent diagrams separating the chaotic and periodic solutions. Right column: Periodicity diagrams, where periodic solutions are plotted with different colours up to period-6. Period-7 or higher solutions (including chaos) can be found in the black regions. The pressure amplitudes \(P_{A1}\) and \(P_{A2}\) are given in bar

Full size image

5.1 The branching phenomenon

Out of the data sets for the 36 relative-frequency combinations, four diagram pairs are shown in Fig. 2 at the four different relative-frequency pairs \((\omega _{R1},\omega _{R2}) = (0.2,0.1), (1,0.1), (3,1)\) and (3, 2) organized in rows and for two different quantities (Lyapunov exponent and period) organized in columns. The left column contains the Lyapunov-exponent diagrams, where the colour-coded area means chaotic solutions (positive exponent) and where in the greyscale domains there are periodic attractors (negative exponent). In the right column, the periods of the (converged) solutions are presented up to period-6. Periodic solutions higher than six including chaos can be found in the black domains. In the upper two rows, the plots correspond to relative frequencies lower than or equal to the linear resonance frequency (\(\omega _{R1,2}\le 1\)), while the lower two rows have relative frequencies higher than or equal to the linear resonance frequency (\(\omega _{R1,2}\ge 1\)).

Since detailed investigations of dual-frequency driven systems for arbitrary driving amplitudes with rational frequency ratio are absent in the literature, only very few information exists about the bifurcation structure shown in Fig. 2. It can be clearly seen that the dual-frequency driving causes a very complex interplay between the resonances originating from the single-frequency driven system (horizontal and vertical axes in Fig. 2), see especially the first two rows of the figure. Their comprehensive topological analysis is beyond the scope of the present study; instead, it intends to add some pieces to our knowledge by looking for special features in the diagrams. In particular, we focus on a very specific phenomenon, the branching mechanism, turning out to be a special feature of dual-frequency driven nonlinear oscillators with rational frequency combinations, which can be used for the control of multistability.

Fig. 3
figure 3

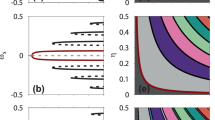
Bi-parametric periodicity diagram at the relative-frequency pair \(\omega _{R1}=3, \omega _{R2}=2\) with increased resolution (\(4001\times 2501\)) of the control parameters \(P_{A1}\) and \(P_{A2}\). The number of the initial conditions is \(5\times 5 =25\) defined on an equidistant grid in the \(y_1\)–\(y_2\) phase plane. The colour code is the same as in the right column of Fig. 2. The pressure amplitudes \(P_{A1}\) and \(P_{A2}\) are given in bar. (Color figure online)

Full size image

Observe that on the horizontal axis in the third row and second column of Fig. 2, three period-3 branches emerge from the segment marked by P3B3 (period: 3, number of the branches: 3). Similarly, three branches appear from the segments P4B3 and P3B3 on the horizontal axis, and two branches are merged together at segments P2B2 and P3B2 on the vertical axis in the last row and second column of Fig. 2, better to be seen in the enlargement and extension in Fig. 3. Observe also that the number of the branches is exactly the same as the value of the corresponding relative frequency along the respective axis. This phenomenon will be referred to as branching mechanism throughout the paper and will be investigated in more detail for the case \(\omega _{R1}=3, \omega _{R2}=2\).

In order to get a deeper insight into the branching mechanism at the relative-frequency pair \(\omega _{R1}=3, \omega _{R2}=2\), computations were repeated with much higher resolution of the pressure amplitudes (Fig. 3). The ranges of the control parameters are \(P_{A1}\in [0, 8]\,\mathrm {(bar)}\) and \(P_{A2}\in [0, 5]\,\mathrm {(bar)}\) with resolutions 4001 and 2501, respectively. The number of initial conditions at a control parameter pair \((P_{A1},P_{A2})\) is increased from 10 to \(5\times 5 = 25\) defined on an equidistant grid on the \(y_1\)–\(y_2\) phase plane. Thus, \(2501\times 4001\times 25\approx 250\,\mathrm {million}\) initial-value problems have to be solved. This huge amount of computations is divided into \(5\times 8=40\) (\(\varDelta P_{A1,2}=1\,\mathrm {bar}\)) segments and distributed to different GPUs.

At first sight, Fig. 3 contains only slightly more information about the branching mechanism than the bottom right diagram in Fig. 2, since it is hard to represent the many coexisting attractors in a single plot obtained by the increased number of initial conditions (in case of coexistence, the solution with the highest period is plotted). Investigating the system period-by-period, however, this high-resolution bi-parametric scan becomes very helpful to understand the branching mechanism (explored rigorously in the next sections); in particular, to identify the connected branches with different periods confidently, such as the ones originating from P4B3, P3B3, P2B3, P3B2 or P2B2, where, for instance, P2B3 and P2B2 are connected.

Typical colour combinations can be seen at the border of the branch families. The three green P2 bands are bordered each by a yellow (period-4) band at the right border (a period-doubled zone) followed by a thin black line (indicating period-8 and higher periods including chaos that are encoded that way). Similarly, the three dark blue P3 bands are bordered each by a light blue (period-6) band, again indicating the start of a period-doubling sequence. In addition, the three yellow P4 bands are bordered by a thin black line, presumably also the beginning of a period-doubling sequence to be seen only at higher resolution. Note that also other dark blue areas are bordered on one side by a period-doubled zone of light blue followed by black. Thus, the branches themselves are period-doubling objects. It should also be noted that in any case, two of the three branches in each \(PnB3, n=2, 3, 4\), turn to the left (lower driving amplitudes \(P_{A1}\)) and one to the right (higher driving amplitudes \(P_{A1}\)).

5.2 Coexisting period-1 solutions

Although the red period-1 domain in Fig. 3 shows no sign of multiple branches, the examination of its inner structure—the organization of the coexisting period-1 orbits—reveals important features of the branching mechanism. They turn out to be general for other periods as well. By filtering the results for period-1 orbits and by counting the number of the different attractors at a given control parameter pair, the structure of the coexisting period-1 solutions can be made visible in the \(P_{A1}\)–\(P_{A2}\) plane, see Fig. 4 with a magnification of the zone near the origin in the bottom panel. Domains with different colours represent areas with a different number of coexisting attractors up to four. These domains are bounded by saddle-node (\(\textit{SN}\), solid) and period-doubling (\(\textit{PD}\), dashed) curves computed by the boundary-value problem solver AUTO introduced in more detail later. The boundaries computed by AUTO are continuous curves. Some fractal-like shapes in the colour-coded domains are an artefact of the lack of a sufficient number of initial conditions or the presence of extremely long transients during the initial-value-problem computation Crossing one of the boundaries means the increment or decrement of the number of the attractors by one.

Multiple stable period-1 orbits in a bi-parametric space usually originate via cusp bifurcations forming pairs of \(\textit{SN}\) points (hysteresis) and giving rise to hysteresis zones. The overlapping of such hysteresis zones may produce domains with a high number of coexisting period-1 attractors [53]. The sole cusp bifurcation in the bottom panel of Fig. 4, however, cannot explain the mosaic-type pattern of the period-1 structure. The investigation of the two special cases, where one of the amplitudes of the dual-frequency driving \(P_{A1}\) or \(P_{A2}\) is zero (vertical or horizontal axis in Fig. 4), can help to understand this pattern.

Fig. 4
figure 4

Number of coexisting period-1 orbits in the \(P_{A1}\)–\(P_{A2}\) parameter plane at the relative-frequency pair \(\omega _{R1}=3, \omega _{R2}=2\). The saddle-node (\(\textit{SN}\), solid) and period-doubling (\(\textit{PD}\), dashed) curves, computed by the boundary-value problem solver AUTO, are the boundaries of the domains with a different number of coexisting attractors. The pressure amplitudes \(P_{A1}\) and \(P_{A2}\) are given in bar

Full size image

5.3 The limiting case \(P_{A1}=0\) and the period-reducing phenomenon

The bifurcation structure with \(P_{A1}=0\,\mathrm {bar}\) is shown in Fig. 5, where the first component of the Poincaré section \(\varPi (y_1)\) is plotted as a function of \(P_{A2}\). The colour code is the same as in the cases of Fig. 3 and the right column of Fig. 2. For instance, red, green and blue curves are period-1, -2 and -3 orbits, respectively. Some of the periodic orbits are also marked by \(N \times \textit{PX}\), where N is the number of the coexisting attractors of period X. The pitchfork, saddle-node and period-doubling bifurcation points are indicated by \(\textit{PF}, \textit{SN}\) and \(\textit{PD}\), respectively.

Fig. 5
figure 5

One-dimensional bifurcation structure with \(P_{A1}=0\) at the relative-frequency pair \(\omega _{R1}=3\), \(\omega _{R2}=2\), where the first component of the Poincaré section \(\varPi (y_1)\) is plotted as a function of the control parameter \(P_{A2}\). The colour code is the same as in the cases of Fig. 3 and the right column of Fig. 2. The relevant periodic orbits are marked by \(N \times \textit{PX}\), where N is the number of the coexisting attractors of period X. The pitchfork, saddle-node and period-doubling bifurcation points are marked by \(\textit{PF}, \textit{SN}\) and \(\textit{PD}\), respectively

Full size image
Fig. 6
figure 6

The period-reducing phenomenon. Top panel: Bubble radius versus time curves \(y_{1}(\tau )\) (pressure amplitude \(P_{A1}=0\,\mathrm {bar}\) \(P_{A2}=1\,\mathrm {bar}\)) starting at the black dots at \(\tau =0\) marked by the bold numbers 1 and 2 in Fig. 5. Bottom panel: The signal of the single-frequency driving with period \(\tau =T_2\). The global Poincaré section applied during the present computations is defined by T (dashed, red vertical line). (Color figure online)

Full size image

The period-reducing phenomenon discussed in detail in Sect. 4 plays an important role in the period-1 bifurcation structure. Observe that the applied frequency combination is the same as in Fig. 1; furthermore, the first component of the dual-frequency driving is zero. Consequently, the driving is a purely harmonic function proportional to the blue curve in Fig. 1, and an originally period-2k solution is observed only as period-k orbit. Thus, the first bifurcation of the stable period-1 curve originating from the equilibrium solution \(y_{1E}\) (both amplitudes are zero) is a pitchfork point \(\textit{PF}\), instead of a period-doubling point \(\textit{PD}\), which gives birth of two period-1 branches \(2 \times P1\). Only the subsequent bifurcations exhibit a Feigenbaum cascade (\(2 \times P2 \rightarrow 2 \times P4 \rightarrow \cdots \)). Similarly, the first bifurcation point in a cascade must be a symmetry-breaking bifurcation in case of a symmetric orbit in a symmetric nonlinear oscillator [54].

Two examples of bubble radius versus time curves \(y_1(\tau )\) are plotted in the top panel of Fig. 6 so as to help understanding the period-reducing mechanism. The blue and black period-1 solutions are initiated at \(P_{A2}=1\,\mathrm {bar}\) from the black dots marked by the bold numbers 1 and 2 in Fig. 5, respectively. The blue harmonic function in the bottom panel in Fig. 6 is the purely harmonic driving of the system, see also Fig. 1. It is clear that if the Poincaré sections are taken at time instances \(\tau _n=n\,{ \cdot }\, T\) (\(n=0,1,2,\ldots \)), which is used during the present simulations, the solutions are regarded as period-1 orbits. In contrast, if the Poincaré sections are taken at time instances \(\tau _n=n \cdot T_2\) (\(n=0,1,2,\ldots \)), which is a common choice in case of a purely harmonic driving, the solutions are period-2 orbits. To prevent ambiguity in the definition of the periodicities, solutions will be referred to as “originally” period-N orbits if the latter definition of the Poincaré section is applied. Although the blue and black attractors in Fig. 6 are different (each has its own basin of attraction), the only difference between them is a phase shift in time by one period of the driving (\(\varDelta \tau =1.5\)).

Fig. 7
figure 7

Period-1 bifurcation curves computed by the boundary-value problem solver AUTO. The black and red curves are stable and unstable solutions, respectively. The asterisk, crosses and dots are the pitchfork (\(\textit{PF}\)), period-doubling (\(\textit{PD}\)) and saddle-node (\(\textit{SN}\)) bifurcation points, respectively. The left panel (A) shows the case with \(P_{A1}=0\), while the right panel (B) presents results at pressure amplitude \(P_{A1}=0.3\,\mathrm {bar}\) and at \(P_{A1}=0.6\,\mathrm {bar}\). (Color figure online)

Full size image

Altogether two types of bifurcation scenarios of periodic orbits are observable in Fig. 5. For odd basic periods (period before a bifurcation cascade takes place), the first point is a pitchfork bifurcation followed by a Feigenbaum period-doubling cascade (\(\textit{PF} \rightarrow \textit{PD} \rightarrow \textit{PD} \rightarrow \cdots \)). Some examples are the already investigated period-1 curve P1 starting from \(y_{1E}\), the period-3 orbits P3 originating from a \(\textit{SN}\) point at \(P_{A2}=1.5\,\mathrm {bar}\) or the period-5 branches P5 appearing again via a \(\textit{SN}\) point at \(P_{A2}=2\,\mathrm {bar}\). Observe that the \(\textit{PF}\) points have no influence to the colour, i.e. period. In case of even basic periods, the period is immediately halved (period-reducing phenomenon), and the bifurcation scenario is a classic Feigenbaum cascade without an initial \(\textit{PF}\) point (\(\textit{PD} \rightarrow \textit{PD} \rightarrow \cdots \)). An example here is the originally period-6 solution \(2 \times P3\) generated at \(P_{A2}=2.5\,\mathrm {bar}\).

Fig. 8
figure 8

One-dimensional bifurcation structure with \(P_{A2}=0\) at the relative-frequency pair \(\omega _{R1}=3\), \(\omega _{R2}=2\), where the first component of the Poincaré section \(\varPi (y_1)\) is plotted as a function of the control parameter \(P_{A1}\). The colour code is the same as in the cases of Fig. 3 and the right column of Fig. 2. The relevant periodic orbits are marked by \(N \times \textit{PX}\), where N is the number of the coexisting attractors of period X. The saddle-node and period-doubling bifurcation points are marked by \(\textit{SN}\) and \(\textit{PD}\), respectively. (Color figure online)

Full size image

Through the discussion of Figs. 5 and 6, it has been shown that the definition of the Poincaré section has an important influence on the apparent periodicity of the solutions. However, problems only appear in the two limiting cases of either \(P_{A1}=0\,\mathrm {bar}\) or \(P_{A2}=0\,\mathrm {bar}\). In the first special case of \(P_{A1}=0\,\mathrm {bar}\), a suitable choice can be either \(T_2\) or T, see the bottom panel of Fig. 6. Since the addition of any small value to the first pressure amplitude \(P_{A1}\) will destroy the special structure introduced in Fig. 5, \(T_2\) will be no longer a period of the dual-frequency driving but only T. Therefore, in order to keep the definition unified, the usage of T as a global Poincaré section is advantageous. This, at first sight only technical, extension of the definition to the limiting, purely harmonic-driving case is of great help in ordering and explaining the bifurcation scenarios of dual-frequency driven systems.

In order to illustrate this effect, it is useful to solve and compute complete bifurcation curves of periodic orbits with a boundary-value-problem solver. As an example, in Fig. 7A, the second component of the Poincaré section \(\varPi (y_2)\) of the period-1 curves is plotted as a function of the control parameter \(P_{A2}\) computed by the bifurcation analysis and continuation software AUTO [36]. Here, the first component of the pressure amplitude \(P_{A1}\) is still zero. AUTO is capable of tracking down whole bifurcation curves including the unstable part even if they contain multiple turning points, and it can detect the bifurcations and their types. This is the reason why AUTO is commonly used to study the bifurcation structure of nonlinear systems [5, 53, 55,56,57,58,59,60,61]. In Fig. 7, the stable and unstable parts of the period-1 branches are indicated by the black and red curves, respectively. The curve originating from \(y_{2E}\) becomes unstable via a pitchfork bifurcation \(\textit{PF}\) at \(P_{A2}=0.19\,\mathrm {bar}\) producing two stable coexisting period-1 branches. These stable curves lose their stability approximately at \(P_{A2}=3\,\mathrm {bar}\) by a period-doubling point \(\textit{PD}\).

5.4 Perturbation of the limiting case \(P_{A1}=0\)

The breakup of the structurally unstable pitchfork bifurcation due to the effect of a nonzero value of the amplitude of the first harmonic component of the excitation (\(P_{A1}=0.3\,\mathrm {bar}\)) is clearly seen in Fig. 7B. The curves marked by \(P1_1^E\) and \(P1_2^1\) in Fig. 7A form a single curve \(P1_1^E+P1_2^1\) in Fig. 7B. Likewise, the curves \(P1_1^{E,u}\) and \(P1_2^2\) presented in Fig. 7A form again a single curve \(P1_1^{E,u}+P1_2^2\) in Fig. 7B composed by a stable and an unstable part separated by a saddle-node bifurcation (black dot) at the turning point. Elevating \(P_{A1}\) from \(0.3\,\mathrm {bar}\) to \(0.6\,\mathrm {bar}\), a pair of \(\textit{SN}\) points appears along the branch \(P1_1^E+P1_2^1\) forming a hysteresis. Observe that both curves \(P1_1^E+P1_2^1\) and \(P1_1^{E,u}+P1_2^2\) have their own separate evolution as the amplitude \(P_{A1}\) changes; consequently, the black and blue curves in the top of Fig. 6 must become different (not only by a phase shift in time) for \(P_{A1}>0\,\mathrm {bar}\) as they have their own separate evolution as well. All the pitchfork structures in the bifurcation scenarios initiated from odd basic periods are broken up in the same way as presented in Fig. 7B, except for the formation of the hysteresis which not necessarily happens.

5.5 The limiting case \(P_{A2}=0\)

Shortly in this section, the complex development of the period-1 structure in a wide range of the amplitudes \(P_{A1}\) and \(P_{A2}\) will be discussed in detail. Up to now, it is important only to understand how the period-reducing mechanism works for single-frequency driving, how it decomposes periodic solutions into multiple orbits of lower periodicities, and how these multiple orbits are separated under the perturbation of the amplitude of the other harmonic component. In order to understand the global picture, however, the investigation of the other special case, where the control parameter is \(P_{A1}\) and the amplitude of the second component \(P_{A2}\) is zero, is necessary. The corresponding bifurcation diagram is shown in Fig. 8, where the first component of the Poincaré section \(\varPi (y_1)\) is plotted as a function of the pressure amplitude \(P_{A1}\). The colour code and the notation system are the same as in Fig. 5. At first sight—in view of (2) with \(\theta = 0\)—both cases (\(P_{A1}=0\) and \(P_{A1}=0\)) seem exchangeable. However, switching to the other frequency component, different bifurcation scenarios develop (if the frequencies are distinct).

Fig. 9
figure 9

The period-reducing phenomenon. Dimensionless bubble radius versus time curves of four coexisting stable period-1 orbits at pressure amplitude \(P_{A1}=2\,\mathrm {bar}\) starting from the black dots shown in Fig. 8 at \(\tau =0\). Between the black, red and blue solid curves there is only a phase shift in time with \(\varDelta \tau = 1\) or 2. The dashed curve is a degenerate (i.e. repeating only after \(T_1\) instead of after T), small-bubble-radius-amplitude case that exists stably up to \(P_{A1}\approx 7\,\mathrm {bar}\) where the oscillation period doubles. (Color figure online)

Full size image
Fig. 10
figure 10

Period-1 bifurcation curves computed by the boundary-value problem solver AUTO. The black and red curves are stable and unstable solutions, respectively. The crosses and dots are the period-doubling (\(\textit{PD}\)) and saddle-node (\(\textit{SN}\)) bifurcation points, respectively. The left panel (A) shows the case with \(P_{A2}=0\), while the right panel (B) presents results of the \(3 \times P1\) curves at the pressure amplitude of \(P_{A2}=0.1\,\mathrm {bar}\). The arrows in panel (B) show the motion of the \(\textit{SN}\) bifurcation points, two of them towards lower \(P_{A1}\), one of them towards larger \(P_{A1}\). (Color figure online)

Full size image

There are two types of bifurcation scenarios of periodic orbits. If the basic (original) period is divisible by 3, then the period reducing takes place immediately decreasing the period of the orbits from 3k to k followed by a Feigenbaum cascade as usual (\(\textit{PD} \rightarrow \textit{PD} \rightarrow \cdots \)). Notable examples are the branches \(3 \times P1\) and \(3 \times P3\) both appearing via \(\textit{SN}\) bifurcations at \(P_{A1}=1.2\,\mathrm {bar}\) and at \(P_{A1}=4.1\,\mathrm {bar}\), respectively. For other basic periods, there is no period-reducing phenomenon, but only a period-doubling cascade. Examples of this scenario are the period-1 curve departing from the equilibrium solution \(y_{1E}\), the period-4 orbits generated at \(P_{A1}=1.5\,\mathrm {bar}\) or the period-5 branches initiated at \(P_{A1}=4.6\,\mathrm {bar}\). Observe that there are no pitchfork or other special bifurcations present in these cases.

Figure 8 explains how the coexistence is possible of altogether four period-1 stable solutions highlighted in Fig. 4 by the yellow domain. The period-1 orbit P1 emerges from the equilibrium point \(y_{1E}\) and remains stable up to the pressure amplitude \(P_{A1}\approx 7\,\mathrm {bar}\). It loses its stability there via a period-doubling bifurcation. The originally period-3 family of solutions \(3 \times P1\) appearing through a \(\textit{SN}\) point is decoupled into three period-1 branches existing between the amplitudes \(P_{A1}\approx 1.19\,\mathrm {bar}\) and \(P_{A1}\approx 4.67\,\mathrm {bar}\). Therefore, there is a wide range of amplitudes \(P_{A1}\) where four period-1 attractors exist. Figure 9 shows these coexisting orbits at \(P_{A1}=2\,\mathrm {bar}\) starting from the black dots in Fig. 8. The dashed curve is the period-1 orbit related to the curve originating from \(y_{1E}\). The black, red and blue solid curves are the orbits of the period-reduced \(3 \times P1\) branches, where the only difference between them is again a phase shift in time, in this case of one or two periods \(T_1\) (\(\varDelta \tau = 1\) or 2).

5.6 Perturbation of the limiting case \(P_{A2}=0\)

Again, the boundary-value-problem solver AUTO can help to understand the behaviour of the system under a small perturbation of the amplitude of the second, harmonic component of the driving (\(P_{A2}>0\)). The bifurcation curves related to the four period-1 orbits can be seen in Fig. 10A for \(P_{A2}=0\,\mathrm {bar}\). The black and red curves mean stable and unstable orbits, respectively. The bifurcation of the saddle-node (\(\textit{SN}\)) and period-doubling (\(\textit{PD}\)) points are also detected. They are marked by dots (\(\textit{SN}\)) and crosses (\(\textit{PD}\)). Observe that the \(P_{A1}\)-ranges of the stable (black) segments in Fig. 10A coincide with the domain of existence of the corresponding parts of the red curves in Fig. 8. On the right hand side of Fig. 10, only the evolution of the curves \(3 \times P1\) is presented by increasing the amplitude \(P_{A2}\) from zero to \(0.1\,\mathrm {bar}\). It is clear that while the saddle-node bifurcations (black dots) take place at the same value of \(P_{A1}\) when \(P_{A2}=0\,\mathrm {bar}\) (see the vertical thin line in Fig. 10B), the locations of these bifurcation points differ when \(P_{A2}>0\). This means that each of the three bifurcation curves have their own evolution as the amplitude \(P_{A2}\) changes. Consequently, the black, red and blue solid curves in Fig. 9 become different (not only by a phase shift in time) for \(P_{A2}>0\).

6 Period 1: the complete picture

Due to the exhaustive discussion in the preceding sections, it is clear now how the system behaves under single-frequency driving when a second, harmonic component is added as a perturbation. The huge amount of results presented in Fig. 3 can help to establish a global overview of the evolution of all the period-1 solutions by means of filtering the results by period, here period-1. Figure 11 shows these period-1 solutions represented in a three-dimensional plot, where the second component of the Poincaré section, \(\varPi (y_2)\), the bubble wall velocity, is plotted as a function of the two main control parameters \(P_{A1}\) and \(P_{A2}\). The different period-1 orbits can be decomposed into several layers indicated by the blue, black, red and green surfaces. In the limit cases when one of the pressure amplitudes is zero (planes \(\varPi (y_2)\)–\(P_{A1}\) or \(\varPi (y_2)\)–\(P_{A2}\)), the points are plotted with bigger markers to be able to distinguish such special solutions more easily. These solutions, which form complete bifurcations curves presented in Figs. 7A and 10A, are marked by \(P1_n^m\), where n is the original period and \(m\,=1,\dots ,n\) is a serial number, P1 means period-1 solution. When both \(P_{A1}\) and \(P_{A2}\) are zero then the system is in equilibrium and the dimensionless bubble wall velocity and its Poincaré section \(y_{2E}\) are zero (it is the origin of the diagram). The black period-1 surface originating from this point is marked by \(P1_1^E\) (instead of \(P1_1^1\), emphasizing the equilibrium origin E). There is only one curve of this type, which is a surface of small-amplitude bubble oscillations.

Fig. 11
figure 11

3D representation of the stable period-1 orbits (Poincaré section points of the bubble wall velocity) above the parameter plane \(P_{A1}\)–\(P_{A2}\) by filtering the results presented in Fig. 3 by period, here period-1. The period-1 orbits can be separated into four different layers marked by the blue, black, red and green surfaces. The indication of the curves in the \(\varPi (y_2)\)–\(P_{A1}\) (Fig. 10) or \(\varPi (y_2)\)–\( P_{A2}\) (Fig. 7) planes is \(P1_n^m\), where n is the original period and \(m=1,\,\dots ,n\) is a serial number, P1 means period-1 solution. The black surface originating from the equilibrium solution of the system is marked by \(P1_1^E\) (instead of \(P1_1^1\) to show the connection with the equilibrium point). (Color figure online)

Full size image
Fig. 12
figure 12

A 3D representation of the bifurcation structure, computed by AUTO, of the blue and black layers presented in Fig. 11. The black and red curves are the stable and unstable solutions, respectively. The blue and green curves form the skeleton of the limit cases of \(P_{A1}=0\,\mathrm {bar}\) or \(P_{A2}=0\,\mathrm {bar}\). Panel B is an enlargement of the near-origin zone to better show the bifurcation-point area. (Color figure online)

Full size image

Figure 11 indicates a very interesting phenomenon, namely the originally period-2 solutions on \(P1_2^1\) can be transformed into the originally period-3 solutions on \(P1_3^1\) through the blue surface. Similarly, orbits on \(P1_2^2\) can be transformed into orbits on \(P1_3^2\) via the green surface. These are smooth transformations by means of the continuous change of the amplitudes \(P_{A1}\) and \(P_{A2}\) of the dual-frequency driving. Naturally, all these orbits are considered as period-1 attractors due to the specific choice of the global Poincaré section. Consider, however, the following scenario of parameter variations visualized by the supplementary movie file (Online Resource 1) where the top panel shows the dimensionless bubble radius curves \(y_1\) as a function of the dimensionless time \(\tau \), and the bottom panel represents the dual-frequency driving signal \(P_A(\tau )\) (excluding the static ambient pressure).

Firstly, let us start the investigation with a solution lying on the bifurcation curve \(2 \times P1\) in Fig. 5 (\(P1_2^1\) or \(P1_2^2\) in Fig. 11) so that the amplitude of the single-frequency excitation is somewhere between \(P_{A2}=1.4\,\mathrm {bar}\) and \(P_{A2}=2.9\,\mathrm {bar}\) (\(P_{A1}=0\,\mathrm {bar}\)) with relative frequency \(\omega _{R2}=2\). Specifically, in Online Resource 1, the pressure amplitude is chosen to be \(P_{A2}=2.5\,\mathrm {bar}\). In this video, besides the originally period-2 (red) attractor, which is the initial state of the transformation, an originally period-3 (blue) attractor coexists regarded as a final target of the control problem. The colour code of these attractors is the same both in Fig. 5 and in the top panel of Online Resource 1; in addition, by comparing the top and bottom panels, the periodicities of the attractors are clearly visible.

Secondly, guide the period-2 orbit smoothly to the curve \(3 \times P1\) shown in Fig. 8 (either \(P1_3^1\) or \(P1_3^2\) in Fig. 11) by varying the pressure amplitudes continuously. By the end of the second operation, the system is again driven by a single frequency (\(\omega _{R1}=3\)) with pressure amplitude between \(P_{A1}=1.2\,\mathrm {bar}\) and \(P_{A1}=4.7\,\mathrm {bar}\) (\(P_{A2}=0\,\mathrm {bar}\)). In Online Resource 1, this transformation takes place along a circle in the \(P_{A1}\)–\(P_{A2}\) plane with radius \(2.5\,\mathrm {bar}\); that is, the final value of the first pressure amplitude is \(P_{A1}=2.5\,\mathrm {bar}\). The continuously changing trajectory during the transformation is marked by the black curve in the top panel.

Fig. 13
figure 13

A 3D representation of the bifurcation structure, computed by AUTO, of the red layer presented in Fig. 11. The black and red curves are the stable and unstable solutions, respectively. The blue and green curves form the skeleton of the limit cases of \(P_{A1}=0\,\mathrm {bar}\) or \(P_{A2}=0\,\mathrm {bar}\). (Color figure online)

Full size image
Fig. 14
figure 14

A 3D representation of the bifurcation structure, computed by AUTO, of the green layer presented in Fig. 11. The black and red curves are the stable and unstable solutions, respectively. The blue and green curves form the skeleton of the limit cases of \(P_{A1}=0\,\mathrm {bar}\) or \(P_{A2}=0\,\mathrm {bar}\). (Color figure online)

Full size image

Thirdly, keep the single-frequency driving but change both the amplitude \(P_{A1}\) and the relative frequency \(\omega _{R1}\) of the driving (in general) to transform the solution from the red curve \(3 \times P1\) in Fig. 8 to the blue curve P3 in Fig. 5. This third step is possible, since both the \(3 \times P1\) and the P3 curves are related to the same subharmonic resonance of order 1 / 3, which forms a continuous domain in the pressure amplitude—frequency parameter plane [53, 61]. Therefore, a smooth transformation of a period-2 solution into a period-3 orbit of a single-frequency driven system is possible by a temporary addition of a second harmonic component to the driving. This is an efficient way to control multistability in harmonically driven nonlinear oscillators. According to the best of the authors’ knowledge, this phenomenon has not yet been published in the literature. During this third step in Online Resource 1, the change of \(P_{A1}\) is not necessary and kept constant. Observe how the initial and the final parameter set become identical; that is, single-frequency driving with amplitude \(P_{A1,2}=2.5\,\mathrm {bar}\) at \(\omega _{R1,2}=2\). The only difference is the state of the system: operation on the period-3 (blue) instead on the period-2 (red) attractor.

In order for a better visualization of the surfaces presented in Fig. 11, hundreds of bifurcation curves are computed by AUTO departing from the results shown in Fig. 10A. These surfaces, composed by lines, are summarized in Figs. 12, 13 and 14. The stable and unstable parts are the black and red curves, respectively. As a skeleton, all the bifurcation curves of the limit cases (\(P_{A1}=0\,\mathrm {bar}\) or \(P_{A2}=0\,\mathrm {bar}\)) are presented by the blue (stable) and the green (unstable) curves, which can help to identify the surfaces more easily (compare also with Figs. 7A, 10A). As usual, the pitchfork (\(\textit{PF}\)), saddle-node (\(\textit{SN}\)) and period-doubling (\(\textit{PD}\)) bifurcation points are marked by asterisk, dots and crosses, respectively. The left hand side of these figures represents the surfaces in the full parameter domain, while the right hand side is a magnification of the interesting parts.

Fig. 15
figure 15

Number of the coexisting period-3 orbits (top panel) and period-4 orbits (bottom panel) in the \(P_{A1}\)–\(P_{A2}\) parameter plane at relative frequencies \(\omega _{R1}=3\) and \(\omega _{R2}=2\)

Full size image

From Fig. 12, it is clear that the blue and black surfaces in Fig. 11 are connected for very small values of \(P_{A1}\). The separation takes place approximately at \(P_{A1}=0.33\,\mathrm {bar}\) via a cusp bifurcation forming a hysteresis, see also the bottom panel of Fig. 4. An example for this hysteresis, which exists between the regions of \(P_{A1}>0.33\,\mathrm {bar}\) and \(P_{A1}<1.19\,\mathrm {bar}\), is already introduced in Fig. 7B for \(P_{A1}=0.6\,\mathrm {bar}\). As expected, the red, standalone surface in Fig. 11 has no connections with other surfaces, see Fig. 13. The green surface in Fig. 11 together with its unstable counterpart forms a simple banded, dual-layer surface presented in Fig. 14.

7 Higher periods

If the smooth transformation works between certain period-2 and period-3 orbits, there must be other combinations of periodic solutions where the transformation is possible. In order to investigate these other possibilities, the number of the coexisting period-3 and period-4 attractors is plotted in the top and the bottom panels of Fig. 15, respectively. The colour codes are the same as in case of Fig. 4 (period-1 orbits). Let us focus only on those parts of the complex bifurcation structures where the transformations take place. In the top panel of Fig. 15, there are two branches along which the following conversion occurs: \(2 \times P3 = P6 \leftrightarrow 3 \times P3 = P9\); that is, an originally period-6 solution is transformed into an originally period-9 orbit. Similarly, the bottom panel of Fig. 15 shows four bands converting originally period-8 orbits into period-12 orbits (\(2 \times P4 = P8 \leftrightarrow 3 \times P4 = P12\)). As a generalization, the present study found that applying the relative-frequency combination \(\omega _{R1}=3\) and \(\omega _{R2}=2\), a transformation between period-2k and period-3k attractors is possible, here \(k=1,2,\ldots \).

8 Winding numbers and compatibility of periodic orbits

Naturally, not every kind of period-2k and period-3k orbits can be transformed into each other; in other words, there is a “compatibility” condition. Observe that the first \(\textit{PD}\) points of the period-1 branches in Fig. 5 (\(2 \times P1\)) and in Fig. 8 (\(3 \times P1\)) are connected via the period-doubling curve \(\textit{PD}\) shown in the top panel of Fig. 4. It is well known in the literature that the quantity called winding number \(w=nk/mk\) is invariant and rational near a period-doubling or a saddle-node point [62, 63]. Here, mk is the period of a given attractor and nk is the number of the rotations of a nearby trajectory around the attractor during one period. Therefore, to each bi-parametric \(\textit{PD}\) or \(\textit{SN}\) bifurcation curve a single, rational winding number can be associated. When a transformation between period-2k and period-3k orbits is possible, then it must be possible between their corresponding bifurcation points as well, see, for instance, the \(\textit{PD}\) curve in Fig. 4 which has the winding number \(w=1/2\). Consequently, the transformation is possible only if the winding numbers of such bifurcation points are compatible; that is, when they are equal.

9 Discussion

According to the literature, the only option to directly target an attractor in case of multistability is to apply a feedback control technique. The main drawback of the feedback control methods is that explicit knowledge of the state space (modified targeting method [33], bush-like paths to a pre-selected attractor [64], reinforcement learning [65]) or the properties of the targeted attractor (trajectory selection by a periodic feedback [34]) is necessary. Control of multistability is possible by delay feedback as well, which can be combined with chaos control easily [66]. In that case, the feedback stabilizes one of the unstable orbits embedded in a chaotic attractor. Unfortunately, it just stabilizes an unstable orbit and does not target directly an already existing attractor. Parenthetically, the feedback control can stabilize an attractor against external noise by employing the Jacobian of the attractor as a feedback [67]. However, the state of the system must be already near to the desired orbit; that is, the application of one of the above targeting techniques is mandatory.

If feedback control is possible then the aforementioned controls work very well; otherwise, the application of a non-feedback method (including a stochastic one) is inevitable. The main advantage of the non-feedback control technique presented in this study is the ability to target the desired attractor directly, which is not possible with traditional non-feedback controls. For instance, the attractor selection by short pulses [31] (kick the system) introduces randomness to the control; that is, it cannot be guaranteed that the final state of the system after the kick is the desired attractor. Moreover, extremely long transients in the presence of transient chaos [68] are also possible. With the continuous transformation of attractors such transients can be avoided. The attractor annihilation techniques by pseudo-periodic forcing [69] or by harmonic perturbation of a state variably or a parameter [32] cannot target an attractor directly either. Roughly speaking, both techniques destruct attractors in the order of the size of their basin of attraction with increasing forcing or perturbation amplitudes.

The applicability of the method presented here has also requirements/limitations. Firstly, in many cases, there is the requirement that the system should not be modified appreciably during the control. Therefore, all non-feedback techniques apply only small perturbations. It is absolutely not fulfilled in the present method as large deviations from the original system parameters is usually necessary. However, by the end of the control, the system goes back exactly to the same parameter set and additional control is no longer required to sustain the desired state (attractor). It must be also noted that if the basin of attraction of the targeted attractor is small then slow transformation may be necessary.

Secondly, due to the large parameter variation during the control, detailed knowledge on the topology of the periodic orbits in a large parameter space must be available. This is usually a minor problem since the bifurcation structure of many nonlinear oscillators have the same basic building blocks [70]. If there is no information about a state variable, the orientation in the topology can be supported; for instance, by measuring and Fourier transforming an indirect quantity connected to the dynamics (in case of bubbles their emitted pressure signal). The peaks presented in the spectra can provide valuable information about the nature of the actual attractor [71], see also the studies of Lauterborn and Cramer [72] and Lauterborn and Suchla [73] where complete period-doubling scenarios could be measured in this way of harmonically forced bubbles represented via spectral bifurcation diagrams. Another requirement related to the topology is that the transformed trajectories must be compatible in terms of winding numbers as already discussed in Sect. 8.

It must be emphasized that it is possible to combine the present non-feedback control technique with other methods. For instance, with stochastic control, attractors with small basins can be annihilated to “simplify” the state spaces during the transformation. Moreover, even if feedback control is possible in an application, the method introduced here is still a good candidate for targeting a desired attractor, and after the continuous transformation, the attractor can be stabilized against external noise with the feedback control. Similarly, the delay feedback control can stabilize an unstable orbit that replaces the originally stable chaotic attractor. After that, the continuous transformation technique can be applied between the resulting coexisting stable states if necessary and if it is possible. In this way, chaos control and targeting an attractor directly is accomplished simultaneously. There are case studies where the application of two different kinds of controls may be successful when the usage of only one of the control fails [74].

Since the control technique is demonstrated numerically only on a specific system (Keller–Miksis equation describing bubble dynamics) and on a very specific example, many questions arise: Is it possible to “bypass” somehow the winding number compatibility condition? Is it possible to transform a chaotic attractor into a stable periodic orbit and vice versa? Is this method applicable to other systems? In order to answer these question correctly, additional detailed analyses are mandatory; however, preliminary conjectures can be made.

Even if a continuous transformation between two coexisting attractors does not exist applying a single-frequency pair, it may be possible to find a transformation by using subsequent frequency pairs one after another, and reaching the desired attractor step-by-step hopping onto “intermediate” attractors. The transformation of chaotic attractors into periodic orbits fits into the large topic of chaos control [21]. Since chaos control is possible with the addition of a second sinusoidal component to the driving [24, 75], the main issue is that how chaos is annihilated (a smooth inverse Feigenbaum cascade or a sudden crises) during the parameter tuning, and what is the resulting periodic orbit which is interesting from the winding number compatibility point of view. It is well known that chaos control is possible merely by adjusting the phase shift between the sinusoidal components of the driving [76]; therefore, the effect of the phase shift must also be thoroughly investigated. It can also play an important role between the transformation of the period-2 and period-3 orbits itself shown in Fig. 11. The period-2 solutions can always be transformed into one of the period-3 orbits through the blue or the green surfaces. In contrast, if the period-3 attractor is in a phase in time described by the red surface then transformation is not possible in the opposite direction (from period-3 to period-2), see again Fig. 11.

It is very likely that the control technique of continuous transformation is possible for other systems as well. As it was already mentioned, the topology of many nonlinear oscillators is composed by the same building blocks. Moreover, in recent publications, a phenomenon called replication of periodic domains is reported by applying a second sinusoidal component to the driving [40, 77], or a single periodic perturbation in case of maps [78, 79]. We believe that the replication of periodic domains and the branching mechanism introduced in Sect. 5.1 have the same dynamical origin.

Finally, it is worth mentioning that any application using dual-frequency driving can benefit (at least indirectly) from the results presented in this study due to the very detailed investigation. Some possible applications are acoustic cavitation [80,81,82,83], Faraday waves [84], stability of traveling beams [85, 86] or laser-driven dissociation of molecules [87].

10 Conclusion

In the present study, a new non-feedback technique to control multistability in harmonically driven nonlinear oscillators is introduced. It is based on the observation that two attractors which cannot be exchanged by tuning the system parameters may be transformed continuously into each other by temporarily adding a second sinusoidal component to the driving. The process to target a desired attractor directly was tested at a relevant example, the Keller–Miksis equation—a second-order ordinary differential equation describing bubble dynamics—and visualized via an animation (Online Resource 1). If this technique is proven to be applicable to other systems as well, it may become an excellent candidate to accomplish non-feedback control without long transients and/or randomness.