Skip to main content
SpringerLink
Log in

Two-frequency parametric excitation and internal resonance of a moving viscoelastic beam

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

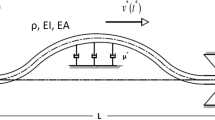
In this paper, analytical and numerical approach is applied to find the steady-state and dynamic behaviors of an axially accelerating viscoelastic beam subject to two-frequency parametric excitation in presence of internal resonance. Direct method of multiple scales is employed to solve the cubic nonlinear integro-partial differential equation. As a result, the governing equation of motion is reduced to a set of nonlinear first-order partial differential equations. These equations are solved through continuation algorithm approach to find the frequency and amplitude response curves and their stability and bifurcation. The system reveals the presence of Hopf, saddle node, and pitchfork bifurcations. The dynamic bevavior of the system is estimated through phase portraits, time traces, Poincare maps, and FFT power spectra obtained via direct time integration. The evolution of maximum Lyapunov exponent reveals the system parameter where the dynamic response changes from stable periodic to unstable chaotic motion of the system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24

Similar content being viewed by others

References

  1. Mote Jr, C.D., Wu, W.Z., Schajer, G.S.: Band saw and circular saw vibration and stability. Shock Vib. Dig. 14(2), 19–25 (1982)

    Article  Google Scholar 

  2. Wickert, J.A., Mote Jr, C.D.: Current research on the vibration and stability of axially moving materials. Shock Vib. Dig. 20, 3–13 (1988)

    Article  Google Scholar 

  3. Abrate, S.: Vibrations of belts and belt drives. Mech. Mach. Theory 27(6), 645–659 (1992)

    Article  Google Scholar 

  4. Chen, L.-Q.: Analysis and control of transverse vibrations of axially moving strings. Appl. Mech. Rev. 98, 91–116 (2005)

    Article  Google Scholar 

  5. Pellicano, F., Vestroni, F.: Nonlinear dynamics and bifurcations of an axially moving beam. J. Vib. Acoust. 122, 21–30 (2000)

    Article  Google Scholar 

  6. Riedel, C.H., Tan, C.A.: Coupled, forced response of an axially moving strip with internal resonance. Int. J. Non Linear Mech. 37, 101–116 (2002)

    Article  MATH  Google Scholar 

  7. Marynowski, K.: Non-linear dynamic analysis of an axially moving viscoelastic beam. J. Theor. Appl. Mech. 40, 465–482 (2002)

    MATH  Google Scholar 

  8. Marynowski, K., Kapitaniak, T.: Kelvin–Voigt versus Burgers internal damping in modelling of axially moving viscoelastic web. Int. J. Non Linear Mech. 37(7), 1147–1161 (2002)

    Article  MATH  Google Scholar 

  9. Marynowski, K., Kapitaniak, T.: Zener internal damping in modeling of axially moving viscoelastic beam with time dependent tension. Int. J. Non Linear Mech. 42, 118–131 (2007)

    Article  MATH  Google Scholar 

  10. Chen, S.H., Huang, J.L., Sze, K.Y.: Multidimensional Lindstedt–Poincare method for nonlinear vibration of axially moving beams. J. Sound Vib. 306, 1–11 (2007)

    Article  Google Scholar 

  11. Ozkaya, E., Bagdatli, S.M., Oz, H.R.: Nonlinear transverse vibrations and 3:1 internal resonances of a beam with multiple supports. J. Vib. Acoust. 130(2), 1–11 (2008)

    Article  Google Scholar 

  12. Bagdatli, S.M., Oz, H.R., Ozkaya, E.: Nonlinear transverse vibrations and 3:1 internal resonances of a tensioned beam on multiple supports. Math. Comput. Appl. 16(1), 203–215 (2011)

    MathSciNet  Google Scholar 

  13. Ozhan, B.B., Pakdemirli, M.: A general solution procedure for the forced vibrations of a system with cubic nonlinearities: primary resonance case. J. Sound Vib. 325, 894–906 (2009)

    Article  Google Scholar 

  14. Ozhan, B.B., Pakdemirli, M.: A general solution procedure for the forced vibrations of a system with cubic nonlinearities: three-to-one internal resonances with external excitation. J. Sound Vib. 329, 2603–2615 (2010)

    Article  Google Scholar 

  15. Huang, J.L., Su, R.K.L., Li, W.H., Chen, S.H.: Stability and bifurcation of an axially moving beam tuned to three-to-one internal resonances. J. Sound Vib. 330, 471–485 (2011)

    Article  Google Scholar 

  16. Ghayesh, M.H., Kafiabad, H.A., Reid, T.: Sub- and super-critical nonlinear dynamics of a harmonically excited axially moving beam. Int. J. Solids Struct. 49, 227–243 (2012)

    Article  Google Scholar 

  17. Chen, L.-Q., Tang, Y.-Q.: Combination and principal parametric resonances of axially accelerating viscoelastic beams: recognition of longitudinally varying tensions. J. Sound Vib. 330, 5598–5614 (2011)

    Article  Google Scholar 

  18. Ghayesh, M.H., Kazemirad, S., Amabili, M.: Coupled longitudinal-transverse dynamics of an axially moving beam with an internal resonance. Mech. Mach. Theory 52, 18–34 (2012)

    Article  Google Scholar 

  19. Ghayesh, M.H.: Coupled longitudinal–transverse dynamics of an axially accelerating beam. J. Sound Vib. 331, 5107–5124 (2012)

    Article  Google Scholar 

  20. Ghayesh, M.H., Amabili, M., Farokhi, H.: Coupled global dynamics of an axially moving viscoelastic beam. Int. J. Non Linear Mech. 51, 54–74 (2013)

    Article  Google Scholar 

  21. Han, Q., Wang, J., Li, Q.: Parametric instability of a cantilever beam subjected to two electromagnetic excitations: experimental and analytical validation. J. Sound Vib. 330, 3473–3487 (2011)

    Article  Google Scholar 

  22. Sarigul, M., Boyaci, H.: Nonlinear vibrations of axially moving beams with multiple concentrated masses Part I: primary resonance. Struct. Eng. Mech. 36(2), 149–163 (2010)

    Article  Google Scholar 

  23. Sahoo, B., Panda, L.N., Pohit, G.: Parametric and internal resonances of an axially moving beam with time dependent velocity. Model. Simul. Eng. Article ID 919517, 18 pp (2013)

  24. Sahoo, B., Panda, L. N., Pohit, G.: Stability and bifurcation analysis of an axially accelerating beam. In: Sinha, J.K. (ed.) Vibration Engineering and Technology of Machinery (Mech. Mach. Sci. 23). Springer International Publishing Switzerland (2015). doi:10.1007/978-3-319-09918-7_81

  25. Nayfeh, A.H.: Response of two degree of freedom systems to multifrequency parametric excitations. J. Sound Vib. 88, 1–10 (1983)

    Article  MathSciNet  Google Scholar 

  26. Nayfeh, A.H.: The response of non-linear single degree of freedom systems to multifrequency excitations. J. Sound Vib. 102(3), 403–414 (1985)

    Article  MathSciNet  Google Scholar 

  27. Nayfeh, A.H., Jebril, A.E.S.: The response of two-degree-of-freedom systems with quadratic and cubic nonlinearities to multifrequency parametric excitations. J. Sound Vib. 115(83), 83–101 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  28. Plaut, R.H., Gentry, J.J., Mook, D.T.: Nonlinear oscillations under multifrequency parametric excitation. Int. J. Non Linear Mech. 25, 187–198 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  29. Parker, R.G., Lin, Y.: Parametric instability of an axially moving media subjected to multifrequency tension and speed fluctuations. J. Appl. Mech. 68, 49–57 (2001)

    Article  MATH  Google Scholar 

  30. El-Bassiouny, A.F.: Principal parametric resonances of non-linear mechanical system with two-frequency and self-excitations. Mech. Res. Commun. 32, 337–350 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  31. Michon, G., Manin, L., Parker, R.G., Dufour, R.: Duffing oscillator with parametric excitation: analytical and experimental investigation on a belt-pulley system. J. Comput. Non Linear Dyn. 3, 031001-1-6 (2008)

    Google Scholar 

  32. Michon, G., Manin, L., Remond, D., Dufour, R., Parker, R.G.: Parametric instability of an axially moving belt subjected to multi-frequency excitations: experiments and analytical validation. J. Appl. Mech. 75, 041004-1-8 (2008)

    Article  Google Scholar 

  33. Yang, T., Fang, B., Chen, Y., Zhen, Y.: Approximate solutions of axially moving viscoelastic beams subject to multi-frequency excitations. Int. J. Non Linear Mech. 44, 230–238 (2009)

    Article  Google Scholar 

  34. Chakraborty, G., Mallik, A.K.: Non-linear vibration of traveling beam having an intermediate guide. Nonlinear Dyn. 20, 247–265 (1999)

    Article  MATH  Google Scholar 

  35. Paidoussis, M.P.: Flutter of conservative systems of pipe conveying incompressible fluid. J. Mech. Eng. Sci. 17(1), 19–25 (1975)

    Article  Google Scholar 

  36. Wickert, J.A.: Nonlinear vibration of a traveling tensioned beam. Int. J. Non Linear Mech. 27, 503–517 (1992)

    Article  MATH  Google Scholar 

  37. Chakraborty, G., Mallik, A.K., Hatwal, H.: Non-linear vibration of traveling beam. Int. J. Non Linear Mech. 34, 655–670 (1999)

    Article  MATH  Google Scholar 

  38. Oz, H.R., Pakdemirli, M., Boyaci, H.: Nonlinear vibrations and stability of an axially moving beam with time-dependent velocity. Int. J. Non Linear Mech. 36, 107–115 (2001)

    Article  Google Scholar 

  39. Nayfeh, A.H.: Introduction to Perturbation Techniques. Wiley, New York (1981)

    MATH  Google Scholar 

  40. Chin, C.M., Nayfeh, A.H.: Three-to-one internal resonance in parametrically excited hinged-clamped beams. Nonlinear Dyn. 20, 131–158 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  41. Dhooge, A., Govaerts, W., Kuznetsov, Yu., A., Mestrom, W., Riet, A.M, Sautois, B.: Matcont and CL\(\_\)Matcont: Continuation toolboxes in Matlab. Gent University, Belgium and Utrecht University, Netherland (2006)

  42. Cheng, G., Zu, J.W.: Nonstick and stick-slip motion of a coulomb-damped belt drive system subject to multi-frequency excitations. J. Appl. Mech. 70, 871–884 (2003)

    Article  MATH  Google Scholar 

Download references

Acknowledgments

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Mechanical Engineering Department, IIIT, Bhubaneswar, India

    Bamadev Sahoo

  2. Mechanical Engineering Department, CET, Bhubaneswar, India

    L. N. Panda

  3. Mechanical Engineering Department, Jadavpur University, Kolkata, India

    Goutam Pohit

Authors
  1. Bamadev Sahoo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. N. Panda
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Goutam Pohit
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bamadev Sahoo.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

Appendix

Appendix

$$\begin{aligned} \varGamma _{1}= & {} - 2 i\omega _{1} A^{\prime }_{1} \phi _{1} - 2 v_{0} A^{\prime }_{1} \phi ^{\prime }_{1} - 2i\mu \omega _{1} A_{1} \phi _{1} - 2i\alpha \omega _{1} A_{1} \phi ^{{\prime }{\prime }{\prime }{\prime }}_{1} +\,\frac{1}{2}v_\mathrm{l}^{2} \left\{ {2A_{1}^{2} \bar{A}_{1} \phi ^{\prime \prime }_{1} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }^{\prime }_{1} \mathrm{d}x_{1}} } \right. \\&+\, A_{1}^{2} \bar{A}_{1} \bar{\phi }^{\prime \prime }\int \limits _{0}^{1} {\phi ^{\prime {2}}_{1} \mathrm{d}x} + 2A_{1} A_{2} \bar{A}_{2} \bar{\phi }^{\prime \prime }_{2} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \phi ^{\prime }_{2} \mathrm{d}x} +\, \left. {2A_{1} A_{2} \bar{A}_{2} \phi ^{\prime \prime }_{1} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }^{\prime }_{2} \mathrm{d}x} + 2A_{1} A_{2} \bar{A}_{2} \phi ^{\prime \prime }_{2} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }^{\prime }_{2} \mathrm{d}x}} \right\} \\ \varGamma _{2}= & {} \frac{1}{2}v_\mathrm{l}^{2} \left\{ {2\bar{A}_{1}^{2} A_{2} \bar{\phi }^{\prime \prime }_{1} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }^{\prime }_{1} \mathrm{d}x} + \bar{A}_{1}^{2} A_{2} \phi ^{\prime \prime }_{2} \int \limits _{0}^{1} \bar{\phi }^{\prime 2}_{1} \mathrm{d}x} \right\} \end{aligned}$$
$$\begin{aligned} \varGamma _{5}= & {} - 2 i\omega _{2} A^{\prime }_{2} \phi _{2} - 2 v_{0} A^{\prime }_{2} \phi ^{\prime }_{2} - 2\mu i\omega _{2} A_{2} \phi _{2} - 2\alpha i\omega _{2} A_{2} \phi ^{{\prime }{\prime }{\prime }{\prime }}_{2} +\, \frac{1}{2}v_\mathrm{l}^{2} \left\{ {A_{2}^{2} \bar{A}_{2} \bar{\phi }^{{\prime }{\prime }}_{2} \int \limits _{0}^{1} {\phi ^{\prime {2}}_{2} \mathrm{d}x}} \right. \\&\left. + 2A_{1} \bar{A}_{1} A_{2} \phi ^{\prime \prime }_{2} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }^{\prime }_{1}} \mathrm{d}x\right. + 2A_{1} \bar{A}_{1} A_{2} \bar{\phi }^{{\prime }{\prime }}_{1} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \phi ^{\prime }_{2} \mathrm{d}x} \left. + 2A_{2}^{2} \bar{A}_{2} \phi ^{\prime \prime }_{2} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }^{\prime }_{2} \mathrm{d}x} + 2A_{1} \bar{A}_{1} A_{2} \phi ^{\prime \prime }_{1} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }^{\prime }_{1} \mathrm{d}x} \right\} \\ \varGamma _{6}= & {} \frac{1}{2}v_\mathrm{l}^{2} \left\{ {A_{1}^{3} \phi ^{\prime \prime }_{1} \int \limits _{0}^{1} {\phi ^{\prime 2}_{1} \mathrm{d}x}} \right\} \\ \varGamma _{7}= & {} A_{1} \left\{ { - v_{1} \omega _{1} \phi ^{\prime }_{1} - \frac{{ v_{1} \varOmega _{1}}}{2}\phi ^{\prime }_{1} + i v_{0} v_{1} \phi ^{{\prime }{\prime }}_{1}} \right\} \\ \varGamma _{9}= & {} \bar{A}_{1} \left\{ {v_{1} \omega _{1} \bar{\phi }^{\prime }_{1} - \frac{{v_{1} \varOmega _{1}}}{2}\bar{\phi }^{\prime }_{1} + iv_{0} v_{1} \bar{\phi }^{\prime \prime }_{1}} \right\} \\ \varGamma _{{10}}= & {} A_{2} \left\{ {v_{1} \omega _{2} \phi ^{\prime }_{2} - \frac{{v_{1} \varOmega _{1}}}{2}\phi ^{\prime }_{2} - iv_{0} v_{1} \phi ^{\prime \prime }_{2}} \right\} \\ \varGamma _{{11}}= & {} \bar{A}_{2} \left\{ {v_{2} \omega _{2} \bar{\phi }^{\prime }_{2} - \frac{{v_{2} \varOmega _{2}}}{2}\bar{\phi } ^{\prime }_{2} + iv_{0} v_{2} \bar{\phi }^{\prime \prime }_{2}} \right\} \end{aligned}$$
$$\begin{aligned} S_{1}= & {} \frac{{\frac{1}{{16}}v_\mathrm{l}^{2} \left\{ {2\int \limits _{0}^{1} {\phi ^{\prime \prime }_{1} \bar{\phi }_{1} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }^{\prime }_{1} \mathrm{d}x} + \int \limits _{0}^{1} {\bar{\phi }^{\prime \prime }_{1} \bar{\phi }_{1} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime {2}}_{1} \mathrm{d}x}} \right\} }}{{ - \left\{ {i\omega _{1} \int \limits _{0}^{1} {\phi _{1} \bar{\phi }_{1} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }_{1} \mathrm{d}x}} \right\} }}; \\ S_{2}= & {} \frac{{\frac{1}{8}v_\mathrm{l}^{2} \left\{ {\int \limits _{0}^{1} {\bar{\phi }^{\prime \prime }_{2} \bar{\phi }_{1} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \phi ^{\prime }_{2} \mathrm{d}x} + \int \limits _{0}^{1} {\phi ^{\prime \prime }_{1} \bar{\phi }_{1} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }^{\prime }_{2} \mathrm{d}x} + \int \limits _{0}^{1} {\phi ^{\prime \prime }_{2} \bar{\phi }_{1} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }^{\prime }_{2} \mathrm{d}x}} \right\} }}{{ - \left\{ {i\omega _{1} \int \limits _{0}^{1} {\phi _{1} \bar{\phi }_{1} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }_{1} \mathrm{d}x}} \right\} }}; \\ S_{3}= & {} \frac{{\frac{1}{8}v_\mathrm{l}^{2} \left\{ {\int \limits _{0}^{1} {\phi ^{\prime \prime }_{2} \bar{\phi }_{2} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }^{\prime }_{1} \mathrm{d}x} + \int \limits _{0}^{1} {\bar{\phi }^{\prime \prime }_{1} \bar{\phi }_{2} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \phi ^{\prime }_{2} \mathrm{d}x} + \int \limits _{0}^{1} {\phi ^{\prime \prime }_{1} \bar{\phi }_{2} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }^{\prime }_{2} \mathrm{d}x}} \right\} }}{{ - \left\{ {i\omega _{2} \int \limits _{0}^{1} {\phi _{2} \bar{\phi }_{2} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }_{2} \mathrm{d}x}} \right\} }}; \\ S_{4}= & {} \frac{{\frac{1}{{16}}v_\mathrm{l}^{2} \left\{ {2\int \limits _{0}^{1} {\phi ^{\prime \prime }_{2} \bar{\phi }_{2} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }^{\prime }_{2} \mathrm{d}x} + \int \limits _{0}^{1} {\bar{\phi }^{\prime \prime }_{2} \bar{\phi }_{2} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime {2}}_{2} \mathrm{d}x}} \right\} }}{{ - \left\{ {i\omega _{2} \int \limits _{0}^{1} {\phi _{2} \bar{\phi }_{2} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }_{2} \mathrm{d}x}} \right\} }}; \\ C_{1}= & {} \frac{{ - i\omega _{1} \int \limits _{0}^{1} {\phi _{1} \bar{\phi }_{1} \mathrm{d}x}}}{{ - \left\{ {i\omega _{1} \int \limits _{0}^{1} {\phi _{1} \bar{\phi }_{1} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }_{1} \mathrm{d}x}} \right\} }}; \end{aligned}$$
$$\begin{aligned} C_{2}= & {} \frac{{ - i\omega _{2} \int \limits _{0}^{1} {\phi _{2} \bar{\phi }_{2} \mathrm{d}x}}}{{ - \left\{ {i\omega _{2} \int \limits _{0}^{1} {\phi _{2} \bar{\phi }_{2} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }_{2} \mathrm{d}x}} \right\} }}; \\ e_{1}= & {} \frac{{ - i\omega _{1} \int \limits _{0}^{1} {\phi ^{{\prime }{\prime }{\prime }{\prime }}_{1} \bar{\phi }_{1} \mathrm{d}x}}}{{ - \left\{ {i\omega _{1} \int \limits _{0}^{1} {\phi _{1} \bar{\phi }_{1} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }_{1} \mathrm{d}x}} \right\} }}; \\ e_{2}= & {} \frac{{ - i\omega _{2} \int \limits _{0}^{1} {\phi ^{{\prime }{\prime }{\prime }{\prime }}_{2} \bar{\phi }_{2} \mathrm{d}x}}}{{ - \left\{ {i\omega _{2} \int \limits _{0}^{1} {\phi _{2} \bar{\phi }_{2} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }_{2} \mathrm{d}x}} \right\} }}; \\ g_{1}= & {} \frac{{\frac{1}{{16}}v_\mathrm{l}^{2} \left\{ {2\int \limits _{0}^{1} {\bar{\phi }^{\prime \prime }_{1} \bar{\phi }_{1} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }^{\prime }_{1} \mathrm{d}x} + \int \limits _{0}^{1} {\phi ^{\prime \prime }_{2} \bar{\phi }_{1} \mathrm{d}x} \int \limits _{0}^{1} {\bar{\phi }^{\prime {2}}_{1} \mathrm{d}x}} \right\} }}{{ - \left\{ {i\omega _{1} \int \limits _{0}^{1} {\phi _{1} \bar{\phi }_{1} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }_{1} \mathrm{d}x}} \right\} }}; \\ g_{2}= & {} \frac{{\frac{1}{{16}}v_\mathrm{l}^{2} \left\{ {\int \limits _{0}^{1} {\phi ^{\prime \prime }_{1} \bar{\phi }_{2} \mathrm{d}x} \int \limits _{0}^{1} {\phi ^{\prime {2}}_{1} \mathrm{d}x}} \right\} }}{{ - \left\{ {i\omega _{2} \int \limits _{0}^{1} {\phi _{2} \bar{\phi }_{2} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }_{2} \mathrm{d}x}} \right\} }}; \end{aligned}$$
$$\begin{aligned} K_{1}= & {} \frac{{\frac{1}{2}\left\{ {v_{1} \omega _{1} \int \limits _{0}^{1} {\bar{\phi }^{\prime }_{1} \bar{\phi }_{1} \mathrm{d}x} - \frac{{v_{1} \varOmega _{1}}}{2}\int \limits _{0}^{1} {\bar{\phi }_{1}^{\prime }} \bar{\phi }_{1} \mathrm{d}x + i v_{0} v_{1} \int \limits _{0}^{1} {\bar{\phi }^{\prime \prime }_{1} \bar{\phi }_{1} \mathrm{d}x}} \right\} }}{{ - \left\{ {i\omega _{1} \int \limits _{0}^{1} {\phi _{1} \bar{\phi }_{1} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }_{1} \mathrm{d}x}} \right\} }}; \\ K_{2}= & {} \frac{{\frac{1}{2}\left\{ {v_{1} \omega _{2} \int \limits _{0}^{1} {\phi _{2}^{\prime } \bar{\phi }_{1} \mathrm{d}x} - \frac{{v_{1} \varOmega _{1}}}{2}\int \limits _{0}^{1} {\phi _{2}^{\prime }} \bar{\phi }_{1} \mathrm{d}x - i v_{0} v_{1} \int \limits _{0}^{1} {\phi _{2}^{{\prime \prime }} \bar{\phi }_{1} \mathrm{d}x}} \right\} }}{{ - \left\{ {i\omega _{1} \int \limits _{0}^{1} {\phi _{1} \bar{\phi }_{1} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{1} \bar{\phi }_{1} \mathrm{d}x}} \right\} }}; \\ K_{3}= & {} \frac{{\frac{1}{2}\left\{ { - v_{1} \omega _{2} \int \limits _{0}^{1} {\phi _{1}^{\prime } \bar{\phi }_{2} \mathrm{d}x} - \frac{{v_{1} \varOmega _{1}}}{2}\int \limits _{0}^{1} {\phi _{1} ^{\prime }} \bar{\phi } \,\mathrm{d}x + i v_{0} v_{1} \int \limits _{0}^{1} {\phi _{1}^{{\prime }{\prime }} \bar{\phi }_{2} \mathrm{d}x}} \right\} }}{{ - \left\{ {i\omega _{2} \int \limits _{0}^{1} {\phi _{2} \bar{\phi }_{2} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }_{2} \mathrm{d}x}} \right\} }}; \\ K_{7}= & {} \frac{{\frac{1}{2}\left\{ {v_{2} \omega _{2} \int \limits _{0}^{1} {\bar{\phi }_{2}^{\prime } \bar{\phi }_{2} \mathrm{d}x - \frac{{v_{2} \varOmega _{2}}}{2}\int \limits _{0}^{1} {\bar{\phi }_{2}^{\prime }} \bar{\phi }_{2}} \mathrm{d}x + i v_{0} v_{2} \int \limits _{0}^{1} {\bar{\phi }_{2}^{{\prime \prime }} \bar{\phi }_{2} \mathrm{d}x}} \right\} }}{{ - \left\{ {i\omega _{2} \int \limits _{0}^{1} {\phi _{2} \bar{\phi }_{2} \mathrm{d}x} + v_{0} \int \limits _{0}^{1} {\phi ^{\prime }_{2} \bar{\phi }_{2} \mathrm{d}x}} \right\} }}; \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sahoo, B., Panda, L.N. & Pohit, G. Two-frequency parametric excitation and internal resonance of a moving viscoelastic beam. Nonlinear Dyn 82, 1721–1742 (2015). https://doi.org/10.1007/s11071-015-2272-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2272-1

Keywords

Search

Navigation