Skip to main content
SpringerLink
Log in

Control and observability aspects of phase synchronization

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

Synchronization phenomena have been studied from a control point of view for many years. However, the vast majority of papers consider complete synchronization, and very few have been devoted to phase synchronization. This paper addresses control and observability aspects of phase synchronization. In order to focus on fundamental aspects, a feedback control framework related to master–slave synchronization is considered. Comparing results using Cartesian and cylindrical coordinates in the context of such a framework and with three known oscillator models, it is argued that (1) observability does not play a significant role in phase synchronization, although it is granted that it might be relevant for complete synchronization, and (2) a practical difficulty is faced when phase synchronization is aimed at, but the control action is not a direct function of the phase error, as it is usually the case in synchronization studies. This difficulty with its fundamental and practical consequences is investigated in some detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Notes

  1. In case of bidirectional coupling (not directly investigated in this paper), the term \(k_2[x_1(t)-x_2(t)]\) would be added to the first equation of the second oscillator, and the oscillators are no longer called master or slave.

  2. Ideally, this signal should be a function of the phase error, e.g., \(e(t)=\phi _2(t)-\phi _1(t)\).

  3. A common nonlinear and \(2\pi \)-periodic control action is \(m_\phi (t)=k_\phi \sin [r_\phi (t)-\phi _1(t)]\). In this paper we use a \(2\pi \)-periodic control action \(m_\phi (t)=k_\phi \mathtt{wraptopi} [r_\phi (t)-\phi _1(t)]\), where wraptopi wraps angles to the range \((-\pi ,\,\pi ]\).

  4. In 2D this boils down to polar coordinates. Because in this paper 2D and 3D oscillators are considered, the term cylindrical coordinates will be used.

  5. The arctangent function is considered with two arguments: atan2(\(y,\,x\)), where the angle information can be obtained in the four quadrants.

  6. As for the origin of this system the following quotation is relevant “Since the first description of two-dimensional radially symmetric differential equations with limit cycles was given by Poincaré, we propose that these systems be called Poincaré oscillators” [31, p. 25]. However, it is pointed out that the denomination is used for a class of two-dimensional differential equations and the specific oscillator in (8) is not considered in that reference.

Abbreviations

CA:

Control action

CS:

Complete synchronization

MV:

Manipulated variable

PS:

Phase synchronization

References

  1. Boccaletti, S., Kurths, J., Osipov, G., Valladares, D.L., Zhou, C.S.: The synchronization of chaotic systems. Phys. Rep. 366(1–2), 1–101 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  2. Osipov, G.V., Kurths, J., Zhou, C.: Synchronization in Oscillatory Networks. Springer, Berlin (2007)

    Book  MATH  Google Scholar 

  3. Fujisaka, H., Yamada, T.: Stability theory of synchronized motion in coupled-oscillator systems. Prog. Theor. Phys. 69(1), 32–47 (1983). https://doi.org/10.1143/PTP.69.32

    Article  MathSciNet  MATH  Google Scholar 

  4. Kapitaniak, T.: Synchronization of chaos using continuous control. Phys. Rev. E 50(2), 1642–1644 (1994)

    Article  Google Scholar 

  5. Rosenblum, M.G., Pikovsky, A.S., Kurths, J.: Phase synchronization of chaotic oscillators. Phys. Rev. Lett. 76(11), 1804–1807 (1996)

    Article  MATH  Google Scholar 

  6. Piqueira, J.R.C.: Network of phase-locking oscillators and a possible model for neural synchronization. Commun. Nonlinear Sci. Numer. Simul. 16(9), 3844–3854 (2011). https://doi.org/10.1016/j.cnsns.2010.12.031

    Article  MathSciNet  MATH  Google Scholar 

  7. Kurths, J., Romano, M.C., Thiel, M., Osipov, G.V., Ivanchenko, M.V., Kiss, I.Z., Hudson, J.L.: Synchronization analysis of coupled noncoherent oscillators. Nonlinear Dyn. 44, 135–149 (2006). https://doi.org/10.1007/s11071-006-1957-x

    Article  MathSciNet  MATH  Google Scholar 

  8. Pereira, T., Batista, M.S., Kurths, J.: General framework for phase synchronization through localized sets. Phys. Rev. E 75, 026216 (2007). https://doi.org/10.1103/PhysRevE.75.026216

    Article  MathSciNet  Google Scholar 

  9. Belykh, V.N., Osipov, G.V., Kuckländer, N., Blasius, B., Kurths, J.: Automatic control of phase synchronization in coupled complex oscillators. Physica D 200(1–2), 81–104 (2005). https://doi.org/10.1016/j.physd.2004.10.008

    Article  MathSciNet  MATH  Google Scholar 

  10. Letellier, C., Aguirre, L.A.: Interplay between synchronization, observability, and dynamics. Phys. Rev. E 82, 016204 (2010). https://doi.org/10.1103/PhysRevE.82.016204

    Article  MathSciNet  Google Scholar 

  11. Aguirre, L.A., Letellier, C.: Controllability and synchronizability: are they related? Chaos Solitons Fractals 83, 242–251 (2016). https://doi.org/10.1016/j.chaos.2015.12.009

    Article  MathSciNet  MATH  Google Scholar 

  12. Sendiña-Nadal, I., Boccaletti, S., Letellier, C.: Observability coefficients for predicting the class of synchronizability from the algebraic structure of the local oscillators. Phys Rev E 94, 042205 (2016). https://doi.org/10.1103/PhysRevE.94.042205

    Article  Google Scholar 

  13. Parlitz, U., Junge, L., Kocarev, L.: Synchronization-based parameter estimation from time series. Phys. Rev. E 54(6), 6253–6259 (1996). https://doi.org/10.1103/PhysRevE.54.6253

    Article  Google Scholar 

  14. Maybhate, A., Amritkar, R.E.: Use of synchronization and adaptive control in parameter estimation from a time series. Phys. Rev. E 59, 284–293 (1999). https://doi.org/10.1103/PhysRevE.59.284

    Article  Google Scholar 

  15. Freitas, U.S., Macau, E.E.N., Grebogi, C.: Using geometric control and chaotic synchronization to estimate an unknown model parameter. Phys. Rev. E 71(4), 047203 (2005). https://doi.org/10.1103/PhysRevE.71.047203

    Article  Google Scholar 

  16. Sedigh-Sarvestani, M., Schiff, S.J., Gluckman, B.J.: Reconstructing mammalian sleep dynamics with data assimilation. PLoS Comput. Biol. 8(11), e1002788 (2012). https://doi.org/10.1371/journal.pcbi.1002788

    Article  MathSciNet  Google Scholar 

  17. Buscarino, A., Frasca, M., Branciforte, M., Fortuna, L., Sprott, J.C.: Synchronization of two Rössler systems with switching coupling. Nonlinear Dyn. 88, 673–683 (2016). https://doi.org/10.1007/s11071-016-3269-0

    Article  Google Scholar 

  18. Mahmoud, G.M., Mahmoud, E.E.: Phase and antiphase synchronization of two identical hyperchaotic complex nonlinear systems. Nonlinear Dyn. 61, 141–152 (2010). https://doi.org/10.1007/s11071-009-9637-2

    Article  MathSciNet  MATH  Google Scholar 

  19. Das, S., Srivastava, M., Leung, A.Y.T.: Hybrid phase synchronization between identical and nonidentical three-dimensional chaotic systems using the active control method. Nonlinear Dyn. 73, 2261–2272 (2013). https://doi.org/10.1007/s11071-013-0939-z

    Article  MathSciNet  MATH  Google Scholar 

  20. Stone, E.F.: Frequency entrainment of a phase coherent attractor. Phys. Lett. A 163, 367–374 (1992)

    Article  MathSciNet  Google Scholar 

  21. Kuramoto, Y.: Self-entrainment of a population of coupled non-linear oscillators. In: Araki, H. (ed.) Lecture Notes in Physics, vol. 39, pp. 420–422. Springer, Berlin (1975)

    Google Scholar 

  22. Dörfler, F., Bullo, F.: Synchronization in complex networks of phase oscillators: a survey. Automatica 50, 1539–1564 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  23. Josić, K., Mar, D.J.: Phase synchronization of chaotic systems with small phase diffusion. Phys. Rev. E 64, 056234 (2001). https://doi.org/10.1103/PhysRevE.64.056234

    Article  Google Scholar 

  24. Hsieh, G.C., Hung, J.C.: Phase-locked loop techniques—a survey. IEEE Trans. Industr. Electron. 43(6), 609–615 (1996)

    Article  Google Scholar 

  25. Kalman, R.E.: On the general theory of control systems. In: Proceedings of the First IFAC Congress Automatic Control, Butterworths, London, pp. 481–492 (1960)

  26. Hermann, R., Krener, A.J.: Nonlinear controllability and observability. IEEE Trans. Autom. Control 22(5), 728–740 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  27. Parlitz, U., Schumann-Bischoff, J., Luther, S.: Local observability of state variables and parameters in nonlinear modeling quantified by delay reconstruction. Chaos 24, 024411 (2014). https://doi.org/10.1063/1.4884344

    Article  MathSciNet  MATH  Google Scholar 

  28. Letellier, C., Aguirre, L.A., Maquet, J.: Relation between observability and differential embeddings for nonlinear dynamics. Phys. Rev. E 71, 066213 (2005)

    Article  MathSciNet  Google Scholar 

  29. Pecora, L.M., Carroll, T.L.: Synchronization in chaotic systems. Phys. Rev. Lett. 64(8), 821–824 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  30. Rosenblum, M., Pikovsky, A.S., Kurths, J.: From phase to lag synchronization in coupled chaotic oscillators. Phys. Rev. Lett. 78(22), 4193–4196 (1997)

    Article  MATH  Google Scholar 

  31. Glass, L., Mackey, M.C.: From Clocks to Chaos: The Rhythms of Life. Princeton University Press, Princeton (1988)

    MATH  Google Scholar 

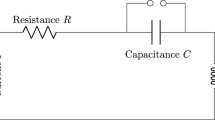
  32. van der Pol, B.: Forced oscillations in a circuit with non-linear resistance. Philos. Mag. J. Sci. 3(13), 65–80 (1927). https://doi.org/10.1080/14786440108564176

    Article  Google Scholar 

  33. Rössler, O.E.: An equation for continuous chaos. Phys. Lett. 57A(5), 397–398 (1976)

    Article  MATH  Google Scholar 

  34. Mormann, F., Lehnertz, K., David, P., Elger, C.E.: Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients. Physica D 144, 358–369 (2000)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

LAA gratefully acknowledges the financial support from CNPq. LF is grateful to IFMG Campus Betim for an academic leave. The authors thank Christophe Letellier for commenting on an early draft of this paper.

Funding

Funding was provided by Conselho Nacional de Desenvolvimento Científico e Tecnológico (Grant No. 302079/2011-4).

Author information

Authors and Affiliations

  1. Departamento de Engenharia Eletrônica, Universidade Federal de Minas Gerais, Av. Antônio Carlos 6627, Belo Horizonte, MG, 31.270-901, Brazil

    Luis A. Aguirre

  2. Programa de Pós-Graduação em Engenharia Elétrica, Universidade Federal de Minas Gerais, Av. Antônio Carlos 6627, Belo Horizonte, MG, 31.270-901, Brazil

    Luis A. Aguirre & Leandro Freitas

  3. Instituto Federal de Educação, Ciência e Tecnologia de Minas Gerais Campus Betim, Betim, MG, 32.677-564, Brazil

    Leandro Freitas

Authors
  1. Luis A. Aguirre
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Leandro Freitas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Luis A. Aguirre.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aguirre, L.A., Freitas, L. Control and observability aspects of phase synchronization. Nonlinear Dyn 91, 2203–2217 (2018). https://doi.org/10.1007/s11071-017-4009-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-4009-9

Keywords

Search

Navigation