Projective lag quasi-synchronization of coupled systems with mixed delays and parameter mismatch: a unified theory

Abstract

This paper investigates the projective lag quasi-synchronization by feedback control of a coupled dynamical system with delays and parameter mismatches on arbitrary time domains. Being formulated on time scales, our results are valid simultaneously for continuous- and discrete-time models as well as for any non-standard time domain. Furthermore, the controller design respects the structure of the equations so that we can characterize the stabilization by a limited controller action. Our proofs rely on the unified matrix-measure theory and the generalized Halanay inequality on time scales. We validate our theoretical results with several simulation examples on various time domains.

1 Introduction

Synchronization is a fundamental property of dynamic systems, where two or more systems achieve a coordinated behaviour, typically through the use of coupling or external forces. It has been an interesting problem since the seminal work of Pecora and Carroll [1] and has applications in many fields of engineering and science, such as image encryption [2], signal and image processing [3], and secure communication [4]. As a result, in the last two decades, many authors have studied the synchronization problem for various types of continuous-time and discrete-time dynamic systems; see, for example, [5,6,7,8,9,10,11,12,13,14,15,16], and the references cited therein. To establish the synchronization results, the authors mainly used two techniques: one is the Lyapunov technique or functional method, see, for instance, [5,6,7,8,9,10]. The second technique is based on the direct method or matrix-measure method which comes with a general algebraic approach to stability or stabilizability as opposed to the often problem-specific construction of Lyapunov functions. The stability and synchronization problem using the matrix-measure method has been studied, for example, in [11,12,13,14,15].

In the literature, researchers have developed different types of synchronization schemes such as exponential synchronization [17, 18], quasi-synchronization [19, 20], lag synchronization [21], and projective synchronization [22]. Among these schemes, projective lag synchronization [23] is a scheme that includes both the projective and lag factors. Here, the state of the response system y lags behind the state of the master system x proportionally after a transient time, i.e. $y(t) = \alpha x (t-\varsigma )$, where $\varsigma >0$ is the lag delay and $\alpha$ is a projective real constant. This scheme has been used in secure communication to extend binary digital to M-nary digital and achieve fast communication [23] and has received more attention in recent years [24,25,26,27]. Particularly, in [25], the authors investigated projective lag synchronization in spatiotemporal chaotic systems with disturbances and time delay using the sliding mode control technique. In [26], the finite-time generalized projective lag synchronization of neutral-type neural networks with delay was studied by using the Gronwall–Bellman inequality and nonlinear feedback control. Additionally, [27] addressed function projective lag synchronization in chaotic systems by utilizing nonlinear adaptive impulsive control and the Lyapunov stability theory.

Further, in many practical applications, parameter mismatches between the drive and response systems are a common issue which can significantly impact the convergence rate of synchronization or even completely prevent synchronization from occurring. Therefore, it is important to establish synchronization results in systems with parameter mismatches. Recently, few authors have investigated the parameter mismatches systems (see, for example, [28,29,30,31,32,33,34,35,36,37,38]). In particular, the authors in Zou et al. [31] proposed two novel protocols for leader–follower and leaderless scenarios using the reference trajectory-based method. They also investigated finite-time consensus in second-order multi-agent systems with non-identical nonlinear dynamics under directed networks by using graph theory, Lyapunov functional method, and finite-time stability theory. In Huang et al. [32] and Yuan et al. [33], the authors discussed the projective lag synchronization and lag quasi-synchronization of coupled systems with parameter mismatch and mixed delays by using the intermittent control and Lyapunov techniques, while in Chen and Cao [34] and He et al. [35], the authors studied the projective synchronization and lag quasi-synchronization results of two coupled delayed systems with parameter mismatch by using the feedback control, generalized Halanay inequality, and matrix-measure method. Additionally, in Huang et al. [36], the authors investigated the weak projective lag synchronization results for coupled neural networks with parameter mismatch and delay by using the feedback control and Lyapunov stability theorem. In Feng and Yang [37], the authors studied the projective lag synchronization results for two different discrete-time chaotic systems by using the feedback controller and Lyapunov method, and in Xiao and Huang [38], the problem of quasi-synchronization for discrete-time inertial neural networks with delay was studied by using the matrix-measure method.

It is worth noting that all the aforementioned results about synchronization have been studied for continuous-time and discrete-time systems but separately. Apart from these separate studies being possibly partially redundant, there exist physical models that consider continuous and discrete evolution at the same time or on some different timelines. For example, in a simple RLC circuit (see Fig. 1), a dynamical scenario with a discharge of the capacitor that takes $\delta >0$ time units and occurs periodically after l time units can conveniently be modelled on the time domain [39]: $T = \cup _{l=0}^\infty [l, l+1-\delta ].$

Fig. 1

A simple RLC circuit

Further, the life span of several species including Pharaoh-Cicada, Magi-Cicada Cassini, and Magi-Cicada Septendecim is represented by the union of equal-length closed time intervals with some gap, i.e. they grow continuously as well as discretely in different stages of their life, and hence, to examine the dynamic properties of these species, one may consider a time domain $T = \cup _{l=0}^\infty [l(c + d), l(c+d) + d],$ where $c, d \in {\mathbb {R}}^+$ [39]. Furthermore, certain neurons in our brain are active during the day and inactive at night, and this process continues with respect to time. The active dynamics of neurons can be intuitively viewed in the time domain ${\mathbb {T}} = \cup _{l=0}^\infty [24l, 24l+d_l],$ where $d_l$ denotes the number of active hours of the neurons in each day (see Fig. 2).

Fig. 2

Red lines denote the active time of neurons in day, while the gap shows the inactive time of neurons at night (color figure online)

Since these types of models evolve in both continuous- and discrete-time domains, in order to study their dynamic behaviour more accurately, we require a dynamic system that can simultaneously incorporate both continuous and discrete-time domains. In this regard, Hilger [40] introduced the concept of time scales theory (measure chain theory), which unifies, extends, and bridges the conventional continuous and discrete dynamical systems into a single unified theory. The results obtained on time scales are not only applicable to discrete and continuous-time domains but also valid for any hybrid-type time domains (a combination of discrete and continuous-time domain, non-uniform discrete sets) which are useful in the study of various complex dynamical systems. For further study on time scales calculus, see [39, 41].

In recent years, time scales theory has gained significant attention due to its diverse applications in science and engineering, including control theory [42], economics [43], and epidemiology [44]. Qualitative properties of dynamic equations on time scales, such as positivity, observability, controllability, and stability, have been extensively studied (see, for instance, [45,46,47,48] and references therein). However, few studies have investigated the synchronization of coupled dynamic systems on time scales [49,50,51,52,53,54,55,56]. Particularly, in Lu et al. [52], synchronization results were investigated for complex dynamical networks with delays on time scales by using the unified Wirtinger-based inequality, while in Ali and Yogambigai [53], global exponential synchronization results of dynamical networks with delays on time scales were studied by employing the Lyapunov–Krasovskii functional and unified Jensen’s inequalities. The works in Wang et al. [54] investigated the problem of synchronization of non-autonomous recurrent neural networks with delays on time scales by applying the comparison lemma and Lyapunov techniques. In Huang et al.  [55], the authors studied quasi-synchronization results for neural networks with parameter mismatches on time scales using the Lyapunov functional method. Recently, Kumar et al. [56] investigated the exponential lag synchronization results of Cohen–Grossberg-type neural networks with mixed delays on time scales by using the matrix-measure and Halanay inequality. It should be noted that the synchronization results for continuous and discrete systems with parameter mismatches have been studied in [28,29,30, 32, 34,35,36, 38], with some utilizing the Lyapunov method [28, 32, 36] and others employing the matrix-measure method [29, 30, 34, 35, 38]. However, these results cannot be easily applied and extended to the hybrid time domains. Also, to the best of the authors’ knowledge, there is no work reported on the projective lag quasi-synchronization (PLQS) of coupled dynamic systems on hybrid-type time domains.

When it comes to considering coupled systems on time scales, several relevant questions arise, such as: What type of time scales conditions must be met for different types of synchronization? Does any relationship exist between synchronization and time scale? It is well known that for computational purposes, continuous-time systems described by differential equations are discretized, in such cases, how can one ensure the selection of an appropriate discrete-time system? Can the synchronization error bound in the existing literature be further refined? Motivated by the above discussion and questions, this manuscript aims to establish PLQS results for coupled dynamic systems with mixed delays and parameter mismatches on time scales using the matrix-measure technique. The main contributions of this manuscript can be highlighted as follows.

• We apply the time scales approach to investigate the problem of PLQS for coupled dynamic systems on arbitrary time domains with mixed delays and parameter mismatches.

• Continuous and discrete-time domains are the particular cases of time scales, and hence, the obtained PLQS scheme is not just true for the continuous-time or discrete-time state analysis, but additionally hold for any mixture of these two, which provides a wider range of applications.

• We refine the theoretical error bound so that it is close to the simulation error.

• We also provide conditions under which the obtained results can be extended to the case of projective quasi-synchronization, lag quasi-synchronization, and quasi-synchronization.

• Three examples are presented to validate the analytical outcomes of this manuscript.

The rest of the manuscript is structured as follows: We provide fundamental notations, definitions, and lemmas in Sect. 2. Section 3 presents the statement of the proposed problem. We establish the main results of this manuscript in Sect. 4. Finally, in Sect. 5, we provide three illustrative examples to validate the obtained analytical results.

2 Preliminaries

We use ${{\,\textrm{Id}\,}}$ to represent the identity matrix of suitable order and superscript T for matrix transpose. The symbol $\emptyset$ denotes the empty set. The space ${\mathbb {R}}^n$ refers to the n-dimensional Euclidean space. The collection of all continuous functions from $[a, b]_{\mathbb {T}}$ into ${\mathbb {R}}^n$, represented by $C([a,b]_{\mathbb {T}},{\mathbb {R}}^n)$, form a Banach space equipped with the induced norm $\Vert x\Vert _p = \sup _{t \in [a,b]_{\mathbb {T}}} \Vert x(t)\Vert _p$, where $p \in \{ 1,2,\infty \}$ and $\Vert \cdot \Vert _p$ is a vector norm. For any $x \in {\mathbb {R}}^n$ and $p=1,2,\infty$, the vector norm is defined as

$$\begin{aligned} \Vert x\Vert _1 = \sum _{k=1}^n \vert x_k \vert , \ \Vert x\Vert _2 = \sqrt{\sum _{k=1}^n x_k^2}, \ \Vert x\Vert _\infty = \max _{1 \le k \le n} \vert x_k \vert . \end{aligned}$$

Next, we recall some basic definitions of time scales and matrix-measure which will be used in the subsequent sections.

A time scale is a non-empty closed subset of the real numbers ${\mathbb {R}}$ which inherits its topology and ordering from ${\mathbb {R}}$. Now onwards, we denote a time scale by ${\mathbb {T}}$. ${\mathbb {R}}$, $h{\mathbb {Z}}$ for $h>0$, and ${\mathbb {P}}_{c,d} = \bigcup _{l=0}^\infty [l(c+d), l(c+ d ) + d], c,d \in {\mathbb {R}}^+$ are some typical examples of time scales. We represent a time scale interval as $[c,d]_{\mathbb {T}}$, which is defined as the set ${t \in {\mathbb {T}}: c \le t \le d}$.

The backward and forward jump operators $\rho , \sigma : {\mathbb {T}} \rightarrow {\mathbb {T}}$ are defined as $\rho (t) = \sup \{ r < t: r \in {\mathbb {T}}\}$ and $\sigma (t) = \inf \{r> t: r \in {\mathbb {T}}\}$, respectively, with the substitutions $\sup \emptyset = \inf {\mathbb {T}}$ and $\inf \emptyset = \sup {\mathbb {T}}$. Additionally, we define the graininess function $\mu : {\mathbb {T}}\rightarrow [0,\infty )$ as $\mu (t) = \sigma (t) - t$. For $t\in {\mathbb {T}}$, if $t < \sup {\mathbb {T}}$ and $\sigma (t) = t$, then t is called right-dense point of ${\mathbb {T}}$.

Let us define the set ${\mathbb {T}}^\kappa$ as follows:

$$\begin{aligned} {\mathbb {T}}^\kappa = {\left\{ \begin{array}{ll} {\mathbb {T}}^\kappa \setminus (\rho (\sup ({\mathbb {T}})), \sup ({\mathbb {T}})] \quad &{}\text {if} \ \sup {\mathbb {T}} < \infty ,\\ {\mathbb {T}} \quad &{}\text {if} \ \sup {\mathbb {T}} = \infty . \end{array}\right. } \end{aligned}$$

Now, we will provide the definition of the delta derivative (also known as the Hilger derivative), which extends the notions of the ordinary derivative and difference operator.

Definition 1

([54], Def. 1) Let $f: {\mathbb {T}} \rightarrow {\mathbb {R}}$ be a function and $t\in {\mathbb {T}}^\kappa$. The Hilger (or delta) derivative of f at t, denoted by $f^\Delta (t)$, is defined as the number (if it exists) such that for any given $\epsilon > 0$, there exists a neighbourhood U of t satisfying the inequality

$$\begin{aligned} \vert [f(\sigma (t))- f(s)] - f^\Delta (t)[\sigma (t)-s] \vert \le \epsilon \vert \sigma (t)-s \vert \end{aligned}$$

for all $s \in U$. Furthermore, the delta derivative can be referred to as the upper right Dini-$\Delta$-derivative denoted by $D^+_\Delta f(t)$, if the right-sided neighbourhood $U^+$ replaces the neighbourhood U.

Remark 1

In Definition 1, if we consider

• ${\mathbb {T}}=h{\mathbb {Z}}$, $h>0$, then the delta derivative $f^\Delta (t)$ becomes the usual h-difference forward operator, i.e. $f^\Delta (t)=\Delta ^h f(t)= \frac{f(t+h)-f(t)}{h}$.

• ${\mathbb {T}}={\mathbb {R}}$, then the delta derivative $f^\Delta (t)$ becomes the usual ordinary derivative $f^ \prime (t)$ and the upper right Dini-$\Delta$-derivative $D^+_\Delta f(t)$ becomes the ordinary upper right Dini-derivative $D^+ f(t)$.

Theorem 1

([39], Theorem 1.16) Assume that $f: {\mathbb {T}} \rightarrow {\mathbb {R}}$ is differentiable at $t \in {\mathbb {T}}^\kappa$, then we have

$$\begin{aligned} f(\sigma (t)) = f(t) + \mu (t)f^\Delta (t). \end{aligned}$$

A function $f: {\mathbb {T}} \rightarrow {\mathbb {R}}$ is said to be regressive (or positive regressive) if $1+\mu (t)f(t)\ne 0$ (or $>0$) for all $t\in {\mathbb {T}}$. Further, f is said to be a regulated function if its right and left side limit exists (finitely) at all right and left dense points of ${\mathbb {T}}$, respectively. Additionally, a regulated function f is said to be rd-continuous, if it is continuous at all the right-dense points of ${\mathbb {T}}$. The sets of all rd-continuous functions and rd-continuous regressive (positive) functions on ${\mathbb {T}}$ are denoted by $C_{rd}({\mathbb {T}},{\mathbb {R}})$ and ${\mathcal {R}} ({\mathcal {R}}^+)$, respectively.

The generalized delta integral on time scales is defined as follows.

Definition 2

( [39], Def. 1.71) A function $F: {\mathbb {T}} \rightarrow {\mathbb {R}}$ is said to be an anti-derivative of a regulated function $f: {\mathbb {T}} \rightarrow {\mathbb {R}}$, if for all $t \in {\mathbb {T}}^\kappa$, the relation $F^\Delta (t) = f(t)$ holds. Further, the Cauchy integral is defined by

$$\begin{aligned} \int _{c}^d f(s) \Delta s = F(d)-F(c) \ \ \text {for all } c,d \in {\mathbb {T}}. \end{aligned}$$

Theorem 2

([39], Theorem. 1.77) Let $c, d \in {\mathbb {T}}$ and $f \in C_{rd}({\mathbb {T}},{\mathbb {R}})$, then, for

• ${\mathbb {T}}=h {\mathbb {Z}} = \{hk: k \in {\mathbb {Z}}\}$, where $h > 0$, we have

  $$\begin{aligned} \int _c^d f(s) \Delta s = {\left\{ \begin{array}{ll} \sum _{k=\frac{c}{h} }^{\frac{d}{h}-1} h f(kh) \quad &{} \text {if} \ c<d,\\ 0 &{} \text {if} \ c=d,\\ - \sum _{k=\frac{c}{h} }^{\frac{d}{h}-1} h f(kh) \quad &{} \text {if} \ c>d. \end{array}\right. } \end{aligned}$$

• $\mathbb {T=R}$, we have

  $$\begin{aligned} \int _c^d f(s) \Delta s = \int _c^d f(s) ds. \end{aligned}$$

In the next definition, we are defining the classical matrix-measure.

Definition 3

([57], Def. 2.1) For a real square matrix $A = (a_{kl})_{n \times n}$, the classical matrix-measure with respect to the $p-$norm $(p=1, 2$ or $\infty )$ is defined as

$$\begin{aligned} \Upsilon _p (A) = \lim _{s \rightarrow 0^+} \dfrac{\Vert {{\,\textrm{Id}\,}}+ s A\Vert _p - 1}{s}, \end{aligned}$$

where $\Vert \cdot \Vert _p$ is the induced matrix norm on ${\mathbb {R}}^{n \times n}$. Table 1 provides the matrix norms and related measures.

Table 1 Matrix norms and related measures

Next, we recall how the matrix-measure is generalized to time scales:

Definition 4

([48], Def. 2 ) For a real square matrix $A = (a_{kl})_{n \times n}$, the unified matrix-measure on an arbitrary time scale ${\mathbb {T}}$ with respect to the $p-$norm $(p=1, 2$ or $\infty )$ is defined as

$$\begin{aligned} M_p(A,{\mathbb {T}}) = {\left\{ \begin{array}{ll} &{} \max \biggl \{ \dfrac{\Vert {{\,\textrm{Id}\,}}+ \mu (t) A\Vert _p - 1}{\mu (t)}:t \in {\mathbb {T}}\biggr \}, \text {if } \ \mu (t)> 0, \forall \ t\in {\mathbb {T}},\\ &{} \max \biggl \{ \Upsilon _p(A), \ \max \Bigl \{ \dfrac{\Vert {{\,\textrm{Id}\,}}+ \mu (t) A\Vert _p - 1}{\mu (t)}:\ t \in {\mathbb {T}},\mu (t)>0\Bigr \} \biggr \}, \ \text {else.} \end{array}\right. } \end{aligned}$$

Note that for ${\mathbb {T}}= {\mathbb {R}}$, Definition 4 reduces to Definition 3. Also, for ${\mathbb {T}} = h{\mathbb {Z}}$, $h>0$, which means that $\mu (t)=h$ for all $t\in {\mathbb {T}}$, Definition 4 reads

$$\begin{aligned} \omega _p (A,h) = \dfrac{\Vert {{\,\textrm{Id}\,}}+ h A\Vert _p - 1}{h}. \end{aligned}$$

We are ending this section by giving the following important result:

Theorem 3

(Halanay inequality [41], Theorem 2.1) Let $z(t) \in C_{rd}({\mathbb {T}},{\mathbb {R}})$ be a nonnegative function satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} D^+_\Delta z(t) &{} \le - a(t) z(t) + b(t) \sup _{s \in [t-\vartheta , t]_{\mathbb {T}}} z(s) + c(t), \ t \in [0, \infty )_{\mathbb {T}}, \\ z(s) &{} = \Phi (s), \ s \in [-\vartheta ,0]_{\mathbb {T}}, \end{array}\right. } \end{aligned}$$

where $\vartheta >0, a(t), b(t), c(t)$ are nonnegative rd-continuous functions, $\Phi \in C_{rd}([-\vartheta ,0]_{\mathbb {T}},{\mathbb {R}})$, and $-a(t) \in {\mathcal {R}}^+$. If there exist constants $\delta >0$ and $k\in (0,1)$ such that

$$\begin{aligned} a(t)-b(t)\ge \delta>0, \ \ k a(t) - b(t) >0, \ t \in [0,\infty )_{\mathbb {T}}, \end{aligned}$$

then for any given $\epsilon >0$, there exists a $T =T(M, \epsilon ) > 0$ such that

$$\begin{aligned} z(t) \le \dfrac{c}{\delta } + \epsilon , \ t \in [T,\infty )_{\mathbb {T}}, \end{aligned}$$

where $c= \sup _{t \ge -\vartheta } c(t)$ and $M = \sup _{s \in [-\vartheta ,0]_{\mathbb {T}}} \vert \Phi (s) \vert$.

3 Problem description

We consider the following coupled dynamical system with discrete and distributed delays on time scales:

$$\left\{ {\begin{array}{*{20}l} \begin{gathered} x^{\Delta } (t) = \widehat{{\mathcal{Q}}}x(t) + \widehat{{\mathcal{R}}}{\mathcal{F}}(x(t)) + \widehat{{\mathcal{S}}}{\mathcal{G}}(x(t - \vartheta _{1} (t))) + \widehat{{\mathcal{T}}}\int_{{t - \vartheta _{2} (t)}}^{t} {\mathcal{H}} (x(s))\Delta s, \; t \in [0,\infty )_{{\mathbb{T}}} , \hfill \\ \end{gathered} \hfill \\ {x(s) = \hat{\phi }(s),\;s \in [ - \vartheta ,0]_{{\mathbb{T}}} ,} \hfill \\ \end{array} } \right.$$

(1)

where $x(t) \in {\mathbb {R}}^n;$ ${\hat{\mathcal {Q}}}, {\hat{\mathcal {R}}}, {\hat{\mathcal {S}}}, {\hat{\mathcal {T}}} \in {\mathbb {R}}^{n \times n}$ are constant matrices; $\vartheta _1(t)(>0)$ is the discrete delay such that $t-\vartheta _1(t) \in {\mathbb {T}}$ and $0 \le \vartheta _1(t) \le \eta _1$ for all $t \in {\mathbb {T}}$; $\vartheta _2(t)(>0)$ is the distributed delay such that $t-\vartheta _2(t) \in {\mathbb {T}}$ and $0 \le \vartheta _2(t) \le \eta _2$ for all $t \in {\mathbb {T}}$; $\eta _1$ and $\eta _2$ are positive constants; $\eta = \max \{\eta _1,\eta _2\}$; ${\hat{\phi }} \in C_{rd}([-\eta ,0]_{\mathbb {T}}, {\mathbb {R}}^n)$; and $\mathcal {F}(x(\cdot )), \mathcal {G}(x(\cdot )), \mathcal {H}(x(\cdot ))$ are functions in ${\mathbb {R}}^n$ which satisfy certain conditions to be specified later.

Let us consider the system (1) as the drive system and the corresponding response system with parameter mismatches in the coefficient matrices as

$$\left\{ {\begin{array}{*{20}l} \begin{gathered} y^{\Delta } (t) = {\mathcal{Q}}y(t) + {\mathcal{R}\mathcal{F}}(y(t)) + {\mathcal{S}\mathcal{G}}(y(t - \vartheta _{1} (t))) \\ \quad \quad \quad \;\;+ {\mathcal{T}}\int_{{t - \vartheta _{2} (t)}}^{t} {\mathcal{H}} (y(s))\Delta s \hfill + u(t),\;t \in [0,\infty )_{{\mathbb{T}}} , \hfill \\ \end{gathered} \hfill \\ {y(s) = \phi (s),\;s \in [ - \eta ,0]_{{\mathbb{T}}} ,} \hfill \\ \end{array} } \right.$$

(2)

where $y(t) \in {\mathbb {R}}^n$; $\mathcal {Q}, \mathcal {R}, \mathcal {S}, \mathcal {T}\in {\mathbb {R}}^{n \times n}$ are constant matrices such that ${\hat{\mathcal {Q}}} \ne \mathcal {Q}, {\hat{\mathcal {R}}} \ne \mathcal {R}, {\hat{\mathcal {S}}} \ne \mathcal {S}, {\hat{\mathcal {T}}} \ne \mathcal {T}$; $\phi \in C_{rd}([-\eta ,0]_{\mathbb {T}}, {\mathbb {R}}^n)$. Due to the finite speed of transmission and spreading, there is a time delay associated with the signal travelling from the master system to the slave system. To account for this delay, we introduce the following controller

$$\begin{aligned} u(t) = -\mathcal {K}(y(t) - \alpha x(t-\varsigma )), \end{aligned}$$

(3)

where $\mathcal {K}$ is the coupling matrix, $\alpha$ is the projective constant, and $\varsigma$ is the transmittal delay with $t-\varsigma \in {\mathbb {T}}$.

Let’s define the error by $e(t) = y(t) - \alpha x(t-\varsigma )$, between the drive system (1) and the response system (2), so that the related error dynamical system can be written as

$$\begin{aligned} e^\Delta (t)&= (\mathcal {Q}-\mathcal {K})e(t) + \mathcal {R}{\bar{\mathcal {F}}}(e(t)) + \mathcal {S}{\bar{\mathcal {G}}}(e(t-\vartheta _1(t))) \nonumber \\&\quad + \mathcal {T}\int _{t-\vartheta _2(t)}^t {\bar{\mathcal {H}}}(e(s)) \Delta s \nonumber \\&\quad + F(x,\vartheta _1(t),\vartheta _2(t),\alpha ,\varsigma ), \end{aligned}$$

(4)

where $e(t)\in {\mathbb {R}}^n$; ${\bar{\mathcal {F}}}(e(\cdot )):= \mathcal {F}(y(\cdot )) - \mathcal {F}(y(\cdot ) - e(\cdot ))$; ${\bar{\mathcal {G}}}(e(\cdot )):= \mathcal {G}(y(\cdot )) - \mathcal {G}(y(\cdot ) - e(\cdot ))$; ${\bar{\mathcal {H}}}(e(\cdot )):= \mathcal {H}(y(\cdot )) - \mathcal {H}(y(\cdot ) - e(\cdot ))$ and

$$\begin{aligned}&F (x, \vartheta _1(t),\vartheta _2(t),\alpha ,\varsigma )\\&:= \alpha (\mathcal {Q}-{\hat{\mathcal {Q}}}) x(t-\varsigma ) + \mathcal {R}\mathcal {F}(\alpha x(t-\varsigma )) - \alpha {\hat{\mathcal {R}}} \mathcal {F}(x(t-\varsigma )) \\&\quad + \mathcal {S}\mathcal {G}(\alpha x(t-\varsigma - \vartheta _1(t))) - \alpha {\hat{\mathcal {S}}} \mathcal {G}(x(t-\varsigma -\vartheta _1(t))) \\&\quad + \int _{t-\vartheta _2(t)}^t (\mathcal {T}\mathcal {H}(\alpha x (s-\varsigma )) -\alpha {\hat{\mathcal {T}}} \mathcal {H}(x(s-\varsigma )) ) \Delta s. \end{aligned}$$

To account for the delays, we set $x(s) = {\hat{\phi }}(-\eta )$ for all $s \in [-\eta -\varsigma , -\eta ]_{\mathbb {T}}$ and

$$\begin{aligned} \psi (s) = {\left\{ \begin{array}{ll} {\hat{\phi }}(s), \ s \in [-\eta , 0]_{\mathbb {T}},\\ {\hat{\phi }}(-\eta ), \ s \in [-\eta -\varsigma , -\eta ]_{\mathbb {T}}. \end{array}\right. } \end{aligned}$$

The initial condition for the error dynamics (4) can be defined by

$$\begin{aligned} e(s) = \phi (s) - \psi (s-\varsigma ), \ s \in [-\eta ,0]_{\mathbb {T}}. \end{aligned}$$

It could be noticed that, due to the parameter mismatches between the drive systems (1) and response system (2), the origin $e=0$ is not an equilibrium point of the error system (4); therefore, complete projective lag synchronization is not possible. However, we provide the PLQS scheme which synchronizes the drive-response systems up to a small error bound. Mathematically we can define the PLQS as follows.

Definition 5

The drive system (1) and the response system (2) are said to be projective lag quasi-synchronized to an error bound $\epsilon _p$ in the timescale sense if it holds that

$$\begin{aligned} \Vert y(t) - \alpha x(t-\varsigma )\Vert _p \le \epsilon _p \ \text {as} \ t \rightarrow \infty . \end{aligned}$$

Remark 2

In Definition 5, the drive system (1) and the response system (2) are called

• projective quasi-synchronized to the error bound $\epsilon _p$, if $\varsigma = 0$;

• lag quasi-synchronized to the error bound $\epsilon _p$, if $\alpha = 1$;

• quasi-synchronized to the error bound $\epsilon _p$, if $\alpha = 1$ and $\varsigma =0$.

To prove the main results, we need the following assumptions.

Assumption 1

(Ass. 3 in [34]) The state x of the drive system evolves in a bounded state space $\Omega \subset {\mathbb {R}}^n$. In particular, there exists a constant $\beta _p$ so that $\Vert x(t) \Vert _p \le \beta _p$ for $p=1,2,\infty$.

Assumption 2

(Ass. 1 in [34]) $\mathcal {F}, \mathcal {G},$ and $\mathcal {H}$ are Lipschitz on $\Omega$, i.e. for any $z_1, z_2 \in \Omega$, there exist positive constants $L_\mathcal {F}, L_\mathcal {G},$ and $L_\mathcal {H}$ such that

$$\begin{aligned} \Vert \mathcal {F}(z_1)-\mathcal {F}(z_2)\Vert _p&\le L_{\mathcal {F}} \Vert z_1-z_2\Vert _p, \\ \Vert \mathcal {G}(z_1)-\mathcal {G}(z_2)\Vert _p&\le L_{\mathcal {G}} \Vert z_1-z_2\Vert _p, \\ \Vert \mathcal {H}(z_1)-\mathcal {H}(z_2)\Vert _p&\le L_{\mathcal {H}} \Vert z_1-z_2\Vert _p \end{aligned}$$

for $p=1,2,\infty .$

Remark 3

Note that in many applied neural networks, typical choices of the activation functions like tanh or Sigmoid fulfil Assumption 2. Moreover, in Assumption 2, we do not require $f(0)=0$ and $g(0)=0$ which is required in some existing works [29, 34]. This implies that a broad spectrum of nonlinear functions satisfies Assumption 2.

Remark 4

In the previous studies [5, 6], time delays have been considered as differentiable, but in this study, we do not require such assumption.

Remark 5

Since $\mathcal {F}, \mathcal {G},$ and $\mathcal {H}$ are Lipschitz on $\Omega ,$ they are also bounded on $\Omega .$ This means that there exist positive constants $K_\mathcal {F}, K_\mathcal {G},$ and $K_\mathcal {H}$ such that $\Vert \mathcal {F}(z)\Vert _p \le K_{\mathcal {F}},$ $\Vert \mathcal {G}(z)\Vert _p \le K_{\mathcal {G}}$, and $\Vert \mathcal {H}(z)\Vert _p \le K_{\mathcal {H}}$ for all $z \in \Omega$ and $p=1,2,\infty .$

4 Projective lag quasi-synchronization

In this section, we will derive some sufficient conditions for PLQS of the drive system (1) and the response system (2) by using the matrix-measure theory and generalized Halanay inequality. Prior to that, we introduce an important lemma that is required to establish these conditions.

Lemma 1

Under Assumptions 1 and 2, $F(x,\vartheta _1(t), \vartheta _2(t), \alpha , \varsigma )$ is bounded by a constant $c_p>0$, i.e.

$$\begin{aligned} \Vert F(x,\vartheta _1(t), \vartheta _2(t), \alpha , \varsigma )\Vert _p \le c_p, \end{aligned}$$

where

$$\begin{aligned} c_p&= \vert \alpha \vert \Vert (\mathcal {Q}-{\hat{\mathcal {Q}}})\Vert _p \beta _p + (\Vert \mathcal {R}\Vert _p + \vert \alpha \vert \Vert {\hat{\mathcal {R}}}\Vert _p )K_\mathcal {F}\\&\quad + (\Vert \mathcal {S}\Vert _p + \vert \alpha \vert \Vert {\hat{\mathcal {S}}}\Vert _p )K_\mathcal {G}\\&\quad + \eta _2 (\Vert \mathcal {T}\Vert _p + \vert \alpha \vert \Vert {\hat{\mathcal {T}}}\Vert _p ) K_\mathcal {H}. \end{aligned}$$

Proof

For any $x \in \Omega$, we have

$$\begin{aligned}&\Vert F(x,\vartheta _1(t), \vartheta _2(t), \alpha , \varsigma ) \Vert _p\nonumber \\&\le \Vert \alpha (\mathcal {Q}-{\hat{\mathcal {Q}}}) x(t-\varsigma ) \Vert _p + \Vert \mathcal {R}\mathcal {F}(\alpha x(t-\varsigma )) - \alpha {\hat{\mathcal {R}}} \mathcal {F}(x(t-\varsigma )) \Vert _p \nonumber \\&\quad + \Vert \mathcal {S}\mathcal {G}(\alpha x(t-\varsigma - \vartheta _1(t))) - \alpha {\hat{\mathcal {S}}} \mathcal {G}(x(t-\varsigma -\vartheta _1(t))) \Vert _p \nonumber \\&\quad + \Vert \int _{t-\vartheta _2(t)}^t (\mathcal {T}\mathcal {H}(\alpha x (s-\varsigma )) -\alpha {\hat{\mathcal {T}}} \mathcal {H}(x(s-\varsigma )) ) \Delta s \Vert _p. \end{aligned}$$

(5)

Now, from Assumptions 1 and 2, we get

$$\begin{aligned}&\Vert \mathcal {R}\mathcal {F}(\alpha x(t-\varsigma )) - \alpha {\hat{\mathcal {R}}} \mathcal {F}(x(t-\varsigma )) \Vert _p \nonumber \\& \quad \le \Vert \mathcal {R}\mathcal {F}(\alpha x(t-\varsigma )) \Vert _ p + \Vert \alpha {\hat{\mathcal {R}}} \mathcal {F}(x(t-\varsigma )) \Vert _p \nonumber \\& \quad \le \Vert \mathcal {R}\Vert _p K_\mathcal {F}+ \vert \alpha \vert \Vert {\hat{\mathcal {R}}}\Vert _p K_\mathcal {F}. \end{aligned}$$

(6)

Similarly, we obtain

$$\begin{aligned}&\Vert \mathcal {S}\mathcal {G}(\alpha x(t-\varsigma -\vartheta _1(t))) - \alpha {\hat{\mathcal {S}}} \mathcal {G}(x(t-\varsigma -\vartheta _1(t))) \Vert _p \nonumber \\& \quad \le \Vert \mathcal {S}\Vert _p K_\mathcal {G}+ \vert \alpha \vert \Vert {\hat{\mathcal {S}}}\Vert _p K_\mathcal {G} \end{aligned}$$

(7)

and

$$\begin{aligned}&\int _{t-\vartheta _2(t)}^t (\Vert \mathcal {T}\mathcal {H}(\alpha x(s-\varsigma )) - \alpha {\hat{\mathcal {T}}} \mathcal {H}(x(t-\varsigma )) \Vert _p) \Delta s \nonumber \\& \quad \le \eta _2 \Vert \mathcal {T}\Vert _p K_\mathcal {H}+ \eta _2 \vert \alpha \vert \Vert {\hat{\mathcal {T}}}\Vert _p K_\mathcal {H}. \end{aligned}$$

(8)

Therefore, from the equations (5), (6), (7) and (8), we get

$$\begin{aligned}&\Vert F(x,\vartheta _1(t), \vartheta _2(t), \alpha , \varsigma ) \Vert _p\\& \quad \le \vert \alpha \vert \Vert (\mathcal {Q}-{\hat{\mathcal {Q}}})\Vert _p \beta _p + (\Vert \mathcal {R}\Vert _p + \vert \alpha \vert \Vert {\hat{\mathcal {R}}}\Vert _p )K_\mathcal {F}+ (\Vert \mathcal {S}\Vert _p \\&\quad + \vert \alpha \vert \Vert {\hat{\mathcal {S}}}\Vert _p )K_\mathcal {G}+ \eta _2 (\Vert \mathcal {T}\Vert _p + \vert \alpha \vert \Vert {\hat{\mathcal {T}}}\Vert _p ) K_\mathcal {H}\\& \quad= c_p, \end{aligned}$$

where $c_p>0$ is a constant. $\square$

Remark 6

In Lemma 1, if $\alpha =1$, then the constant $c_p$ can be calculated as

$$\begin{aligned} c_p&= \Vert (\mathcal {Q}-{\hat{\mathcal {Q}}})\Vert _p \beta _p + (\Vert \mathcal {R}\Vert _p - \Vert {\hat{\mathcal {R}}}\Vert _p )K_\mathcal {F}\\&\quad + (\Vert \mathcal {S}\Vert _p - \Vert {\hat{\mathcal {S}}}\Vert _p )K_\mathcal {G}+ \eta _2 (\Vert \mathcal {T}\Vert _p - \Vert {\hat{\mathcal {T}}}\Vert _p ) K_\mathcal {H}. \end{aligned}$$

Now, we are in a position to give the first main result of PLQS for the drive system (1) and response system (2) as follows.

Theorem 4

Let Assumptions 1 and 2 hold, then the drive system (1) and the response system (2) are projective lag quasi-synchronized with an error level

$$\begin{aligned} \epsilon _p =\dfrac{\Vert \mathcal {B}^{-1}\Vert _p \Vert \mathcal {B}\Vert _p c_p}{\delta _p}, \end{aligned}$$

if, for some $p\in \{1,2,\infty \}$, there exist a non-singular matrix $\mathcal {B}$, a coupling matrix $\mathcal {K}$, and a constant $k \in (0,1)$ such that

$$\begin{aligned} {\mathcal {M}}_{(1,p)} - {\mathcal {M}}_{(2,p)} \ge \delta _p>0, \ k {\mathcal {M}}_{(1,p)} - {\mathcal {M}}_{(2,p)} >0 \end{aligned}$$

and $-{\mathcal {M}}_{(1,p)} \in {\mathcal {R}}^+$, where

$$\begin{aligned} {\mathcal {M}}_{(1,p)}&= - (M_p(\mathcal {B}(\mathcal {Q}-\mathcal {K})\mathcal {B}^{-1},{\mathbb {T}}) + L_\mathcal {F}\Vert \mathcal {B}\Vert _p \Vert \mathcal {R}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p),\\ {\mathcal {M}}_{(2,p)}&= L_\mathcal {G}\Vert \mathcal {B}\Vert _p \Vert \mathcal {S}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p + \eta _2 L_\mathcal {H}\Vert \mathcal {B}\Vert _p \Vert \mathcal {T}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p \end{aligned}$$

and $c_p$ is the same as defined in Lemma 1.

Proof

Let us define

$$\begin{aligned} V(t) = \Vert \mathcal {B}e(t)\Vert _p. \end{aligned}$$

For any point $t \in {\mathbb {T}}$, there are two possibilities: either $\mu (t) = 0$ or $\mu (t) >0$. As a result, we separate the proof into two cases as follows:

Case 1: When $\mu (t)>0$, then we have

$$\begin{aligned}&\dfrac{\Vert \mathcal {B}e(\sigma (t)) \Vert _p -\Vert \mathcal {B}e(t) \Vert _p }{\mu (t)} \nonumber \\& \quad = \dfrac{1}{\mu (t)} \bigg \{ \Vert \mathcal {B}e(t) + \mu (t) \mathcal {B}e^\Delta (t) \Vert _p -\Vert \mathcal {B}e(t) \Vert _p \bigg \} \nonumber \\& \quad = \dfrac{1}{\mu (t)} \bigg \{ \Vert \mathcal {B}e(t) + \mu (t) \mathcal {B}((\mathcal {Q}-\mathcal {K})e(t) + \mathcal {R}{\bar{\mathcal {F}}}(e(t)) \nonumber \\& \quad \quad + \mathcal {S}{\bar{\mathcal {G}}}(e(t-\vartheta _1(t))) + \mathcal {T}\int _{t-\vartheta _2(t)}^t {\bar{\mathcal {H}}}(e(s)) \Delta s \nonumber \\& \quad \quad + F(x,\vartheta _1(t),\vartheta _2(t),\alpha ,\varsigma ) \Vert _p - \Vert \mathcal {B}e(t)\Vert _p \bigg \} \nonumber \\& \quad \le \dfrac{1}{\mu (t)} \bigg \{ \Vert \mathcal {B}e(t) + \mu (t)\mathcal {B}(\mathcal {Q}-\mathcal {K})e(t)\Vert _p -\Vert \mathcal {B}e(t) \Vert _p \bigg \} \nonumber \\& \quad \quad + \Vert \mathcal {B}\mathcal {S}{\bar{\mathcal {G}}}(e(t-\vartheta _1(t)))\Vert _p + \Vert \mathcal {B}\mathcal {T}\int _{t-\vartheta _2(t)}^t \mathcal {H}(e(s)) \Delta s \Vert _p \nonumber \\& \quad \quad + \Vert \mathcal {B}\mathcal {R}{\bar{\mathcal {F}}}(e(t))\Vert _p + \Vert \mathcal {B}F(x,\vartheta _1(t),\vartheta _2(t),\alpha ,\varsigma ) \Vert _p. \end{aligned}$$

(9)

Now, from Assumption 2, we have

$$\begin{aligned} \Vert {\bar{\mathcal {F}}}(e(t))\Vert _p&= \Vert \mathcal {F}(y(t)) - \mathcal {F}(y(t) - e(t)) \Vert _p \nonumber \\&\le L_\mathcal {F}\Vert y(t) -\alpha x(t-\varsigma ) \Vert _p = L_\mathcal {F}\Vert e(t)\Vert _p. \end{aligned}$$

(10)

Similarly, we obtain

$$\begin{aligned} \Vert {\bar{\mathcal {G}}}(e(t-\vartheta _1(t)))\Vert _p&\le L_\mathcal {G}\Vert e(t-\vartheta _1(t))\Vert _p \end{aligned}$$

(11)

and

$$\begin{aligned} \Vert {\bar{\mathcal {H}}}(e(t))\Vert _p&\le L_\mathcal {H}\Vert e(t)\Vert _p. \end{aligned}$$

(12)

Now, from the inequalities (9), (10), (11), (12) and Lemma 1, we obtain

$$\begin{aligned}&\dfrac{\Vert \mathcal {B}e(\sigma (t)) \Vert _p -\Vert \mathcal {B}e(t) \Vert _p}{\mu (t)} \\&\le \dfrac{\Vert {{\,\textrm{Id}\,}}+ \mu (t) \mathcal {B}(\mathcal {Q}-\mathcal {K})\mathcal {B}^{-1}\Vert _p -1 }{\mu (t)} \Vert \mathcal {B}e(t) \Vert _p \\&\quad + L_\mathcal {F}\Vert \mathcal {B}\Vert _p \Vert \mathcal {R}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p \Vert \mathcal {B}e(t)\Vert _p \\&\quad + L_\mathcal {G}\Vert \mathcal {B}\Vert _p \Vert \mathcal {S}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p \Vert \mathcal {B}e(t-\vartheta _1(t))\Vert _p \\&\quad + \eta _2 L_\mathcal {H}\Vert \mathcal {B}\Vert _p \Vert \mathcal {T}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p \sup _{s \in [t-\eta _2,t]} \Vert \mathcal {B}e(s)\Vert _p + \Vert \mathcal {B}\Vert _p c_p \\&\le ( M_p(\mathcal {B}(\mathcal {Q}-\mathcal {K})\mathcal {B}^{-1},{\mathbb {T}}) + L_\mathcal {F}\Vert \mathcal {B}\Vert _p \Vert \mathcal {R}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p ) \Vert \mathcal {B}e(t) \Vert _p \\&\quad + \Vert \mathcal {B}\Vert _p c_p + (L_\mathcal {G}\Vert \mathcal {B}\Vert _p \Vert \mathcal {S}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p \\&\quad + \eta _2 L_\mathcal {H}\Vert \mathcal {B}\Vert _p \Vert \mathcal {T}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p ) \sup _{s \in [t-\eta ,t]} \Vert \mathcal {B}e(s)\Vert _p \\&\le -{\mathcal {M}}_{(1,p)} \Vert \mathcal {B}e(t)\Vert _p + {\mathcal {M}}_{(2,p)} \sup _{s \in [t-\eta , t]_{\mathbb {T}}} \Vert \mathcal {B}e(s)\Vert _p + \Vert \mathcal {B}\Vert _p c_p. \end{aligned}$$

Hence, using Definition 1, we obtain

$$\begin{aligned} D^+_\Delta V(t)&\le -{\mathcal {M}}_{(1,p)} V(t) + {\mathcal {M}}_{(2,p)} \sup _{s \in [t-\eta , t]_{\mathbb {T}}}V(s) \nonumber \\&\quad + \Vert \mathcal {B}\Vert _p c_p. \end{aligned}$$

(13)

Case 2: When $\mu (t)=0$, the delta derivative becomes the ordinary derivative, i.e. $z^\Delta (t) = z'(t)$. Accordingly, by applying the formula $z (t + h) = z(t) + z'(t)h + \textrm{r}_z(h)$ with $\lim _{h\rightarrow 0} \dfrac{\Vert \textrm{r}_z(h)\Vert _p}{h} = 0$, we obtain

$$\begin{aligned}&\lim _{h \rightarrow 0^+} \dfrac{\Vert \mathcal {B}e(t+h) \Vert _p -\Vert \mathcal {B}e(t) \Vert _p }{h} \\&= \lim _{h \rightarrow 0^+} \dfrac{1}{h} \bigg \{ \Vert \mathcal {B}e(t) + h \mathcal {B}e^\Delta (t) + \textrm{r}_e(h) \Vert _p -\Vert \mathcal {B}e(t) \Vert _p \bigg \} \\&\le \lim _{h \rightarrow 0^+} \dfrac{1}{h} \bigg \{ \Vert \mathcal {B}e(t) + h \mathcal {B}((\mathcal {Q}-\mathcal {K})e(t) + \mathcal {R}{\bar{\mathcal {F}}}(e(t)) \\&\quad + \mathcal {S}{\bar{\mathcal {G}}}(e(t-\vartheta _1(t))) + \mathcal {T}\int _{t-\vartheta _2(t)}^t {\bar{\mathcal {H}}}(e(s)) \Delta s \\&\quad + F(x,\vartheta _1(t),\vartheta _2(t),\alpha ,\varsigma ) + \textrm{r}_e(h) \Vert _p - \Vert \mathcal {B}e(t)\Vert _p \bigg \} \\&\le ( M_p(\mathcal {B}(\mathcal {Q}-\mathcal {K})\mathcal {B}^{-1},{\mathbb {T}}) + L_\mathcal {F}\Vert \mathcal {B}\Vert _p \Vert \mathcal {R}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p ) \Vert \mathcal {B}e(t) \Vert _p \\&\quad + \Vert \mathcal {B}\Vert _p c_p + (L_\mathcal {G}\Vert \mathcal {B}\Vert _p \Vert \mathcal {S}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p \\&\quad + \eta _2 L_\mathcal {H}\Vert \mathcal {B}\Vert _p \Vert \mathcal {T}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p ) \sup _{s \in [t-\eta ,t]} \Vert \mathcal {B}e(s)\Vert _p \\&\le -{\mathcal {M}}_{(1,p)} \Vert \mathcal {B}e(t)\Vert _p + {\mathcal {M}}_{(2,p)} \sup _{s \in [t-\eta , t]_{\mathbb {T}}} \\&\quad \Vert \mathcal {B}e(s)\Vert _p + \Vert \mathcal {B}\Vert _p c_p. \end{aligned}$$

Therefore, by utilizing Definition 1, we obtain the same inequality as (13).

As a result of the above two cases, for each $t \in {\mathbb {T}}$, we obtain

$$\begin{aligned} D^+ _\Delta V(t) \le -{\mathcal {M}}_{(1,p)} V(t) + {\mathcal {M}}_{(2,p)} \sup _{s \in [t-\eta , t]_{\mathbb {T}}} V(s) + \Vert \mathcal {B}\Vert _p c_p. \end{aligned}$$

Therefore, from Lemma 3, we get

$$\begin{aligned} V(t) \le \dfrac{\Vert \mathcal {B}\Vert _p c_p}{\delta _p} + \epsilon . \end{aligned}$$

Subsequently, we obtain

$$\begin{aligned} \Vert e(t) \Vert _p&= \Vert \mathcal {B}^{-1} \mathcal {B}e(t) \Vert _p \\&\le \Vert \mathcal {B}^{-1}\Vert _p \Vert V(e(t))\Vert _p \\&\le \dfrac{\Vert \mathcal {B}^{-1}\Vert _p \Vert \mathcal {B}\Vert _p c_p}{\delta _p} + \Vert \mathcal {B}^{-1}\Vert _p \Vert \mathcal {B}\Vert _p \epsilon . \end{aligned}$$

Hence, the drive system (1) and the response system (2) are projective lag quasi-synchronized to the error level $\epsilon _p = \dfrac{\Vert \mathcal {B}^{-1}\Vert _p \Vert \mathcal {B}\Vert _p c_p}{\delta _p}$. $\square$

Remark 7

The error bound level $\epsilon _p$ depends on the bound on F. The estimate of F obtained in Lemma 1 is optimal (smallest and least assumptions) but certainly not practical. Therefore, based on a slight strengthening of the assumptions (Lipschitz is almost differentiable and in applications, this is typically no restriction), we provide better error estimates that take into account the parameter mismatch and the projection.

Assumption 3

The functions $\mathcal {F},\mathcal {G}, \mathcal {H}: \Omega \rightarrow {\mathbb {R}}^n$ are differentiable, and there exist some positive constants $M_\mathcal {F}, M_\mathcal {G}$ and $M_\mathcal {H}$ such that

$$\begin{aligned} \Vert \mathcal {F}' (z) \Vert _p \le M_\mathcal {F}, \ \Vert \mathcal {G}' (z)\Vert _p \le M_\mathcal {G}\ \text {and} \ \Vert \mathcal {H}'(z)\Vert _p \le M_\mathcal {H}\end{aligned}$$

for all $z \in \Omega$ and $p=1,2,\infty$.

Lemma 2

Under the additional Assumption 3, the constant $c_p$ as in Theorem 4 can be replaced by $C_p$, where

$$\begin{aligned} C_p&= \vert \alpha \vert \Vert (\mathcal {Q}-{\hat{\mathcal {Q}}})\Vert _p \beta _p + \vert 1-\alpha \vert (\Vert \mathcal {R}\Vert _p M_\mathcal {F}\\&\quad + \Vert \mathcal {S}\Vert _p M_\mathcal {G}+ \eta _2 \Vert \mathcal {T}\Vert _p M_\mathcal {H}) \\&\quad + \Vert \mathcal {R}\Vert _p \Vert \textrm{r}_\mathcal {F}((\alpha -1)x(t-\varsigma ) ) \Vert _p \\&\quad + \Vert \mathcal {S}\Vert _p \Vert \textrm{r}_\mathcal {G}((\alpha -1)x(t-\varsigma ) ) \Vert _p \\&\quad + \eta _2 \Vert \mathcal {T}\Vert _p \Vert \textrm{r}_\mathcal {H}((\alpha -1)x(t-\varsigma ) \Vert _p \\&\quad + \vert \alpha \vert ( \Vert {\hat{\mathcal {R}}} - \mathcal {R}\Vert _p K_\mathcal {F}+ \Vert {\hat{\mathcal {S}}} - \mathcal {S}\Vert _p K_\mathcal {G}+ \eta _2 \Vert {\hat{\mathcal {T}}} - \mathcal {T}\Vert _p K_\mathcal {H}), \end{aligned}$$

where $\textrm{r}_f((\alpha -1) x(t-\varsigma ))$ denotes the remainder term of the linear approximation of f that, for fixed x, goes to zero faster than $(\alpha -1)$ approaches zero.

Proof

For any $x \in \Omega$, we have

$$\begin{aligned}&\Vert F(x,\vartheta _1(t), \vartheta _2(t), \alpha , \varsigma ) \Vert _p \le \Vert \alpha (\mathcal {Q}-{\hat{\mathcal {Q}}}) x(t-\varsigma ) \Vert _p \nonumber \\&\quad + \Vert \mathcal {R}\mathcal {F}(\alpha x(t-\varsigma )) - \alpha {\hat{\mathcal {R}}} \mathcal {F}(x(t-\varsigma )) \Vert _p \nonumber \\&\quad + \Vert \mathcal {S}\mathcal {G}(\alpha x(t-\varsigma - \vartheta _1(t))) - \alpha {\hat{\mathcal {S}}} \mathcal {G}(x(t-\varsigma -\vartheta _1(t))) \Vert _p \nonumber \\&\quad + \bigg \Vert \int _{t-\vartheta _2(t)}^t (\mathcal {T}\mathcal {H}(\alpha x (s-\varsigma )) -\alpha {\hat{\mathcal {T}}} \mathcal {H}(x(s-\varsigma )) ) \Delta s \bigg \Vert . \end{aligned}$$

(14)

Now, from Assumption 3, $\mathcal {F}$ is differentiable, and hence, we can write

$$\begin{aligned} \mathcal {F}(\alpha x(t-\varsigma ))&= \mathcal {F}(x(t-\varsigma ) + (\alpha -1) x(t-\varsigma )) \\&= \mathcal {F}(x(t-\varsigma )) + (\alpha -1) x(t-\varsigma ) \\&\quad + \mathcal {F}' (x(t-\varsigma )) ) + \textrm{r}_\mathcal {F}((\alpha -1) x(t-\varsigma )). \end{aligned}$$

Therefore, we can calculate

$$\begin{aligned} \mathcal {R}\mathcal {F}( \alpha x (t-\varsigma )&- \alpha (\mathcal {R}+({\hat{\mathcal {R}}}-\mathcal {R}) )\mathcal {F}(x(t-\varsigma )) \\&= \mathcal {R}(\mathcal {F}(x(t-\varsigma )) + (\alpha -1) x(t-\varsigma ) \mathcal {F}' (x(t-\varsigma )) ) \\&\quad + \textrm{r}_\mathcal {F}((\alpha -1) x(t-\varsigma )) - \alpha \mathcal {R}\mathcal {F}(x(t-\varsigma )) \\&\quad - \alpha ({\hat{\mathcal {R}}}-\mathcal {R}) \mathcal {F}(x(t-\varsigma )). \end{aligned}$$

Thus, by using Assumptions 1, 2 and 3

$$\begin{aligned}&\Vert \mathcal {R}\mathcal {F}( \alpha x (t-\varsigma ) - \alpha (\mathcal {R}+({\hat{\mathcal {R}}}-\mathcal {R}) )\mathcal {F}(x(t-\varsigma ))\Vert _p \nonumber \\&\le \vert (1-\alpha ) \vert \Vert \mathcal {R}\Vert _p \Vert (\mathcal {F}' (x(t-\varsigma )) x(t-\varsigma ) ) \Vert _p \nonumber \\&\quad + \Vert \mathcal {R}\Vert _p \Vert \textrm{r}_\mathcal {F}((\alpha -1)x(t-\varsigma ))\Vert _p \nonumber \\&\quad + \vert \alpha \vert \Vert ({\hat{\mathcal {R}}}-\mathcal {R})\Vert _p \Vert \mathcal {F}(x(t-\varsigma ))\Vert _p \nonumber \\&\le \vert (1-\alpha ) \vert \Vert \mathcal {R}\Vert _p M_\mathcal {F}+ \Vert \mathcal {R}\Vert _p \Vert (\textrm{r}_\mathcal {F}((\alpha -1)x(t-\varsigma ))\Vert _p \nonumber \\&\quad + \vert \alpha \vert \Vert ({\hat{\mathcal {R}}}-\mathcal {R})\Vert _p K_\mathcal {F}. \end{aligned}$$

(15)

Similarly, we obtain

$$\begin{aligned}&\Vert \mathcal {S}\mathcal {G}(\alpha x(t-\varsigma -\vartheta _1(t))) - \alpha {\hat{\mathcal {S}}} \mathcal {G}(x(t-\varsigma -\vartheta _1(t))) \Vert _p \nonumber \\&\le \vert (1-\alpha )\vert \Vert \mathcal {S}\Vert _p M_\mathcal {G}+ \Vert \mathcal {S}\Vert _p \Vert \textrm{r}_\mathcal {G}((\alpha -1)x(t-\varsigma ))\Vert _p \nonumber \\&\quad + \vert \alpha \vert \Vert ({\hat{\mathcal {S}}}-\mathcal {S})\Vert _p K_\mathcal {G} \end{aligned}$$

(16)

and

$$\begin{aligned}&\int _{t-\vartheta _2(t)}^t (\Vert \mathcal {T}\mathcal {H}(\alpha x(s-\varsigma )) - \alpha {\hat{\mathcal {T}}} \mathcal {H}(x(t-\varsigma )) \Vert _p) \Delta s \nonumber \\&\le \eta _2 \vert (1-\alpha )\vert \Vert \mathcal {T}\Vert _p M_\mathcal {H}+ \eta _2 \Vert \mathcal {T}\Vert _p \Vert \textrm{r}_\mathcal {H}((\alpha -1)x(t-\varsigma ))\Vert _p \nonumber \\&\quad + \eta _2 \vert \alpha \vert \Vert ({\hat{\mathcal {T}}}-\mathcal {T})\Vert _p K_\mathcal {H}. \end{aligned}$$

(17)

Therefore, from the inequalities (14), (15), (16) and (17), we get

$$\begin{aligned} \Vert F(x,\vartheta _1(t), \vartheta _2(t), \alpha , \varsigma ) \Vert _p&\le C_p. \end{aligned}$$

Hence, the result follows. $\square$

Remark 8

Note that the bounds in Lemma 2 scale with the mismatch $\Vert {\hat{\mathcal {R}}} -\mathcal {R}\Vert _p, \Vert {\hat{\mathcal {S}}} -\mathcal {S}\Vert _p$, and $\Vert {\hat{\mathcal {T}}} -\mathcal {T}\Vert _p$. Therefore, the estimate obtained in Lemma 2 is likely sharper than the estimate obtained in Lemma 1 (see Sect. 5).

Remark 9

Assumption 3 is stronger than Assumption 2 but still satisfied by many nonlinear functions and well-known activation functions in applied neural networks, such as tanh, Sigmoid or Logistic, and Gaussian. However, there are some nonlinear functions, like modulus function, which are not differentiable at certain points of the domain. Exploring the behaviour of these functions and developing results for such cases could be an interesting direction for future research.

Remark 10

Based on Theorem 4, we can design a control gain matrix that incorporates considerations for parameter mismatches and synchronization error levels. For convenience, we consider $\mathcal {B}={{\,\textrm{Id}\,}}$.

Step 1: Calculate the parameter mismatches bound or uncertainty bound $c_p \ (or \ C_p)$ from Lemma 1 (or Lemma 2).

Step 2: Chose an appropriate error level $\epsilon _p>0$, and calculate $\delta _p$ from $\epsilon _p =\frac{c_p}{\delta _p} \ (\text {or} \ \frac{C_p}{\delta _p})$.

Step 3: Compute ${\mathcal {D}} = -\delta _p - L_\mathcal {G}\Vert \mathcal {S}\Vert _p - \eta _2 L_\mathcal {H}\Vert \mathcal {T}\Vert _p - L_\mathcal {F}\Vert \mathcal {R}\Vert _p.$

Step 4: Determine the feedback gain matrix $\mathcal {K}$ such that $M_p(\mathcal {Q}-\mathcal {K},{\mathbb {T}}) \le {\mathcal {D}}$.

We note that the determination of the constants like $C_p$ contain upper and worst-case bounds to the parameter mismatches like ${\mathcal {Q}}-\hat{{\mathcal {Q}}}$ so that they naturally cover unmodelled mismatches that are smaller than assumed. Furthermore, the constants that bound the states of the drive system are inferred from a simulation which would also simply include modelling errors in the drive system. Finally, the matrix-measure continuously depends on perturbations in the coefficients as can be seen from the formulas for the particular realizations for the different norms in Table 1. Overall, we can state that the presented procedure is robust with respect to unknown perturbations in the systems.

Next, we provide a remark for different choices of $\mathcal {B}$ and $\mathcal {K}$ as follows.

Remark 11

In Theorem 4,

• if we choose $\mathcal {B}={{\,\textrm{Id}\,}}$, then the values of ${\mathcal {M}}_{(1,p)}$, ${\mathcal {M}}_{(2,p)}$, and $\epsilon _p$ will be replaced by $- (M_p((\mathcal {Q}-\mathcal {K}),{\mathbb {T}}) + L_\mathcal {F}\Vert \mathcal {R}\Vert _p \Vert )$, $L_\mathcal {G}\Vert \mathcal {S}\Vert _p + \eta _2 L_\mathcal {H}\Vert \mathcal {T}\Vert _p$, and $\frac{ c_p}{\delta _p}$, respectively;

• if $\mathcal {K}$ is a time-varying matrix, i.e. $\mathcal {K}=\mathcal {K}(t)$, then the values of ${\mathcal {M}}_{(1,p)}$ will be replaced by $- (M_p(\mathcal {B}(\mathcal {Q}-\mathcal {K}(t))\mathcal {B}^{-1},{\mathbb {T}}) + L_\mathcal {F}\Vert \mathcal {B}\Vert _p \Vert \mathcal {R}\Vert _p \Vert \mathcal {B}^{-1}\Vert _p)$ for all $t \in [0,\infty )_{\mathbb {T}}$;

• if we choose $\mathcal {B}={{\,\textrm{Id}\,}}$ and $\mathcal {K}=\mathcal {K}(t)$, then the values of ${\mathcal {M}}_{(1,p)}$, ${\mathcal {M}}_{(2,p)}$, and $\epsilon _p$ will be replaced by $- (M_p((\mathcal {Q}-\mathcal {K}(t)),{\mathbb {T}}) + L_\mathcal {F}\Vert \mathcal {R}\Vert _p \Vert )$, $L_\mathcal {G}\Vert \mathcal {S}\Vert _p + \eta _2 L_\mathcal {H}\Vert \mathcal {T}\Vert _p$, and $\frac{ c_p}{\delta _p}$, respectively, for all $t \in [0,\infty )_{\mathbb {T}}$.

The next remark discusses some immediate results from the above-obtained results.

Remark 12

Similarly to Theorem 4, Lemma 2, and Remark 11, one can establish the similar results for

• lag quasi-synchronization of the system (1) and (2), when $\alpha =1$;

• projective quasi-synchronization of the system (1) and (2), when $\varsigma =0$;

• quasi-synchronization of the system (1) and (2), when $\alpha =1$ and $\varsigma = 0$.

Remark 13

When there are no distributed time delays (i.e. $\vartheta _2(t)= 0$), all the above discussed results can be proven by setting the respective terms to zero in the computation of the constants ${\mathcal {M}}_{(1,p)}, {\mathcal {M}}_{(2,p)}$ and the estimates on the mismatch.

Remark 14

Theorem 4 covers the problem in all generality; therefore, for specific time scales like continuous time or discrete time, the matrix measures in ${\mathcal {M}}_{(1,p)}$ are readily computed by the known formulas.

Next, some special cases of the considered problem for different time scales including real, discrete, and non-overlapping time intervals are considered and show how our results generalize and extend the existing results. \\  Case 1. For the continuous-time domain, i.e. when ${\mathbb {T}} = {\mathbb {R}}$, the drive system (1) reduces to

$$\begin{aligned} x^\prime (t)&= {\hat{\mathcal {Q}}} x(t) + {\hat{\mathcal {R}}} \mathcal {F}(x(t)) + {\hat{\mathcal {S}}} \mathcal {G}(x(t-\vartheta _1(t))) \nonumber \\&\quad + {\hat{\mathcal {T}}} \int _{t-\vartheta _2(t)}^t \mathcal {H}(x(s)) d s \end{aligned}$$

(18)

and the response system (2) reduces to

$$\begin{aligned} y^\prime (t)&= \mathcal {Q}y(t) + \mathcal {R}\mathcal {F}(y(t)) + \mathcal {S}\mathcal {G}(y(t-\vartheta _1(t))) \nonumber \\&\quad + \mathcal {T}\int _{t-\vartheta _2(t)}^t \mathcal {H}(y(s)) d s + u(t), \end{aligned}$$

(19)

where $t \in [0,\infty )$ and the remaining parameters are equal to those defined previously.

Remark 15

As far as we know, the PLQS of the continuous-time system (18)–(19) using the Halanay inequality and matrix-measure approach has not yet been investigated in the existing literature. Hence, the findings presented in this paper are entirely novel, even in the context of continuous-time systems. A few authors [29, 34] have investigated different synchronization results for the system (18)–(19) by using the different techniques. Notably, our results are particularly significant when $\varsigma =0$, where they become the main outcomes of [34]. Further, in contrast to the impulsive control approach utilized in [29], we utilize a feedback controller and provide simpler criteria for achieving PLQS. Our numerical simulations show that to achieve the same error bounds, our proposed method greatly reduces the required feedback gain as compared to [29] (see Example 2), underscoring the efficacy of our approach.

Remark 16

The synchronization results for the continuous-time system (18)–(19) without distributed time delay, i.e. when $\vartheta _2(t)=0$, have been investigated in [28, 32, 33, 35]. In particular, if $\alpha = 1$, our results coincide with those of [35]. Further, in comparison with the intermittent technique developed in [33], our results significantly reduce the required feedback gain to achieve the same error bound, as shown in Example 3. This further demonstrates that the results of this paper are non-trivial extensions and generalizations of the existing results.

Case 2. For the $h-$difference discrete-time domain, i.e. when ${\mathbb {T}}=h{\mathbb {Z}}$, $h>0$, the drive system (1) reduces to

$$\begin{aligned} x(t+h)&= x(t) + h({\hat{\mathcal {Q}}} x(t) + {\hat{\mathcal {R}}} \mathcal {F}(x(t)) + {\hat{\mathcal {S}}} \mathcal {G}(x(t-\vartheta _1(t))) \nonumber \\&\quad + {\hat{\mathcal {T}}} \int _{t-\vartheta _2(t)}^t \mathcal {H}(x(s)) \Delta s ) \end{aligned}$$

(20)

and the response system (2) reduces to

$$\begin{aligned} y(t+h)&= y(t) + h(\mathcal {Q}y(t) + \mathcal {R}\mathcal {F}(y(t)) + \mathcal {S}\mathcal {G}(y(t-\vartheta _1(t))) \nonumber \\&\quad + \mathcal {T}\int _{t-\vartheta _2(t)}^t \mathcal {H}(y(s)) \Delta s + u(t)), \end{aligned}$$

(21)

where $t \in [0,\infty )_{h {\mathbb {Z}}}$.

Remark 17

The discrete-time systems have been studied in [13, 18, 20], but to the best of our knowledge, there is no paper that discussed the PLQS results for the discrete-type system (20)–(21). However, we have formulated our problem by using the time scales theory; therefore, our results can also be applied to the discrete-time systems of the form (20)–(21), as demonstrated in Case 2 of Example 1.

Case 3. For the mixed time domain ${\mathbb {T}} = hP_{c,d}$, i.e. ${\mathbb {T}}=\cup _{l=0}^\infty h[l(c+d), l(c+d)+d], \ h,c,d>0,$ which is different from the traditional discrete-time domain and continuous-time domain, the drive system (1) becomes

$$\left\{ \begin{gathered} x^{\prime } (t) = \widehat{{\mathcal{Q}}}x(t) + \widehat{{\mathcal{R}}}{\mathcal{F}}(x(t)) + \widehat{{\mathcal{S}}}{\mathcal{G}}(x(t - \vartheta _{1} (t))) \hfill \\ \quad \quad \; + \widehat{{\mathcal{T}}}\int_{{t - \vartheta _{2} (t)}}^{t} {\mathcal{H}} (x(s))ds,\;t \in h{\mathbb{P}}_{{c,d}} { \setminus } \cup _{{l = 0}}^{\infty } h\{ l(c + d) + d\} , \hfill \\ x(t + hc) = x(t) + hc(\widehat{{\mathcal{Q}}}x(t) + \widehat{{\mathcal{R}}}{\mathcal{F}}(x(t)) + \widehat{{\mathcal{S}}}{\mathcal{G}}(x(t - \vartheta _{1} (t))) \hfill \\ \quad \quad \quad \quad \; + \widehat{{\mathcal{T}}}\int_{{t - \vartheta _{2} (t)}}^{t} {\mathcal{H}} (x(s))\Delta s),\;t = \cup _{{l = 0}}^{\infty } h\{ l(c + d) + d\} \hfill \\ \end{gathered} \right.$$

(22)

and the response system (2) becomes

$$\left\{ {\begin{array}{*{20}l} {y^{\prime } (t) = {\mathcal{Q}}y(t) + {\mathcal{R}\mathcal{F}}(y(t)) + {\mathcal{S}\mathcal{G}}(y(t - \vartheta _{1} (t)))} \hfill \\ \begin{gathered} \quad \quad \; + {\mathcal{T}}\int_{{t - \vartheta _{2} (t)}}^{t} {\mathcal{H}} (y(s))ds + u(t),\;t \in h{\mathbb{P}}_{{c,d}} { \setminus } \cup _{{l = 0}}^{\infty } h\{ l(c + d) + d\} , \hfill \\ y(t + hc) = y(t) + hc({\mathcal{Q}}y(t) + {\mathcal{R}\mathcal{F}}(y(t)) + {\mathcal{S}\mathcal{G}}(y(t - \vartheta _{1} (t))) \hfill \\ \quad \quad \quad \quad \; + {\mathcal{T}}\int_{{t - \vartheta _{2} (t)}}^{t} {\mathcal{H}} (y(s))\Delta s + u(t)),\;t = \cup _{{l = 0}}^{\infty } h\{ l(c + d) + d\} . \hfill \\ \end{gathered} \hfill \\ \end{array} } \right.$$

(23)

We are ending up this section by giving the final remark as follows.

Remark 18

Standard and generalized matrix-measure theory can be used to establish results for regular time-domain systems, such as continuous and discrete-time systems. However, for irregular time-domain systems like (22) and (23), these results cannot be directly studied using discrete-time and continuous-time system theories. Instead, the time scales and unified matrix-measure theory can be used to study these results easily (see case 3 of Example 1).

5 Illustrative examples

In this section, we provide three examples to illustrate the obtained results for different time domains. Whereas the first example is tailored to best illustrate the potential of our theoretical results with respect to arbitrary time domains, the second example is borrowed from [29] to show the general applicability of our methods. In the final example, we consider the Lu oscillator from [33] and show that our results can be applied to a variety of dynamical systems.

Example 1

Consider the following coefficients for the drive system (1) and the response system (2)

$$\begin{aligned}&{\hat{\mathcal {Q}}} = \begin{bmatrix} -0.5 &{} 0.0 \\ 0.0 &{} -0.4 \end{bmatrix},\ {\hat{\mathcal {R}}} = \begin{bmatrix} 0.4 &{} 0.4 \\ 0.4 &{} 0.3 \end{bmatrix},\\&{\hat{\mathcal {S}}} = \begin{bmatrix} -0.4 &{} 0.1\\ -0.2 &{} 0.5 \end{bmatrix}, \ {\hat{\mathcal {T}}} = \begin{bmatrix} 0.2 &{} -0.1 \\ 0.1 &{} -0.4 \end{bmatrix}, \\&\mathcal {Q}= \begin{bmatrix} -0.51 &{} 0.0 \\ 0.0 &{} -0.41 \end{bmatrix}, \ \mathcal {R}= \begin{bmatrix} 0.401 &{} 0.401 \\ 0.401 &{} 0.311 \end{bmatrix}, \\&\mathcal {S}= \begin{bmatrix} -0.401 &{} 0.11 \\ -0.21 &{} 0.5001 \end{bmatrix}, \ \mathcal {T}= \begin{bmatrix} 0.201 &{} -0.101\\ 0.101 &{} -0.4001 \end{bmatrix}, \\&\mathcal {F}(x(\cdot ))=\mathcal {G}(x(\cdot ))= \begin{bmatrix} 0.7 \tanh (x_1(\cdot )) \\ 0.8 \tanh (x_2(\cdot )) \end{bmatrix}, \\&\mathcal {H}(x(\cdot )) = \begin{bmatrix} 0.8 \tanh (x_1(\cdot )) \\ 0.7 \tanh (x_2(\cdot )) \end{bmatrix}, \\&{\hat{\phi }}(s) = \begin{bmatrix} -0.2 \\ -0.1 \end{bmatrix},\ \phi (s) = \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix} \ \text {for } s \in [-\eta ,0]_{\mathbb {T}}, \\&\alpha = 0.5,\ \mathcal {B}=\begin{bmatrix} 1 &{} 0 \\ 0 &{} 1 \end{bmatrix}. \end{aligned}$$

Clearly, for the considered coefficients, Assumption 1 holds. Also, one can see that $\mathcal {F}, \mathcal {G},$ and $\mathcal {H}$ satisfy Assumption 2 and Assumption 3. Now, we consider the following three different time domains as follows.

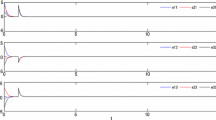
Case 1. ${\mathbb {T}} = {\mathbb {R}}$, i.e. $\mu (t)=0$ for all t. We set $\vartheta _1(t) = \vartheta _2(t)=\frac{\exp (t)}{2+\exp (t)}$ and $\varsigma = 0.4$; then, $\eta =1$. The synchronization errors and error norm between the drive system (1) and the response system (2) without feedback controller are shown in Fig. 3.

Fig. 3

Trajectories of the errors $e_1$, $e_2$, and error norm $\Vert e\Vert _2$ of the uncontrolled system when ${\mathbb {T}}={\mathbb {R}}$

Fig. 4

Trajectories of the errors $e_1$, $e_2$, and error norm $\Vert e\Vert _2$ of the controlled system when ${\mathbb {T}}={\mathbb {R}}$

Now, for the coupling matrix

$$\begin{aligned} \mathcal {K}= \begin{bmatrix} 3.81 &{} 0.0\\ 0.0 &{} 3.91 \end{bmatrix}, \end{aligned}$$

we can calculate

$$\begin{aligned} {\mathcal {M}}_{(2,1)} = 0.8897, \ {\mathcal {M}}_{(2,2)} = 0.8505, \ {\mathcal {M}}_{(2,\infty )} = 0.9690 \end{aligned}$$

and

$$\begin{aligned}&\Upsilon _1(\mathcal {Q}-\mathcal {K}) = -4.32, \ \Upsilon _2(\mathcal {Q}-\mathcal {K}) =-8.64,\ \Upsilon _\infty (\mathcal {Q}-\mathcal {K}) = -4.32. \end{aligned}$$

Hence,

$$\begin{aligned} {\mathcal {M}}_{(1,1)}&= 3.6784 ,\quad {\mathcal {M}}_{(1,2)} = 8.0327, \ \text {and } {\mathcal {M}}_{(1,\infty )} = 3.6784. \end{aligned}$$

Therefore, we can see that $-{\mathcal {M}}_{(1,p)} \in {\mathcal {R}}^+$ for $p \in \{ 1,2, \infty \}$ and

$$\begin{aligned}&{\mathcal {M}}_{(1,1)}-{\mathcal {M}}_{(2,1)} \ge 2.7887>0, \\&{\mathcal {M}}_{(1,2)}-{\mathcal {M}}_{(2,2)} \ge 7.1822>0, \\&{\mathcal {M}}_{(1,\infty )}-{\mathcal {M}}_{(2,\infty )} \ge 2.70940. \end{aligned}$$

Also, for $k=0.5$ and $p \in \{ 1,2, \infty \}$, the inequality $k {\mathcal {M}}_{(1,p)} - {\mathcal {M}}_{(2,p)}>0$ holds. Thus, all of the requirements of Theorem 4 and Lemma 2 are satisfied, and as a result, the drive system (1) and the response system (2) are projective lag quasi-synchronized. The synchronization errors and error norm between the drive system (1) and the response system (2) with feedback controller (3) are shown in Fig. 4.

The theoretical error bounds for different values of p are given in Table 2. Clearly, the theoretical error bound obtained from Lemma 2 is fairly close to the computed error as shown in Fig. 4.

Table 2 Error bounds from Theorem 4 and Lemma 2 when ${\mathbb {T}}={\mathbb {R}}$

Case 2. ${\mathbb {T}} = 0.2 {\mathbb {Z}}$, i.e. $\mu (t)=0.2$ for all $t \in 0.2 {\mathbb {Z}}$. We set $\vartheta _1(t) = \vartheta _2(t)=0.2$ and $\varsigma = 0.4$; then, $\eta =0.2$. The synchronization errors and error norm between the drive system (1) and the response system (2) without feedback controller (3) are shown in Fig. 5.

Fig. 5

Trajectories of the errors $e_1$, $e_2$, and error norm $\Vert e\Vert _2$ of the uncontrolled system when ${\mathbb {T}}=\frac{1}{5}{\mathbb {Z}}$

Fig. 6

Trajectories of the errors $e_1$, $e_2$, and error norm $\Vert e\Vert _2$ of the controlled system when ${\mathbb {T}}=\frac{1}{5}{\mathbb {Z}}$

Now, for the coupling matrix

$$\begin{aligned} \mathcal {K}= \begin{bmatrix} 4.49 &{} 0.0\\ 0.0 &{} 4.59 \end{bmatrix}, \end{aligned}$$

we can calculate

$$\begin{aligned} {\mathcal {M}}_{(2,1)} = 0.5690, \ {\mathcal {M}}_{(2,2)} = 0.5674, \ {\mathcal {M}}_{(2,\infty )} = 0.6483 \end{aligned}$$

and

$$\begin{aligned}&\omega _1(\mathcal {Q}-\mathcal {K}) = -5.0, \ \omega _2(\mathcal {Q}-\mathcal {K}) = -5.0, \ \omega _\infty (\mathcal {Q}-\mathcal {K}) = -5.0. \end{aligned}$$

Hence,

$$\begin{aligned} {\mathcal {M}}_{(1,1)} = 4.3584,\quad {\mathcal {M}}_{(1,2)} = 4.3927, \ \text {and } {\mathcal {M}}_{(1,\infty )} = 4.3584. \end{aligned}$$

Therefore, we can see that $-{\mathcal {M}}_{(1,p)} \in {\mathcal {R}}^+$ for $p \in \{ 1,2, \infty \}$ and

$$\begin{aligned}&{\mathcal {M}}_{(1,1)}-{\mathcal {M}}_{(2,1)} \ge 3.7894>0, \\&{\mathcal {M}}_{(1,2)}-{\mathcal {M}}_{(2,2)} \ge 3.8253>0, \\&{\mathcal {M}}_{(1,\infty )}-{\mathcal {M}}_{(2,\infty )} \ge 3.7101>0. \end{aligned}$$

Also, for $k=0.5$ and $p \in \{ 1,2, \infty \}$, the inequality $k {\mathcal {M}}_{(1,p)} - {\mathcal {M}}_{(2,p)}>0$ holds. Thus, all of the requirements of Theorem 4 and Lemma 2 are satisfied, and as a result, the drive system (1) and the response system (2) are projective lag quasi-synchronized. The synchronization errors and error norm between the drive system (1) and the response system (2) with feedback controller (3) are shown in Fig. 6.

The theoretical error bounds for different values of p are given in Table 3. Here also, the theoretical error bound obtained from Lemma 2 is fairly close to the computed error as shown in Fig. 6.

Table 3 Error bounds from Theorem 4 and Lemma 2 when ${\mathbb {T}}=\frac{1}{5}{\mathbb {Z}}$

Case 3. ${\mathbb {T}} = {\mathcal {P}} = [-1,0] \cup _{l=0}^\infty 0.5[l, (l+0.7)]$. Here, $\mu (t)$ is given by

$$\mu (t) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {t \in [ - 1,0] \cup _{{l = 0}}^{\infty } [0.5l,0.5(l + 0.7)),} \hfill \\ {0.15,} \hfill & {t = \cup _{{l = 0}}^{\infty } \{ 0.5(l + 0.7)\} .} \hfill \\ \end{array} } \right.$$

We set $\vartheta _1(t) = \vartheta _2(t)=0.5$ and $\varsigma = 1$; then, $\eta =0.5$. The synchronization errors and error norm between the drive system (1) and the response system (2) without feedback controller (3) are shown in Fig. 7.

Fig. 7

Trajectories of the errors $e_1$, $e_2$, and error norm $\Vert e\Vert _2$ of the uncontrolled system when ${\mathbb {T}}={\mathcal {P}}$

Fig. 8

Trajectories of the errors $e_1$, $e_2$, and error norm $\Vert e\Vert _2$ of the controlled system when ${\mathbb {T}}={\mathcal {P}}$

Now, for the coupling matrix

$$\begin{aligned} \mathcal {K}= \begin{bmatrix} 6.15 &{} 0.0\\ 0.0 &{} 6.25 \end{bmatrix}, \end{aligned}$$

we can calculate

$$\begin{aligned} {\mathcal {M}}_{(2,1)} =0.6892, \ {\mathcal {M}}_{(2,2)} = 0.6736, \ {\mathcal {M}}_{(2,\infty )} = 0.7685 \end{aligned}$$

and

$$\begin{aligned}&M_1((\mathcal {Q}-\mathcal {K}),{\mathcal {P}}) =-6.66, \ M_2((\mathcal {Q}-\mathcal {K}),{\mathcal {P}}) = -6.66,\ \\&M_\infty ((\mathcal {Q}-\mathcal {K}),{\mathcal {P}})= -6.66. \end{aligned}$$

Hence,

$$\begin{aligned}{} & {} {\mathcal {M}}_{(1,1)} = 6.0184,\quad {\mathcal {M}}_{(1,2)} = 6.0527, \ \text {and } \\{} & {} {\mathcal {M}}_{(1,\infty )} = 6.0184. \end{aligned}$$

Therefore, we can see that $-{\mathcal {M}}_{(1,p)} \in {\mathcal {R}}^+$ for $p \in \{ 1,2, \infty \}$ and

$$\begin{aligned}&{\mathcal {M}}_{(1,1)}-{\mathcal {M}}_{(2,1)} \ge 5.3292>0, \\&{\mathcal {M}}_{(1,2)}-{\mathcal {M}}_{(2,2)} \ge 5.3791>0, \\&{\mathcal {M}}_{(1,\infty )}-{\mathcal {M}}_{(2,\infty )} \ge 5.2499>0. \end{aligned}$$

Also, for $k=0.5$ and $p \in \{ 1,2, \infty \}$, the inequality $k {\mathcal {M}}_{(1,p)} - {\mathcal {M}}_{(2,p)}>0$ holds. Thus, all of the requirements of Theorem 4 and Lemma 2 are satisfied, and as a result, the drive system (1) and the response system (2) are projective lag quasi-synchronized. The synchronization errors and error norm between the drive system (1) and the response system (2) with feedback controller (3) are shown in Fig. 8.

The theoretical error bounds for different values of p are given in Table 4. In this case also, the theoretical error bound obtained from Lemma 2 is fairly close to the computed error as shown in Fig. 8.

Table 4 Error bounds from Theorem 4 and Lemma 2 when ${\mathbb {T}}={\mathcal {P}}$

Example 2

Consider the continuous-time case of the drive and response systems (18)–(19) with the following coefficients as in [29]

$$\begin{aligned}&{\hat{\mathcal {Q}}} = \begin{bmatrix} -1.0 &{} 0.0 \\ 0.0 &{} -1.0 \end{bmatrix},\ {\hat{\mathcal {R}}} = \begin{bmatrix} 2.0 &{} -0.1 \\ 5.0 &{} 4.5 \end{bmatrix},\\&{\hat{\mathcal {S}}} = \begin{bmatrix} -1.5 &{} -0.1\\ -0.2 &{} -4.0 \end{bmatrix}, \ {\hat{\mathcal {T}}} = \begin{bmatrix} -0.3 &{} 0.1 \\ 0.1 &{} -0.2 \end{bmatrix}, \\&\mathcal {Q}= \begin{bmatrix} -1.0 &{} 0.0 \\ 0.0 &{} -1.0 \end{bmatrix}, \ \mathcal {R}= \begin{bmatrix} 1.8 &{} -0.15 \\ -0.52 &{} 3.5 \end{bmatrix}, \\&\mathcal {S}= \begin{bmatrix} -1.7 &{} -0.12 \\ -0.26 &{} -2.5 \end{bmatrix}, \ \mathcal {T}= \begin{bmatrix} 0.6 &{} 0.15\\ 2.0 &{} -0.12 \end{bmatrix}, \\&\mathcal {F}(x(\cdot ))=\mathcal {G}(x(\cdot ))=\mathcal {H}(x(\cdot ))= \begin{bmatrix} \tanh (x_1(\cdot )) \\ \tanh (x_2(\cdot )) \end{bmatrix}, \ \mathcal {B}=\begin{bmatrix} 1 &{} 0 \\ 0 &{} 1 \end{bmatrix}, \\&\vartheta _1(t) =1, \vartheta _2(t)=0.2, \alpha = 0.5,\ {\hat{\phi }}(s) = \begin{bmatrix} 0.01 \\ 0.1 \end{bmatrix},\\&\phi (s) = \begin{bmatrix} 0.02 \\ 0.01 \end{bmatrix} \ \text {for } s \in [-1,0]. \end{aligned}$$

Clearly, for the considered coefficients, Assumption 1 holds. Also, one can see that $\mathcal {F}, \mathcal {G},$ and $\mathcal {H}$ satisfy Assumption 2 and Assumption 3. The synchronization errors and error norm between the drive system (1) and the response system (2) without feedback controller are shown in Fig. 9.

Fig. 9

Trajectories of the errors $e_1$, $e_2$, and error norm $\Vert e\Vert _2$ of the uncontrolled system

Fig. 10

Trajectories of the errors $e_1$, $e_2$, and error norm $\Vert e\Vert _2$ of the controlled system

Now, for the coupling matrix

$$\begin{aligned} \mathcal {K}= \begin{bmatrix} 10.1557 &{} 0.0\\ 0.0 &{} 10.1557 \end{bmatrix}, \end{aligned}$$

we can calculate ${\mathcal {M}}_{(2,2)} = 2.9619 \ \text {and} \ \Upsilon _2(\mathcal {Q}-\mathcal {K}) =-22.3114.$ Hence, ${\mathcal {M}}_{(1,2)} =15.8442.$ Therefore, we can see that ${\mathcal {M}}_{(1,2)}-{\mathcal {M}}_{(2,2)} =12.8824 >0$ and $-{\mathcal {M}}_{(1,2)} \in {\mathcal {R}}^+$. Also, for $k=0.5$, the inequality $k {\mathcal {M}}_{(1,2)} - {\mathcal {M}}_{(2,2)}>0$ holds. Thus, all of the requirements of Theorem 4 and Lemma 2 are satisfied, and as a result, the drive system (1) and the response system (2) are projective lag quasi-synchronized. The synchronization errors and error norm between the drive system (1) and the response system (2) with feedback controller (3) are shown in Fig. 10.

Further, for $p=2$, we can calculate $C_2=3.1471$. Hence, the theoretical error bound $\epsilon _2=\frac{C_2}{\delta _2}$ is 0.2443. Comparing the results quantitatively, we note that to achieve the error bound 0.2443, we used the feedback gain $\mathcal {K}= {{\,\textrm{diag}\,}}\{10.1557, 10.1557\},$ while to achieve the same error bound, the authors in [29] used a gain of $\mathcal {K}= {{\,\textrm{diag}\,}}\{20, 20\}$, which is approximate double of our gain.

Finally, we present our third example as follows.

Example 3

Consider the continuous-time Lu oscillator given by the drive and response systems (18)–(19) with the following coefficients as in [33]

$$\begin{aligned}&{\hat{\mathcal {Q}}} = \begin{bmatrix} -1.0 &{} 0.0 \\ 0.0 &{} -1.0 \end{bmatrix},\ {\hat{\mathcal {R}}} = \begin{bmatrix} 2.0 &{} -0.1 \\ 5.0 &{} 3.2 \end{bmatrix},\\&{\hat{\mathcal {S}}} = \begin{bmatrix} -1.5 &{} -0.1\\ -0.18 &{} -2.5 \end{bmatrix}, \\&\mathcal {Q}= \begin{bmatrix} -0.99 &{} 0.0 \\ 0.0 &{} -1.1 \end{bmatrix}, \ \mathcal {R}= \begin{bmatrix} 2.1 &{} -0.1 \\ -0.51 &{} 3.1 \end{bmatrix}, \\&\mathcal {S}= \begin{bmatrix} -1.5 &{} -0.11 \\ -0.16 &{} -2.4 \end{bmatrix}, \\&\mathcal {F}(x(\cdot ))=\mathcal {G}(x(\cdot ))= \begin{bmatrix} \tanh (x_1(\cdot )) \\ \tanh (x_2(\cdot )) \end{bmatrix}, \ \mathcal {B}=\begin{bmatrix} 1 &{} 0 \\ 0 &{} 1 \end{bmatrix}, \\&\vartheta _1(t) =1, \vartheta _2(t)=0.0, \alpha = 0.9,\ \varsigma = 0.02, \ p=2, \\&{\hat{\phi }}(s) = \begin{bmatrix} 0.2 \\ -0.3 \end{bmatrix},\ \phi (s) = \begin{bmatrix} -0.1 \\ 0.1 \end{bmatrix} \ \text {for } s \in [-1,0]. \end{aligned}$$

Clearly, for the considered coefficients, Assumption 1 holds. Also, one can see that $\mathcal {F}, \mathcal {G},$ and $\mathcal {H}$ satisfy Assumption 2 and Assumption 3. The synchronization errors and error norm between the drive system (1) and the response system (2) without feedback controller are shown in Fig. 11.

Fig. 11

Trajectories of the errors $e_1$, $e_2$, and error norm $\Vert e\Vert _2$ of the uncontrolled system

Fig. 12

Trajectories of the errors $e_1$, $e_2$, and error norm $\Vert e\Vert _2$ of the controlled system

Now, for the coupling matrix

$$\begin{aligned} \mathcal {K}= \begin{bmatrix} 10.4848 &{} 0.0\\ 0.0 &{} 10.3748 \end{bmatrix}, \end{aligned}$$

we can calculate ${\mathcal {M}}_{(2,2)} = 2.42 \ \text {and} \ \Upsilon _2(\mathcal {Q}-\mathcal {K}) =-22.9496.$ Hence, ${\mathcal {M}}_{(1,2)} =16.6950.$ Therefore, we can see that ${\mathcal {M}}_{(1,2)}-{\mathcal {M}}_{(2,2)} =14.2750 >0$ and $-{\mathcal {M}}_{(1,2)} \in {\mathcal {R}}^+$. Also, for $k=0.5$, the inequality $k {\mathcal {M}}_{(1,2)} - {\mathcal {M}}_{(2,2)}>0$ holds. Thus, all of the requirements of Theorem 4 and Lemma 2 are satisfied, and as a result, the drive system (1) and the response system (2) are projective lag quasi-synchronized. The synchronization errors and error norm between the drive system (1) and the response system (2) with feedback controller (3) are shown in Fig. 12.

Further, for $p=2$, we can calculate $C_2=3.5259$. Hence, the theoretical error bound $\epsilon _2=\frac{C_2}{\delta _2}$ is 0.2470. Comparing the results quantitatively, we note that to achieve the error bound 0.2470, we used the feedback gain $\mathcal {K}= {{\,\textrm{diag}\,}}\{10.4848, 10.3848\},$ while to achieve the same error bound, the authors in [33] used the intermittent control technique with a feedback gain of $\mathcal {K}= {{\,\textrm{diag}\,}}\{40, 40\}$, which is approximate four times of our gain.

Remark 19

Previous works, such as [28, 29, 32,33,34,35], have considered similar types of examples on either continuous or discrete-time domains. To the best of our knowledge, there is currently no other example in the literature that has addressed PLQS of coupled systems on hybrid-type time domains (as presented in case 3 of Example 1).

Remark 20

In this paper, we have derived protocols for achieving asymptotic quasi-synchronization. However, it is important to note that these protocols only guarantee convergence with an infinite settling time. In order to address this limitation, an interesting future direction could be to investigate the finite-time quasi-synchronization, where the synchronization is achieved within a specific finite-time period instead of an infinite duration. Furthermore, the continuous feedback controller we used in our approach can be costly in terms of implementation and computational resources. Therefore, another potential future direction could be to develop alternative controllers, like impulsive controllers and event-triggered controllers which have the advantage of reducing implementation and computational costs compared to continuous feedback control.

6 Conclusions

In this study, we have presented a feedback control law that successfully establishes projective lag quasi-synchronization for coupled dynamical systems with parameter mismatches and mixed time-varying delays on arbitrary time domains. More precisely, we first formulated the problem on time scales, allowing the results to be valid for arbitrary time domains. Next, we derived various sufficient conditions for projective lag quasi-synchronization and obtained corresponding error bounds. Additionally, by setting some particular values to the parameters, we provided different conditions for projective quasi-synchronization, quasi-synchronization, and lag synchronization. Our study has also extended and refined existing results by generalizing them using the time scales theory. The analytical outcomes have been validated using time scales calculus, unified matrix-measure, and generalized Halanay inequality. In the last, we provided some numerical examples for different time domains and showed that the error bounds obtained analytically are very close to the simulated error bounds.

Overall, this study provides a comprehensive understanding of the problem of projective lag quasi-synchronization and offers a generic solution for synchronizing parameter mismatched coupled dynamical systems with mixed time-varying delays on continuous, discrete and also arbitrary time domains. It can be used as a foundation for future research in the field of synchronization of deterministic and stochastic dynamical systems. An immediate valuable extension would be the inclusion of impulsive effects with time-dependent delays. Furthermore, a promising application where memory terms, delays, and on-off behaviour as it can be naturally modelled by time scales are relevant lies in the synchronization of connected memristors [16].