Use of independent volume parameters in the development of new large displacement ANCF triangular plate/shell elements

Abstract

In this paper, a new unified kinematic description, obtained from Bezier geometry using linear mapping and position vector gradients associated with three independent parameters, is used to develop large displacement plate/shell finite elements (FE). Contrary to the conventional FE method, in the approach developed in this paper based on the absolute nodal coordinate formulation (ANCF), no distinction is made between plate and shell structures. The proposed ANCF triangular plate/shell elements have 12 coordinates per node: three position coordinates and nine position gradient coordinates that define vectors tangent to coordinate lines at the nodes. The fundamental differences between the conventional FE and the new ANCF parameterizations are highlighted. In this investigation, two different parameterizations, each of which employs independent coordinates, are used. In the first parameterization, called volume parameterization, coordinate lines along the sides of the triangular element in the straight (un-deformed) configuration are used in order to facilitate the development of closed-form cubic shape functions. In the second parameterization, called Cartesian parameterization, coordinate lines along the global axes of the structure (body) coordinate system are used to facilitate the element assembly. The element transformation between the volume and the Cartesian parameterizations is developed and used to define the structure inertia and elastic forces. Three new fully parameterized ANCF triangular plate/shell elements are developed in this investigation: a four-node mixed-coordinate element (FNMC) and two three-node elements (TN1 and TN2). All the elements developed in this investigation lead to a constant mass matrix and zero Coriolis and centrifugal forces. A non-incremental total Lagrangian procedure is used for the numerical solution of the nonlinear equations of motion. The performance of the proposed ANCF triangular plate/shell elements is analyzed by comparison with the ANCF rectangular plate element and conventional three-node linear (TNL) and six-node quadratic (SNQ) triangular plate elements.

Appendix

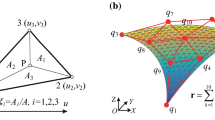
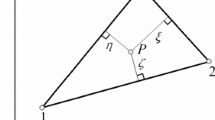
In this appendix, the shape functions of the TNL and SNQ elements that use extensible directors are presented [77]. Considering a general node k, both the TNL and SNQ elements have the nodal position vector $\mathbf{r}^{k}$ and the slope vector $\mathbf{r}_z^k$ as nodal coordinates. The linear shape functions $s_k ,k=1,2,\ldots ,6$, of the conventional TNL element can be explicitly written in terms of the set of volume coordinates $\xi , \eta , \zeta$, and $\chi$ as follows:

$$\begin{aligned} \left. \begin{array}{ll} s_1 &{}=\xi ,\quad s_2 =\frac{W}{2}\xi \chi ,\quad s_3 =\eta ,\quad s_4 =\frac{W}{2}\eta \chi ,\\ s_5 &{}=\zeta ,\quad s_6 =\frac{W}{2}\zeta \chi \end{array}\right\} \end{aligned}$$

(A.1)

where W is the TNL element thickness. The pairs of shape functions $s_i$ and $s_j , i=1,3,5, j=2,4,6$, are, respectively, associated with the TNL nodal positions and slopes of the corner nodes $k, k=1,2,3$.

The quadratic shape functions $s_k ,k=1,2,\ldots ,12$, of the SNQ element can be written in terms of the set of volume coordinates $\xi , \eta , \zeta$, and $\chi$ as

$$\begin{aligned} \left. \begin{array}{ll} s_1 &{}=\xi \left( {\xi -\left( {\eta +\zeta } \right) } \right) ,\quad s_2 =\frac{W}{2}\xi \chi \left( {1-2\left( {\eta +\zeta } \right) } \right) ,\\ s_3 &{}=\eta \left( {\eta -\left( {\zeta +\xi } \right) } \right) , \\ s_4 &{}=\frac{W}{2}\eta \chi \left( {1-2\left( {\zeta +\xi } \right) } \right) ,\\ s_5 &{}=\zeta \left( {\zeta -\left( {\xi +\eta } \right) } \right) ,\quad s_6 =\frac{W}{2}\zeta \chi \left( {1-2\left( {\xi +\eta } \right) } \right) , \\ s_7 &{}=4\xi \eta ,\quad s_8 =2W\xi \eta \chi ,\\ s_9 &{}=4\eta \zeta ,\quad s_{10} =2W\eta \zeta \chi ,\\ s_{11} &{}=4\zeta \xi ,\quad s_{12} =2W\zeta \xi \chi \end{array}\right\} \end{aligned}$$

(A.2)

where W is the SNQ element thickness. While the pairs of shape functions $s_i$ and $s_j , i=1,3,5, j=2,4,6$, are, respectively, associated with the SNQ nodal positions and slopes of the corner node $k, k=1,2,3$, the pairs of shape functions $s_i$ and $s_j , i=7,9,11, j=8,10,12$, are, respectively, associated with the nodal positions and slopes of the middle node $k, k=4,5,6$, on the sides of the element.