Contact interaction of two rectangular plates made from different materials with an account of physical nonlinearity

Abstract

A mathematical model of a contact interaction between two plates made from materials with different elasticity modulus is derived taking into account physical and design nonlinearities. In order to study the stress–strain state of this complex mechanical structure, the method of variational iteration has been employed allowing for reduction of partial differential equations to ordinary differential equations (ODEs). The theorem regarding convergence of this method is formulated for the class of similar-like problems. The convergence of the proposed iterational procedure used for obtaining a solution to contact problems of two plates is proved. In the studied case, the physical nonlinearity is introduced with the help of variable parameters associated with plate stiffness. The work is supplemented with a few numerical examples. Both Fourier and Morlet power spectra are employed to detect and analyse regular and chaotic vibrations of two interacting plates.

1 Introduction

Many researchers have indicated that several structural materials may exhibit different tensile and compression response under flexural testing. For instance, composites fabricated from carbon fibres pre-impregnated by epoxy polymer usually present different elastic responses under tension and compression in the principal material directions. This phenomenon has been observed for the first time by Jones [1], who introduced the name of multi-modulus materials.

The multi-modulus materials, such as concrete, are widely employed in civil engineering [2]. While investigating radial and tangential stresses around boreholes, it was found that a slope of the linearized relationship in compression is almost always higher than that in tension [3]. Different stress–strain characteristics of cast iron and Poisson’s coefficient in tension and compression were reported by Gilbert [4].

Patel et al. [5] carried out both theoretical and experimental investigations of material properties of a calendared ply of numerous composites widely used in the body and belt of radial tires. They detected bi-modulus behaviour under tension and compression.

Barak et al. [6] employed electronic speckle pattern interferometry to measure concurrently the compressive and tensile strains in cortical bone beams tested in bending. It was reported that the tensile Young’s modulus is slightly (6%) greater than the compressive Young’s modulus.

Bertoldi et al. [7] developed a micromechanical model for nacre (mother of pearl) by using a homogenization approach. In the small-strain regime, the nacre exhibited strong difference in directional stiffness and bi-modular effects (different Young’s moduli in compression and tension).

It should be emphasized that even graphene, the strongest material having minimum electric resistance, shows greater compression modulus than tension modulus [8, 9]. Graphite, which is a descendant of graphene, was investigated by Yao et al. [10] and different tensile and compressive elastic moduli were measured in this study. In addition, buckling tests were performed while studying the buckling behaviour of a graphite rod. The analytical and finite element numerical models demonstrated to be reliable.

Yao and Ye [11] proposed the analytical/numerical model of thermal stresses for a structure with different moduli.

In the last century, a few mathematical models were developed to study behaviour of the multi-modulus materials. The first one was proposed by Bert [12], who studied a certain composite material exhibiting different Poisson compliance when loaded transversally to the fibres than when loaded parallelly to the fibres. The proposed method has been commonly used in multi-layer composites [13,14,15,16]. The second widely accepted model was proposed by Amburtsmian [17] and was validated for isotropic materials. It allows for estimation of different tension and compression moduli based on the positive/negative sign of the fundamental stresses, which play an important role in engineering application.

Furthermore, Jones [18] proposed the modified and improved model called the weighted compliance matrix (WCM) material model, which satisfies the criteria for isotropic and orthotropic bodies under plane stresses. The state of the art of the multi-modulus materials was presented, for instance, in reference [19] and thus is omitted here.

The contact problems have a long history in mechanics, and at the beginning, mathematical approaches were applied to solve them. The problem of a point contact between elastic bodies was formulated for the first time by Hertz [20]. Nowadays, a rapid development of technology and fabrication tools has attracted numerous researchers to revisit modelling of the contact problem, which stands for one of the most challenging problems in the field of mechanics of deformable rigid bodies. The complexity of the problem requires rather sophisticated mathematical approaches aimed at finding precise, reliable, and validated solutions. In particular, the complexity and difficulty of the mentioned problems increase while dealing with the contact interactions of structural members made from materials having different moduli.

Duvant and Lion [21] proposed the first attempt to study contact problems with the help of evolutionary variational inequalities. A deeper state of the art of mathematical approaches can be found in references [22,23,24]. More recently, quasi-static and dynamical frictional non-standard contact states belonging to a new class, including also effects of memory, have been studied in piezoelectric materials [25, 26].

The so far briefly reviewed state of the art emphasizes the importance of analysing the phenomena associated with contact problems of plates taking into account the different moduli of the used materials. Our work brings a contribution to this problem by derivation of a mathematical model of the contact interaction of two plates, where the physical nonlinearity is also taken into account. The paper is organized in the following manner.

Section 2 of the paper deals with derivation of the partial differential equations (PDEs) governing the dynamics of two plates made from bi-modulus material. In addition, the plates are of variable thicknesses and are separated by a clearance. Reduction of PDEs to ODEs is described in Sect. 3, including a numerical example. Section 4 presents theorems associated with the MVI (method of variational iterations) convergence putting emphasis on our formulated theorems. Contact interaction of two square plates and numerical examples is reported in Sect. 5. Section 6 presents dynamic problems of contact interaction with employment of Fourier and Morlet wavelet spectra aimed at investigating regular and chaotic vibration of the structural package. The paper ends with a Sect. 7 containing concluding remarks associated with the obtained results.

2 Statement of the problem

We consider a problem dealing with one-constrained mechanical interaction between two rectangular plates of variable thickness. The plates are treated as thin, and their stress–strain state (SSS) can be described by the classical Kirchhoff theory supplemented with physical nonlinearity and considered in the frame of the theory of small elastic-plastic deformations. We assume that the contact pressure (normal to the surface of generated stress) is much less in comparison with the normal stress occurred in the plates cross sections, and hence, a free slip of the contacting plates is allowed. A choice of the classical theory of plates (the Kirchhoff model) is motivated by an observation that, in comparison with the transversal crushing in a contact zone, the deformation of the transverse shear has a negligible influence on both the SSS and the distribution of the contact pressure [27]. This validated observation stands for us as the main purpose of developing and further employing our theoretical background.

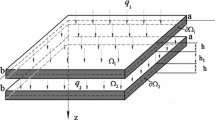
Let us present a system of the input PDEs for two contacting plates in the following form [27]:

$$\begin{aligned} \left\{ \begin{array}{l} A_{1}w_{1}(x,y)=q_{1}(x,y)-q_{k}\psi \\ A_{2}w_{2}(x,y)=q_{2}(x,y)-q_{k}\psi \end{array}\right. \end{aligned}$$

(1)

where $w_i (x,y)$—vector functions; $q_i (x,y)$—vector of the external load; $i = 1, 2$—number of a plate coinciding with a positive sense of the normal; $\varOmega _{1} =\{a_1 (x,y)\le z\le b_1 (x,y)\}, \varOmega _{2} =\{a_2 (x,y)\le z\le b_2 (x,y)\}$—volumes occupied by plates; $z=a_i (x,y)$ and $z= b_{i}(x,y)$, $(x, y)\in \varOmega _{i}$ are the functions governing forms of external surfaces of the plates, which allow to take into account changes in thickness of each plate (Fig. 1).

Fig. 1

Geometric parameters of the plates

The influence of different plate moduli on the plate behaviour is investigated based on Zhao and Ye [28] as well as He et al. [29] proposals. Each plate is divided into two subspaces by means of employing a concept of the so-called elastic neutral layer $z=c_i (x,y)$: $\varOmega _i^+ =\{a_i (x,y)\le z\le c_i (x,y)\}, \varOmega _i^- =\{c_i (x,y)\le z\le b_i (x,y)\}$. The material in the space $\varOmega _i^+$ is defined by Young’s modulus $E_i^+ (x,y,z,e_i^+ )$ and Poisson’s coefficient $\nu _i^+ (x,y,z,e_i^+ )$ corresponding to extension (+), whereas the space $\varOmega _i^-$ is defined by Young’s modulus $E_i^- (x,y,z,e_i^- )$ and Poisson’s coefficient $\nu _i^- (x,y,z,e_i^- )$ corresponding to compression (–). Furthermore, $e_i^{+/-}$ stands for the deformation intensity. The stress–strain state, owing to reference [29], is defined by non-constant elasticity modulus and Poisson’s coefficient, and the following relations hold

$$\begin{aligned} \sigma _x^{+/-}= & {} \frac{E_i^{+/-} }{ 1-\left( {\nu _i^{+/-} } \right) ^{2}}\left[ {\varepsilon _x +\nu _i^{+/-} \varepsilon _y } \right] , \\ \sigma _y^{+/-}= & {} \frac{E_i^{+/-} }{ 1-\left( {\nu _i^{+/-} } \right) ^{2}}\left[ {\varepsilon _y +\nu _i^{+/-} \varepsilon _x } \right] ,\\ \tau _{xy}^{+/-}= & {} -\frac{E_i^{+/-} z}{ 1+\left( {\nu _i^{+/-} } \right) }\varepsilon _{xy} . \end{aligned}$$

In physically linear problems, based on the introduced assumptions, the operator $A_i\,(i = 1,2)$ takes the following form

$$\begin{aligned} A_i w_i \left( {x ,y} \right)= & {} D_i \left[ \frac{\partial ^{2}}{\partial x^{2}}\left( {\frac{\partial ^{2}w_i }{\partial x^{2}}+\frac{\partial ^{2}w_i }{\partial y^{2}}} \right) \right. \nonumber \\&\left. +\,\frac{\partial ^{2}}{\partial y^{2}}\left( {\frac{\partial ^{2}w_i }{\partial x^{2}}+\frac{\partial ^{2}w_i }{\partial y^{2} }} \right) \right] , \end{aligned}$$

(2)

where

$$\begin{aligned} D_i =\frac{E_i^+ \int _{a_i (x,y)}^{c_i (x,y)} {z^{2}\hbox {d}z} }{ 1-\left( {\nu _i^+ } \right) ^{2}}+\frac{E_i^- \int _{c_i (x,y)}^{b_i (x,y)} {z^{2}\hbox {d}z} }{ 1-\left( {\nu _i^- } \right) ^{2}}. \end{aligned}$$

On the other hand, for physically nonlinear stress–strain problem of plates with non-constant thickness and made from a material with different moduli, the operator $A_i\,(i = 1,2)$ has the following form

$$\begin{aligned} A_i w_i \left( {x ,y} \right)= & {} \frac{\partial ^{2}}{\partial x^{2}}\left( {B_{11,i} \frac{\partial ^{2}w_i }{\partial x^{2}}+B_{10,i} \frac{\partial ^{2}w_i }{\partial y^{2}}} \right) \nonumber \\&+\,\frac{\partial ^{2}}{\partial y^{2}}\left( {B_{10,i} \frac{\partial ^{2}w_i }{\partial x^{2}}+B_{11,i} \frac{\partial ^{2}w_i }{\partial y^{2} }} \right) \nonumber \\&+\,2\frac{\partial ^{2}}{\partial x \partial y}\left( {\left( {B_{11,i} -B_{10,i} } \right) \frac{\partial ^{2}w_i }{\partial x \partial y}} \right) ,\nonumber \\ \end{aligned}$$

(3)

where

$$\begin{aligned} B_{mn,i}= & {} \frac{1}{2}\left[ \frac{E_{11,i} }{E_{01,i} }+\left( {-1} \right) ^{m}\frac{E_{10,i} }{E_{00,i}}\right. \\&\left. -\,E_{21,i} +\left( {-1} \right) ^{n}E_{20,i} \right] ,\\ E_{mn,i}= & {} \int \limits _{a_i (x,y)}^{c_i (x,y)} {\frac{E_i^+ z^{m}}{1+(-1)^{n}\nu _i^+ }} \;\hbox {d} z\\&+\,\int \limits _{c_i (x,y)}^{b_i (x,y)} {\frac{E_i^- z^{m}}{1+(-1)^{n}\nu _i^- }} \;\hbox {d} z,\\&\quad n=0, 1;\quad m=i=1, 2. \end{aligned}$$

The operators $A_i\,(i = 1,2)$ are defined as follows (linear case)

$$\begin{aligned} A_i w_i \left( {x ,y} \right)= & {} D_i \left[ \frac{\partial ^{2}}{\partial x^{2}}\left( {\frac{\partial ^{2}w_i }{\partial x^{2}}+\frac{\partial ^{2}w_i }{\partial y^{2}}} \right) \right. \nonumber \\&\left. +\,\frac{\partial ^{2}}{\partial y^{2}}\left( {\frac{\partial ^{2}w_i }{\partial x^{2}}+\frac{\partial ^{2}w_i }{\partial y^{2} }} \right) \right] , \end{aligned}$$

(4)

and where $D_i =\frac{E_i h^{3}}{12 \left( {1-\nu _i ^{2}} \right) }$ stands for a cylindrical stiffness, $E _i$ is Young modulus, and $\nu _i$ is Poisson’s coefficient.

In a nonlinear problem governing the SSS of plates of variable thickness and made from bi-modulus material, the operators $A_i$ $(i = 1,2)$ have the following form

$$\begin{aligned} A_i w_i \left( {x ,y} \right)= & {} \frac{\partial ^{2}}{\partial x^{2}}\left( {B_{11,i} \frac{\partial ^{2}w_i }{\partial x^{2}}+B_{10,i} \frac{\partial ^{2}w_i }{\partial y^{2}}} \right) \nonumber \\&+\,\frac{\partial ^{2}}{\partial y^{2}}\left( {B_{10,i} \frac{\partial ^{2}w_i }{\partial x^{2}}+B_{11,i} \frac{\partial ^{2}w_i }{\partial y^{2} }} \right) \nonumber \\&+\,2\frac{\partial ^{2}}{\partial x \partial y}\left( {\left( {B_{11,i} -B_{10,i} } \right) \frac{\partial ^{2}w_i }{\partial x \partial y}} \right) , \end{aligned}$$

(5)

where

$$\begin{aligned} B_{mn,i}= & {} \frac{1}{2}\left[ \frac{E_{11,i} }{E_{01,i} }+\left( {-1} \right) ^{n+1}\frac{E_{10,i} }{E_{00,i} }\right. \nonumber \\&\left. -\,E_{21,i} +\left( {-1} \right) ^{n}E_{20,i} \right] , \\ E_{mn,i}= & {} \int \limits _{a_i (x,y)}^{b_i (x,y)} {\frac{E_i z^{m}}{1+(-1)^{n}\nu _i }} \;\hbox {d} z,\\&\quad n=0, 1,\quad m=i=1, 2. \end{aligned}$$

The following notation is employed: $z=a_i \left( {x,y} \right)$ and/or $z=b_{i}({x,y}),(x,y)\epsilon \varOmega _{i}$ denote equations of external surfaces of the plates, which allow for inclusion of variable thickness of each plate; $E_{i } (x,y,z,e_i^{(i)} ), \nu _{i} (x,y,z,e_i^{(i)} )$ describe different stiffness modulus and Poisson’s coefficients, respectively; $e_i^{(i)}$ stands for intensity of deformation of i-th plate.

It should be emphasized that the method of variable parameters of stiffness [30], employed in our physically nonlinear problem, is based on observation that $E_i (x, y, z, e_i^{(i)} )_{, }v_i (x, y, z, e_i^{(i)} )$ are non-constant parameters dependent on the deformation state in a plate point, and they are governed by the following formulas

$$\begin{aligned} E_i =\frac{9K_{1i} G_i }{3K_{1i} +G_i }, \quad \nu _i =\frac{1}{2}\frac{3K_{1i} -2G_i }{3K_{1i} +G_i }, \end{aligned}$$

(6)

where $K_{1i} = \hbox {const}$. The theory of deformation yields the following shear modulus

$$\begin{aligned} G_i =\frac{1}{3}\frac{\sigma _i^{(i)} \left( e_i^{(i)} \right) }{e_i^{(i)} }, \end{aligned}$$

(7)

where $\sigma _i^{(i)}$, $e_i^{(i)}$ stand for intensity of stresses and deformations of a plate, respectively, and

$$\begin{aligned} e_k^{(i)}= & {} \frac{\sqrt{2}}{3}\left[ \left( {e_{xx}^{(i)} -e_{yy}^{(i)} } \right) ^{2}+\left( {e_{yy}^{(i)} -e_{zz}^{(i)} } \right) ^{2}\right. \nonumber \\&\left. \quad +\,\left( {e_{xx}^{(i)} -e_{zz}^{(i)} } \right) ^{2}+1.5\left( {e_{xy}^i } \right) ^{2} \right] ^{1/2}, \\ e_{xx}^{(i)}= & {} -z\frac{\partial ^{2}w_i }{\partial x^{2}},\quad e_{yy}^{(i)} =-z\frac{\partial ^{2}w_i }{\partial y^{2}},\quad e_{xy}^{(i)} =-2z\frac{\partial ^{2}w_i }{\partial x\partial y}. \end{aligned}$$

The value of $e_{zz}^{(i)}$ is defined through the condition of a plane stress state $(s_{zz} =0)$:

$$\begin{aligned} e_{zz}^{(i)} =-\frac{\nu _{i}}{1-\nu _i }\left( e_{xx}^{(i)} +e_{yy}^{(i)}\right) . \end{aligned}$$

(8)

Two types of boundary conditions are analysed, i.e.

• (i) simple support

  $$\begin{aligned} w_i \Big |_{\partial \varOmega } =\frac{\partial ^{2}w_{i} }{\partial n^{2}} \Big |_{\partial \varOmega } =0,\quad i=1,2; \end{aligned}$$

  (9)

• (ii) rigid clamping

  $$\begin{aligned} w_i \Big |_{ \partial \varOmega } =\frac{\partial w_i }{\partial n} \Big |_{\partial \varOmega } =0,\quad i=1,2. \end{aligned}$$

  (10)

Note that in mathematical models (1), (4), (9), (10) and (1), (5), (9), (10), the contact pressure is proportional to the transversal crushing $w_1 -h_1 -w_2$ in a zone of contact between plates, i.e. we have

$$\begin{aligned} q_k (x,y)=k\frac{E}{h}(w_1 -h_1 -w_2 ), \end{aligned}$$

(11)

and the function $\psi$ has the following form

$$\begin{aligned} \psi ={\left[ {1+\hbox {sign}(w_1 -h_1 -w_2 )} \right] }/2. \end{aligned}$$

(12)

Here $h_1$ stands for a clearance between plates, and k is the stiffness coefficient of the transverse crushing of the plates.

Due to occurrence of the multiplier $\psi$ in (1), the system of equations becomes nonlinear, and consequently the entire problem becomes nonlinear. The design nonlinearity governs the possibility of switching on/off of the one-sided constraint. Furthermore, inclusion of the physical nonlinearity in the considered problem makes it impossible to solve the problem via classical analytical, semi-analytical, or numerical approaches. Therefore, we employ here the method of successive approximations matched with a simultaneous process of improvements of the borders of the contact zones.

Observe that formula (11) holds for the case of a contact between plates having the same thickness h and the same parameters E and k. In the case of contact problems of Kirchhoff’s plates, Winkler-type coupling between the crushing zone and the contact pressure is utilized. If there is a thin layer between plates, it can be also taken into account by means of changing the parameter k.

If the initial plates configuration (function $h_{1})$ and the employed load correspond to lack of contact between the deformed plates, then $\psi \equiv$ 0, and the system (1) is split into two separate subsystems. Otherwise, two subsystems (plates) are coupled. Substituting (11) into (1) yields

$$\begin{aligned} \left\{ {\begin{array}{l} A_1 w_1 (x,y)=q_1 (x,y)-k\frac{E_1 }{h}(w_1 -h_1 -w_2 )\psi , \\ A_2 w_2 (x,y)=q_2 (x,y)+k\frac{E_2 }{h}(w_1 -h_1 -w_2 )\psi . \end{array}} \right. \end{aligned}$$

(13)

Observe that the system (13) is of the eight orders and hence it should be studied together with the boundary conditions (9), (10). It includes both design and physical nonlinearity.

In order to solve the derived design-nonlinear problem (13), one has to construct an iterational process allowing (for each step of loading) for solving only one of the equations of the system (13). This procedure yields a decrease in the systems order twice for a two-layer package and, consequently, into n times while dealing with a package of n layers. The iterational procedure has the following form

$$\begin{aligned} \left\{ {\begin{array}{l} A _1 \left( w _1^{(n)} \right) +k\frac{E}{h} \psi _{(n-1)} w_1^{(n)} =q_1 (x,y)\\ \quad +\,k\frac{E_1 }{h}\left( h_1 +w_2^{(n-1)} \right) \psi _{(n-1)} , \\ A_2 \left( w_2^{(n)} \right) +k\frac{E}{h} \psi _{(n-1)} w_2^{(n)} =q_2 (x,y)\\ \quad +\,k\frac{E_2 }{h}\left( w_1^{(n-1)} -h _1 \right) \psi _{(n-1)} . \end{array}} \right. \end{aligned}$$

(14)

The system (14) should be supplemented with the corresponding boundary conditions (6) or (7) for the i-th plate. If the values of E and h are different, then for the upper/lower plate we use notation $E_1 ,h_1 /E_2 ,h_2$, and we have

$$\begin{aligned} q_k (x,y)=2k\frac{E_1 }{h_1 } \left( {1+\frac{E_1 h_2 }{E_2 h_1 }} \right) (w_1 -h_j -w_2 ). \end{aligned}$$

(15)

In the case of fixed/frozen contact zone, Eq. (14) can be solved using one of the methods devoted to reduction of PDEs to ODEs. Those methods are briefly discussed in the next sections of the paper.

3 Reduction of PDEs to ODEs

Nowadays, there exist a few methods aiming at reducing the PDEs to ODEs. The principal concepts and ideas of those methods will be discussed using the operator-type equation of the form

$$\begin{aligned} Aw\left( {x ,y} \right) =q\left( {x y} \right) , \quad \left( {x ,y} \right) \in \varOmega =\left( {a ,b} \right) \times \left( {c ,d} \right) , \end{aligned}$$

(16)

where A—operator of a boundary problem including both differential operator and boundary conditions; q(x, y)—known function (vector function of the system of equations); w(x, y)—function being searched (vector function of the system of equations).

3.1 The method of Kantorovich–Vlasov (MKV)

Owing to the MKV, the following form of solution to (16) can be assumed [31, 32]:

$$\begin{aligned} w_N \left( {x ,y} \right) =\sum _{i=1}^N {\varphi _i \left( x \right) } \psi _i \left( y \right) , \end{aligned}$$

(17)

where $\varphi _i (x)$ are given functions satisfying the boundary conditions (9) or (10), whereas $\psi _i (y)$ are the being searched functions defined by the following system of projected equations

$$\begin{aligned} (Aw_N -q,\varphi _j (x))_{H(a,b)} =0 j=1,2,\ldots ,N, \end{aligned}$$

(18)

Here $(A u_N -q,\varphi _j (x))$ stands for notation of a scalar product in the space ${H(a,b), H = H(a,b) \times H(c,d)}$ is the space in which the exact solution $w_0$ to Eq. (16) exists. The procedure (18) reduces the problem of PDEs to ODEs by employing the Bubnov–Galerkin method regarding one of the coordinates. This procedure, in fact, generalizes the classical Bubnov–Galerkin method [33].

Disadvantages If the expected solution (17) should obey the same symmetry property with regard to all variables, then the MKV method sometimes cannot exhibit this property due to the limited number of terms used in the series. In other words, in case of taking a limited number of the series terms, the mentioned symmetry can be lost.

Advantages Independence of the basic functions versus one of the variables (here y) on the form of the boundary conditions.

3.2 Method of Vaindiner (MV)

In this case a solution to Eq. (15) is assumed to be as follows [34]:

$$\begin{aligned} w_N (x,y)=\sum _{i=1}^N {\varphi _{i} (x)\;\psi _i (y)} +u_{i}(x) v_i (y), \end{aligned}$$

(19)

where $\psi _i (y)$ and $u_i (x)$ are given functions, $\varphi _i (x)$ and $v_i (x)$ are the being searched functions satisfying the system of projected equations of the following form

$$\begin{aligned} (A w_N -q,\psi _j (y))_{H(c,d)}= & {} 0, \nonumber \\ (A w_N -q,u_j (x))_{H(a,b)}= & {} 0, \quad j=1,2,\ldots ,N,\nonumber \\ \end{aligned}$$

(20)

where $H((a,b)\times (c,d)) = H(a,b) \times H(c,d)$ is the space, where the exact solution $w_0$ exists.

Drawbacks There is a need to choose a full coordinate system of equations; there exists a dependence of accuracy of the obtained solutions on a number of equations in the system of approximating equations 2N, i.e. the number of equations is twice increased in comparison with the MKV.

Advantages In spite of the same advantages as those exhibited by MKV, there is a possibility of obtaining a symmetric solution with respect to all variables, if the being searched exact solutions have the mentioned symmetry.

3.3 Method of variational iteration (MVI)

This method presents a modification of the MKV [35]. Owing to MVI, a solution to Eq. (16) can be searched in the form of (17), where the functions $\varphi _i (x)$ and $\psi _i (y)$ are defined through the following equations

$$\begin{aligned}&(A u_N -q,\varphi _j (x))_{H(a,b)} =0, \end{aligned}$$

(21)

$$\begin{aligned}&(A u_N -q,\psi _j (y))_{H(c,d)} =0 \quad j=1,2,\ldots ,N, \end{aligned}$$

(22)

in the following way. A certain system of N functions with regard to one of the variables, let us say $\varphi _{j}^{0} (x) j=1,2,\ldots ,N$, is given. Then, the system (21) defines a system of functions $\psi _j^{(1)} (y)$, which are substituted into the system (22), and a new choice with regard to the variable x is defined as $\varphi _j^{(2)} (x)$. Then, using the chosen functions, the system (21) yields a new function $\psi _j^{(3)} (y)$ with respect toy,  and so on. Truncating the process of searching for the functions $\varphi _{j} (x)$ and $\psi _{j}(y)$ on the k-th step, we define the following function

$$\begin{aligned} w_N =\sum _{i=1}^N {\varphi _i^{(k-1)} (x)\psi _j^{(k)} (y)} , \end{aligned}$$

(23)

which serves as an approximate solution to Eq. (14).

Disadvantages The accuracy of the obtained approximate solution depends on a number of the series terms of (17).

Advantages There is no need to define the initial approximations satisfying, for instance, the boundary conditions; symmetry of the approximate solutions, if it is a priori known, holds; it is possible to achieve the maximum allowed accuracy of the approximate solutions even for a bounded number of terms approximating the solutions.

3.4 Method of Arganovskiy–Baglay–Smirnov (MABS)

The so far discussed method of variational iterations (MVI) coincides with the first term of the series of the method developed by Arganovskiy and Baglay [36], Baglay and Smirnov [37]. The formal scheme of the MABS can be briefly summarized in the following way.

A solution to Eq. (16) in the first approximation ($N=1$) is searched in a way similar to the MVI, i.e. we take

$$\begin{aligned} w_1 =\varphi _1^{(k-1)} (x) \;\psi _1^{(k)} (y). \end{aligned}$$

(24)

The new equation is defined as follows

$$\begin{aligned} Aw_2 (x,y)=q(x,y)-Aw_1 (x,y), \end{aligned}$$

(25)

i.e. we have changed the right-hand side of Eq. (16). Equation (16) is solved again with the help of MVI, and its first approximation yields

$$\begin{aligned} w_2 (x,y)=\varphi _2^{(k-1)} (x) \psi _2^{(k)} (y). \end{aligned}$$

(26)

The next new equation follows: $Aw_3 (x,y)=q(x,y)-Aw_1 (x,y)-Aw_2 (x,y)$, and then one employs the MVI again in the first approximation, and so on.

Finally, the following series is used as the input solution:

$$\begin{aligned} w(x,y)=\sum _{n=1}^N {w_n (x,y)} . \end{aligned}$$

(27)

Drawbacks This method cannot be used to solve a class of problems (for instance, if the boundary conditions are changed in a rectangular plate).

Advantages The advantages are analogous to those of MVI. Furthermore, each of the defined right-hand sides of the type of Eq. (25) can be solved by the MVI only in the first approximation, which generates algebraic systems of a small dimension.

3.5 Combined method (MC)

This method is a combination of the MV, MABS, and MVI. Owing to the MC, the approximate solution is searched in the following form

$$\begin{aligned} w^{(k)}(x,y)=\varphi ^{(k)}(x) \psi ^{(k-1)}(y)+u^{(k-1)}(x) v^{(k)}(y), \end{aligned}$$

(28)

where $\psi ^{0}(y)$ and $u^{0}(x)$ are assumed as known functions; $\varphi ^{(1)}(x)$ and $v^{(1)}(y)$ are the being searched functions defined by the projected Eq. (16). However, on the contrary to the MV, where the searched functions $\varphi ^{(1)}(x)$ and $v^{(1)}(y)$ have been treated as the final ones, here they are taken as known functions used to define the new $\psi ^{(2)}(y)$ and $u^{(2)}\left( x \right)$ unless the accuracy between $u^{(k)}(x,y)$ and $u^{(k-1)}(x,y)$ exceeds the assumed magnitude. We are looking for a solution of the equations

$$\begin{aligned} Aw_2 (x,y)=q(x,y)-Aw_1 (x,y) \end{aligned}$$

(29)

defined through the so far described way, i.e.

$$\begin{aligned} w_2 (x,y)=\varphi _2^{(k)} (x) \psi _2^{(k-1)} (y)+u_2^{(k-1)} (x) v^{(k)}(y). \end{aligned}$$

If the error between $u_1$ and $(u_1 +u_2 )$ is less than a given quantity, then the process is terminated. If not, then the following equation is constructed

$$\begin{aligned} Aw_3 (x,y)=q(x,y)-Aw_1 (x,y)-Aw_2 (x,y), \end{aligned}$$

(30)

and $w_3 (x, y)$ is defined, and so on. The final solution to Eq. (16) is defined by the following series

$$\begin{aligned} w_N (x,y)=\sum _{j=1}^N {w_j (x,y)} . \end{aligned}$$

(31)

Advantages This method includes all advantages of MV and MABS; furthermore, it may be used for a wide class of problems (for example, for the problems of rectangular variable boundary conditions along their contours).

3.6 Matching of the methods of Kantorovich–Vlasov and Arganovskiy–Baglay–Smirnov ($\hbox {MKV}+\hbox {MABS}$)

The key idea of this matching is the application of the procedure of MABS to the MKV without the employment of the method of variational iterations (MVI).

Owing to the method, an approximate solution of Eq. (16) is found based on the Kantorovich–Vlasov method, assuming its following form

$$\begin{aligned} w_N \left( {x ,y} \right) =\sum _{i=1}^N {\varphi _i \left( x \right) } \psi _i \left( y \right) , \end{aligned}$$

(32)

where $\varphi _i (x)$ are the given functions satisfying the corresponding boundary conditions (9) or (10), $\psi _i (y)$ are the searched functions defined by the system of projection Eq. (18). However, if the functions $w_1 (x,y)$ found in the MKV are the final ones, they can be employed to construct the operator $Aw _1 (x,y)$ on the right-hand side of equation

$$\begin{aligned} Aw_2 (x,y)=q(x,y)-Aw_1 (x,y), \end{aligned}$$

(33)

which is solved using the MKV.

If the error between $w_1$ and $w_1 +w_2$ is smaller than a given quantity, then the iterative process is stopped. If this is not the case, than we construct the following equation

$$\begin{aligned} Aw_3 (x,y)=q(x,y)-Aw_1 (x,y)-Aw_2 (x,y), \end{aligned}$$

(34)

and we define $w_3 (x, y)$ with the help of the MKV, and so on. The terminal/final solution to Eq. (16) is given by the following formula

$$\begin{aligned} w_N (x,y)=\sum _{j=1}^N {w_j (x,y)} . \end{aligned}$$

(35)

3.7 Matching of the methods of Vaindiner and the Arganovskiy–Baglay–Smirnov ($\hbox {MV}+\hbox {MABS}$)

In this case the method of Vaindiner (MV) is supplemented with the procedure of the MABS but without a procedure of MVI.

A solution to Eq. (15) is searched in the following form:

$$\begin{aligned} w_N (x,y)=\sum _{i=1}^N {\varphi _i (x)\;\psi _i (y)} +u_i (x) v_i (y), \end{aligned}$$

(36)

where $\psi _i (y)$ and $u_i (x)$ are the given functions, $\varphi _i (x)$ and $v_i (x)$ are the searched functions defined by the system of projection Eq. (18).

However, while the found function $w_1 (x,y)$ is treated as the final one in the MV, it is used to define the operator $Aw _1 (x,y)$ on the right-hand side of the following equation

$$\begin{aligned} Aw_2 (x,y)=q(x,y)-Aw_1 (x,y), \end{aligned}$$

(37)

which is solved by the MV.

If the error between $w_1$ and $w_1 +w_2$ is smaller than a given quantity, then the iterative process is stopped. Otherwise, we construct the following equations

$$\begin{aligned} Aw_3 (x,y)=q(x,y)-Aw_1 (x,y)-Aw_2 (x,y), \end{aligned}$$

(38)

and we define $w_3 (x, y)$ with the help of the MKV. As the final solution of Eq. (16), we take the following

$$\begin{aligned} w_N (x,y)=\sum _{j=1}^N {w_j (x,y)} . \end{aligned}$$

(39)

3.8 Matching of the methods of Vaindiner with the method of variational iterations ($\hbox {MV}+\hbox {MVI}$)

In this case the method of Vaindiner (MV) is extended to include a procedure of the variational iterations.

Table 1 Comparison of the results obtained with different methods

The approximate solution to the problem is searched in the following form

$$\begin{aligned} w^{(k)}(x,y)=\varphi ^{(k)}(x) \psi ^{(k-1)}(y)+u^{(k-1)}(x) v^{(k)}(y), \end{aligned}$$

(40)

where $\psi ^{0}(y)$ and $u^{0}(x)$ are known functions, $\varphi ^{(1)}(x)$ and $v^{(1)}(y)$ are the searched functions defined by the system of projection Eq. (16). However, if the functions $\varphi ^{(1)}(x)$ and $v^{(1)}(y)$ found with the help of MV are the final ones, they are taken as known functions, and the being searched solution takes the form

$$\begin{aligned} w^{(2)}(x,y)=\varphi ^{(1)}(x) \psi ^{(1)}(y)+u^{(1)}(x) v^{(1)}(y). \end{aligned}$$

(41)

Employment of the MVI yields new functions $\psi ^{(2)}(y)$ and $u^{(2)}(x),$ and so on. The iterative procedure is carried out until the error between $w^{(k)}(x,y)$ and $w^{(k-1)}(x,y)$ is smaller than a priori given value.

3.9 Numerical example

In order to compare the accuracy of each of the discussed methods, we consider the problem of a linear bending of the Germain–Lagrange plate governed by the following PDE

$$\begin{aligned} A_ w(x,y)=D\nabla ^{2}\nabla ^{2}w(x,y)=q(x,y), \end{aligned}$$

(42)

which has known exact solution.

The following boundary conditions are applied:

• (i) simple support

  $$\begin{aligned} w\Big |_{\partial \varOmega } =\frac{\partial ^{2}w}{\partial n^{2}} \Big |_{\partial \varOmega } =0; \end{aligned}$$

  (43)

• (ii) stiff clamping

  $$\begin{aligned} w\Big |_{ \partial \varOmega } =\frac{\partial w}{\partial n} \Big |_{\partial \varOmega } =0. \end{aligned}$$

  (44)

The space $\varOmega =( {0,a})\left( {0,b} \right)$ has the boundary $\partial \varOmega$. The differential operator (42) and the employed boundary conditions are presented in their counterpart non-dimensional form

$$\begin{aligned}&x=\bar{{x}}a, \quad y=\bar{{y}}b, \quad w=\bar{{w}}h,\nonumber \\&\lambda =a/b, \quad \bar{{q}}(x,y)=\frac{q(x,y)}{12(1-\nu ^{2})}\;\frac{a^{4}}{E h^{4}},\nonumber \\&\overline{\nabla }^{4}\overline{w} =\frac{\partial ^{4}\overline{w} }{\partial \overline{x} ^{4}}+2\lambda ^{2}\frac{\partial ^{4}\overline{w} }{\partial \overline{x} ^{2}\partial \overline{y} ^{2}}+\lambda ^{4}\frac{\partial ^{4}\overline{w} }{\partial \overline{y} ^{4}}, \end{aligned}$$

(45)

and the bars over the non-dimensional quantities are further omitted.

Note that a system of integral–differential equations yielded by the Kantorovich–Vlasov procedure can be solved through the method of finite differences (FDM) with the successive employment of the Gauss method while solving a system of algebraic equations produced during looking for the solutions. The solution to the stated problems has been solved using unitary and doubled accuracy. The interval [0, 1] has been divided into 30 nodes. Further increase in nodes number has not changed the obtained results. The relative error of computations has been traced using the formula $\varepsilon =\left| {\frac{w^{k}(x,y)-w^{k-1}(x,y)}{w^{k}(x,y)}} \right| <10^{-3}$. The obtained results are reported in Table 1 for $\bar{{q}}(x,y)=50$.

The so far described methods as well as the results of the numerical experiment allow one to conclude that the MC has the highest accuracy in comparison with other methods and it yields the results being close to the exact solution. However, a drawback of this method is associated with the increase in the number of differential equations, and hence, one more iteration should be involved to get reliable results, which implies an increase in the computational time. However, the method of variational iterations is free from this drawback, and the yielded results are also close to the exact ones. Therefore, particularly in the case of complex problems, the MVI is recommended.

4 Mathematical background

4.1 Theorems on convergence of MVI

In the case of a fixed contact zone, the procedure of the MVI [35] is constructed (see the comments given in Sect. 3.3) together with the method of variable parameters of stiffness (MVPS) [30] unless the required accuracy is achieved. A successive improvement of a contact zone is achieved due to the method of direct iteration. Then the solution procedure is repeated, i.e. we employ three iterational procedures nested in each other. Scheme of MVI can be formally described in the following way. We are aimed at finding a solution to equation

$$\begin{aligned} Aw(x,y)=q(x,y); \quad x, y \in \varOmega (x,y), \end{aligned}$$

(46)

where A stands for a certain operator defined on the manifold D(A) of the Hilbert space $L_2 (\varOmega ); q(x, y)$ stands for a given function of two variables x, y; w(x, y) is a searched function; $\varOmega (x, y)$ is a space associated with variations of x and y.

If $\varOmega (x, y)=X\times Y$ (X—a certain bounded set of variables x; Y—a bounded set of y), then a solution to Eq. (46) has the following form

$$\begin{aligned} w_N (x,y)=\sum _{i=1}^N {u_i (x)v_i (y)} , \end{aligned}$$

(47)

where the functions $u_i (x)$ and $v_i (y)$ are defined by the following system of equations

$$\begin{aligned} \begin{array}{l} \int \limits _X {\left( {Aw_N -q} \right) u_1 \left( x \right) \hbox {d}x = 0, } \int \limits _Y {\left( {Aw_N -q} \right) v_1 \left( y \right) \hbox {d}y = 0,} \\ \int \limits _X {\left( {Aw_N -q} \right) u_N \left( x \right) \hbox {d}x = 0, } \int \limits _Y {\left( {Aw_N -q} \right) v_N \left( y \right) \hbox {d}y = 0,} \\ \end{array} \end{aligned}$$

(48)

in the following way. A certain system composed of N functions with respect to one of the variables, for instance, $u_1^0 (x), u_2^0 (x),\ldots , u_N^0 (x)$ is given. Then, the first N equations of the system (48) yield N functions $v_1^1 (x), v_2^1 (x),\ldots , v_N^1 (x)$. Next, the obtained functions are employed to create a new set of functions $x - u_1^2 (x), u_2^2 (x),\ldots , u_N^2 (x)$, which is further used to construct a set of new functions with respect to the variable y, i.e. $v_1^3 (x), v_2^3 (x),\ldots , v_N^3 (x)$, and so on.

In the case of the iterational procedure MVI [35], proofs of the theorems constituting the theoretical background of the MVI convergence were given for the problems of the theory of plates.

Theorem 1

If A is a positively defined operator with its action space $D(A)\subset H_A ,$ then the sequence of elements $\alpha =\parallel w_{1}^{k}(x,y)-w_{0}\parallel _{H_A}$ is monotonously decreasing, i.e. for arbitrary and j,  if only $i\ge j,$ then

$$\begin{aligned} \left\| {w_1^i -w_0 } \right\| _{H_T } \le \left\| {w_1^j -w_0 } \right\| _{H_T } . \end{aligned}$$

(49)

Theorem 2

Let each element of the basis system of the space $\mathop {W_2^m }\limits ^0(X\times Y)$ has the form

$$\begin{aligned} \theta _i (x,y)=\varphi _i (x)\psi _i (y), \end{aligned}$$

(50)

where is a basis system in the space $\mathop {W_2^m }\limits ^0(X \times Y),$ and, respectively, $\{\varPsi _{i}(X \times Y)\}$ in the space $\mathop {W_2^m }\limits ^0 (Y),$ and in order to get an arbitrary -th approximation regarding MVI, the components of the elements of the basis system $\{\theta _{i}(X \times Y)\}$ are taken as initial conditions. Then, for sufficiently large N, the MVI gives a unique approximate solution, and the sequence $\{W_{N}\}$ is convergent with regard to the norm of the space $\mathop {W_2^m }\limits ^0(X \times Y),$ and tends to the exact solution $\omega _{0}$ independently of a number of steps k, which can be defined for each of the N-th approximation, i.e. $\parallel w_{N}^{k}-w_{0}\parallel \mathop {W_2^m }\limits ^0, N \rightarrow \infty$

The ordinary differential equations obtained on each step of the iterational procedure by the method of variational iterations can be solved with numerous methods such as reduction of the problem to the algebraic equations by FDM with the successive solutions of the obtained algebraic equations by the Gauss method.

The method of variational iterations (MVI) removes the necessity of constructing the system of approximating functions, on the contrary to the widely employed Bubnov–Galerkin and Ritz methods [38, 39]. The initially given arbitrary functions (perhaps satisfying the well-known conditions of smoothness) are modified in the process of computations through MVI beginning with a solution of the input system of PDEs governing the plates behaviour. Therefore, in a natural way, the MVI constructs the approximating functions in the form of a product of two functions, where one of them depends on one argument in a way similar to the Fourier method. This implies the necessity of solving two ODEs instead of one. In fact, the method of variational iterations generalizes the Fourier method.

The most fascinating result is that the procedure of the MVI is converged even if functions not satisfying the boundary condition (9), (10) in the form: $w_1 (x)=1; w_2 (y)=1$ are taken as the initial approximations.

The MVI procedure was stopped already on the fourth step of the variational iterations. Remarkably, almost accurate coincidence with the exact solution has been obtained, i.e. the boundary conditions (6)/(7) correspond to the difference between the approximate and exact solution in percentage of 0.1/0.6%.

4.2 Convergence theorem

In what follows, we formulate a theorem (without a proof) regarding convergence of the iterational procedure (14) associated with solving our formulated problem aimed at designing a nonlinear system composed of two plates made from materials of different moduli.

Let $R^{2}$ be an Euclidean plane with a Descartes basis: $\varOmega _{i} \epsilon R^{2}$—area on a plane with the boundary $\partial \varOmega _{i} \left( {i=1,2}\right) , \bar{{\varOmega }}_{i} =\varOmega _{i} \cup \partial \varOmega _{i} \left( {x,y} \right) \epsilon \varOmega _{i} ;\varOmega ^{*}$—sub-area of $\varOmega _{i}, \forall i,\varOmega ^{*}\subseteq \varOmega _{I};n_{i}$—external normal to $\partial \varOmega _{i}$.

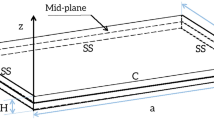
We consider a space plate-type object composed of two contacting plates (Fig. 2) obeying Kirchhoff’s hypotheses and governed by the following PDEs:

$$\begin{aligned}&A_1 \left( w_1 (x,y)\right) +k\frac{E_1 }{h}w_1 \psi (x,y)\nonumber \\&\quad =q_1 +k\frac{E_1 }{h}(w_2 +h_1 ) \psi (x,y), \nonumber \\&A_2 \left( w_2 (x,y)\right) +k\frac{E_2 }{h}w_2 \psi (x,y)\nonumber \\&\quad =q_2 \left( 1-\psi (x,y)\right) +k\frac{E_2 }{h}(w_1 -h_1 ) \psi (x,y),\nonumber \\ \end{aligned}$$

(51)

with the boundary conditions (10). The function defining the contact zone $\varOmega ^{*}$ of the plates is as follows

$$\begin{aligned} \psi (x,y)=\left\{ {\begin{array}{l} 1, (x,y)\in \varOmega {*,} \\ 0,(x,y)\notin \varOmega *, \\ \end{array}} \right. \end{aligned}$$

(52)

and $q_{1}{ (x, y), q}_{2}(x, y)$ are the functions of external load acting on the first and the second plate, respectively; the operators $A_i (w_i )$ have the form (5), which in the case of elastic problems is governed by (4); $\Vert \cdot \Vert _{\mathrm{A}}$—norm in a normalized space A; ($\cdot$, $\cdot )$—scalar product in the Hilbert space $L_{2}$. The employed notation of the functional spaces coincides with that given in reference [40], whereas $E_1 , E_2$ stand for different moduli in tension and compression.

In order to solve the problem (51), (10), the following iterational algorithm is employed:

$$\begin{aligned}&A_1 \left( w_1^{(n+1)} (x,y)\right) +k\frac{E_1 }{h}w_1^{(n+1)} \psi (x,y)=q_1\nonumber \\&\qquad +\,k\frac{E_1 }{h}\left( w_2^{(n)} +h_1 \right) \psi (x,y), \nonumber \\&A_2 \left( w _2^{(n+1)} (x,y)\right) +k\frac{E_2 }{h}w_2^{(n)} \psi (x,y)\nonumber \\&\quad =q_2 \left( 1-\psi (x,y)\right) \nonumber \\&\qquad +\,k\frac{E_2 }{h}\left( w_1^{(n)} -h_1 \right) \psi (x,y), \end{aligned}$$

(53)

$$\begin{aligned}&w_1^{(n+1)} \mathop |\nolimits _{\partial \varOmega _1 } =\frac{\partial w_1^{(n+1)} }{\partial n_1 }\mathop |\nolimits _{\partial \varOmega _1 } =0, \nonumber \\&w_2^{(n+1)} \mathop |\nolimits _{\partial \varOmega _2 } =\frac{\partial w_2^{(n+1)} }{\partial n_2 }\mathop |\nolimits _{\partial \varOmega _2 } =0. \end{aligned}$$

(54)

Then, the following theorem holds.

Theorem Let $\varOmega _{i}, (i = 1,2)$ are bounded spaces and let their boundaries $\partial \varOmega _{\mathrm{i}}$ satisfy conditions of the Sobolev embedding theorems [40], where $\varOmega ^{*}$ stands for a measurable space, $q_i ({x,y})\subseteq L_{2} (\varOmega _{i} )$ and besides, there exist real constants $c_{i}> 0, D_{i} > 0$ such that

$$\begin{aligned}&D_1 \left\| { \varDelta \left( {w_i } \right) } \right\| _{L_2 \left( {\varOmega ^{*}} \right) }^2 \nonumber \\&\quad \le \left( {B_{11, i} } \right. \frac{\partial ^{2}w_i }{\partial x^{2}} + B_{10, i} \frac{\partial ^{2}w_i }{\partial y^{2}} , \frac{\partial ^{2}w_i }{\partial x^{2}} \left. \right) _{L_2 \left( {\varOmega _2 } \right) } \nonumber \\&\qquad + \,\left( {B_{10, i} \frac{\partial ^{2}w_i }{\partial x^{2}}} \right. +B_{11, i} \frac{\partial ^{2}w_i }{\partial y^{2}} , \left. {\frac{\partial ^{2}w_i }{\partial y^{2}}} \right) _{L_2 \left( {\varOmega _2 } \right) } \nonumber \\&\qquad +\,\left[ \left( {B_{11, i} } \right. + B_{10, i} )\frac{\partial ^{2}w_i }{\partial x\partial y} , \frac{\partial ^{2}w_i }{\partial x\partial y} \right] _{L_2 \left( {\varOmega _2 } \right) } \nonumber \\&\quad \le c_i \left\| {\varDelta (w_i )} \right\| _{L_2 (\varOmega _i )}^2 . \end{aligned}$$

Then:

• (1) $\forall n$, $w_i^{(n)} \in W_2^4 (\varOmega _i )\bigcap {\dot{W}_2^2 } (\varOmega _i ) i=1,2;$

• (2) There exist functions $w_{i}^*(x,y)\in \dot{W}_{2}^{2} (\varOmega _{i}) i=1,2$ being solutions to the problems (14), (10) and $\mathop {\lim \limits _{n\rightarrow \infty }} \left\| {w_i^{(n)} -w_i^*} \right\| _{W_2^2 (\varOmega _i )} =0$.

Remark 1

The method of the variable stiffness parameters allows one to study SSS of the plates and plate-type constructions made from materials of different moduli, i.e. materials having different values of the elastic modulus and the Poisson’s coefficients regarding tension and compression.

Remark 2

The given theorem implies the theorem reported in reference [39] valid for a material with one modulus.

5 Contact interaction of two square plates

In this section we consider bending of two squared plates made from materials having different moduli in tension and compression, taking the physical nonlinearity into account (see Fig. 2).

Fig. 2

Two plates with a clearance

If values of the material parameters $E^{+},\;E^{-}, \nu ^{+},\nu ^{-}$ are slightly changed, the change in the elastic neutral layer (surfaces of the zeroth order) can be neglected [28, 29]. This observation has been taken into account in our further considered computational examples.

In order to investigate the stress–strain state of the plate-type structures made from materials of different moduli, one needs to use two different dependencies of the stress intensity on deformation. Let $\sigma _i^{(i)+} (e_i^{(i)+} )$ and $\sigma _i^{(i)-} (e_i^{(i)-} )$ be dependencies of the stress on deformation for the i-th plate. (“+” refers to tension, whereas “–” refers to compression.) Depending on a sign of the averaged stress of i-th plate $\sigma _v^{(i)} =\frac{1}{3}\left( {\sigma _X^{(i)} +\sigma _Y^{(i)} +\sigma _Z^{(i)} } \right)$, one may construct a diagram $\sigma _i^{(i)} (e_i^{(i)} )$ corresponding to either tension or compression for each of the plates. In this case, the previously implemented algorithm, including the method of variable elasticity parameters, method of variational iterations, iterational method of variational iterations, and iterational method of contact interaction, is employed.

5.1 Computational examples

We consider an example of a computation of the contact interaction between the square plates made from materials of different tension/compression moduli.

The plate material is a pure aluminium, and its nonlinear diagram is governed by the following formula

$$\begin{aligned} \sigma _i^ =\sigma _{s} \left[ {1-\exp \left( -\frac{e_{i}}{e_{is}} \right) } \right] , \end{aligned}$$

(55)

where $e_{iS} =\frac{\sigma _{S}}{3\sigma _{0}}$ is a conventional intensity of plasticity deformation, and hence,

$$\begin{aligned} \sigma =\sigma _{1} \frac{e_{is}}{e_{i}}\left[ {1-\exp \left( {-\frac{e_{i}}{e_{is}}} \right) } \right] . \end{aligned}$$

(56)

Fig. 3

The diagram $\sigma _{i} (e_i )$

While approximating the $\sigma _{i} (e_{i} )$ dependence shown in Fig. 3, one may use the following formula

$$\begin{aligned} \sigma _{i} =\sigma _{s} \left[ {1-\exp \left( {-\frac{e_{i} }{e_{is} }\left\{ {1+\frac{e_{i} }{e_{is}}} \right\} } \right) } \right] . \end{aligned}$$

(57)

The coefficient b can be identified assuming that the curve L goes through the point $(\sigma _i^{(*)} , e_i^{(*)} )\in L$, and hence,

$$\begin{aligned} b=-\frac{e_{i}}{e_{is}}\left[ {1+\frac{e_{iS}}{e_i{*}}\ln \left( {1-\frac{\sigma _{i}^{*}}{\sigma _{s}}} \right) } \right] . \end{aligned}$$

(58)

This allows for more feasible tracing of the velocity of approximating $\sigma _{s}$ by $\sigma _{i}^{*}$ with an increase in $e_{i}$. In the case of a material with different moduli (Fig. 4) and with an account of $\sigma _{i} \left( {e_i} \right)$ in the case of physical nonlinearity, we have

$$\begin{aligned} \sigma _{i}\pm =\alpha \sigma _{s}^{\pm } \left[ {1-\exp \left( {-\frac{e_{i}\pm }{e_{is}^\pm }} \right) } \right] . \end{aligned}$$

(59)

The conventionally recognized notation ± for $\sigma _{i} , e_{i}$, $e_{is}$ denotes the values of the stress, deformation and plasticity deformation, respectively, for the case of tension (+) and compression (–). The coefficient $\alpha$ may have values larger or smaller than 1 in both cases of deformation, i.e. tension or compression.

Fig. 4

Diagram $\sigma _{i} \left( {e_{i} } \right)$ for the material of different moduli and with physical nonlinearity

As an example, we consider two square plates simply supported along their contours [see (10)] for $\lambda =\frac{a}{b}=1$ and for their relative thickness $a/h=12.5$. Each plate is made from aluminium and exhibits the stress plasticity threshold $\sigma _S =1023\times 10^{5}$ Pa, $G_1 =G_2 =0.383\times 10^{11}$ Pa (here stresses are measured with respect to $G_1 (h/a)^{2})$, the non-dimensional deformations $\overline{e} =e_i (a/h)^{2}$, whereas the plasticity deformations are described by the formula $\overline{e_{S} } =e_{iS} (a/h)^{2}$. In reference [41], it has been shown that the properties of aluminium are well approximated by the dependencies $\sigma _{i}\left( {e_{i}} \right)$ through formulas (55), (56) and they are validated experimentally. Owing to the data reported in this reference, we take $k=k_{1} =2G_{1}$, and the $\sigma _i^{(i)} (e_i^{(i)} )$ function is governed by the following formula

$$\begin{aligned} \sigma _i^{(i)\pm } =\alpha ^{\pm }\sigma _s^{(i)} \left[ {1-\exp \left( {-\frac{e_i^{(i)\pm } }{e_s^{(i)\pm } }} \right) } \right] , \end{aligned}$$

(60)

the algorithms developed by us for estimating the dependence $\sigma _i^{(i)} (e_i^{(i)} )$ can be given in an arbitrary way, i.e. either in a tabular form (digits) or in an analytical way.

Fig. 5

The load–deflection dependence of the upper plate (both plates are made from material of different moduli)

The volume of each plate is covered by a mesh $B_i$ with respect to x, y, z of the resolution $30\times 30\times 8.$ In each point of two volumes, the following quantities have been computed $\sigma _{av}$, $E_i , \nu _i$ ($i = 1,2$) as a result of employment of the formulas reported in Sect. 2, and hence, the iterational procedures have been constructed.

The load–deflection dependence in the centre plate of the upper plate $\overline{q} (w_1 (0.5,0.5))$ is reported in Fig. 5, where $\left( {\bar{{q}}(x,y)=\frac{q(x,y)}{12(1-\nu _1 ^{2})}\;\frac{a^{4}}{E_1 h^{4}}} \right)$. The values of $\alpha ^{-}$ are shown in the figure, whereas $\alpha ^{+ }= 1.0$ for all investigated variants. Observe that an increase in the loading yields essential differences in SSS in comparison with decreasing $\alpha ^{- }$. The value of the threshold load decreases on amount of 2.1% with a decrease in $\sigma _{s}$ on amount of 5%.

Now we consider the SSS of the contact two-layer construction simply supported along the contour (9). Here the upper plate is made from a material of different moduli and physically nonlinear (solid curves), whereas the lower plate is made from one-modulus material (dashed curves). Relations $q(w_1 (0.5,0.5))$ are reported in Fig. 6.

The value of deflection, for which a contact occurred, is denoted by a dot $\left( {w_1 =0.01} \right)$. In the case of contact problems, the differences exhibited by the curves $q(w_1 )$ are essentially less than for the one-layer plates for $\alpha ^{-} = 0.8; 0.95$; 1.0. Analysis of the SSS of the plates implies that although the qualitative behaviour of the one-modulus $(\alpha ^{-} = 1)$ and different moduli ($\alpha ^{-} \ne 1$) materials is the same, there is an essential quantitative difference.

Fig. 6

The load–deflection dependence of the upper plate (only upper plate is made from material of different moduli)

Fig. 7

Surfaces $M_{x}(x,y)$ for different (a) and the same (b) modulus corresponding to the upper and lower plate, respectively

Fig. 8

Surfaces $M_{x}(x,y)$ for the upper plate with $\alpha ^{-} = 0.8$ (a) and $\alpha ^{-} = 1.0$ (b), respectively

The surface ${\bar{M}}_x (x,y)=-\frac{\partial }{\partial x}\left( {\overline{D_1 } \frac{\partial w}{\partial x}} \right)$ for different modulus $\alpha ^{-}= 0.8$ of the first plate and one modulus of the second (lower) plate is shown in Fig. 7a, b, respectively. Figure 8a, b shows the surfaces $\bar{{M}}_x (x,y)$ for the upper plate for the same parameters $\alpha ^{-} = 0.8$, and 1.0, respectively. Analysis of the plates SSS implies that their qualitative behaviour is similar in both cases $(a^{-}=1),$ and ($\alpha ^{-}\ne$ 1), but there is an essential quantitative difference.

6 Dynamics of a contact interaction

It should be emphasized that the phenomenon of contact interplay exhibited by mechanical systems composed of multi-layer plates coupled by boundary conditions is reported in this paper for the first time.

The further employed wavelet-based analysis allows one to study different kinds of vibration character in a given time interval. It allows also for detection of a birth/death of a frequency and time of its occurrence/vanishment. Although there exist different types of wavelets [42, 43], the Morlet wavelet is the most suitable for our purpose. The analysis of advantages and disadvantages of different wavelet types to be employed in the study of shells can be found in reference [44].

A phase synchronization means phase locking of chaotic vibrational signals in time, although amplitudes of the mentioned signals remain uncoupled with each other and exhibit chaotic behaviour. Furthermore, phase locking implies frequency locking (resonance phenomenon). The wavelet surface $w(s,t_{0})=\Vert w(s,t_{0}\Vert \exp [j\varphi _{s}(t_{0})])$ characterizes the system behaviour in each time interval s at an arbitrary time instant $t_{0}$. The quantity $\Vert w(s,t_{0})\Vert$ describes the occurrence and intensity of the corresponding time interval s at the time instant $t_{0}$. The integral energy distribution of the wavelet spectrum with respect to time intervals $E(s)=\int \Vert w(s,t_{0})\Vert ^{2}\hbox {d}t_{0}$ is introduced. The studied phase is defined as $\varphi _{s}=\arg W(s,t)$ for each time interval s, i.e. one can characterize behaviour of each time interval s with the help of the associated phase $\varphi _{s} (t)$. In particular, we have employed the Morlet wavelet while investigating the synchronization phenomenon of the considered mechanical structures.

Chaotic phase synchronization plays a key role in modern theory of nonlinear vibrations. The occurrence of the chaotic phase synchronization has been experimentally validated in radio-frequency generators, electromechanical oscillators, lasers, heart beating, and many others. It has also a significant influence on robustness of information transmission with the help of deterministic chaotic vibration.

Equations governing the dynamics of two-layer package of physically linear elastic plates have the following form (see Fig. 2)

$$\begin{aligned}&\left[ {\frac{E_1^+ \int _{a_i (x,y)}^{c_i (x,y)} {z^{2}\hbox {d}z} }{ 1-\left( {\nu _i^+ } \right) ^{2}}+\frac{E_1^- \int _{c_i (x,y)}^{b_i (x,y)} {z^{2}\hbox {d}z} }{ 1-\left( {\nu _i^- } \right) ^{2}}} \right] \nabla _\lambda ^{4}w_1 \nonumber \\&\quad +\,\frac{\gamma }{g}h\frac{\partial ^{2}w_1 }{\partial t^{2}}+\varepsilon \frac{\gamma }{g}h\frac{\partial w_1 }{\partial t}\nonumber \\&\quad -\,\frac{k}{h}E_1^+ (w_1 -w_2 -h*)\psi =q(t), \nonumber \\&\left[ {\frac{E_2^+ \int _{a_i (x,y)}^{c_i (x,y)} {z^{2}\hbox {d}z} }{ 1-\left( {\nu _i^+ } \right) ^{2}}+\frac{E_2^- \int _{c_i (x,y)}^{b_i (x,y)} {z^{2}\hbox {d}z} }{ 1-\left( {\nu _i^- } \right) ^{2}}} \right] \nabla _\lambda ^{4}w_2 \nonumber \\&\quad +\,\frac{\gamma }{g}h\frac{\partial ^{2}w_2 }{\partial t^{2}}+\varepsilon \frac{\gamma }{g}h\frac{\partial w_2 }{\partial t}\nonumber \\&\quad +\,\frac{k}{h}E_2^- (w_1 -w_2 -h*)\psi =0. \end{aligned}$$

(61)

In a particular case of one-modulus ($E_1^{+/-} =E_2^{+/-} =E$ and $\nu _1^{+/-} =\nu _2^{+/-} =\nu )$ physically linear material ($E=\hbox {const}$, $\nu =\hbox {const}$), PDEs (61) can be reduced to the counterpart non-dimensional form as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{1}{12(1-\nu ^{2})}\left( {\nabla _\lambda ^{4}w_1 } \right) +\frac{\partial ^{2}w_1 }{\partial t^{2}}+\varepsilon \frac{\partial w_1 }{\partial t}\\ \quad -K(w_1 -w_2 -h*)\varPsi =q(t), \\ \frac{1}{12(1-\nu ^{2})}\left( {\nabla _\lambda ^{4}w_2 } \right) +\frac{\partial ^{2}w_2 }{\partial t^{2}}+\varepsilon \frac{\partial w_2 }{\partial t}\\ \quad +K(w_1 -w_2 -h*)\varPsi =0. \end{array}} \right. \end{aligned}$$

(62)

System of Eq. (62) has been obtained by the following introduced relations between dimensional and non-dimensional parameters: $x=a\overline{x} , y=a\bar{{y}}; q=\overline{q} \frac{E(h)^{4}}{a^{2}b^{2}}, \tau =\frac{ab}{h}\sqrt{\frac{\gamma }{Eg}}, \lambda =\frac{a}{b}$, where a, b—plate dimension with respect to x and y, respectively; t—time; $\varepsilon$—damping coefficient; w—deflection; h—plate thickness; $\nu =0.3$—Poisson’s coefficient; g—the gravity of Earth; E—Young’s modulus; q(x, y, t)—transverse load; $\gamma$—specific material weight. Note that bars over non-dimensional quantities have been omitted in (62) for simplicity reasons.

Fig. 9

Characteristics of the plate contact interactions (see text for more details)

As boundary conditions, simple support along a contour is taken:

$$\begin{aligned}&w_m =0;\quad {w}''_m |_x =0; \hbox {for}\,x =0;1, w_m =0;\nonumber \\&{w}''_m |_y =0; \hbox {for}\,y=0;1; m=1,2. \end{aligned}$$

(63)

The initial conditions are as follows

$$\begin{aligned} w_m (x,y)|_{t=0} =0,\quad \dot{w}_m |_{t=0} =0, \quad m=1, 2. \end{aligned}$$

(64)

We take the control function $\psi =\frac{1}{2}[ 1+\hbox {sign}( w_1 -h*-w_2 ) ]$; $\varPsi =1,$ if $\hbox {w}_{1} >w_2 +h_k$, i.e. there is contact between plates; otherwise $\varPsi =0$; $w_1 ,w_2$—function of deflection of upper and lower plates, respectively; K—stiffness coefficient of transverse clamping in the contact zone; $h*$—clearance between plates, and $q(t)=q_0 \sin (\omega _0 t)$.

A solution to system (60)–(62) is being searched by the Faedo–Galerkin method, and the problem is reduced to investigating nonlinear ODEs (the Cauchy problem). The function $w_i , i=1,2$ is approximated by a function being a product of two functions (one depending on time and the other depending on coordinates) of the following form

$$\begin{aligned} w_{m} =\sum _{i=1}^N {\sum _{j=1}^N {A^{(m)}_{ij} (t)\sin (i\pi x)\sin (j\pi y),}}\quad m=1,2 \end{aligned}$$

(65)

The derived Cauchy problem has been solved using the fourth-order Runge–Kutta method.

As an example, let us consider vibration of the plates under the sinusoidal and uniformly distributed load for the following fixed parameters: $q_0 =2$, $K=5000$, $h*=0.01$, $\varepsilon =0.5$, $\omega _0 =5.0887$. (The last one stands for the fundamental frequency of linear plate vibration.)

It has been shown that to verify convergence of the numerical results obtained by the Faedo–Galerkin method for $N=1, 3, 5$, it is sufficient to take only three first terms of the series in formula (65). It has been found that once a contact between two plates takes place, vibration become chaotic. The character of plates vibration has been investigated with the help of qualitative methods of nonlinear dynamical systems, i.e. we have employed Fourier and wavelet-based analysis, studied contact pressure between plates, and monitored the phase difference of plate vibration.

Graphs of simultaneous vibration of the centres of both plates w(t), their contact pressure Pq(t), time history of phases difference $\varDelta \varphi _s (t)$ as well as the Fourier power spectrum $F(\omega )$ and 2D/3D wavelet spectrum for each of the plate, respectively, are presented in Fig. 9.

Time histories of plate deflections (a) and time histories of contact pressures (b) exhibit complex chaotic interaction of the plates. A dark colour used in the plots showing the phase difference (c) exhibits the frequencies zone $\omega \in [4,8]$ where the phase synchronization has been detected. Vibrations exhibit clearly the frequency $\omega _0 ,$ i.e. the vibrations take place on the fundamental frequency of free vibrations of the two-layer structural package.

This is validated by the Fourier spectrum (d, g) and the Morlet spectrum (e, h, f, i). The latter exhibits energetic component of each of the frequencies at a given time instant.

Remark 1

It should be mentioned that the so far solved dynamical problems and used methodology can be successfully employed also to solve static counterpart problems. The method is known as the relaxation method and has been used by us earlier to solve different nonlinear problems [45]. From the mathematical point of view, the relaxation method belongs to a class of iterational methods devoted to solve a system of algebraic nonlinear equations where each time step creates a new approximation to a being searched solution. This method is of high accuracy, and it is robust to the choice of the initial approximation. This observation is motivated by physical correspondence of Eq. (50) to vibrations of plates embedded into a viscous environment.

Remark 2

In the case of the studied nonlinear dynamical problems, after transition from PDEs to ODEs, one can (on each time interval) improve the system of approximating functions $w_n (x,y)$, where a solution to the dynamical problem can be presented in the following form

$$\begin{aligned} w(x,y,t)=A(t)w_n (x,y), \end{aligned}$$

(66)

by using one of the earlier described methods (Sects. 3.2–3.5). This approach can be used particularly to the problems where the boundary conditions are changed due to vibrations.

7 Concluding remarks

The following general conclusions can be formulated as a result of the carried out research.

• 1. The proposed approach is convenient for analysis of SSS of multi-layer plates and beams with welded layers and with the occurrence of separated contacting zones due to the technological and exploitation reasons.

• 2. The method offers a possibility of studying the constructions with contacts between layers, when the contact condition may depend on coordinates and all non-homogeneity properties of the studied contact.

• 3. Important results yielded by our theoretical investigations concern removal of the function describing the contact interaction between the structural members from a number of unknowns.

• 4. The given algorithm allows one to study SSS of the structures, in which the dependencies $\sigma _i^{(i)} (e_i^{(i)} )$ can be given either in digital forms or can be formulated analytically.

• 5. In the case of a two-layer plate–plate package with design nonlinearity, phase synchronization takes place in the frequency interval $\omega \in \left[ {4, 8} \right]$, where there is lack of synchronization (bright zones in the graphs of the phase difference) in certain time intervals, but amplitude locking phenomena appear instead.

Appendices

Appendix A

Coupling of contact pressure and transverse clamping of a thin beam

Let us show that in order to take into account the transverse clamping, one can employ the Winkler’s hypothesis. To solve this problem, we begin with a solution to the problem of contact of a layer of thickness $2l_1$ with a rigid die. Let the layer be under pressure q in a zone of the length 2l symmetrically distributed with respect to axes x, z (see Fig. 10). We restrict the considerations to the plane case and we develop pressure into a trigonometric infinite series of the following form

$$\begin{aligned} q(x)=\sum _{m=0}^\infty {A_m } \cos \frac{m\pi x}{l} . \end{aligned}$$

The stresses are derived in reference [46], and they take the following form

$$\begin{aligned}&\sigma _x =2\sum {A_m } F_m^- (z) \cos \beta x, \nonumber \\&\sigma _z=2\sum {A_m } F_m^+ (z) \cos \beta x, \nonumber \\&F_m^\pm =\frac{(\beta l_1 ch\beta l_1 \pm sh\beta l_1 ) ch\beta z-\beta z sh\beta z sh\beta l_1 }{sh2\beta l_1 +2\beta l_1 } ,\nonumber \\&\beta =\frac{m\pi }{l}. \end{aligned}$$

(A.1)

Fig. 10

Contact between a thin layer of the thickness $2l_{1}$ and a die

We take $q(x)=-\sigma _z (x,l_1 ).$ In the case of a plane in a deformable state, we have

$$\begin{aligned} \varepsilon _z =\frac{\partial u_z \left( {x,z} \right) }{\partial z}=\frac{1}{E}\left[ {(q-\upsilon ^{2})\sigma _z -\upsilon \left( {1+\upsilon } \right) \sigma _z } \right] .\nonumber \\ \end{aligned}$$

(A.2)

It should be emphasized that the so far described model of the transverse clamping in contact zones can be also employed in frame of the classical kinematical Bernoulli–Euler hypothesis. The latter statement has been illustrated and discussed in reference [47], where both normal load and contact pressure satisfy the same requirement: they are considerably less in comparison with normal stresses in transverse shell cross sections and, consequently, they can be neglected in Hook’s law relations.

Integrating (A.2) with respect to z, and taking into account that $\int \nolimits _{0}^{l_1}\sigma _{x}\hbox {d}z=0$ and since there is no load in the x direction, we obtain

$$\begin{aligned} u_{z} \left( {x,l_1 } \right)= & {} \frac{1-\upsilon ^{2}}{E}\int \limits _{0}^{l_1 } {\sigma _z \hbox {d}z} \nonumber \\= & {} 2\left( {1-\upsilon ^{2}} \right) \sum _m{A_m\varDelta } \frac{ch2\beta l_1 -1}{\beta \left( {sh2\beta l_1 +2\beta l_1 } \right) }\cos \beta x.\nonumber \\ \end{aligned}$$

(A.3)

Both nominator and denominator of (A.3) are developed into a series with regard to $\beta l_1 \equiv c,$ and hence, (A.3) yields

$$\begin{aligned} u_z (x,l_1 )= & {} \frac{1-\upsilon ^{2}}{E}l_1 \sum _m {A_m \frac{1+\frac{c^{2}}{3}+\frac{2c^{4}}{45}+\ldots }{1+\frac{c^{2}}{3}+\frac{3c^{4}}{45}+\ldots }} \nonumber \\ \cos \beta x= & {} \frac{1-\upsilon ^{2}}{E}l_1 \sum _m {A_m } \left( 1-\frac{c^{4}}{45}+\ldots \right) \cos \beta x \nonumber \\= & {} \frac{1-\upsilon ^{2}}{E}l_1 \left[ q(\bar{{x}})-\frac{1}{45}(\bar{{l}}_1 )^{4}q_x^{IV} (\bar{{x}})\right. \nonumber \\&\left. +\cdots \right] , \bar{{x}}=\frac{x}{l } , \bar{{l}}_1 =\frac{l_1 }{l}. \end{aligned}$$

(A.4)

Now, introducing the notation $2l_1 =h$, we obtain a formula for coupling of the transverse clamping $\varDelta =2u_z \left( {x,t} \right)$ and the function $q(\bar{{x}})$ of the following form

$$\begin{aligned} \frac{1}{1-\upsilon ^{2}}\frac{E}{h}\varDelta =q(\bar{{x}})-\frac{1}{720}\left( {\frac{h}{l}} \right) ^{4}q_{\bar{{x}}}^{IV} \left( \bar{{x}}, {\small \triangle } t\right) +\cdots \nonumber \\ \end{aligned}$$

(A.5)

Next, we consider clamping of the same layer two smooth, symmetrically located with respect to axes x, z (Fig. 10), dies. In this case, a solution to the contact problem, where the function $u_z (x,l_1 )$ is given on the interval $-l\le x\le l$, satisfies the following equation

$$\begin{aligned} \int \limits _{-\infty }^\infty {q(\xi ) K\left( {\frac{x-\xi }{l_1 }} \right) } \hbox {d}\xi =\pi s_0 u_z (x,l_1 ) , \end{aligned}$$

(A.6)

assuming that the condition $\sigma _z =\tau =0$ is satisfied on the interval $\left| x\right| \le l$ for $\left| z \right| =l_1$, where

$$\begin{aligned}&K(p)=\int \limits _0^\infty {\frac{ch2u-1}{sh2u+2u}} \frac{\cos up}{u}\hbox {d}u\equiv \int \limits _0^\infty {\frac{L(u)}{u}} \cos up \hbox {d}u, \nonumber \\&\overline{s_0 } =\frac{E}{2(1-\upsilon ^{2})}. \end{aligned}$$

(A.7)

Fig. 11

Contact between a thin layer and two symmetrically located dies

Solution to Eq. (A.6) in the form

$$\begin{aligned} q(x)= & {} \frac{\overline{s_0 } }{\pi l_1^2 }\int \limits _{-\infty }^\infty {u_z } (\xi ,l_1 ) K^{*}\left( \frac{x-\xi }{l_1 }\right) \hbox {d}\xi , \nonumber \\ K^{*}(p)= & {} \int \limits _0^\infty {\frac{u \cos pu}{L(u)}} \hbox {d}u \end{aligned}$$

(A.8)

was reported in reference [48], where the approximation $\frac{u}{L(u)}=\frac{1}{A}+\sum \nolimits _{i=1}^\infty {B_i } u^{(2i)}(p)$ was used to obtain the following relation: $K^{*}(p)=\frac{\pi }{A}\delta _0 (p)+\pi \sum \nolimits _{i=1}^\infty {(-1)^{i}} B_i \delta ^{(2i)}(p)$ where $\delta _0^{(2i)}$ stands for the derivative of 2i-th order (Fig. 11).

In what follows, we find the solution in an explicit form of the mentioned formulas [48]:

$$\begin{aligned}&\delta _0 (p)=\delta _0 \left( \frac{x-\xi }{l_1 }\right) =l_1 \delta _0 (x-\xi ) , \delta _0 (x-\xi )\nonumber \\&\quad =-\delta _0 (\xi -x), \nonumber \\&\int \limits _{-l}^l {f(\xi )} \delta _0 (x-\xi ) \hbox {d}\xi =f(x) ,\nonumber \\&\int \limits _{-l}^l {f(\xi )} \delta _0^{(2i)} (x-\xi ) \hbox {d}\xi =f^{(2i)}(x),\quad \left| x \right| \le l. \end{aligned}$$

(A.9)

Owing the evenness of the function $K^{*}(p)$, we have $K^{*}\left( {\frac{\xi -x}{l_1 }} \right) =K^{*}\left( {\frac{x-\xi }{l_1 }} \right)$.

Substituting the series of u / L(u) into the solution of Eq. (A.6), carrying out the integration in the interval $-l,l$, and taking into account the already known relations for the generalized functions, we get

$$\begin{aligned} q(x)= & {} \frac{1}{2(1-\upsilon ^{2})}\frac{E}{l_1 }\Big [ u_z (x,l_1 )-B_1 l_1^2 u_z \nonumber \\&+\,B_2 l_1^4 u_z^{IV} -\cdots \Big ]. \end{aligned}$$

(A.10)

Let us develop u / L(u) into the following series

$$\begin{aligned} \frac{u}{L(u)}=\frac{u(sh2u+2u)}{ch2u-1}=2\left( {1+\frac{1}{45}u^{4}+\cdots } \right) .\nonumber \\ \end{aligned}$$

(A.11)

Then, taking into account (A.10) and (A.11), we obtain: $1/A=2 , B_1 =0 , B_2 =2/45$.

The so far carried out analysis yields

$$\begin{aligned} q(\bar{{x}})=\frac{1}{1-\upsilon ^{2}}\frac{E}{h}\left[ {\varDelta +\frac{1}{720}\left( {\frac{h}{l}} \right) ^{4}\varDelta ^{IV}+\cdots } \right] .\nonumber \\ \end{aligned}$$

(A.12)

One can verify that the relations (A.5) and (A.12) are mutually inverse. They imply that when there are no bending deformations and elongations of the middle beam surfaces, in the two so far studied tasks, a coupling between clamping and contact pressure differs from Winkler’s model only by the derivative of the fourth order multiplied by small coefficients. Even for $h/l=1$ (l stands for a characteristic dimension of a contact zone), the first coefficient of the so far mentioned coefficients is equal to 1/720, where usually $h<<l$.

The so far well-judged considerations yield a conclusion that Winkler’s model (A.12) exhibits high enough accuracy. The latter conclusion has been also validated by the authors of reference [49] under support of the asymptotic analysis as well as by the author of reference [47] where a wide class of contact problems of symmetric shells has been solved.

If one takes into account tangential deformations yielded by bending and elongation of the contacting beams, the coefficient $\varDelta$ changes, and small additive terms appear. For instance, the formula of clamping in the case of plates yields $q_k =\frac{3(1-\upsilon )}{4(1+\upsilon )(1-2\upsilon )}\frac{E}{h}\big [ \varDelta +o(h^{2}\varDelta _0 w) \big ]$. In the case of beams, taking into account the Poisson’s coefficient $\upsilon =0$, it yields $q_k =\frac{3}{4}\frac{E}{h}\left[ {\varDelta +o(h^{2}\varDelta _0 w)} \right]$.

Analogous formulas have been also obtained and studied in references [50, 51]. They differ only in the coefficient K standing by $\mathrm{E}/h,$ which in all related formulas is close to one (1).

Taking into account the so far carried out considerations and owing to the mentioned dedicated references while solving the contact problems of Kirchhoff theory of shells, Winkler’s model of coupling between the clamping and contact pressure has been validated.

In what follows, we express the contact pressure between the Euler–Bernoulli beam and the dies by the difference $\varDelta =w-a,$ where w stands for a normal displacement of the middle surface [49, 52,53,54], and the following simple formula holds

$$\begin{aligned} q_k =K\frac{E}{h}\left( {w-a} \right) , a>0. \end{aligned}$$

(A.13)

In the case of contact between two beams, formula (A.13) takes the following counterpart form

$$\begin{aligned} q_k =K\frac{E}{h}(w_1 -a-w_2 ). \end{aligned}$$

(A.14)

Numbering of beams corresponds to a positive sense of a normal to the beam surface. If there is contact, then $q_k >0.$ As it has been already mentioned, the coefficient K is close to one.