Skip to main content
SpringerLink
Log in

Tangential velocity during impact with friction in three-dimensional rigid multibody systems

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

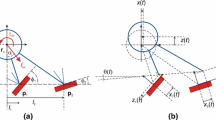
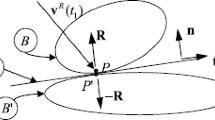
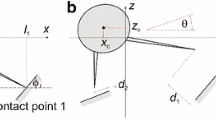
This paper introduces an analysis of tangential velocity of the contact point during a single-point impact with friction in three-dimensional rigid multibody systems. Considering the normal component of impulse at the contact point as the independent variable, a system of nonlinear differential equations describing the progress of the tangential velocity is derived. Quartic algebraic equations for the invariant and the flow change directions are obtained. The system of differential equations could have a discontinuity problem if the tangential velocity instantaneously vanishes. Effectively, this problem is mathematically solved and the new sliding direction is specified. During impact, the sliding direction could continuously change or the sliding could stop and the non-sliding continues or the sliding could restart along a new direction. The stick-slip effect could also have its influence. Two friction models are used, and an appropriate numerical procedure is suggested that can handle all the possible sliding scenarios. To verify the proposed method, the numerical solution is compared to the analytical solution for a special case of a homogeneous ellipsoid that collides with a horizontal fixed rough surface. A case study of a four-degrees-of-freedom spatial robot that collides with its environment is considered. The bifurcation associated with the variation of the kinetic coefficient of friction is investigated, and a set of threshold values of it are determined. Some phase portraits are drawn, and the invariant directions and flow change directions are drawn for all portraits. Each portrait represents all the flow trajectories of the tangential velocity for different initial conditions with a specific kinetic coefficient of friction. This qualitative analysis not only helps in understanding the behavior of multibody systems in such situations but also it gives insight to the physical phenomenon of impact itself.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Routh, E.J.: Dynamics of a System of Rigid Bodies, 6th edn. Macmillan and Co., London (1897)

    MATH  Google Scholar 

  2. Whittaker, E.T.: A. Treatise on the Analytical Dynamics of Particles and Rigid Bodies. Cambridge University Press, Cambridge (1904)

    MATH  Google Scholar 

  3. Kane, T.R., Levinson, D.A.: Dynamic: Theory and Applications. McGraw-Hill, New York (1985)

    Google Scholar 

  4. Keller, J.B.: Impact with friction. J. Appl. Mech-T. ASME 53, 1–4 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  5. Stronge, W.J.: Rigid body collisions with friction. Proc. R. Soc. Lond. A431, 169–181 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  6. Elkaranshawy, H.A., Mohamed, K.T., Ashour, A.S., Alkomy, H.M.: Solving Painlevé paradox: (P–R) sliding robot case. Nonlinear Dyn. 88(3), 1691–1705 (2017)

    Article  Google Scholar 

  7. Stronge, W.J.: Swerve during three-dimensional impact of rough rigid bodies. J. Appl. Mech-T. ASME 61, 605–611 (1994)

    Article  MATH  Google Scholar 

  8. Bhatt, V., Koechling, J.: Partitioning the parameter space according to different behaviors during three-dimensional impact. J. Appl. Mech-T. ASME 62, 740–746 (1995)

    Article  MATH  Google Scholar 

  9. Bhatt, V., Koechling, J.: Three-dimensional frictional rigid-body impact. J. Appl. Mech-T. ASME 62, 893–898 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  10. Battle, J.A.: The sliding velocity flow of rough collisions in multi-body systems. J. Appl. Mech-T. ASME 63, 804–809 (1996)

    Article  Google Scholar 

  11. Batlle, J.A., Cardona, S.: The jamb (self-locking) process in three-dimensional collisions. J. Appl. Mech-T. ASME 65, 417–423 (1998)

    Article  Google Scholar 

  12. Mirtich, B., Canny, J.: Impulse-based simulation of rigid bodies. In: Proceedings of the Symposium on Interactive 3D Graphics, pp. 181–189 (1995)

  13. Zhang, Y., Sharf, I.: Rigid body impact modeling using integral formulation. J. Comput. Nonlin. Dyn. 2, 98–102 (2007)

    Article  Google Scholar 

  14. Elkaranshawy, H.A.: Rough collisions in three-dimensional rigid multi-body system. Proc. Inst. Mech. Eng. Part K J. Multi Body Dyn. 221, 541–550 (2007)

    Google Scholar 

  15. Elkaranshawy, H.A.: Spatial robotic systems subjected to impact with friction. In: Proceedings of the IASTED International Conference on Robotics, Pittsburgh, pp. 269–277 (2011). doi:10.2316/P.2011.752-047

  16. Elkaranshawy, H.A., Abdelrazek, A.M., Ezzat, H.M.: Power series solution to sliding velocity in three-dimensional multibody systems with impact and friction. Int. J. Math. Comput. Phys. Electr. Comput. Eng. 9(10), 585–588 (2015)

    Google Scholar 

  17. Zhen, Z., Liu, C.: The analysis and simulation for three-dimensional impact with friction. Multibody Syst. Dyn. 18, 511–530 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  18. Djerassi, S.: Three-dimensional, one-point collision with friction. Multibody Syst. Dyn. 27, 173–195 (2012). doi:10.1007/s11044-011-9287-2

    Article  MATH  MathSciNet  Google Scholar 

  19. Jia, Y., Wang, F.: Analysis and computation of two body impact in three dimensions. J. Comput. Nonlinear Dyn. 12(4), 041012 (2017). doi:10.1115/1.4035411

    Article  Google Scholar 

  20. Jia, Y.-B.: Three-dimensional impact: energy-based modeling of tangential compliance. Int. J. Robot. Res. 32, 56–83 (2013). doi:10.1177/0278364912457832

    Article  Google Scholar 

  21. Stronge, W.J.: Planar impact of rough compliant bodies. Int. J. Impact Eng. 15(4), 435–450 (1994)

    Article  Google Scholar 

  22. Jia, Y.-B., Mason, M.T., Erdmann, M.: Multiple impacts: a state transition diagram approach. Int. J. Robot. Res. 32, 84–114 (2013). doi:10.1177/0278364912461539

    Article  Google Scholar 

  23. Zhao, Z., Liu, C., Chen, T.: Docking dynamics between two spacecrafts with APDSes. Multibody Syst. Dyn. 37, 245–270 (2016). doi:10.1007/s11044-015-9477-4

    Article  MATH  MathSciNet  Google Scholar 

  24. Goldsmith, W.: Impact: The Theory and Physical Behaviour of Colliding Solids. Edward Arnold Ltd., London (1960)

    MATH  Google Scholar 

  25. Guida, D., Nilvetti, F., Pappalardo, C.M.: Instability induced by dry friction. Int. J. Mech. 3(3), 44–51 (2009)

    Google Scholar 

  26. Guida, D., Nilvetti, F., Pappalardo, C.M.: Dry friction influence on cart pendulum dynamics. Int. J. Mech. 3(2), 31–38 (2009)

    Google Scholar 

  27. Pennestrì, E., Rossi, V., Salvini, P., Valentini, P.P.: Review and comparison of dry friction force models. Nonlinear Dyn. 83(4), 1785–1801 (2016)

    Article  MATH  Google Scholar 

  28. Marques, F., Flores, P., Claro, J.C.P., Lankarani, H.M.: A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 86(3), 1407–1443 (2016)

    Article  MathSciNet  Google Scholar 

  29. Battle, J.A.: Rough balanced collisions. J. Appl. Mech-T. ASME 63, 168–172 (1996)

    Article  Google Scholar 

  30. Schiehlen, W. (ed.): Multibody Systems Handbook. Springer, New York (1990)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Mathematics and Physics, Faculty of Engineering, Alexandria University, Alexandria, Egypt

    Hesham A. Elkaranshawy, Amr M. Abdelrazek & Hossam M. Ezzat

Authors
  1. Hesham A. Elkaranshawy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Amr M. Abdelrazek
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hossam M. Ezzat
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hesham A. Elkaranshawy.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Elkaranshawy, H.A., Abdelrazek, A.M. & Ezzat, H.M. Tangential velocity during impact with friction in three-dimensional rigid multibody systems. Nonlinear Dyn 90, 1443–1459 (2017). https://doi.org/10.1007/s11071-017-3737-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3737-1

Keywords

Search

Navigation