Stability of a convex order one periodic solution of unilateral asymptotic type

Abstract

In this paper, we consider semi-continuous dynamical systems with linear impulsive conditions, which have a convex order one periodic solution of unilateral asymptotic type. By constructing a sequence of switched systems and using the square approximation of the order one periodic solution, some stability criteria of the order one periodic solution are obtained. Compared with the continuous dynamical system, these criteria are very similar and also easily to be applied in the research of practical problems.

1 Introduction

Impulsive semi-dynamical systems have played an important role in describing the sudden change during the process of continuous development. These systems consist of two parts: differential equations that describe continuous variation of state and impulsive conditions that describe the discontinuity points of the solution at the moments of impulse. The theoretic research of this kind of system is of great importance. In recent decades, more and more attentions have been attracted and considerable work has been done [1,2,3,4,5,6,7,8,9,10,11,12,13].

However, for the stability of the solution of an impulsive semi-dynamical system, there is still very limited results. Besides the famous Analogue of Poincar$\acute{e}$ Criterion [13, 14] which has been popularly used, researchers have been attempting to obtain more available methods. Tian et al. [15] studied the stability of the positive order one periodic solution for a solvable semi-continuous dynamical system by using geometric approach. E. M. Bonotto et al. and his partners considered Lyapunov stability of closed sets and Poisson stability in impulsive semi-dynamical systems [4, 5] and also got a different version of the Poincar$\acute{e}$–Bendixson theorem [3]. Successor functions are also directly applied to analyze the stability of the order one periodic solution [10, 11, 16, 17]. Furthermore, several researchers have made attempts to generalize the stability theory of continuous dynamical systems into impulsive semi-dynamical systems [18,19,20,21]. Although there are so many researchers taking part in this work, there is still little result that can be easily applied to show the stability of a solution for impulsive semi-dynamical systems. Even the well-known Analogue of Poincar$\acute{e}$ Criterion is limited to use because the stability is closely related to the initial value of the periodic solution. Previously, researchers [18,19,20,21] mainly focused on getting related stability results for some specific impulsive semi-dynamical systems. However, to the best of our knowledge, there were no general stability criteria for the order one periodic solutions of impulsive semi-dynamical systems. The purpose of this paper is to establish the stability theory for order one periodic solutions of impulsive semi-dynamical systems.

In this paper, we mainly discuss the stability of a convex order one periodic solution of unilateral asymptotic type. The paper is organized as follows. In Sect. 2, some notation and definitions of the semi-continuous dynamical systems are given. In Sect. 3, we mainly discuss the stability of the order one periodic solution by using the square approximation of switched systems. An applied example is given in Sect. 4 and the paper ends with a brief conclusion.

2 Preliminaries

In this section, some notation and definitions of semi-continuous dynamical systems are given. They will be used in the following discussions.

Definition 2.1

([10]) Consider the state-dependent impulsive differential equations

$$\begin{aligned} \left\{ \begin{array}{ll} \left. \begin{array}{l} {\displaystyle \frac{\mathrm{{d}} x}{\mathrm{{d}}t}}={P}(x,y),\\ \\ {\displaystyle \frac{\mathrm{{d}}y}{\mathrm{{d}}t}}={Q}(x,y),\end{array}\right\} \ \ \ (x,y)\notin M\{x, y\},\\ \\ \left. \begin{array}{l} \triangle x=\alpha (x,y),\\ \\ \triangle y=\beta (x,y), \end{array}\right\} \ \ \ (x,y)\in M\{x, y\}.\\ \\ \end{array}\right. \end{aligned}$$

(1)

The dynamical system consisting of the solution mappings of the system (1) is defined as a semi-continuous dynamical system which is denoted by $(\Omega , f, \varphi , M)$. The initial point P is required not in the set $M\{x, y\}$, that is, $P \in \Omega = R_+^2\setminus M\{x, y\}$, and $\varphi$ is a continuous mapping that satisfies $\varphi (M)=N$. We call $\varphi$ the impulse mapping. $M\{x, y\}$ and $N\{x, y\}$ stand straight lines or curves in $R_+^2$, and we call $M\{x, y\}$ and $N\{x, y\}$ the impulse set and phase set, respectively.

Definition 2.2

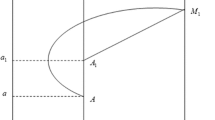
([10]) Let $f(P,t):\Omega \rightarrow \Omega$ be the solution mapping of system (1). If there exists a point $A\in N\{x,y\}$ and a T such that $f(A,T)=B\in M\{x,y\}$ and $\varphi (B) = \varphi (f(A,T))= A\in N\{x,y\}$, then f(A, t) is called an order one periodic solution of system (1) with period T ( see Fig.1, denoted by ). The orbit of the order one periodic solution is called an order one cycle ( see Fig.1, denoted by ).

Definition 2.3

Suppose $\Gamma =f(P,t)$ is an order one periodic solution of system (1). If for any $\varepsilon >0$, there must exist $\delta >0$ and $t_0\ge 0$, such that for any point $P_{1}\in U (P,\delta )\cap N\{x,y\}$, we have $\rho (f({P_{1}},t),\Gamma )<\varepsilon$ for $t>t_0$ , then we call the order one periodic solution $\Gamma$ is orbitally stable.

Definition 2.4

([10]) Suppose that both the impulse set M and phase set N of system (1) are straight lines, then a coordinate system can be defined in the phase set N. Consider point $A\in N$, and its coordinate is a. Assume the trajectory starting from point A intersects the impulse set M at a point $A'$, and point $A'$ is mapped to point $A_1\in N$ after impulsive effect. Denote the coordinate of $A_1$ by $a_1$, then we call point $A_1$ the successor point of point A and call $F(A)=a_1-a$ the successor function of point A.

Lemma 2.1

([10]) The successor function F(A) is continuous on N.

Lemma 2.2

([10]) If there are two points $A\in N, B\in N$ such that $F(A)F(B)<0$, then there exists a point $C\in N$ between A and B such that $F(C)=0$.

Fig. 1

Three types of order one periodic solutions

For order one circles (denoted by for convenience of description ), suppose the trajectory is not tangent to the impulse set M, that is to say, point B is not a point of tangency. For any point $\bar{D}$ in the phase set N near point A, we are interested in the position of its successor point $\bar{E}$. According to the position relationship of points $\bar{D}$ , $\bar{E}$ and the order one periodic solution , all of order one cycles can be classified into the following three types:

Type 1 the order one circle is convex, and points $\bar{D}$ , $\bar{E}$ are at the same side of . We call this type of order one periodic solution a convex order one periodic solution of unilateral asymptotic type (see Fig. 1a);

Type 2 the order one circle is not convex, but points $\bar{D}$ , $\bar{E}$ are still at the same side of (see Fig. 1b);

Type 3 points $\bar{D}$ , $\bar{E}$ are at different sides of (see Fig. 1c).

Theorem 2.5

Consider the order one periodic solution of type 1, suppose any point D in the $\epsilon$-neighborhood of point A, there must exist a point $\bar{D}$ in the phase set N such that the trajectory through point $\bar{D}$ passes through point D. If for any point D whose corresponding point $\bar{D}$ is above point A and the successor function of $\bar{D}$ satisfies $F(\bar{D})<0$, then the order one periodic solution is unidirectional stable.

In the next section, we mainly discuss the stability of an order one periodic solution of the type 1 for a kind of semi-continuous dynamical system with linear impulse functions.

3 Main results

Consider the following dynamical system with impulsive state feedback control where the impulse functions are linear:

$$\begin{aligned} \left\{ \begin{array}{ll} \left. \begin{array}{l} {\frac{\mathrm{{d}}x(t)}{\mathrm{{d}}t} = P(x,y),}\\ \\ {\frac{\mathrm{{d}}y(t)}{\mathrm{{d}}t} = Q(x,y),}\end{array}\right\} \ \ \ x<h,\\ \\ \left. \begin{array}{l} \Delta x(t)=-\alpha x, \quad \Delta y(t)=-\beta y(t), \end{array}\right\} \ \ \ x=h. \end{array}\right. \end{aligned}$$

(2)

Suppose is a convex order one periodic solution of unilateral asymptotic type with period T of system (2) (see Fig. 2a). We denote it by $\Gamma$ and suppose is not tangent to the impulse set $x=h$. For any point D in the $\epsilon -$neighborhood of A, there must exist a point $\bar{D}$ in the phase set N such that the trajectory through $\bar{D}$ passes through point D. If for any point D, both of whose corresponding points $\bar{D}$ and $\bar{E}$ are above point A and $F(\bar{D})<0$, then the order one periodic solution $\Gamma$ is unidirectional stable by Theorem 2.5 (see Fig. 2b). What we need to do in the following is to find a method to verify that the successor function $F(\bar{D})<0$.

So far, however, there is still no available method for the calculation of the successor function of order one periodic solutions. In this paper, with the aid of square approximation of the order one periodic solution and the stability analysis of hybrid limit cycles of a kind of switched system, we will give a computing method for the successor function of order one periodic solutions which is similar to the method for continuous dynamical systems.

Fig. 2

The order one periodic solution of system (2) and its square approximation

For the order one periodic solution of system (2), we denote A by $A(x_a,y_a)$ and B by $B(x_b,y_b)$. Since point B is mapped to point A by the impulsive mapping, the time spent by this behavior is 0. In order to use the square approximation of the order one periodic solution, we assume that the time spent by the impulsive mapping is T / n ( see Fig. 2c) and construct the following systems

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\mathrm{{d}}x(t)}{\mathrm{{d}}t} = P(x,y),\\ \\ \displaystyle \frac{\mathrm{{d}}y(t)}{\mathrm{{d}}t} = Q(x,y) \end{array}\right. \end{aligned}$$

(3)

and

$$\begin{aligned} \left\{ \begin{array}{l} {\displaystyle \frac{\mathrm{{d}}x(t)}{\mathrm{{d}}t}} =-\frac{\alpha nh}{T}\triangleq P_1(x,y),\\ \\ {\displaystyle \frac{\mathrm{{d}}y(t)}{\mathrm{{d}}t}} =\frac{n(y_a-y_b)}{T} \triangleq Q_1(x,y),\quad n=1,2,\ldots . \end{array}\right. \end{aligned}$$

(4)

These two systems motivate us to consider an approximation of switched systems for the semi-continuous dynamical system (2). Hence, in order to study the stability of the order one periodic solution of system (2), we formulate the following hybrid system (switched system whose switching law is determined by states):

$$\begin{aligned} \left\{ \begin{array}{ll} \left. \begin{array}{l} {\displaystyle \frac{\mathrm{{d}}x(t)}{\mathrm{{d}}t}} = P(x,y),\\ \\ {\displaystyle \frac{\mathrm{{d}}y(t)}{\mathrm{{d}}t}} = Q(x,y), \end{array}\right\} \ \ \ \text{ initial } \text{ values } \text{ in } \text{ the } \text{ phase } \text{ set }\quad x=(1-\alpha )h,\\ \\ \left. \begin{array}{l} {\displaystyle \frac{\mathrm{{d}}x(t)}{\mathrm{{d}}t}} =-\frac{\alpha nh}{T}\triangleq P_1(x,y),\\ \\ {\displaystyle \frac{\mathrm{{d}}y(t)}{\mathrm{{d}}t}} =\frac{n(y_a-y_b)}{T} \triangleq Q_1(x,y), \end{array}\right\} \ \ \ \text{ initial } \text{ values } \text{ in } \text{ the } \text{ pulse } \text{ set } \quad x=h.\\ \end{array}\right. \end{aligned}$$

(5)

For simplicity, we introduce the following denotations

$$\begin{aligned} Z(x,y),\quad X^1(P(x,y),Q(x,y)),\quad X^2(P_1(x,y),Q_1(x,y)), \end{aligned}$$

then the system (5) can be rewritten as

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}t}[Z(x,y)]=c_1X^1+c_2X^2, \end{aligned}$$

(6)

or

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{\mathrm{{d}}x(t)}{\mathrm{{d}}t} =Z_1(x,y)= c_1P(x,y)+c_2P_1(x,y),\\ \\ \displaystyle \frac{\mathrm{{d}}y(t)}{\mathrm{{d}}t} =Z_2(x,y)= c_1Q(x,y)+c_2Q_1(x,y), \end{array}\right. \end{aligned}$$

(7)

where $c_1=0,c_2=1$ if initial values are in the pulse set $x=h$ and $c_1=1,c_2=0$ if initial values are in the phase set $x=(1-\alpha )h$.

For system (2), we assume the closed curve consisting of curve and line segment $\overline{BA}$ is an order one periodic circle. Arbitrarily choose a point $S_0$ in the phase set $x=(1-\alpha )h$ which is near point A, then there exists a range of points:

$$\begin{aligned} \{S_1,S_2,\ldots ,S_k,S_{k+1},\ldots \}, \end{aligned}$$

where $S_1$ is the successor point of $S_0$, $S_2$ is the successor point of $S_1$, and so on (see Fig. 3a).

Fig. 3

The successor points of systems (2) and (7)

Establish a coordinate system at the phase set such that the coordinate of A is 0. Let $s_0, s_1,\ldots , s_k, s_{k+1},\ldots$ be the coordinates of points $S_0,S_1,\ldots ,S_k,S_{k+1},\ldots ,$ respectively.

Lemma 3.1

For any point $S_0$ in the phase set which is near point A, if the point range $S_k\rightarrow A, \quad k\rightarrow \infty$, i.e., the sequence $s_k\rightarrow 0, \quad k\rightarrow \infty$, then the order one periodic solution is asymptotically stable (unidirectional).

Lemma 3.2

(Königs) Assume $\bar{s}=f(s)$ is a continuous transform of line segment L to itself and $s=0$ is a fixed point. If the part of the curve $\bar{s}=f(s)$ which is near the origin of the plane $(s,\bar{s})$ lies in the interior of the area

$$\begin{aligned} |\frac{\bar{s}}{s}|\le 1-\varepsilon ({\ge }1+\varepsilon ),\quad \varepsilon >0, \end{aligned}$$

then the fixed point $s=0$ is stable (unstable).

Proof

We just prove the stability when $|\frac{\bar{s}}{s}|\le 1-\varepsilon$, otherwise, the discussion is similar.

Select $\eta >0$ small enough such that for any s in the noncentral neighborhood $U^0(0,\eta )$ of the fixed point $s=0$ satisfies

$$\begin{aligned} |\frac{\bar{s}}{s}|\le 1-\varepsilon =\delta <1, \end{aligned}$$

then we have $\bar{s}\le \delta |s|<|s|$.

For arbitrary point range $\{s_k\}\subset U^0(0,\eta )$ which are obtained by the transform starting from point $s_0$, we can easily get $|s_1|<\delta |s_0|, |s_2|<\delta |s_1|,\cdots$, then we have $|s_n|\le \delta ^n|s_0|$ and $|s_n|\rightarrow 0$ when $n\rightarrow \infty$, which means the fixed point $s=0$ is stable. The proof is completed. $\square$

Corollary 1

Assume that function $\bar{s} = f (s)$ is derivable at $s = 0$, then the fixed point $s=0$ is stable (unstable) if $|\frac{\mathrm{{d}}\bar{s}}{\mathrm{{d}}s}|_{s=0}<1 ({>}1)$.

Lemma 3.3

Assume H(x, y) has continuous partial derivatives with respect to x and y on $R^2$, x and y are functions of t, S is a closed curve that starts from point A in the direction as indicated by the arrow (see Fig. 4) and the period is T, then

$$\begin{aligned} \oint _S\left[ \frac{\mathrm{{d}}}{\mathrm{{d}}t}H(x,y)\right] \mathrm{{d}}t=\int _0^T\left[ \frac{\mathrm{{d}}}{\mathrm{{d}}t}H(x,y)\right] \mathrm{{d}}t=0. \end{aligned}$$

Fig. 4

The periodic solution of the switch system (7)

Proof

According to the derivation rule of the multi-variable function, we have $\frac{\mathrm{{d}}}{\mathrm{{d}}t}H(x,y)=\frac{\partial H}{\partial x}\frac{\mathrm{{d}}x}{\mathrm{{d}}t}+\frac{\partial H}{\partial y}\frac{\mathrm{{d}}y}{\mathrm{{d}}t},$ then the left of the above equation can be rewritten as

$$\begin{aligned} \oint _S\left[ \frac{\mathrm{{d}}}{\mathrm{{d}}t}H(x,y)\right] \mathrm{{d}}t= & {} \oint _S\left[ \frac{\partial H}{\partial x}\frac{\mathrm{{d}}x}{\mathrm{{d}}t}+\frac{\partial H}{\partial y}\frac{\mathrm{{d}}y}{\mathrm{{d}}t}\right] \mathrm{{d}}t\\= & {} \oint _S\left[ \frac{\partial H}{\partial x}\mathrm{{d}}x+\frac{\partial H}{\partial y}\mathrm{{d}}y\right] . \end{aligned}$$

Let $P(x,y)=\frac{\partial H}{\partial x}, Q(x,y)=\frac{\partial H}{\partial y}.$ Since the necessary and sufficient condition of line integral independent of the path is

$$\begin{aligned} \frac{\partial P}{\partial y}=\frac{\partial ^2 H}{\partial x\partial y}=\frac{\partial ^2 H}{\partial y\partial x}=\frac{\partial Q}{\partial x}, \end{aligned}$$

(8)

if the two second order mixed partial derivatives $\frac{\partial ^2 H}{\partial x\partial y}$ and $\frac{\partial ^2 H}{\partial y\partial x}$ are continuous in the area of interest, then they must be equal and we can easily get

$$\begin{aligned} \oint _S\left[ \frac{\mathrm{{d}}}{\mathrm{{d}}t}H(x,y)\right] \mathrm{{d}}t=\int _0^T\left[ \frac{\mathrm{{d}}}{\mathrm{{d}}t}H(x,y)\right] \mathrm{{d}}t=0. \end{aligned}$$

The proof is completed. $\square$

In Fig. 2, we see the periodic solution $\Gamma _n$ whose period is $(1+\frac{1}{n})T$ (see Fig. 2c) as the square approximation of the order one periodic solution $\Gamma$ whose period is T (see Fig. 2a), then for any continuously differentiable function D(x(t), y(t)), we have the following result

Lemma 3.4

Assume continuous periodic solutions $\Gamma _n$ is the square approximation of the order one periodic solution $\Gamma$ of unilateral asymptotic type, then

$$\begin{aligned} \int _\Gamma D(x(t),y(t))\mathrm{{d}}t=\lim \limits _{n\rightarrow \infty } \oint _{\Gamma _n} D(x(t),y(t))\mathrm{{d}}t. \end{aligned}$$

For the order one periodic solution of system (2), we have given the successor point of any point near A on the phase set. Correspondingly, we also consider the periodic solution of the switched system (7) and give the successor point of any point a near A ( see Fig. 3b).

Arbitrarily choose a point a in the phase set which is near point A, then there exists a range of points:

$$\begin{aligned} \{a_1^+,a_2^+,\ldots ,a_k^+,a_{k+1}^+,\ldots \}, \end{aligned}$$

where A is the successor point of A, $a_1^+$ is the successor point of a, $a_2^+$ is the successor point of $a_1^+$, and so on (see Fig. 3b).

In order to get the explicit expression of the successor function of the point near the order one periodic solution $\Gamma$, we firstly give the expression of the successor function of the point near the square approximate periodic solution $\Gamma _n$. Here, calculation methods to solve the successor function for continuous systems are supposed to be applied. To this end, we transform the successor point in the rectangular coordinate system into the successor point in the curvilinear coordinate system.

Fig. 5

The curvilinear coordinate system of the switch system

We still denote the convex order one periodic solution of unilateral asymptotic type of system (2) by and the periodic solution of the square approximate switched system (7) by ( see Fig. 5 ). We want to calculate the successor function $F(S_k)$ of any point $S_k$ near point A. For this purpose, we firstly establish coordinate system at the phase set N, and the coordinate of any point in the phase set is its coordinate on y axis. Suppose the coordinate of point $S_k$ is $y_{S_k}$, the trajectory passing through point $S_k$ intersects the pulse set at a point b. Point c is the phase point of point b and its coordinate is $y_c$, then the successor function of point $S_k$ is $F(S_k)=y_c-y_{S_k}<0$ (see Fig. 5).

According to Theory 2.5, the necessary and sufficient condition for the unidirectional stability of the order one periodic solution is: for any point $S_k$ above point A,

$$\begin{aligned} F(S_k)=y_c-y_{S_k}<0 \end{aligned}$$

is satisfied.

So what we need to do is finding a method to calculate the value of $F(S_k)$.

Along the direction of the trajectory of , we introduce the curvilinear coordinates (s, n), where s is the arc length starting from point A, and its increasing direction is consistent with the increasing direction of time t; n is the length of the normal, and its positive direction is to the left side when traveling along the periodic orbit ( see Fig. 5 ). The trajectory through point $S_k$ intersects n axis at point a and intersects impulse set M at b, while the trajectory through point c intersects n axis at point d. We define the successor function of point $S_k$ in the curvilinear coordinate system is

$$\begin{aligned} F_1^\oplus (S_k)=n_d-n_a<0. \end{aligned}$$

According to Theory 2.5, the necessary and sufficient condition for the unidirectional stability of the order one periodic solution is: for any point $S_k$ above point A,

$$\begin{aligned} F(S_k)=y_c-y_{S_k}<0\Leftrightarrow F_1^\oplus (S_k)=n_d-n_a<0 \end{aligned}$$

is satisfied.

In order to study the stability of the convex order one periodic solution of unilateral asymptotic type, we assume P(x, y) and Q(x, y) in system (2) have derivatives of any order. Suppose the equations of orbital curve are $x=f(t), y=g(t),t\in [0,T]$, which is also consistent with that the period of the order one periodic solution $\Gamma$ is T. For the curvilinear coordinate system (s, n) , take arc length s as a parameter, the equations of the orbital curve are

$$\begin{aligned} x=\varphi (s), y=\psi (s). \end{aligned}$$

For the switched system (7), the orbital curve segment $\overline{BA}$ is the orbital curve of system (4), and its equations are

$$\begin{aligned} x=\varphi _1(s), y=\psi _1(s), \end{aligned}$$

so the equations of the periodic solution $\Gamma _n$ is

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle x =\Phi (s)= c_1\varphi (s)+c_2\varphi _1(s),\\ \\ \displaystyle y = \Psi (s)= c_1\psi (s)+c_2\psi _1(s), \end{array}\right. \end{aligned}$$

(9)

where $c_1=0,c_2=1$ if initial values are in the pulse set $x=h$ and $c_1=1,c_2=0$ if initial values are in the phase set $x=(1-\alpha )h$.

Assume that the curvilinear coordinate of A is $(\Phi (s),\Psi (s))$ (here, $\Phi (s)$ and $\Psi (s)$ are not smooth at points A and B, so we need make a smoothing approximation for $\Phi (s)$ and $\Psi (s)$ at points A and B by drawing new curve in a small enough neighborhood of points A and B, see Fig. 4 ), then for point a , the relationship between its rectangular coordinates (x, y) and curvilinear coordinates (s, n) is:

$$\begin{aligned} x=\Phi (s)-n \Psi '(s), \quad y=\Psi (s)+n \Phi '(s). \end{aligned}$$

Let $Z_{10}(x,y), Z_{20}(x,y)$ represent the value of $Z_{1}(x,y), Z_{2}(x,y)$ at periodic solution $\Gamma _n$, that is,

$$\begin{aligned} Z_{10}(x,y)=Z_1(\Phi (s),\Psi (s)), \quad Z_{20}(x,y)=Z_2(\Phi (s),\Psi (s)). \end{aligned}$$

According to system (7), we can easily get

$$\begin{aligned} \frac{\mathrm{{d}}y}{\mathrm{{d}}x}= & {} \frac{\Psi '(s)+\Phi '(s)\frac{\mathrm{{d}}n}{\mathrm{{d}}s}+n \Phi ''(s)}{\Phi '(s)-\Psi '(s)\frac{\mathrm{{d}}n}{\mathrm{{d}}s}-n \Psi ''(s)}\\= & {} \frac{Z_2(\Phi (s)-n \Psi '(s),\Psi (s)+n \Phi '(s) )}{Z_1(\Phi (s)-n \Psi '(s),\Psi (s)+n \Phi '(s) )} \end{aligned}$$

and

$$\begin{aligned} \frac{\mathrm{{d}}n}{\mathrm{{d}}s}=\frac{Z_2 \Phi '-Z_1\Psi ' -n(Z_1 \Phi ''+Z_2 \Psi '')}{Z_1 \Phi '+Z_2 \Psi '}=F(s,n). \end{aligned}$$

(10)

Suppose $Z_1,Z_2$ have continuous partial derivatives, then F(s, n) has continuous first-order partial derivative with respect to n and (10) can be rewritten as

$$\begin{aligned} \frac{\mathrm{{d}}n}{\mathrm{{d}}s}=F'_n(s,n)|_{n=0}+o(n). \end{aligned}$$

(11)

After simple calculations, we have

$$\begin{aligned}&\!\!\!F'_n(s,n)|_{n=0}\nonumber \\&=Z_{10}\frac{Z_{10}^2Z_{2y0}-Z_{10}Z_{20}(Z_{1y0}+Z_{2x0}) +Z_{20}^2Z_{1x0}}{(Z_{10}^2+Z_{20}^2)^{\frac{3}{2}}}=H(s) \nonumber \\ \end{aligned}$$

(12)

where $Z_{1x0}, Z_{1y0}, Z_{2x0}$ and $Z_{2y0}$ denote partial derivatives of $Z_1$ and $Z_2$ when $n = 0$, respectively. H(s) denotes the curvature of the curvilinear trajectory at point A, so the approximate equation of (10) is

$$\begin{aligned} \frac{\mathrm{{d}}n}{\mathrm{{d}}s}=H(s) n, \end{aligned}$$

and by simple calculations, we can get

$$\begin{aligned} n=n_0 \exp \left( \int _0^s H(s')ds'\right) , n_0=n(0). \end{aligned}$$

(13)

Theorem 3.1

Assume that $\gamma$ is the length of the periodic curve of system (7), then the periodic solution $\Gamma _n$ is stable provided

$$\begin{aligned} \int _0^\gamma H(s)ds<0. \end{aligned}$$

(14)

Proof

Consider the trajectory abcd (see Fig. 5), the coordinates of a and b in the coordinate system (s, n) is denoted by $n_0$ and n, respectively. According to (13), if $\int _0^\gamma H(s)ds<0$, then we have $|n(\gamma )|<|n_0|$. By Lemmas 3.1 and  3.2, the periodic solution $\Gamma _n$ is stable. The proof is completed. $\square$

Corollary 2

(Dilibereto) Along the periodic solution $\Gamma _n$, if $H(s) < 0$, then the periodic solution $\Gamma _n$ is stable.

Let $\mathrm{{d}}s=\sqrt{Z_{10}^2+Z_{20}^2}\mathrm{{d}}t$, then the left of the inequality (14) can be rewritten as

$$\begin{aligned}&\int _0^\gamma H(s)\mathrm{{d}}s\\&\quad = \int _0^{T+\frac{T}{n}} \frac{1}{Z_{10}^2+Z_{20}^2}[Z_{10}^2Z_{2y0}\\&\qquad -Z_{10}Z_{20}(Z_{1y0}+Z_{2x0})+Z_{20}^2Z_{1x0}] \mathrm{{d}}t\\&\quad =\int _0^{T+\frac{T}{n}}[Z_{1x0}+Z_{2y0}\\&\qquad \left. -\frac{Z_{10}^2 Z_{1y0}+ Z_{10}Z_{20}(Z_{1y0}+Z_{2x0})+Z_{20}^2Z_{1x0}}{Z_{10}^2+Z_{20}^2}\right] \mathrm{{d}}t \\&\quad =\int _0^{T+\frac{T}{n}}(Z_{1x0}+Z_{2y0})\mathrm{{d}}t -\frac{1}{2}\oint _{\Gamma _n} \frac{d(Z_{10}^2+Z_{20}^2)}{Z_{10}^2+Z_{20}^2}\mathrm{{d}}t \\&\quad =\int _0^{T+\frac{T}{n}}(Z_{1x0}+Z_{2y0})\mathrm{{d}}t. \end{aligned}$$

Theorem 3.2

If the integral along the periodic solution $\Gamma _n$ of system (7) satisfies

$$\begin{aligned} \int _0^{T+\frac{T}{n}}(Z_{1x0}+Z_{2y0})\mathrm{{d}}t<0, \end{aligned}$$

then $\Gamma _n$ is orbital asymptotical stable.

Furthermore, according to (3) and (4), we have

$$\begin{aligned} Z_{1x0} =\frac{\partial Z_1}{\partial x}=\frac{\partial P}{\partial x}, \quad Z_{2y0} =\frac{\partial Z_2}{\partial y}=\frac{\partial Q}{\partial y}, \end{aligned}$$

then we can easily get

$$\begin{aligned} \int _0^{T+\frac{T}{n}}(Z_{1x0}+Z_{2y0})\mathrm{{d}}t=\int _0^{T+\frac{T}{n}}\left( \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y} \right) \mathrm{{d}}t. \end{aligned}$$

Theorem 3.3

If the integral along the periodic solution $\Gamma _n$ of system (7) satisfies

$$\begin{aligned} \int _0^{T+\frac{T}{n}}\left( \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right) \mathrm{{d}}t<0, \end{aligned}$$

then $\Gamma _n$ is orbital asymptotical stable.

Since

$$\begin{aligned} \Gamma _n\rightarrow \Gamma , \frac{T}{n}\rightarrow 0,\quad T+\frac{T}{n}\rightarrow T,\quad n\rightarrow \infty , \end{aligned}$$

by Lemma 3.4 we can get

Theorem 3.4

If the semi-continuous dynamical system (2) has a convex order one periodic solution of unilateral asymptotic type with period T, and the integral along the periodic solution $\Gamma$ satisfies

$$\begin{aligned} \int _0^{T}\left( \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y} \right) \mathrm{{d}}t<0, \end{aligned}$$

then the order one periodic solution $\Gamma$ is orbital stable (but not necessarily orbital asymptotical stable ).

Corollary 3

If the semi-continuous dynamical system (2) has a convex order one periodic solution of unilateral asymptotic type with period T, and the region G that contains the periodic solution $\Gamma$ satisfies

$$\begin{aligned} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y} <0, \end{aligned}$$

then the order one periodic solution $\Gamma$ is orbital stable.

4 Applied example

In this example, a cooperative system with state feedback impulsive harvesting is presented. Let x(t) and y(t) be the densities of two different populations at time t, respectively. There is an adjustable constant threshold value h for the density of the first population, and it will be harvested with proportion $\alpha$ when its density x reaches h. Then the system is

$$\begin{aligned} \left\{ \begin{array}{ll} \left. \begin{array}{l} {\frac{\mathrm{{d}}x(t)}{\mathrm{{d}}t} = x(t)(r_1-a x(t)+ by(t)) ,}\\ \\ {\frac{\mathrm{{d}}y(t)}{\mathrm{{d}}t} = y(t)(r_2+cx(t)-dy(t)),}\end{array}\right\} \ \ \ x<h,\\ \\ \left. \begin{array}{l} x(t^+)=(1-\alpha )x(t), \quad y(t^+)= y(t), \end{array}\right\} \ \ \ x=h, \\ \\ x(0)=x_0<h,\quad y(0)=y_0 \end{array}\right. \end{aligned}$$

(15)

where $r_1$ and $r_2$ are intrinsic growth rates, a and d are density dependent coefficients and the population interaction is governed by b and c.

Fig. 6

Existence of order one periodic solution of system (15) when $ad-bc\le 0$ and when $ad-bc>0$ and $h<\frac{r_1d+r_2b}{ad-bc}$

Without impulsive effect, we can easily get the equilibria of the ordinary differential system that consists of the first two equations of system (15). There are always three boundary equilibria: an unstable node O(0, 0) and two saddle points $A(r_1/a,0)$ and $B(0,r_2/d)$. If $ad-bc>0$, there is another interior node $(x^*,y^*)$ that is globally stable in the first quadrant, where $x^*=\frac{r_1d+r_2b}{ad-bc}, y^*=\frac{ar_2+cr_1}{ad-bc}$.

We assume $h\le \frac{r_1d+r_2b}{ad-bc}$ when $ad-bc>0$. In fact, if $h>\frac{r_1d+r_2b}{ad-bc}$, the population level of x will not be in a high state to be harvested because it will tend to $\frac{r_1d+r_2b}{ad-bc}$ eventually without human intervention.

To discuss the existence of the order one periodic solution of system (15), we firstly build coordinate system on the phase set $x=(1-\alpha )h$. For any point $M(x_\mathrm{{M}},y_\mathrm{{M}})$ in the phase set, let its coordinate be $y_M$. Then we have the following result

Theorem 4.1

Assume that $ad-bc\le 0$ (or $ad-bc>0, h\le \frac{r_1d+r_2b}{ad-bc}$), then system (15) has a positive order one periodic solution.

Proof

Suppose that the isocline $r_2+c x- dy=0$ intersects the vertical lines $x=(1-\alpha )h$ and $x=h$ at points $C((1-\alpha )h, y_C)$ and $D(h,y_D)$, respectively. Points $E((1-\alpha )h,y_E)$ and $G((1-\alpha )h,y_G)$ are on the phase set $x=(1-\alpha )h$, where $y_E=y_D$ and point G is above and sufficiently close to the point C (see Fig. 6, where (a) for the case $ad-bc\le 0$ and (b) for the case $ad-bc>0$).

Since $r_2+c x- dy=0$ is the horizontal isocline, variable y decreases above this horizontal isocline in the vector field and increases in the lower half of the vector field. Consider the trajectory of system (15) starting from point E, it must intersect the impulse set $x=h$ at a point $E'$, and after impulsive effect, the point $E'$ is mapped to a point $E_1$ which is in the phase set $x=(1-\alpha )h$. Since $y_{E_1}=y_{E'}<y_D=y_E$, the successor function of point E satisfies $F(E)=y_{E_1}-y_{E}<0$. Furthermore, the trajectory starting from point G must intersect the impulse set $x=h$ at a point $G'$, and after impulsive effect, the point $G'$ is mapped to a point $G_1$ in the phase set $x=(1-\alpha )h$. Since G is sufficiently close to point C, $y_{G'}>y_C$ and $y_{G_1}=y_{G'}>y_G$, the successor function of point G satisfies $F(G)=y_{G_1}-y_{G}>0$. According to Lemma 2.2, there must exist a point N between points E and G on the phase set $x=(1-\alpha )h$ such that $F(N)=0$, that is to say, there must exist an order one periodic solution passing through point N. The proof is completed. $\square$

Theorem 4.2

If $ad-bc\le 0$ (or $ad-bc>0, h\le \frac{r_1d+r_2b}{ad-bc}$), then the order one periodic solution of system (15) is orbital stable.

Proof

Obviously, the order one periodic solution of system (15) we have given in Theorem 4.1 can be classified into Type 1, that is, it is a convex order one periodic solution of unilateral asymptotic type. Now we use the results we have obtained in Sect. 3 to show the orbital stability of the periodic solution.

Since the divergence of the system (15)

$$\begin{aligned} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}=r_1+r_2+(c-2a)x+(b-2d)y \end{aligned}$$

is not a constant, and we cannot determine it is positive or negative.

Let $B(x,y)=\frac{1}{xy}$, then

$$\begin{aligned} \frac{\partial PB}{\partial x}+\frac{\partial QB}{\partial y}=-\left( \frac{a}{y}+\frac{d}{x}\right) <0, \end{aligned}$$

according to the Dulacs theorem, Theorems 3.3 and  3.4, we know the order one periodic solution of system (15) is orbital stable. The proof is completed. $\square$

5 Conclusion

In this paper, we studied a kind of semi-continuous dynamical system with linear impulsive conditions. The focus has been mainly on the stability analysis of the order one periodic solution. To the best of our knowledge, the calculation of the successor function in semi-continuous dynamical systems is not easy. Because the dissmoothness at the pulse point, stability criteria of continuous dynamical systems cannot be applied directly. Although researchers in the recent years have created several methods to prove the stability of an order one periodic solution, these methods always have no generality and applied only to particular models. Even the famous Analogue of Poincar$\acute{e}$ Criterion is not convenient in practical use for the stability of the order one periodic solution can only be judged with the aid of the initial value.

In order to give a general stability criterion of order one periodic solutions which can be used easily, we firstly classified all order one periodic solutions into three types. In this paper, we just studied the type 1, that is, the closed convex order one periodic solution of unilateral asymptotical type. To make use of theoretic results of continuous dynamical systems, we constructed a sequence of switched systems, each of which has a hybrid limit cycle. These hybrid limit cycles can form a square approximation for the order one periodic solution. Similar to the stability analysis in continuous dynamical systems, we got stability criteria for these hybrid limit cycles, then obtained the stability results for the order one periodic solution by using square approximation. The classification method of order one cycles is first proposed in this paper, and for the type 1 order one cycle, we successfully generalized the stability criteria of continuous dynamical systems into impulsive semi-dynamical systems.

Our ultimate goal is to solve the stability of the order one periodic solution of all the three types, but the current method we introduced in this paper is only applicable to closed convex ones of unilateral asymptotical type. The study of the other two types is under our future explorations.