Three-dimensional energy channeling in the unit-cell model coupled to a spherical rotator I: bidirectional energy channeling

Abstract

This work is the first one in a two part series devoted to the analysis of the complex nonlinear mechanism of three-dimensional energy channeling emerging in a locally resonant three-dimensional, single-cell unit. The system under consideration comprises of an external mass subjected to a three-dimensional linear local potential with an internal spherical rotator. In the present study we focus on the analysis of the regimes of three-dimensional, bidirectional energy transport realized in the limit of low-energy excitations. Unlike the previously reported studies, this system under consideration exhibits rich nonlinear phenomena concerning the dynamics and the bifurcation structure of highly non-stationary regimes. Thus, in the considered limit we unveil analytically the two distinct families of non-stationary regimes corresponding to the in-plane as well as the out-of-plane bidirectional energy channeling. This phenomenon of bidirectional energy channeling is manifested by the three-dimensional, recurrent transformation of general in-plane oscillations of the external element to the orthogonally reoriented in-plane and out-of-plane ones. This three-dimensional energy flow is fully controlled by the internal spherical rotator coupled to the external mass. Here we also show that the regimes corresponding to the bidirectional energy channeling as well as spontaneous energy locking reported in the previously considered planar cases can be generalized analytically to the three-dimensional case. To this end we use a regular multi-scale analysis which enables to characterize and predict the intrinsic mechanisms governing the highly non-stationary regimes of the three-dimensional energy flow. Numerical simulations are found to be in extremely good correspondence with the analysis.

Appendices

Appendix 1: Dynamics of the rotator considered in Cartesian coordinates

In Sect. 2 we have used Euler angles to model the dynamics of the internal rotator. In fact such a description is natural to model such systems, although they have their own disadvantages. It is well known that spherical angular coordinates (in this case Euler angles) can lead to singularities in the configuration space. Such singular points can lead to blow up of the vector field of the dynamical system resulting in failure of the numerical simulation. In order to avoid this pitfall, we consider Cartesian coordinates to define the configuration of the internal rotator and an appropriate constraint to specify the constant radius of the internal rotator. Accordingly, the kinetic and the potential energy are given by,

$$\begin{aligned} T= & {} \frac{m}{2}\left\{ \left( \frac{\hbox {d}x_{m}}{\hbox {d}t} \right) ^{2}+\left( \frac{\hbox {d}y_{m}}{\hbox {d}t} \right) ^{2}+\left( \frac{\hbox {d}z_{m}}{\hbox {d}t} \right) ^{2} \right\} \nonumber \\&+\,\frac{M}{2}\left\{ \left( \frac{\hbox {d}x_{M}}{\hbox {d}t} \right) ^{2}+\left( \frac{\hbox {d}y_{M}}{\hbox {d}t} \right) ^{2}+\left( \frac{\hbox {d}z_{M}}{\hbox {d}t} \right) ^{2} \right\} \nonumber \\ \end{aligned}$$

(A1.1)

$$\begin{aligned} V= & {} \left\{ \frac{k_{1}}{2}x_{M}^{2} \right\} +\left\{ \frac{k_{2}}{2}y_{M}^{2} \right\} +\left\{ \frac{k_{3}}{2}z_{M}^{2} \right\} \end{aligned}$$

(A1.2)

where all the variables and parameters have the usual meaning as defined in Sect. 2. However, we have a holonomic constraint relating the constant radius of the internal rotator with its coordinates. The Lagrangian after introducing the constraint equation with the Lagrange multiplier ($\lambda$)

$$\begin{aligned} L=T-V+\tilde{\lambda }\left( x_{m}^{2}+y_{m}^{2}+z_{m}^{2}-r^{2} \right) \end{aligned}$$

(A1.3)

The dimensional EOMs take the form,

$$\begin{aligned}&\left( M+m \right) \frac{\hbox {d}^{2}x_{M}}{\hbox {d}t^{2}}+m\frac{\hbox {d}^{2}x_{m}}{\hbox {d}t^{2}}+k_{1}x_{M}=0\nonumber \\&\left( M+m \right) \frac{\hbox {d}^{2}y_{M}}{\hbox {d}t^{2}}+m\frac{\hbox {d}^{2}y_{m}}{\hbox {d}t^{2}}+k_{2}y_{M}=0\nonumber \\&\left( M+m \right) \frac{\hbox {d}^{2}z_{M}}{\hbox {d}t^{2}}+m\frac{\hbox {d}^{2}z_{m}}{\hbox {d}t^{2}}+k_{3}z_{M}=0\nonumber \\&m\left( \frac{\hbox {d}^{2}x_{M}}{\hbox {d}t^{2}}+\frac{\hbox {d}^{2}x_{m}}{\hbox {d}t^{2}} \right) -2\tilde{\lambda }x_{m}=0\nonumber \\&m\left( \frac{\hbox {d}^{2}y_{M}}{\hbox {d}t^{2}}+\frac{\hbox {d}^{2}y_{m}}{\hbox {d}t^{2}} \right) -2\tilde{\lambda }y_{m}=0\nonumber \\&m\left( \frac{\hbox {d}^{2}z_{M}}{\hbox {d}t^{2}}+\frac{\hbox {d}^{2}z_{m}}{\hbox {d}t^{2}} \right) -2\tilde{\lambda }z_{m}=0\nonumber \\&x_{m}^{2}+y_{m}^{2}+z_{m}^{2}-r^{2}=0 \end{aligned}$$

(A1.4)

Using the non-dimensional variables $\left( x=\frac{x_{M}}{r},\tilde{x}=\frac{x_{m}}{r}, \tau =t\sqrt{ \frac{K_{1}}{\left( m+M \right) }} , \varepsilon =\frac{m}{\left( m+M \right) }, \lambda =\frac{\tilde{\lambda }}{K_{1}}\right)$, we have

$$\begin{aligned}&\ddot{x}+\varepsilon \ddot{\tilde{x}}+x=0\nonumber \\&\ddot{y}+\varepsilon \ddot{\tilde{y}}+y=0\nonumber \\&\ddot{z}+\varepsilon \ddot{\tilde{z}}+z=0\nonumber \\&\varepsilon \left( \ddot{x}+\ddot{\tilde{x}} \right) -2\lambda \tilde{x}=0\nonumber \\&\varepsilon \left( \ddot{y}+\ddot{\tilde{y}} \right) -2\lambda \tilde{y}=0\nonumber \\&\varepsilon \left( \ddot{z}+\ddot{\tilde{z}} \right) -2\lambda \tilde{z}=0\nonumber \\&\tilde{x}^{2}+\tilde{y}^{2}+\tilde{z}^{2}-1=0 \end{aligned}$$

(A1.5)

where $\dot{x}=\frac{\hbox {d}x}{\hbox {d}\tau }$.

The corresponding Lagrange multiplier is,

$$\begin{aligned} \lambda =\frac{\varepsilon }{2}\left\{ \left( \ddot{x}+\ddot{\tilde{x}} \right) \tilde{x}+\left( \ddot{y}+\ddot{\tilde{y}} \right) \tilde{y}+\left( \ddot{z}+\ddot{\tilde{z}} \right) \tilde{z} \right\} \end{aligned}$$

(A1.6)

Differentiating the constraint equation twice yields

$$\begin{aligned} \tilde{x}\ddot{\tilde{x}}+\tilde{y}\ddot{\tilde{y}}+\tilde{z}\ddot{\tilde{z}}=-\left( \dot{\tilde{x}}^{2}+\dot{\tilde{y}}^{2}+\dot{\tilde{z}}^{2} \right) \end{aligned}$$

(A1.7)

The Lagrange multiplier ($\lambda )$ takes the form,

$$\begin{aligned} \lambda =\frac{\varepsilon }{2}\left\{ \ddot{x}\tilde{x}+\ddot{y}\tilde{y}+\ddot{z}\tilde{z}-\left( \dot{\tilde{x}}^{2}+\dot{\tilde{y}}^{2}+\dot{\tilde{z}}^{2} \right) \right\} \end{aligned}$$

(A1.8)

Inserting the Lagrange multiplier from (A1.8) in (A1.5) and rearranging the terms we have the non-dimensional equations of motion in the following form

$$\begin{aligned}&\ddot{x}+\varepsilon \ddot{\tilde{x}}=-x\nonumber \\&\ddot{y}+\varepsilon \ddot{\tilde{y}}=-y\nonumber \\&\ddot{z}+\varepsilon \ddot{\tilde{z}}=-z\nonumber \\&\ddot{x}\left( 1-\tilde{x}^{2} \right) -\tilde{x}\tilde{y}\ddot{y}-\tilde{x}\tilde{z}\ddot{z}+\ddot{\tilde{x}}=-\left( \dot{\tilde{x}}^{2}+\dot{\tilde{y}}^{2}+\dot{\tilde{z}}^{2} \right) \tilde{x}\nonumber \\&\ddot{y}\left( 1-\tilde{y}^{2} \right) -\tilde{x}\tilde{y}\ddot{x}-\tilde{y}\tilde{z}\ddot{z}+\ddot{\tilde{y}}=-\left( \dot{\tilde{x}}^{2}+\dot{\tilde{y}}^{2}+\dot{\tilde{z}}^{2} \right) \tilde{y}\nonumber \\&\ddot{z}\left( 1-\tilde{z}^{2} \right) -\tilde{y}\tilde{z}\ddot{y}-\tilde{x}\tilde{z}\ddot{x}+\ddot{\tilde{z}}=-\left( \dot{\tilde{x}}^{2}+\dot{\tilde{y}}^{2}+\dot{\tilde{z}}^{2} \right) \tilde{z}\nonumber \\ \end{aligned}$$

(A1.9)

In essence the equations of motion (A1.9) and (5) model the dynamics of the same mechanical model illustrated in Fig. 1 and are equivalent. However, it is worth noting that while (5) represents a five degree of freedom system, whereas (A1.9) represents a six degree of freedom system with an inherent holonomic constraint. As described in Sect. 2, (5) can lead to unbounded solutions at the singular points during numerical simulations. However, the above model (A1.9) can be numerically integrated without encountering singular points and thereby resulting in bounded solutions.

Appendix 2: Coefficients corresponding to the slow-flow equations of the three translational coordinates

The coefficients corresponding to Eq. (20) are given

$$\begin{aligned} A_{1}= & {} -\cos \left( \delta _{12} \right) \cos \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \sin \left( \eta \right) \nonumber \\&-\,\cos \left( \delta _{12}+\delta _{23} \right) \sin \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \cos \left( \xi \right) \nonumber \\&+\,\sin \left( \xi \right) \cos \left( \eta \right) \sin ^{2}\left( \psi _{0} \right) \end{aligned}$$

(A2.1)

$$\begin{aligned} A_{2}= & {} \sin \left( \delta _{12} \right) \cos \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \sin \left( \eta \right) \nonumber \\&+\,\sin \left( \delta _{12}+\delta _{23} \right) \sin \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \cos \left( \xi \right) \nonumber \\ \end{aligned}$$

(A2.2)

$$\begin{aligned} B_{1}= & {} -\cos \left( \delta _{12} \right) \cos \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \cos \left( \eta \right) \nonumber \\&-\,\cos \left( \delta _{23} \right) \cos \left( \theta _{0} \right) \sin \left( \theta _{0} \right) \sin ^{2}\left( \psi _{0} \right) \cos \left( \xi \right) \nonumber \\&+\,\left( 1-\cos ^{2}\left( \theta _{0} \right) \sin ^{2}\left( \psi _{0} \right) \right) \sin {\left( \xi \right) \sin \left( \eta \right) } \end{aligned}$$

(A2.3)

$$\begin{aligned} B_{2}= & {} -\sin \left( \delta _{12} \right) \cos \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \cos \left( \eta \right) \nonumber \\&+\,\sin \left( \delta _{23} \right) \cos \left( \theta _{0} \right) \sin \left( \theta _{0} \right) \sin ^{2}\left( \psi _{0} \right) \cos \left( \xi \right) \end{aligned}$$

(A2.4)

$$\begin{aligned} C_{1}= & {} -\cos \left( \delta _{23} \right) \cos \left( \theta _{0} \right) \sin \left( \theta _{0} \right) \sin ^{2}{\left( \psi _{0} \right) \sin \left( \xi \right) \sin \left( \eta \right) }\nonumber \\&-\,\cos \left( \delta _{12}+\delta _{23} \right) \sin \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \cos \left( \eta \right) \nonumber \\&-\,\sin ^{2}\left( \theta _{0} \right) \sin ^{2}\left( \psi _{0} \right) \cos \left( \xi \right) +\cos \left( \xi \right) \end{aligned}$$

(A2.5)

$$\begin{aligned} C_{2}= & {} -\sin \left( \delta _{23} \right) \cos \left( \theta _{0} \right) \sin \left( \theta _{0} \right) \sin ^{2}{\left( \psi _{0} \right) \sin \left( \xi \right) \sin \left( \eta \right) }\nonumber \\&-\,\sin \left( \delta _{12}+\delta _{23} \right) \sin \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \cos \left( \eta \right) \nonumber \\ \end{aligned}$$

(A2.6)

Appendix 3: Conservation of angular momentum

The presence of a conserved quantity (integral of motion) of a dynamical system effectively reduces the dimensionality of the system. Thus, finding an integral of motion is imperative when studying higher-dimensional systems, such as the one considered in this study. The Hamiltonian system [(5) or (20)] described in Sects. 2 and 4 has three more integrals of motion in addition to the first integral corresponding to energy. The three conserved quantities are the angular momentums ($L_{x}, L_{y},L_{z})$ along the three perpendicular directions. To find the integral of motion, we calculate the angular momentum in the original coordinates [corresponding to (5)], complexify the expressions and then average the expression with respect to the fast time scale corresponding to the Hamiltonian slow-flow model (20). Accordingly (as per the notation in “Appendix 1”), we have

$$\begin{aligned}&\dot{\tilde{x}}(\tau )=\dot{x}(\tau )-\dot{\psi }\mathrm {cos}(\psi (\tau )) \end{aligned}$$

(A3.1)

$$\begin{aligned}&\dot{\tilde{y}}(\tau )=\dot{y}(\tau )+\dot{\psi }\cos \left( \theta \left( \tau \right) \right) \cos \left( \psi \left( \tau \right) \right) \nonumber \\&\quad -\dot{\theta }\sin \left( \theta \left( \tau \right) \right) \cos \left( \psi \left( \tau \right) \right) \end{aligned}$$

(A3.2)

$$\begin{aligned}&\dot{\tilde{z}}(\tau )\mathrm {=}\dot{z}(\tau )+\dot{\psi }{\sin \left( \theta \left( \tau \right) \right) \cos \left( \psi \left( \tau \right) \right) }\nonumber \\&\quad +\dot{\theta }\cos \left( \theta \left( \tau \right) \right) \sin \left( \psi \left( \tau \right) \right) \end{aligned}$$

(A3.3)

The angular momentums about the three perpendicular directions are as follows

$$\begin{aligned} C_{x}= & {} \varepsilon \left\{ -\dot{\tilde{y}}\tilde{z}+\tilde{y}\dot{\tilde{z}} \right\} +\left( 1-\varepsilon \right) \left\{ -\dot{y}z+y\dot{z} \right\} \end{aligned}$$

(A3.4)

$$\begin{aligned} C_{y}= & {} \varepsilon \left\{ -\dot{\tilde{z}}\tilde{x}+\tilde{z}\dot{\tilde{x}} \right\} +\left( 1-\varepsilon \right) \left\{ -\dot{z}x+z\dot{x} \right\} \end{aligned}$$

(A3.5)

$$\begin{aligned} C_{z}= & {} \varepsilon \left\{ -\dot{\tilde{x}}\tilde{y}+\tilde{x}\dot{\tilde{y}} \right\} +\left( 1-\varepsilon \right) \left\{ -\dot{x}y+x\dot{y} \right\} \end{aligned}$$

(A3.6)

The averaged equation corresponding to the three angular momentums ($L_{x}, L_{y},L_{z})$ are

$$\begin{aligned} L_{x}= & {} \frac{1}{2i}\left\{ y_{0}z_{0}^{*}-y_{0}^{*}z_{0} \right\} +\sin ^{2}\left( \psi _{0} \right) \theta _{0}^{\prime } \end{aligned}$$

(A3.7)

$$\begin{aligned} L_{y}= & {} \frac{1}{2i}\left\{ z_{0}x_{0}^{*}-z_{0}^{*}x_{0} \right\} -\frac{\cos \left( \theta _{0} \right) \sin \left( 2\psi _{0} \right) }{2}\theta _{0}^{\prime }\nonumber \\&\quad -\sin \left( \theta _{0} \right) \psi _{0}^{\prime }\end{aligned}$$

(A3.8)

$$\begin{aligned} L_{z}= & {} \frac{1}{2i}\left\{ x_{0}y_{0}^{*}-x_{0}^{*}y_{0} \right\} -\frac{\sin \left( \theta _{0} \right) \sin \left( 2\psi _{0} \right) }{2}\theta _{0}^{\prime }\nonumber \\&\quad +\cos \left( \theta _{0} \right) \psi _{0}^{\prime } \end{aligned}$$

(A3.9)

Using the spherical coordinate transformation we have in the simplified notation

$$\begin{aligned} L_{x}= & {} a_{1}+a_{2}\theta _{0}^{\prime } \end{aligned}$$

(A3.10)

$$\begin{aligned} L_{y}= & {} -b_{1}-b_{2}\theta _{0}^{\prime }-b_{3}\psi _{0}^{\prime } \end{aligned}$$

(A3.11)

$$\begin{aligned} L_{z}= & {} c_{1}-c_{2}\theta _{0}^{\prime }+c_{3}\psi _{0}^{\prime } \end{aligned}$$

(A3.12)

where the coefficients are defined as,

$$\begin{aligned} a_{1}= & {} \frac{1}{2}N^{2}\sin \left( \delta _{23} \right) \sin \left( \eta \right) \sin \left( 2\xi \right) \end{aligned}$$

(A3.13)

$$\begin{aligned} a_{2}= & {} \sin ^{2}\left( \psi _{0} \right) \end{aligned}$$

(A3.14)

$$\begin{aligned} b_{1}= & {} \frac{1}{2}N^{2}\sin \left( \delta _{12}+\delta _{23} \right) \cos \left( \eta \right) \sin \left( 2\xi \right) \end{aligned}$$

(A3.15)

$$\begin{aligned} b_{2}= & {} \frac{\cos \left( \theta _{0} \right) \sin \left( 2\psi _{0} \right) }{2} \end{aligned}$$

(A3.16)

$$\begin{aligned} b_{3}= & {} \sin \left( \theta _{0} \right) \end{aligned}$$

(A3.17)

$$\begin{aligned} c_{1}= & {} \frac{1}{2}N^{2}\sin \left( \delta _{12} \right) \sin \left( 2\eta \right) \sin ^{2}\left( \xi \right) \end{aligned}$$

(A3.18)

$$\begin{aligned} c_{2}= & {} \frac{\sin \left( \theta _{0} \right) \sin \left( 2\psi _{0} \right) }{2} \end{aligned}$$

(A3.19)

$$\begin{aligned} c_{3}= & {} \cos \left( \theta _{0} \right) \end{aligned}$$

(A3.20)

Appendix 4: In-plane, bidirectional, recurrent energy channeling across two orthogonal directions

As discussed toward the end of Sect. 4.2, the system under consideration can exhibit both in-plane and out-of-plane energy channeling regimes. The out-of-plane energy channeling mechanism has been quite extensively dealt with in Sect. 4.2. The in-plane energy channeling mechanism has been considered in [33] for a planar system. However, the system under consideration can exhibit such in-plane energy channeling in three orthogonal planes. For the sake of comprehensiveness and completeness, we describe all these three mechanisms. To this end we can deduce additional integrals of motion by considering localization of motion to a particular plane. Similar to the analysis in Sect. 4.2, introducing $L_{x}=L_{y}=L_{z}=0$ in the reduced slow-flow model (23), we have,

• 1. For localization in $x{-}y$ plane we have an integral of motion $C_{x\leftrightarrow y}=2N^{2}\cos \left( 2\eta \right) +\cos \left( 2\psi _{0} \right)$ corresponding to $\xi =\pi /2, \delta _{12}=\pi /2, \delta _{23}=0, \theta _{0}=0$ and the corresponding reduced order slow-flow equations take the form

  $$\begin{aligned} \begin{array}{ll} \xi ^{\prime }=0 &{}\qquad \psi _{0}^{\prime }=-\frac{1}{2}\sin \left( 2\eta \right) \\ \eta ^{\prime }=\frac{1}{4}\sin \left( 2\psi _{0} \right) &{} \qquad \theta _{0}^{\prime }=0 \end{array} \end{aligned}$$

  (A4.1)

• 2. For localization in $x{-}z$ plane we have $C_{x\leftrightarrow z}=-2N^{2}\cos \left( 2\xi \right) +\cos \left( 2\psi _{0} \right)$ corresponding to $\eta =0, \delta _{12}=\pi /2, \delta _{23}=0, \theta _{0}=\pi /2$ and the reduced order slow-flow equations take the form

  $$\begin{aligned} \begin{array}{ll} \xi ^{\prime }=-\frac{1}{4}\sin \left( 2\psi _{0} \right) &{}\qquad \psi _{0}^{\prime }=-\frac{1}{2}\sin \left( 2\xi \right) \\ \eta ^{\prime }=0&{}\qquad \theta _{0}^{\prime }=0 \end{array} \end{aligned}$$

  (A4.2)

• 3. For localization in $y{-}z$ plane by we have $C_{y\leftrightarrow z}=-2N^{2}\cos \left( 2\xi \right) +\cos \left( 2\theta _{0} \right)$ corresponding to $\eta =\pi /2, \delta _{12}=0, \delta _{23}=\pi /2, \psi _{0}=\pi /2$ and the reduced order slow-flow equations take the form

  $$\begin{aligned} \begin{array}{ll} \xi ^{\prime }=-\frac{1}{4}\sin \left( 2\theta _{0} \right) &{} \qquad \qquad \psi _{0}^{\prime }=0\\ \eta ^{\prime }=0&{}\qquad \qquad \theta _{0}^{\prime }=-\frac{1}{2}\sin \left( 2\xi \right) \end{array}\nonumber \\ \end{aligned}$$

  (A4.3)

Fig. 14

Schematic of in-plane energy exchange mechanism, a angular coordinates corresponding to external mass, b rotational angles corresponding to the internal rotator. (Color figure online)

Fig. 15

Projection of the slow-flow phase space onto the $\psi _{0}-\xi$ plane corresponding to $\eta =0$ for $N=0.6$. Blue and black curves correspond to returning trajectories, red curves to channeling window and bold-red curve to complete energy channeling trajectory. (Color figure online)

Fig. 16

Response corresponding to channeling trajectory (Point A in Fig. 15: $\eta =0, \xi =\pi /2, N=0.6)$ for initial conditions $x\left( 0 \right) =0.006, y\left( 0 \right) =0, z\left( 0 \right) =0,\theta \left( 0 \right) =\pi /2, \psi \left( 0 \right) =1.19$, a x displacement, b y displacement, c z displacement of external mass, d rotator angle $\theta$, e rotator angle $\psi$

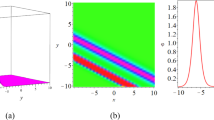
It is interesting to note that the three cases described above are similar, and therefore analyzing the dynamics corresponding to any one case is sufficient. The primary objective of the present section is to find the critical value of N above which the regimes of recurrent bidirectional energy channeling are not possible. The in-plane energy channeling mechanism in $x{-}y$ plane has been previously explored in [34]. In the present section we consider the mechanism of in-plane energy channeling confined to the $x{-}z$ plane. Arguing exactly as in Sect. 4, we project the dynamics of system (A4.2) onto the $\psi _{0}-\xi$ using the additional conserved quantity $C_{x\leftrightarrow z}$. In Fig. 15 we illustrate the projection of the phase space onto the $\psi _{0}-\xi$ plane. The thin-red trajectories of Fig. 15 correspond to channeling window, while the bold-red trajectory to the regimes of complete energy channeling. Accordingly we define

$$\begin{aligned} \psi _{0}^{-}= & {} \psi _{0}(\xi =0)\nonumber \\ \psi _{0}^{+}= & {} \psi _{0}\left( \xi =\frac{\pi }{2} \right) \end{aligned}$$

(A4.4)

where $\psi _{0}^{+}$ and $\psi _{0}^{-}$ correspond to localization along z and x directions, respectively. Thus,

$$\begin{aligned} C^{-}= & {} -2N^{2}+\cos \left( 2\psi _{0}^{-} \right) ; \xi =0\nonumber \\ C^{+}= & {} 2N^{2}+\cos \left( 2\psi _{0}^{+} \right) ; \xi =\frac{\pi }{2} \end{aligned}$$

(A4.5)

However, exactly as we mentioned above, whenever there is a formation of energy channeling regimes, the conserved should remain a constant, i.e., $C^{-}=C^{+}=C$ and we have the relations

$$\begin{aligned}&\cos \left( 2\psi _{0}^{-} \right) +\cos \left( 2\psi _{0}^{+} \right) =2C\nonumber \\&\cos \left( 2\psi _{0}^{-} \right) -\cos \left( 2\psi _{0}^{+} \right) =4N^{2} \end{aligned}$$

(A4.6)

The solvability of (A4.6) yields

$$\begin{aligned} N_{\mathrm{cr}}=\frac{1}{\sqrt{2} }; C_{\mathrm{cr}}=1 \end{aligned}$$

(A4.7)

Thus, for $N_{\mathrm{cr}}>\frac{1}{\sqrt{2} }, C_{\mathrm{cr}}>1$ one would observe only returning and disconnected trajectories similar to the one shown in Fig. 8c. Next, solving for $\cos \left( 2\psi _{0}^{-} \right)$ and $\cos \left( 2\psi _{0}^{+} \right)$ in (A4.6) and considering the solvability ($\cos \left( 2\psi _{0}^{-} \right) \le 1, \cos \left( 2\psi _{0}^{+} \right) \le 1)$, we have the window for channeling as,

$$\begin{aligned} \left| C+2N^{2} \right| \le 1\quad \hbox {and}\quad \left| C-2N^{2} \right| \le 1 \end{aligned}$$

(A4.8)

Thus, the channeling trajectories satisfy the conditions

$$\begin{aligned} 2N^{2}-1\le C\le 1-2N^{2}\quad \hbox {and}\quad N\le N_{\mathrm{cr}} \end{aligned}$$

(A4.9)

The Hamiltonian for the considered system is

$$\begin{aligned} H= & {} -\frac{1}{8}N^{2}\sin \left( 2\psi _{0} \right) \sin \left( 2\xi \right) \cos \left( \delta _{12}+\delta _{23} \right) \nonumber \\&+\,\frac{1}{8}N^{2}\cos \left( 2\psi _{0} \right) \cos \left( 2\xi \right) +\frac{1}{2}\left( D_{1}\psi _{0} \right) ^{2}\nonumber \\ \end{aligned}$$

(A4.10)

As described previously, along the channeling trajectory, the Hamiltonian can be described as,

$$\begin{aligned} H^{-}= & {} H\left( \xi =0 \right) =\frac{1}{8}N^{2}\cos \left( 2\psi _{0}^{-} \right) \end{aligned}$$

(A4.11)

$$\begin{aligned} H^{+}= & {} H\left( \xi =\frac{\pi }{2} \right) =-\frac{1}{8}N^{2}\cos \left( 2\psi _{0}^{+} \right) \end{aligned}$$

(A4.12)

Further, the Hamiltonian is constant along the channeling trajectory, i.e., $H^{-}=H^{+}$. Accordingly we have

$$\begin{aligned} \cos \left( 2\psi _{0}^{-} \right) +\cos \left( 2\psi _{0}^{+} \right) =0 \end{aligned}$$

(A4.13)

It can be shown that, for the solvability of (A4.13) and the first equation of (A4.6), one needs to have $C=0$. Thus, it can be concluded that the necessary and sufficient condition for the existence of bidirectional, in-plane energy channeling is $C=0$ and $N<N_{\mathrm{cr}}$.

In Fig. 14 we present a schematic of the mechanism of the in-plane ($x{-}z)$ bidirectional, energy channeling described above. Here we note that along the entire process of bidirectional energy channeling, the coordinates of the external mass satisfy $\eta =\eta ^{\prime }=0$ and $\xi ^{\prime }\ne 0$, whereas the internal rotator performs periodic in-plane oscillations ($\theta =\pi /2$ such that $\theta ^{\prime }=0$ and $\psi ^{\prime }\ne 0)$. In Fig. 15 we present the contour corresponding to $C_{x\leftrightarrow z}$ projected onto the plane $\psi _{0}-\xi$ where the description of the trajectories has been already elaborated in Sect. 4.2.2. The response of the external mass corresponding to complete bidirectional energy channeling between x- and z-directions is presented in Fig. 16a–c. As described previously, $y\left( \tau _{1} \right) =0$ and one can observe complete and recurrent energy exchange between x- and z-directions. The response of the internal rotator is shown in Fig. 16d, e wherein $\theta =\pi /2$, $\theta ^{\prime }=0$ and $\psi ^{\prime }\ne 0$.