Skip to main content

Advertisement

SpringerLink
Log in

A numerical mapping of energy gains in a powered Swing-By maneuver

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

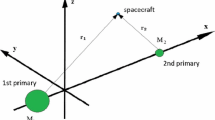
The present paper studies the effects of a powered Swing-By maneuver, considering the particular and important situations where there are energy gains for the spacecraft. The objective is to map the energy variations obtained from this maneuver as a function of the three parameters that identify the pure gravity Swing-By with a fixed mass ratio (angle of approach, periapsis distance and velocity at periapsis) and the three parameters that define the impulsive maneuver (direction, magnitude and the point where the impulse is applied). The mathematical model used here is the version of the restricted three-body problem that includes the Lemaître regularization, to increase the accuracy of the numerical integrations. It is developed and implemented by an algorithm that obtains the energy variation of the spacecraft with respect to the largest primary of the system in a maneuver where the impulse is applied inside the sphere of influence of the secondary body, during the passage of the spacecraft. The point of application of the impulse is a free parameter, as well as the direction of the impulse. The results make a complete map of the possibilities, including the maximum gains of energy, but also showing alternatives that can be used considering particularities of the mission.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Prado, A.F.B.A.: Powered Swing-By. J. Guid. Control Dyn. 19(5), 1142–1147 (1996)

    Article  MATH  Google Scholar 

  2. Da Silva Ferreira, A.F., Prado, A.F.B.A., Winter, O.C.: A numerical study of powered Swing-Bys around the Moon. Adv. Space Res. 56(2), 252–272 (2015)

    Article  Google Scholar 

  3. Araujo, R.A.N., Winter, O.C., Prado, A.F.B.A., Vieira Martins, R.: Sphere of influence and gravitational capture radius: a dynamical approach. Mon. Not. R. Astron. Soc. 391(2), 675–684 (2008)

    Article  Google Scholar 

  4. Casalino, L., Colasurdo, G., Pastrone, D.: Simple strategy for powered Swing-By. J. Guid. Control Dynam. 22(1), 156–159 (1999)

    Article  Google Scholar 

  5. Uphoff, C.: The art and science of lunar gravity assist In: AAS/GSFC Symposium, (1989). (AAS 89-170)

  6. Nock, K.T., Upholf, C.W.: Satellite aided orbit capture (1979). (AAS/AIAA paper 79-165)

  7. Flandro, G.: Fast reconnaissance missions to the outer solar system utilizing energy derived from the gravitational field of jupiter. Astronaut. Acta 12(4), 329–337 (1966)

    Google Scholar 

  8. Kohlhase, C.E., Penzo, P.A.: Voyager mission description. Sp. Sci. Rev. 21(2), 77–101 (1977)

    Article  Google Scholar 

  9. Byrnes, D.V., D’amario, L.A.: A combined Halley flyby Galileo mission. AIAA/AAS Astrodynamics Conference, San Diego, CA, AIAA paper 82-1462 (1982)

  10. Dunham, D., Davis, S.: Optimization of a multiple Lunar-Swingby trajectory sequence. J. Astronaut. Sci. 33(3), 275–288 (1985)

    Google Scholar 

  11. Carvell, R.: Ulysses-the Sun from above and below. Space 1, 18–55 (1985)

    Google Scholar 

  12. Broucke, R.A., Prado, A.F.B.A.: Planar close encounter trajectories for spacecraft passing near Jupiter. Adv. Sp. Res. 36(3), 561–568 (2005)

    Article  Google Scholar 

  13. Prado, A.F.B.A., Broucke, R.A.: Júpiter Swing-By trajectories passing near the Earth. Adv. Astronaut. Sci. 82(Part 2), 1159–1176 (1993). (AAS—AIAA Spaceflight Mechanics Meeting, 3, 22–24)

    Google Scholar 

  14. Prado, A.F.B.A., Broucke, R.A.: A classification of Swing-By trajectories using the Moon. Appl. Mech. Rev. 48(11), 138–142 (1995)

    Article  Google Scholar 

  15. Sukhanov, A.: Close approach to sun using gravity assists of the inner planets. Acta Astronaut. 45(4–9), 177–185 (1999)

    Article  Google Scholar 

  16. Casalino, L., Colasurdo, G., Pasttrone, D.: Optimal low-thrust scape trajectories using gravity assist. J. Guid. Control Dyn. 22(5), 637–642 (1999)

    Article  Google Scholar 

  17. Longuski, J.M., Strange, N.J.: Graphical method for gravity-assist trajectory design. J Spacecr. Rockets 39(1), 9–16 (2002)

    Article  Google Scholar 

  18. McConaghy, T.T., Debban, T.J., Petropulos, A.E., Longuski, J.M.: Design and optimization of low-thrust gravity trajectories with gravity assist. J Spacecr. Rockets 40(3), 380–387 (2003)

    Article  Google Scholar 

  19. Heaton, A.F., Strange, N.J., Longuski, J.M.: Automated design of the Europa orbiter tour. J Spacecr. Rockets 39(1), 17–22 (2002)

    Article  Google Scholar 

  20. Longman, R.W., Schneider, A.M.: Use of Jupiter’s moons for gravity assist. J Spacecr. Rockets 7(5), 570–576 (1970)

    Article  Google Scholar 

  21. Lynam, A.E., Kloster, K.W., Longuski, J.M.: Multiple-satellite-aided capture trajectories at Jupiter using the Laplace resonance. Celest. Mech. Dyn. Astron. 109, 59–84 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  22. Longuski, J.M., Williams, S.N.: The last grand tour opportunity to Pluto. J. Astronaut. Sci. 39, 359–365 (1991)

    Google Scholar 

  23. Hollister, W.M., Prussing, J.E.: Optimum transfer to Mars via Venus. Astronaut. Acta 12(2), 169–179 (1966)

    Google Scholar 

  24. Striepe, S.A., Braun, R.D.: Effects of a Venus Swing-By periapsis burn during an Earth–Mars trajectory. J. Astronaut. Sci. 39(3), 299–312 (1991)

    Google Scholar 

  25. Muhonen, D., Davis, S., Dunham, D.: Alternative gravity-assist sequences for the ISEE-3 escape trajectory. J. Astronaut. Sci. 33(3), 255–273 (1985)

    Google Scholar 

  26. Broucke, R.A.: The celestial mechanics of gravity assist. AIAA/AAS Astrodynamics Conference, Minneapolis, MN, AIAA paper 88-4220 (1988)

  27. Araujo, R.A.N., Winter, O.C., Prado, A.F.B.A.: The Swing-By effect in the Vesta-Magnya case. Single and multiple encounters. WSEAS Trans. Syst. 11(6), 187–197 (2012)

    Google Scholar 

  28. Okutsu, M., Yam, C.H., Longuski, J.M.: Low-thrust trajectories to jupiter via gravity assists from Venus, Earth and Mars. AIAA/AAS Astrodynamics Specialist Conference, Keystone, CO, AIAA Paper 2006-6745 (2006)

  29. Santos, D.P.S., Prado, A.F.B.A., Casalino, L., Colasurdo, G.: Optimal trajectories towards near-earth-objects using solar electric propulsion (sep) and gravity assisted maneuver. J. Aerosp. Eng. 1(2), 51–64 (2008)

    Google Scholar 

  30. McNutt Jr., R.L., Solomon, S.C., Grard, R., Novara, M., Mukai, T.: An international program for mercury exploration: synergy of messenger and bepicolombo. Adv. Sp. Res. 33(12), 2126–2132 (2004)

    Article  Google Scholar 

  31. McNutt Jr., R.L., Solomon, S.C., Gold, R.E., Leary, J.C.: The messenger mission to mercury: development history and early mission status. Adv. Sp. Res. 38(4), 564–571 (2006)

    Article  Google Scholar 

  32. Grard, R.: Mercury: the messenger and bepicolombo missions a concerted approach to the exploration of the planet. Adv. Sp. Res. 38(4), 563 (2006)

    Article  Google Scholar 

  33. Jehn, R., Companys, V., Corral, C., Yárnoz, D.G., Sánchez, N.: Navigating BepiColombo during the weak-stability capture at Mercury. Adv. Sp. Res. 42(8), 1364–1369 (2008)

    Article  Google Scholar 

  34. Gomes, V.M., Prado, A.F.B.A.: Swing-by maneuvers for a cloud of particles with planets of the solar system. WSEAS Trans. Appl. Theor. Mech. 3(11), 869–878 (2008)

    Google Scholar 

  35. Gomes, V.M., Formiga, J., de Moraes, R.V.: Studying close approaches for a cloud of particles considering atmospheric drag. Math. Probl. Eng. (2013). doi:10.1155/2013/468624

  36. Gomes, V.M., Prado, A.F.B.A.: A study of the impact of the initial energy in a close approach of a cloud of particles. WSEAS Trans. Math. 9, 811–820 (2010)

    Google Scholar 

  37. Murray, C.D., Dermott, S.F.: Solar System Dynamics, 1st edn. Cambridge University Press, Cambridge (1999)

    MATH  Google Scholar 

  38. Szebehely, V.: Theory of Orbits. Academic Press, New York (1967)

    Google Scholar 

  39. Pourtakdoust, S.H., Sayanjali, M.: Fourth body gravitation effect on the resonance orbit characteristics of the restricted three-body problem. Nonlinear Dyn. 76(2), 955–972 (2014)

    Article  MathSciNet  Google Scholar 

  40. Zotos, E.E.: Classifying orbits in the restricted three-body problem. Nonlinear Dyn. 82(3), 1233–1250 (2015)

    Article  MathSciNet  Google Scholar 

  41. Qian, Y.J., Zhang, W., Yang, X.D., Yao, M.H.: Energy analysis and trajectory design for low-energy escaping orbit in Earth–Moon system. Nonlinear Dyn 85(1), 463–478 (2016)

    Article  MathSciNet  Google Scholar 

  42. Vieira Neto, E., Winter, O.C.: Time analysis for temporary gravitational capture: satellites of Uranus. Astron. J. 122(1), 440–448 (2001)

    Article  Google Scholar 

Download references

Acknowledgements

The authors wish to express their appreciation for the support provided by Grants # 304700/2009-6 from the National Council for Scientific and Technological Development (CNPq); Grants # 2011/08171-3 and 2014/06688-7, from São Paulo Research Foundation (FAPESP) and the financial support from the National Council for the Improvement of Higher Education (CAPES).

Author information

Authors and Affiliations

  1. Instituto Nacional de Pesquisas Espaciais, São José dos Campos, São Paulo, 12227-010, Brazil

    Alessandra F. S. Ferreira & Antônio F. B. A. Prado

  2. Universidade Estadual Paulista, Guaratinguetá, São Paulo, 12516-410, Brazil

    Othon C. Winter

Authors
  1. Alessandra F. S. Ferreira
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Antônio F. B. A. Prado
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Othon C. Winter
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alessandra F. S. Ferreira.

Appendices

Appendix 1: Detailed information about the trajectories in the Earth–Moon system

It is shown here the maximum energy variations \((\Delta E_{\max })\) and its corresponding data, as the true anomaly of the point where the impulse is applied \((\theta )\), the angle that gives the direction of the impulse \((\alpha )\), the deflection angle \((\zeta )\), the escape velocity \((V_{\infty +})\) and R, which is the distance between the spacecraft and the secondary body at the instant that the impulse is applied.

Appendix 2: Details of the trajectories for the Sun–Jupiter system

It is shown here the maximum energy variations \((\Delta E_{\max })\) and its corresponding data, as the true anomaly of the point where the impulse is applied \((\theta )\), the angle that gives the direction of the impulse \((\alpha )\), the deflection angle \((\zeta )\), the escape velocity \((V_\infty +)\) and R, which is the distance between the spacecraft and the secondary body at the instant that the impulse is applied.

Appendix 3: Coefficients of the empirical equations that describe the maximum energy variation

Equations (24) and (28) describe the coefficients of Eq. 20 as a function of the magnitude of the impulse \((\delta {V})\).

$$\begin{aligned} a_1= & {} -\left( {6.9093\times 10^{-10}} \right) \delta V^{8}+\left( {1.2491\times 10^{-8}} \right) \delta V^{7}\nonumber \\&-\,\left( {9.4632\times 10^{-8}} \right) \delta V^{6}+\left( {3.8896\times 10^{-7}} \right) \delta V^{5}\nonumber \\&-\,\left( {9.3631\times 10^{-7}} \right) \delta V^{4} +\left( {1.3226\times 10^{-6}} \right) \delta V^{3}\nonumber \\&-\,\left( {1.0262\times 10^{-6}} \right) \delta V^{2}+\left( {3.6004\times 10^{-7}} \right) \delta V\nonumber \\&-\,\left( {2.1218\times 10^{-8}} \right) \end{aligned}$$
(24)
$$\begin{aligned} b_1= & {} \left( {8.1943\times 10^{-7}} \right) \delta V^{8}-\left( {1.4749\times 10^{-5}} \right) \delta V^{7}\nonumber \\&+\,0.00011121\delta V^{6}-0.00045486\delta V^{5}\nonumber \\&+\,0.0010895\delta V^{4} -0.0015315\delta V^{3}\nonumber \\&+\,0.0011831\delta V^{2} -0.00041416\delta V\nonumber \\&+\,\left( {2.4623\times 10^{-5}} \right) \end{aligned}$$
(25)
$$\begin{aligned} c_1= & {} -0.00036168\delta V^{8}+0.0064807\delta V^{7}\nonumber \\&-\,0.048632\delta V^{6}+0.19791\delta V^{5}-0.47159\delta V^{4}\nonumber \\&+\,0.65953\delta V^{3}-0.50708\delta V^{2} +0.17702\delta V\nonumber \\&-\,0.010831 \end{aligned}$$
(26)
$$\begin{aligned} d_1= & {} 0.07033\delta V^{8}-1.2546\delta V^{7} +9.3694\delta V^{6}\nonumber \\&-\,37.935\delta V^{5} +89.917\delta V^{4}-125.08\delta V^{3}\nonumber \\&+\,95.691\delta V^{2}-33.267\delta V +2.1306 \end{aligned}$$
(27)
$$\begin{aligned} e_1= & {} -0.74231\delta V^{9}+7.6992\delta V^{8} -1.701\delta V^{7}\nonumber \\&-\,311.82\delta V^{6} +1875.7\delta V^{5}-5229\delta V^{4}\nonumber \\&+\,7892.5\delta V^{3}-6304.6\delta V^{2} +2239.9\delta V-151.11\nonumber \\ \end{aligned}$$
(28)

Equations (29) and (33) describe the coefficients of Eq. (21) as a function of the magnitude of the impulse \((\delta {V})\).

$$\begin{aligned} a_2= & {} -\left( {2.0996\times 10^{-10}} \right) \delta V^{8}+\left( {3.7802\times 10^{-9}} \right) \delta V^{7}\nonumber \\&-\,\left( {2.8519\times 10^{-8}} \right) \delta V^{6}+\left( {1.1676\times 10^{-7}} \right) \delta V^{5}\nonumber \\&-\,\left( {2.8016\times 10^{-7}} \right) \delta V^{4}+\left( {3.951\times 10^{-7}} \right) \delta V^{3}\nonumber \\&-\,\left( {3.071\times 10^{-7}} \right) \delta V^{2}+\left( {1.0911\times 10^{-7}} \right) \delta V\nonumber \\&-\,\left( {5.1707\times 10^{-9}} \right) \end{aligned}$$
(29)
$$\begin{aligned} b_2= & {} \left( {2.2047\times 10^{-7}} \right) \delta V^{8}-\left( {4.0258\times 10^{-6}} \right) \delta V^{7}\nonumber \\&+\,\left( {3.0831\times 10^{-5}} \right) \delta V^{6}-0.00012824\delta V^{5}\nonumber \\&+\,0.00031282\delta V^{4}-0.00044882\delta V^{3}\nonumber \\&+\,0.00035537\delta V^{2} -0.00012942\delta V\nonumber \\&+\,\left( {7.0061\times 10^{-6}} \right) \end{aligned}$$
(30)
$$\begin{aligned} c_2= & {} -\left( {7.2312\times 10^{-5}} \right) \delta V^{9}+0.0011587\delta V^{8}\nonumber \\&-\,0.0073561\delta V^{7}+0.022503\delta V^{6}-0.027767\delta V^{5}\nonumber \\&-\,0.019652\delta V^{4}+0.10125\delta V^{3}\nonumber \\&-\,0.11473\delta V^{2}+0.049405\delta V-0.0031216 \end{aligned}$$
(31)
$$\begin{aligned} d_2= & {} 0.016556\delta V^{9}-0.26995\delta V^{8}+1.7661\delta V^{7}\nonumber \\&-\,5.7542\delta V^{6}+8.7551-1.0826\delta V^{4}-15.562\delta V^{3}\nonumber \\&+\,20.553\delta V^{2}-9.344\delta V+0.70129 \end{aligned}$$
(32)
$$\begin{aligned} e_2= & {} -1.3364\delta V^{9}+22.003\delta V^{8}-146.32\delta V^{7}\nonumber \\&+\,492.14\delta V^{6}-817.07\delta V^{5}+345.12\delta V^{4}\nonumber \\&+\,902.47\delta V^{3}-1390.6\delta V^{2}+659.13\delta V-56.513\nonumber \\ \end{aligned}$$
(33)

Equations (34) and (44) describe the coefficients of Eq. (22) as a function of the magnitude of the impulse \((\delta {V})\).

$$\begin{aligned} a_3= & {} \left( {1.6042\times 10^{-17}} \right) \delta V^{8}-\left( {2.5231\times 10^{-16}} \right) \delta V^{7}\nonumber \\&+\,\left( {1.6116\times 10^{-15}} \right) \delta V^{6}-\left( {5.3638\times 10^{-15}} \right) \delta V^{5}\nonumber \\&+\,\left( {9.9236\times 10^{-15}} \right) \delta V^{4}-\left( {1.0104\times 10^{-14}} \right) \delta V^{3}\nonumber \\&+\,\left( {5.3072\times 10^{-15}} \right) \delta V^{2}-\left( {1.2438\times 10^{-15}} \right) \delta V\nonumber \\&+\,\left( {8.7211\times 10^{-17}} \right) \end{aligned}$$
(34)
$$\begin{aligned} b_3= & {} -\left( {4.3206\times 10^{-14}} \right) \delta V^{8}+\left( {6.7949\times 10^{-13}} \right) \delta V^{7}\nonumber \\&-\,\left( {4.3399\times 10^{-12}} \right) \delta V^{6}+\left( {1.4442\times 10^{-11}} \right) \delta V^{5}\nonumber \\&-\,\left( {2.6716\times 10^{-11}} \right) \delta V^{4}+\left( {2.72\times 10^{-11}} \right) \delta V^{3}\nonumber \\&-\,\left( {1.4287\times 10^{-11}} \right) \delta V^{2}+\left( {3.3473\times 10^{-12}} \right) \delta V\nonumber \\&-\,\left( {2.3467\times 10^{-13}} \right) \end{aligned}$$
(35)
$$\begin{aligned} c_3= & {} \left( {5.2025\times 10^{-11}} \right) \delta V^{8}-\left( {8.1812\times 10^{-10}} \right) \delta V^{7}\nonumber \\&+\,\left( {5.2248\times 10^{-9}} \right) \delta V^{6}-\left( {1.7385\times 10^{-8}} \right) \delta V^{5}\nonumber \\&+\,\left( {3.2158\times 10^{-8}} \right) \delta V^{4}-\left( {3.2737\times 10^{-8}} \right) \delta V^{3}\nonumber \\&+\,\left( {1.7197\times 10^{-8}} \right) \delta V^{2}-\left( {4.0281\times 10^{-9}} \right) \delta V\nonumber \\&+\,\left( {2.8236\times 10^{-10}} \right) \end{aligned}$$
(36)
$$\begin{aligned} d_3= & {} -\left( {3.6871\times 10^{-8}} \right) \delta V^{8}+\left( {5.7978\times 10^{-7}} \right) \delta V^{7}\nonumber \\&-\,\left( {3.7024\times 10^{-6}} \right) \delta V^{6}+\left( {1.2318\times 10^{-5}} \right) \delta V^{5}\nonumber \\&-\,\left( {2.2783\times 10^{-5}} \right) \delta V^{4}+\left( {2.3193\times 10^{-5}} \right) \delta V^{3}\nonumber \\&-\,\left( {1.2185\times 10^{-5}} \right) \delta V^{2}+\left( {2.8537\times 10^{-6}} \right) \delta V\nonumber \\&-\,\left( {2.0002\times 10^{-7}} \right) \end{aligned}$$
(37)
$$\begin{aligned} e_3= & {} \left( {1.7033\times 10^{-5}} \right) \delta V^{8}-0.00026781\delta V^{7}\nonumber \\&+\,0.00171\delta V^{6}-0.005689\delta V^{5}+0.010521\delta V^{4}\nonumber \\&-\,0.01071\delta V^{3}+0.0056279\delta V^{2}\nonumber \\&-\,0.001318\delta V+\left( {9.2376\times 10^{-5}} \right) \end{aligned}$$
(38)
$$\begin{aligned} f_3= & {} -0.0066105\delta V^{9}+0.10848\delta V^{8}\nonumber \\&-\,0.7349\delta V^{7}+2.6606\delta V^{6}\nonumber \\&-\,5.5748\delta V^{5}+6.8616\delta V^{4}\nonumber \\&-\,4.8323\delta V^{3}+1.8036\delta V^{2}\nonumber \\&-\,0.29959\delta V+0.014695 \end{aligned}$$
(39)
$$\begin{aligned} g_3= & {} 1.4437\delta V^{9}-23.699\delta V^{8}\nonumber \\&+\,160.63\delta V^{7}-581.9\delta V^{6}+1220.3\delta V^{5}\nonumber \\&-\,1503.8\delta V^{4}+1060.6\delta V^{3}\nonumber \\&-\,396.53\delta V^{2}+66.039\delta V-3.2517 \end{aligned}$$
(40)
$$\begin{aligned} h_3= & {} -214.76\delta V^{9}+3526.6\delta V^{8}-23914\delta V^{7}\nonumber \\&+\,86691\delta V^{6}-\left( {1.8196\times 10^{-5}} \right) \delta V^{5}\nonumber \\&+\,\left( {2.245\times 10^{-5}} \right) \delta V^{4}-\left( {1.5858\times 10^{-5}} \right) \delta V^{3}\nonumber \\&+\,59393\delta V^{2}-9916.8\delta +490.14 \end{aligned}$$
(41)
$$\begin{aligned} i_3= & {} 20824\delta V^{9}-\left( {3.4209\times 10^{-5}} \right) \delta V^{8}\nonumber \\&+\,\left( {2.3209\times 10^{-6}} \right) \delta V^{7}-\left( {8.4193\times 10^{-6}} \right) \delta V^{6}\nonumber \\&+\,\left( {1.7688\times 10^{-7}} \right) \delta V^{5}-\left( {2.1851\times 10^{-7}} \right) \delta V^{4}\nonumber \\&+\,\left( {1.5459\times 10^{-7}} \right) \delta V^{3}-\left( {5.8\times 10^{-6}} \right) \delta V^{2}\nonumber \\&+\,\left( {9.7087\times 10^{-5}} \right) \delta V-48163 \end{aligned}$$
(42)
$$\begin{aligned} j_3= & {} -\left( {1.1884\times 10^{-6}} \right) \delta V^{9}+\left( {1.953\times 10^{-7}} \right) \delta V^{8}\nonumber \\&-\,\left( {1.3257\times 10^{-8}} \right) \delta V^{7}+\left( {4.8126\times 10^{-8}} \right) \delta V^{6}\nonumber \\&-\,\left( {1.0121\times 10^{-9}} \right) \delta V^{5}+\left( {1.2518\times 10^{-9}} \right) \delta V^{4}\nonumber \\&-\,\left( {8.8709\times 10^{-8}} \right) \delta V^{3}+\left( {3.334\times 10^{-8}} \right) \delta V^{2}\nonumber \\&-\,\left( {5.5947\times 10^{-7}} \right) \delta V+\left( {2.7855\times 10^{-6}} \right) \end{aligned}$$
(43)
$$\begin{aligned} k_3= & {} \left( {3.0312\times 10^{-7}} \right) \delta V^{9}-\left( {4.9835\times 10^{-8}} \right) \delta V^{8}\nonumber \\&+\,\left( {3.3847\times 10^{-9}} \right) \delta V^{7}-\left( {1.2296\times 10^{-10}} \right) \delta V^{6}\nonumber \\&+\,\left( {2.5884\times 10^{-10}} \right) \delta V^{5}-\left( {3.2059\times 10^{-10}} \right) \delta V^{4}\nonumber \\&+\,\left( {2.2755\times 10^{-10}} \right) \delta V^{3}-\left( {8.5671\times 10^{-9}} \right) \delta V^{2}\nonumber \\&+\,\left( {1.4412\times 10^{-9}} \right) \delta V-\left( {7.2007\times 10^{-7}} \right) \end{aligned}$$
(44)

Equations (45) and (55) describe the coefficients of Eq. (23) as a function of the magnitude of the impulse \((\delta V)\).

$$\begin{aligned} a_4= & {} -\left( {1.0705\times 10^{-18}} \right) \delta V^{9}+\left( {1.6883\times 10^{-17}} \right) \delta V^{8}\nonumber \\&-\left( {1.1045\times 10^{-16}} \right) \delta V^{7}+\left( {3.9381\times 10^{-16}} \right) \delta V^{6}\nonumber \\&-\left( {8.5765\times 10^{-16}} \right) \delta V^{5}+\left( {1.2342\times 10^{-15}} \right) \delta V^{4}\nonumber \\&-\left( {1.229\times 10^{-15}} \right) \delta V^{3}+\left( {7.7792\times 10^{-16}} \right) \delta V^{2}\nonumber \\&-\left( {1.9375\times 10^{-16}} \right) \delta V+\left( {9.8868\times 10^{-18}} \right) \end{aligned}$$
(45)
$$\begin{aligned} b_4= & {} \left( {4.2985\times 10^{-15}} \right) \delta V^{8}-\left( {6.1705\times 10^{-14}} \right) \delta V^{7}\nonumber \\&+\left( {3.4654\times 10^{-13}} \right) \delta V^{6}-\left( {9.4239\times 10^{-13}} \right) \delta V^{5}\nonumber \\&+\left( {1.1863\times 10^{-12}} \right) \delta V^{4}-\left( {3.4127\times 10^{-13}} \right) \delta V^{3}\nonumber \\&-\left( {4.98\times 10^{-13}} \right) \delta V^{2}+\left( {1.9964\times 10^{-13}} \right) \delta V\nonumber \\&-\left( {7.101\times 10^{-15}} \right) \end{aligned}$$
(46)
$$\begin{aligned} c_4= & {} -\left( {3.1033\times 10^{-12}} \right) \delta V^{9}+\left( {4.8112\times 10^{-11}} \right) \delta V^{8}\nonumber \\&-\left( {3.0786\times 10^{-10}} \right) \delta V^{7}+\left( {1.0691\times 10^{-9}} \right) \delta V^{6}\nonumber \\&-\left( {2.2718\times 10^{-9}} \right) \delta V^{5}+\left( {3.2536\times 10^{-9}} \right) \delta V^{4}\nonumber \\&-\left( {3.3468\times 10^{-9}} \right) \delta V^{3}+\left( {2.2308\times 10^{-9}} \right) \delta V^{2}\nonumber \\&-\left( {5.6288\times 10^{-10}} \right) \delta V+\left( {2.8565\times 10^{-11}} \right) \end{aligned}$$
(47)
$$\begin{aligned} d_4= & {} \left( {3.8859\times 10^{-9}} \right) \delta V^{8}-\left( {5.6072\times 10^{-8}} \right) \delta V^{7}\nonumber \\&+\left( {3.1746\times 10^{-7}} \right) \delta V^{6}-\left( {8.761\times 10^{-7}} \right) \delta V^{5}\nonumber \\&+\left( {1.1436\times 10^{-6}} \right) \delta V^{4}-\left( {4.2105\times 10^{-7}} \right) \delta V^{3}\nonumber \\&-\left( {3.5995\times 10^{-7}} \right) \delta V^{2}+\left( {1.5266\times 10^{-7}} \right) \delta V\nonumber \\&-\left( {5.3446\times 10^{-9}} \right) \end{aligned}$$
(48)
$$\begin{aligned} e_4= & {} -\left( {8.8741\times 10^{-7}} \right) \delta V^{9}+\left( {1.3434\times 10^{-5}} \right) \delta V^{8}\nonumber \\&-(8.3238\times 10^{-5})\delta V^{7}+0.00027751\delta V^{6}\nonumber \\&-\,0.0005667\delta V^{5}+0.00080599\delta V^{4}-0.00087623\delta V^{3}\nonumber \\&+\,0.00063143\delta V^{2}-0.00016252\delta V\nonumber \\&+\left( {8.1928\times 10^{-6}} \right) \end{aligned}$$
(49)
$$\begin{aligned} f_4= & {} 0.00025791\delta V^{9}-0.0038432\delta V^{8}\nonumber \\&+\,0.023289\delta V^{7}-0.075357\delta V^{6}\nonumber \\&+\,0.14916\delta V^{5}-0.21108\delta V^{4}+0.23989\delta V^{3}\nonumber \\&-\,0.18269\delta V^{2}+0.047668\delta V-0.0023935 \end{aligned}$$
(50)
$$\begin{aligned} g_4= & {} -0.051179\delta V^{9}+0.74788\delta V^{8} -4.4036\delta V^{7}\nonumber \\&+\,13.676\delta V^{6} -25.859\delta V^{5}+36.334\delta V^{4}\nonumber \\&-\,44.11\delta V^{3}+36.119\delta V^{2} -9.5874\delta V\nonumber \\&+\,0.47923 \end{aligned}$$
(51)
$$\begin{aligned} h_4= & {} 6.8442\delta V^{9}-97.59\delta V^{8}+553.12\delta V^{7}\nonumber \\&-\,1619.3\delta V^{6}+2845\delta V^{5} -3950.4\delta V^{4}\nonumber \\&+\,5330.8\delta V^{3} -4813.3\delta V^{2}+1305.2\delta V-64.903 \end{aligned}$$
(52)
$$\begin{aligned} i_4= & {} -588.65\delta V^{9}+8132.2\delta V^{8}-43715\delta V^{7}\nonumber \\&+\left( {1.1669\times 10^{5}} \right) \delta V^{6}-\left( {1.7871\times 10^{5}} \right) \delta V^{5}\nonumber \\&+\left( {2.4225\times 10^{5}} \right) \delta V^{4}-\left( {3.9806\times 10^{5}} \right) \delta V^{3}\nonumber \\&+\left( {4.1292\times 10^{5}} \right) \delta V^{2}-\left( {1.15\times 10^{5}} \right) \delta V+5684.5 \nonumber \\\end{aligned}$$
(53)
$$\begin{aligned} j_4= & {} 29286\delta V^{9}-\left( {3.8778\times 10^{5}} \right) \delta V^{8}\nonumber \\&+\left( {1.9269\times 10^{6}} \right) \delta V^{7}-\left( {4.355\times 10^{6}} \right) \delta V^{6}\nonumber \\&+\left( {4.6593\times 10^{6}} \right) \delta V^{5}-\left( {5.8182\times 10^{6}} \right) \delta V^{4}\nonumber \\&+\left( {1.5982\times 10^{7}} \right) \delta V^{3}-\left( {2.053\times 10^{7}} \right) \delta V^{2}\nonumber \\&+\left( {5.9161\times 10^{6}} \right) \delta V-\left( {2.9038\times 10^{5}} \right) \end{aligned}$$
(54)
$$\begin{aligned} k_4= & {} -\left( {6.389\times 10^{5}} \right) \delta V^{9}+\left( {7.9757\times 10^{6}} \right) \delta V^{8}\nonumber \\&-\left( {3.4901\times 10^{7}} \right) \delta V^{7}+\left( {5.3272\times 10^{7}} \right) \delta V^{6}\nonumber \\&+\left( {2.0075\times 10^{7}} \right) \delta V^{5}-\left( {5.2271\times 10^{7}} \right) \delta V^{4}\nonumber \\&-\left( {2.3901\times 10^{8}} \right) \delta V^{3}+\left( {4.4785\times 10^{8}} \right) \delta V^{2}\nonumber \\&-\left( {1.3483\times 10^{8}} \right) \delta V+\left( {6.5623\times 10^{6}} \right) \end{aligned}$$
(55)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ferreira, A.F.S., Prado, A.F.B.A. & Winter, O.C. A numerical mapping of energy gains in a powered Swing-By maneuver. Nonlinear Dyn 89, 791–818 (2017). https://doi.org/10.1007/s11071-017-3485-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3485-2

Keywords

Search

Navigation