1 Introduction

Tuned mass dampers (TMD) are widely used for damping of unwanted oscillations of mechanical and structural systems. The first record of TMD-like device can be found in the work by Watts [1] from 1883. In 1909, Frahm [2] described and patented the classic TMD. His device is extremely effective in reducing the response of the damped structure only in the principal resonance. Den Hartog proposed to add a viscous damper to Frahm’s system design [3] to expand its range of effectiveness. Thanks to that simple modification, the TMD can reduce vibrations of the main body in wide range of excitation frequencies around the principal resonance. Another way to broaden the range of TMD’s effectiveness was proposed by Roberstson [4] and Arnold [5] who interchange the linear spring of TMD by the nonlinear one (with the linear and nonlinear parts of stiffness). Recently, there are many papers considering new or modified designs as well as new applications of TMDs [6,7,8]

In this paper, we investigate the effects of adding an inerter to the TMD taking into account the influence of inerter nonlinearites of different types. The inerter—introduced in early 2000s by Smith [9]—is a two terminal element which has the property that the force generated at its ends is proportional to the relative acceleration of its terminals (the idealized model). Its constant of proportionality is called an inertance and is measured in kilograms. In the first successful application, the inerter was used in cars’ suspensions [9,10,11], but now, we can find a number of studies on other possible application areas. For example, in railway vehicles’, suspensions [12,13,14], in devices that absorb impact forces [15] or protect buildings from earthquakes [16, 17]. In [18], authors study the influence of the inerter on the natural frequencies of vibration systems. They propose different constructional solutions of one- and two-degree-of-freedom systems and present how the inerter influences their dynamics. In [19], authors review the effects of the application of the inerter in the tuned mass absorber. In very new papers [20,21,22,23], one can find the idea of usage of the inerter as a part of the TMD. They prove that by adding the inerter we are able to improve the TMD damping properties. Numerical results presented in the aforementioned publications prove that optimally designed TMD with the inerter outperforms classical TMDs. In our recent paper [28], we describe a novel TMD design which besides the above advantages has a wider range of effectiveness and is not susceptible to detuning.

Recently, a new device consisting of a soft spring connected to a rotary damping tube with the inertial mass was proposed by Saito et al. [24]. It is called tuned viscous mass damper (TVMD) system [25]. This device was studied mostly to improve the seismic performance of a single-degree-of-freedom structures, and it proved to outperform other well-known devices. Recently, a TVMD-like device was applied to a steel structure in Japan [26]. Additionally, one can find studies about multiple-degree-of-freedom system with TVMD [27].

The general mathematical model of the inerter proposed by Smith et. al. [9] is very simple. Nevertheless, the practical realizations do not follow the mathematical model strictly. It is mainly caused by factors such as internal motions resistances, friction, play in gear and others. Most of these effects are modeled using nonlinear functions that are much more complex than the formula proposed by Smith. The effects of the inerter nonlinearites were investigated both numerically and experimentally [29, 30]. These investigations refer only to some of the proposed applications of inerters due to the differences between the roles of the inerter in the distinct devices. In this paper, we distinguish the sources of nonlinearities that mechanical gear-based inerters bring to the TMD. Then, we investigate their influence on the dynamics of the system with TMD. We focus on the TMD damping efficiency and its range of effectiveness. We describe and compare the results obtained for different factors. Finally, we investigate the full model of TMD with inerter and propose its simplification.

The paper is organized as follows: Sect. 2 includes the description of the overall model of the system with TMD and the inerter. We also list factors that we take into account. In Sect. 3, we analyze the influence of TMD inertia composition between its main mass and the inertance introduced by the inerter. Section 4 is devoted to the investigation and description if the influence of viscous damping on the TMD efficiency. In Sect. 5, we consider dry friction, and then, in Sect. 6, we describe the influence of play in the inerter gear. In Sect. 7, we consider the full model of the TMD containing all elements earlier analyzed and present its simplification. Finally, we summarize the conclusions of our work in Sect. 8.

2 Model of the system

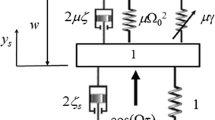
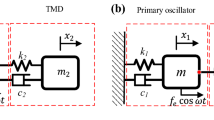
The analyzed system is shown in Fig. 1. It consists of the base oscillator that can move in vertical direction and the TMD connected to its top. The base oscillator has the mass M and is connected with the support via the spring of stiffness K and a viscous damper described by the damping coefficient C. It is excited by a harmonic force of amplitude F and frequency \(\omega \). The TMD is used to mitigate the vibrations of the base structure. The TMD has the mass m and is connected to the main body via four links: spring of stiffness k, viscous damper with damping coefficient c, element that corresponds to dry friction described by parameter \(d_{f}\) and the inerter. We use the model of the inerter with play [31] that is described by four parameters: inertance I, stiffness \(k_{i}\), viscous damping coefficient \(c_{i}\) and dimension of the backlash gap \(\varepsilon \).

The motion of the system is described by four generalized coordinates two of which are used to describe the dynamics of the inerter with play. The vertical displacement of the base oscillator is given by coordinate x. To describe the position of the TMD, we use coordinate y. The model of play uses coordinates r and u, where r describes the distance between the two nodes of the inerter, while u defines the actual gap in the system. For more detailed description of the play model, we refer to [31].

Fig. 1
figure 1

Model of the considered system and notation of system’s parameters

Full size image

The motion of the system presented in Fig. 1 is described by the following set of equations:

$$\begin{aligned}&M\ddot{x}+Kx+C\dot{x}+F_\mathrm{stiffness}+F_\mathrm{damping}+F_\mathrm{friction}\nonumber \\&\quad +F_\mathrm{inerter}=F\cos \left( \omega t\right) , \end{aligned}$$
(1)
$$\begin{aligned}&m\ddot{y}-F_\mathrm{stiffness}-F_\mathrm{damping}-F_\mathrm{friction}-F_\mathrm{inerter}=0,\nonumber \\ \end{aligned}$$
(2)

The first link that connects the TMD with the main mass is the linear spring. The force generated by the spring is given by the following formula: \(F_\mathrm{stiffness}=k\left( x-y\right) \). There are three other links connecting TMD with the main mass—namely viscous damper, dry friction component and the inerter. Forces corresponding to each link are not fixed during our analysis and depend on the type of configuration of TMD we investigate. We assume the following values of the base structure parameters: \(M=100\,(\hbox {kg})\), \(K=4\times 10^{4}\,({\hbox {N}}/{\hbox {m}})\), \(C=100\,({\hbox {N\,s}}/{\hbox {m}})\) (which corresponds to 2.5% of the critical damping). Its natural frequency of vibrations is equal to \(20\,(\hbox {Hz})\). During our investigation, we assume constant amplitude of forcing \(F=200\,(\hbox {N})\) and variable frequency of excitation \(\omega \) varying in ranges from \(15\,(\hbox {Hz})\) to \(25\,(\hbox {Hz})\). Aforementioned parameters of TMD’s are changed during investigation, but we fix the stiffness of the TMD spring to \(k=4\times 10^{3}\,({\hbox {N}}/{\hbox {m}})\), and we assume that constant overall inertia of the TMD is equal to \(10\,(\hbox {kg})\). This means that the sum of the TMD mass m and inertance I persists the same: \(m+I=10\,(\hbox {kg})\). Both stiffness and inertia of TMD are equal to 10% of the equivalent parameters of the base structure which ensures that their natural frequencies of vibrations are equal.

Table 1 Formulas that are used to calculate \(F_\mathrm{damping}\), \(F_\mathrm{friction}\), \(F_\mathrm{inerter}\) on different stages of our investigation
Full size table

In this paper, we analyze four factors which influence the property of inerters and change the dynamics and the efficiency of the TMD:

  1. 1.

    The I to m ratio—The overall inertia of the TMD is a composition of its main mass m and the inertance I. Depending on the I to m ratio the system behaves differently. In Sect. 3, we present how this ratio influences the efficiency of the TMD and its range of effectiveness.

  2. 2.

    Viscous damping—Inerters, the same as every mechanical element/device, dissipate some amount of energy during operation. The energy dissipation is often modeled by adding the viscous damper. In Sect. 4, we describe how the value of viscous damping coefficient c influences the efficiency of the TMD.

  3. 3.

    Dry friction—There are numerous embodiments of inerters mentioned in the literature [9, 30]. All of them contain elements that introduce friction to the system. In Sect. 5, we use simple continuous model of dry friction to show how it affects the dynamics of the considered structure.

  4. 4.

    Play—Most of inerter embodiments contain gears [9, 30, 32] in which we observe play [29, 30]. In Sect. 6, we present the influence of play on the dynamics and efficiency of the TMD. For that purpose, we use the model of play described by Scheibe and Smith [31].

After considering the influence of I to m ratio in Sect. 3, we pick three characteristic cases. In Case 1 \(m=9\,(\hbox {kg})\), \(I=1\,(\hbox {kg})\), so the main mass of the TMD is dominant and the inerter plays minor role, i.e., to adjust overall inertia of the TMD. In the second Case 2, we assume that the overall inertia is equally splitted between mass m and inertance I (\(m=5\,(\hbox {kg})\), \(I=5\,(\hbox {kg})\)). Finally, in Case 3, the inerter plays dominant role and main mass of TMD is minor: \(m=1\,(\hbox {kg})\), \(I=9\,(\hbox {kg})\).

For each of the three cases, we describe the influence of viscous damping, dry friction and play. Then, in Sect. 7, we describe the dynamics of the full model of the TMD that contains all four factors above described. We also propose the simplification of the full model which significantly facilitates the computer simulations. In Table 1, we show the formulas that we use to calculate \(F_\mathrm{damping}\), \(F_\mathrm{friction}\), \(F_\mathrm{inerter}\) and the values of influencing parameters of the system (names in the first column correspond to titles and numbers of sections where given property is analyzed).

3 Influence of the I to m ratio

In this section, we investigate the influence of the TMD inertia distribution. We fix the overall inertia of the TMD which is a sum of its main mass m and inertance I: \(m+I=10\,(\hbox {kg})\). By changing the ratio between I and m, we describe the effects of different compositions of inertia. For simplicity, instead of using directly I to m ratio, we use the ratio between inertance and overall inertia of TMD and name it \(I_\mathrm{ratio}=\frac{I}{I+m}\) expressed in percentage. Thanks to that our marker is within the range of \(\left\langle 0{-}100\right) \%\) and the higher the value the bigger part of inertia is introduced by the inerter itself. We want to investigate the efficiency of the TMD not only in the main resonance but in a wider range of excitation frequencies. It is because in most practical application, we prefer devices with broadband effectiveness. We use frequency response curves (FRCs) of the base oscillator to present the mitigation properties of the TMD. In Fig. 2a, we present two-parameter diagram showing the amplitude of the base oscillator with respect to excitation frequency \(\omega \) and \(I_\mathrm{ratio}\). The value of the amplitude is expressed with a color scale that is shown on the right side of the plot. Additionally, in Fig. 2b, we present five FRC of the base system. The black line presents the response of the structure without the device while the other four curves are calculated for different values of \(I_\mathrm{ratio}\):

Fig. 2
figure 2

Influence of the \(I_\mathrm{ratio}\) on the system’s dynamics. Subplot (a) is a two-parameter diagram showing the changes of the maximum amplitude of the base oscillator for different \(\omega \) and \(I_\mathrm{ratio}\). In subplot (b), we present five FRCs calculated for different sets of parameters (the values are also marked in subplot (a))

Full size image

  • yellow line for \(I_\mathrm{ratio}=0\), \(m=10\,(\hbox {kg})\), \(I=0\,(\hbox {kg})\)—for that case we have classical TMD without the inerter.

  • red line for \(I_\mathrm{ratio}=0.1\), \(m=9\,(\hbox {kg})\), \(I=1\,(\hbox {kg})\)—for that case inerter plays minor role and the main mass of the TMD m is dominant. This corresponds to the situation when the inerter is used to adjust the overall inertia of the device. Because of the practical importance, we pick this case for further investigation and name it “Case 1”.

  • green line for \(I_\mathrm{ratio}=0.5\), \(m=5\,(\hbox {kg})\), \(I=5\,(\hbox {kg})\)—here the inertia is equally distributed between the mass of TMD and the inerter. The main mass is significantly complemented by the inerter which role is now crucial. We name it “Case 2”.

  • blue line for \(I_\mathrm{ratio}=0.9\), \(m=1\,(\hbox {kg})\), \(I=9\,(\hbox {kg})\)—now the inerter is strongly dominant and the main mass of TMD is minor. It corresponds to the situation when we want to minimize the mass of the device. Minimization of the TMD’s mass is often the practical engineering problem [33]. We name this case “Case 3”.

Results presented in Fig. 2 prove that the value of \(I_\mathrm{ratio}\) strongly influences the response of the structure. In Fig. 2a, we show the two dimensional plot (\(I_\mathrm{ratio}\) versus \(\omega \)) which in color presents the maximum amplitude of the base system. For low values of \(I_\mathrm{ratio}\), we observe two resonances for significantly different frequencies \(\omega \). With increasing the ratio, the distance between resonance frequencies starts to reduce, and finally, for \(I_\mathrm{ratio}=1.0\), they merge. For \(I_\mathrm{ratio}=1.0\), mass of the TMD is equal to zero; hence, it has not influence on the dynamics of the base system. Analyzing FRCs from Fig. 2b, we see that with the increase of \(I_\mathrm{ratio}\) the height of the resonance peaks changes, and so for small \(I_\mathrm{ratio}\) the first resonance peak—that occurs before the main resonant frequency—is higher than the second one (after the main resonant frequency). That difference in height decreases with the increase of \(I_\mathrm{ratio}\).

From practical point of view, we see that if TMD is designed to mitigate vibrations of one precise frequency, inertance can be dominant part of the overall TMD inertia. But if we want to design the device that will damp vibrations in some significant range of frequencies, then we have to compose the overall inertia carefully. Although there are many methods of enhancing the range of TMD effectiveness, the tendency in positioning of main resonance peaks that is shown in Fig. 2 is always present.

4 Influence of viscous damping

In this section, we analyze and describe the influence of viscous damping on the dynamics and efficiency of the TMD. In the considered model, energy is dissipated via classical viscous dampers. The first damper connects main mass M and describes internal damping of the damped structure. Its damping coefficient is given by the parameter C which has a constant value \(C=100\,({\hbox {N\,s}}/{\hbox {m}})\). The second damper connects the main mass with the mass m of the TMD. Its damping coefficient is given by c, and it varies during our investigation. The idea of using viscous damper as a connecting link between the TMD and damped structure was proposed by Den Hartog [3] who proved that it can vastly improve the range of the TMD effectiveness. In our previous publication [34], we proposed a numerical algorithm that can be used to optimize the value of the damping coefficient. The influence of viscous dampers on the dynamics of TMDs has been widely investigated. In this paper, we describe the interplay between the inertance and viscous damping coefficient.

We consider three different Cases of TMDs’ parameters with different \(I_\mathrm{ratio}\) that we describe in Sect. 3. We show that by changing the composition of TMD inertia, we can alter the effects caused by viscous damper. For each of the three Cases, we change the value c from 0 (no viscous damper) up to \(100\,({\hbox {N\,s}}/{\hbox {m}})\) and analyze the response of the base system. The highest considered value of c corresponds to 25% of critical damping of the TMD with \(I_\mathrm{ratio}=0\). In Fig. 3, we present the influence of viscous damping coefficient on the maximum amplitude of base structure vibrations for different values of excitation frequency (we consider \(\omega \epsilon \left\langle 15,\,25\right\rangle \,(\hbox {Hz})\)). First two subplots of Fig. 3 refer to Case 1 (\(I_\mathrm{ratio}=0.1\)). In subplot (a), we show two-parameter plot presenting the amplitude of the base oscillator with respect to excitation frequency \(\omega \) and \(I_\mathrm{ratio}\). The value of the amplitude is expressed with a color scale that is shown on the right side of the plot. Additionally, in Fig. 3b, we present five FRCs of the base system. The black line is a reference and presents the response of the structure without TMD. Yellow curve is the response of the structure with the TMD without viscous damper. Then, curves red, green and blue were calculated for growing value of viscous damping coefficient: \(c=10\,({\hbox {N\,s}}/{\hbox {m}})\), \(c=56.38\,({\hbox {N\,s}}/{\hbox {m}})\) and \(c=90\,({\hbox {N\,s}}/{\hbox {m}})\), respectively. We picked these values for the following reasons:

  • \(c=10\,({\hbox {N\,s}}/{\hbox {m}})\)—it corresponds to relatively small value of damping coefficient, i.e., 2.5% of critical damping of the TMD with \(I_\mathrm{ratio}=0\). Such a small value of damping coefficient is often used to model the energy dissipation present in the real systems due to imperfections, dry friction, internal damping, etc. [35]. Hence, the FRC calculated for \(c=10\,({\hbox {N\,s}}/{\hbox {m}})\) (red line in Fig. 3b) can be treated as a curve received from practical realization of TMD without additional viscous damper.

  • \(c=56.38\,({\hbox {N\,s}}/{\hbox {m}})\)—it is the optimized value of c received from numerical optimization procedure described in [34], i.e., 14% of critical damping of TMD with \(I_\mathrm{ratio}=0\). We expect that for this value the TMD is highly efficient in a wide range of excitation frequencies \(\omega .\) The FRC calculated for optimized value of c has green color in Fig. 3b.

  • \(c=90\,({\hbox {N\,s}}/{\hbox {m}})\)—it corresponds to relatively high value of damping coefficient, i.e., 22.5% of critical damping of TMD with \(I_\mathrm{ratio}=0\). We picked this value to present how the response of the system changes when we drastically increase the viscous damping coefficient. The FRC of the TMD with \(c=90\,({\hbox {N\,s}}/{\hbox {m}})\) has blue color (Fig. 3b).

Fig. 3
figure 3

Influence of the viscous damping coefficient c on the system’s dynamics. Subplots (a, b) refer to Case 1 embodiment, (c, d) to Case 2 and (e, f) to Case 3. Subplots (a, c, e) are two-parameter diagrams showing the changes of the base oscillator amplitude for different \(\omega \) and c. On subplots (b, d, f), we present five FRCs calculated for different sets of parameters

Full size image

We performed similar calculations also for Case 2 and Case 3. The results for Case 2 are presented in subplots (c, d) of Fig. 3, and for Case 3 in subplots (e, f) of the same figure. FRCs presented in subplot (d) were calculated for: \(c=10\,({\hbox {N\,s}}/{\hbox {m}})\)—red line; \(c=31.73\,({\hbox {N\,s}}/{\hbox {m}})\) (which is an optimized value for that Case)—green line and \(c=90\,({\hbox {N\,s}}/{\hbox {m}})\)—blue line. For Case 3, optimized value of viscous damping coefficient is \(c=6.45\,({\hbox {N\,s}}/{\hbox {m}})\), and we present the FRC for that case using green color in Fig. 3f. Similarly as for previous Cases, red and blue lines in subplot (f) were calculated for \(c=10\,({\hbox {N\,s}}/{\hbox {m}})\) and \(c=90\,({\hbox {N\,s}}/{\hbox {m}})\), respectively.

Results received for Case 1 are similar to the ones obtained for classical TMD without the inerter. It is because in Case 1 embodiment the inerter plays minor role and the main mass m is 90% of the overall TMD inertia. Interesting conclusions can be drawn after comparing the results obtained for three considered Cases. Firstly, we see that when \(I_\mathrm{ratio}\) rises the optimum value of c decreases. It is because critical value of damping coefficient depends on the mass of TMD m which decreases with the increase of \(I_\mathrm{ratio}\). It does not depend on the overall inertia of TMD which is constant and depends on m and the value of inertance I. So, if we want the inerter to create the majority of the overall TMD inertia and still receive satisfactory damping efficiency, we should ensure low damping coefficient. What is equally important is the fact that the range of c for which TMD has good damping properties decreases with the rise of \(I_\mathrm{ratio}\). This means that if the inerter plays a dominant role over the main mass m we have to be very careful when adjusting the value of c. Moreover, the FRC received for optimal value of c differs strongly for each considered case. This explains the trade off that we should deal with when designing TMD with the inerter. In other words, inerters can help to reduce the overall mass of the TMD but with the increase of \(I_\mathrm{ratio}\) we observe the narrowing of the range in which TMD is highly efficient, and we have to ensure high precision when adjusting the other TMD parameters’ values.

5 Influence of dry friction

In this section, we describe the influence of dry friction. Instead of using viscous damper we introduce dry friction model to the system. We use continuous model of dry friction. The force it generates is given by the following formula:

$$\begin{aligned} F_\mathrm{friction}=d_{f}\frac{2\arctan \left( 10^{6}(\dot{x}-\dot{y})\right) }{\pi } \end{aligned}$$
(3)

To describe the effects of dry friction, we perform similar analysis to the one presented in the previous section. We change the value of \(d_{f}\) parameter in the range \(\left\langle 0,\,100\right\rangle \,(\hbox {N})\) and check the response of the base structure. We consider 3 Cases to describe how the effects of dry friction depend on the inertance value. The results are presented in Fig. 4. First two subplots (a, b) correspond to Case 1 for which \(I_\mathrm{ratio}=0.1\) and inerter plays minor role. In subplot (a), we show two-parameter density plot of the amplitude of the base structure, and in subplot (b), we show 4 FRCs calculated for:

  • \(d_{f}=0\,(\hbox {N})\)—reference TMD without dry friction—yellow line.

  • \(d_{f}=10\,(\hbox {N})\)—small value of dry friction force. Such model corresponds to inherent dry friction that is present in most inerter embodiments—red line.

  • \(d_{f}=45.78\,(\hbox {N})\)—that is numerically optimized value of dry friction force—green line.

  • \(d_{f}=90\,(\hbox {N})\)—relatively large value of dry friction force. This case corresponds to the TMD with some imperfections or with additional friction elements. It let us show what happens when there is significant dry friction force—blue line.

Fig. 4
figure 4

Influence of dry friction amplitude \(d_{f}\) on the system’s dynamics. Subplots (a, b) refers to Case 1 embodiment, (c, d) to Case 2 and (e, f) to Case 3. Subplots (a, c, e) are two-parameter diagrams showing the changes of the base oscillator amplitude for different \(\omega \) and c. On subplots (b, d, f) we present 5 FRCs calculated for different sets of parameters

Full size image

In subplots (c, d), we show the results obtained for Case 2 and in (c, d) for Case 3. FRCs presented in subplot (d) were calculated for: \(d_{f}=10\,(\hbox {N})\)—red line; \(d_{f}=37.65\,(\hbox {N})\) (which is an optimized value for Case 2)—green line and \(d_{f}=90\,(\hbox {N})\)—blue line. For Case 3, optimized value of dry friction parameter is \(d_{f}=15.44\,(\hbox {N})\), and we present the FRC for that case using green color in Fig. 3f. Similarly as for previous Cases, red and blue lines in subplot (f) were calculated for \(d_{f}=10\,(\hbox {N})\) and \(d_{f}=90\,(\hbox {N})\), respectively.

Analyzing the presented results, we can draw the following conclusions. As expected, when \(I_\mathrm{ratio}\) is small, the effects caused by dry friction are similar to the results obtained for the TMD without inerter. If the dry friction element is properly chosen, it can enhance the range of effectiveness and improve the overall efficiency of TMD. For Case 1, the range of \(d_{f}\) for which we observe significant improvement in damping efficiency is relatively large. When we increase the value of \(I_\mathrm{ratio}\), the role of the inerter grows and TMD behaves differently. Similarly as for viscous damping, the optimum value of dry friction parameter \(d_{f}\) is somehow connected to the main mass of TMD m which value decreases with the rise of \(I_\mathrm{ratio}\). That is why the optimum values of \(d_{f}\) are the smaller, the bigger the inertance. Also, the range of \(d_{f}\) values shrinks when we increase \(I_\mathrm{ratio}\). Summing up, we can say that the effects of dry friction changes with the change of \(I_\mathrm{ratio}\) value similarly as for viscous damping case described in the previous section.

Simultaneously, comparing the effects of dry friction and viscous damping, we can say that the changes of FRC curves are more sudden for dry friction than for viscous damping. The other thing is that for large values of \(d_{f}\) parameter, the FRC curve does not have significant resonance peak as we can find for large viscous damping coefficients. Around the resonant frequency, the relation between the amplitude of the base oscillator and the excitation frequency can be estimated as a decreasing linear function. This effect is especially visible for Case 1 and Case 2 (subplots (d, f) of Fig. 3).

6 Influence of play in inerter gear

Most of inerter realizations that have been described up to this moment contain gears with backlash. Still, there is a number of scientific works which proves that in many applications the play does not jeopardize potential benefits inerters can bring. There is also a number of methods to utilize the unwanted play. However, to decide, if we need to eliminate play when designing a highly efficient TMD with the inerter, we have to describe precisely how it affects the TMD efficiency. In this section, we investigate this influence using the model of play described by Scheibe and Smith [31].

Full description of the modeling approach can be found in [31] but for sake of clarity, and here, we recall the mathematical formulas governing the behavior of the system with play. Firstly, we recall that for the system with play we have four degrees of freedom (namely \(x,\, y,\, u,\, r\)) instead of just two which describe the position of the damped body x and TMD y. Coordinates u and r are used to describe the position of nodes connecting the inerter, parallel spring-damper element and play element in series. Hence, the model that consists of formulas 1 and 2 has to be accompanied by additional equations. The first formula has been already presented in the Table 1, and it states that the force produced in the inerter (given by \(I\left( \ddot{r}-\ddot{x}\right) \)) is equal to the force in spring-damper element (given by \(k_{i}\left( r-u\right) +c_{i}\left( \dot{r}-\dot{u}\right) \)). So, we get:

$$\begin{aligned} I\left( \ddot{r}-\ddot{x}\right) =k_{i}\left( r-u\right) +c_{i}\left( \dot{r}-\dot{u}\right) \end{aligned}$$
(4)

Then, depending on the current state of the system, we add another equation. When modeling the extension of the engaged inerter (assuming that there is no more gap in gears), we assume that \(u=y-\varepsilon \). Then, when the inerter is engaged but compressing, we have \(u=y+\varepsilon \). Finally, in disengagement state, we know only that \(\left| y-u\right| <\varepsilon \) but in that state the force generated in both elements (inerter and spring-damper) is equal to zero. Therefore, we know that both sides of Eq. 4 are equall to 0 which gives us the following two equations:

$$\begin{aligned}&I\left( \ddot{r}-\ddot{x}\right) =0 \end{aligned}$$
(5)
$$\begin{aligned}&k_{i}\left( r-u\right) +c_{i}\left( \dot{r}-\dot{u}\right) =0 \end{aligned}$$
(6)

Using the above description, we are always able to fully describe the motion of the system with play in the inerter.

In the model, we have to pick two-parameters values: the stiffness \(k_{i}\) and viscous damping coefficient \(c_{i}\). The mesh stiffness of a single gear depends on many factors such as tooth module, material, manufacturing technology and thermal treatment. Nevertheless, authors usually assume values from the range: \(\left( 10^{7},\,10^{9}\right) ({\hbox {N}}/{\hbox {m}})\) [36, 37]. Conforming the aforementioned works, we assume the following parameters of the play model: stiffens connected with the play element \(k_{i}=2\times 10^{7}\,({\hbox {N}}/{\hbox {m}})\) and its viscous damping coefficient \(c_{i}=0.01\,({\hbox {N\,s}}/{\hbox {m}})\). We assumed slightly lower value of \(k_{i}\) to include the flexibility of gear rack, gear shafts, etc. Knowing that in most applications we can assume \(\varepsilon =1\times 10^{-4}\,(\hbox {m})\) as a standardized play gap [38], we consider much larger range of play gap \(\varepsilon \epsilon \left\langle 0,\,0.002\right\rangle \,(\hbox {m})\) to show how this value influences the response of system in the most extreme cases (lack of gap and large gap). We investigate 3 Cases that are described in Sect. 3 and show the results of numerical simulations in Fig. 5. In the upper row of Fig. 5, we show two-parameter density plots showing how the response on the system changes with the increase of play gap up to \(\varepsilon =0.002\,(\hbox {m})\). We see that basically there is no overall macroscopic influence of play on the base system amplitude (\(MAX\,[x]\)). Still, with the increase of the play gap \(\varepsilon \), the dynamics of the system changes. To present the effects of increasing the play gap, we show phase portraits of the base structure calculated for two different frequencies of excitations. We picked one value after the main resonance \(\omega =21\,(\hbox {Hz})\) (subplots (d, e, f) and one before the main resonance \(\omega =19\,(\hbox {Hz})\) (subplots (g, h, i). On each graph (d–i), we show phase portrait of the base structure oscillator calculated for four different values of \(\varepsilon \):

  • \(\varepsilon =0\,(\hbox {m})\)—for which there is no play gap. Such value corresponds to the idealized model of the system with perfect backlash elimination or to the usage of inerter realization with no gears (i.e., hydraulic inerter [39]—black lines.

  • \(\varepsilon =0.5\times 10^{-4}\,(\hbox {m})\)—this value corresponds to the half of standardized play gap. We pick it as a model of gear that are assembled in a way to minimize the play gap—green lines.

  • \(\varepsilon =1\times 10^{-4}\,(\hbox {m})\)—standarized play gap—red lines.

  • \(\varepsilon =1\times 10^{-3}\,(\hbox {m})\)—ten times of a standardized play gap. We pick it as a model of imperfect or heavily worn gear—blue lines.

Analyzing Fig. 5d–i, we see that with the increase of play gap we observe less smooth trajectories with more numbers of more significant fluctuations. Still the difference in the amplitude of the base structure is barely visible. Nevertheless, from practical point of view, fluctuation that are present when the play gap is significant are highly undesirable. They cause higher loads in the system which may impede operation and lead to rapid wear of the device elements. Subplots (a, d, g) correspond to Case 1 while (b, e, h) and (c, f, i) to Case 2 and Case 3, respectively. Comparing the results obtained for different \(I_\mathrm{ratio}\), we can say that the effects of play do not depend on that value. Hence, the situation is completely different from the one observed for viscous damping and dry friction.

Fig. 5
figure 5

Influence of play \(\varepsilon \) in inerter gear on the system’s dynamics. Subplots (a, d, g) refers to Case 1 embodiment, (b, e, h) to Case 2 and (c, f, i) to Case 3. Subplots (a, b, c) are two-parameter diagrams showing the changes of the base oscillator amplitude for different \(\omega \) and \(\varepsilon \). On subplots (d, e, f), we present phase portraits of the base oscillator calculated for \(\omega =21\,(\hbox {Hz})\), while in subplots (g, h, i), we present phase portraits for \(\omega =19\,(\hbox {Hz})\). On each subplot (d–i), we plot four different curves that corresponds to different values of play, i.e., \(\varepsilon =0\,(\hbox {m})\)—black lines, \(\varepsilon =0.00005\,(\hbox {m})\)—green lines, \(\varepsilon =0.0001\,(\hbox {m})\)—red lines and \(\varepsilon =0.001\,(\hbox {m})\)—blue lines. (Color figure online)

Full size image

It is important to notice that the considered model of the base system (with the assumed parameters values) corresponds to a large scale construction in which we observe vibrations of a large amplitude. In general, we can say that when the TMD is active, the amplitude of the damped body is at least 100 times bigger than the play gap. This fact may be one of the reasons why we observe almost no overall macroscopic influence of play on the systems dynamics. Still, the effects caused by the backlash in inerter gears can be different if the amplitude of vibrations is comparable to the play itself, but it is a subject for another investigation.

7 Full model of TMD with inerter

In this section, we investigate the dynamics of the full model of the TMD with the inerter. The system includes viscous damper, dry friction and model of play [31]. We continue our approach and consider 3 Cases with different \(I_\mathrm{ratio}\). For each Case, we compare the effects introduced by each element and investigate how they change in the presence of the others. Results are presented in Fig. 6. Subplots (a, b) correspond to Case 1 (\(I_\mathrm{ratio}=0.1\)). In Fig. 6a, we show 5 FRC curves calculated for the following conditions:

  • \(c=0\,({\hbox {N\,s}}/{\hbox {m}})\), \(d_{f}=0\,(\hbox {N}),\) \(\varepsilon =0\,(\hbox {m}),\) \(k_{i}\rightarrow \infty \,({\hbox {N}}/{\hbox {m}})\), \(c_{i}=0\,({\hbox {N\,s}}/{\hbox {m}})\)—It is the most simple TMD without any of the considered elements. We treat it as a reference response— black line marked as “1”.

  • \(c=0\,({\hbox {N\,s}}/{\hbox {m}})\), \(d_{f}=0\,(\hbox {N}),\) \(\varepsilon =0.0001\,(\hbox {m}),\) \(k_{i}=2\times 10^{7}\,({\hbox {N}}/{\hbox {m}})\), \(c_{i}=0.01\,({\hbox {N\,s}}/{\hbox {m}})\)— Model of the TMD with play caused by the presence of inerter gear assuming standardized play gap—yellow line marked as “2” (overlapped by the black line).

  • \(c=10\,({\hbox {N\,s}}/{\hbox {m}})\), \(d_{f}=0\,(\hbox {N})\), \(\varepsilon =0\,(\hbox {m}),\) \(k_{i}\rightarrow \infty \,({\hbox {N}}/{\hbox {m}})\), \(c_{i}=0\,({\hbox {N\,s}}/{\hbox {m}})\)—Classical TMD with viscous damper. The model often used to introduce simple model of the energy dissipation present in real systems—blue line marked as “3”.

  • \(c=0\,({\hbox {N\,s}}/{\hbox {m}})\), \(d_{f}=10\,(\hbox {N})\), \(\varepsilon =0\,(\hbox {m}),\) \(k_{i}\rightarrow \infty \,({\hbox {N}}/{\hbox {m}})\), \(c_{i}=0\,({\hbox {N\,s}}/{\hbox {m}})\)—TMD with dry friction element. The other way of modeling energy dissipation. Rarely used because of nonlinearity of the function—red line marked as “4”.

  • \(c=10\,({\hbox {N\,s}}/{\hbox {m}})\), \(d_{f}=10\,(\hbox {N})\), \(\varepsilon =0.0001\,(\hbox {m}),\) \(k_{i}=2\times 10^{7}\,({\hbox {N}}/{\hbox {m}})\), \(c_{i}=0.01\,({\hbox {N\,s}}/{\hbox {m}})\)— Full model of TMD with all considered elements—green line marked as “5”.

Comparing the FRCs from Fig. 6a, we see that the effects caused by viscous damping and dry friction are qualitatively the same while the play itself does not cause macroscopic changes to the shape of FRC. In the literature, authors often use simple model of TMD with viscous damper because it is simple and mathematically convenient. Our results prove that such a model can also well simulate the behavior of TMDs with inerters but only when viscous damping coefficient and dry friction parameters are relatively small (see previous sections). Practically, this means that simplified model is sufficient to model the device without additional damper (TMD which consists only of mass connected with the main body via spring and inerter).

To investigate the accuracy of the simplified model, we calculate one more FRC for TMD with only viscous damper. This time we adjust the value of damping coefficient to imitate FRC received for the full model. For simplicity, we assume the value 50% grater than reference value which for Case 1 gives us \(c_\mathrm{opt}(Case\,1)=15\,({\hbox {N\,s}}/{\hbox {m}})\)). In Fig. 6b, we compare FRCs calculated for the full model (green line “5”) and for TMD with adjusted viscous damping coefficient \(c_\mathrm{opt}(Case\,1)=15\,({\hbox {N\,s}}/{\hbox {m}})\) (orange line “6”). The area between the curves is marked using gray color and indicates the difference in the responses. We see only slight disagreement between the curves which proves that— especially for engineering applications—there is no need to use the full model for TMD with the inerter.

Fig. 6
figure 6

Comparison between the effects caused by four investigated elements. In subplots (a, c, e), we present FRC calculated for models with each investigated factor and the full model that contains all of them. In subplots (b, d, f), we magnify and compare the results obtained for the full model (green curves) and the simplified model (orange curves). (Color figure online)

Full size image

We perform similar analysis for Case 2 and Case 3 and present the results in subplots (c, d) and (e, f) of Fig. 6, respectively. For Case 2, parameters’ values and colors of the lines are exactly the same as for Case 1 (see the list above). Also, we use the same value of the adjusted damping coefficient \(c_\mathrm{opt}(Case\,2)=15\,({\hbox {N\,s}}/{\hbox {m}})\). Analyzing the results obtained for the Case 2, we come to the same conclusions as formulated for Case 1.

When investigating Case 3, we also follow the procedure described above, but we reduce the values of viscous damping coefficient and dry friction parameter by half (\(c=5\,({\hbox {N\,s}}/{\hbox {m}})\), \(d_{f}=5\,(\hbox {N})\)). It is because in Case 3 the main mass of the TMD is much smaller \(m=1\,(\hbox {kg})\). Also, the adjusted value of viscous damping coefficient for a simplified model is by half smaller: \(c_\mathrm{opt}(Case\,3)=7,5\,({\hbox {N\,s}}/{\hbox {m}})\). For Case 3, we observe even grater agreement between the full model and the simplified one in Fig. 6f.

Comparing the results for the 3 considered cases, we see that the simplified model can be used despite the value of \(I_\mathrm{ratio}\) and the agreement between the results is the grater, the bigger \(I_\mathrm{ratio}\). Still, it is true only for relatively small values of viscous damping coefficient and dry friction parameter \(d_{f}\). Recalling the results presented in previous sections, we have to remember that the effects of increasing the viscous damping coefficient and dry friction parameter strongly depend on \(I_\mathrm{ratio}\).

8 Conclusions

In this paper, we present and analyze the effects of inerter nonlinearities on the dynamics and efficiency of TMD. We consider the following factors: I to m ratio, viscous damping, dry friction, play and the full model containing all the factors. Analyzing the results, we can draw the following conclusions.

The composition of the TMD overall inertia has crucial influence on the response of the damped body. Increasing the \(I_\mathrm{ratio}=\frac{I}{I+m}\), we observe the narrowing of the distance between the new resonance peaks. We pick three specific cases that refer to different inerter functions. Case 1 in which the inerter plays minor role and \(I_\mathrm{ratio}=0.1\). Case 2 with TMD inertia equally splitted between inerter and moving mass (\(I_\mathrm{ratio}=0.5\)) and finally Case 3 with the dominant role of the inertance - \(I_\mathrm{ratio}=0.9\). Because all of the cases have practical importance, we consider them during further analysis.

The second factor we investigate is viscous damping. We analyze the influence of damping coefficient c for the 3 cases. Each time we observe strong influence of c on the FRC of the main structure. But, with the increase of \(I_\mathrm{ratio}\), we observe the decrease of the range of c for which we observe best damping properties. This means that although we can use the inerter as a main part of TMD inertia, it leads to some difficulties when tuning other parameters values.

We come to the similar conclusions after examining the influence of dry friction (changing \(d_{f}\) parameter value). Comparing the effects of both types of energy dissipation, we can say that dry friction causes more sudden changes of the FRCs than the ones caused by viscous damping coefficient. Moreover, for large values of \(d_{f}\) parameter, the FRCs have no significant resonance peaks which are always recognizable with viscous damping.

Next, we analyze the influence of play in inerter gears. This investigation is particulary significant as most of inerter realizations have many gears which introduce some discontinuities into the model. Our results prove that if the amplitude of the damped structure is sufficient, then even relatively large play gaps do not influence the overall efficiency of the TMD. Nevertheless, the bigger the play gap, the less smooth the trajectories we receive with more significant fluctuations. Although the difference in the base structure amplitude is barely visible, in practice we always should minimize play gap close to reference value. It is because larger gaps cause fluctuation that can impede operation and lead to rapid wear of the device elements. The interesting observation is that the effects introduced by play do not depend on \(I_\mathrm{ratio}\) value. Still, we have to remember that the results were obtained for the model that corresponds to a large scale construction in which we observe vibrations of a large amplitude. The effects caused by the increase of the play gap can be different for systems of a smaller scale.

Finally, we analyzed the full model of TMD that contains all four factors that we previously consider. For the investigation, we pick parameter values that correspond to TMD with typical inerter. So, we assume relatively small energy dissipation via viscous damping and dry friction, and reference play gap. After comparing the results, we can say that the effects introduced by viscous damping and dry friction are qualitatively comparable while play does not have macroscopic influence on the system’s dynamics.

The most common model of TMD with the inerter consists of moving mass connected to the damped structure via linear spring, viscous damper and the inerter. In the last part of the paper, we compare the results obtained using the full model with the common model in which we adjust the value of damping coefficient (by increasing its value by 50%). The results demonstrate good compliance despite the value of \(I_\mathrm{ratio}\). Still, the simplified model is genuine only for relatively small values of viscous damping coefficient and dry friction parameter \(d_{f}\).

Numerical results presented in this paper prove that the composition of overall inertia of TMD is crucial for its efficiency. The nonlinearities introduced to the system by the presence of the inerter also affect the dynamics of the system. The effects they cause strongly depend on \(I_\mathrm{ratio}\). In many cases, we can use the simplified model with just viscous damper added and receive results with satisfactory precision.