Stable periodic orbits in a pair of chaotic oscillators coupled by an extremely weak diffusive connection

Abstract

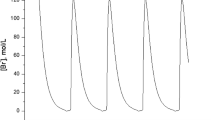
The present paper numerically and experimentally demonstrates that an extremely weak diffusive connection can induce a stable periodic orbit in coupled chaotic oscillators, where each individual oscillator has an unstable periodic orbit which dominates its chaotic attractor. The connection-induced stable periodic orbit is quite close to the unstable periodic orbit. The mechanism of this phenomenon is clarified on the basis of bifurcation analysis: When the coupling strength is varied from zero to an extremely small positive value, the unstable periodic orbit embedded within each individual chaotic attractor becomes stable via a period-doubling bifurcation and then disappears via a saddle-node bifurcation. These results are numerically observed in well-known chaotic oscillators, such as Rössler oscillators and logistic maps. Furthermore, an experimental verification of this phenomenon in coupled chaotic electronic circuits is presented.

Appendices

Appendix A: Circuit implementation

This appendix provides detailed information on our circuit implementation. The nonlinear elements illustrated in Fig. 7 are implemented as diodes (1S1588). The inductor $L$ is realized by the equivalent circuit shown in Fig. 13a: $L=R_{1}R_{3}C_{4}R_{5}/R_{2}=10\,\mathrm{mH}$, where $R_{1}=100$ $\Omega$, $R_{2}=100$ $\Omega$, $R_{3}=100$ $\Omega$, $C_{4}=100$ nF, $R_{5}=1$ k$\Omega$. This is because real inductors inevitably include a resistive component, which cannot be neglected. The negative conductance $-g$ is realized as illustrated in Fig. 13b. The conductance $g$ is adjusted by the variable resistor $r$: $g=1/r$. For accurate adjustment of the coupling strength and the negative conductance, 10-turn precision potentiometers (7274R) are used for $R$ and $r$.

Fig. 13

Implementation of inductor $L$ and negative conductance $-g$: a $L$, b $-g$

Appendix B: Measurement procedure

This appendix presents our measurement procedure for the bifurcation points shown in Fig. 12. As illustrated in Fig. 9, the voltages $v_{1,2}^{a}$ in our circuits powered by a DC voltage source (KENWOOD PW18-2) are measured by digital oscilloscopes (IWATSU DS-5314). The following steps allow us to obtain the bifurcation points.

For step (i), $g$ in each individual oscillator ($1/R=0\,\mathrm{mS}$) is fixed at the PD bifurcation point (period $3 \rightarrow 6$): The fixed values for the oscillators 1 and 2 are denoted by $g_\mathrm{1}$ and $g_\mathrm{2}$, respectively. They are slightly different ($g_{1} \ne g_{2}$) due to errors in the circuit devices. This difference is denoted by $\varDelta g:= g_{1} - g_{2}$, and their average $g_\mathrm{ave}:=(g_{1} + g_{2})/2$ is recorded as $g$. For step (ii), the coupling resistor $R$ is carefully varied and then the lower and upper values of the dotted lines, wherein the connection-induced stable period-three orbit shown in Figs. 10b and 11b can be observed, are plotted. For step (iii), $g_{1}$ and $g_{2}$ are changed, but their difference $\varDelta g$ is maintained. For step (iv), return to step (ii). These experimental data strongly depend on the experiment environment; thus, these are slightly different every time we measure. However, we always obtain the similar tendency as bifurcation points in Fig. 12. Remark that we experimentally found that some other attractors coexist with the orbit: There is room for further investigation.