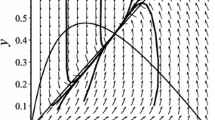
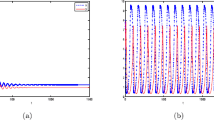
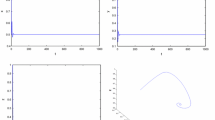
Appendix
In this Appendix section, we shall study the stability of bifurcated periodic solutions arising through Hopf bifurcations by applying the normal form theory and center manifold theorem [27, 28]. Without loss of generality, we denote any one of these critical values \(\tau =\tau _j (j=0,1,\ldots )\) by \(\tilde{\tau }\), at which the characteristic Eq. (2.3) has a pair of purely imaginary roots \(\pm i\omega _+\).
We denote \(\tau \) as \(\tau =\tilde{\tau }+\mu \), \(\mu \in \mathbb {R}\). Then \(\mu =0\) is Hopf bifurcation value of system (2.1). We first rescale the time by \(t\rightarrow t/\tau \) to normalize the delay so that (2.1) can be written as
$$\begin{aligned} u'(t)=L_\mu u_{t}+F(u_{t},\mu ), \end{aligned}$$
(5.1)
in the phase space \(C=C([-1,0],\mathbb {R}^{2})\), where \(u=(u_1,u_2)^T\in C,\) and \(L_\mu : C\rightarrow \mathbb {R}, F: \mathbb {R}\times C\rightarrow \mathbb {R}\) are given respectively by
$$\begin{aligned} L_\mu \phi =(\tilde{\tau }+\mu )\left( \begin{array}{c}\alpha _{11}\phi _{1}(0) +a_{11}\phi _{1}(-1) +\alpha _{12}\phi _{2}(0) \\ \alpha _{21}\phi _{1}(0)+ \alpha _{22}\phi _{2}(0)\end{array}\right) ,\nonumber \\ \end{aligned}$$
(5.2)
and
$$\begin{aligned} F(\phi ,\mu )=(\tilde{\tau }+\mu )\left( \begin{array}{c} \sum \nolimits _{i+j\ge 2}\frac{1}{i!j!}f^{(1)}_{ij}\phi ^i_1(0)\phi ^j_2(0)\\ \sum \nolimits _{i+j\ge 2}\frac{1}{i!j!}f^{(2)}_{ij}\phi ^i_1(0)\phi ^j_2(0) \end{array}\right) .\nonumber \\ \end{aligned}$$
(5.3)
We introduce the formal Taylor expansions about \(\phi =(\phi _1,\phi _2)^T\) as follows
$$\begin{aligned} F(\phi ,\mu )=\frac{1}{2!}F_2(\phi ,\mu ) +\frac{1}{3!}F_3(\phi ,\mu )+o(|\phi |^4), \end{aligned}$$
where
$$\begin{aligned} \frac{1}{m!}F_m(\phi ,\mu )=(\tilde{\tau }+\mu )\left( \begin{array}{c} \sum \nolimits _{i+j=m}\frac{1}{i!j!}f^{(1)}_{ij}\phi ^i_1(0)\phi ^j_2(0)\\ \sum \nolimits _{i+j=m}\frac{1}{i!j!}f^{(2)}_{ij}\phi ^i_1(0)\phi ^j_2(0) \end{array}\right) . \end{aligned}$$
where \(m=2,3\).
Then \(L_\mu \) is a continuous linear function mapping \(C([-1,0],\mathbb {R}^{2})\) into \(\mathbb {R}^{2}\). By the Riesz representation theorem, there exists a matrix whose components are bounded variation functions \(\eta (\theta ,\mu )\) in \([-1,0]\), such that
$$\begin{aligned} L_\mu \phi =\int _{-1}^{0}d\eta (\theta ,\mu )\phi (\theta ),\ \ \phi \in C([-1,0],\mathbb {R}^{2}). \end{aligned}$$
(5.4)
In fact, we choose
$$\begin{aligned} \eta (\theta ,\mu )&= (\tilde{\tau }+\mu ) \left( \begin{array}{c@{\quad }c} \alpha _{11} &{}\alpha _{12} \\ \alpha _{21} &{}\alpha _{22} \end{array} \right) \delta (\theta )\nonumber \\&\quad -\,(\tilde{\tau }+\mu ) \left( \begin{array}{c@{\quad }c} a_{11} &{} 0 \\ 0&{}0 \end{array} \right) \delta (\theta +1), \end{aligned}$$
(5.5)
where \(\delta (\theta )\) is Dirac function. Then (5.4) is satisfied.
For \(\phi \in C^{1}([-1,0],\mathbb {R}^{2})\), define
$$\begin{aligned} A(\mu )\phi = \left\{ \begin{array}{l@{\quad }l} \frac{d\phi (\theta )}{d\theta } , &{} -1\le \theta <0,\\ \int _{-1}^{0}d\eta (s,\mu )\phi (s) ,&{} \theta =0, \end{array} \right. \end{aligned}$$
(5.6)
and
$$\begin{aligned} R(\mu )\phi =\left\{ \begin{array}{l@{\quad }l} 0 , &{} -1\le \theta <0, \\ F(\phi ,\mu ) ,&{}\theta =0. \end{array} \right. \end{aligned}$$
(5.7)
Then system (5.1) can be transformed into a operator differential equation of the form
$$\begin{aligned} u'_{t}=A(\mu )u_{t}+R(\mu )u_{t}, \end{aligned}$$
(5.8)
where \(u_{t}=u(t+\theta ), \theta \in [-1,0]\).
The adjoint operator \(A^{*}\) of \(A\) is defined by
$$\begin{aligned} A^{*}(\mu )\psi =\left\{ \begin{array}{l@{\quad }l} -\frac{d\psi (s)}{ds},&{} 0<s\le 1, \\ \int _{-1}^{0}\psi (-t)d\eta (t,0),&{} s=0, \end{array} \right. \end{aligned}$$
(5.9)
associated with a bilinear form
$$\begin{aligned}&<\psi (s),\phi (s)>= \overline{\psi (0)}\phi (0)\nonumber \\&\quad -\int _{\theta =-1}^{0}\int _{\xi =0}^{\theta }\overline{ \psi }^{T}(\xi -\theta )d\eta (\theta )\phi (\xi )d\xi , \end{aligned}$$
(5.10)
where \(\eta (\theta )=\eta (\theta ,0)\), we know that \(\pm i\omega _{+}\tilde{\tau }\) are eigenvalues of \(A(0)\). Thus they are also eigenvalues of \(A^{*}\).
It is easy to verify that
$$\begin{aligned} <q^*,q>=1,<q^*,\overline{q}>=0, \end{aligned}$$
where
$$\begin{aligned}&\begin{aligned} q(\theta )&=(1,\zeta )^{T}e^{i\theta \omega _{+}\tilde{\tau }}\\&= \left( 1,\frac{i\omega _{+}-\alpha _{11}-a_{11}e^{i \omega _{+}\tilde{\tau }}}{\alpha _{12}}\right) ^{T} e^{i\theta \omega _{+}\tilde{\tau }},\end{aligned}\\&\begin{aligned} q^{*}(s)&=D(\zeta ^{*},1)e^{is\omega _{+}\tilde{\tau }}\\&=D\left( \frac{-i\omega _{+}-\alpha _{22}}{\alpha _{12}},1 \right) e^{is\omega _{+}\tilde{\tau }}, \end{aligned} \end{aligned}$$
and
$$\begin{aligned} \overline{D}=\frac{1}{\overline{\zeta }^*+\zeta -\tilde{\tau }[\alpha _{11}\zeta ^*+a_{11}\zeta ^*+\alpha _{21} +\alpha _{21}\zeta ^*\zeta +\alpha _{22}\zeta ]e^{-i\omega _{+}\tilde{\tau }}}. \end{aligned}$$
From [27], we first compute the coordinates to describe the center manifold \(C_0\) at \(\mu =0\). Let \(u_{t}\) be the solution of Eq. (5.1) when \(\mu =0\).
Define
$$\begin{aligned} z(t)=<q^{*}(s),u_{t}(\theta )>, \end{aligned}$$
$$\begin{aligned} W(t,\theta )&= (W^{(1)}(t,\theta ),W^{(2)}(t,\theta ))^T\nonumber \\&= u_{t}(\theta )-2Re\{z(t)q(\theta )\}. \end{aligned}$$
(5.11)
On the center manifold \(C_{0}\), we have
$$\begin{aligned} W(t,\theta )=W(z(t),\overline{z(t)},\theta ), \end{aligned}$$
where
$$\begin{aligned} W(z(t),\overline{z(t)},\theta )&= W_{20}(\theta )\frac{z^{2}}{2}+ W_{11}(\theta )z\overline{z}\nonumber \\&\quad +\,W_{02}(\theta )\frac{ \overline{z}^{2}}{2}+\cdots . \end{aligned}$$
(5.12)
In fact, \(z(t)\) and \(\overline{z(t)}\) are local coordinates of center manifold \(C_{0}\) in the direction of \(q\) and \(q^{*}\), respectively. For the solution \(u_{t}\in C_{0}\) of (5.8), since \(\mu =0\), we can obtain that \(<\psi ,A\phi >=<A^{*}\psi ,\phi >,\) for \((\phi ,\psi )\in D(A)\times D(A)\), then
$$\begin{aligned} z'(t)&= <q^{*},u_t'>=<q^{*},Au_{t}+Ru_{t}>\\&= <q^{*},Au_{t}>+<q^{*},Ru_{t}> \\&= <A^{*}q^{*},u_{t}>+<q^{*},Ru_{t}>\\&= \omega _{+}\tilde{\tau }zi+\overline{q}^{*}(0)F_{0}(z,\bar{z}). \end{aligned}$$
Thus
$$\begin{aligned} z'(t)=\omega _{+}\tilde{\tau } zi+\overline{q}^{*}(0)F_{0}(z,\bar{z}), \end{aligned}$$
(5.13)
that is
$$\begin{aligned} z'(t)=\omega _{+}\tilde{\tau }zi+g(z,\overline{z}), \end{aligned}$$
(5.14)
where
$$\begin{aligned} g(z,\overline{z})&= \frac{1}{2}g_{20}z^{2}+ g_{11}z\overline{z}+\frac{1}{2}g_{02}\overline{z}^{2}\nonumber \\&\quad +\,\frac{1}{2}g_{21}z^{2}\overline{z}+\cdots . \end{aligned}$$
(5.15)
From (5.11), we get
$$\begin{aligned} u_{t}(\theta )=(u_{1t}(\theta ),u_{2t}(\theta )) =W(t,\theta )+zq+\overline{z} \overline{q}, \end{aligned}$$
where
$$\begin{aligned} u_{i}(t+\theta )=W^{(i)}(t,\theta )+zq^{(i)} +\overline{z}\overline{q}^{(i)},(i=1,2,3). \end{aligned}$$
Thus, we have
$$\begin{aligned} g(z,\overline{z})&= \overline{q}^{*}(0)F_{0}(z,\overline{z})\\&= \overline{D}\tilde{\tau }(\overline{\zeta }^{*},1) \left( \begin{array}{c} \sum \nolimits _{i+j\ge 2}\frac{1}{i!j!}f^{(1)}_{ij}\phi ^i_1(0)\phi ^j_2(0)\\ \sum \nolimits _{i+j\ge 2}\frac{1}{i!j!}f^{(2)}_{ij}\phi ^i_1(0)\phi ^j_2(0) \end{array}\right) . \end{aligned}$$
Comparing the coefficients with (5.15), we have
$$\begin{aligned} g_{20}&= 2\overline{D}\tilde{\tau }\left( \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20} +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}\zeta ^2 +\overline{\zeta }^{*}f^{(1)}_{11}\zeta \right. \\&\quad \left. +\,\frac{1}{2}f^{(2)}_{20} +\frac{1}{2}f^{(2)}_{02}\zeta ^2 +f^{(2)}_{11}\zeta \right) , \\ g_{11}&= \overline{D}\tilde{\tau }\left( \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20}2 +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}2\zeta \overline{\zeta } +\overline{\zeta }^{*}f^{(1)}_{11}(\zeta +\overline{\zeta })\right. \\&\quad \left. +\,\frac{1}{2}f^{(2)}_{20}2 +\frac{1}{2}f^{(2)}_{02}2\zeta \overline{\zeta } +f^{(2)}_{11}(\zeta +\overline{\zeta })\right) , \\ g_{02}&= 2\overline{D}\tilde{\tau }\left( \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20} +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}\overline{\zeta }^2 +\overline{\zeta }^{*}f^{(1)}_{11}\overline{\zeta }\right. \\&\quad \left. +\,\frac{1}{2}f^{(2)}_{20} +\frac{1}{2}f^{(2)}_{02}\overline{\zeta }^2 +f^{(2)}_{11}\overline{\zeta } \right) ,\\ g_{21}&= 2\overline{D}\tilde{\tau }\left[ \left. \overline{\zeta }^{*}f^{(1)}_{20}\left( W_{11}^{(1)}(0)+\frac{W_{20}^{(1)}(0)}{2}\right) \right. \right. \\&\quad +\,\overline{\zeta }^{*}f^{(1)}_{02} \left( W_{11}^{(2)}(0)\zeta +\frac{W_{20}^{(2)}(0)\overline{\zeta }}{2} \right) \\&\quad +\,\overline{\zeta }^{*}f^{(1)}_{11}\left( W_{11}^{(1)}(0)\zeta +\frac{W_{20}^{(1)}(0)\overline{\zeta }}{2}\right. \\&\quad \left. +\,W_{11}^{(2)}(0)+\frac{W_{20}^{(2)}(0)}{2}\right) +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{30} +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{03}\zeta ^2\overline{\zeta } \\&\quad +\,\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{21}(2\zeta +\overline{\zeta })+\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{12}(2\zeta \overline{\zeta }+\zeta ^2)\\&\quad \times \, f^{(2)}_{20}\left( W_{11}^{(1)}(0)+\frac{W_{20}^{(1)}(0)}{2}\right) \\&\quad +\,f^{(2)}_{02}\left( W_{11}^{(2)}(0)\zeta +\frac{W_{20}^{(2)}(0)\overline{\zeta }}{2} \right) \\&\quad +\,f^{(2)}_{11}\left( W_{11}^{(1)}(0)\zeta +\frac{W_{20}^{(1)}(0)\overline{\zeta }}{2}\right. \\&\quad \left. +\,W_{11}^{(2)}(0)+\frac{W_{20}^{(2)}(0)}{2}\right) +\frac{1}{2}f^{(2)}_{30} +\frac{1}{2}f^{(2)}_{03}\zeta ^2\overline{\zeta } \\&\quad \left. +\,\frac{1}{2}f^{(2)}_{21}(2\zeta +\overline{\zeta })+\frac{1}{2}f^{(2)}_{12}(2\zeta \overline{\zeta }+\zeta ^2) \right] . \end{aligned}$$
According to (5.8), (5.11) and (5.13), we can obtain that
$$\begin{aligned} W'&= u_{t}-z'q-\overline{z}'\overline{q}\nonumber \\&= \left\{ \begin{array}{l@{\quad }l} A(0)W(t,\theta )-2Re[\overline{q}^{*}(0)F_{0}q(\theta )], &{}-1\le \theta \le 0,\\ A(0)W(t,\theta )-2Re[\overline{q}^{*}(0)F_{0}q(\theta )]+F_{0},&{} \theta =0 .\end{array} \right. \nonumber \\ \end{aligned}$$
(5.16)
Let
$$\begin{aligned} W'=A(0)W(t,\theta )+G(z,\overline{z},\theta ), \end{aligned}$$
(5.17)
where
$$\begin{aligned} G(z,\overline{z},\theta )=G_{20}(\theta )\frac{z^{2}}{2}+ G_{11}z\overline{z}+G_{02}\frac{\overline{z}^{2}}{2}+\cdots . \end{aligned}$$
According to (5.12), we have
$$\begin{aligned} A(0)W(t,\theta )&= A(0)W_{20}(\theta )\frac{z^{2}}{2}+ A(0)W_{11}(\theta )z\overline{z}\nonumber \\&\quad +\,A(0)W_{02}(\theta ) \frac{\overline{z}^{2}}{2}+\cdots . \end{aligned}$$
(5.18)
Differentiating two sides of (5.12) with respect to \(t\), we get
$$\begin{aligned} W'=W_{z}z'+W_{\overline{z}}\overline{z}'. \end{aligned}$$
(5.19)
From (5.18) and (5.19), we can obtain that
$$\begin{aligned}&[A(0)-2i\omega _+\tilde{\tau }I]W_{20}(\theta )\frac{z^{2}}{2}+ A(0)W_{11}(\theta )z\overline{z}\nonumber \\&\qquad +\,A(0)W_{02}(\theta ) \frac{\overline{z}^{2}}{2}+\cdots \nonumber \\&\quad =-G_{20}(\theta )\frac{z^{2}}{2}- G_{11}z\overline{z}-G_{02}\frac{\overline{z}^{2}}{2}-\cdots . \end{aligned}$$
(5.20)
Comparing the coefficients with (5.20), we can know that
$$\begin{aligned}&[A(0)-2i\omega _{+}\tilde{\tau }I]W_{20}(\theta ) =-G_{20}(\theta ),\end{aligned}$$
(5.21)
$$\begin{aligned}&A(0)W_{11}(\theta )=-G_{11}(\theta ). \end{aligned}$$
(5.22)
From (5.17), we have
$$\begin{aligned} G(z,\overline{z},\theta )&= -\overline{q}^{*}(0)F_{0}q(\theta ) -q^{*}(0)\overline{F}_{0}\overline{q}(\theta )\nonumber \\&= -g(z,\overline{z})q(\theta )-\overline{g}(z, \overline{z})\overline{q}(\theta ), \ -1\le \theta <0.\nonumber \\ \end{aligned}$$
(5.23)
So, we get
$$\begin{aligned}&G_{20}(\theta )=-g_{20}q(\theta )-\overline{g}_{02} \overline{q}(\theta ),\end{aligned}$$
(5.24)
$$\begin{aligned}&G_{11}(\theta )=-g_{11}q(\theta )-\overline{g}_{11} \overline{q}(\theta ). \end{aligned}$$
(5.25)
Then, together with (5.21) and (5.24), we can know that
$$\begin{aligned} W'_{20}=2i\omega _+\tilde{\tau }W_{20}+g_{20}q(\theta ) +\overline{g}_{20}\overline{q}(\theta ), \end{aligned}$$
(5.26)
so
$$\begin{aligned} W_{20}(\theta )&= \frac{ig_{20}q(0)}{\omega _{+} \tilde{\tau }}e^{i\omega _{+}\tilde{\tau }\theta } -\frac{\overline{g}_{02}\overline{q}(0)}{3i\omega _{+}\tilde{\tau }} e^{-i\omega _{+}\tilde{\tau }\theta }\nonumber \\&\quad +\,E_{1}e^{2i\omega _{+}\tilde{\tau }\theta }. \end{aligned}$$
(5.27)
Similarly, we get
$$\begin{aligned} W_{11}(\theta )&= \frac{g_{11}q(0)}{i\omega _{+} \tilde{\tau }}e^{i\omega _{+}\tilde{\tau }\theta }- \frac{\overline{g}_{11}\overline{q}(0)}{i\omega _{+} \tilde{\tau }}e^{-i\omega _{+}\tilde{\tau }\theta }\nonumber \\&\quad +\,E_{2}e^{2i\omega _{+}\tilde{\tau }\theta }, \end{aligned}$$
(5.28)
where
$$\begin{aligned} E_{1}=(E^{(1)}_{1},E^{(2)}_{1}), E_{2}=(E^{(1)}_{2},E^{(2)}_{2}). \end{aligned}$$
Next we focus on the computation of \(E_{1}\), \(E_{2}\). From (5.21) and (5.22), we get
$$\begin{aligned} \int _{-1}^{0}d\eta (\theta )W_{20}(\theta )&= 2i\omega _{+}\tilde{\tau }W_{20}(\theta )-G_{20}(\theta ),\end{aligned}$$
(5.29)
$$\begin{aligned} \int _{-1}^{0}d\eta (\theta )W_{11}(\theta )&= -G_{11}(\theta ). \end{aligned}$$
(5.30)
From (5.27), we can obtain that
$$\begin{aligned} \int _{-1}^{0}d\eta (\theta )W_{20}(\theta )&= \frac{ig_{20}}{\omega _{+}\tilde{\tau }}\dot{q}(0) -\frac{\overline{g}_{02}}{3i\omega _{+}\tilde{\tau }} \dot{\overline{q}}(0)\nonumber \\&\quad +\,\int _{-1}^{0}d\eta (\theta )e^{2i\omega _{+}\tilde{\tau }\theta }E_{1}\nonumber \\&= -g_{20}q(0)+\frac{\overline{g}_{02}}{3}\overline{q}(0)\nonumber \\&\quad +\,\int _{-1}^{0}d\eta (\theta )e^{2i\omega _{+}\tilde{\tau } \theta }E_{1}, \end{aligned}$$
(5.31)
and
$$\begin{aligned} 2i\omega _+\tilde{\tau }W_{20}(0)&= -2g_{20}q(0) -\frac{2\overline{g}_{02}}{3}\overline{q}(0)\nonumber \\&\quad +\,2i\omega _ +\tilde{\tau }E_1. \end{aligned}$$
(5.32)
Therefore, (5.29) becomes
$$\begin{aligned} G_{20}(0)&= -g_{20}q(0)-\overline{g}_{02}\overline{q}(0)\nonumber \\&\quad +\,\left( 2i\omega _+\tilde{\tau }I -\int _{-1}^{0}d\eta (\theta )e^{2i\omega _{+}\tilde{\tau }\theta }\right) E_1. \end{aligned}$$
(5.33)
Similarly, we have
$$\begin{aligned} G_{11}(0)=-g_{11}q(0)-\overline{g}_{11}\overline{q}(0) -\int _{-1}^{0}d\eta (\theta )E_2. \end{aligned}$$
(5.34)
In addition, we get
$$\begin{aligned}&G_{20}(0)=-g_{20}q(0)-\overline{g}_{02}\overline{q}(0)\nonumber \\&\quad +\,2\tilde{\tau }\left( \begin{array}{c} \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20} +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}\zeta ^2 +\overline{\zeta }^{*}f^{(1)}_{11}\zeta \\ \frac{1}{2}f^{(2)}_{20} +\frac{1}{2}f^{(2)}_{02}\zeta ^2 +f^{(2)}_{11}\zeta \end{array}\right) ,\end{aligned}$$
(5.35)
$$\begin{aligned}&G_{11}(0)=-g_{11}q(0)-\overline{g}_{11}\overline{q}(0)\nonumber \\&\quad +\,2\tilde{\tau }\left( \begin{array}{c} \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20}2 +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}2\zeta \overline{\zeta } +\overline{\zeta }^{*}f^{(1)}_{11}(\zeta +\overline{\zeta })\\ \frac{1}{2}f^{(2)}_{20}2 +\frac{1}{2}f^{(2)}_{02}2\zeta \overline{\zeta } +f^{(2)}_{11}(\zeta +\overline{\zeta }) \end{array}\right) .\nonumber \\ \end{aligned}$$
(5.36)
Substituting (5.35) and (5.36) into (5.33) and (5.34), respectively, then
$$\begin{aligned}&\left( i\omega _{+}\tilde{\tau }I-\int _{-1}^{0}e^{i\omega _{+} \tilde{\tau }\theta }d\eta (\theta )\right) q(0)=0,\\&\left( -i\omega _{+}\tilde{\tau }I-\int _{-1}^{0} e^{-i\omega _{+}\tilde{\tau }\theta }d\eta (\theta )\right) \overline{q}(0)=0. \end{aligned}$$
We have
$$\begin{aligned}&\left( 2i\omega _{+}\tilde{\tau }I- \int _{-1}^{0}e^{2i\omega _{+}\tilde{\tau }\theta }d \eta (\theta )\right) E_{1}\\&\quad =2\tilde{\tau }\left( \begin{array}{c} \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20} +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}\zeta ^2 +\overline{\zeta }^{*}f^{(1)}_{11}\zeta \\ \frac{1}{2}f^{(2)}_{20} +\frac{1}{2}f^{(2)}_{02}\zeta ^2 +f^{(2)}_{11}\zeta \end{array}\right) , \end{aligned}$$
namely,
$$\begin{aligned}&\left( \begin{array}{c@{\quad }c}2i\omega _{+}-\alpha _{11}-a_{11}e^{-2i \omega _{+}\tilde{\tau }}&{}-\alpha _{12} \\ -\alpha _{21} &{} 2i\omega _{+}-\alpha _{22} \end{array}\right) E_{1}\nonumber \\&\quad =2\left( \begin{array}{c} \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20} +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}\zeta ^2 +\overline{\zeta }^{*}f^{(1)}_{11}\zeta \\ \frac{1}{2}f^{(2)}_{20} +\frac{1}{2}f^{(2)}_{02}\zeta ^2 +f^{(2)}_{11}\zeta \end{array}\right) . \end{aligned}$$
Thus, we get
$$\begin{aligned}&E^{(1)}_{1}=\frac{2}{B_1}\left| \begin{array}{c@{\quad }c} \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20} +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}\zeta ^2 +\overline{\zeta }^{*}f^{(1)}_{11}\zeta &{}-\alpha _{12} \\ \frac{1}{2}f^{(2)}_{20} +\frac{1}{2}f^{(2)}_{02}\zeta ^2 +f^{(2)}_{11}\zeta &{} 2i\omega _{+}-\alpha _{22}\end{array}\right| ,\\&E^{(2)}_{1}=\frac{2}{B_1}\left| \begin{array}{c@{\quad }c} 2i\omega _{+}-\alpha _{11}-a_{11}e^{-2i\omega _{+}\tilde{\tau }}&{} \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20} +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}\zeta ^2 +\overline{\zeta }^{*}f^{(1)}_{11}\zeta \\ -\alpha _{21} &{} \frac{1}{2}f^{(2)}_{20} +\frac{1}{2}f^{(2)}_{02}\zeta ^2 +f^{(2)}_{11}\zeta \end{array}\right| , \end{aligned}$$
where
$$\begin{aligned} B_1=\left| \begin{array}{c@{\quad }c}2i\omega _{+}-\alpha _{11} -a_{11}e^{-2i\omega _{+}\tilde{\tau }} &{}-\alpha _{12} \\ -\alpha _{21} &{} 2i\omega _{+}-\alpha _{22} \end{array}\right| . \end{aligned}$$
Similarly,
$$\begin{aligned}&E^{(1)}_{2}=\frac{2}{B_2}\left| \begin{array}{c@{\quad }c} \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20}2 +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}2\zeta \overline{\zeta } +\overline{\zeta }^{*}f^{(1)}_{11}(\zeta +\overline{\zeta })&{}-\alpha _{12} \\ \frac{1}{2}f^{(2)}_{20}2 +\frac{1}{2}f^{(2)}_{02}2\zeta \overline{\zeta } +f^{(2)}_{11}(\zeta +\overline{\zeta })&{} -\alpha _{22}\end{array}\right| ,\\&E^{(2)}_{2}=\frac{2}{B_2}\left| \begin{array}{c@{\quad }c} -\alpha _{11}-a_{11}e^{-2i\omega _{+}\tilde{\tau }}&{} \frac{\overline{\zeta }^{*}}{2}f^{(1)}_{20}2 +\frac{\overline{\zeta }^{*}}{2}f^{(1)}_{02}2\zeta \overline{\zeta } +\overline{\zeta }^{*}f^{(1)}_{11}(\zeta +\overline{\zeta }) \\ -\alpha _{21}e^{-2i\omega _{+}\tilde{\tau }} &{} \frac{1}{2}f^{(2)}_{20}2 +\frac{1}{2}f^{(2)}_{02}2\zeta \overline{\zeta } +f^{(2)}_{11}(\zeta +\overline{\zeta })\end{array}\right| , \end{aligned}$$
where
$$\begin{aligned} B_2=\left| \begin{array}{c@{\quad }c}-\alpha _{11}-a_{11}e^{-2i \omega _{+}\tilde{\tau }}&{}-\alpha _{12} \\ -\alpha _{21} &{}-\alpha _{22} \end{array}\right| . \end{aligned}$$
Then, \(g_{21}\) can be determined by the parameters. Thus, we can compute the following values:
$$\begin{aligned}&C_{1}(0)=\frac{i}{2\omega _{+}\tilde{\tau }} \left( g_{20}g_{11}-2|g_{11}|^{2}-\frac{|g_{02}|^{2}}{3}\right) +\frac{g_{21}}{2},\\&\quad \mu _{2}=-\frac{Re\{C_{1}(0)\}}{Re\{\lambda '(\tilde{\tau })\}} \text { and } \beta _{2}=2Re\{C_{1}(0)\}. \end{aligned}$$
Theorem 5.1
-
(i)
\(\mu _{2}\) determines the directions of Hopf bifurcation. If \(\mu _{2}>0\)
\((<0)\), then the Hopf bifurcation is supercritical (subcritical);
-
(ii)
\(\beta _{2}\) determines the stability of bifurcated periodic solutions. If \(\beta _{2}<0\)
\((>0),\) the bifurcated periodic solutions are stable (unstable).