Tropical or extratropical cyclones: what drives the compound flood hazard, impact, and risk for the United States Southeast Atlantic coast?

Abstract

Subtropical coastlines are impacted by both tropical and extratropical cyclones. While both may lead to substantial damage to coastal communities, it is difficult to determine the contribution of tropical cyclones to coastal flooding relative to that of extratropical cyclones. We conduct a large-scale flood hazard and impact assessment across the subtropical Southeast Atlantic Coast of the United States, from Virginia to Florida, including different flood hazards. The physics-based hydrodynamic modeling skillfully reproduces coastal water levels based on a comprehensive validation of tides, almost two hundred historical storms, and an in-depth hindcast of Hurricane Florence. We show that yearly flood impacts are two times as likely to be driven by extratropical than tropical cyclones. On the other hand, tropical cyclones are 30 times more likely to affect people during rarer 100-year events than extratropical cyclones and contribute to more than half of the regional flood risk. With increasing sea levels, more areas will be flooded, regardless of whether flooding is driven by tropical or extratropical cyclones. Most of the absolute flood risk is contained in the greater Miami metropolitan area. However, several less populous counties have the highest relative risks. The results of this study provide critical information for understanding the source and frequency of compound flooding across the Southeast Atlantic Coast of the United States.

1 Introduction

A large and growing share of the world's population lives in coastal regions and is vulnerable to extreme events, such as tropical cyclones. Merkens et al. (2016) estimated that 680 million people live in the low-lying coastal zone worldwide and that this amount could reach more than one billion by 2050. The high concentration of people in coastal areas has resulted in many economic benefits, including improved transportation, industrial and urban development, revenue from tourism, food production, and many more. However, the high concentration of people also concentrates exposure to natural hazards in the coastal zone. Humans are not the only species in the coastal regions that can be affected by extreme events. Beaches, dunes, and tidal wetlands are diverse ecosystems in the coastal zone that are sensitive to climate change and extreme events. For example, Dewald and Pike (2014) showed that hurricanes affect 97% of the sea turtle nesting beaches in the Northwestern Atlantic and Northeastern Pacific Oceans.

Sea-level rise (SLR) increases coastal flooding (e.g., Vitousek et al. 2017; Taherkhani et al. 2020; Sweet et al. 2022). Coastal flooding is driven by many complex factors, including changes in sea level, storms, high tides, or a combination of the three. Storms, both tropical cyclones (TCs) and extratropical cyclones (ETCs, or migratory cyclones/storms of middle and high latitudes), can result in storm surge, high waves, and rainfall that can contribute to or result in flooding. Moreover, the intensity, duration, and occurrence of these storm impacts are expected to change in the coming decades due to climate change. For example, as a consequence of warmer waters and a warmer, more humid atmosphere, Knutson et al. (2015) showed that global average TC intensity, rainfall rates, and occurrence of very intense TCs are projected to increase. In addition, global climate models (GCMs) show a projected poleward shift in midlatitude ETC tracks, with varying changes in the strength of storms across the globe (Chang et al. 2012; Chemke et al. 2022).

In recent years, more focus has been given to coastal compound flooding, caused by the co-occurrence of high tides, coastal storm surges, waves, precipitation, and/or river discharge (Wahl et al. 2015). Storm events, such as Hurricane Florence (2018), have highlighted the importance of compound events and the need to include all relevant drivers of flooding to assess local and regional coastal flood risk. Hurricane Florence resulted in large amounts of rainfall in North and South Carolina. For example, locally, Swansboro and Elizabethtown, N.C., recorded close to 90 cm (Callaghan 2020) of rain. Rainfall together with other drivers resulted in a large compound flood zone in the low-lying coastal zone where ocean, precipitation, and river discharge were all of importance (Ye et al. 2021). However, a priori, the relative contribution of each physical driver to the flooding is often unknown. Whereas flooding hazards from each physical process may be realized, quantifying hazards due to the combination of two or more processes is difficult due to a large number of possible combinations and non-linear physical interactions (e.g., Huang et al. 2021). One solution is to apply multivariate extreme value theory, which requires dynamic downscaling of many events to define the critical region where flooding occurs. Ideally, all possible combinations need to be simulated by either the use of extensive computational resources or computationally efficient methods. Computationally efficient methods can be achieved by an acceleration of the direct simulations, developing a series of event reduction techniques, or by a combination of the two, for example, through hybrid downscaling (Bakker et al. 2022).

In addition to the general challenges of modeling compound flooding (Santiago-Collazo et al. 2019), estimating return periods (RPs) of TC-included flooding remains a significant obstacle. This challenge is related to two factors. First, TCs are poorly resolved in many synoptic-scale and global climate datasets used for meteorological forcing due to coarse spatial and temporal resolution, causing an underestimation in TC intensity (Roberts et al. 2020) and, consequently, storm surge and wave conditions (Murakami and Sugi 2010). Second, the limited record length of available meteorological forcing data, in combination with the low probability of TCs, means the number of TCs is too small to estimate RPs robustly (e.g., Lin and Emanuel 2016; Leijnse et al. 2022). In flood risk assessment, it is possible to overcome some of these limitations via synthetic emulation of TC tracks (e.g., Vickery et al. 2000; Bloemendaal et al. 2020; Nederhoff et al. 2021a, b) or other statistical techniques such as the joint probability method (JPM; Resio and Irish 2015; Gonzalez et al. 2019; Nadal-Caraballo et al. 2022). Still, these approaches suffer from parameterizations of key physics (e.g., land–sea interactions or sea water temperature) and are based on datasets with limited temporal length. Alternatives could be the pseudo-global warming approach (Jyoteeshkumar Reddy et al. 2021) or the full dynamical approach (Mori and Takemi 2016) which is only available to a few nationwide research centers with very high computing capacity (Mori et al. 2021).

In recent years, the scientific community has increasingly focused on (TC-induced) compound events. In all these efforts, coupling procedures between marine (tide and surge) and inland processes (rainfall and riverine discharge) are paramount to capture the complex physical interactions. For example, at the local-watershed scale, Bilskie and Hagen (2018) showed local impacts on water levels in the flood transition zone when considering different techniques for combining marine and inland flooding. Gori et al. (2020) simulated all the physical iterations of multiple flood drivers for many synthetic TC events to produce probabilistic hazard maps, including a breakdown of rainfall versus surge-dominated flood zones. Bates et al. (2021) took this one step further and provided the first integrated and high-resolution view of the U.S. fluvial, coastal, and pluvial flood hazard, as a single layer, driven by both TC and ETC events. However, that study did not provide an estimate of the contribution of TCs to compound flooding. Booth et al. (2016) provided a breakdown between TCs and ETCs for the U.S. mid-Atlantic and Northeast Coasts based on observational data and showed that TCs typically dominate the most extreme events (e.g., 100-year event) while more common events (e.g., yearly) driven by ETCs are equally important. However, no study has yet estimated the relative contribution of TCs and ETCs to compound flooding using an integrated physics-based model that encapsulates inland and coastal processes across thousands of kilometers. The contributions of TC and ETC to compound flooding matter because the weather phenomena have different characteristics and patterns of movement, which affect the time scale, intensity, and spatial distribution of the flooding and, consequently, hazards and impacts.

In this paper, we introduce, validate, and apply a workflow for analyzing and predicting compound flooding hazards, impacts, and risks for both tropical and extratropical cyclones. This approach is applied on large spatial scales and for dozens of realizations in the future climate and for seven SLR scenarios. This work is part of a broader project led by the U.S. Geological Survey (USGS) to map future coastal flooding and erosion hazards across the Southeast United States due to SLR and storms in a changing climate (Barnard et al. 2023a, b; Parker et al. 2023). This work focuses on the overland coastal flooding component of the study. The novelty of this manuscript is investigating the contribution of TC and ETC events to flood hazards and how this will change with SLR. The paper is structured as follows. First, we describe the regional domain in this study. Second, the materials and methods applied in this workflow are described. Third, the results are presented, which (a) focus on the validation of tide, historical conditions, and Hurricane Florence, and (b) on the application of the model to assess flood hazards and impacts on the future climate and SLR scenarios. Lastly, we present our discussion and conclusions sections.

2 The Southeast Atlantic coastal zone

The Southeast Atlantic Coast includes vast stretches of coastal and inland low-lying areas, the southern reach of the Appalachian Mountains, several high-growth metropolitan areas (e.g., Miami, Jacksonville, Savannah, Charleston, Wilmington, and Norfolk), and large rural expanses. This study focuses on the coastal zone of the Southeast Atlantic Coast, ranging from Biscayne Bay, Florida in the south up to the mouth of the Chesapeake Bay in the north (gray counties shown in Fig. 1a). The coastal zone is manually defined here as the area between the present-day shoreline and about the 10 m elevation contour relative to NAVD88. This Low Elevation Coastal Zone (McGranahan et al. 2007) typically extends about 100 km inland in this region.

Fig. 1

The study area (shown in gray) consists of the coastal counties in the United States Southeast Atlantic Coast states of Florida, Georgia, South Carolina, North Carolina, and parts of Virginia. Also, shown are the SFINCS (Super-Fast Inundation of CoastS) flood model domains (white outlines), offshore boundary (blue line), sources (green dots), and observation points (red dots). Model domains typically reach about 100 km inland to about 10 m above NAVD88 (the landward boundary of the model in white). Several major city names are presented to orient the reader. © Esri, DigitalGlobe, GeoEye, i-cubed, USDA FSA, USGS, AEX, Getmapping, Aerogrid, IGN, IGP, swisstopo, and the GIS User Community

The Southeast Atlantic Coast is rapidly urbanizing. For example, the Southeast Atlantic Coast contains many of the fastest-growing metropolitan areas in the country, including several of the top 20 fastest-growing urban regions in 2020 (U.S. Census 2020). This shift is on top of existing sizeable urban city centers such as the greater Miami area (Miami-Dade, Broward, and Palm Beach counties). These trends toward a more urbanized Southeast are expected to persist, creating new vulnerabilities by increasing population exposure to areas in the flood hazard zone (e.g., 100-year flood map).

Flood hazards are expected to increase significantly in the future due to rising global sea levels (Vitousek et al. 2017; Taherkhani et al. 2020; Sweet et al. 2022). The average global mean sea level (GMSL) has risen about 21–24 cm from 1880 to 2021 and is 97 mm above 1993 levels (NOAA 2022). This rise in SLR has been accelerating since 1990 (Dangendorf et al. 2017; Sweet et al. 2022) and is projected to continue to accelerate due, for example, to the increased mass loss of the Antarctic ice sheet (Le Bars et al. 2017). Recent downscaled projections for the Southeast Atlantic Coast by Sweet et al. (2022) suggested rates and an increase in local sea levels, relative to the 2000 range, of 0.3–0.5 m for 2050, 0.5–1.6 m for 2100, and 0.7–2.7 m for 2150. SLR will significantly alter flooding frequency in many already vulnerable communities.

Many cities across the Southeast Atlantic Coast are starting to plan for the impacts rising waters are likely to have on their infrastructure. For example, flood events in Charleston, S.C., have been increasing and are projected to increase substantially more in the future with sea-level rise; the city has prepared a Sea-Level Rise Strategy Plan (City of Charleston 2015). The city is also planning to undertake subsequent steps to further protect the city and its inhabitants from nuisance flooding.

Besides high tide events, which will be exacerbated due to SLR, the Southeast Atlantic Coast is regularly impacted by extreme weather events. TCs can bring strong winds, heavy rainfall, and high surges and waves in the summer and fall. Some of these TCs, such as Hurricane Andrew (1992), were extremely powerful and devastated communities on the Southeast Atlantic Coast. ETC events can also trigger a large amount of flooding due to wind and precipitation and subsequent storm surges and high waves. For example, in October 2015, a significant rainfall nor'easter caused historic flash flooding across North and South Carolina, resulting in $2.5 billion in damages (NCEI 2022). Hurricane Florence in 2018 resulted in $24 billion in wind and water damage (NHC 2019).

3 Materials and methods

3.1 Overview

The modeling approach is based broadly on the Coastal Storm Modeling System (CoSMoS: Barnard et al. 2014, 2019; Erikson et al. 2018; O'Neill et al. 2018), initially developed for the West Coast of the United States, but with significant modifications and updates to address the need to capture and resolve TCs as well as pluvial contributions to flooding. Figure 2 shows a conceptual framework as applied in this study. The numerical computation of overland flooding is based on the open-source hazard model SFINCS (Super-Fast INundation of CoastS; Leijnse et al. 2021). Five computational domains were created for the study region (Fig. 1) based on topo-bathymetry, soil type, and land cover data across the region (Sect. 3.2.1). Boundary conditions for water levels, discharges, and atmospheric conditions (Sect. 3.2.2) for tens of thousands of emulated extratropical and tropical storms were provided (Sect. 3.5.1). First, we simulated a validation period and compared results to validation data (Sect. 3.3) to determine model skill (Sect. 4.1). Secondly, storms for the climate projection period were simulated for different sea level rise scenarios. Results per storm were used in an extreme value analysis (Sect. 3.5.2) to determine their frequency and downscaled at higher spatial resolution. High-resolution water depth maps were used as input for the open-source impact model Delft-FIAT (Flood Impact Assessment Tool; Sect. 3.2.3) to determine impacts and risks. Compound flood hazards and impacts are described in Sect. 4.2. The latter includes a breakdown of the contribution of TC versus ETCs. In subsequent paragraphs, input data and individual methodological and model components are described, followed by detailed explanations of the numerical methods and computational framework.

Fig. 2

Conceptual workflow of the CoSMoS framework. Green data boxes are data sources, purple terminator boxes are analysis steps, predefined blue processes are numerical models SFINCS (hazard model) and Delft-FIAT (impact model), and yellow database symbols are the eventual outputs used as results

3.2 Input data

3.2.1 Topo-bathymetry, soil type, land cover

Before generating the overland flood models, elevation datasets were extracted along the entirety of the Southeast Atlantic Coast from the area's Coastal National Elevation Database (CoNED) topographic model (Danielson et al. 2016; Tyler et al. 2022), Continuously Updated Digital Elevation Model (CUDEM; CIRES 2014), and Coastal Relief Model (NOAA National Geophysical Data Center 2001). Topo-bathymetric data were applied in the order listed to cover the entire area and fill data gaps. The model landward extent was manually determined to allow for minimal inflow boundary locations and typically reaches + 10 m elevation relative to NAVD88. The seaward extent was set to around NAVD88 − 10 m. This depth suffices for overland flood modeling purposes. Maximum dune elevations along the coast were derived from CoNED and cross-checked with Doran et al. (2017) to include coastal flood defenses in the overland flooding models.

Information from the National Land Cover Database (Homer et al. 2020) was converted to roughness values using Manning's coefficients and approaches as described by Nederhoff et al. (2021a, b) to define a spatially varying roughness map across each SFINCS model (see Table 2). Friction in open water was set to a typical coastal value of 0.020 and was thus not used for calibration purposes.

Data from the U.S. General Soil Map (STATSGO2; U.S. Department of Agriculture; USDA 2020) provided the input for the Curve Number infiltration method used in the overland flooding models. STATSGO2 is an inventory developed by the U.S. Department of Agriculture and includes soil characteristics information across the Continental U.S. The hydrologic soil group (HSG) information and hydraulic conductivity (Ks) from the surface layer were used for this study. In particular, HSG information was combined with a landcover map to estimate the curve numbers according to USDA (1986).

3.2.2 Boundary conditions: water levels, discharges, and meteorological conditions

Water level time series were applied at the offshore boundary of the SFINCS models. These time series were derived from a linear superposition of the Global Tide and Surge Model (GTSM; Muis et al. 2016, 2022) outputs and wave setup; wave setup was computed with a parameterized empirical formula (Stockdon et al. 2006) and waves from the ERA5 reanalysis (Hersbach et al. 2020) and projection time-periods (Erikson et al. 2022). Statistical corrections were applied to improve modeled water level components. In particular, a correction on the tidal components, seasonality, and non-tidal residual (NTR) was performed to improve the skill of the boundary conditions. For more information on this correction, one is referred to Parker et al. (2023). For the TC simulations, water levels from the coupled numerical hydrodynamic and wave model setup (ADCIRC + STWAVE; see Massey et al. 2021), which includes tide, wind-driven surge, and wave-driven setup, were used.

Discharges for 74 rivers flowing into the study domain were derived from the NOAA National Water Model (NWM) continental United States Retrospective Dataset (NOAA 2021). This river discharge reanalysis dataset was used directly for the hindcast (validation) period. River discharge for the projection period was derived using a relationship between NWM discharge and historical precipitation and applying this relationship to estimate future discharge rates. In particular, the upstream watershed location of each river was identified from the network of river-reach IDs used by the NWM (Liu et al. 2018). For each watershed, cumulative precipitation was computed and the best correlation using a linear fit with a variable time lag between cumulative daily precipitation and discharge was found. This linear fit was then applied to the projected precipitation, yielding projected future discharge for each of the streams. The projected future discharge was bias-corrected, based on the historical NWM discharge using empirical quantile matching (Li et al. 2010). A baseflow, as calculated from NWM using a digital filter method from the HydRun toolbox (Tang and Carey 2017), was also applied in the TC simulations. Baseflow was included to get an estimate of discharge-driven compound flooding during TCs.

All the model domains were forced with the same meteorological conditions (wind, sea-level pressure, and rainfall). The meteorological conditions used for the hindcast (validation) period (1980–2018) were based on ERA5 (Hersbach et al. 2020) for wind and pressure. For the same period, the North American Land Data Assimilation System (NLDAS; Chang et al. 2012) was used for rainfall. For the projection period (2020–2050), conditions were applied from the Coupled Model Intercomparison Project—Phase 6 (CMIP6). In particular, an ensemble of three CMIP6 models was used from the High-Resolution Model Intercomparison Project (HighResMIP) based on the SSP5-8.5 greenhouse gas concentration scenario: CMCC-CM2-VHR4 (Scoccimarro et al. 2017), GFDL-CMC4C192 (Guo et al. 2018), and HadGEM3 (Roberts 2019a). These models were chosen because of their increased atmospheric and ocean resolution as fine as 25–50 km, which is expected to better resolve coastal storm events that are not adequately resolved with the native resolution of most GCMs (Roberts et al. 2020). The chosen CMIP6 models, at the time of this study, had data from 2020 to 2050. All 31 years of data from all three models were used for this study. No bias corrections were performed on the projection period meteorological conditions (wind, pressure, and rainfall data fields from CMIP6). Implications of the lack of bias correction for CMIP6 are described in the discussion section.

Multi-decadal-scale hindcast, reanalysis, and General Circulation Models, such as ERA5 and CMIP6-HighResMIP, allow for an analysis of the long-term evolution of the climate and how it affects global processes. However, model resolutions are often insufficient to fully resolve TCs and have a limited temporal length (see Introduction). The U.S. Army Corps of Engineers (USACE) Coastal Hazards System (CHS; Nadal-Caraballo et al. 2020) synthetic TC dataset was applied to overcome these limitations. The CHS (https://chs.erdc.dren.mil) is primarily a probabilistic analysis and machine learning framework based on the Joint Probability Method (JPM). It also encompasses high-resolution numerical simulation of thousands of synthetic TCs under current and future climates. For more information on the CHS and the JPM method, refer to Nadal-Caraballo et al. (2022). In the present study, the probabilities of the CHS synthetic TCs were updated to reflect climate change in which more intense hurricanes are likely to be observed more frequently in the study area from northern Florida northward. This change is related to higher sea surface temperatures. For information on how this was done, one is referred to Appendix 10.1. Rainfall for TCs was based on the Interagency Performance Evaluation Task Force Rainfall Analysis (IPET 2006) method. The IPET method relates pressure deficit to rainfall which decreases exponentially as a function of the TC radius. Within the eye of the storm, rainfall rates are constant. No asymmetry and/or rainfall bands are included in this method.

For the historical periods, we assumed that ERA5-NLDAS had sufficient resolution to resolve TC activity for validation purposes (Dullaart et al. 2020). On the other hand, for the projection period, we assumed TC events were missing in CMIP6 and only ETCs were included (Han et al. 2022).

3.2.3 Exposure and vulnerability data

Impact computations for computed flood maps were performed with HydroMT (Hydro Model Tools), an open-source Python wrapper (Eilander and Boisgontier 2022) for the Delft-FIAT (Flood Impact Assessment Tool). Delft-FIAT is a flexible open-source toolset for building and running flood impact models which are based on the unit-loss method (De Bruijn 2005). Inputs for Delft-FIAT are a hazard layer (water depth), exposure layer (object map with population), and vulnerability (depth–damage curves).

The exposure layer used in Delft-FIAT was based on a method that combines the Global Urban Footprint (GUF; Esch et al. 2017) for the presence of buildings and the Global Human Settlement Layer (GHSL; Florczyk et al. 2019) for population density. In other words, the GHSL estimates the number of people in certain areas, which are distributed over the building footprints provided by GUF. The result is a method that can produce an exposure layer for any place on the globe. In this paper, we calibrated the population per county using the 2020 Census, which resulted in a total population size of 18,828,520 for the area of interest. Vulnerability curves are based on Huizinga et al. (2017). Flood impact is defined here as the population affected via the vulnerability curve. Flood risk is defined as the product of the probability of a flood event and potential adverse consequences for humans (Kron 2005).

3.3 Validation data

A comprehensive set of validation data was used to assess model skill. First, all observed 6-min interval water levels from all long-term National Oceanic and Atmospheric Administration (NOAA) water level stations (CO-OPS 2022) between 1980 and 2018 for the area of interest were collected and processed into continuous time series. In total, 24 NOAA stations were included in the validation (see Figs. 1, 3, or 5 for their locations). Validation focused both on the tidal prediction (Sect. 4.1.1) and storms across the region (Sect. 4.1.2).

The observed water levels were used to determine tidal constituents using UTide (Codiga 2011) for each NOAA gauge. In addition, the XTide database (retrieved via Delft Dashboard; van Ormondt et al. 2020) was also used to identify 68 locations with observed tidal amplitude and phases for model validation. See Fig. 3 for the location of both the NOAA and XTide stations.

Special attention was given to validating Hurricane Florence (2018), which made landfall near Wilmington, N.C. (Sect. 4.1.3). For this singular event, an additional 156 pressure gauges and 396 high water marks (HWM) made available by the U.S. Geological Survey (USGS) were also used to validate the model (U.S. Geological Survey 2021; see Fig. 6 for their locations). Note that this is not the only hurricane that was validated (see Sects. 3.5.1 and 4.1.2), but special attention was given to Florence since this work was funded in the aftermath of the event (see Funding disclosure).

3.4 Numerical method: overland flooding with SFINCS

3.4.1 Overview

SFINCS (Leijnse et al. 2021) was successfully applied to simulate compound flooding, including dynamic hydraulic processes such as tidal propagation, rainfall, and river runoff while maintaining computational efficiency (e.g., Sebastian et al. 2021) and was therefore chosen to predict overland flooding for this study. The physics model dynamically computes water propagation throughout the domain with a computational time step of several seconds (varies per simulation). High-resolution topo-bathymetry and land roughness were included in the native 1 × 1 m resolution utilizing subgrid lookup tables (Leijnse et al. 2020). The continuity and momentum computations were performed on a coarse 200 × 200 m resolution grid to save computational expense. Subgrid bathymetry features were included to account for maximum dune height based on the topo-bathymetry to control overflow during storm conditions. Leijnse et al. (2020) showed water level computations for Hurricane Irma (2017) were still accurate when including subgrid features based on the high-resolution elevation data. The SFINCS model was not calibrated but instead applied with default parameters throughout this study. Advection was deactivated to save computational time but was not found to influence the results (typical in non-wave-driven flooding applications; Leijnse et al. 2021).

Derived overland maximum flood levels were subsequently downscaled to 10 × 10 m resolution water depths using the nearest neighbor interpolation for the water level in combination with a box filter of 3 neighboring grid cells. The five computational SFINCS domains overlap to overcome any possible boundary effects. Results from overlapping model domains were merged by taking the average water level.

The water levels (described by the tide, NTR, and wave setup components) were imposed at the offshore boundary (see Fig. 1 for the location). Hence, we apply SFINCS not just as an overland flood model but also to propagate water levels through the domain, solving the same governing equations describing overland flooding as well as being responsible for tidal propagation (Leijnse et al. 2021). In particular, the model accounts for various factors influencing propagation, such as bathymetry (water depth), bottom friction, Coriolis force, wind stress, and external boundary conditions. Water levels were imposed approximately every 500 m alongshore at the ocean boundary. Incoming short and infragravity waves were not accounted for (except through statistical downscaling of wave setup from offshore wave conditions) since dynamically downscaling this was computationally prohibitive (increasing computation times ~ 1000-fold¹). Implications of the model setup are described in the discussion section. River discharges are accounted for as a vertical point source, linked to the closest grid cell center, and at each time step mass according to the discharge time series is added.

3.4.2 Curve number method

Infiltration was computed at every computational time step with the newly implemented Curve Number method in SFINCS. This method is based on the Soil Conservation Service (SCS; currently known as Natural Resource Conservation Service) Curve Number method for evaluating the volume of rainfall resulting in direct surface runoff. SCS was first developed in 1954 and is described in most hydrology handbooks and textbooks (e.g., Bedient et al. 2013). This method was added to SFINCS to take advantage of most practicing engineers’ familiarity with this method and the availability of tabulated curve numbers for a wide range of land use and soil groups. The Curve Number method is a combined loss method that estimates the net loss due to interception, depression storage, and infiltration to predict the total rainfall excess from a rainfall event.

The Curve Number model uses the following equations to relate total event runoff Q to total event precipitation P.

$$Q=\frac{\left(P-I_a\cdot S_{max}\right)^2}{P+(1-I_a)S_{max}}$$

(1)

$$S_{max} = \left( {\frac{100}{{CN}} - 10} \right)0.0254$$

(2)

in which I_a is the initial abstraction percentage (default 20%), S_max is the retention after runoff begins. CN is the Curve Number and note that here we directly convert the original curve number in inches to meters via the computation of S_max. Since SFINCS is a continuous model, the Curve Number computation is done at a time-step level (order of seconds). It computes the infiltration rate by subtracting the total precipitation with runoff and dividing by the time step (forward differences).

The moisture storage capacity of the soil can be depleted during wet periods and replenished during dry periods. To model this behavior with the Curve Number method, whether it rains or not, we implemented the effective storage capacity (S_e), which is tracked during the simulation. During rainfall, the capacity is slowly filled (Eqs. 1 and 2). During a period with no precipitation, the effective moisture storage capacity is assumed to be replenished at a rate proportional to S_max. Here, we related the recovery constant to the soil saturation akin to the approach used in the Storm Water Management Model (SWMM; U.S. Environmental Protection Agency 2015). In particular, the continuous recovery k_r is estimated with the following equation $k_{r} = \sqrt {K_{s} } /75$, in which K_s is the hydraulic conductivity in inch/h and k_r is the recovery in the percentage of S_max per hour. At the start of new simulations, the cumulative variables are reset to 0, and S_e is set equal to 50% of S_max. Implications of the 50% saturation assumption are described in the discussion section.

The Curve Number infiltration methodology goes hand-in-hand with precipitation. In particular, we first compute the gross rainfall rate per grid cell. Second, we compute the infiltration rate with the methodology outlined in this paragraph. Lastly, we compute the effective rainfall rate by subtracting the infiltration rate from the gross rainfall. The effective rainfall is accounted for by adding the net water volume at each grid cell and each time step as part of the continuity updating step in SFINCS.

3.5 Computational framework

3.5.1 Storm selection

Two slightly different approaches were followed to define the storms. The first one is used to define storms to be run in the validation period. The second one is used for the climate projection period.

First, using all the observed water level data between 1980 and 2018 retrieved from all NOAA tide gauges within the region, the observed linear sea level trend was removed from each individual gauge. Next, unique observed storm peaks were detected via the peak-over-threshold method by finding, on average, three maximum water levels yearly per gauge (39 years × 3 peaks = 117 peaks for most gauges). The threshold was detected automatically on a gauge-by-gauge basis and set at a relatively low value of three. This threshold ensures the inclusion of all significant events over decadal time periods while keeping computational constraints in mind of not being able to model all events. A minimum of 7 days between peak events at each gauge was imposed to guarantee independence between the storms. This detection of storms resulted in a total of 198 historical storms, used here for validation purposes. In regard to duration, each validation storm is simulated for at least 7 days around the middle of the peak when the storm is characterized by a single peak, and for longer in case of containing multiple peaks. In this case, the minimum and maximum peak date defines the duration of the storm and, consequently, the simulation time. Concerning the hydrograph characterization of the storm, the simulation starts at low water of NAVD88 − 0.5 m to avoid low-lying flooding areas since SFINCS initializes water levels across the domain based on the starting water level.

Second, for the 31 years of climate projection record, particular storms per CMIP6 model, were selected based on three independent criteria. In a similar fashion as for the observed data, for each offshore water level boundary point, we detect water level peaks in which the threshold is set to identify, on average, three extreme water level events yearly. A similar method was used for discharge and rainfall. The peaks were identified for all 74 discharge points and for the total rainfall per SFINCS domain, combined, and run similarly to the validation runs. Common peaks were found as a result of these methods; however, only the unique storms were combined per SFINCS domain, resulting in 263–347 events per domain per CMIP6 model. This method was chosen to reduce computational expense since, in this way, we simulated around ~ 20% of the total record and could run simulations in parallel. The main difference between both periods is that fluvial and pluvial data were included as criteria for selecting storms in the climate projection period. However, for the validation period the available validation data were limited to tide gauges and therefore, only these data were used to define storms.

For the TC simulations, a total of 1059 tracks were included. Each track had a probability, location of landfall, heading, forward speed, and intensity based on the synthetic dataset from Nadal-Caraballo et al. (2020). Specific TCs were neglected if a track resulted in less than 20 cm of storm surge everywhere in each domain. The number of neglected tracks varies per domain (126–260, or 12–25%, were neglected, leaving 799–933 from the total of 1059 that were included).

3.5.2 Extreme value analysis

Flood hazards per numerical (SFINCS) grid cell were determined using empirical estimates of exceedance probabilities, without regressing return period estimates using any extreme value parametric distribution. In this way, the full set of potential candidates for compound flooding is simulated without making any a priori inference on the underlying processes beyond compound flooding (Anderson et al. 2019). The maximum computed water level, maximum depth-averaged flow velocity, and wet duration per event and per grid cell were stored. Each storm is ranked on maximum water level, and gives the same frequency resulting in an estimate of the probability of m/(n + 1) in which m is the ranking and n is the number of years, here 31 (i.e., Weibull plotting position; Weibull 1939). TC probability per simulation is derived from the CHS JPM-based input dataset, and the probability is estimated by integrating the discrete storm probability weights over the range of predicted water levels. Per sorted event, the associated maximum depth-averaged flow velocity and wet duration are provided to inform possible conditions during these events.

To combine ETC and TC runs, we first determined the extreme value distribution for high water per grid cell for ETC and TC runs separately. For the three CMIP6 models, we determined the extreme value distribution per model and used the ensemble mean as the estimate for ETC. Afterward, the extremes were combined by taking the inverse of the sum of the TC and ETC yearly exceedance frequency. We follow Dullaart et al. (2021) and for a given high water, we calculated its return period as follows:

$$RP(x)=\frac{1}{\frac{1}{{RP}_{ETC}(x)}+\frac{1}{{RP}_{TC}(x)}}$$

(3)

where RP is the return period in x years of high water. RP_TC and RP_ETC refer to the return period of the TC and ETC water level at the same value of water level. Examples of the probability of high water levels by ETC, TC, and jointly for six stations throughout the domain can be found in the Appendix (Fig. 17). No storm conditions were based on a tide-only simulation of 30 days, chosen to cover a full spring-neap tidal cycle. This cycle, influenced by the Moon and Sun's gravity, causes varying tidal strengths: higher and lower tides during spring tides and milder tides during neap tides. During this stimulation, a baseflow from rivers was included but the effects of waves and rainfall were excluded. No-storm simulations were included to provide an estimate of nuisance flooding.

3.6 Simulation periods and computational expense

Flood predictions were made for two time periods: historical (1980–2018) and future projections (2020–2050).

For validation of the model skill, historical conditions were simulated for 1980–2018. First tidal conditions were simulated and compared to NOAA and XTide stations across the U.S. Southeast. This simulation is based on a 365-day-long simulation without meteorological conditions and baseflow discharge rates for the year 2016. Secondly, 198 historical storms were simulated to assess model skill in reproducing extreme water levels. Thirdly, an in-depth analysis of Hurricane Florence (2018) was performed.

Flood hazard, impact, and risk computations were performed for 2020–2050 using CMIP6 ETC storm events outlined above and TCs from the USACE-CHS framework. Additionally, all ETC and TC model simulations were repeated for seven SLR scenarios: 0-, 0.25-, 0.50-, 1.00-, 1.50-, 2.00- and 3.00-m compared to the year 2005. These scenarios cover the range of plausible sea level projections for the U.S. Southeast through 2100, as reported by Sweet et al. (2022).

Model simulations were performed on the Deltares Netherlands Linux-based High-Performance Computing platform using 54 Intel Xeon CPU E3-1276 v3. On average, a 7-day simulation (typical duration for an individual event) took about 41 min on a single core. Running all 80,000 events (all TCs + ETCs for seven SLR scenarios) took 31 days.

3.7 Model skill

To quantify the skill of the model to reproduce water levels, several accuracy metrics were calculated: model bias, mean-absolute-error (MAE; Eq. 4), root-mean-square-error (RMSE; Eq. 5), and unbiased RMSE (uRMSE; RMSE with bias removed from the predicted value)

$$MAE = \frac{1}{N}\sum \left( {\left| {y_{i} - x_{i} } \right|} \right)^{ }$$

(4)

$$RMSE = \sqrt {\frac{1}{N}\sum \left( {y_{i} - x_{i} } \right)^{2} }$$

(5)

where N is the number of data points, y_i is the i-th predicted (modeled) value, x is the i-th measurement.

4 Results

4.1 Validation

4.1.1 Tidal validation

Model skill in reproducing tidal amplitudes and phases is assessed at 24 NOAA stations and 56 XTide stations across the area of interest and presented in Fig. 3 and Table 3 in the Appendix. The model framework can reproduce tide with a median MAE of 8.3 cm and a median RMSE for high water of 9.9 cm (median computed over the different stations). Across the region, MAE is typically lower than 20 cm (80% of the stations). The most significant model error is shown at Savannah, GA, (MAE of 32 cm). The model error generally increases farther away from the ocean boundary in narrow estuaries and harbors. The model-computed tidal amplitude at these locations is typically underestimated compared to observations. We hypothesize that the underestimation of tidal amplitudes has to do with the (a) SFINCS model resolution and (b) high roughness values from land that may be mapped to the channel in some locations due to the coarse resolution of the land cover map.

Fig. 3

Overview of the Mean Absolute Error (MAE) of tidal water levels at 24 NOAA stations (depicted with station ID) and 68 XTide stations (shown with names) across the study area. For more detailed information on the model skill is provided in Table 3. Several major city names are presented to orient the reader. © Esri, DigitalGlobe, GeoEye, i-cubed, USDA FSA, USGS, AEX, Getmapping, Aerogrid, IGN, IGP, swisstopo, and the GIS User Community

4.1.2 Storm validation across the region

Four examples of time series of modeled and observed water levels are presented in Fig. 4 for large historical hurricanes for stations from north to south: Irene (2009), Hugo (1989), Matthew (2006), and Wilma (2008). Observed and modeled water levels and tides are shown. Tides are based on astronomical components only. The tidal component of the water levels visually matches well the observations before the hurricane's arrival, except for Money Point, VA. (#8,639,348). At this station, there is an underestimation of the tidal amplitude, and the tide arrives too late (i.e., overestimating phase). The lower skill for tidal modeling at #8,639,348 can also be seen in the Appendix (Table 2). The peak water levels are particularly skillful. Computed NTR is also found to match well with the observations since the median MAE increased from 8.3 cm for tide only to 11.9 cm for the water level signal over all storms.

Fig. 4

Time series of observed (red), computed (blue), and tidal (green) still water levels for four events across the area of interest. Panel A depicts Hurricane Irene (2009) in a time series at Money Point, Virginia. Panel B shows Hurricane Hugo (1989) at Charleston, South Carolina, C Hurricane Matthew (2016) at Fernandina Beach, Florida, and D depicts Hurricane Wilma (2005) at Virginia Key, Florida. Stations are listed from north to south. Skill scores are presented in the top left corner

The accuracy of the proposed model framework is presented in Table 1 and Fig. 5. Model skill is good, with a median MAE between 8 and 20 cm (25–75 percentile). However, biases per station do exist. For example, Duck, N.C. (#8651370), has a median bias of + 25 cm, while I-295 Buckman Bridge, FL (#8,720,357) has a median bias of − 19.2 cm. We hypothesize that Duck's overestimation is driven by the inclusion of an open-coast wave setup, which is not measured at the NOAA station (see Parker et al. 2023). On the other hand, the underestimation at the I-295 bridge, being situated inland along the St. John’s River, might be driven by an underestimation of pluvial/fluvial processes or by an underestimation of the tide.

Table 1 Overview of skill scores (mean-absolute-error; MAE, unbiased root-mean-square error; uRMSE and bias) for 24 NOAA observations across 198 events from 1980 to 2018

Fig. 5

Overview of the median Mean Absolute Error (MAE) of storm water levels at 24 NOAA stations (depicted with station ID) across the study area. For more detailed information on model skill, refer to Table 3. Several major city names are presented to orient the reader. © Esri, DigitalGlobe, GeoEye, i-cubed, USDA FSA, USGS, AEX, Getmapping, Aerogrid, IGN, IGP, swisstopo, and the GIS User Community

4.1.3 Hurricane Florence

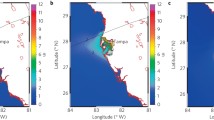
In this section, the SFINCS model setup is validated for Hurricane Florence (2018). The spatial extent of this detailed validation covers about 500 km alongshore and centered around Wilmington, N.C., where Florence made landfall, and includes all data available within the cross-shore extent of the SFINCS domains (~ 100 km). Figure 6a shows the orientation compared to the rest of the study area including the track of Florence. Merged model results for SFINCS domains #4 and #5 were used in this section. Figure 6b presents the stations used for the in-depth validation of Florence, a combination of permanent NOAA gauges and USGS-deployed rapid deployment gauges and highwater marks (HWMs; U.S. Geological Survey 2021). The validation focuses first on reproducing six time series in the area, after which the HWMs are discussed. These time series are randomly chosen across a range of stations to show coastal, riverine, and mixed locations with various degrees of model skill.

Fig. 6

Observational data and model extent for the detailed validation of Hurricane Florence (2018). Panel A: overview figure for the entire study area showing the five different SFINCS (Super-Fast INundation of CoastS) domains, the track of Hurricane Florence (green) and the area of interest Panel B: USGS stations used for the validation of Hurricane Florence model results. USGS gauges have been divided into coastal (pink) and inland (orange) locations based on the classification given when the data were released. Gauges and high water marks (HWM) are marked, respectively, with upward-pointing and downward-pointing triangles. The best track is based on the International Best Track Archive for Climate Stewardship (IBTrACS; Knapp et al. 2010). The coordinate system of this figure is WGS 84 / UTM 17 N (EPSG 32617). © Microsoft Bing Maps

The time series of the water levels for six gauges around the landfall of Hurricane Florence is shown in Fig. 7. The first gauge shows Oyster Landing, N.C. (#8,662,245). At this station, the model reproduces the tide well (as shown in previous sections). Oyster Landing is located southwest of the location of landfall, which explains the decrease in water-levels (setdown) caused by offshore directed wind after landfall of the TC. The second gauge, USGS SCHOR14330, located in a local creek and about 1 km from the shoreline, mainly shows the impact of rainfall runoff, albeit slightly influenced by tides. The model can reproduce both signals. Gauges 3, 4, and 6 show a similar pattern of tidal oscillation with a slight increase in mean water level with the hurricane's landfall. These temporarily placed gauges were only partially inundated, so they only provided a signal to compare the model with at higher water levels. Gauge 5 was in a salt marsh near the town of Sneads Berry, N.C., close to the New River estuary. The observations show a tidally influenced riverine behavior where the water level rises due to rainfall until several days after landfall, after which time the water level slowly falls again. The model underestimates the peak of the water level, possibly due to the underestimation of the TC precipitation boundary condition. Moreover, the model drains too quickly compared to observations, which could be caused by hydrological processes such as infiltration via the Curve Number method or underestimation with friction.

Fig. 7

Water level time series as observed (red) and modeled (blue) during Hurricane Florence (2018). The dashed black line is the moment of landfall. The location of the six gauges is shown on the map in Fig. 6 and stations are listed from west to east

High water marks are compared to the modeled water depth and water level in Fig. 8. A clear flooding pattern of the hinterland is both computed and observed (Fig. 8—panel a). The model underestimates the HWM (Fig. 8—panel b). Based on the division between coastal and riverine points, the underestimation is already present in the coastal points (30 cm); however, the bias reaches 91 cm for the riverine points. These biases affect the model skill, resulting in an MAE for all the points of 69 cm. A similar result is shown for the linear regression fit (green line), which has an offset that gets worse with higher water levels. It is hypothesized that this underestimation is driven by a difference in modeled (input) and actual precipitation and river discharge. This situation would explain why the time-series model skill is higher than the HWM skill.

Fig. 8

Validation of the maximum water depth and level for Hurricane Florence (2018). Panel a: maximum water depth with high water marks (HWMs; circles) compared to spatial color for the model. Panel b maximum water level for the same HWMs. Different colors represent either coastal (pink) or riverine (orange) points. ‘Linear’ is a least-squares linear fit on all the data points and shows the tendency for underestimation of the modeled HWM (negative bias) that increases with water level. Note the increasing dealignment between the green line and the dashed black line. Model estimates of extreme water levels have substantial scatter and bias which increases with water level. The latter explains the higher error for riverine versus coastal points. The coordinate system of this figure is WGS 84/UTM 17 N (EPSG 32617). © Microsoft Bing Maps

4.2 Projected flood hazards and impact

4.2.1 Flood hazards

While flood hazards are calculated on a high detail level (tens of meters) for over 1000 km of coastline, for clarity only a limited region around Charleston, S.C. is presented, as an example of the output (Fig. 9). Panels A and B show the water level (A) and Panel B the water depth, both (A and B) for a return period of 50 years and the SLR scenario of 100 cm. Panel C presents the range of flooding for progressively larger events for the SLR scenario of 100 cm with colors indicating a flooded grid cell and associated lowest return frequency. Finally, panel D presents the progressing effects of sea level for a 50-year storm. The color represents which SLR scenario, given a 50-year event (2% chance per year), results in flooding. Data for all return periods and SLR scenarios can be accessed via Barnard et al. (2023a, b).

Fig. 9

Example output for Charleston, S.C. Panel a Water level for a 50-year return period storm in combination with a 100 cm SLR. Panel b Water depth 50-year return period storm in combination with a. Panel c progressing flood extent for different storm frequencies for an SLR scenario of 100 cm. Panel D: Progressing flood extent for different SLR scenarios for a 50-year return period. The progressing flood extent (c and d) shows with which lowest storm frequency or sea level rise scenario the area gets flooded. The coordinate system of this figure is WGS 84 / UTM 17 N (EPSG 32617). © Microsoft Bing Maps

A regional analysis of flood-hazard area (minimum threshold water depth of 10 cm) over the entire U.S. Southeast is shown in Fig. 10. Only grid cells with a bed level above NAVD88 + 1 m are considered, to exclude low-lying flooding of natural systems. The area of interest is defined as the Low Elevation Coastal Zone above NAVD88 + 1 m. Flood hazards can occur during no-storm conditions (i.e., flooding during regular tides together with SLR, considered here as nuisance flooding, shown in panel A) or storm conditions with a specific return period (panel b). A relatively small area currently gets flooded under regular (non-storm) conditions, representing ~ 2000 km² or 1% of the area of interest. This flood hazard area increases significantly with SLR. The increases with SLR are initially small but increase at more than a linear rate. For example, an increase of the mean sea level from the current level to 50 cm increases the non-storm flood hazard by ~ 560 km²(+ 26%). The same mean sea level increase from 100 to 150 cm results in an increase of flooded areas by > 4200 km² (+ 750% increase). In other words, increasing sea levels inundate disproportionally more and more area. Storm hazards increase with the return period and rising sea level (Fig. 10—panel B). Yearly storm events without SLR (SLR of 0 m) flood around 13,000 km² or 6.2% of the study area and are projected to increase to 8.0 and 11.7% for 100 and 200 cm of SLR, respectively. The 100-year flood event, without SLR, floods almost 4.5 times as much area compared to the annual event. Moreover, Fig. 10b shows a well-described phenomenon in the scientific literature (e.g., Vitousek et al. 2017), where, for instance, a 20-year flood hazard at current sea level will, with 200 cm SLR, be the new 3-year event (i.e., decreased return period).

Fig. 10

Flood hazard for the no storm (daily; tide-only) condition (left panel a) and storms (right panel b). Color depicts different sea level scenarios of current sea level (red), 25 cm (blue), 50 cm (green), 100 cm (orange), 150 cm (yellow), 200 cm (brown) and 300 cm (pink). Note that A and B share the same y-axes. For absolute numbers use the left y-axis and for a relative of the total the right y-axis. Hazards increase with increasing SLR scenarios, which means that the same area is flooded with lower return periods and that the same storm return period gets more severe. The relative increase in surface area is larger for lower return periods than for higher return periods and increases more than linear for higher SLR scenarios

Analyzing the entire area of interest together allows for the quantification of flood impact in the number of people affected by both non-storm (i.e., nuisance flooding; Fig. 11a) and storm conditions (Fig. 11b). Model results indicate that on average 150,000 people are currently affected yearly by compound flooding in the coastal zone. People are impacted as a function of the hazard (water depth), exposure (where people are located), and vulnerability (depth-damage curve; see also Materials and Methods section). The number of affected people by flooding grows to 2,210,000 for a 100-year event (1% chance). That is an increase from 1 to 14% of the total population of the area of interest. A 100-year flood impact today will be a yearly impact with a 200 cm SLR. Moreover, the 20-year impact increases from 1.4 to 3.3 million people for 150 cm of SLR. This is an increase of 132% and is substantially higher than the increase in flood hazard for the same return period and SLR scenario (14%). Also, the number of people expected to be negatively affected by non-storm conditions (i.e., nuisance flooding) is likely to increase to almost 3 million for 300 cm of SLR.

Fig. 11

Flood impact in terms of people affected by the no storm condition (left panel a) and storms (right panel b). Note that a and b share the same y-axes. For absolute numbers use the left y-axis and for a relative of the total the right y-axis. Color depicts different sea level scenarios of current sea level (red), 25 cm (blue), 50 cm (green), 100 cm (orange), 150 cm (yellow), 200 cm (brown) and 300 cm (pink). Impacts increase with increasing SLR scenarios and have a large relative increase compared to hazards (Fig. 10)

Flood impacts per return period can be integrated over frequency to provide an estimate of annual risk. This process, which will be referenced throughout the rest of the paper as (absolute) flood risk, is used in generating the results shown in Figs. 12, 13, 14 and 15. The non-storm scenario is not included in the flood risk estimate. In particular, we integrated the affected people per storm frequency and computed the Expected Annual Affected People (EAAP; Giardino et al. 2018). Figure 12 presents the EAAP as a function of SLR for the 14 most populous counties in the area of interest. The most considerable contribution of the total compound flood risk is for the three southeast Florida counties of Miami-Dade, Broward, and Palm Beach Counties (i.e., the greater Miami metropolitan area), which comprise 62–72% of the total EAAP.

Fig. 12

Flood risk in Expected Annual Affected People (EAAP) as a function of sea-level-rise (SLR) for absolute numbers (left y-axis) and percentage of total (right y-axis). Color depicts the top affected 14 counties, including the 15th color for all the other counties (gray). EAAP increases strongly with SLR, and Florida’s Miami-Dade, Broward, and Palm Beach Counties account in absolute relative terms for the largest EAAP

Fig. 13

Relative flood risk as a function of population size for an SLR projection of 1 m color-coded in Expected Annual Affected People (EAAP). The bar shows the change from the current sea level to 1 m (lower value) and the increase from 1 to 2 m. Several smaller, less populous counties have the highest relative risk in the area

Fig. 14

Color-coded relative flood risk per county as a function of sea-level-rise (SLR). Different panels (a–f) represent different SLR scenarios (no SLR to 300 cm). 25 cm SLR results are not shown, for conciseness of the Figure. Relative flood risk is projected to increase with SLR. The coordinate system of this figure is WGS 84/UTM 17 N (EPSG 32617). © Microsoft Bing Maps

Fig. 15

The division TC/ETC (black line) and contribution of TC-only (red) versus ETC-only (green) or either (blue) for compound flooding. Panel a. Flood hazard as a function of return period for SLR scenario of 100 cm. Panel b. Flood impact as a function of return period for SLR scenario of 100 cm. Panel C. Flood risk in EAAP for different SLR scenarios. The contribution of TCs increases with the return period for both hazards and impacts but decreases for flood risk as a function of SLR

Similar to flood hazards, there is a stronger than linear increase in the impact of flood risk as a function of SLR. The first 50 cm SLR results in an increase in EAAP from 480,000 to 700,000 people. That is an increase of 220,000 people (+ 45%). SLR scenarios of 100, 150, and 200 cm result in increases of 360,000, 530,000, and 840,000 EAAP (+ 119, + 240, and + 413% or fourfold increase).

Absolute flood risk or EAAP strongly follows exposure; thus, densely populated areas generally have the most significant flood risk in this analysis. Relative flood risk can be computed by dividing the EAAP by the county's total population (Fig. 13). Vulnerable counties such as Miami-Dade and Broward Counties are both populous and have a high relative flood risk. However, a county like Poquoson in Virginia does not show up in the previous (absolute) analysis but does in terms of relative risk because a high percentage of the population would be exposed to flooding (Fig. 13). In a situation without SLR, these communities can be negatively affected during rare but severe storms (e.g., 100-year events). For the example of Poquoson County, with 1.6 m of SLR, what is currently a 100-year flood impact event will become the new yearly event with dire consequences regarding relative flood risk.

Relative flood risk provides a framework to identify when significant proportions of counties will start to face negative consequences because of SLR. Figure 14 shows the relative flood risk per county for the different SLR scenarios analyzed (25 cm SLR results are not shown, for conciseness of the figure). Higher sea levels result in more relative risk. In particular, only one county (Hyde County) has a relative compound flood risk greater than 10% for the current sea level. This value is expected to increase to 12 counties for an SLR of 100 cm and 41 for 300 cm for a total of 94 counties analyzed. Similarly, no county has a 20% or higher flood risk for the current sea level (see also Fig. 13). With 100 cm of SLR, four counties (Poquoson, Tyrrell, Monroe, Hyde) will have this level of relative flood risk, and this increases to 29 counties with 300 cm of SLR. Note a low risk does not mean that a county cannot be impacted by floods. It means there is a lower likelihood that a large percentage of the county's population is negatively impacted by flooding.

4.2.2 Tropical versus extratropical

The relative portion of TCs, ETCs, or either physical driver can be determined by the differences between the combined results and the TC- or ETC-only results for flood hazards (Fig. 15—panel a; flooded area), flood impact (Fig. 15—b; impacted people), and flood risk (Fig. 15—c; EAAP). For example, the combined flood hazard zone of the whole area with 100 cm of SLR and an annual return period event is 16,489 km². Only considering TCs results in a hazard area of 7360 km² and ETCs alone gives 9201 km². Combining the TC-only and ETC-only areas gives an area larger than the combined flood hazard zone by 72 km², indicating the portion of the combined flood hazard zone that can be flooded by either driver (meaning here TC or ETC: 0.4%). Of the combined flood hazard zone, the portion that is due to ETCs-only is thus 55.4% (9129 km²), and the portion due to TCs only is 44.2% (7288 km²). Therefore, we estimate that ETCs dominate the annual flood hazards compared to TCs (division is 55.6% ETC and 44.4% TCs). The division between TCs and ETCs are computed by dividing the area flooded uniquely by ETCs compared to the total area that is uniquely flooded by ETCs and TCs.

Flood hazards (Fig. 15—panel a), regardless of the driver, increase considerably as a function of the return period from ~ 16,500 km² for the annual return period (8% area) to ~ 60,000 km² (29% area) for the 100-year event. For higher return periods, TCs drive an increasingly larger share of the division. For example, a 2-year event (50% annual probability) is 47.2% driven uniquely by TCs versus 24.5% uniquely by ETC and 28.3% by either driver. This percentage of uniquely flooded areas results in a breakdown of 66% for TCs and 34% for ETCs. This breakdown increases to 96% for TCs and 4% for ETCs for the 100-year event (1% annual probability). The increasing dominance of the third category, “either physical driver” (Fig. 15—blue colors), is due to the binary nature of flood hazards (i.e., wet or dry). In other words, low-lying areas will get flooded for the most extreme events regardless of whether the driving force is a TC or ETC, and in our analysis, we cannot differentiate between the two. The analysis only reveals if areas get flooded uniquely by TCs or ETCs. We apply the ratio to establish the division between ETC and TC. For a visual impression of this analysis, see in the Appendix a detailed breakdown for Charleston, S.C., flooding with annual frequency, 10-year, and 100-year (Fig. 18).

A similar trend emerges for the flood impacts (Fig. 15—panel b). For an SLR scenario of 100 cm, it is estimated that ~ 530,500 people (3.4%) are negatively affected annually by flooding. This impact increases to almost 3,743,000 people (or 24.3% of the population) for the 100-year event. The annual impact is about 22.7% uniquely driven by TCs, 42.8% by ETCs, and 34.5% by either driver. In other words, ETCs result in almost twice the amount of negative impact with a yearly frequency based on the division estimate (division TC/ETC 35–65%). However, for the 100-year event, 58.3% is driven by TCs versus 2.0% by ETCs and 39.8% by either driver (i.e., 30 × more TC-driven impact). The lack of a linear correlation between hazards and impacts is noteworthy.

Regarding flood risk (Fig. 15—panel c), TCs generally dominate over ETCs. For the current sea level, 52.2% of the flood risk is uniquely related to TCs. In comparison, 24.1% is related to ETCs and 23.7% to either driver. In other words, TC-induced flood risk is about twice that of ETCs based on the division TC/ETC. This distribution of risk decreases to 17.3% TCs, 14.0% ETCs, and 68.7% for either driver for the 300 cm SLR scenario. Higher SLR scenarios result in more and more flood risk regardless of the ETCs or TCs. The contribution of TCs to compound flood risk decreases from 70 to 55% from no SLR to 300 cm (or 30 and 45% ETCs).

5 Discussion

The validation shows that the presented workflow and the developed five SFINCS domains can skillfully reproduce tidal (median MAE 8.3 cm; Fig. 3) and coastal extreme water levels (median MAE 11.9 cm; Fig. 5). It is hypothesized that this model skill has been achieved by (1) nesting the overland flow domains into large-scale hydrodynamic and wave models that provide statistically corrected boundary conditions and (2) including relevant bathymetry features. Computational efficiency was prioritized to allow for the deterministic computation of flood hazards and impacts of thousands of events. Limited computational resources did constrain the utilized approach to a relatively coarse model resolution of 200 × 200 m in combination with subgrid lookup tables that resolve fine-scale flood features at the resolution of the 1-m Digital Elevation Model. Similar to other approaches (e.g., Volp et al. 2013; Sehili et al. 2014), the subgrid approach substantially reduced computational cost without significant accuracy loss. The underestimation of tides at several stations is likely driven by incorrect friction, as derived from the landcover map, and not a limitation in the subgrid method itself. The accuracy of the boundary conditions could also play a role (see Parker et al. 2023). Moreover, as part of sensitivity testing, it was found that model skill versus computational cost seems optimal at a model resolution of 200 × 200 m. More refined model simulations did minimally increase model skill but with a considerable increase in computational cost. The SFINCS domains were also not calibrated and instead ran with default parameters. Calibration of, for example, bottom friction could further increase model skill. The near-continuous computations allowed for the usage of empirical extreme value statistics on a cell-by-cell basis. This method eliminated the need to fit statistical distributions that could potentially yield incorrect results when limited data points are presented. The latter mainly occurs for overland compound flooding, where only several (rare) storms result in flooding.

The version of SFINCS applied in this manuscript does not include a stationary wave solver, infragravity waves, sediment transport, or morphology. Wave setup was used at the offshore boundary based on the empirical formula of Stockdon et al. (2006) and presented in Parker et al. (2023). Still, the accuracy of this correction was not able to be assessed. A more in-depth validation at a case study site with good observational data might provide insight. The lack of infragravity waves, sediment transport, and morphological change is a limitation since breaches and overtopping are commonly reported during extreme events (e.g., during Hurricane Florence; Biesecker and Kastanis, 2018 or more recently during Ian and Nicole in the 2022 season). This restriction would, most likely, result in underestimating the computed flood hazards and impacts. In this paper, we have assessed flood hazards and impacts given SLR scenarios but without taking into account morphological and societal changes such as population dynamics and construction of flood risk management features. The natural system will respond given changes in climate (Antolínez et al. 2018), for example, shorelines are projected to undergo a large recession (e.g., Bruun 1954; Ranasinghe et al. 2012). Moreover, the U.S. Southeast is projected to continue its economic growth (Hauer 2019), but any local mitigation and adaptation measures taken will be beholden to the question of how flood hazards and risks develop in the future. These changes are not considered in this paper. Additionally, no validation of the impact computation was performed. Lastly, Lockwood et al. (2022) showed that sea level rise and changes in the meteorological conditions correlate; however, in this paper, they were assumed independent to allow for the computation of several sea level rise scenarios under one future projected climate.

Hydrological processes were resolved in this paper by (1) applying the NWM for riverine inflow into the SFINCS domains and (2) computing rainfall run-off by including rainfall and estimating infiltration with the Curve Number method. Validation for Hurricane Florence did show clear observed and modeled inland flooding, including raised water levels in the analyzed time series of observations and models due to precipitation and riverine flow (Fig. 8). However, the error in reproducing the HWM with an MAE of 63 cm is much higher than the other errors presented in this paper, but they are in the same order as other Hurricane Florence validations (e.g., Ye et al. 2021 reported an average MAE of 73 cm). In addition, dynamic processes such as groundwater and (managed) urban drainage systems are not included, which could substantially influence results locally. For example, South Florida is known for its permeable karst substrate in combination with regulated channels, which affects the risk of flooding (Czajkowski et al. 2018; Sukop et al. 2018). Moreover, it is unclear how the assumption of 50% saturation in the Curve Number at the start of each simulation has influenced the results. Sensitivity testing showed that the soil saturation assumption influences results for milder more-frequent storms. Nonetheless, the impact of more substantial events, such as Hurricane Florence, was restricted due to the considerable overall precipitation relative to the infiltration capacity (see for example Leijnse et al. 2023 and sensitivity testing in Appendix 10.2). Whereas the 50% saturation value was held constant for the sea level rise scenarios, one might expect increased soil saturation through changes in precipitation patterns and rising temperatures associated with a warming climate. Continuous, deterministic, simulations could overcome this limitation but were deemed computationally too expensive for this large-scale study. Arguably, the absolute amount of precipitation is a larger source of uncertainty relative to the runoff concepts and assumptions applied, especially when moving toward the climate projections. Besides these limitations, the SFINCS-based estimate of flood hazards and impacts across the region provides valuable information to coastal managers and policymakers on an unprecedented scale and resolution. In particular, we hypothesize that reported hazards, impacts, and risk values can provide relative insights due to the physics-based derivation despite model shortcomings.

The simulation and detailed analysis of both TCs and ETCs allowed quantifying the contribution of tropical and extratropical events. Similar to Dullaart et al. (2021), this paper also found that it is vital to include TCs, especially for infrequent events. Here, we estimate a dominance in TC risk across the study area to be around 55–68%, which is in the same order of magnitude as Dullaart et al. (2021), who provided estimates for storm surge across the globe or Booth et al. (2016) who provided its estimate based observational water level data. A limitation of our study is the record length of 31 years for ETCs and, therefore, implicitly assuming dominance of TCs for higher return periods. However, in this study, we do see that TCs dominate the signal earlier in the frequency range for the Southeast Atlantic Coast. For other areas (e.g., West Coast or New England states), this dominance of TCs is most likely not the case, and another method needs to be explored.

In this study, we directly applied an ensemble of three high-resolution CMIP6 models to determine ETC-driven flooding for the projected climate. This approach was necessitated by the unavailability of historical high-resolution CMIP6 data at the time of our study, which would have allowed for bias correction or an assessment of percent change between the historical and future periods. However, GCMs are known to have biases, which propagate and can thus influence the simulations (e.g., Xu et al. 2021). On the other hand, high-resolution CMIP6 models (~ 25 km) are starting to be sufficient to resolve the relevant meteorological features for large-scale flood assessments (e.g., Roberts et al. 2020). For example, a recent study by Muis et al. (2023) showed a positive bias of ~ 10% in computed storm surge levels corresponding to a 10-year return period between a HighResMIP ensemble and ERA5 reanalysis along the eastern North Atlantic U.S. coast which gives confidence these products start to resolve relevant features flood assessments. Moreover, taking an ensemble, as was done in this study, is expected to perform better than individual members (Tebaldi and Knutti 2007), and preserves event consistency among meteorological forcings for projected storm events (wind, pressure, and rain). We do acknowledge the limitation of bias and are exploring the possibility of incorporating historical and projected scenarios based on the same CMIP6 models to overcome possible biases in meteorological forcing. Other methods include working with historical climate forcing such as the ERA5 reanalysis to overcome these potential biases.

6 Conclusions

Using well-calibrated numerical models, it is shown that predicting both tropical and extratropical cyclones is vital for accurately assessing coastal hazards and impacts. Extratropical cyclones are mainly responsible for frequent flooding events. In particular, we find that for the current sea level, extratropical cyclones contribute to half of the flooded area. These events affect almost twice the amount of people compared to tropical cyclones with a yearly frequency. However, tropical cyclones drive the majority of the infrequent flood hazards. For example, for the 100-year event, tropical cyclones contribute ~ 96% of the flooded area and likely affect 30 times the number of people. Additionally, we find that tropical cyclones contribute to more than half of the total coastal compound flood risk. The relative importance of tropical cyclones to compound flood risk does decrease with sea level rise.

The relative impact of flood hazards from annual storm events is limited to 6.3% of low-lying areas of the U.S. Southeast Atlantic coast at the current sea level. In comparison, 100-year events flood 27.2% of the considered area. With sea-level rise (SLR), flooding increases significantly. In particular, annual hazards increase from 6.3% today to 8.0 and 11.7% with 100 and 200 cm, respectively, of sea level rise. This change makes rare events more severe and decreases the return period for current extreme events. For example, a 100-year flood impact today will be a yearly impact with a 200 cm SLR. Also, flood impacts are projected to have a larger relative increase compared to flood hazards for the same return period and SLR scenario. Flood risk is expected to grow non-linearly from roughly 3.1% (0.5 million people) today to 6.9 and 16.1% (1.1 and 2.6 million people) for 100 and 200 cm, respectively, of sea level rise. Impacts are mainly driven by exposure in the most populous counties in the area (Miami-Dade, Broward, and Palm Beach County together comprise 62–70% of the total risk in the area). However, several smaller, less populous counties have the highest relative risk of the study area compared to the high absolute flood risk for the populated southeast Florida region. This contrast highlights the importance of using relative risk, calculated as the ratio of people affected to the total population of a county, as a critical metric for informing policy decisions.

While our methodology is targeted at coastal flooding, precipitation and hydrology are included to capture coastal compound flooding. In particular, the model framework developed in this study can skillfully reproduce coastal water levels. Model errors in these areas are driven by errors in tide (median mean-absolute-error, MAE, 8.3 cm) and storms (median MAE 11.9 cm). As demonstrated in the validation of Hurricane Florence, the model error increased farther inland due to less well-resolved hydrological processes such as rainfall, infiltration, and riverine flow.

Appendix

1.1 Updating synthetic tropical cyclone probabilities to reflect climate change

We conducted a comparative analysis of tropical cyclone (TC) characteristics in a CMIP6 multi-model ensemble for historical (1980–2014) and future (2016–2050) periods to assess the need for modifying probabilities in the USACE CHS synthetic TC dataset. For the TC comparisons between the historical and future model ensembles, we examined TC storm parameters (frequency, location, heading, forward speed, radius of maximum winds, and intensity based on central sea level pressure deficit) at a 600 km radius around USACE shoreline locations. In particular, we utilized eight atmosphere–ocean coupled CMIP6 models and the tracks of TCs using the TRACKS method (Roberts 2019b). Our analysis revealed a change in the sea level pressure deficit for the most intense storms within our region. The other TC parameters did not change. The strongest 2% of storms in the 8-model ensemble showed increased storm strength from northern Florida northward, indicating more frequent intense TCs in this area. These alterations were incorporated into the USACE CHS synthetic TC dataset, leading to recalculated probabilities that reflect this intensification.

1.2 Sensitivity tests for saturation percentage

In this study, we assessed the sensitivity of the Curve Number method to the assumption of 50% saturation focused on the computed flood extents for Hurricane Florence (Sect. 4.1.3). A series of tests were conducted using saturation percentages that varied from 0% (indicative of full saturation, yielding a S_e value of 0) to 100% (representing complete insaturation, leading to a S_e value of S_max) in 25% increments. Throughout the study, we applied a 50% value (see Sect. 3.4.2). The sensitivity analysis of this parameter for Hurricane Florence revealed a maximum variation in flood extent ranging from + 2.6% to − 0.3% (Fig. 16—panel b). Notably, the most pronounced disparities were observed in the range of 0–50% saturation, indicating the fully saturated spectrum of the parameter. Furthermore, these differences were predominantly evident further inland and further away from the hurricane's landfall (Fig. 16—panel a). We hypothesize that such variations can be attributed to the substantial cumulative rainfall concentrated within the storm's eye, which surpasses infiltration capacity irrespective of the initial saturation percentage. Additionally, further inland, the primary flooding source tends to be rainfall-induced, in contrast to coastal areas where tidal surges predominantly contribute to flooding events (Fig. 16).

Fig. 16

Senstivity testing on the saturation percentages on the flood extent computed for Hurricane Florence (2018). Panel A: overview figure for spatial difference in flood extent (colors), domains (gay) and the track of Hurricane Florence (black dashed). Panel B: Difference in relative flood extent area relative to a 50% saturation percentage. The best track is based on International Best Track Archive for Climate Stewardship (IBTrACS; Knapp et al. 2010).The coordinate system of this figure is WGS 84/UTM 17 N (EPSG 32617)

Fig. 17

Extreme water level return levels and periods for TC-only simulation (red), ETC-only (green) and the combined results (black dashed lines). The return values presented throughout this study are the yearly, 2-, 5-, 10-, 20-, 50- and 100-year estimates and are shown as black dots. The dominance of ETC versus TC varies per station and return period

Fig. 18

Breakdown of flooding for Charleston, South Carolina, for annual, 10- and 100-year flooding. Color-coded is the source of the flooding. Most of the grid cells are flooded by both TC & ETC (either driver; blue color). Flooding with a yearly frequency is driven more by ETC-only drivers (green) while 100-year events are driven more by TC-only (red)

1.3 List of acronyms used

Acrnyom	Meaning
CHS	Coastal hazards system
CMIP6	Coupled model intercomparison project—Phase 6
CoNED	Coastal National Elevation Database
CoSMoS	Coastal storm modeling system
CUDEM	Continuously updated digital elevation model
Delft-FIAT	Flood impact assessment tool
EAAP	Expected annual affected people
ETC	Extratropical cyclone
GCM	Global climate model
GHSL	Global human settlement layer
GMSL	Global mean sea level
GTSM	Global Tide and Surge Model
GUF	Global urban footprint
HSG	Hydrologic soil group
HydroMT	Hydro model tools
IPET	Interagency performance evaluation task force rainfall analysis
JPM	Joint probability method
MAE	Mean-absolute-error
MSL	Mmean sea level
NLDAS	North American land data assimilation system
NOAA	National Oceanic and Atmospheric Administration
NTR	Non-tidal residual
NWM	National water model
RMSE	Root-mean-square-error
RP	Return period
SCS	Soil conservation service
SFINCS	Super-Fast INundation of Coast
SLR	Sea level rise
SWMM	Storm water management model
TC	Tropical cyclone
USACE	U.S. Army Corps of Engineers
USGS	U.S. Geological Survey

1.4 Additional figures and tables

See Tables 2 amd 3, Figs. 17 and 18.

Table 2 Lookup table for conversion of National Land Cover Database Land to roughness values using Manning's coefficients

Table 3 Overview of tidal skill scores for 24 NOAA and 43 XTIDE locations (68 in total)