1 Introduction

Water infiltration into soil is one of the main triggering factors of slope instability. It may result in water content increase, matric suction reduction and, consequently, shear strength decrease, which may induce slope failure (Anderson and Sitar 1995; Alonso et al. 1995; Li et al. 2005a; Lu et al. 2010). The infiltration into the soil is mostly affected by the soil hydraulic characteristics (Ng and Shi 1998; Rahimi et al. 2010; Shuin et al. 2012; Hou et al. 2021) and the permeability of soil–bedrock interface, if present (Greco et al. 2017). The evaporation of water from the ground surface is another process that affects water infiltration, increasing soil suction. When modelling the hydrological processes of unsaturated slopes, however, evaporation is often neglected or rarely considered, to avoid unpredictability in the transient seepage analysis (Ng et al. 2008; Li et al. 2005a; Fredlund et al. 2012) and, in slope stability problems variables other than rainfall are seldom included. In addition, when vegetation is present, the transpiration due to roots uptake must be included into the evapotranspiration flux. Experimental studies conducted on the hydraulic response of pyroclastic ashy soils on evapotranspiration and rainfall infiltration (Rianna et al. 2014; Pagano et al. 2014) outlined that neglecting vegetation can lead to incorrect estimation of the pore-water pressure regime over long time periods. In fact, some authors started to evaluate hydrological responses of these soils by also considering the presence of vegetation (Chirico et al. 2013; Comegna et al. 2013; McGuire et al. 2016; Pagano et al. 2019; Capobianco et al. 2020), which may play an important role in stabilizing slopes. Prone-to-failure slopes, especially if located in vulnerable areas, need proper monitoring. Intelligent solutions for landslide mitigation (Capobianco et al. 2022), monitoring and early warning can help to safeguard society and infrastructure from climate-induced geohazards.

This study proposes a four-phase approach to set up a local landslide early warning system (Lo-LEWS, Piciullo et al. 2018) at slope scale with the Internet of Things (IoT). This paper focuses on the first two phases of the proposed approach, i.e. real-time monitoring and modelling of the slope behaviour, with some preliminary analyses on the conditions leading to failure, specifically, on the most relevant hydrological variables that influence the factor of safety (FS).

The methodology proposed in this study is applied to a monitored unsaturated steep slope in Norway that is threating a double railway line in Eidsvoll municipality. In the literature, there are several contributions on the response of partially saturated soils in natural slopes to rainfall. Examples can be found for volcanic soils in Italy (Casagli et al. 2006; Cascini et al. 2010De Vita et al. 2012), residual soils in Hong Kong and Singapore (Ng and Pang 2000; Li et al. 2005b; Rahardjo et al. 2005; Rahimi et al. 2011), silty sand and silty clay in India (Sarma et al. 2015), flysch materials in Croatia (Peranić et al. 2019), and in bluffs in Washington area, USA (Godt and McKenna 2008). However, few studies on monitored partially saturated slopes in Norway are available in the literature (Krzeminska et al. 2019; Capobianco et al. 2021; Oguz et al. 2022). The slope under investigation has been monitored since 2016 and has been included as a pilot study within the Centre for Research-based Innovation (CRI) Klima2050 (http://www.klima2050.no/). The importance of considering climate drivers and vegetations has been defined comparing the results of different simulations with in situ measurements using Taylor diagrams. Then, the best simulation has been considered for a sensitivity analysis of the saturated horizontal hydraulic conductivity (kx) and of the ratio between vertical and horizontal hydraulic conductivity (ky/kx). Anisotropy has been taken into account since considering a slope made up of homogeneous material has a strong limitation on modelling real case studies (Yeh and Tsai 2018). In addition, the effectiveness of the best hydrological model was tested for different time spans: 6-month, 1 year, 1.25-year. A stability analysis was carried out to assess the variation of the FS with time. Finally, a machine learning random forest algorithm has been applied to predict the FS from the monitored hydrological variables. The importance of every variable in predicting the FS has been also defined. In the literature, machine learning algorithms are often used to predict landslides at a regional scale (Liu et al. 2020; Ng et al. 2021) and seldom at a slope scale.

So far, no deformations have been recorded at the slope location. However, as landslides are likely to become more frequent with climate change (Gariano and Guzzetti 2016), and future climate in the Nordic region is forecasted to be wetter and more erratic (Hanssen-Bauer et al. 2017), the need and use of a IoT-based monitoring and early warning for situational awareness of slope stability are becoming urgent (Oguz et al. 2022). The possibility to have all the monitored data collected by means of a data logger and stored in real time into a cloud system, which can directly feed the machine learning algorithms to forecast in advance a possible instability and to warn the infrastructure owner, is the final aim of this pilot study in Eidsvoll, Norway.

2 Framework for a IoT-based stability analysis as local landslide early warning system (Lo-LEWS)

Rainfall-induced landslide is usually triggered by a combination of wet antecedent conditions followed by one or more days of relatively intense rainfall (Baum et al. 2005). The transient reduction of suction during infiltration and, thus, increment of soil water content, can be used to identify periods when moisture conditions and rainfall concur to trigger landslides in unsaturated slopes (Godt et al. 2009). Identifying the conditions that may lead to the potential failure of a slope can help defining threshold values for landslide early warning purposes (Piciullo et al. 2020).

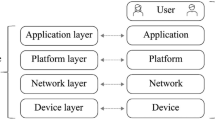
In this regard, Fig. 1 proposes a framework for the definition of a IoT-based slope stability analysis and Lo-LEWS (Piciullo et al. 2018). The framework is based on the following four phases: monitoring, modelling, forecasting and warning. The monitoring phase is necessary to provide real-time or near-real-time input data to both the modelling and forecasting phases. The monitored data, specifically hydrological (i.e., pore water pressure regime, soil water content) and climate data (i.e. daily and hourly rainfall, snowmelt, air temperature, relative humidity, wind speed), are used as input parameters for the hydrological modelling together with soil properties. These latter are usually obtained by laboratory or field tests.

Fig. 1
figure 1

Conceptualization of the phases for a IoT-based slope stability analysis and warning at a slope scale

Full size image

In the hydrological modelling, the climate data can be input as water flux boundary conditions. The water flux can be either extremely simplified, i.e., an entering water flux simulating the rainfall infiltration, or it can include additional factors, such as plant evapotranspiration, interception, and runoff. When evapotranspiration is included, additional climate variables are needed, together with vegetation properties, as discussed more in detail in Sect. 4.5. The calibration of the hydrological model consists in fine-tuning the initial hydraulic conditions to fit as much as possible the measured data. The validation consists in comparing predicted (by the model) and observed (by in situ monitoring) hydrological data to define the best simulation that fits the in situ conditions, for a given period of analysis.

Then, the best simulation obtained with the modelling is used for slope stability analysis. The slope stability modelling results are used as dataset, together with the monitored variable and predicted climate variables, for training machine learning algorithms. In the forecasting phase, forecasted values of precipitation, temperature, snowmelting can be used as input data for trained machine learning algorithms, with the aim of predicting time frames where slope instabilities are likely to occur. When predefined thresholds are exceeded or FS values less than 1 are computed, warning protocols and emergency plans need to be activated.

3 Monitoring of an unsaturated slope in Norway

3.1 Case study and hydrological monitoring instruments

The study area is located in the municipality of Eidsvoll, Norway (60°19′23.376", 11°14′44.646"). The slope under analysis is 25–30 m high, with an inclination of about 45° in the upper part. As part of an InterCity railway project in Eastern Norway, an additional railway track is being constructed next to an already existing railway line at its toe. So far, the slope has not shown any deformations; however, it represents a threat to both the existing and the proposed new railway lines. In addition, its location is right at the eastern side of a cultural heritage area, with an old church from the twelfth century and its graveyard, which makes impossible the realization of physical slope stability measures on top of the slope. For the above-described reasons, the slope has been instrumented with several sensors.

Volumetric water content (VWC) and pore-water pressure (PWP) sensors were installed in late spring/early summer of 2016 to monitor the hydrological conditions. Delta-T SM150T has been used as sensor type for measuring both VWC and temperature with an accuracy, respectively, of ± 3% and ± 0.5 °C. The sensors use an electromagnetic field to measure the dielectric permittivity of the surrounding medium. The SM150T sensor is engineered to withstand long-term burial. Two general soil calibrations were available: organic and mineral. The calibration for mineral soils has been used since it can characterize predominantly sand, silt and clay. The sensors are connected to the GP2 data logger to provide long-term moisture and temperature data.

Geotech PVT electronic piezometer with logging memory is used to measure positive and negative PWP. It operates without the need of additional battery, logging box or any kind of permanently installed external equipment—just two wires are visible on the surface. The piezometer has a high-precision laser-trimmed ceramic sensor, and it is suitable for long-term installations. The output from the piezometer is digital and is not affected by cable length. At each measurement, the user gets the serial number of the gauge, the pore pressure, temperature, date and time. Currently, the piezometers need to be read manually.

The slope has been schematized with the following layering: a sand/silt layer of circa 6 m, a smaller layer of clayey silt material (about 3 m thick), a firm marine clay layer to large depths (Fig. 2).

Fig. 2
figure 2

a Cross section of the studied slope, with soil stratigraphy and location of the sensors and b a picture of the vegetation cover along the slope

Full size image

In the top part of the sand/silt layer, Delta-T SM150T sensors are installed for the combined measurement of VWC and ground temperature. The installation depths are, respectively, 0.1-, 0.5-, 1-, 2-, 4-and 6-m. In addition, Geotech electronic piezometers have been installed, from the top of the slope (circa 171 m a.s.l.), respectively, at 6-, 9-, 15- and 23-m depths. The two deepest piezometers (15 and 23 m) are located within the clay layer (Fig. 2). The piezometer sensor at 9-m depth is in a transition zone between silt and clay layers, while the uppermost piezometer, 6-m depth, is installed in the silt layer. Two more piezometers are installed at the toe of the slope (circa 144 m a.s.l.) at 5- and 12-m depths.

Figure 2 shows the position of the sensors in a slope cross section. The VWC and PWP sensors are monitored in real time with 1-h frequency. Readings are collected online through Deltalink-cloud software (see Sect. 3.2 for more details).

3.2 IoT-based monitoring system

The data acquisition system used at the Eidsvoll site is based on the Delta-T GP2 Data Logger and Delta-T 3G-DLC-BX1/SP solar-powered 3G/2G Modem Gateway box. The GP2 is a versatile and rugged 12-channel data logger, ready-made for outdoor installation, and can log most sensor types and accepts voltage, resistance, current, potentiometer, counter, frequency, and digital state inputs. The GP2’s analog inputs can be fully customized. Each channel can have its own input type and recording parameters. DeltaLINK software gives the user control over reading frequency, thresholds, and units and provides statistical recording options for average, minimum, maximum, standard deviation and more. At the Eidsvoll site, the SDI-12 protocol is used to interface the DeltaLINK with sensors, which is a standard communication protocol used in a wide range of environmental, agricultural and industrial applications. The data logger includes 4 MB of flash memory to enable storage of up to 2.5 million readings.

At the case site, the GP2 data logger and the modem gateway are enclosed in separate cabinets, both sharing power supply from the Delta-T 2G-DLC-BX1-SP. Initially the GP2 only used internal batteries as its power source, but to reduce the need for frequent visits, reduced hours for replacing batteries, to reduce the chance for losing data, the system was then upgraded with the Delta-T 3G-DLC-BX1/SP solar-powered 3G/2G Modem Gateway solution. This consists of a FTX0009 2G modem gateway, 30-W solar panel, solar regulator, and a 10-Ah lead acid battery. Due to problems with power outages, as a consequence of low-light conditions during the Norwegian winter months, the included solar power battery was upgraded to a 12-V 200Ah AGM solar power battery and was installed in a third separate container.

Currently, the data logger is configured to measure and store data from the sensors every hour and transmit this data to the Delta-T Cloud API every 6 h. The data acquisition timing and the transmission frequency can be increased to up to 5 min. The complete updated dataset is available both graphically and for downloading from the Delta-T Cloud service.

3.3 Monitoring data

PWP and VWC monitoring started in May 2016, and the data are shown in Fig. 3a, b. The soil temperature is also monitored at each depth (Fig. 3c). The measurements were processed to remove unreliable values (i.e., VWC < 0%), due to either maintenance or contact problems. About the piezometers installed from the top of the slope, although there is a lack of PWP data at 6-m depth, between February 2017 and March 2019 (Fig. 3a), it is possible to observe that the PWP values at 9-, 15- and 23-m depths, remained almost constant, after the first month of stabilization due to the installation. The PWP measurements indicate that the water table is circa 7 m deep from the surface, with negative values of about -10 kPa measured at 6-m depth. From October 2019, a PWP increase is observed, until a peak of about 6 kPa is reached around April, after which the PWP decreases again with the beginning of the summer season. The fluctuation of the PWP from 10 to 6 kPa indicates that the water table changes seasonally from 7 m depth in spring–summer to 5.5–6 m in fall–winter. The two piezometers installed from the toe of the slope at 5- and 12-m depths have monitored data only until September 2017, because they were removed due construction works related to the railway line. They showed a water table located at circa 2 m depth from the toe of slope.

Fig. 3
figure 3

a Pore-water pressures monitored at four depths from the top of the slope from May 2016 to August 2020, and at two depths from the top from May 2016 to September 2017; b VWC monitoring data at six depths of the instrumented slope from May 2016 until August 2020 (the grey bars represent the periods with data unavailability, due to either maintenance or contact problems.); c Monitored temperature at six depths of the instrumented slope and rainfall-snowmelt data from senorge.no

Full size image

The VWC is influenced by both freezing and snow melting periods. Freezing periods can be easily detected by the soil temperature reaching values below 0 °C, while snow melting is typical occurring in spring. Temperature and precipitation values are shown in Fig. 3c, where precipitation accounts for both daily rainfall and daily snowmelt (see Sect. 4.5 for details). Drops in logged VWC due to pore water transformed into ice were observed at shallow depths (0.1 m and 0.5 m) each year at the beginning of the winter. It is worth mentioning that the low VWC values recorded in periods with temperature below zero do not realistically represent the in situ soil VWC. At the beginning of the spring, with exception of 2019–2020, peaks of VWC due to snowmelt were recorded at shallow depths (Fig. 3b). Smaller peaks can be observed also at 1-m depth, where the water infiltration, due to snowmelt, arrives with a delay, providing a small shift of the VWC trend. VWC values at larger depths show a rather constant behaviour, except at 6-m depth, where an initial drop was recorded at the beginning of the monitored period and an increase around December 2019.

4 Hydrological and slope stability modelling

4.1 Numerical modelling

The commercial software GeoStudio (GEO-SLOPE International, Ltd. 2012a; b) was used to perform the hydrological modelling and the slope stability analysis. Two modules of the software were used, namely SEEP/W (analysis of unsaturated groundwater flow) and SLOPE/W (slope stability computation), to define a reliable model able to represent the in situ conditions. The 2D finite element module SEEP/W was used to analyse the transient seepage and obtain PWP and VWC variations in the soil. The governing equation in SEEP/W is Richards’ equation (Richards 1931), which describes two-dimensional flow in unsaturated soils, as shown in Eq. (1)

$$\frac{\partial }{\partial x}\left({k}_{x}\frac{\partial h}{\partial x}\right)+\frac{\partial }{\partial y}\left({k}_{y}\frac{\partial h}{\partial y}\right)+Q=\frac{\partial \theta }{\partial t}$$
(1)

where x and y are spatial coordinates; θ is the volumetric water content; h is the hydraulic head; kx and ky are a function of θ and represent the hydraulic conductivities in the x and y directions, respectively; Q is water flux; and t is time.

The SEEP/W transient analysis was saved every 24 h and used as input in the form of a pore-water pressure distribution for the slope stability analysis. The SLOPE/W module was used to perform slope stability analysis using the limit equilibrium method (LEM) and calculation of the safety factor assuming the rotational failure model proposed by Morgenstern and Price (1965). Examples of numerical modelling coupling transient seepage and slope stability analyses are available in the literature, to assess rainfall infiltration effects on riverbank stability (Duong et al. 2019; Capobianco et al. 2021) and on a residual soil (Heyerdahl et al. 2018; Peranić et al. 2019).

4.2 Calibration and validation procedures of the volumetric water content (VWC)

The analyses with SEEP/W were carried out starting from June 2019. At the beginning of the selected period of analysis, the VWC in the soil was inevitably influenced by antecedent precipitation conditions and evapotranspiration processes. With the SEEP/W software, it is not possible to manually assign a customized VWC profile before starting the simulation. To overcome this issue, a prelaminar calibration procedure has been carried out. It consisted in fitting the measured VWC profile with the modelled one, acting on the input water flux (see Sect. 4.5). The calibration procedure was performed before starting the simulations. For validation purposes, the results of SEEP/W simulations were compared to the observed data for the whole period of analysis. A comparison of the back-analysed monitored variables obtained with and without this preliminary calibration is provided in Sect. 5.1.

The agreement between in situ measured VWC (i.e., observations) and modelled VWC (i.e., predictions) was evaluated considering an approach used for satellite-based soil moisture products (Albergel et al. 2012; Liu et al. 2018) and global climate models. Taylor diagrams (Taylor 2001) were used to describe the statistical relationship between predicted and observed data. The correlation coefficient (R, Eq. 2), the normalized standard deviation (SDV, Eq. 3) and the centred root-mean-square difference (RMSD, Eq. 4) were used to quantify the agreement between the VWC predicted by different simulations and the measured ones. The bias was also calculated and included in the diagram (Eq. 5). Taylor diagrams were finally used to compare the different predictions with the observation, using a single graph per each monitored depth.

$$R = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left[ {\left( {{\text{VSWC}}_{{{\text{pre}},i}} - \overline{{{\text{VWC}}_{{{\text{pre}}}} }} } \right) * \left( {{\text{VSWC}}_{{{\text{obs}},i}} - \overline{{VWC_{{{\text{obs}}}} }} } \right)} \right]}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {{\text{VSWC}}_{{{\text{obs}},i}} - \overline{{{\text{VWC}}_{obs} }} } \right)^{2} } * \sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {{\text{VSWC}}_{{{\text{pre}},i}} - \overline{{{\text{VWC}}_{{{\text{pre}}}} }} } \right)^{2} } }}$$
(2)
$${\text{SDV}} = \frac{{\sigma_{{{\text{pre}}}} }}{{\sigma_{{{\text{obs}}}} }}$$
(3)
$${\text{RMSD}} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left[ {\left( {{\text{VSWC}}_{{{\text{pre}},i}} - \overline{{{\text{VWC}}_{{{\text{pre}}}} }} } \right) - \left( {{\text{VSWC}}_{{{\text{obs}},i}} - \overline{{{\text{VWC}}_{{{\text{obs}}}} }} } \right)} \right]^{2} }}{n}}$$
(4)
$${\text{Bias}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left[ {{\text{VSWC}}_{{{\text{pre}},i}} - {\text{ VSWC}}_{{{\text{obs}},i}} } \right]}}{n}$$
(5)

The R, SDV, centred RMSD are related by the following normalized formula:

$${\text{centred}}\,{\text{RMSD}}^{2} = {\text{SDV}}^{2} + 1 - 2*{\text{SDV}}*R$$
(6)

The construction of the diagram is based on the similarity of the above equation and the law of cosines (Taylor 2001):

$$c^{2} = a^{2} + b^{2} - 2*a*b*\cos \theta$$
(7)

4.3 Soil physical and mechanical properties

Grain size distribution analyses have been carried out for several representative samples taken at different depths (Heyerdahl et al. 2018). The results have been interpreted identifying the following three layers, from the top: a 6-m unsaturated sandy silt, followed by a 3-m layer of clayey silt, in partially saturated condition, laying on top of a firm marine clay extending to large depth (Table 1). Natural gravimetric water content values were measured on samples taken at different depths. More than one sample was taken from each layer; thus, in Table 1, the range of water content is indicated for each soil type.

Table 1 Slope layers and conditions
Full size table

Material properties were obtained: by triaxial tests for layer 1 (Heyerdahl et al. 2018) and layer 3 (NGI report 20160131‐02‐R); by literature (Statens Vegvesen 2018; Melchiorre and Frattini 2012) for layer 2. The material properties of the layers are summarized in Table 2. To be conservative, the unsaturated shear strength angle (\(\phi^{b}\)), representing shear strength increase due to the matric suction (Fredlund and Rahardjo 1993), was considered equal to \(\phi^{\prime } /2\), and no additional unsaturated strength was considered as a function of the VWC (Vanapalli et al. 1996). The extended Mohr–Coulomb failure envelope (Fredlund et al. 1978) was used to define the shear strength criteria as shown in Eq. (7):

$$\tau = c^{\prime } + \left( {\sigma - u_{{\text{a}}} } \right)\tan \phi + \left( {u_{{\text{a}}} - u_{{\text{w}}} } \right) \tan \phi^{b}$$
(7)

where \(\tau\) is the shear stress on the failure plane at failure; \(c^{\prime }\) is the intercept of the "extended" Mohr–Coulomb failure envelope on the shear stress axis when the net normal stress and the matric suction at failure are equal to zero, also referred as the "effective cohesion"; \(\left( {\sigma - u_{{\text{a}}} } \right)\) is the net normal stress at failure; \(\phi^{\prime }\) is the angle of internal friction associated with the net normal stress state variable;\(\left( {u_{{\text{a}}} - u_{{\text{w}}} } \right)\) is the matric suction at failure and \(\phi^{b}\) the angle represents shear strength increase due to the matric suction.

Table 2 Soil properties for slope stability analysis in SLOPE/W
Full size table

4.4 Soil water retention curves

The experimental soil water retention curves (SWRCs) of the unsaturated layers of the slope were obtained through pressure plate testing (Lin and Cerato 2012; Heyerdahl et al. 2018) performed at NGI labs. The van Genuchten (1980) SWRC equation was used to calculate the water content as function of the matric suction as follows:

$$\theta = \theta_{{\text{r}}} + \frac{{\theta_{{\text{s}}} - \theta_{{\text{r}}} }}{{\left[ {1 + \left( {\frac{\psi }{\alpha }} \right)^{n} } \right]^{m} }}$$
(8)

where \(\theta\) is the actual soil water content (m3/m3); \(\theta_{{\text{r}}}\) the residual water content (m3/m3); \(\theta_{{\text{s}}}\) the saturated water content (m3/m3); \(\psi\) the matric suction (kPa); \(\alpha\) is a scaling factor (kPa); n and m = (1–1/n) are fit parameters of the model related to the shape of the curve.

The hydraulic conductivity was calculated as follows:

$$k_{{\text{w}}} = k_{{\text{s}}} { }\frac{{\left[ {1 - \left( {\alpha \psi^{{\left( {n - 1} \right)}} } \right)\left( {1 + \left( {\alpha \psi^{n} } \right)^{ - m} } \right)} \right]^{2} }}{{\left( {\left( {\left( {1 + \alpha \psi^{n} } \right)} \right)^{\frac{m}{2}} } \right)}}$$
(9)

where \(k_{{\text{w}}}\) is the actual hydraulic conductivity (m/s) and \(k_{{\text{s}}}\) is the saturated hydraulic conductivity.

Figure 4 shows the soil water retention curves for the drying phase obtained interpolating the results of the pressure plate tests. Batch1, Batch2 and Batch3 between 1.5 and 6 m could be considered to have comparatively equal retention properties, while Batch 4 at 6–7 m was different. The curves obtained for Batch1 and Batch4 have been considered in the following analyses, respectively, for layer 1 and layer 2.

Fig. 4
figure 4

Soil water retention curves for the drying phase obtained interpolating the results of the pressure plate tests. a for sand silt layer from 0 to 6-m depth; b for clayey silt layer from 6 to 7-m depth

Full size image

In Table 3, the van Genuchten best-fit parameters \(\alpha\), n and m are shown, together with the saturated hydraulic conductivity (ksat) taken from Heyerdahl et al. (2018). The saturated hydraulic conductivity for layer 1 was measured with the constant head method on undisturbed specimens in the conventional triaxial apparatus. The values for Layer 2 and Layer 3 have been assumed considering laboratory tests carried out on similar soils in the area.

Table 3 van Genuchten best-fit parameters for SWRC and saturated permeability
Full size table

It is important to specify that tests for the determination of the SWRCs during the absorption phase cannot be performed with the pressure plate apparatus; thus, the hysteresis in the soil retention behaviour was not taken in consideration, although it is generally recommended to use the wetting curve, for better characterization of unsaturated flow conditions leading to slope failure (Ebel et al. 2008; Chen et al. 2017).

4.5 Modelling set-up

The slope geometry modelled is shown in Fig. 5. Initial total head values were assumed, respectively, on the left and on the right boundaries, of 163 m and 142 m. The total head values were defined considering the 4 piezometers installed on top of the slope and 2 other piezometers at the toe of the slope (Fig. 2). Daily precipitation (rainfall and snowmelt) data were used to define the flux boundary conditions along the slope surface in the SEEP/W program. To discretize the domain, quadrilateral and triangular elements of about 1-m resolution were used (Fig. 4), with a total of 2460 elements and 2566 nodes.

Fig. 5
figure 5

Slope geometry with mesh distributions, boundary conditions and regions used in the model

Full size image

The measured initial VWC profile, at the time 0 of the analysis (i.e., 04 June 2019), showed a nonlinear trend (Fig. 6), because, in general, shallowest layers are more prone to wetting and drying cycles determined by short-term rainfall, evaporation and evapotranspiration, which would slightly affect deeper layers (Comegna et al. 2016a, b; Capobianco et al. 2020). The VWC profile shows an increasing trend from 4-m depth towards the surface and a saturated conditions below 6 m (Fig. 6). In this regard, two series of simulations starting from different VWC initial conditions (IC) were considered: (i) non-calibrated (NC), with a linear trend of negative pressure head up to 5-m depth (Model_NC in Fig. 6), and (ii) calibrated (C), with a VWC profile resulting from a preliminary hydrological adjustment (Model_NC in Fig. 6). The calibrated VWC profile was obtained by applying an initial condition of steady-state analysis with a constant surface unit flux equal to the recorded monthly rainfall of the antecedent month (180 mm).

Fig. 6
figure 6

Initial VWC profiles: measured to date 03 June 2019 (continuous blue line), modelled non-calibrated (NC) and modelled calibrated (C)

Full size image

For each series, a total of three simulations were carried out, respectively, considering different boundary conditions: (1) precipitation (R), (2) precipitation and evaporation (CL), and (3) precipitation and evapotranspiration due to vegetation (VE). To assess the evaporation flux, SEEP/W module uses by default the Penman–Monteith equation (Allen et al. 1998). For the cases with climate boundary conditions (CL and VE), a set of climate variables (i.e., air temperature, relative humidity, wind speed and solar radiation) were provided to feed the Penman–Monteith equation to determine the evaporation flux. The climate variables used for modelling were taken from the closest meteorological station, located about 11 km north from the slope. The precipitation (rainfall and snowmelt) dataset was obtained from the daily gridded raster file on the Norwegian website senorge.no (http://www.senorge.no), evaluated combining weather stations and radar measurements. SeNorge provides high-resolution fields of daily total precipitation for applications requiring long-term datasets at regional or national level. The dataset constitutes a valuable meteorological input for snow and hydrological simulations; it is updated daily and presented on a high-resolution 1 km grid (Lussana et al. 2018). Snowmelt is estimated by the Snow map model (Saloranta 2012).

Furthermore, additional information related to the vegetation was also needed to determine the evapotranspiration flux. An overview of the effects of vegetation on the hydraulic modelling and the Penman–Monteith equation using SEEP/W was provided in a recent study (Capobianco et al. 2021). Specifically, the following values for the vegetation features were used. The leaf area index (LAI), defined as the projected area of leaves over a unit of land, was set equal to 1.5 for the period May–September) and equal to 0 for the autumn and winter period (October–April). The Plant Moisture limit (PML) was set equal to suggested default value from SEEP/W manual (Geoslope 2012). An arbitrary value of 1 m was selected for the root depth (RD), and the normalized root density (NRD) was considered to have a negative linear trend. Finally, the soil cover fraction (SCF), representing the percentage of soil covered by the canopy, was a proportional function of the LAI (for LAI = 0, SCF = 0; for LAI = 1.5, SCF = 1), and the vegetation height, equal to 3 m, is an average between bushes and tree heights present along the slope. Vegetation may change the soil water retention capability of the root-permeated soil (Scholl et al. 2014; Ng et al. 2016; Leung et al. 2018; Foresta et al. 2019; Capobianco et al. 2020); however, there still is an open debate on whether the presence of roots reduces or increases the soil water conductivity. Similarly, frost action and drying can be important for infiltration in shallow layers due to shrinkage/cracking and soil heave. Since these aspects go beyond the scope of this work, the same hydraulic properties of the unsaturated layers were adopted in all simulated cases (Table 3), including those with vegetation. The variables needed for each simulation are listed in Table 4.

Table 4 Simulations in SEEP/W and list of climate and vegetation variables needed for each simulation
Full size table

5 Results and discussion

5.1 Preliminary correlation between predicted and observed VWC

The predicted VWC calculated with the SEEP/W module was compared to the observed values (i.e., in situ measurements) for a 6-month period (i.e., June 2019–December 2019), considering all the 6 measured depths. A common and simple approach to compare predicted and observed data is to regress predicted and observed values and compare slope and intercept parameters against the 1:1 bisector line that represents the perfect correlation between the two variables. The disposition of the variables is important because, although the correlation value is the same, the intercept and the slope of each regression differ and, in turn, may change the result of the model evaluation (Piñeiro et al. 2008). Pairs of observed–predicted VWC values were, respectively, plotted in the y-axis and x-axis for each of the 6 sensor depths. Figure 7 shows the pairs of observed–predicted VWC for the 6 simulated cases on a daily basis, with on the left side the non-calibrated series, and on the right side, the calibrated ones (see Table 4). For almost all the depths, the non-calibrated data series (Fig. 7a–c) are more scattered, whereas for the calibrated simulations (Fig. 7d–f), the values are less spread and closer to the 1:1 line. At 2- and 4-m depths, the discrepancy between observed and predicted data is visible as the points are spread horizontally.

Fig. 7
figure 7

Regression between observed (y-axis) and predicted (x-axis) VWC values and comparison against the 1:1 line (perfect correspondence) for the following simulated cases a NC_R, b NC_CL, c NC_Cl-VE, d C_R, e C_Cl, and f C_CL_VE

Full size image

The simulations were conservative at almost all depths (apart from 6-m depth), since the predicted VWC points are mostly all located either on the 1:1 line or below it (Fig. 7). This means that the predicted VWC values are generally higher than the observed values. This discrepancy can be justified by the SWRCs used to perform the analyses, since the curves are calculated for the drying phase based on drying tests. For soils with hysteretic behaviour, for the same values of suction, the corresponding VWC in the drying path is higher than the one in the wetting path (Childs and Collis-George 1950; Croney and Coleman 1954; Millington and Quirk 1959; Kunze et al. 1968; Hogarth et al. 1988; Pham et al. 2005; Maqsoud et al. 2006; Nuth and Laloui 2008; Malaya and Sreedeep 2012, Sorbino and Nicotera 2013; Rianna et al. 2019; Capparelli and Spolverino 2020; Comegna et al. 2021). It is also worth mentioning that the SWRCs were obtained in laboratory, while experimental in situ tests can give different results even though are more difficult to perform. In fact, the impact of soil structure on water retention curves and hydraulic conductivity in the field, compared to small core samples, has been recognized in previous studies (Mirus 2015; Fatichi et al. 2020). In addition, the variability of hydraulic parameters for a field-based SWRC is also smaller compared to a laboratory-based or texture-based SWRC (Thomas et al. 2018). Finally, another limitation of the modelling software is that it can only simulate homogeneous layers, while it has been observed in Heyerdahl et al. (2018) that soil layers 1 (0–6 m) and 2 (6–9 m) are not completely homogeneous, as the proportions of silt, sand and clay are not constant with depth. This is also confirmed by the SWRC experimental points measured in laboratory for the first layer (i.e., Batch3, Fig. 4a). Few measured pairs of VWC-suction values obtained from Batch 3 are not as consistent as the points obtained for Batch1 and Batch2.

5.2 Validation of the hydrogeological model with Taylor diagrams

The comparison between observed and predicted VWC patterns was quantified in terms of correlation (R, Eq. 2), standard deviations ratio (SDV, Eq. 3), centred root-mean-square difference (RMSD, Eq. 4) and bias (Eq. 5). R coefficient (Eq. 2), SDV (Eq. 3) RMSD (Eq. 4) and bias (Eq. 5). These parameters were calculated for each couple of predicted–observed VWC datasets. The results were plotted (Fig. 8) in the Taylor diagrams (Taylor 2001).

Fig. 8
figure 8

Taylor diagrams comparing modelled and measured VWC, respectively, for the following depth: a 0.1 m, b 0.5 m, c 1 m, d 2 m, e 4 m and f 6 m. The purple diamond in correspondence to the point 1 of SDV and R, and 0 of RMSD, represents the in-situ condition

Full size image

Each diagram plots the comparison between predicted and observed VWC values at different soil depths (0.1, 0.5, 1, 2, 4, 6 m). Every diamond is representative of a simulation case from Table 4 and is plotted in the diagram as a function of the calculated 'R' coefficient (black curves), SDV (blue curves) and RMSD (green curves); the diamond colour is representative of the bias. The position of each diamond on the plot quantifies how closely that model's VWC patterns match the observations. Ideally, a good model would have relatively high correlation, low RMS errors (Taylor 2001) and SDV around 1. Furthermore, the darker is the diamond colour, the lower is the bias in predicting the VWC values.

Series-wise, it is possible to confirm that the best simulations are those that belong to the C-series, where an initial calibration of the VWC was performed. At almost all depths, the C-series were closer to the observed in situ VWC values and trends.

Figure 8 shows that the simulation C_CL_VE generally agrees better than the other simulations with the observations at almost all depths. C_CL_VE shows a better agreement with the observed VWC at 0.1 and 0.5 m, despite the bigger variability of data observed at the shallowest layers, mostly due to the short response to atmospheric drivers. On the contrary, the simulation C_CL_VE was less able to model the VWC at 2 m. Even though at 2 m (Fig. 8d) there is a fairly high correlation (0,77), SDV and RMSD were high (respectively 9,7 and 9,5), and the bias was about 6%. This indicates less agreement between the predicted and observed values. However, it is important to underline that none of the simulations can correctly model the VWC at 2-m depth. At 4-m depth (Fig. 8e), the C_CL_VE simulation showed a good agreement with the observed data, with a bias circa 6%. At 6-m depth (Fig. 8f), high correlation (0,97) and low bias, but high SDV (3,5) indicates that the model was able to reasonably predict the trend and the values, but with bigger variations of the predicted values compared to the measured ones. In summary, these results show that for modelling in situ VWC it is important to carry out an initial calibration and to perform the analyses considering both vegetation and climatic variables. Climate variables and vegetation can significantly influence the hydrological behaviour of unsaturated slopes. For example, temperature can change the VWC of the shallowest layers from one season to another, while roots can improve the permeability of the rhizosphere, thus promoting lateral diversion of rainwater and acting like a natural lateral drainage (Balzano et al. 2019).

Furthermore, the preliminary validation process was useful to prove that the SEEP/W modelling, specifically simulation C_CL_VE, was better than the others to back analyse the hydrogeological conditions within the slope at almost all depths. Possibility to further improve the match between observed and predicted hydrological variables (i.e. VWC and PWP) trends and values are described in the following section.

5.3 Sensitivity analysis of the hydraulic conductivity for the best-fit model (C_CL_VE)

As a second step of the validation process, a sensitivity analysis of the hydraulic conductivity has been performed. The sensitivity of different model outputs and the importance of each layer within the model have been described in the following. Specifically, the saturated hydraulic conductivity and the permeability anisotropy ratio (\(k_{y}^{\prime } /k_{x}^{\prime }\)) have been varied. Generally, the saturated hydraulic conductivity is assumed to be the same in both directions in engineering practice; however, this does not account for possible inhomogeneities in the soil texture that are often found in situ (Wang et al. 2018; Hong et al. 2019).

Simulation C_CL_VE is the best one, resulting from the previous preliminary validation, in back-calculating the observed VWC and it has been considered, herein, for the sensitivity analysis. In order to improve the reliability of the model, the results of the different simulations, described in this section, have been compared not only with VWC but also with PWP measurements. The list of simulations carried out is provided in Table 5. As a reference for comparing the observed data with the predictions, the PWP and VWC sensors at 6-m depth only have been considered. The reason is because these sensors are located in the fluctuation zone of the water table and are showing more long-term variations compared to other depths.

Table 5 List of simulations carried out varying the saturated horizontal hydraulic conductivity and the permeability anisotropy ratio
Full size table

Figure 9 summarizes the main findings of the sensitivity analysis. Figure 9a, c and Fig. 9b, d show, respectively, how changing the hydraulic conductivity and the ratio influences the model result. Specifically, Fig. 9a,c shows that increasing the hydraulic conductivity of layer 1, from 2.4E−06 m/s (C_CL_VE_0) to 5E−06 m/s (C_CL_VE_1), a faster infiltration process and earlier VWC and PWP responses are observed. This change influences the VWC within layer 1; C_CL_VE_1 has lower VWC values at all depth except at 6-m, i.e., the interface with layer 2. This second layer has a lower hydraulic conductivity that leads to water accumulation at the interface. For this reason, the VWC at 6-m depth increases. The same consideration can be done for the PWP, which increases at 6-m depths. In general, this change shows a better correspondence between observed and predicted VWC and PWP.

Fig. 9
figure 9

Comparison between different simulation predictions and the observed VWC and PWP at 6-m depth

Full size image

Increasing the hydraulic conductivity of layer 2, from 1E−07 m/s (C_CL_VE_0) to 5E−07 m/s (C_CL_VE_2), shows a reduced peak and a smoothed trend (Fig. 9a, c) of both VWC and PWP values. (The curves are less steep and the initial PWP is closer to the observed one.) The change in layer 2 influences only the deepest VWC sensor, located at 6-m, at the interface between layers 1 and 2. A simulation increasing the hydraulic conductivity of both layer 1 and layer 2 (i.e. C_CL_VE_11 in Fig. 9a, c), has been carried out, obtaining VWC and PWP trends between C_CL_VE_1 and C_CL_VE_2. The VWC curve obtained shows a good match with the observed one (Fig. 9a). The observed and predicted PWP curves have a similar shape, but the predicted one seems to be shifted in time (Fig. 9c).

The best simulation obtained varying the hydraulic conductivity of each layer (C_CL_VE_11) has been considered for parametric analysis of the permeability anisotropy ratio. Increasing the permeability anisotropy ratio of layer 1 from 1 to 2.5 (C_CL_VE_12) varies the infiltration response to climate drivers and vegetation. The similarity between predicted and observed PWP increases (Fig. 9d), but the predicted VWC overestimates the actual VWC values (Fig. 9b). A better agreement for the VWC is observed by reducing the ratio to 1.5 (C_CL_VE_13). However, the best simulation able to adequately represent both VWC and PWP trends is obtained considering a ratio of 2 (C_CL_VE_17).

Changing the ratio of layer 2 and layer 3 does not show any variations in the different simulations for the PWP and the VWC within layer 1. Moreover, soft marine clays do not show relevant permeability anisotropy as showed also by Leroueil et al. (1990) and Hong et al. (2019).

Figures 10 and 11 compare, respectively, the predicted VWC and PWP of the best simulation (C_CL_VE_17) with the observed data at different depths.

Fig. 10
figure 10

Comparison between the best simulation prediction (orange line) and the observed VWC (OBSV, blue line) at different depths: 0.1, 0.5, 1, 2, 4, 6 m

Full size image
Fig. 11
figure 11

Comparison between the best simulation prediction (orange line) and the observed PWP (OBSV, blue line) at different depths: 6, 9, 15, 23 m

Full size image

5.4 Effectiveness of the hydrogeological model with time

The previous section shows that the simulation C_CL_VE_17, including a preliminary calibration, climate drivers and vegetation, is able to replicate the monitored in situ PWP and VWC conditions. This section aims to assess the effectiveness of the hydrological model C_CL_VE_17 of back-calculating the VWC throughout the year. The observed VWC has been compared with the predicted data at 0.1-, 0.5-, 1-, 6-m depths. The other two depths (i.e., 2- and 4-m) have been excluded from the comparison since the model was not able to replicate the VWC values and trends at these depths.

Three different time spans have been considered for comparison: a 6-month period (6M), June 2019–December 2019; a 12-month period (1Y), June 2019–June 2020; and a 14-month period (1.25Y), June 2019–August 2020. Figure 12 shows the comparison between the predicted VWC variables (simulation C_CL_VE_17) with the in situ measurements for the three different time spans using Taylor diagrams.

Fig. 12
figure 12

Taylor diagrams comparing modelled and measured VWC of the combination C_CL_VE_17 for 6 months (6M), 12 months (1Y) and 14 months (1.25Y) period, respectively, for the following depths: a 0.1 m, b 0.5 m, c 1 m, d 6 m. The purple diamond in correspondence to the point 1 of SDV and R, and 0 of RMSD represents the in situ condition

Full size image

The analysis shows that, for 0.1, 0.5, 1-m depths, the 6M comparison has a high R (> 0.75), a SDV of circa 1, the lowest RSMD among the other time spans and the bias always lower than 7% (Fig. 12). For the 6-m depth, the 6M comparison shows a high R (> 0.85), with a low bias (circa 1%) but a high SDV (5.4) and, consequently a high RSMD (Fig. 12). The reason lies on the flat trend showed by the measured VWC in the 6M time span (see Fig. 10), with an almost constant VWC value in time. On the contrary, the simulation C_CL_VE_17 shows an increase of the VWC slightly before (i.e. from November) the one observed for the measured data (i.e., from December). Consequently, the SDV is high (5.4) even though the observed and predicted VWC are both low, respectively, 0.25 for the measured data and 1.3 for the modelled one.

Analysing the 1Y comparison, it emerges that, apart from 0.1-m depth, the performance of the model to predict the in situ condition is still good. In general, at all depths, R is higher than 0.78, SDV is around 1 and bias lower than 5% (Fig. 12), except at 0.1-m depth, where R decreases to 0.5, SDV is lower than 1 and bias is circa 5%. This can be justified by the freezing cycles during the winter experienced by the soil at shallow depths (see Fig. 3), when the sensor is reading very low values of VWC (see Sect. 3.3).

After these considerations, the simulation C_CL_VE_17 for the time span 1Y can be still considered to satisfactorily replicate the VWC at all depths. The results show that for this case study a recalibration of the numerical modelling is not necessary for up to 1 year. However, a recalibration after 6M could be recommended.

5.5 Machine learning preliminary analysis for factor of safety forecasting

A machine learning analysis has been carried out to predict the FS from the modelled 1Y VWC. The VWC values are the variables measured in real time on the slope. For this reason, the possibility to predict the FS from VWC would be very important for the implementation of a real-time slope stability analysis as a Lo-LEWS for the slope. The FS values have been obtained from the coupled analysis of SEEP and Slope (GEOSLOPE International Ltd.) for C_CL_VE_17.

A supervised, regression machine learning analysis has been carried out using a random forest machine learning model. The analysis is supervised because the data are known. The VWC at all depths, air temperature, precipitation, PWP at 6-m depth are named features, while the FS are the targets. In the training phase, the random forest model receives both the features and the targets, and it learns how to predict the FS given the features. The dataset with features and targets has been randomly split into training (75%) and testing sets (25%). The days with missing monitoring data have been excluded from the analyses. No anomalous values have been found in the dataset. In the training phase, relations between feature and target values are defined. In the testing one, the model predicts the FS.

A baseline computing the train targets average has been evaluated. A baseline is a method that uses heuristics, simple summary statistics or randomness, to create predictions for a dataset. The baseline's accuracy has been calculated (98.32%). It represents the reference value to compare the machine learning algorithm performance with. Moreover, to quantify the usefulness of all the input features used in the random forest model, the relative importance has been calculated. The importance describes how much a particular feature improves the prediction.

The prediction accuracy is calculated for different combination of features (i.e. monitored variables) used to predict the FS, and it is compared with the baseline accuracy (Table 6). Air temperature and precipitation have been considered in all the combinations. However, their contribution alone slightly increases the prediction accuracy (98.78%). The highest accuracy (99.78%) is obtained considering the PWP at 6-m (Table 6). A similar accuracy (99.77%) is reached considering precipitation, air temperature and the VWC at 0.1-, 0.5-, 1-, 6-m depths. This result highlights the possibility to predict the FS knowing the VWC. The VWC is monitored in near real time; thus, they can be used as warning parameters in the IoT-based Lo-LEWS. A higher accuracy is reached if considering also the PWP at 6-m (99.83%). However, the PWP measures are currently not automatic, and manual in situ readings are needed.

Table 6 Comparison between baseline and prediction accuracies for different considering features
Full size table

Figure 13 shows the importance of the variables considered for predicting the FS with combination #6 (Table 6), i.e., considering VWC, precipitation and air temperature. The most important variables are (Fig. 13): the VWC at 1-m (0.54), 6-m (0.28) depths and air temperature (0.12). The daily precipitation and the VWC at 0.1 and 0.5-m depths show a low importance in predicting the FS for the 1Y period. It is interesting to notice that the daily temperature has a higher importance compared to the daily precipitation; this finding highlights once more the importance of the temperature in controlling the evapotranspiration, the hydrological balance (Scaringi and Loche 2022) and, thus, the stability of an unsaturated slope (Bordoni et al. 2015).

Fig. 13
figure 13

Relative importance of the features used to predict the FS (histograms). The red dashed line represents the 95% of importance. The green continuous line is the cumulative accuracy

Full size image

6 Concluding remarks

This work presents a framework for a IoT-based early warning at a slope scale (i.e. Lo-LEWS). The paper applies the first two phases of the framework to an unsaturated slope in Norway. The monitoring and modelling phases have been described, with emphasis on the hydrological model, its effectiveness in time and ML analysis to predict the FS from the monitored variables.

Two series of simulations were carried out: one considering an initial calibration of the VWC profile (C) and another one where no initial calibration has been conducted (NC). For each series, a total of three simulations were performed, respectively, including precipitation; precipitation and climate parameters; precipitation, climate parameters and effects of vegetation. The paper describes the validation of the different simulations with the observed in situ VWC measurements. The comparison carried out using Taylor diagrams showed the importance of including a VWC preliminary calibration as well as precipitation (rainfall and snowmelt), climate variables and vegetation for back-calculating the hydrological behaviour of the slope. A sensitivity analysis of the hydraulic conductivity and permeability anisotropy has been conducted to improve the agreement between predicted and observed hydrogeological variables (i.e., VWC and PWP). The sandy silt layer on top of the slope showed a permeability anisotropy with an hydraulic conductivity ratio greater than 1, highlighting a higher vertical hydraulic conductivity compared to the horizontal one, as also showed by Hong et al. (2019), for sandy soils.

The simulation C_CL_VE_17 was able to adequately reproduce the observed in situ VWC conditions at 0.1-, 0.5- ,1- and 6-m depths. On the contrary, at 2- and 4-m depths, the model was not able to predict the observed VWC, which maintain a quite flat trend with very low VWC values. However, the absolute discrepancy between predicted and observed VWC for both depths was not exceeding 5%. The reasons for this discrepancy can be ascribed to the possible presence of higher hydraulic conductivity soil lens located between 2 and 4 m depth, and the use of drying curves as SWRC. This would explain the very low VWC recorded in situ. However, moisture content in a slope is subject to spatial variability that a 2D model cannot fully capture (Uhlemann et al. 2017).

The effectiveness of the hydrological model in back-calculating VWC was tested for 3 different time spans: 6M, 1Y, 1.25Y. The results showed that the accuracy and performance of the SEEP/W model decreased with time. The analysis outlines that the C_CL_VE_17 model was able to replicate the VWC at 4 depths (0.1, 0.5, 1, 6 m) for up to 1Y. Despite this finding, the re-calibration period might change from year to year as a function of the slope and the environment under investigation. A slope stability analysis has been carried coupling the hydrological modelling with a LEM. The calculated FS, the temperature, the precipitation and the monitored WVC and PWP have been used as input for a ML analysis. The ML analysis has shown the possibility to predict the FS using the monitored VWC. This finding is very important since it proved the possibility to use monitored real-time data in a Lo-LEWS, with the aim of informing and warning the railway authority of the increased probability of having a landslide.

In conclusion, the procedure described in this paper can be seen as a first step towards a IoT-based Lo-LEWS. The importance of using monitored data to back-calculate and validate a hydrological model has been highlighted. Moreover, the possibility to use VWC to predict the FS has been investigated. However, forecasting and warning phases still need to be detailed to operate the IoT-based Lo-LEWS for the studied slope. About the forecasting phase, conditions leading to failure (i.e. VWC, PWP, precipitation and temperature values/thresholds) need to be determined. In the analysis carried out herein, the FS values used to train the ML algorithm have always been above one; indeed, no deformation has been observed in situ. Additional simulations need to be carried out considering extreme climate inputs with the aim of considering climate changes and detecting combinations of variables leading to failure (i.e., FS < 1) that can serve as dataset for training machine learning algorithms. Moreover, an automatized procedure to compute the FS considering the monitored hydrological variables and the forecasted climate ones need to be implemented. About the warning phase, different warning levels as a function of the monitored and forecasted variables needed to be distinguished, as well as procedures and emergency plans to adopt in each level.

Further effort will be also spent to couple VWC measurements with recently installed tensiometers in the unsaturated layer. This dataset will provide more information on the in situ wetting–drying cycles of the slope, leading to a better evaluation of the SWRC, improving the modelling phase. On top of the slope, a local weather station was installed in June 2022, which will allow more accurate measurements of the climate variables (precipitation, wind speed, air temperature, relative humidity) in the near future, improving the monitoring phase.