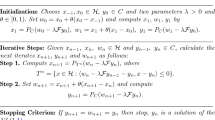New Inertial Projection Methods for Solving Multivalued Variational Inequality Problems Beyond Monotonicity

Abstract

In this paper, we present two new inertial projection-type methods for solving multivalued variational inequality problems in finite-dimensional spaces. We establish the convergence of the sequence generated by these methods when the multivalued mapping associated with the problem is only required to be locally bounded without any monotonicity assumption. Furthermore, the inertial techniques that we employ in this paper are quite different from the ones used in most papers. Moreover, based on the weaker assumptions on the inertial factor in our methods, we derive several special cases of our methods. Finally, we present some experimental results to illustrate the profits that we gain by introducing the inertial extrapolation steps.

1 Introduction

Assume that C is a nonempty closed and convex subset of $\mathbb {R}^{N}$ and $F:C\rightrightarrows \mathbb {R}^{N}$ a multivalued mapping with nonempty values. The Multivalued Variational Inequality Problem (MVIP) associated with F and C consists in finding x^∗∈ C and u ∈ F(x^∗) such that

$$ \begin{array}{@{}rcl@{}} \langle u, y-x^{*}\rangle\geq 0,~\forall y\in C. \end{array} $$

(1)

MVIP (1) was first introduced and studied by Browder (1965) as an important generalization of the classical Variational Inequality Problem (VIP). The MVIP is also known to be a useful generalization of the class of multivalued complementarity problems (see Dong et al. 2017; Facchinei and Pang 2003; He et al. 2019), as well as constrained convex non-smooth optimization problems (see Dong et al. 2017; He et al. 2019; Rockafellar 1970). Therefore, problem (1) is quite general and provides a unified treatment for the study of a wide class of problems such as price equilibrium problems, oligopolistic market equilibrium problems, Nash equilibrium problems, fixed point problems for multivalued mappings, game theory, among others (see Attouch and Cabot 2019b; Brouwer 1912; Carey and Ge 2012; He et al. 2019; Nadler1969; Oggioni et al. 2012; Raciti and Falsaperla 2007 and the references therein).

When F is a singlevalued mapping in Eq. 1 (i.e., the case of the classical VIP), many methods have been designed by numerious authors for solving the VIP. These include, the gradient projection methods, extragradient methods (Korpelevich 1976), the subgradient extragradient methods (Censor et al. 2011), Tseng’s method (Tseng 2000), among others (see, for example, Vuong 2019). We note that these methods for solving the classical VIP are not simply transformed to the case of MVIP since it is very difficult to handle the multivalued mapping associated with the MVIP. Thus, the methods for solving the MVIP are quite different. In 2014, Fang and Chen (2014) extended the subgradient extragradient method for solving the MVIP (1) in finite dimensional spaces. By employing the Procedure A below, they proposed the following Algorithm 1.1.

Procedure A (Konnov 1998)

• Input: a point $x\in \mathbb {R}^{N}$.

• Output: a point R(x) ∈ C, where $C:=\{x\in \mathbb {R}^{N}~|~g(x)\leq 0\}$, $g:\mathbb {R}^{N} \to \mathbb {R}$ is a convex function.

• Step 1: set n = 0 and x_n = x.

• Step 2: if g(x_n) ≤ 0, then stop and set R(x) = x_n. Otherwise, go to Step 3.

• Step 3: choose a point w_n ∈ ∂g(x_n), where ∂g(x) denotes the subdifferential of g at x, set

  $$x_{n+1}=x_{n}-2g(x_{n}) \frac{w_{n}}{\|w_{n}\|^{2}},$$

  and set n := n + 1 go back to Step 2.

Algorithm 1.1.

• Step 0: Choose $\bar {x}_{1}\in \mathbb {R}^{N}$ and two parameters γ, δ ∈ (0,1). Set n = 1.

• Step 1. Apply Procedure A with $x=\bar {x}_{n}$ and set $x_{n}=R(\bar {x}_{n})$.

• Step 2. Choose u_n ∈ F(x_n) and let k_n be the smallest nonnegative integer satisfying $v_{n}\in F(P_{C}(x_{n}-\gamma ^{k_{n}}u_{n})),$

  $$ \begin{array}{@{}rcl@{}} \gamma^{k_{n}}\|u_{n}-v_{n}\|\leq (1-\delta)\|x_{n}-P_{C}(x_{n}-\gamma^{k_{n}}u_{n})\|. \end{array} $$

  (2)

  Set $\rho _{n}=\gamma ^{k_{n}}$ and z_n = P_C(x_n − ρ_nu_n). If x_n = z_n, stop.

• Step 3. Compute $\bar {x}_{n+1}=P_{C_{n}}(x_{n}-\rho _{n} v_{n}),$ where $C_{n}=\{y\in \mathbb {R}^{N} : \langle x_{n}-\rho _{n} u_{n}-z_{n}, y-z_{n}\rangle \leq 0\}$. Let n = n + 1 and return to Step 1.

Inspired by Algorithm 1.1, Dong et al. (2017) proposed the following projection and contraction method for solving the MVIP (1).

Algorithm 1.2.

• Step 0: Choose $\bar {x}_{1}\in \mathbb {R}^{N}$ and four parameters τ > 0, γ, δ ∈ (0,1) and α ∈ (0,2). Set n = 1.

• Step 1. Apply Procedure A with $x=\bar {x}_{n}$ and set $x_{n}=R(\bar {x}_{n})$.

• Step 2. Choose u_n ∈ F(x_n) and find the smallest nonnegative integer l_k such that $\rho _{n}=\tau \gamma ^{l_{k}}$ and v_n ∈ F(P_C(x_n − ρ_nu_n)), which satisfies

  $$ \begin{array}{@{}rcl@{}} \rho_{n}\|u_{n}-v_{n}\|\leq (1-\delta)\|x_{n}-P_{C}(x_{n}-\rho_{n} u_{n})\|. \end{array} $$

  (3)

  Set y_n = P_C(x_n − ρ_nu_n). If x_n = y_n, stop.

• Step 3. Compute $\bar {x}_{n+1}=x_{n}-\alpha {\upbeta }_{n} d(x_{n}, y_{n}),$ where d(x_n, y_n) − ρ_n(u_n − v_n), ϕ(x_n, y_n) := 〈x_n − y_n, d(x_n, y_n)〉 and ${\upbeta }_{n}:=\frac {\phi (x_{n}, y_{n})}{\|d(x_{n}, y_{n})\|^{2}}$.

Let n = n + 1 and return to Step 1.

We comment that the Armijo-type linesearch procedures (2) and (3) of Algorithm 1.1 and Algorithm 1.2, respectively, involve the computation of projection onto C multiple times in each linesearch. They also involve the evaluation of the multivalued mapping F too many times in each search. To overcome some of these shortcomings, He et al. (2019), proposed the following projection-type method for solving MVIP (1):

Algorithm 1.3.

• Step 0: Choose $x_{1}\in \mathbb {R}^{N}$ as an initial point and fix four parameters γ, σ ∈ (0,1) and $0<\rho ^{0}\leq \rho ^{1}<\infty$. Set $C_{1}=\mathbb {R}^{N}, \bar {x}_{1}=x_{1},$ and n = 1.

• Step 1: Apply Procedure A to obtain $x_{n}=R(\bar {x}_{n})$.

• Step 2: Choose u_n ∈ F(x_n) and ρ_n ∈ [ρ⁰, ρ¹]. Set y_n = P_C(x_n − ρ_nu_n). If x_n = y_n, then stop. Otherwise, compute z_n = α_ny_n + (1 − α_n)x_n and choose the largest α ∈{γ⁰, γ, γ², γ³,⋯ } such that there exists w_n ∈ F(z_n) satisfying

  $$ \begin{array}{@{}rcl@{}} \langle w_{n},x_{n}-y_{n}\rangle \geq \sigma\langle u_{n},x_{n}-y_{n} \rangle. \end{array} $$

• Step 3: Taking a point v_n ∈ F(y_n), set d(x_n, y_n) = (x_n − y_n) − ρ_n(u_n − v_n) and compute $\bar {v}_{n}=x_{n}-{\upbeta }_{n}d(x_{n},y_{n}),$ where ${\upbeta }_{n} =\frac {\phi (x_{n},y_{n})}{\|d(x_{n},y_{n})\|^{2}},~~~ \phi (x_{n},y_{n})=\langle x_{n}-y_{n},d(x_{n},y_{n})\rangle$.

• Step 4: Set $C_{n}=\{y\in \mathbb {R}^{N}|\langle w_{n},y-z_{n}\rangle \leq 0\}$ for n ≥ 2 and $C^{*}_{n}=\cap ^{n}_{i=1}C_{i}$.

  Compute $\bar {x}_{n+1}=P_{{C^{*}_{n}}}(\bar {v}_{n})$.

  If $\bar {x}_{n+1}=x_{n},$ then stop. Otherwise, let n := n + 1 and return Step 1.

As observed in He et al. (2019, Section 4), Algorithm 1.1, Algorithm 1.2 and Algorithm 1.3 do not work well in some settings because of the presence of Procedure A in the iterative steps. Hence, the authors in He et al. (2019) proposed the following projection-type method without Procedure A for solving MVIP (1), which can be implemented in such settings.

Algorithm 1.4.

• Step 0: Choose $x_{1}\in \mathbb {R}^{N}$ as an initial point and fix four parameters γ, σ ∈ (0,1) and $0<\rho ^{0}\leq \rho ^{1}<\infty$. Set $C_{1}=\mathbb {R}^{N}$ and n = 1.

• Step 1: Choose u_n ∈ F(x_n) and ρ_n ∈ [ρ⁰, ρ¹]. Set y_n = P_C(x_n − ρ_nu_n). If x_n = y_n, then stop. Otherwise, compute z_n = α_ny_n + (1 − α_n)x_n and choose the largest α ∈{γ⁰, γ, γ², γ³,⋯ } such that there exists w_n ∈ F(z_n) satisfying

  $$ \begin{array}{@{}rcl@{}} \langle w_{n},x_{n}-y_{n}\rangle \geq \sigma\langle u_{n},x_{n}-y_{n} \rangle. \end{array} $$

• Step 2: Taking a point v_n ∈ F(y_n), set d(x_n, y_n) = (x_n − y_n) − ρ_n(u_n − v_n) and compute $\bar {x}_{n}=x_{n}-{\upbeta }_{n}d(x_{n},y_{n}),$ where ${\upbeta }_{n} =\frac {\phi (x_{n},y_{n})}{\|d(x_{n},y_{n})\|^{2}},~~~ \phi (x_{n},y_{n})=\langle x_{n}-y_{n},d(x_{n},y_{n})\rangle$.

• Step 3: Set $C_{n}=\{y\in \mathbb {R}^{N}|\langle w_{n},y-z_{n}\rangle \leq 0\}$ for n ≥ 2 and $C^{*}_{n}=\cap ^{n}_{i=1}C_{i}$. Compute $x_{n+1}=P_{C\cap {C^{*}_{n}}}(\bar {x}_{n})$.

  If x_n+ 1 = x_n, then stop. Otherwise, let n := n + 1 and return Step 1.

Notice that the linesearch procedure in Algorithm 1.3 and Algorithm 1.4 involve the computation of the projection onto C only one time in each search trial. Thus, Algorithm 1.3 and Algorithm 1.4 seem more efficient than Algorithm 1.1 and Algorithm 1.2. Moreover, He et al. (2019) showed numerically that their methods perform better than Algorithm 1.2 of Dong et al. (2017). However, Algorithm 1.3 and Algorithm 1.4 still involve the evaluation of the multivalued mapping at least 3 times in each iteration.

Recently, inertial type algorithms for solving optimization problems have become of great interest to numerous researchers. Since Polyak (1964) studied an inertial extrapolation process for solving the smooth convex minimization problems, there have been growing interests in the design and study of iterative methods with inertial term. For example, inertial forward-backward splitting methods (Attouch et al. 2000; Cholamjiak et al. 2018; Ochs et al. 2015), inertial Douglas-Rachford splitting method (Bot et al. 2015), inertial ADMM (Bot and Csetnek 2016), and inertial forward-backward-forward method (Lorenz and Pock 2015). The inertial term is based upon a discrete analogue of a second order dissipative dynamical system (Attouch et al. 2000) and known for its efficiency in improving the convergence rate of iterative methods. The inertial type algorithms have been tested in the solution of certian number of problems (for example, imaging and data analysis problems, motion of a body in a potential field) and the tests show that they actually give remarkable speed-up when compared with corresponding algorithms without inertial term (see, for example, Attouch and Cabot 2019a; Attouch and Cabot2019b; Attouch et al. 2000; Beck and Teboulle 2009; Bot and Csetnek2016; Lorenz and Pock 2015; Ochs et al. 2015; Polyak 1964; Shehu and Cholamjiak 2019; Shehu et al. 2019; Shehu et al. 2019 and the references therein).

Inspired by this recent trend on inertial extrapolation type methods for solving optimization problems, our aim in this paper is to design some modifications of Algorithms 1.3 and 1.4, together with new inertial extrapolation techniques to solve problem (1). We present two inertial projection-type methods for solving MVIP (1) when the multivalued mapping F is only assumed to be locally bounded without any monotonicity assumption. The first method uses a linesearch as in Algorithm 1.3 and Algorithm 1.4 while the second method uses a different linesearch procedure with the aim of minimizing the number of evaluation of the multivalued mapping F in each search. Furthermore, the inertial techniques that we employ in this paper are quite different from the ones used in most papers (see for example Cholamjiak et al. 2018; Chuang 2017; Lorenz and Pock 2015; Mainge 2008; Moudafi and Oliny2003; Ochs et al. 2015; Polyak 1964; Shehu and Cholamjiak 2019; Shehu et al. 2019; Shehu et al. 2019; Thong and Hieu 2018; Thong and Hieu 2017and the references therein). Moreover, based on the weaker assumptions on the inertial factor in our methods, we derive several special cases of our methods. Finally, we provide some numerical implementations of our methods and compare them with the methods in He et al. (2019), in order to show the profits that we gain by introducing the inertial extrapolation steps.

We organize the rest of the paper as follows: We first recall some basic results in Section 2. Some discussions about our methods are given in Section 3. In Section 4, we investigate the convergence analysis of our first method. In Section 5, we analyze the convergence of our second method. In Section 6, we give some numerical experiments to support our theoretical findings. Then, we conclude with some final remarks in Section 7.

2 Preliminaries

The metric projection, denoted by P_C, is a map defined on $\mathbb {R}^{N}$ onto C which assigns to each $x\in \mathbb {R}^{N}$, the unique point in C, denoted by P_Cx such that

$$\|x-P_{C}x\|=\inf \{\|x-y\|:~y\in C\}.$$

It is well known that P_C is nonexpansive, and characterized by the inequality

$$ \begin{array}{@{}rcl@{}} \langle x-P_{C}x, y-P_{C} x\rangle\leq 0~~\forall y\in C. \end{array} $$

(4)

Furthermore, the P_C is known to possess the following property

$$ \begin{array}{@{}rcl@{}} \|P_{C}x-x\|^{2}\leq \|x-y\|^{2}-\|P_{C}x-y\|^{2}~\forall y\in C. \end{array} $$

(5)

It is also known that P_C satisfies

$$ \begin{array}{@{}rcl@{}} \langle x-z, x-P_{C}z\rangle \geq \|x-P_{C}z\|^{2},~\forall x\in C, ~z\in \mathbb{R}^{N}. \end{array} $$

(6)

For more information and properties of P_C, see Goebel and Reich (1984) and He (2006).

Definition 2.1

A multivalued mapping $F:C\rightrightarrows \mathbb {R}^{N}$ is said to be

• outer-semicontinuous at x ∈ C if and only if the graph of F is closed;

• inner-semicontinuous at x ∈ C if for any sequence {x_n} converging to x and y ∈ F(x), then there exists a sequence {y_n} in F(x_n) such that {y_n} converges to y;

• continuous at x ∈ C if it is both outer-semicontinuous and inner-semicontinuous at x;

• locally bounded on C if for every x ∈ C, there exists a neighborhood U of x such that F(U) is bounded, where F(U) = ∪_x∈UF(x).

Definition 2.2

A multivalued mapping $F:C\rightrightarrows \mathbb {R}^{N}$ is said to be

• monotone on C if for any x, y ∈ C,

  $$\langle u-v, x-y\rangle\geq 0,~\forall u\in F(x),~v\in F(y);$$

• pseudomonotone on C if for any x, y ∈ C,

  $$\text{there exists}~u\in F(x) : \langle u, y-x\rangle\geq 0~\text{implies}~\forall v\in F(y)~:~\langle v, y-x\rangle\geq 0;$$

• quasimonotone on C if for any x, y ∈ C,

  $$\text{there exists}~u\in F(x) : \langle u, y-x\rangle> 0~\text{implies}~\forall v\in F(y)~:~\langle v, y-x\rangle\geq 0.$$

Proposition 2.3

(Rockafellar and Wets 2004) A multivalued mapping $F:C\rightrightarrows \mathbb {R}^{N}$ is said to be locally bounded if and only if for any bounded sequence {x_n} with u_n ∈ F(x_n), the sequence {u_n} is bounded.

Proposition 2.4

(He et al. 2019) Assume that the solution set of problem (1) Γ is nonempty and that $F:C\rightrightarrows \mathbb {R}^{N}$ is continuous. If either

• (i) F is monotone or pseudomonotone on C;

• (ii) F is quasimonotone on C and for any x^∗∈Γ with u^∗∈ F(x^∗) satisfying (1) such that

  $$\text{there exists}~~y^{*}\in C~:~\langle u^{*}, y^{*}-x^{*}\rangle\neq 0;$$

• (iii) F is quasimonotone on C with int C≠∅ and 0∉F(x^∗) for all x^∗∈Γ.

Then,

$$ \begin{array}{@{}rcl@{}} \langle u, y-x^{*}\rangle \geq 0~~\forall y\in C,~ u\in F(y), ~x^{*}\in {\Gamma}. \end{array} $$

(7)

Remark 2.5

We can see from Proposition 2.4 that condition (7) is a weaker condition than various monotonicity conditions. Thus, we shall assume for the rest of this paper, that the solution set of problem (1) Γ is nonempty and that Eq. 7 is satisfied.

Following Attouch and Cabot (2019a, pages 5, 10), we note that if x_n+ 1 = x_n + 𝜃_n(x_n − x_n− 1), then for all n ≥ 1, we have that

$$x_{n+1}-x_{n}=\left( \prod\limits_{j=1}^{n}\theta_{j}\right)(x_{1}-x_{0}),$$

which implies that

$$x_{n}=x_{1}+\left( \sum\limits_{j=1}^{n-1} \prod\limits_{j=1}^{l}\theta_{j}\right)(x_{1}-x_{0}).$$

Thus, {x_n} converges if and only if x₁ = x₀ or if $\sum \limits _{l=1}^{\infty }\prod \limits _{j=1}^{l}\theta _{j} <\infty$.

Therefore, we assume henceforth that

$$ \begin{array}{@{}rcl@{}} \sum\limits_{l=i}^{\infty}\left( \prod\limits_{j=i}^{l} \theta_{j}\right)<\infty~~\forall i\geq 1. \end{array} $$

(8)

Then, we can define the sequence {t_i} in $\mathbb {R}$ by

$$ \begin{array}{@{}rcl@{}} t_{i}:=\sum\limits_{l=i-1}^{\infty}\left( \prod\limits_{j=i}^{l} \theta_{j}\right)=1+\sum\limits_{l=i}^{\infty}\left( \prod\limits_{j=i}^{l} \theta_{j}\right), \end{array} $$

(9)

with the convention $\prod \limits _{j=i}^{i-1} \theta _{j}=1~\forall i\geq 1$.

Remark 2.6

Assumption (8) ensures that {t_i} is well-defined in Eq. 9 and

$$ \begin{array}{@{}rcl@{}} t_{i}=1+\theta_{i} t_{i+1},~\forall i\geq 1. \end{array} $$

(10)

The following proposition provides a criterion for ensuring assumption (8). In fact, this condition makes it possible to cover the usual situations.

Proposition 2.7

(Attouch and Cabot 2019a, Proposition 3.1) Let {𝜃_n} be a sequence such that 𝜃_n ∈ [0,1) for every n ≥ 1. Assume that

$$ \begin{array}{@{}rcl@{}} \lim\limits_{n\rightarrow \infty}\left( \frac{1}{1-\theta_{n+1}}-\frac{1}{1-\theta_{n}}\right)=c, \end{array} $$

for some c ∈ [0,1). Then, we have

• (i) Condition Eq. 8 holds, and $t_{n+1}\sim \frac {1}{(1-c)(1-\theta _{n})}$ as $n\rightarrow \infty$.

• (ii) The equivalence $1-\theta _{n} \sim 1-\theta _{n+1}$ holds true as $n\rightarrow \infty$. Hence, $t_{n+1}\sim t_{n+2}$ as $n\rightarrow \infty$.

Remark 2.8

Example of a sequence satisfying the assumptions of Proposition 2.7 (therefore, satisfying assumption (8)) is $\theta _{n}=1-\frac {\bar {\theta }}{n},$ $\bar {\theta }>1$.

Clearly,

$$ \begin{array}{@{}rcl@{}} \left( \frac{1}{1-\theta_{n+1}}-\frac{1}{1-\theta_{n}}\right)=\frac{1}{\bar{\theta}}(n+1)-\frac{1}{\bar{\theta}}n=\frac{1}{\bar{\theta}}. \end{array} $$

Hence,

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow \infty}\left( \frac{1}{1-\theta_{n+1}}-\frac{1}{1-\theta_{n}}\right)=\frac{1}{\bar{\theta}}. \end{array} $$

Recall that the above example falls within the setting of Nesterov’s extrapolation methods (for instance, see Attouch and Cabot 2019a; Beck and Teboulle 2009; Chambolle and Dossal 2015, Nesterov 1983).

The corresponding finite sum expression of {t_i} is defined for i, n ≥ 1, by

$$ \begin{array}{@{}rcl@{}} t_{i, n}:=\begin{cases} \sum\limits_{l=i-1}^{n-1}\left( \prod\limits_{j=i}^{l} \theta_{j}\right)=1+\sum\limits_{l=i}^{n-1}\left( \prod\limits_{j=i}^{l} \theta_{j}\right), & i\leq n,\\ 0, & \text{otherwise}. \end{cases} \end{array} $$

(11)

In the same manner, we have that {t_{i, n}} is well-defined and (see also Attouch and Cabot 2019a)

$$ \begin{array}{@{}rcl@{}} t_{i, n}=1+\theta_{i} t_{i+1, n} ~\forall i\geq 1,~n\geq i+1. \end{array} $$

(12)

The sequences {t_i} and {t_{i, n}} are very crucial to our convergence analysis. In fact, their effect can be seen in the following lemma which also plays a crucial role in establishing our convergence results.

Lemma 2.9

(Attouch and Cabot 2019a, page 42, Lemma B.1). Let {a_n},{𝜃_n} and {w_n} be sequences of real numbers satisfying

$$ \begin{array}{@{}rcl@{}} a_{n+1}\leq \theta_{n}a_{n}+w_{n} ~~~\text{for every} ~~n\geq 1. \end{array} $$

Assume that 𝜃_n ≥ 0 for every n ≥ 1.

• (a) For every n ≥ 1, we have

  $$ \begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{n}a_{i}\leq t_{1,n}a_{1}+\sum\limits_{i=1}^{n-1}t_{{i+1},n}w_{i}, \end{array} $$

  where the double sequence {t_{i, n}} is defined by Eq. 11.

• (b) Under Eq. 8, assume that the sequence {t_i} defined by Eq. 9 satisfies $\sum \limits _{i=1}^{\infty }t_{i+1}[w_{i}]_{+}<\infty$. Then, the series $\sum \limits _{i\geq 1}[a_{i}]_{+}$ is convergent, and

  $$ \begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{\infty}[a_{i}]_{+}\leq t_{1}[a_{1}]_{+}+\sum\limits_{i=1}^{\infty}t_{i+1}[w_{i}]_{+}~, \end{array} $$

  where $[t]_{+}:=\max \limits \{t,0\}$ for any $t\in \mathbb {R}$.

The following lemmas will also be needed in our convergence analysis.

Lemma 2.10

(Facchinei and Pang 2003) A point x^∗∈Γ if and only if x^∗ = P_C(x^∗− ρu) for some u ∈ F(x^∗) and ρ > 0.

Lemma 2.11

(Attouch and Cabot 2019a, page 7, Lemma 2.1). Let {x_n} be a sequence in $\mathbb {R}^{N}$, and let {𝜃_n} be a sequence of real numbers. Given $z\in \mathbb {R}^{N}$, define the sequence {Γ_n} by ${\Gamma }_{n}:=\frac {1}{2}\|x_{n}-z\|^{2}$. Then

$$ \begin{array}{@{}rcl@{}} {\Gamma}_{n+1}-{\Gamma}_{n}-\theta_{n}({\Gamma}_{n}-{\Gamma}_{n-1})&=& \frac{1}{2}(\theta_{n}+{\theta_{n}^{2}})\|x_{n}-x_{n-1}\|^{2}+\langle x_{n+1}-y_{n}, x_{n+1}-z\rangle \\ &&-\frac{1}{2}\|x_{n+1}-y_{n}\|^{2}, \end{array} $$

(13)

where y_n = x_n + 𝜃_n(x_n − x_n− 1).

Lemma 2.12

The following is well-known:

$$2\langle x,y\rangle=\|x\|^{2}+\|y\|^{2}-\|x-y\|^{2}=\|x+y\|^{2}-\|x\|^{2}-\|y\|^{2}~~\forall~x,y\in \mathbb{R}^{N}.$$

Lemma 2.13

(Konnov 1998) The number of iterations in Procedure A is finite and for any given $x\in \mathbb {R}^{N}$, it holds that

$$\|R(x)-y\|\leq \|x-y\|,~~\forall y\in C.$$

3 Proposed Methods

In this section, we present our methods and discuss their features. We begin with the following assumptions under which we obtain our convergence results.

Assumption 3.1

Suppose that the following hold:

• (a) The feasible set C is nonempty, closed and convex subset of $\mathbb {R}^{N}$.

• (b) $F:\mathbb {R}^{N}\rightrightarrows \mathbb {R}^{N}$ is locally bounded and continuous.

• (c) Γ is nonempty and satisfies condition (7).

• (d) 𝜃_n ∈ [0,1[ for all n ≥ 1 and there exists ε ∈ (0,1) such that for n large enough, we have

  $$ \begin{array}{@{}rcl@{}} (1-\varepsilon)(1-\theta_{n-1})\geq \theta_{n} t_{n+1}\left( 1+\theta_{n}+\left[\theta_{n-1}-\theta_{n}\right]_{+}\right). \end{array} $$

  (14)

We now present some criteria that guarantee assumptions (8) and (14).

Proposition 3.1

Assume that {𝜃_n} is a nondecreasing sequence that satisfies 𝜃_n ∈ [0,1[ ∀n ≥ 1 with $\lim \limits _{n \rightarrow \infty }\theta _{n}=\theta$ such that the following condition holds:

$$ \begin{array}{@{}rcl@{}} 1-3\theta>0. \end{array} $$

(15)

Then assumptions (8) and (14) hold.

Proof

Observe that 𝜃_n ≤ 𝜃 ∀n ≥ 1. Thus, we have that assumption (8) is satisfied and $t_{n}=\frac {1}{1-\theta } ~~\forall n\geq 1$ (see Attouch and Cabot 2019a). Now, observe that 1 − 3𝜃 > 0 implies that $(1-\theta )>\frac {\theta (1+\theta )}{1-\theta }$. This further implies that there exists 𝜖 ∈ (0,1) such that

$$ \begin{array}{@{}rcl@{}} (1-\epsilon)(1-\theta)\geq \frac{\theta(1+\theta)}{1-\theta}. \end{array} $$

(16)

Since 𝜃_n ≤ 𝜃 ∀n ≥ 1, we obtain from Eq. 16 that

$$ \begin{array}{@{}rcl@{}} (1-\epsilon)(1-\theta_{n-1})\geq \frac{\theta(1+\theta)}{1-\theta}\geq \theta_{n}t_{n+1}(1+\theta_{n}), \end{array} $$

(17)

for some 𝜖 ∈ (0,1). Since 𝜃_n− 1 ≤ 𝜃_n ∀n ≥ 1, we obtain that

$$ \begin{array}{@{}rcl@{}} \theta_{n}t_{n+1}(1+\theta_{n})=\theta_{n}t_{n+1}(1+\theta_{n}+[\theta_{n-1}-\theta_{n}]_{+}). \end{array} $$

Combining this with Eq. 17, we get that the assumption (14) is satisfied. □

Proposition 3.2

Suppose that 𝜃_n ∈ [0,1) and there exists $c\in [0,\frac {1}{2})$ such that

$$ \begin{array}{@{}rcl@{}} \lim_{n\rightarrow \infty}\left( \frac{1}{1-\theta_{n+1}}-\frac{1}{1-\theta_{n}}\right)=c \end{array} $$

(18)

and

$$ \begin{array}{@{}rcl@{}} \liminf\limits_{n\rightarrow \infty}(1-\theta_{n})^{2}>\limsup\limits_{n\rightarrow \infty}\frac{\theta_{n}(1+\theta_{n})}{1-2c}. \end{array} $$

(19)

Then assumption (14) holds.

Proof

From Eq. 19, we obtain that

$$ \begin{array}{@{}rcl@{}} \liminf\limits_{n\rightarrow \infty}(1-\theta_{n-1})^{2}>\limsup\limits_{n\rightarrow \infty}\frac{\theta_{n}(1+\theta_{n})}{1-2c}. \end{array} $$

(20)

Thus, there exists 𝜖 ∈ (0,1) sufficiently small enough such that

$$ \begin{array}{@{}rcl@{}} \liminf\limits_{n\rightarrow \infty}(1-\theta_{n-1})^{2}>\limsup\limits_{n\rightarrow \infty}\frac{\theta_{n}(1+\theta_{n})}{1-2c-\epsilon(1-c)}>\limsup\limits_{n \rightarrow \infty}\frac{\theta_{n}(1+\theta_{n})}{1-2c}. \end{array} $$

(21)

This implies that

$$ \begin{array}{@{}rcl@{}} (1+o(1))\theta_{n}(1+\theta_{n})&\leq [1-2c-\epsilon(1-c)+o(1)](1-\theta_{n-1})^{2}\\ &=[(1-\epsilon)(1-c)-(2c-c+o(1))](1-\theta_{n-1})^{2}\\ &\leq [(1-\epsilon)(1-c)-\theta_{n}(c+o(1))](1-\theta_{n-1})^{2}, \end{array} $$

which implies that

$$ \begin{array}{@{}rcl@{}} (1-\epsilon)(1-c)(1-\theta_{n-1})^{2} &\geq (1+o(1))\theta_{n}\left( 1+\theta_{n}+(1-\theta_{n-1})^{2}+o\left( (1-\theta_{n-1})^{2}\right)\right). \end{array} $$

(22)

Now, observe from Eq. 18 that

$$ \begin{array}{@{}rcl@{}} \theta_{n-1}-\theta_{n}+c(1-\theta_{n-1})(1-\theta_{n})=o\left( (1-\theta_{n-1})(1-\theta_{n})\right), \end{array} $$

which implies from Proposition 2.7(ii) that

$$ \begin{array}{@{}rcl@{}} \theta_{n-1}-\theta_{n} &=-c(1-\theta_{n-1})(1-\theta_{n})+o\left( (1-\theta_{n-1})(1-\theta_{n})\right)\\ &=-c(1-\theta_{n-1})^{2}+o(1-\theta_{n-1})^{2}~~ \text{as~~}~~ n\rightarrow \infty. \end{array} $$

This implies that

$$ \begin{array}{@{}rcl@{}} |\theta_{n-1}-\theta_{n}|&=|-c(1-\theta_{n-1})^{2}+o(1-\theta_{n-1})^{2}|\\ &\leq c(1-\theta_{n-1})^{2}+o(1-\theta_{n-1})^{2} ~~ \text{as~~}~~ n\rightarrow \infty. \end{array} $$

(23)

Combining (22) and (23), we obtain that

$$ \begin{array}{@{}rcl@{}} (1-\epsilon)(1-c)(1-\theta_{n-1})^{2} &\geq \left( 1+o(1)\right)\theta_{n}\left( 1+\theta_{n}+[\theta_{n-1}-\theta_{n}]_{+}\right). \end{array} $$

(24)

By Proposition 2.7, we have that $t_{n+1}\sim t_{n} \sim \frac {1}{(1-c)(1-\theta _{n-1})}$ as $n\rightarrow \infty$. Hence, Eq. 24 is equivalent to

$$ \begin{array}{@{}rcl@{}} (1-\epsilon)(1-c)(1-\theta_{n-1})^{2}&\geq \frac{\theta_{n}}{(1-c)(1-\theta_{n-1})}t_{n+1}\left( 1+\theta_{n}+[\theta_{n-1}-\theta_{n}]_{+}\right), \end{array} $$

which implies that assumption (14) holds. □

Remark 3.3

We mention that Proposition 3.1 and Proposition 3.2 provide some sufficient conditions for ensuring that assumptions (14) and (8) hold. That is, assumptions (14) and (8) are much more weaker conditions than the assumptions in both propositions. Note that similar conditions as in Propositions 3.1 and 3.2 have been used by other authors to ensure convergence of inertial methods (see Lorenz and Pock 2015; Thong and Hieu 2018; Thong and Hieu 2017 and the references therein). In fact, we shall see later that using the conditions in Proposition 3.1 and Proposition 3.2, we derive some corollaries of our results.

We now present the first method of this paper.

Algorithm 3.2.

• Step 0: Choose the sequence {𝜃_n} in [0,1) such that the condition from Eqs. 8 and 14 hold. Let $x_{1}, x_{0}\in \mathbb {R}^{N}$ be given arbitrary and fix $\gamma , \sigma \in (0, 1), 0<\rho _{0}\leq \rho _{1}<\infty$. Set $C_{1}=\mathbb {R}^{N}$ and n = 1.

• Step 1. Set

  $$ v_{n}=x_{n}+\theta_{n}(x_{n}-x_{n-1})$$

  and choose u_n ∈ F(v_n) and ρ_n ∈ [ρ₀, ρ₁]. Then, compute

  y_n = P_C(v_n − ρ_nu_n). If v_n = y_n: STOP. Otherwise, go to Step 2.

• Step 2. Compute

  $$z_{n}=\alpha_{n}y_{n}+(1-\alpha_{n}) v_{n}$$

  and choose the largest $\alpha \in \{\gamma , \gamma ^{2}, \gamma ^{3}, \dots \}$ such that there exists a point w_n ∈ F(z_n) satisfying

  $$ \begin{array}{@{}rcl@{}} \langle w_{n}, v_{n}-y_{n}\rangle \geq \sigma\langle u_{n}, v_{n}-y_{n}\rangle. \end{array} $$

  (25)

• Step 3. Set $C_{n}=\{y\in \mathbb {R}^{N} : \langle w_{n}, y-z_{n}\rangle \leq 0\}$ for n ≥ 2 and $C_{n}^{*}=\cap _{i=1}^{n} C_{i}$. Then, compute

  $$x_{n+1}=P_{C_{n}^{*}}(v_{n}).$$

Set n := n + 1 and go back to Step 1.

Lemma 3.4

Step 2 of Algorithm 3.2 is well-defined.

Proof

Let v ∈ C and u ∈ F(v). Define y := P_C(v − ρu),ρ > 0. If v = y, then by Lemma 2.10, we have that v is a solution. Now, if v≠y, then by Eq. 4,

$$ \begin{array}{@{}rcl@{}} \langle u, v-y\rangle=\frac{1}{\rho} \langle y-(v-\rho u)+(v-y), v-y\rangle\geq \frac{1}{\rho} \langle v-y, v-y\rangle>0. \end{array} $$

(26)

Now, suppose on the contrary that Step 2 is not well-defined, then we will have that, for any α > 0 and w ∈ F(z) with z = αy + (1 − α)v,

$$ \begin{array}{@{}rcl@{}} \langle w, v-y\rangle<\sigma\langle u, v-y\rangle. \end{array} $$

(27)

In particular, for $\alpha _{n}=\frac {1}{n^{2}}$ with z_n = α_ny + (1 − α_n)v, we have that z_n → v as $n\to \infty$. Since F is continuous, it is inner-semicontinuous. Thus, there exists w_n ∈ F(z_n) such that w_n → u with u ∈ F(v). Taking w as w_n in Eq. 27, and taking limit as $n\to \infty$, we obtain that

$$(1-\sigma)\langle u, v-y\rangle \leq 0,$$

which contradicts (26). Hence, Step 2 of Algorithm 3.2 is well-defined. □

Remark 3.5

Observe that Assumption 3.1 (c) ensures that Step 3 of Algorithm 3.2 is well-defined since ${\Gamma }\subset C_{n}^{*}$ and hence $C_{n}^{*}\neq \emptyset$ for all n ≥ 2. Indeed, for z ∈Γ, we obtain from Assumption 3.1 (c) that 〈w_n, z − z_n〉≤ 0 ∀n ≥ 2. Thus, z ∈ C_n ∀n ≥ 2, which follows that $z\in C_{n}^{*}~\forall n\geq 2$.

In the following, we present another method with a new linesearch (different from Eq. 25) with the aim of minimizing the number of evaluation of the multivalued mapping F in each search.

Algorithm 3.3.

• Step 0: Choose the sequence {𝜃_n} such that the condition from Eqs. 8 and 14 hold. Let $x_{1}, x_{0}\in \mathbb {R}^{N}$ be given arbitrary and fix $\gamma , \sigma \in (0, 1), 0<\rho _{0}\leq \rho _{1}<\infty$. Set $C_{1}=\mathbb {R}^{N}$ and n = 1.

• Step 1. Set

  $$ v_{n}=x_{n}+\theta_{n}(x_{n}-x_{n-1})$$

  and choose u_n ∈ F(v_n) and ρ_n ∈ [ρ₀, ρ₁]. Then, compute

  y_n = P_C(v_n − ρ_nu_n). If v_n = y_n: STOP. Otherwise, go to Step 2.

• Step 2. Compute

  $$z_{n}=\alpha_{n}y_{n}+(1-\alpha_{n}) v_{n}$$

  and choose the largest $\alpha \in \{\gamma , \gamma ^{2}, \gamma ^{3}, \dots \}$ such that there exists a point w_n ∈ F(z_n) satisfying

  $$\langle w_{n}, v_{n}-y_{n}\rangle\geq \frac{\sigma}{2} \|v_{n}-y_{n}\|^{2}.$$

• Step 3. Set $C_{n}=\{y\in \mathbb {R}^{N} : \langle w_{n}, y-z_{n}\rangle \leq 0\}$ for n ≥ 2 and $C_{n}^{*}=\cap _{i=1}^{n} C_{i}$. Then, compute

  $$x_{n+1}=P_{C_{n}^{*}}(v_{n}).$$

Set n := n + 1 and go back to Step 1.

Remark 3.6

• (a) Observe that if we choose a point u ∈ F(x) with y := P_C(x − ρu), then, by setting z = x − ρu in Eq. 6, we obtain that

  $$ \begin{array}{@{}rcl@{}} \langle u, x-y\rangle\geq \frac{\sigma}{2}\|x-y\|^{2}. \end{array} $$

  (28)

  Thus, using Eq. 28 and the continuity of F, we can see that Step 2 of Algorithm 3.3 is well-defined.

• (b) Our Algorithm 3.2 and Algorithm 3.3 have fewer evaluations of multivalued mapping F than Algorithm 1.3 and Algorithm 1.4.

4 Convergence Analysis for Algorithm 3.2

Lemma 4.1

Let {x_n} be a sequence generated by Algorithm 3.2 and {Γ_n} be defined by ${\Gamma }_{n}=\frac {1}{2}\|x_{n}-z\|^{2}$ for any z ∈Γ. Then, under assumption (8) and Assumption 3.1(c),(d), we have that

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{i=1}^{n-1}\left[t_{i+1, n}\left( (1-3\theta_{i})-(1-\theta_{i})\right)+t_{i, n}(1-\theta_{i-1})\right] \|x_{i}-x_{i-1}\|^{2}\\ &&{\kern22pt}\leq 2t_{1}|{\Gamma}_{1}-{\Gamma}_{0}|+2{\Gamma}_{0}+t_{1}(1-\theta_{0})\|x_{1}-x_{0}\|^{2}, \end{array} $$

where {t_{i, n}} is defined in Eq. 11.

Proof

First observe that

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x_{n}\|^{2}&=&\|x_{n+1}-2x_{n}+x_{n-1}-(x_{n-1}-x_{n})\|^{2}\\ &=& \|x_{n+1}-2x_{n}+x_{n-1}\|^{2}+\|x_{n-1}-x_{n}\|^{2}\\ &&+2\langle x_{n+1}-2x_{n}+x_{n-1}, x_{n}-x_{n-1}\rangle, \end{array} $$

which implies that

$$2\langle x_{n+1}-2x_{n}+x_{n-1}, x_{n}-x_{n-1}\rangle =\|x_{n+1}-x_{n}\|^{2}- \|x_{n+1}-2x_{n}+x_{n-1}\|^{2}-\|x_{n-1}-x_{n}\|^{2}.$$

Thus, we obtain that

$$ \begin{array}{@{}rcl@{}} {}\|x_{n+1}-v_{n}\|^{2}&=&\|x_{n+1}-x_{n}-(x_{n}-x_{n-1})+(1-\theta_{n})(x_{n}-x_{n-1})\|^{2}\\ &=& \|x_{n+1}-2x_{n}+x_{n-1}\|^{2}+(1-\theta_{n})^{2}\|x_{n}-x_{n-1}\|^{2}\\ &&+2(1-\theta_{n})\langle x_{n+1}-2x_{n}+x_{n-1}, x_{n}-x_{n-1}\rangle \\ &=& \|x_{n+1}-2x_{n}+x_{n-1}\|^{2}+(1-\theta_{n})^{2}\|x_{n}-x_{n-1}\|^{2}\\ &&+(1-\theta_{n})\left[\|x_{n+1}-x_{n}\|^{2}- \|x_{n}-x_{n-1}\|^{2}-\|x_{n+1}-2x_{n}+x_{n-1}\|^{2}\right]\\ &=& \theta_{n} \|x_{n+1}-2x_{n}+x_{n-1}\|^{2}+(1-\theta_{n})^{2}\|x_{n}-x_{n-1}\|^{2}\\ &&+(1-\theta_{n})\left[\|x_{n+1}-x_{n}\|^{2}- \|x_{n}-x_{n-1}\|^{2}\right]\\ &\geq & (1-\theta_{n})^{2}\|x_{n}-x_{n-1}\|^{2}+(1-\theta_{n})\left[\|x_{n+1}-x_{n}\|^{2}- \|x_{n}-x_{n-1}\|^{2}\right]. \end{array} $$

(29)

Let z ∈Γ, then by Remark 3.5, we have that $z\in C_{n}^{*}$. Thus, we obtain from Lemma 2.11 and Eq. 29 that

$$ \begin{array}{@{}rcl@{}} {}{\Gamma}_{n+1}-{\Gamma}_{n}-\theta_{n}({\Gamma}_{n}-{\Gamma}_{n-1})&=& \frac{1}{2}(\theta_{n}+{\theta_{n}^{2}})\|x_{n}-x_{n-1}\|^{2}+\langle x_{n+1}-v_{n}, x_{n+1}-z\rangle \\ &&-\frac{1}{2}\|x_{n+1}-v_{n}\|^{2}\\ &\leq & \frac{1}{2}(\theta_{n}+{\theta_{n}^{2}})\|x_{n}-x_{n-1}\|^{2}-\frac{1}{2}\|x_{n+1}-v_{n}\|^{2}\\ &\leq & \frac{1}{2}(\theta_{n}+{\theta_{n}^{2}})\|x_{n}-x_{n-1}\|^{2}-\frac{1}{2}(1-\theta_{n})^{2}\|x_{n}-x_{n-1}\|^{2}\\ &&-\frac{1}{2}(1-\theta_{n})\left[\|x_{n+1}-x_{n}\|^{2}- \|x_{n}-x_{n-1}\|^{2}\right]\\ &=& \frac{1}{2}(3\theta_{n}-1)\|x_{n}-x_{n-1}\|^{2} -\frac{1}{2}(1-\theta_{n})\\ &&\times\left[\|x_{n+1}-x_{n}\|^{2}- \|x_{n}-x_{n-1}\|^{2}\right], \end{array} $$

(30)

which implies from Lemma 2.9 (a) that

$$ \begin{array}{@{}rcl@{}} &&{\Gamma}_{n}-{\Gamma}_{0}= \sum\limits_{i=1}^{n}\left( {\Gamma}_{i}-{\Gamma}_{i-1}\right)\\ &\leq & t_{1, n}\left( {\Gamma}_{1}-{\Gamma}_{0}\right)+ \sum\limits_{i=1}^{n-1}t_{i+1, n}\left[\frac{1}{2}(3\theta_{i}-1)\|x_{i}-x_{i-1}\|^{2}-\frac{1}{2}(1-\theta_{i})\right.\\ &&\times\left. \left( \|x_{i+1}-x_{i}\|^{2}-\|x_{i}-x_{i-1}\|^{2}\right)\right]. \end{array} $$

Notice that t_1,n ≤ t₁. Thus, we obtain that

$$ \begin{array}{@{}rcl@{}} && \sum\limits_{i=1}^{n-1}t_{i+1, n}\left[(1-3\theta_{i})\|x_{i}-x_{i-1}\|^{2}+(1-\theta_{i})\left( \|x_{i+1}-x_{i}\|^{2}-\|x_{i}-x_{i-1}\|^{2}\right) \right]\\ &\leq & 2t_{1, n}({\Gamma}_{1}-{\Gamma}_{0})+2({\Gamma}_{0}-{\Gamma}_{n})\\ &\leq & 2t_{1}|{\Gamma}_{1}-{\Gamma}_{0}|+2{\Gamma}_{0}. \end{array} $$

(31)

□

Now, observe that

$$ \begin{array}{@{}rcl@{}} && \sum\limits_{i=1}^{n-1}t_{i+1, n}(1-\theta_{i})\left( \|x_{i+1}-x_{i}\|^{2}-\|x_{i}-x_{i-1}\|^{2}\right)\\ &= & \sum\limits_{i=1}^{n-1}\left( t_{i, n}(1-\theta_{i-1})-t_{i+1, n}(1-\theta_{i})\right)\|x_{i}-x_{i-1}\|^{2}\\ &&+t_{n, n}(1-\theta_{n-1})\|x_{n}-x_{n-1}\|^{2}-t_{1, n}(1-\theta_{0})\|x_{1}-x_{0}\|^{2}\\ &\geq & \sum\limits_{i=1}^{n-1}\left( t_{i, n}(1-\theta_{i-1})-t_{i+1, n}(1-\theta_{i})\right)\|x_{i}-x_{i-1}\|^{2}-t_{1}(1-\theta_{0})\|x_{1}-x_{0}\|^{2}. \end{array} $$

(32)

Combining (31) and (32), we get that

$$ \begin{array}{@{}rcl@{}} && \sum\limits_{i=1}^{n-1}t_{i+1, n}(1-3\theta_{i})\|x_{i}-x_{i-1}\|^{2}+\sum\limits_{i=1}^{n-1}\left( t_{i, n}(1-\theta_{i-1})-t_{i+1, n}(1-\theta_{i})\right)\|x_{i}-x_{i-1}\|^{2}\\ &\leq & 2t_{1}|{\Gamma}_{1}-{\Gamma}_{0}|+2 {\Gamma}_{0}+t_{1}(1-\theta_{0})\|x_{0}-x_{1}\|^{2}. \end{array} $$

That is,

$$ \begin{array}{@{}rcl@{}} && \sum\limits_{i=1}^{n-1}\left[t_{i+1, n}\left( (1-3\theta_{i})-(1-\theta_{i})\right)+t_{i, n}(1-\theta_{i-1})\right]\|x_{i}-x_{i-1}\|^{2}\\ &\leq & 2t_{1}|{\Gamma}_{1}-{\Gamma}_{0}|+2 {\Gamma}_{0}+t_{1}(1-\theta_{0})\|x_{0}-x_{1}\|^{2}. \end{array} $$

(33)

Lemma 4.2

Let {x_n} be a sequence generated by Algorithm 3.2. Then, under assumption (8) and Assumption 3.1(c),(d), we have that $\sum \limits _{n=1}^{\infty }(1-\theta _{n-1}) \|x_{n}-x_{n-1}\|^{2} < \infty$ and $\sum \limits _{n=1}^{\infty }\theta _{n}t_{n+1} \|x_{n}-x_{n-1}\|^{2}<\infty$.

Proof

From Eq. 12 and since t_i+ 1,n ≤ t_i+ 1, we obtain

$$ \begin{array}{@{}rcl@{}} &&t_{i+1, n}\left[(1-3\theta_{i})-(1-\theta_{i})\right]+t_{i, n}(1-\theta_{i-1})\\ &= & t_{i+1, n}\left[(1-3\theta_{i})-(1-\theta_{i})\right]+(1-\theta_{i-1})+\theta_{i} t_{i+1, n}(1-\theta_{i-1})\\ &= & t_{i+1, n}\left[(1-3\theta_{i})-(1-\theta_{i})+\theta_{i} (1-\theta_{i-1})\right]+(1-\theta_{i-1})\\ &= & (1-\theta_{i-1})-\theta_{i} t_{i+1, n}\left( 1-\theta_{i-1}\right)\\ &\geq & (1-\theta_{i-1})-\theta_{i} t_{i+1}\left( 1-\theta_{i-1}\right)\\ &\geq & (1-\theta_{i-1})-\theta_{i} t_{i+1}\left( 1+\theta_{i}+\left[\theta_{i-1}-\theta_{i}\right]_{+}\right). \end{array} $$

(34)

Using Eq. 34 in Lemma 4.1, we obtain that

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{i=1}^{n-1}(1-\theta_{i-1})-\theta_{i} t_{i+1}\left( 1+\theta_{i}+\left[\theta_{i-1}-\theta_{i}\right]_{+}\right)\|x_{i}-x_{i-1}\|^{2}\\ &\leq & 2t_{1}|{\Gamma}_{1}-{\Gamma}_{0}|+2 {\Gamma}_{0}+t_{1}(1-\theta_{0})\|x_{0}-x_{1}\|^{2}. \end{array} $$

We may assume without loss of generality that assumption (14) holds for every n ≥ 1. Then, we obtain that

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{n-1}\varepsilon (1-\theta_{i-1})\|x_{i}-x_{i-1}\|^{2} &\leq & 2t_{1}|{\Gamma}_{1}-{\Gamma}_{0}|+2 {\Gamma}_{0}+t_{1}(1-\theta_{0})\|x_{0}-x_{1}\|^{2}. \end{array} $$

Now, taking limit as $n\to \infty$, we get that

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{\infty}(1-\theta_{i-1}) \|x_{i}-x_{i-1}\|^{2} < \infty. \end{array} $$

(35)

Thus, the first conclusion of the lemma is established. To establish the second conclusion of the lemma, we employ assumption (14) again in Eq. 35 and obtain

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{\infty}\theta_{i} t_{i+1} \|x_{i}-x_{i-1}\|^{2} < \infty. \end{array} $$

□

Lemma 4.3

Let {x_n} be a sequence generated by Algorithm 3.2. Then, under assumption (8) and Assumption 3.1(c),(d), we have that

• (a) $\lim \limits _{n\to \infty } \|x_{n}-z\|$ exists for all z ∈Γ.

• (b) $\lim \limits _{n\to \infty } \|v_{n}-x_{n+1}\|=0$.

Proof

• (a) From Eq. 30, we obtain that

  $$ \begin{array}{@{}rcl@{}} {\Gamma}_{n+1}-{\Gamma}_{n} &\leq & \theta_{n}({\Gamma}_{n}-{\Gamma}_{n-1})+ \frac{1}{2}(\theta_{n}+{\theta_{n}^{2}})\|x_{n}-x_{n-1}\|^{2}-\frac{1}{2}\|x_{n+1}-v_{n}\|^{2}\\ &\leq & \theta_{n}({\Gamma}_{n}-{\Gamma}_{n-1})+\theta_{n}\|x_{n}-x_{n-1}\|^{2}-\frac{1}{2}\|x_{n+1}-v_{n}\|^{2}\\ &\leq & \theta_{n}({\Gamma}_{n}-{\Gamma}_{n-1})+\theta_{n}\|x_{n}-x_{n-1}\|^{2}. \end{array} $$

  (36)

  Thus, from Lemma 4.2 and Lemma 2.9 (b), we obtain that $\sum \limits _{n=1}^{\infty } \left [{\Gamma }_{n}-{\Gamma }_{n-1}\right ]_{+}<\infty$. This implies that $\lim \limits _{n\to \infty }{\Gamma }_{n}=\lim \limits _{n\to \infty }\frac {1}{2}\|x_{n}-z\|^{2}$ exists, which further gives that $\lim \limits _{n\to \infty }\|x_{n}-z\|$ exists for all z ∈Γ.

• (b) Now, using Eq. 36 and Lemma 2.9 (a), we obtain that

  $$ \begin{array}{@{}rcl@{}} {\Gamma}_{n}-{\Gamma}_{0}&=&\sum\limits_{i=1}^{n}\left( {\Gamma}_{i}-{\Gamma}_{i-1}\right)\\ &\leq & t_{1, n}\left( {\Gamma}_{1}-{\Gamma}_{0}\right)+\sum\limits_{i=1}^{n-1}t_{i+1, n}\left[\theta_{i} \|x_{i}-x_{i-1}\|^{2}-\frac{1}{2}\|x_{i+1}-v_{i}\|^{2}\right]. \end{array} $$

  (37)

  Since t_i+ 1,n ≤ t_i+ 1, we obtain from Eq. 37 and Lemma 4.2 that

  $$ \begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{n-1}t_{i+1, n}\|x_{i+1}-v_{i}\|^{2}{}&\leq &{} 2 {\Gamma}_{0}+2t_{1, n}({\Gamma}_{1}-{\Gamma}_{0}) +2\sum\limits_{i=1}^{n-1}t_{i+1, n}\theta_{i} \|x_{i}-x_{i-1}\|^{2}\\ {}&\leq &{}2 {\Gamma}_{0}{}+{}2t_{1}|{\Gamma}_{1}{}-{}{\Gamma}_{0}| +2\sum\limits_{i=1}^{\infty}t_{i+1}\theta_{i} \|x_{i}-x_{i-1}\|^{2}<\infty. \end{array} $$

  Since t_i+ 1,n = 0 for i ≥ n, letting n tend to $\infty$, we obtain that

  $$ \begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{\infty} t_{i+1}\|x_{i+1}-v_{i}\|^{2}<\infty. \end{array} $$

  (38)

  Replacing i with n in Eq. 38 and since t_n ≥ 1 for every n ≥ 1, we obtain from Eq. 38 that $\sum \limits _{n=1}^{\infty } \|x_{n+1}-v_{n}\|^{2}<\infty$. This implies that $\lim \limits _{n\to \infty } \|v_{n}-x_{n+1}\|=0$.

□

Remark 4.4

The main role of assumption (14) is to guarantee the condition

$$ \begin{array}{@{}rcl@{}} \sum\limits_{n=1}^{\infty}t_{n+1}\theta_{n}\|x_{n}-x_{n-1}\|^{2}<\infty, \end{array} $$

(39)

obtained in Lemma 4.2 above. Note that Lemma 4.3 holds true if we assume condition (39) directly. Moreover, if 𝜃_n ∈ [0,𝜃] for every n ≥ 1, where 𝜃 ∈ [0,1), then $t_{n}\leq \frac {1}{(1-\theta )}~~~\forall n\geq 1$. Under this setting, we have that condition (39) is guaranteed by the condition

$$ \begin{array}{@{}rcl@{}} \sum\limits_{n=1}^{\infty}\theta_{n}\|x_{n}-x_{n-1}\|^{2} <\infty. \end{array} $$

(40)

In other words, if we assume that condition (40) holds for 𝜃_n ∈ [0,𝜃] ∀n ≥ 1, with 𝜃 ∈ [0,1), then Lemma 4.3 holds. This assumption has been used by numerous authors to ensure convergence of inertial methods (see, for example, Alvarez and Attouch 2001; Chuang 2017; Lorenz and Pock 2015; Mainge 2008; Moudafi and Oliny 2003 and the references therein).

Furthermore, under the assumptions of Proposition 3.1, we obtain the following as corollaries of Lemma 4.2 and Lemma 4.3 respectively.

Corollary 4.5

Let {x_n} be a sequence generated by Algorithm 3.2 such that Assumption 3.1(c) holds. Suppose that {𝜃_n} is a nondecreasing sequence that satisfies 𝜃_n ∈ [0,1[ ∀n ≥ 1 with $\lim \limits _{n \rightarrow \infty }\theta _{n}=\theta$ such that 1 − 3𝜃 > 0. Then, we have that $\sum \limits _{n=1}^{\infty }(1-\theta _{n-1}) \|x_{n}-x_{n-1}\|^{2} < \infty$ and $\sum \limits _{n=1}^{\infty }\theta _{n}t_{n+1} \|x_{n}-x_{n-1}\|^{2}<\infty$.

Proof

By Proposition 3.1, we have that assumptions (8) and (14) hold. Hence, the proof follows from Lemma 4.2. □

Corollary 4.6

Let {x_n} be a sequence generated by Algorithm 3.2 such that Assumption 3.1(c) holds. Suppose that {𝜃_n} is a nondecreasing sequence that satisfies 𝜃_n ∈ [0,1[ ∀n ≥ 1 with $\lim \limits _{n \rightarrow \infty }\theta _{n}=\theta$ such that 1 − 3𝜃 > 0. Then,

• (a) $\lim \limits _{n\to \infty } \|x_{n}-z\|$ exists for all z ∈Γ.

• (b) $\lim \limits _{n\to \infty } \|v_{n}-x_{n+1}\|=0$.

Proof

It is similar to the proof of Corollary 4.5. □

Remark 4.7

Observe that Eq. 18 and Proposition 2.7 imply that condition (8) also holds in Proposition 3.2. Hence, by replacing assumptions (8) and (14) with the assumptions of Proposition 3.2 in Lemma 4.2 and Lemma 4.3, we also obtain corollaries of Lemma 4.2 and Lemma 4.3 in the same manner as Corollaries 4.5 and 4.6 respectively.

Remark 4.8

If we take the inertial factor 𝜃_n to be a constant (that is 𝜃_n = 𝜃 ∀n ≥ 1), then we obtain the following corollaries of Lemma 4.2 and Lemma 4.3.

Corollary 4.9

Let {x_n} be a sequence generated by Algorithm 3.2 such that Assumption 3.1(c) holds. Suppose that 𝜃_n = 𝜃 ∀n ≥ 1 with 𝜃 ∈ [0,1) such that

$$ \begin{array}{@{}rcl@{}} (1-\theta)^{2}>\theta(1+\theta). \end{array} $$

(41)

Then, we have that $\sum \limits _{n=1}^{\infty }(1-\theta ) \|x_{n}-x_{n-1}\|^{2} < \infty$ and $\sum \limits _{n=1}^{\infty }\frac {\theta }{1-\theta } \|x_{n}-x_{n-1}\|^{2}<\infty$. Consequently, we have $\sum \limits _{n=1}^{\infty }\|x_{n}-x_{n-1}\|^{2}<\infty$.

Proof

Since 𝜃_n = 𝜃 ∈ [0,1), we obtain for i ≥ 1 that $t_{i}=\sum \limits _{l=i-1}^{\infty }\theta ^{l-i+1}=\frac {1}{1-\theta }<\infty$. Thus, we get that assumption (8) holds. Note also from Eq. 41 that there exists 𝜖 ∈ (0,1) such that

$$ \begin{array}{@{}rcl@{}} (1-\epsilon)(1-\theta)\geq \frac{\theta(1+\theta)}{1-\theta}, \end{array} $$

which is equivalent to condition (14) since 𝜃_n = 𝜃 ∀n ≥ 1. Hence, all the assumptions of Lemma 4.2 are satisfied. Thus, the rest of the proof follows from Lemma 4.2. □

Corollary 4.10

Let {x_n} be a sequence generated by Algorithm 3.2 such that Assumption 3.1(c) holds. Suppose that 𝜃_n = 𝜃 ∀n ≥ 1 with 𝜃 ∈ [0,1) such that (1 − 𝜃)² > 𝜃(1 + 𝜃). Then,

• (a) $\lim \limits _{n\to \infty } \|x_{n}-z\|$ exists for all z ∈Γ.

• (b) $\lim \limits _{n\to \infty } \|v_{n}-x_{n+1}\|=0$.

Proof

The proof is similar to the proof of Corollary 4.9. □

We now return to a very important result for our convergence analysis, whose proof rely on the linesearch given in Algorithm 3.2.

Lemma 4.11

Let assumption (8) and Assumption 3.1 hold, and let the sequence {x_n} be generated by Algorithm 3.2. Then, $\lim \limits _{n\to \infty }\alpha _{n} \|y_{n}-v_{n}\|^{2}=0$. Moreover, if there exists a subsequence $\{x_{n_{k}}\}$ of {x_n} such that $\{x_{n_{k}}\}$ converges to x^∗ and x^∗∉Γ, then

• (a) $\liminf \limits _{k\to \infty } \alpha _{n_{k}}>0$;

• (b) $\lim \limits _{k\to \infty }\|v_{n_{k}}-y_{n_{k}}\|=0$.

Proof

From Eq. 4, Step 1, Step 2 and the fact that $x_{n+1}\in C_{n}^{*},$ we obtain that

$$ \begin{array}{@{}rcl@{}} \alpha_{n}\|v_{n}-y_{n}\|^{2}&=&\alpha_{n}\langle v_{n}-y_{n}, v_{n}-y_{n}\rangle\\ &\leq & \alpha_{n} \langle v_{n}-y_{n}, v_{n}-y_{n}\rangle +\alpha_{n} \langle y_{n}-v_{n}+\rho_{n} u_{n}, v_{n}-y_{n}\rangle\\ &=& \alpha_{n} \rho_{n} \langle u_{n}, v_{n}-y_{n}\rangle\\ &\leq & \frac{\alpha_{n} \rho_{n}}{\sigma} \langle w_{n}, v_{n}-y_{n}\rangle\\ &=& \frac{\rho_{n}}{\sigma} \langle w_{n}, v_{n}-z_{n}\rangle\\ &\leq & \frac{\rho_{n}}{\sigma} \left( \langle w_{n}, v_{n}-x_{n+1}\rangle +\langle w_{n}, x_{n+1}-z_{n}\rangle\right) \\ &\leq &\frac{\rho_{n}}{\sigma} \|w_{n}\| \|v_{n}-x_{n+1}\|. \end{array} $$

(42)

Since by Lemma 4.3, {x_n} is bounded, we have that {z_n} is also bounded. Moreover, since F is locally bounded, we obtain from Proposition 2.3 that {w_n} is bounded. Using this and the boundedness of {ρ_n}, we obtain from Eq. 42 and Lemma 4.3 that

$$ \begin{array}{@{}rcl@{}} \lim\limits_{n\to\infty}\alpha_{n} \|y_{n}-v_{n}\|^{2}=0. \end{array} $$

(43)

• (a) By Step 2, we have that {α_n}⊂ (0,1) is bounded. Thus, there exists a subsequence $\{\alpha _{n_{k}}\}$ of {α_n} such that $\liminf \limits _{k\to \infty } \alpha _{n_{k}}\geq 0$. In fact, we claim that $\liminf \limits _{k\to \infty } \alpha _{n_{k}}> 0$. Suppose on the contrary that $\liminf \limits _{k\to \infty } \alpha _{n_{k}}= 0$. Then, without loss of generality, we can choose a subsequence of $\{\alpha _{n_{k}}\}$ still denoted by $\{\alpha _{n_{k}}\}$ such that $\lim \limits _{k\to \infty } \alpha _{n_{k}}=0$.

Now, define $\bar {\alpha }_{n_{k}}:=\frac {\alpha _{n_{k}}}{\gamma },~~\bar {z}_{n_{k}}:= \bar {\alpha }_{n_{k}}y_{n_{k}}+(1-\bar {\alpha }_{n_{k}}) v_{n_{k}}$. Then, by the boundedness of $\{y_{n_{k}}-v_{n_{k}}\}$ and since $\alpha _{n_{k}}\to 0$ as $k\to \infty$, we obtain that

$$ \begin{array}{@{}rcl@{}} \lim_{k\to\infty}\| \bar{z}_{n_{k}}-v_{n_{k}}\|=0. \end{array} $$

(44)

Also, by Lemma 4.2, we obtain that $\lim \limits _{k\to \infty }\| x_{n_{k}}-v_{n_{k}}\|=\lim \limits _{k\to \infty } \theta _{n_{k}}\|x_{n_{k}}-x_{n_{k}-1}\|=0$. Thus, since $x_{n_{k}}\to x^{*}$, we have that $v_{n_{k}}\to x^{*}$. Using Assumption 3.1 (b), the boundedness of $\{v_{n_{k}}\}$ and Proposition 2.3, we obtain that $\{u_{n_{k}}\}$ is also bounded. Thus, we can choose a subsequence of $\{u_{n_{k}}\}$ still denoted by $\{u_{n_{k}}\}$ such that $u_{n_{k}}\to \bar {u}$. Since F is continuous, it is outer-semicontinuous. Hence, $\bar {u}\in F(x^{*})$. We also assume without loss of generality that $\rho _{n_{k}}\to \rho \in [\rho _{0}, \rho _{1}]$. Therefore, we obtain from the continuity of P_C that $y_{n_{k}}\to y^{*}$ as $k\to \infty$, where $y^{*}=P_{C}(x^{*}-\rho \bar {u})$.

Again, from Eq. 44, we obtain that $\bar {z}_{n_{k}}\to x^{*}$. Since F is inner-semicontinuous and $\bar {u}\in F(x^{*})$, we can choose a subsequence $w_{n_{k}}\in F(\bar {z}_{n_{k}})$ such that $\bar {w}_{n_{k}}\to \bar {u}$.

Now, from the definition of $\bar {z}_{n_{k}}$ and Step 2, we obtain that

$$ \begin{array}{@{}rcl@{}} \langle \bar{w}_{n_{k}}, v_{n_{k}}-y_{n_{k}}\rangle <\sigma \langle u_{n_{k}}, v_{n_{k}}-y_{n_{k}}\rangle. \end{array} $$

(45)

Thus, taking limit as $k\to \infty$, we obtain that

$$ \begin{array}{@{}rcl@{}} \langle \bar{u}, x^{*}-y^{*}\rangle \leq 0. \end{array} $$

(46)

On the hand, since x^∗∉Γ, we have from Lemma 2.10 that x^∗≠y^∗. Hence, we get

$$ \begin{array}{@{}rcl@{}} \langle \bar{u}, x^{*}-y^{*}\rangle=\frac{1}{\rho} \langle y^{*}-(x^{*}-\rho \bar{u})+(x^{*}-y^{*}), x^{*}-y^{*}\rangle>\frac{1}{\rho} \langle x^{*}-y^{*}, x^{*}-y^{*}\rangle>0, \end{array} $$

(47)

which is a contradiction to Eq. 46. Therefore, $\liminf \limits _{k\to \infty } \alpha _{n_{k}}>0$.

• (b) From (a), we have that $\liminf \limits _{k\to \infty } \alpha _{n_{k}}>0$. Thus, we obtain from Eq. 43 that

  $$ \begin{array}{@{}rcl@{}} 0\leq \limsup\limits_{k \rightarrow\infty}\|v_{n_{k}}-y_{n_{k}}\|^{2}&\leq \limsup\limits_{k\rightarrow \infty}\left( \alpha_{n_{k}}\|v_{n_{k}}-y_{n_{k}}\|^{2}\right)\left( \limsup\limits_{k\rightarrow\infty}\frac{1}{\alpha_{n_{k}}}\right)\\ &= \left( \limsup\limits_{k\rightarrow \infty}\alpha_{n_{k}}\|v_{n_{k}}-y_{n_{k}}\|^{2}\right)\left( \frac{1}{\liminf\limits_{k\rightarrow\infty}\alpha_{n_{k}}}\right)\\ &=0. \end{array} $$

  Therefore, we obtain that

  $$\lim\limits_{k\rightarrow\infty}\|v_{n_{k}}-y_{n_{k}}\|=0.$$

□

Now, we are in position to give the main theorem of this section.

Theorem 4.12

Let {x_n} be a sequence generated by Algorithm 3.2. Then, under assumption (8) and Assumption 3.1, we have that {x_n} converges to an element of Γ.

Proof

By Lemma 4.3, {x_n} is bounded. Thus, there exists a subsequence $\{x_{n_{k}}\}$ of {x_n} such that $\{x_{n_{k}}\}$ converges to some point x^∗. Also, we have that

$$ \begin{array}{@{}rcl@{}} \|v_{n_{k}}-x_{n_{k}}\|=\theta_{n_{k}}\|x_{n_{k}}-x_{{n_{k}}-1}\|\to 0,~\text{as}~k\to \infty. \end{array} $$

(48)

We now claim that x^∗∈Γ.

Suppose on the contrary that x^∗∉Γ. Then, it follows from Lemma 4.11 (b) and Eq. 48 that

$$ \begin{array}{@{}rcl@{}} \lim_{k\to \infty} y_{n_{k}}=\lim_{k\to \infty} P_{C}(v_{n_{k}}-\rho_{n_{k}}u_{n_{k}})=\lim_{k\to \infty} x_{n_{k}}=x^{*}. \end{array} $$

(49)

Now, without loss of generality, we may assume that $\rho _{n_{k}}\to {\rho ^{*}}$ and $u_{n_{k}}\to {u^{*}}$. Since F is continuous, it is outer-semicontinuous. Thus, we obtain that u^∗∈ F(x^∗). Therefore, we obtain from Eq. 49 that

$$ P_{C}(x^{*}-\rho^{*}u^{*})=x^{*}.$$

It then follows from Lemma 2.10 that x^∗∈Γ, which is a contraction. Hence, our claim holds.

We now show that {x_n} converges to x^∗.

Replacing z by x^∗ in Lemma 4.3, we obtain that $\lim \limits _{n\rightarrow \infty }\|x_{n}-x^{*}\|^{2}$ exists. Since x^∗ is an accumulation point of {x_n}, we obtain that {x_n} converges to x^∗. □

Remark 4.13

In view of Corollaries 4.5-4.10, we can obtain various corollaries of Theorem 4.12. Furthermore, in the case that 𝜃_n = 0 for all n ≥ 1, assumptions (8) and (14) are automatically satisfied. Moreover, we have in this case that t_n = 1 for all n ≥ 1. Hence, we can employ Procedure A (see page 1) to obtain similar result as in He et al. (2019, Theorem 3.1).

Algorithm 4.1.

• Step 0: Let $x_{1}\in \mathbb {R}^{N}$ be given arbitrary and fix $\gamma , \sigma \in (0, 1), 0<\rho _{0}\leq \rho _{1}<\infty$. Set $C_{1}=\mathbb {R}^{N}$, $\bar {x}_{1}=x_{1}$ and n = 1.

• Step 1. Apply Procedure A to obtain $x_{n}=R(\bar {x}_{n})$.

• Step 2. Choose u_n ∈ F(x_n) and ρ_n ∈ [ρ₀, ρ₁]. Then, compute

  y_n = P_C(x_n − ρ_nu_n). If x_n = y_n: STOP. Otherwise, go to Step 2.

• Step 3. Compute

  $$z_{n}=\alpha_{n}y_{n}+(1-\alpha_{n}) x_{n}$$

  and choose the largest $\alpha \in \{\gamma , \gamma ^{2}, \gamma ^{3}, \dots \}$ such that there exists a point w_n ∈ F(z_n) satisfying

  $$ \begin{array}{@{}rcl@{}} \langle w_{n}, x_{n}-y_{n}\rangle \geq \sigma\langle u_{n}, x_{n}-y_{n}\rangle. \end{array} $$

  (50)

• Step 4. Set $C_{n}=\{y\in \mathbb {R}^{N} : \langle w_{n}, y-z_{n}\rangle \leq 0\}$ for n ≥ 2 and $C_{n}^{*}=\cap _{i=1}^{n} C_{i}$. Then, compute

  $$\bar{x}_{n+1}=P_{C_{n}^{*}}(x_{n}).$$

  If $\bar {x}_{n+1}=x_{n}$, then stop. Otherwise, let n = n + 1 and return to Step 1.

Corollary 4.14 (see for example, He et al. (2019, Theorem 3.1))

Let {x_n} be a sequence generated by Algorithm 4.1 such that the following assumptions hold:

• (a) The set C is described as in procedure A (see page 1).

• (b) $F:C\rightrightarrows \mathbb {R}^{N}$ is locally bounded and continuous.

• (c) Γ is nonempty and satisfies condition (7).

Then, we have that {x_n} converges to an element of Γ.

Proof

It follows carefully from Lemma 2.13 and Theorem 4.12. □

Remark 4.15

Under the settings of Remark 4.13, we can obtain in general, similar result as in He et al. (2019, Theorem 3.2) without Procedure A.

Algorithm 4.2.

• Step 0: Let x₁ ∈ C be given arbitrary and fix $\gamma , \sigma \in (0, 1), 0<\rho _{0}\leq \rho _{1}<\infty$. Set $C_{1}=\mathbb {R}^{N}$ and n = 1.

• Step 1. Choose u_n ∈ F(x_n) and ρ_n ∈ [ρ₀, ρ₁]. Then, compute

  y_n = P_C(x_n − ρ_nu_n). If x_n = y_n: STOP. Otherwise, go to Step 2.

• Step 2. Compute

  $$z_{n}=\alpha_{n}y_{n}+(1-\alpha_{n}) x_{n}$$

  and choose the largest $\alpha \in \{\gamma , \gamma ^{2}, \gamma ^{3}, \dots \}$ such that there exists a point w_n ∈ F(z_n) satisfying

  $$ \begin{array}{@{}rcl@{}} \langle w_{n}, x_{n}-y_{n}\rangle \geq \sigma\langle u_{n}, x_{n}-y_{n}\rangle. \end{array} $$

  (51)

• Step 3. Set $C_{n}=\{y\in \mathbb {R}^{N} : \langle w_{n}, y-z_{n}\rangle \leq 0\}$ for n ≥ 2 and $C_{n}^{*}=\cap _{i=1}^{n} C_{i}$. Then, compute

  $${x}_{n+1}=P_{C}\cap {C_{n}^{*}}(x_{n}).$$

  If x_n+ 1 = x_n, then stop. Otherwise, let n = n + 1 and return to Step 1.

Corollary 4.16 (see, for example, He et al. (2019, Theorem 3.2))

Let {x_n} be a sequence generated by Algorithm 4.2 such that the following assumptions hold:

• (a) The feasible set C is a nonempty closed and convex subset of $\mathbb {R}^{N}$.

• (b) $F:C\rightrightarrows \mathbb {R}^{N}$ is locally bounded and continuous.

• (c) Γ is nonempty and satisfies condition (7).

Then, we have that {x_n} converges to an element of Γ.

Proof

It follows directly from Corollary 4.14. □

5 Convergence Analysis for Algorithm 3.3

Remark 5.1

Notice that Step 2 (the linesearch procedure) of Algorithm 3.2 is not utilized in the proof of Lemma 4.1-Lemma 4.3. Thus, Lemma 4.1-Lemma 4.3 hold automatically if {x_n} is generated by Algorithm 3.3. Therefore, we only need to prove the version of Lemma 4.11 and Theorem 4.12 corresponding to Algorithm 3.3 in this section.

Lemma 5.2

Let the sequence {x_n} be generated by Algorithm 3.3 such that assumption (8) and Assumption 3.1 are satisfied. Then, we have

• (a) $\lim \limits _{n\to \infty }\alpha _{n} \|y_{n}-v_{n}\|^{2}=0$.

• (b) If there exists a subsequence $\{x_{n_{k}}\}$ of {x_n} such that $\{x_{n_{k}}\}$ converges to x^∗, then $\lim \limits _{k\to \infty }\|v_{n_{k}}-y_{n_{k}}\|=0$.

Proof

• (a) From Eq. 4, Step 2 and the fact that $x_{n+1}\in C_{n}^{*},$ we obtain that

  $$ \begin{array}{@{}rcl@{}} \alpha_{n}\|v_{n}-y_{n}\|^{2} &\leq & \frac{2\alpha_{n}}{\sigma} \langle w_{n}, v_{n}-y_{n}\rangle\\ &\leq & \frac{2}{\sigma} \langle w_{n}, v_{n}-z_{n}\rangle\\ &\leq & \frac{2}{\sigma} \left( \langle w_{n}, v_{n}-x_{n+1}\rangle +\langle w_{n}, x_{n+1}-z_{n}\rangle\right) \\ &\leq &\frac{2}{\sigma} \|w_{n}\| \|v_{n}-x_{n+1}\|. \end{array} $$

  (52)

  Since {z_n} is bounded and F is locally bounded, we obtain from Proposition 2.3 that {w_n} is also bounded. Thus, we obtain from Eq. 52 and Lemma 4.3 that

  $$ \begin{array}{@{}rcl@{}} \lim\limits_{n\to\infty}\alpha_{n} \|y_{n}-v_{n}\|^{2}=0. \end{array} $$

  (53)

• (b) Since {α_n}⊂ (0,1) is bounded, we have that $\liminf \limits _{n\to \infty } \alpha _{n}\geq 0$.

We now consider two possible cases:

Case 1: Suppose that $\liminf \limits _{n\to \infty } \alpha _{n}=0$. Then, we can choose a subsequence of {α_n} denoted by $\{\alpha _{n_{k}}\}$ such that $\lim \limits _{k\to \infty } \alpha _{n_{k}}=0$ and

$$ \begin{array}{@{}rcl@{}} \lim\limits_{k\to\infty} \|v_{n_{k}}-y_{n_{k}}\|=t\geq 0. \end{array} $$

(54)

Now, define $\bar {\alpha }_{n_{k}}:=\frac {\alpha _{n_{k}}}{\gamma }$. Then, $\bar {z}_{n_{k}}:= \bar {\alpha }_{n_{k}}y_{n_{k}}+(1-\bar {\alpha }_{n_{k}}) v_{n_{k}}$. Since $\alpha _{n_{k}}\to 0$ as $k\to \infty$, we obtain that $\bar {\alpha }_{n_{k}}\to 0$ as $k\to \infty$. Hence,

$$ \begin{array}{@{}rcl@{}} \lim_{k\to\infty}\| \bar{z}_{n_{k}}-v_{n_{k}}\|=0. \end{array} $$

(55)

Now, from the definition of $\bar {z}_{n_{k}}$ and Step 2, we obtain that

$$\langle \bar{w}_{n_{k}},v_{n_{k}}-y_{n_{k}} \rangle <\frac{\sigma}{2}\|v_{n_{k}}-y_{n_{k}}\|^{2},$$

which implies that

$$ \begin{array}{@{}rcl@{}} 2\langle \bar{w}_{n_{k}}-u_{n_{k}},v_{n_{k}}-y_{n_{k}}\rangle+2\langle u_{n_{k}},v_{n_{k}}-y_{n_{k}} \rangle <\sigma \|v_{n_{k}}-y_{n_{k}}\|^{2}. \end{array} $$

(56)

Now, set $s_{n_{k}}:=v_{n_{k}}-\rho _{n_{k}} u_{n_{k}}$. Then, Eq. 56 becomes

$$2\langle \bar{w}_{n_{k}}-u_{n_{k}}, v_{n_{k}}-y_{n_{k}} \rangle+\frac{2}{\rho_{n_{k}}}\langle v_{n_{k}}- s_{n_{k}}, v_{n_{k}}-y_{n_{k}}\rangle <\sigma \|v_{n_{k}}-y_{n_{k}}\|^{2},$$

which implies that

$$ 2\langle \bar{w}_{n_{k}}-u_{n_{k}}, v_{n_{k}}-y_{n_{k}} \rangle+ \frac{1}{\rho_{n_{k}}}\left( \|v_{n_{k}}-y_{n_{k}}\|^{2}+\|s_{n_{k}}-v_{n_{k}}\|^{2}-\|s_{n_{k}}-y_{n_{k}}\|^{2}\right)<\sigma\|v_{n_{k}}-y_{n_{k}}\|^{2}. $$

That is,

$$ \begin{array}{@{}rcl@{}} \frac{1}{\rho_{n_{k}}}\left( \|s_{n_{k}}-v_{n_{k}}\|^{2}-\|s_{n_{k}}-y_{n_{k}}\|^{2}\right)<(\sigma-\frac{1}{\rho_{n_{k}}})\|v_{n_{k}}-y_{n_{k}}\|^{2}-2\langle \bar{w}_{n_{k}}-u_{n_{k}}, v_{n_{k}}-y_{n_{k}} \rangle. \end{array} $$

(57)

Now, by Lemma 4.2, we obtain that $\lim \limits _{k\to \infty }\| x_{n_{k}}-v_{n_{k}}\|=0$. Thus, since $x_{n_{k}}\to x^{*}$, we have that $v_{n_{k}}\to x^{*}$. Using Assumption 3.1 (b), the boundedness of $\{v_{n_{k}}\}$ and Proposition 2.3, we obtain that $\{u_{n_{k}}\}$ is also bounded. Thus, we can choose a subsequence of $\{u_{n_{k}}\}$ still denoted by $\{u_{n_{k}}\}$ such that $u_{n_{k}}\to \bar {u}$. Since F is continuous, it is outer-semicontinuous. Hence, $\bar {u}\in F(x^{*})$. We also assume without loss of generality that $\rho _{n_{k}}\to \rho \in [\rho _{0}, \rho _{1}]\subset [\rho _{0}, \frac {1}{\sigma })$. Again, from Eq. 55, we obtain that $\bar {z}_{n_{k}}\to x^{*}$. Since F is inner-semicontinuous and $\bar {u}\in F(x^{*})$, we can choose a subsequence $w_{n_{k}}\in F(\bar {z}_{n_{k}})$ such that $\bar {w}_{n_{k}}\to \bar {u}$.

Also, since $\{v_{n_{k}}\}$, $\{u_{n_{k}}\}$, $\{y_{n_{k}}\}$ and $\{\bar {w}_{n_{k}}\}$ are bounded, we can choose a subsequence {k_j} of {k} such that

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{\rho}\left[\limsup_{k\to \infty}\left( \|s_{n_{k}}-v_{n_{k}}\|^{2}-\|s_{n_{k}}-y_{n_{k}}\|^{2}\right)\right]\\ &\leq & \limsup_{k\to\infty}\left[\left( \sigma-\frac{1}{\rho_{n_{k}}}\right)\|v_{n_{k}}-y_{n_{k}}\|^{2}-2\langle \bar{w}_{n_{k}}-u_{n_{k}}, v_{n_{k}}-y_{n_{k}} \rangle\right]\\ &= & \lim_{j\to\infty}\left[\left( \sigma-\frac{1}{\rho_{n_{k_{j}}}}\right)\|v_{n_{k_{j}}}-y_{n_{k_{j}}}\|^{2}-2\langle \bar{w}_{n_{k_{j}}}-u_{n_{k_{j}}}, v_{n_{k_{j}}}-y_{n_{k_{j}}} \rangle\right]. \end{array} $$

Thus, we obtain from Eq. 54 that

$$ \begin{array}{@{}rcl@{}} \limsup_{k\to \infty}\left( \|s_{n_{k}}-v_{n_{k}}\|^{2}-\|s_{n_{k}}-y_{n_{k}}\|^{2}\right)&\leq & {\rho}(\sigma-\frac{1}{\rho})t. \end{array} $$

(58)

At this point, we claim that t = 0. Otherwise, Eq. 58 will become

$$\limsup_{k\to \infty}\left( \|s_{n_{k}}-v_{n_{k}}\|^{2}-\|s_{n_{k}}-y_{n_{k}}\|^{2}\right)\leq {\rho}(\sigma-\frac{1}{\rho})t<0.$$

But for $\varepsilon =\frac {-\rho \left (\sigma -\frac {1}{\rho }\right )}{2}t>0,$ there exists $N\in \mathbb {N}$ such that

$$\|s_{n_{k}}-v_{n_{k}}\|^{2}-\|s_{n_{k}}-y_{n_{k}}\|^{2} \leq \rho\left( \sigma-\frac{1}{\rho}\right)+\varepsilon=\frac{\rho\left( \sigma-\frac{1}{\rho}\right)}{2}<0~~\forall k\in \mathbb{N},~~k\geq N.$$

Thus, we obtain that

$$\|v_{n_{k}}-s_{n_{k}}\|<\|y_{n_{k}}-s_{n_{k}}\|~~~ \forall k\in \mathbb{N},$$

which is a contradiction to the definition of $y_{n_{k}}=P_{C}(v_{n_{k}}-\rho _{n_{k}}u_{n_{k}})$. Therefore, t = 0. Hence, Eq. 54 becomes

$$ \begin{array}{@{}rcl@{}} \lim\limits_{k\to\infty} \|v_{n_{k}}-y_{n_{k}}\|=0. \end{array} $$

Case 2: Suppose that $\liminf \limits _{n\to \infty } \alpha _{n}>0$. Then, we obtain from Eq. 53 that

$$ \begin{array}{@{}rcl@{}} 0\leq \limsup\limits_{k \rightarrow\infty}\|v_{n_{k}}-y_{n_{k}}\|^{2}&\leq \limsup\limits_{k\rightarrow \infty}\left( \alpha_{n_{k}}\|v_{n_{k}}-y_{n_{k}}\|^{2}\right)\left( \limsup\limits_{k\rightarrow\infty}\frac{1}{\alpha_{n_{k}}}\right)\\ &= \left( \limsup\limits_{k\rightarrow \infty}\alpha_{n_{k}}\|v_{n_{k}}-y_{n_{k}}\|^{2}\right)\left( \frac{1}{\liminf\limits_{k\rightarrow\infty}\alpha_{n_{k}}}\right)\\ &=0. \end{array} $$

Therefore, we obtain that

$$\lim\limits_{k\rightarrow\infty}\|v_{n_{k}}-y_{n_{k}}\|=0.$$

□

Theorem 5.3

Let {x_n} be a sequence generated by Algorithm 3.3. Then, under assumption (8) and Assumption 3.1, we have that {x_n} converges to an element of Γ.

Proof

By Lemma 4.3, {x_n} is bounded. Thus, there exists a subsequence $\{x_{n_{k}}\}$ of {x_n} such that $\{x_{n_{k}}\}$ converges to some point x^∗. Thus, we obtain from Lemma 5.2 (b) that

$$ \begin{array}{@{}rcl@{}} \lim\limits_{k\to\infty}\|v_{n_{k}}-y_{n_{k}}\|=0. \end{array} $$

(59)

Also, from Lemma 4.2, we obtain that

$$ \begin{array}{@{}rcl@{}} \lim\limits_{k\to\infty}\|v_{n_{k}}-x_{n_{k}}\|=0. \end{array} $$

(60)

Hence, from Eqs. 59 and 60, we obtain

$$ \begin{array}{@{}rcl@{}} \lim_{k\to \infty} y_{n_{k}}=\lim_{k\to \infty} P_{C}(v_{n_{k}}-\rho_{n_{k}}u_{n_{k}})=\lim_{k\to \infty} x_{n_{k}}=x^{*}. \end{array} $$

(61)

Now, without loss of generality, we may assume that $\rho _{n_{k}}\to {\rho ^{*}}$ and $u_{n_{k}}\to {u^{*}}$. Since F is continuous, it is outer-semicontinuous. Thus, we obtain that u^∗∈ F(x^∗). Therefore, we obtain from Eq. 61 that

$$ P_{C}(x^{*}-\rho^{*}u^{*})=x^{*}.$$

It then follows from Lemma 2.10 that x^∗∈Γ.

We now show that {x_n} converges to x^∗.

Replacing z by x^∗ in Lemma 4.3, we obtain that $\lim \limits _{n\rightarrow \infty }\|x_{n}-x^{*}\|^{2}$ exists. Since x^∗ is an accumulation point of {x_n}, we obtain that {x_n} converges to x^∗. □

Remark 5.4

Following Remark 4.13, we can also obtain various corollaries of Theorem 5.3.

6 Numerical Experiments

In this section, we discuss the numerical behavior of Algorithm 3.2 and Algorithm 3.3 using test examples taken from the literature. We only compare our methods with Algorithms 1.3 and 1.4 of He et al. (2019) since in He et al. (2019, Section 4), we have that the methods in He et al. (2019) are more efficient than most relevant methods in the literature.

The codes are implemented in Matlab 2016 (b). We perform all computations on a personal computer with an Intel(R) Core(TM) i5-2600 CPU at 2.30GHz and 8.00 Gb-RAM.

We consider the same set of examples considered in He et al. (2019, Section 4). We randomly choose $x_{0}, x_{1}\in \mathbb {R}^{N}$ and the inertial factor 𝜃_n satisfying assumptions (8) and (14).

Example 6.1

Consider the following convex non-smooth optimization problem (see also Dong et al. 2017; He et al. 2019)

$$ \begin{array}{@{}rcl@{}} \min\limits_{x \in C}\varphi (x), \end{array} $$

where $\varphi (x)=-x_{1}+20\max \limits \{{x_{1}^{2}}+{x_{2}^{2}}-1,0\}$ and $C=\{x\in \mathbb {R}^{2}_{+}:x_{1}+x_{2}\leq 1\}$. This problem is equivalent to the MVIP (1) with F(x) = ∂φ(x), where ∂φ(x) is the subdifferential of φ at x:

$$ \begin{array}{@{}rcl@{}} \partial \varphi (x)= \left\{ \begin{array}{ll} (-1+ 40x_{1},40x_{2}),&\text{if}~~\|x\|>1; \\ (-1,0),&\text{if}~~\|x\|<1;\\ \{(-1+ 40tx_{1},40tx_{2})|t\in [0,1]\}, &\text{if}~~ \|x\|=1. \end{array} \right. \end{array} $$

Then, we see that x^∗ = (1,0) is the unique solution of the problem, and the multivalued mapping F = ∂φ satisfies the assumptions of Assumption 3.1 (b).

For the parameters, we choose ρ_n ∈ (0,2),σ = 0.8, and γ = 0.7. Furthermore, we take ∥x_n − x^∗∥≤ 𝜖 as the termination criterion. We stress that these choices are the same as the ones considered by He et al. (2019) for their numerical experiments.

For 𝜖 = 10^− 7, we obtain the numerical results listed in Table 1 and Fig. 1, which show that our methods perfom better than Algorithm 1.3 and Algorithm 1.4 of He et al. (2019).

Table 1 Numerical results for Example 6.1 with 𝜖 = 10^− 7

Fig. 1

∥x_n − x^∗∥ vs Iteration numbers (n) for Example 6.1 with 𝜖 = 10^− 7: Top Left: Case 1; Top Right: Case 2; Bottom Left: Case 3; Bottom Right: Case 4

For 𝜖 = 10^− 10, it was observed in He et al. (2019, Section 4) that Algorithm 1.3 of He et al. (2019) does not work well because of the presence of Procedure A in the iterative steps. Therefore, in this setting, we shall compare our methods with only Algorithm 1.4 of of He et al. (2019). For this, we obtain the numerical results reported in Table 2 and Fig. 2, which show that our methods still perform better than Algorithm 1.4 of He et al. (2019).

Table 2 Numerical results for Example 6.1 with 𝜖 = 10^− 10

Fig. 2

∥x_n − x^∗∥ vs Iteration numbers (n) for Example 6.1 with 𝜖 = 10^− 10: Top Left: Case 1; Top Right: Case 2; Bottom Left: Case 3; Bottom Right: Case 4

We consider the following cases for the numerical experiments of Example 6.1.

• Case 1: x₁ = (0.5,− 0.25)^T, x₀ = (0.5,− 0.25)^T and $\theta _{n}=\frac {2n-1}{8n}$.

• Case 2: x₁ = (0.7,0.25)^T, x₀ = (0.5,0.25)^T and $\theta _{n}=\frac {2n-1}{8n}$.

• Case 3: x₁ = (− 1.5,1)^T, x₀ = (1,− 0.2)^T and $\theta _{n}=\frac {n-1}{n+4}$.

• Case 4: x₁ = (− 0.5,1.5)^T, x₀ = (− 0.5,1)^T and $\theta _{n}=\frac {n-1}{n+4}$.

Example 6.2

We next consider the following optimization problem which was also considered in He et al. (2019) and Ye and He (2015).

$$ \begin{array}{@{}rcl@{}} \min\limits_{x\in C}\varphi(x), \end{array} $$

where $C=\left \{x\in \mathbb {R}^{5}:x_{i}\geq 0,~~i=1,2,\cdots ,5,~{\sum }_{i=1}^{5}x_{i}=a,~a>0\right \}$ and $\varphi (x)=\frac {0.5\langle Hx,x \rangle +\langle q,x\rangle +1}{\sum \limits _{i=1}^{5}x_{i}}$. Furthermore, H denotes a positive diagonal matrix with the same element h taken from the interval (0.1,2) and q = (− 1,− 1,− 1,− 1,− 1). Clearly, this problem is equivalent to MVIP (1) with solution set ${\Gamma }=\{\frac {1}{5}(a,\cdots ,a)\},$ where F(x) = (φ₁(x),⋯ ,φ₅(x)) and

$$ \begin{array}{@{}rcl@{}} \varphi_{i}(x)=\frac{\partial \varphi(x)}{\partial x_{i}}=\frac{hx_{i}\sum\limits_{i=1}^{5}x_{i}-0.5h\sum\limits_{i=1}^{5}{x_{i}^{2}}-1}{\left( \sum\limits_{i=1}^{5}x_{i}\right)^{2}}. \end{array} $$

For 𝜖 = 10^− 4, σ = 0.3 and for some randomly chosen values of a, we compare our methods with Algorithm 1.4 of He et al. (2019). We obtain the numerical results displayed in Table 3 and Fig. 3, which show that our methods perform better than Algorithm 1.4 of He et al. (2019).

Table 3 Numerical results for Example 6.2 with 𝜖 = 10^− 4

Fig. 3

∥x_n − x^∗∥ vs Iteration numbers (n) for Example 6.2 with 𝜖 = 10^− 4: Top Left: Case 1; Top Right: Case 2; Bottom Left: Case 3; Bottom Right: Case 4

We consider the following cases for the numerical experiments of Example 6.2.

• Case 1: x₁ = (1,0.5,1,1.5,1)^T, x₀ = (1,0.5,1,1.5,1)^T, a = 5 and $\theta _{n}=\frac {2n-1}{8n}$.

• Case 2: x₁ = (3,2,2,1,2)^T, x₀ = (4.3,2.5,2.2,0.3,0.7)^T, a = 10 and $\theta _{n}=\frac {2n-1}{8n}$.

• Case 3: x₁ = (0.1,0.9,2,0.5,1.5)^T, x₀ = (0.3,0.5,1.2,2.5,0.5)^T, a = 5 and $\theta _{n}=\frac {n-1}{n+4}$.

• Case 4: x₁ = (2.1,2.9,2,1.5,1.5)^T, x₀ = (1.3,1.5,2.2,3.5,1.5)^T, a = 10 and $\theta _{n}=\frac {n-1}{n+4}$.

7 Conclusion

We propose two new inertial extrapolation projection-type methods for solving MVIPs when the multivalued mapping F is only required to be locally bounded without any monotonicity assumption. The first method uses a linesearch as in He et al. (2019, Algorithms 1 and 2) while the second method uses a different linesearch procedure with the aim of minimizing the number of evaluation of the multivalued mapping F in each search. Furthermore, our inertial techniques for establishing the convergence of these methods are quite different from the commonly used ones in most papers (see for example Cholamjiak et al.2018; Chuang 2017; Ochs et al. 2015; Lorenz and Pock 2015; Polyak 1964; Shehu and Cholamjiak 2019; Lorenz and Pock 2015; Mainge 2008; Moudafi and Oliny 2003; Shehu et al. 2019; Shehu et al. 2019; Thong and Hieu2018; Thong and Hieu 2017 and the references therein). Moreover, based on the weaker assumptions on the inertial factor in our methods, we derive several special cases of our methods. Finally, we consider some numerical implementations of our methods and compare them with the methods in He et al. (2019, Algorithms 1 and 2), in order to show the profits that we gain by introducing the new inertial extrapolation steps. In fact, in all our comparisons, the numerical results demonstrate that our methods perform better than the methods in He et al. (2019, Algorithms 1 and 2). Thus, our results improve and generalize many recent important results in this direction.