1 Introduction

With the rapid development of information technology and network science, multi-agent systems (MASs) are gradually applied in numerous aspects, such as autonomous unmanned vehicles [1], unmanned aerial vehicle formation [2], factory automation management [3], etc. Due to the large scale of the MASs, however, it is more difficult for such systems to return to normal state timely when they suffer from network attacks. At this time, each node of a networked system urgently needs to deal with the impact of the attacks to guarantee synchronization or consensus. Synchronization focuses on whether the nodes in the coupled network can achieve the same state, while consensus focuses on designing distributed control protocols for MASs to make the states of agents in the systems tend to be identical. In most cases, consensus is little different to synchronization. They are just for different networked systems. In [4] and [5], synchronization is studied for two kinds of neural networks. Specially, the sufficient conditions for ensuring secure synchronization are derived for the Markov jump neural networks in [4], where the mixed cyber-attack forms of deception attack and denial of service attack are considered.

Common network attacks include denial of service (DoS) attacks [6], distributed denial of service (DDoS) attacks [7], false data injection (FDI) attacks [8], etc. Among them, DoS attacks are relatively destructive. The working principle of DoS attacks is to compel the networked system too busy to process necessary instructions and occupy the key communication resources. DoS attacks will use packets to overwhelm the local system to disturb or intensely stop the corresponding local services answering the reasonable external demand, and sometimes will crumble the local system so that it doesn’t work properly. For example, In [9] and [10], security controls of signed MASs and switching MASs under DoS attacks are studied. In [11], based on the distributed control, group consensus of first-order MAS is achieved under DoS attacks and switching topologies. It can be seen that it is of great significance to further explore the impact of DoS attacks on achieving consensus of a MAS. In particular, the different characteristics of DoS attacks need to be further discussed.

Usually, DoS attacks include periodic DoS attacks, intermittent DoS attacks and random DoS attacks. The attack intervals of periodic DoS attacks are fixed, so it is easy to be implemented. However, long-term periodic DoS attacks are easy to be monitored and defended. In contrast, short-term and uncertain DoS attacks are more covert and not easy to be detected, such as intermittent DoS attacks [12]. In addition, the attack time and other characteristics of random DoS attacks have certain randomness, which will lead to random packet loss. The existing results usually regard random DoS attacks as Markov attacks [13], and apply this perspective to establish a model. This paper adopts the aperiodic DoS attack model, where the duration of DoS attack only needs to satisfy an assumption.

To deal with such attacks, the system needs to have the ability to recover within a limited time after being attacked to ensure that the system achieves the required collective dynamics. Consensus is a typical collective dynamics and a basic research topic in the distributed cooperative coordination of MASs. This means that all agents exchange information based on the local information interaction, therefore, an appropriate distributed consensus protocol (such as event-triggered control [14]) needs to be designed so that all states of agents eventually converge to a common value. Various studies are conducted on coordination of MASs without or with DoS attacks. Specifically, in [15], the finite-horizon robust event-triggered control is studied for nonlinear MASs with state delay, and consensus of nonlinear MASs is further discussed. In [16], due to the different network environment, the states of agents are different, and the consensus convergence state is also different from [15], that is, the finite mean square consensus criterion of second-order nonlinear MAS is established. In some cases, due to the different control strategies, the conditions for reaching consensus are also different. For example, in [17], consensus of MASs is realized via the proposed event-triggered control strategy without collecting global information. For example, in [18], a second-order MAS in directed networks is studied, and practical consensus is reached in a fixed time. Nowadays, the research on the convergence problem of second-order MASs is not rich, so we also choose such systems as the research direction.

When there is a cooperative relationship among agents in a MAS, the MAS is able to achieve consensus. In [19], the event-triggered communication (ETC), self-triggered communication (STC) scheme and the corresponding resilient control protocol are designed, and the sufficient conditions for the system to achieve consensus under DoS attacks are obtained. Both references [19] and [20] apply the event-triggered scheme, however, the MAS in [20] has both cooperative relationship and competitive relationship, so that the system tends to achieve bipartite consensus. In [21], the time factor on the basis of event-triggered control is considered and the leader selection scheme is given, and the sufficient conditions for achieving bipartite consensus are finally obtained. In [22], bipartite consensus of MASs is addressed by dealing with the influence of noise. By designing a time-varying stochastic bipartite consensus protocol to reduce the harmful effects of noise, the necessary and sufficient conditions for the proposed protocol are derived to guarantee mean square bipartite consensus.

With the expansion of the scale of MASs, achieving consensus in the whole system becomes more and more restrictive. Therefore, it is necessary to study group consensus, that is, the system is divided into several subgroups, and consensus can be reached for the agents in the same subgroup. In [23], group consensus of heterogeneous MASs under Markov transformation is considered. Similarly, in [24] and [25], heterogeneous MASs are also studied, and sufficient conditions for achieving group consensus are given. The difference is that [24] considers a system with input time delay and [25] considers a heterogeneous MAS with unknown parameters. In [26], a distributed dynamic event-triggered scheme is designed for MASs with input saturation. At the same time, an algorithm for estimating initial conditions is introduced. Based on the stability theory, the conditions of mean square local group consensus are derived.

Up to now, studies on group consensus of MASs suffered from DoS attacks are relatively rare. Especially under DoS attacks, the problem of group consensus of the MASs with multiple isolated leaders deserves further study.

Enlightened by the above discussions, this article mainly focuses on group consensus of the MAS with multiple isolated leaders. Main contribution of this article are highlighted below.

  1. (1)

    For a class of nonlinear MASs with multiple isolated leaders, group consensus of the nonlinear MASs is analyzed, and sufficient criteria for ensuring group consensus are derived.

  2. (2)

    DoS attacks, which can be conducted aperiodically or randomly, are considered in information interaction among agents. The effect of attack durations on consensus is clearly given.

  3. (3)

    The group consensus problem for a first-order nonlinear MAS is first studied under DoS attacks, and then the theoretical results are further generalized to the second-order nonlinear MAS.

  4. (4)

    Distributed cooperative controllers are designed for both first-order and second-order MASs. In addition, both the information interaction within the group and the information interaction between groups are considered in the controllers.

2 Preliminaries

We suppose that the MASs have M leader agents and N follower agents. These followers can be divided into M groups, and each group has an unique leader, \(N={\textstyle \sum _{j=1}^{M}N_j} \), where \(N_j\) denotes the total number of follower nodes in group \(j,~j=1,2,\ldots ,M\).

Define the set \(I_0=\left\{ N+1,\ldots ,N+M\right\} \), \(I_1=\left\{ 1,2,\ldots ,N_1\right\} \), \(I_k=\left\{ \sum _{j=1}^{k-1}N_j+ 1,\sum _{j=1}^{k-1}N_j +2,\ldots , \sum _{j=1}^{k-1}N_j +N_1\right\} ,~k=2,3,\ldots ,M\), and \(I=I_1\cup I_2\cup \ldots \cup I_M\). The node set is \(V_j=\left\{ n_i \mid i\in I_j\right\} ,~j=0,1,2,\ldots ,M\), where \(V_0\) is the node set of the leaders, and the rest sets are the follower nodes.

The triple \(G=\left( V, E, A \right) \) represents a weighted directed graph and also indicates the relationship among those followers. The set of followers is V, which has a partition \(V=V_1 \cup V_2 \cup \ldots \cup V_M\). The edge set is \(E \subseteq V\times V\). In addition, the adjacency matrix is \(A=\left[ a_{ij} \right] _{N\times N}\), where \(a_{ij}\ne 0\) if there is a directed edge from node j to node i, otherwise \(a_{ij}=0\).

The set of neighbours for node \(n_i\) is defined as:

$$\begin{aligned} N_{k,i}=\left\{ n_j\in V_k \mid \left( n_i, n_j \right) \in E \right\} ,~ k=1,2,\ldots ,M. \end{aligned}$$

Observing the information interaction between two agents in the same subsystem and also between two agents in the different subsystems, this paper divides the agents as follows [27]: \(V_k^{in}=\left\{ n_i\in V_k \mid \bigcup _{l\ne k}N_{l,i}=\emptyset ~\text {and}~n_i\notin \bigcup _{m\in I{\setminus } I_k}N_{k,m}\right\} \) is the k-th node set that does not exchange information with the nodes in other subsystems, and \(V_k^{out}=\left\{ n_i\in V_k \mid \bigcup _{l\ne k}N_{l,i}\ne \emptyset ~\text {or}~n_i\in \bigcup _{m\in I{\setminus } I_k}N_{k,m}\right\} \) is the k-th node set that exchanges information with the nodes in the k-th subsystem and other subsystems. According to the above definition, we can obtain \(V_k=V_k^{in}\cup V_k^{out}\) and \(V_k^{in}\cap V_k^{out}=\emptyset \). Define \(V^{in}=\bigcup _{k=1}^{M}V_k^{in}\) and \(V^{out}=\bigcup _{k=1}^{M}V_k^{out}. \)

Furthermore, let \(L=\left[ l_{ij} \right] _{N\times N} \) be the Laplacian matrix of G with \(l_{ii}=\sum _{j}^{N}a_{ij}\) and \(l_{ij}=-a_{ij}\) for \(i \ne j\).

Assumption 1

The subgraph of each group exists a spanning tree with one leader agent as its root.

DoS attack is one of the most common ways of the network attack, which compels the MASs too busy to process necessary instructions and occupies the key communication resources. Therefore, when the MASs are subjected to the DoS attack, the MASs cannot execute the designed control instructions, in other words, the control fails during the attack period. In this paper, an aperiodic DoS attack model is established. For the sake of storing energy for the next attack, the DoS attack needs to retain in a dormant state for a while after each attack. The specific description of the DoS attack of this paper is introduced below.

Let the DoS attack sequence be \(\left\{ t_\theta \right\} , \theta \in N^{*},~N^{*}=\left\{ 0,1,2,\ldots \right\} \). Then the DoS attack interval can be expressed as \(S_\theta =\left[ t_\theta , t_\theta +\tau _\theta \right) \), where \(\tau _\theta \) is the duration of the DoS attack. The intersection of all intervals where DoS attacks occur is an empty set, that is, there is no overlap, which can be expressed as \(t_\theta +\tau _\theta <t_{\theta +1},~\theta \in N^{*}\). For all given bounded time interval \(\left[ t_0, t \right] ,~t_0<t\), it is impossible to transmit information during the DoS attack time. These time intervals that cannot transmit information can be expressed as \(T_D=\bigcup S_\theta \bigcap \left[ t_0, t \right] \). In that case, the corresponding time interval for information transmission can be expressed as \(T_s=\left[ t_0, t \right] {\setminus } \bigcup S_\theta \).

Definition 1

[28] The DoS attack frequency is defined as \(F_s\left( t_0, t \right) =\frac{N_s\left( t_0, t \right) }{t-t_0}\), where \(N_s\left( t_0, t \right) \) is the number of attacks during the interval \(\left[ t_0, t \right] \).

Assumption 2

With regard to the duration of DoS attack, there exist \(T>1\) and \( \varphi > 0\) such that \(|T_D |< \varphi +\frac{t-t_0}{T}\), where T and \(\varphi \) are both constants, and \(|T_D |\) represents the time length of \(T_D\).

Remark 1

In the DoS attack interval, the communications between two adjacent agents will fail properly. This paper aims to study group consensus of the MASs suffered from DoS attacks and design a suitable controller so that followers in each subgroup can still approach the state information of the corresponding leader in that subgroup.

3 Main Results on Group Consensus

In this section, group consensus of first-order MASs is first analyzed, and then the result is further extended to the second-order MASs. Several sufficient conditions are obtained.

3.1 Group Consensus of First-Order MASs Under DoS Attacks

The leaders are modeled as

$$\begin{aligned} {\dot{x}_{k}^{*}}(t) = f\left( {x_{k}^{*}(t),t}\right) ,~k\in I_{0}, \end{aligned}$$
(1)

and the follower agents are represented as

$$\begin{aligned} {\dot{x}}_{i}(t) = f\left( {x_{i}(t),t}\right) + \mu _{i}(t),~i\in I, \end{aligned}$$
(2)

where \(x_{k}^{*}(t) \in R^{n}\) are the position states of leaders, \( x_{i}(t) \in R^{n}\) are the position states of follower agents, \(f\left( {x_{k}^{*}(t),t} \right) \), \(f\left( {x_{i}(t),t} \right) \in R^{n}\) are nonlinear functions satisfying Lipschitz condition, and \(\mu _{i}(t) \in R^{n}\) are external controllers to be designed.

Definition 2

If first-order nonlinear MASs (1)-(2) are in accord with \(\lim _{t \rightarrow \infty } \left\| x_i\left( t \right) - x_k^*\left( t \right) \right\| =0,~i\in I_k\) under any initial conditions, then the group consensus of MASs (1)-(2) under DoS attacks is said to be realized.

Assumption 3

For arbitrary variables \(w_1,~w_2\in R^{n}\), there is a non-negative real number \(\rho \) such that the nonlinear function satisfies

$$\begin{aligned} \left\| {f\left( {w_1,t} \right) - f\left( {w_2,t} \right) }\right\| \le \rho \left\| {w_1 - w_2} \right\| . \end{aligned}$$

The following rules are made for information interaction.

(i):

When \(n_{i}\) \(\in \) \(V^{in}(i \in I)\) are the nodes whose leader’s state of the subsystem is known, and the information interaction in this subsystem is transmitted by the position state \(x_{i}(t)\), and the error state is expressed as \(e_{i}(t)= x_{i}(t) - x_{i}^{*}(t),\) where \(x_{i}^{*}(t)= x_{k}^{*}(t)\) for \(i \in I_{k},~k = 1,2,\ldots ,M\).

(ii):

When \(n_{i}\) \(\in \) \(V^{out}(i \in I)\) are the nodes whose leader’s state of the subsystem is known, the states of the out-group neighbors are known and the leader’s state of those out-group neighbors is unknown, the information interaction in this subsystem is transmitted by the position state \(x_{i}(t)\) and the out-group information exchange is transmitted by the error of the position state \(e_{i}(t)=x_{i}(t) - x_{i}^{*}(t)\), where \(x_{i}^{*}(t) = x_{k}^{*}(t)\) for \(i \in I_{k},~k = 1,2,\ldots ,M\).

Next, based on the information interaction of the above two rules, that is, the information interaction within the group and the information interaction between groups, we design the external controller for first-order MASs as

$$\begin{aligned} \begin{array}{ll} \mu _{i}(t) = &{} \alpha c\left[ {\sum \limits _{j \in V_{k}}{a_{ij}\left( {x_{j}(t) - x_{i}(t)} \right) }} + b_{i}\left( {x_{k}^{*}(t) - x_{i}(t)} \right) \right. \\ &{}+ \left. {\sum \limits _{j\in \left( V\backslash V_{k} \right) }{a_{ij}\left( {e_j(t) - e_i(t)} \right) }} \right] ,~i \in V_{k}, \end{array} \end{aligned}$$
(3)

where \(c\ge 0\) represents the controller gain and \(\alpha >0\) indicates the coupling strength. When the MASs suffer from DoS attacks, \(c = 0\). Accordingly, when there is no attack, \(c > 0\). \(a_{ij}\) refers to the weight for the edge between the ith node and the jth node. Additionally, \(b_i\) refers to pinning coupling strength of the ith node and its leader. We define matrix \(B=diag\left\{ b_1, b_2,\ldots ,b_N \right\} \), \( H=\left[ h_{ij} \right] _{N\times N}\), \(H=L+B\), \( H^{'}=\frac{H+H^T}{2}\).

Based on the properties of the Laplacian matrix, the external controller (3) can also be transformed to

$$\begin{aligned} \begin{array}{ll} \mu _{i}(t) &{}= \alpha c\left[ \sum \limits _{j \in V_{k}}a_{ij}\left( x_{j}(t) - x_{k}^{*}(t)\right) - \left( \sum \limits _{j \in V_{k}}a_{ij} + b_{i}\right) \left( x_{i}(t) - x_{k}^{*}(t) \right) \right. \\ &{}~~+\left. {\sum \limits _{j \in {V\backslash V}_{k}}{a_{ij}e_{j}(t)}} - {\sum \limits _{j \in {V\backslash V}_{k}}{a_{ij}e_{i}(t)}}\right] \\ &{}= \alpha c\left[ {{\sum \limits _{j \in V_{k}}{a_{ij}e_{j}(t) - \left( {\sum \limits _{j \in V_{k}}{a_{ij} + {\sum \limits _{j \in {V\backslash V}_{k}}{a_{ij}}} + b_{i}}} \right) e_{i}(t)}} + {\sum \limits _{j \in {V\backslash V}_{k}}{a_{ij}e_{j}(t)}}} \right] \\ &{}= \alpha c\left[ {{\sum \limits _{j \in V_{k},i \ne j}{{- l}_{ij}e_{j}(t) - \left( {l_{ii} + b_{i}} \right) e_{i}(t)}} - {\sum \limits _{j \in {V/V}_{k}}{l_{ij}e_{j}(t)}}} \right] \\ &{}= - \alpha c\left[ {{\sum \limits _{j \in V}{l_{ij}e_{j}(t)}} + b_{i}e_{i}(t)} \right] \\ &{}= - \alpha c{\sum \limits _{j \in V}{h_{ij}e_{j}(t)}}, \end{array} \end{aligned}$$

therefore, for \(t\in \left[ t_\theta +\tau _\theta , t_{\theta +1} \right) , ~\theta \in N^{*}\), DoS attack is dormant and the error system of the MASs can be expressed as

$$\begin{aligned} \begin{array}{ll} {\dot{e}}_{i}(t) &{}= {\dot{x}}_{i}(t) - {\dot{x}_{k}^{*}}(t) \\ &{}=- \alpha c{\sum \limits _{j \in V}{h_{ij}e_{j}(t)}} + \left[ {f\left( {x_{i}(t),t} \right) - f\left( {x_{k}^{*}(t),t} \right) } \right] , \end{array} \end{aligned}$$
(4)

where \(e_{i}(t)=x_{i}(t) - x_{i}^{*}(t)\). Reformulate the error systems (4) into a compact form

$$\begin{aligned} \dot{e}(t) = - \alpha c\left( {L + B} \right) \otimes I_n e(t) + F\left( {x,t} \right) = - \alpha cH \otimes I_ne(t) + F(t), \end{aligned}$$
(5)

where \(e(t) = \left[ {e_{1}^{T}(t),e_{2}^{T}(t),\ldots ,e_{N}^{T}(t)} \right] ^{T}\) and \(F\left( {t} \right) = \left[ {F_{1}^{T}(t),F_{2}^{T}(t),\ldots , F_{N}^{T}(t)} \right] ^{T}\) with \(F_{i}(t) = f\left( {x_{i}(t),t} \right) - f\left( {x_{k}^{*}(t),t} \right) ,~i = 1,2,\ldots ,N. \)

When \(t\in \left[ t_{\theta }, t_\theta +\tau _\theta \right) , ~\theta \in N^{*}\), DoS attack is active and the external control is failing, that is \(c=0\). Then, the error system of the MASs can be expressed as

$$\begin{aligned} \dot{e}(t) = F(t). \end{aligned}$$
(6)

In fact, system (6) can be written uniformly to system (5), which becomes system (6) if \(c=0\). Next, we present the theoretical result on guaranteeing group consensus of the first-order MASs (1) and (2) suffered from the DoS attacks via the distributed cooperative controller (3).

Theorem 1

When the assumptions 1 and 3 are true, the first-order MASs (1) and (2) under the DoS attacks can achieve group consensus via the distributed cooperative controller (3) if the following conditions hold:

\((a_1)\) \(c > \frac{\rho ^{2} + 1}{2\alpha \lambda _{\min }\left( H' \right) }\);

\((b_1)\) \(T > \frac{2\alpha c \lambda _{\min }\left( H' \right) }{2\alpha c \lambda _{\min }\left( H' \right) - \rho ^{2} - 1}\).

Proof

Lyapunov function is designed as

$$\begin{aligned} V(t) = \frac{1}{2}e^{T}(t)e(t). \end{aligned}$$

Then, computing the derivative of V(t) derives

$$\begin{aligned} \begin{array}{ll} \dot{V}(t) &{}= e^{T}(t)\dot{e}(t) \\ &{}= e^{T}(t)\left( {- \alpha cH\otimes I_{n}e(t)} \right) + e^{T}(t)F(t) \\ &{}\le e^{T}(t)\left( {- \alpha cH' \otimes I_{n}e(t)} \right) + \frac{1}{2}e^{T}(t)e(t) + \frac{1}{2}F^{T}(t)F(t) \\ &{}{\le e}^{T}(t)\left( {- \alpha c\lambda _{\min }\left( {H'} \right) e(t)} \right) + \frac{1}{2}e^{T}(t)e(t) + \frac{1}{2}\rho ^{2}e^{T}(t)e(t) \\ &{}= e^{T}(t)\left( {- \alpha c\lambda _{\min }\left( {H'} \right) + \frac{1}{2} + \frac{1}{2}\rho ^{2}} \right) e(t) \\ &{}= 2\left( {- \alpha c\lambda _{\min }\left( {H'} \right) + \frac{1}{2} + \frac{1}{2}\rho ^{2}} \right) V(t) \\ &{}= \left( {- 2\alpha c\lambda _{\min }\left( {H'} \right) + 1 + \rho ^{2}} \right) V(t). \end{array} \end{aligned}$$

When \(t \in \left[ t_{\theta },t_{\theta } + \tau _{\theta } \right) \), DoS attacks occur, that is, \(c =0\), therefore,

$$\begin{aligned} \dot{V}(t) \le \left( 1 + \rho ^{2} \right) V(t),t \in \left[ t_{\theta },t_{\theta } + \tau _{\theta } \right) . \end{aligned}$$

When \(t \in \left[ t_{\theta } + \tau _{\theta },t_{\theta + 1} \right) \), \(c >0\), hence,

$$\begin{aligned} \dot{V}(t) \le \left( {- 2\alpha c\lambda _{\min }\left( {H'} \right) + 1 + \rho ^{2}} \right) V(t),t \in \left[ {t_{\theta } + \tau _{\theta },t_{\theta + 1}} \right) . \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{array}{ll} \dot{V}(t) &{}\le V\left( t_{0} \right) e^{{({- 2\alpha c\lambda _{\min }{(H')} + 1 + \rho ^{2}})}{({t - t_{0}})} + (2\alpha c\lambda _{\min }{(H')})(\varphi + \frac{t - t_{0}}{T})} \\ &{}= e^{2\alpha c\lambda _{\min }{(H')}\varphi }e^{{({- 2\alpha c\lambda _{\min }{(H')} + 1 + \rho ^{2} + \frac{2\alpha c\lambda _{\min }{(H')}}{T}})}{({t - t_{0}})}}. \end{array} \end{aligned}$$

According to conditions \((a_1)\) and \((b_1)\),

$$\begin{aligned} - 2\alpha c\lambda _{\min }\left( H' \right) + 1 + \rho ^{2} + \frac{2\alpha c\lambda _{\min }\left( H' \right) }{T} < 0, \end{aligned}$$

consequently, it follows from Lyapunov stability theory that \(\lim _{t \rightarrow \infty } V(t)=0\), that is \(\lim _{t \rightarrow 0}\left\| e(t) \right\| =0\).

In a word, group consensus of the MASs (1) and (2) is reached, and the theorem is proved. \(\square \)

Remark 2

According to Theorem 1, one knows that group consensus has a requirement on the duration of the DoS attacks. In addition, when the controller gain and the attack duration satisfy the conditions \((a_1)\) and \((b_1)\) respectively, group consensus of the MASs (1) and (2) can still be reached based on distributed protocol (3).

3.2 Grouping Consensus of Second-Order MASs Under DoS Attacks

The leaders dynamics are given as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{k}^{*}(t)=v_{k}^{*}(t), \\ \dot{v}_{k}^{*}(t)=f\left( x_{k}^{*}, v_{k}^{*}, t\right) , \end{array} \quad k \in I_{0},\right. \end{aligned}$$
(7)

and the followers dynamics are modeled as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{i}(t)=v_{i}(t), \\ \dot{v}_{i}(t)=f\left( x_{i}(t), v_{i}(t), t\right) +\mu _{i}(t), \end{array} \quad i\in I,\right. \end{aligned}$$
(8)

where \({x}_{k}^{*}(t)\in R^{n}\) are the position states of leaders, \(x_i(t)\) are the position states of follower agents, \({v}_{k}^{*}(t)\in R^{n}\) are the velocity states of the leaders, \(v_i(t)\) are the velocity states of follower agents, \(f\left( {x_{k}^{*}(t),{v}_{k}^{*}(t),t} \right) \), \(f\left( {x_{i}(t),{v}_{i}(t),t} \right) \in R^{n}\) are nonlinear functions satisfying Lipschitz condition, and \(\mu _{i}(t) \in R^{n}\) are external controllers to be designed.

Definition 3

If second-order nonlinear MASs (7) and (8) are in accord with the formulation \(\lim _{t \rightarrow \infty } \left\| x_i\left( t \right) - x_k^*\left( t \right) \right\| =0 \) and \(\lim _{t \rightarrow \infty } \left\| v_i\left( t \right) - v_k^*\left( t \right) \right\| =0\) under any initial conditions for any \(i\in I_k\), then group consensus of MASs (7) and (8) under DoS attacks is said to be realized.

Assumption 4

For any variables \(z_1\), \(z_2\), \(w_1\), \(w_2\) \(\in \) \(R^n\), there are real numbers \(\rho _1\ge 0\) and \(\rho _2\ge 0\) such that

$$\begin{aligned} \left\| f(z_1,z_2,t)-f(w_1,w_2,t)\right\| \le \rho _1 \left\| z_1-w_1 \right\| + \rho _2 \left\| z_2-w_2 \right\| . \end{aligned}$$

The following rules are made for information interaction.

(i) When \(n_{i}\) \(\in \) \(V^{in}(i \in I)\) are the nodes whose leader’s state of the subsystem is known, and the information interaction in this subsystem is transmitted by the position state \(x_{i}(t)\) and the velocity state \(v_{i}(t)\). Additionally, the error states are expressed as \(e_{i}^{(1)}(t) =x_{i}(t) -x_{i}^{*}(t)\) and \( e_{i}^{(2)}(t) =v_{i}(t) -v_{i}^{*}(t)\), where \(x_{i}^{*}(t) = x_{k}^{*}(t)\) and \(v_{i}^{*}(t) =v_{k}^{*}(t)\), \(i \in I_{k}\), \(k=1,2, \ldots , M\).

(ii) When \(n_{i}\) \(\in \) \(V^{out}(i \in I)\) are the nodes whose leader’s state of the subsystem is known, the states of the out-group neighbors are known and the leader’s state of those out-group neighbors is unknown, the information interaction in this subsystem is transmitted by the position state \(x_{i}(t)\) and the velocity state \(v_{i}(t)\) and the out-group information exchange is transmitted by the errors of the position state \(e_{i}^{(1)}(t)=x_{i}(t) -x_{i}^{*}(t)\) and the velocity state \( e_{i}^{(2)}(t) =v_{i}(t) -v_{i}^{*}(t)\), where \(x_{i}^{*}(t) = x_{k}^{*}(t)\) and \(v_{i}^{*}(t) =v_{k}^{*}(t)\), \(i \in I_{k}\), \(k=1,2, \ldots , M\).

Based on the information interaction of the above two rules, which consider the information interaction within the group and the information interaction between groups, the second-order cooperative controller is proposed as

$$\begin{aligned} \begin{array}{ll} \mu _{i}(t)= &{} \alpha c\left[ \sum _{j \in V_{k}} a_{i j}\left( x_{j}(t)-x_{i}(t)\right) +b_{i}\left( x_{k}^{*}(t)-x_{i}(t)\right) + \right. \\ &{}\left. \sum _{j \in \left( V \backslash V_{k}\right) } a_{i j}\left( {e}_{j}^{(1)}(t)-{e}_{i}^{(1)}(t)\right) \right] \\ &{}+\beta c\left[ \sum _{j \in V_{k}} a_{i j}\left( v_{j}(t)-v_{i}(t)\right) +b_{i}\left( v_{k}^{*}(t)-v_{i}(t)\right) + \right. \\ &{}\left. \sum _{j \in \left( V \backslash V_{k}\right) } a_{i j}\left( {e}_{j}^{(2)}(t)-{e}_{i}^{(2)}(t)\right) \right] , \end{array} \end{aligned}$$
(9)

where c refers to the control gain, and \(\alpha \) and \(\beta \) signify the positive coupling strengths. \(c=0\) when the MASs are under DoS attack, and \(c>0\) when no attack occurs. \(a_{i j}\) means the weight for the edge of the ith node and the jth node. Furthermore, \(b_{i}\) denotes the pinning coupling strength of the ith node and its leader.

Represent the cooperative controller as follows:

$$\begin{aligned} \begin{array}{ll} \mu _{i}(t) =- \alpha c\sum \limits _{j \in V}{h_{ij}e_{j}^{\left( 1 \right) }(t)}- \beta c\sum \limits _{j \in V}h_{ij}e_{j}^{\left( 2 \right) }(t). \end{array} \end{aligned}$$

Let

$$\begin{aligned} e^{(1)}(t)^{T} = \left[ e_{1}^{(1)}(t)^{T}, e_{2}^{(1)}(t)^{T}, \ldots ,e_{N}^{(1)}(t)^{T} \right] ^{T}, \\ e^{(2)}(t)^{T} = \left[ e_{1}^{(2)}(t)^{T}, e_{2}^{(2)}(t)^{T}, \ldots ,e_{N}^{(2)}(t)^{T} \right] ^{T}, \end{aligned}$$

and

$$\begin{aligned} \bar{e}(t) = \left[ \begin{array}{l} e^{(1)}(t) \\ e^{(2)}(t) \end{array}\right] . \end{aligned}$$
(10)

Then error systems of systems (7) and (8) can further be reexpressed as the following matrix equation

$$\begin{aligned} \begin{array}{ll} \dot{\bar{e}}(t) &{} = \left[ \begin{array}{cc} 0_{N} &{} I_{N} \\ -\alpha c H &{} -\beta c H \end{array}\right] \otimes I_{n} \bar{e}(t) +\left[ \begin{array}{c} 0_{n N \times 1} \\ {\left[ f\left( x_{i}(t), t\right) -f\left( x_{k}^{*}(t), t\right) \right] _{N \times 1}} \end{array}\right] . \end{array} \end{aligned}$$
(11)

Let \(M = \left[ \begin{array}{cc}0_{N} &{} I_{N} \\ -\alpha c H &{} -\beta c H\end{array}\right] \otimes I_{n}\), and \(\bar{F}(t) = \left[ \begin{array}{c}0_{n N \times 1} \\ F(t)\end{array}\right] \), the system is transformed into

$$\begin{aligned} \dot{\bar{e}}(t) = M \bar{e}(t)+\bar{F}(t). \end{aligned}$$
(12)

Similar to Subsect. 3.1, system (12) can represent both an error system that is not affected by the DoS attacks and an error system that is affected by the DoS attacks. In other words, if \(c=0\) in matrix M, then system (12) represents error system that is not affected by the DoS attacks; if \(c\ne 0\) in matrix M, then system (12) represents error system that is affected by the DoS attacks.

Theorem 2

Under assumptions 2 and 4, and DoS attacks in the communication, the second-order MASs composed of (7) and (8) can reach group consensus, with the distributed cooperative controller (9) if:

\((a_2)\) \(c>\max \left\{ \frac{\alpha }{2 \beta ^{2} \lambda _{\min }\left( H^{\prime }\right) }, \frac{\alpha +2 \alpha \rho _{1}^{2}+\beta \rho _{1}^{2}}{2 \alpha ^{2} \lambda _{\min }\left( H^{\prime }\right) }, \frac{2 \alpha +\beta +2 \alpha \rho _{2}^{2}+2 \beta \rho _{2}^{2}}{2 \beta ^{2} \lambda _{\min }\left( H^{\prime }\right) }\right\} \);

\((b_2)\) \(T>\frac{r_S-r_D}{r_S} \).

Proof

Define \(\Omega =\left[ \begin{array}{cc}2 c H^{\prime } &{} \frac{1}{\beta } I_{N} \\ \frac{1}{\beta } I_{N} &{} \frac{1}{\alpha } I_{N}\end{array}\right] \otimes I_{n} \). From \(\frac{1}{\alpha } I_{N}>0\) and Schur Complement Lemma that \(\Omega >0\) is equivalent to \(2 c H^{\prime }-\frac{\alpha }{\beta ^2}I_N>0\). From condition\((a_2)\), we have \(c>\frac{\alpha }{2 \beta ^{2} \lambda _{\min }\left( H^{\prime }\right) }\). That is, \(2 c\lambda _{\min }\left( H^{\prime }\right) >\frac{\alpha }{ \beta ^{2}}\). Hence, \(2 c H^{\prime }-\frac{\alpha }{\beta ^2}I_N>0\). Furthermore, \(\Omega \) is positive definite. Select following Lyapunov function

$$\begin{aligned} V =\frac{1}{2}\bar{e}^{T} \Omega {\bar{e}}. \end{aligned}$$
(13)

Taking the derivative of V gets

$$\begin{aligned} \begin{array}{ll} \dot{V}&{}=\bar{e}^{T}\Omega \dot{\bar{e}} \\ &{}=\bar{e}^{T}(t) \Omega (M \bar{e}(t)+\bar{F}(x, t)) \\ &{}=\bar{e}^{T}(t)\left( \frac{1}{2} \Omega M+\frac{1}{2} M^{T} \Omega ^{T}\right) \bar{e}(t)+\bar{e}^{T}(t) \Omega \bar{F}(t) \\ &{}=\left[ e^{(1)^T}(t),~ e^{(2)}(t)\right] \left[ \begin{array}{cc} \frac{-\alpha c}{\beta } H^{\prime } &{} 0_N \\ 0_N &{} \frac{1}{\beta } I_N-\frac{\beta c}{\alpha } H^{\prime } \end{array}\right] \otimes I_n\left[ \begin{array}{c} e^{(1)}(t) \\ e^{(2)}(t) \end{array}\right] \\ &{}~~-\frac{1}{\beta } e^{(1)^T}(t) F(t)-\frac{1}{\alpha } e^{(2)^T}(t) F(t) \\ &{}\le -\frac{\alpha c}{\beta } \lambda _{\min }\left( H^{\prime }\right) e^{(1)^T}(t) e^{(1)}(t)+\left( \frac{1}{\beta } I_N-\frac{\beta c}{\alpha } \lambda _{\min }\left( H^{\prime }\right) \right) e^{(2)^T}(t) e^{(2)}(t) \\ &{}~~+\frac{1}{2 \beta } e^{(1)^T}(t) e^{(1)}(t)+\frac{1}{2 \alpha } e^{(2)^T}(t) e^{(2)}(t)+\left( \frac{1}{2 \beta }+\frac{1}{2 \alpha }\right) F(t)^T F(t) \\ &{}\le -\frac{\alpha c}{\beta } \lambda _{\min }\left( H^{\prime }\right) e^{(1)^T}(t) e^{(1)}(t)+\left( \frac{1}{\beta } I_N-\frac{\beta c}{\alpha } \lambda _{\min }\left( H^{\prime }\right) \right) e^{(2)^T}(t) e^{(2)}(t) \\ &{}~~+\frac{1}{2 \beta } e^{(1)^T}(t) e^{(1)}(t)+\frac{1}{2 \alpha } e^{(2)^T}(t) e^{(2)}(t) \\ &{}~~+\left( \frac{1}{\beta }+\frac{1}{\alpha }\right) \left( \rho _1^2 e^{(1)^T}(t) e^{(1)}(t)+\rho _2^2 e^{(2)^T}(t) e^{(2)}(t)\right) \\ &{}=\left( -\frac{\alpha c}{\beta } \lambda _{\min }\left( H^{\prime }\right) +\frac{1}{2 \beta }+\frac{1}{\beta } \rho _1^2+\frac{1}{\alpha } \rho _1^2\right) e^{(1)^T}(t) e^{(1)}(t) \\ &{}~~+\left( -\frac{\beta c}{\alpha } \lambda _{\min }\left( H^{\prime }\right) +\frac{1}{\beta }+\frac{1}{2 \alpha }+\frac{1}{\beta } \rho _2^2+\frac{1}{\alpha } \rho _2^2\right) e^{(2)^T}(t) e^{(2)}(t) \\ &{}=-\bar{e}^T(t)\left[ \begin{array}{cc} m_1I_N &{} 0_N \\ 0_N &{} m_2I_N \end{array}\right] \otimes I_n \bar{e}(t) \le -rV(t), \end{array} \end{aligned}$$
(14)

where \(m_1=\frac{\alpha c}{\beta } \lambda _{\min }\left( H^{\prime }\right) -\frac{1}{2 \beta }-\frac{1}{\beta } \rho _1^2-\frac{1}{\alpha } \rho _1^2\), \(m_2=\frac{\beta c}{\alpha } \lambda _{\min }\left( H^{\prime }\right) -\frac{1}{\beta }-\frac{1}{2 \alpha }-\frac{1}{\beta } \rho _2^2-\frac{1}{\alpha } \rho _2^2\),

and \(r=\frac{2\min \left\{ m_1, m_2 \right\} }{\lambda _{\max } \left( \Omega \right) }\).

When DoS attack occurs, \(c=0\) for \(t \in \left[ t_\theta , t_\theta +\tau _\theta \right) \), then \(m_1=-\frac{1}{2 \beta }-\frac{1}{\beta } \rho _1^2-\frac{1}{\alpha } \rho _1^2\), \(m_2=-\frac{1}{\beta }-\frac{1}{2 \alpha }-\frac{1}{\beta } \rho _2^2-\frac{1}{\alpha } \rho _2^2\) and \(r<0\), set \(r_D=\frac{2}{\lambda _{\max } \left( \Omega \right) }\min \left\{ -\frac{1}{2 \beta }-\frac{1}{\beta } \rho _1^2-\frac{1}{\alpha } \rho _1^2, -\frac{1}{\beta }-\frac{1}{2 \alpha }-\frac{1}{\beta } \rho _2^2-\frac{1}{\alpha } \rho _2^2\right\} \).

When the DoS attack stops, \(c>0\) for \(t\in \left[ t_\theta +\tau _\theta , t_{\theta +1}\right) \), then \(m_1=\frac{\alpha c}{\beta } \lambda _{\min }\left( H^{\prime }\right) -\frac{1}{2 \beta }-\frac{1}{\beta } \rho _1^2-\frac{1}{\alpha } \rho _1^2\), \(m_2=\frac{\beta c}{\alpha } \lambda _{\min }\left( H^{\prime }\right) -\frac{1}{\beta }-\frac{1}{2 \alpha }-\frac{1}{\beta } \rho _2^2-\frac{1}{\alpha } \rho _2^2\) and \(r>0\), set \(r_S=\frac{2}{\lambda _{\max } \left( \Omega \right) }\min \left\{ \frac{\alpha c}{\beta } \lambda _{\min }\left( H^{\prime }\right) -\frac{1}{2 \beta }-\frac{1}{\beta } \rho _1^2-\frac{1}{\alpha } \rho _1^2, \frac{\beta c}{\alpha } \lambda _{\min }\left( H^{\prime }\right) -\frac{1}{\beta }-\frac{1}{2 \alpha }-\frac{1}{\beta } \rho _2^2-\frac{1}{\alpha } \rho _2^2\right\} \).

Therefore,

$$\begin{aligned} \begin{array}{ll} &{}\dot{V} \le {- r_{D}V,~\text {when}~t \in \left[ {t_{\theta },t_{\theta } + \tau _\theta } \right) }, \\ &{}\dot{V} \le {- r_{S}V,~\text {when}~t \in \left[ {t_{\theta } + \tau _\theta ,t_{\theta + 1}} \right) }. \end{array} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{array}{ll} V(t) &{}\le e^{-r_S\left( t-t_\theta -\tau _\theta \right) } V\left( t_\theta +\tau _\theta \right) \\ &{}\le e^{-r_D \tau _\theta -r_S\left( t-t_\theta -\tau _\theta \right) } V\left( t_k\right) \\ &{}\le V\left( t_0\right) e^{\left( r_S-r_D\right) \left( t-t_0\right) \frac{1}{T}-r_D \varphi -r_S\left( t-t_0-\varphi \right) }. \end{array} \end{aligned}$$

According to conditions \((a_2)\) and \((b_2)\)

$$\begin{aligned} \left( r_S-r_D\right) \frac{1}{T}-r_S<0. \end{aligned}$$

In summary, if conditions \((a_2)\) and \((b_2)\) in Theorem 2 are satisfied, the system can achieve group consensus, so Theorem 2 is proved. \(\square \)

Remark 3

According to Definition 3, we know that the implementation of group consensus has a requirement on the duration of DoS attack. When the controller gain and the attack duration satisfy \((a_2)\) and \((b_2)\), respectively, group consensus of systems (7) and (8) can be reached with the distributed controller (9).

Remark 4

According to the conditions \((a_1)\) and \((a_2)\) of theorems 1 and 2 respectively, both first-order and second-order MASs subjected to DoS attacks need a certain amount of coupling strength to achieve group consensus. Meanwhile, \(c>0\) also implies that it is crucial for the external controls to achieve group consensus for the MASs subjected to DoS attacks. Base on the conditions \((b_1)\) and \((b_2)\) of theorems 1 and 2 respectively, T should be greater than a certain value when the first-order or second-order MASs subjected to DoS attacks achieve group consensus. In other words, in order to achieve group consensus for the MASs subjected to DoS attacks, the average interval of DoS attacks should be greater than one value. Additionally, the lower bounds of both coupling strength and constant T can be derived from theorems 1 and 2, respectively.

Remark 5

The existence of four assumptions is necessary. Assumption 1 ensures that the entire network has the basis for information interaction; Assumption 2 limits the duration of the DoS attack interval and ensures that the duration of the attack interval is less than an average; Assumptions 3 and 4 give the corresponding Lipschitz conditions. According to theorems 1 and 2, satisfying these assumptions can ensure group consensus of nonlinear MASs.

4 Simulation Results

In this section, numerical examples are presented to explain the effectiveness of the designed controllers and the obtained theoretical results. Simulations for both first-order MASs and second-order MASs are given.

4.1 Simulations for First-Order MASs

A MAS consisting of three leaders and three groups of ten followers is considered, and their dynamics are described by systems (1) and (2). The adjacency matrix of follower agents is as follows:

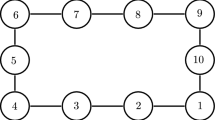
$$\begin{aligned} A= \left( \begin{array}{cccccccccc} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$

Based on the adjacency matrix, the topology of MASs, where the followers in the same group are represented by the same color, is shown in Fig. 1. Ten follower agents are divided into three subgroups. Especially, agents 1, 2 and 3 are chosen as the followers of the first subgroup, agents 4, 5 and 6 are chosen as the followers of the second subgroup, and agents 7, 8, 9 and 10 are chosen as the followers of the third subgroup.

Fig. 1
figure 1

The topology graph of followers

Full size image

The nonlinear function is \(f(x)=\frac{1}{5}\sqrt{x^{2} + 5}\). Obviously, function f(x) is in accord with Assumption 3 with \(\rho =1/5\). In addition, set \(B= \left[ \begin{array}{cccccccccc} 1 ,&0,&0,&0,&1,&0,&0,&0,&0,&2 \end{array} \right] \), implying that the first follower, fifth follower and tenth follower are pinned by the first leader, second leader and third leader, respectively. Only one agent is pinned in each subgroup.

The initial value of all followers is set in the following vector \(x_0= \left[ \begin{array}{cccccccccc} 100,&200,&300,&400,&500,&600,&700,&800,&900,&1000 \end{array} \right] \), and the initial value of three leaders \(x^*\) is set as \(x_0^*= \left[ \begin{array}{ccc} 20,&30,&10 \end{array} \right] .\) By calculating, \(\lambda _{\min }(H')=0.2049\). Set \(\alpha = 1\), \(c=3\) and \(T=7\). Therefore, conditions of Theorem 1 are satisfied. The trajectories of position states of both ten followers and three leaders are depicted in Fig. 2, where three thick lines in red, black and blue indicate the trajectories of three leaders. Figure 2 shows that group consensus is reached. All the followers in each subgroup track the corresponding leader of that subgroup.

Fig. 2
figure 2

The evolutions of position states of agents

Full size image

In addition, the trajectories of controllers are drawn in Fig. 3, where the MASs are affected by a series of DoS attacks. As can be seen from Fig. 3, when the MASs are affected by the DoS attack, the external control fails and the corresponding external control becomes zero; When a period of DoS attack ends, the communication of the MASs is restored and the external control continues to be effective. Furthermore, the controllers of ten followers gradually tend to 0 as group consensus is asymptotically realized.

Fig. 3
figure 3

The evolutions of \(u_i(t), i=1,2,\cdots ,10\)

Full size image

Remark 6

Simulation results of first-order MASs show that when three groups of followers of the MASs are controlled via the controller (3), all the follower agents can asymptotically track the corresponding leaders. This also shows that the controller (3) designed in Subsect. 3.1 is effective for the first-order MASs (1)-(2).

4.2 Simulations for Second-Order MASs

In this subsection, a MAS consisting of three leaders and three groups of followers is considered, and their dynamics are described by systems (7) and (8), where \(f(x)= \frac{1}{20}\sqrt{x^{2} + v^{2} + 5}\) with \(\rho _1=1/20\) and \(\rho _2=1/20\). The topology of second-order MASs is the same as Fig. 1.

Select \(B= \left[ \begin{array}{cccccccccc} 1 ,&0,&0,&0,&1,&0,&0,&0,&0,&2 \end{array} \right] \). The initial values of positions and velocities of followers are selected as \(x_0= \left[ \begin{array}{cccccccccc} 100,&200,&300,&400,&500,&600,&700,&800,&900,&1000 \end{array} \right] \), and \(v_0= \left[ \begin{array}{cccccccccc} 50,&100,&150,&200,&250,&300,&350,&400,&450,&500 \end{array} \right] \), respectively. The initial values of positions and velocities of leaders are set as \(x_0^*= \left[ \begin{array}{ccc} 20,&40,&10 \end{array} \right] \), and \(v_0^*= \left[ \begin{array}{ccc} 15,&25,&30 \end{array} \right] \), respectively.

Nodes 1, 2 and 3 are chosen as the first group of followers; Nodes 4, 5 and 6 are chosen as the second group of followers; Nodes 7, 8, 9 and 10 are chosen as the third group of followers. By calculating, \(r_S=0.0029\), \(r_D=-0.0327\). Set \(\alpha = 1\), \(\beta = 1\), \(c=8\) and \(T=15\). Therefore, conditions of Theorem 2 are satisfied. The evolutions of position states and velocity states of all agents are depicted in Figs. 4 and 5, respectively.

Fig. 4
figure 4

The evolutions of position states of all agents

Full size image
Fig. 5
figure 5

The evolutions of velocity states of all agents

Full size image

Furthermore, the trajectories of controllers are drawn in Fig. 6. where the MASs are affected by a series of DoS attacks.

Fig. 6
figure 6

The evolutions of \(u_i(t), i=1,2,\cdots ,10\)

Full size image

Remark 7

Simulation results of the second-order MASs show that when three groups of followers of the MASs are controlled via the controller (9), all the follower agents can asymptotically track the corresponding leaders. Therefore, the controller (9) is effective for the second-order MASs (7)–(8).

5 Conclusions

In this article, group consensus of both first-order MASs and second-order MASs under DoS attacks was investigated. According to the method of grouping, the controllers for both first-order nonlinear MASs and second-order nonlinear MASs were designed. By means of the Lyapunov function method, group consensus could be achieved when control gain and durations of DoS attacks satisfied the derived conditions. The designed controller and theoretical results were explained by simulation results. In the future, group consensus of the heterogeneous MASs with switching topology and DoS attacks will be further investigated.