1 Introduction

The single-agent deep reinforcement learning (SADRL)-based algorithms using the value function commonly suffer from the overestimation problem [1, 2], which is also known as the maximization bias problem. The main reasons for this problem can be summarized as follows: (1) inadequate exploration in the initial stage of deep reinforcement learning (DRL) training can cause the distribution of the generated samples to deviate from the real probability distribution of policy \(\pi\) in the action-value function (AVF) \(Q\left( {s,a} \right)\); (2) the AVF \(Q\left( {s,a} \right)\) is randomly initialized and then updated iteratively using the Bellman equation to approach the optimal AVF \(Q^{*} \left( {s,a} \right)\) gradually, so there is a variance in the update of \(Q\left( {s,a} \right)\); thus, \(Q\left( {s,a} \right)\) cannot be updated to the target value \(r + \gamma Q\left( {s^{\prime } ,\pi \left( {s^{\prime } } \right)} \right)\) in one step; instead, it will fluctuate around the target value; (3) the AVF \(Q\left( {s,a} \right)\) is in essence an estimated value with a bias, which is to be fitted employing DRL and using a neural network with parameters; this explains the existence of an inherent error between \(Q\left( {s,a} \right)\) and the optimal AVF \(Q^{*} \left( {s,a} \right)\) [3]; (4) the SADRL algorithms based on Q-Learning [4] use the same greedy policy with maximization operation for both action selection and action evaluation, that is, the target value is \(r + \gamma Q\left( {s^{\prime } ,\arg \max_{{a^{\prime } }} Q\left( {s^{\prime } ,a^{\prime } ;\theta_{t} } \right);\theta_{t} } \right)\). Hasselt et al. [2] have proved that estimation errors from any source in the SADRL algorithms can lead to overestimation of action values, which can occur even when the average estimated value of the AVF is correct, and an environment is certain and free of adverse influencing factors such as noise. Moreover, when the maximum value \(\max_{{a^{\prime } }} Q\left( {s^{\prime } ,a^{\prime } } \right)\) in the next state \(s^{\prime }\) is used to update \(Q\left( {s,a} \right)\) using a greedy policy and the bootstrapping updating method, the previously overestimated action values are transferred backward continuously and accumulated, aggravating the overestimation of the action value. As a result, the estimated value deviates far from the true optimal action value, resulting in a suboptimal policy.

Multi-agent deep reinforcement learning (MADRL)-based algorithms using value function decomposition (VFD) [5,6,7,8,9] adopt the Q-Learning [4] or a DQN [10] algorithm to update the joint action-value function (JAVF) \(Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right)\) iteratively. Under the non-stationary influence in a multi-agent system environment [11, 12], an inaccurate estimation of the individual utility function \(Q_{i} \left( {\tau^{i} ,a^{i} } \right)\) of an agent can severely affect the accuracy of the JAVF \(Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right)\), which in turn can lead to the JAVF estimation error. However, most existing VFD algorithms have focused only on how to decompose JAVF \(Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right)\) effectively or how to improve the expressiveness of the decomposition without considering the possible overestimation problem when inaccurate target estimates of JAVF are used to calculate the loss. Therefore, it is necessary to optimize the calculation method of the JAVF updating target to improve the result of centralized training.

The essence of DRL is to generate a large number of samples for iterative updating through the continuous interaction between an agent and an environment and learn an optimal policy for sequential decision problems by optimizing the expectation of cumulative discount reward. Therefore, various problems, such as inadequate exploration, the existence of variance in the update, and estimation bias, are inevitable in the early stage of training. A feasible solution for reducing the overestimation is to minimize the impact of the greedy policy when calculating the updating target. Considering all mentioned, this study proposes an overestimation reduction method named λWD QMIX, which is based on multi-step weighted double estimation. By merely changing the calculation method of the JAVF updating target, a significant improvement in the algorithm’s performance is achieved without performing the augmentation of the network structure and increasing the number of network parameters. The main contributions of this study can be summarized as follows:

  1. (1)

    This paper proves that the estimation bias indeed causes the overestimation problem of the JAVF updating target in the VFD-based MADRL algorithms, and gives the corresponding mathematical proofs and theoretical derivations, and obtains the lower bound of the overestimation error;

  2. (2)

    This paper proposes a MADRL overestimation reduction method based on the multi-step weighted double estimation named λWD QMIX. The proposed method realizes estimation bias correction and multi-step estimation of JAVF using the Weighted Double Q-Learning algorithm based on weighted double estimation and Peng’s \(Q\left( \lambda \right)\) method based on eligibility trace backup, thus effectively reducing the estimation bias and variance and alleviating the problems of overestimation and underestimation in the existing MADRL algorithms;

  3. (3)

    The proposed λWD QMIX only changes the computation of the JAVF updating target without additionally adding or changing any network structure of the baseline algorithm, and thus has good scalability and can in principle be combined with any VFD-based MADRL algorithms.

2 Related Work

Most VFD-based collaborative MADRL algorithms use the centralized training and decentralized execution (CTDE) framework [13, 14] to solve two types of problems: (1) the non-stationary problem that arises when independent learning frameworks [15, 16] are used to solve a problem that can be modeled as a decentralized partially observable Markov decision process (Dec-POMDP) [17, 18]; (2) the problem of difficult learning and poor scalability caused by the excessively large joint state space created when a fully centralized learning framework [19] is used to solve the Dec-POMDP problems. The QMIX algorithm [6] is a typical VFD-based collaborative MADRL algorithm, so studying this algorithm can provide a theoretical basis for the development of other VFD-based algorithms. The main objective of this study is to solve the overestimation problem in the VFD-based collaborative MADRL algorithms effectively. Some of the recently published studies have considered similar problems. For instance, Liu et al. [20] proposed an MC-QMIX algorithm that adopts a voting network to generate a reasonable confidence level for each estimator in the integrated candidate model using a multiple choice learning method and uses the confidence levels to correct the bias in the JAVF estimation. Wu et al. [21] proposed a Sub-AVG extension method that maintains multiple target neural networks. During the training process, this method discards the largest among the previously learned action values and averages the remaining action values, thus obtaining a generally smaller updating target for the JAVF. Fu et al. [22] proposed a Double QMIX algorithm that adopts the Double DQN algorithm [2] to calculate the updating target of the JAVF in the QMIX algorithm, thus reducing the overestimation caused by using the same maximization approach for both action selection and action evaluation processes. Yao et al. [23] developed a multi-step SMIX(λ) algorithm, which extends the SARSA algorithm [24] to the off-policy setting and uses the λ-return to calculate the updating target. This arrangement relaxes the greedy assumption in the learning stage while improving the sample efficiency and accuracy in JAVF estimation. In addition, several studies have introduced multi-step estimation methods, such as TD(λ) [25], into collaborative MADRL algorithms (e.g., DOP [26] and VMIX [27]) based on the AC special structure [28] to improve their overall performance.

3 Preliminaries

3.1 Optimum Action Value Estimation in DRL Algorithms Using Value Function

The main goal of reinforcement learning is to optimize the mapping relationship between states and actions by maximizing the expected cumulative discounted return, thus finding an optimal policy for sequential decision problems [24]. This is a process of constant exploration in an environment using the trial-and-error policy. In the SADRL-based algorithms using the value function, the main goal is commonly achieved by learning the estimate of an optimal AVF \(Q^{*} \left( {s,a} \right)\) for each action. The true value of \(Q\left( {s,a} \right)\) is given by Eq. (1), and it is defined as an expected return obtained by executing an action \(a\) in the current state \(s\) under a given policy \(s\), where \(\gamma\) is the discount factor, \(G_{t}\) is the cumulative discount reward. An optimal policy \(\pi^{*}\) can be obtained by selecting the maximum action value in any state of \(Q^{*} (s,a) = \max_{\pi } Q^{\pi } (s,a)\).

$$ \begin{aligned} Q^{\pi } \left( {s,a} \right) & = E_{{\pi ,p\left( {s^{\prime},r|s,a} \right)}} \left[ {G_{t} |s_{t} = s,a_{t} = a} \right] \\ & = E_{{\pi ,p\left( {s^{\prime},r|s,a} \right)}} \left[ {\sum\limits_{k = 0}^{\infty } {\gamma^{k} r_{t + k + 1} } |s_{t} = s,a_{t} = a} \right] \\ & = E_{{\pi ,p\left( {s^{\prime},r|s,a} \right)}} \left[ {r_{t + 1} + \gamma Q\left( {s_{t + 1} ,a_{t + 1} } \right)|s_{t} = s,a_{t} = a} \right] \\ \end{aligned} $$
(1)

Based on the off-policy temporal difference (TD), the Q-Learning algorithm [4] calculates the updating target by Eq. (2), performing the one-step bootstrapping, thus estimating an optimal AVF. The DQN algorithm [10] employs an experience replay mechanism to sample the training samples, so as to break the correlation between data bits and uses the target network to calculate the updating target by Eq. (3), thus effectively improving the stability and convergence of training. The updating targets of the Double Q-Learning [1] and Double DQN [2] algorithms are given by Eqs. (4) and (5), respectively; both algorithms use different value functions to perform decoupling in action selection and action evaluation, thus solving the overestimation problem caused by performing maximization on the same value function in the optimization process.

$$ \begin{aligned} y_{t}^{Q} & = r_{t + 1} + \gamma \max_{{a_{t + 1} }} Q\left( {s_{t + 1} ,a_{t + 1} ;\theta_{t} } \right) \\ & = r_{t + 1} + \gamma Q\left( {s_{t + 1} ,\arg \max_{{a_{t + 1} }} Q\left( {s_{t + 1} ,a_{t + 1} ;\theta_{t} } \right);\theta_{t} } \right) \\ \end{aligned} $$
(2)
$$ y_{t}^{DQN} = r_{t + 1} + \gamma \max_{{a_{t + 1} }} Q\left( {s_{t + 1} ,a_{t + 1} ;\theta_{t}^{ - } } \right) $$
(3)
$$ y_{t}^{DoubleQ} = r_{t + 1} + \gamma Q\left( {s_{t + 1} ,\arg \max_{{a_{t + 1} }} Q\left( {s_{t + 1} ,a_{t + 1} ;\theta_{t} } \right);\theta^{\prime}_{t} } \right) $$
(4)
$$ y_{t}^{DoubleDQN} = r_{t + 1} + \gamma Q\left( {s_{t + 1} ,\arg \max_{{a_{t + 1} }} Q\left( {s_{t + 1} ,a_{t + 1} ;\theta_{t} } \right);\theta_{t}^{ - } } \right) $$
(5)

3.2 Monotonic Value Function Decomposition

In the fully-cooperative MADRL-based algorithms, the interaction between agents and an environment has usually been modeled as a Dec-POMDP problem composed of a tuple \(M = < N,S,\vec{\varvec{A}},P,\Omega ,O,r,\gamma >\). In the Dec-POMDP problems, agents do not have their own individual rewards, and they can receive only a joint reward \(r\left( {s,\vec{\varvec{a}}} \right)\) from an environment and continuously learn the individual utility function \(Q_{i} \left( {\tau^{i} ,a^{i} } \right)\) in the environment in a hidden mode using their own local observations \(o^{i}\), thus maximizing the expected cumulative discounted joint reward \(E\left[ {G_{t} } \right]\). The collaborative VFD-based MADRL algorithms refine the structural form of the value function by decomposing a JAVF \(Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right)\) and use algorithms, such as the DRQN [29], to perform centralized training, which can effectively solve the problems associated with an unstable environment and decentralized deployment. Theoretically, the VFD-based collaborative learning algorithms abandon global optimality and instead adopt a strong decomposition hypothesis, that is, the individual-Global-Max (IGM) hypothesis [6]. As shown in Eq. (6), the IGM hypothesis states that an optimal joint action resulting from the JAVF \(Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right)\) of all agents is equivalent to the aggregate of optimal actions of the individual utility functions \(Q_{i} \left( {\tau^{i} ,a^{i} } \right)\) of all agents.

$$ \arg \max_{{\vec{\varvec{a}}}} Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right) = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\arg \max_{{a^{1} }} Q_{1} \left( {\tau^{1} ,a^{1} } \right)} \\ \cdots \\ {\arg \max_{{a^{N} }} Q_{N} \left( {\tau^{N} ,a^{N} } \right)} \\ \end{array} } \\ \end{array} } \right) $$
(6)

Further, as given in Eq. (7), the QMIX algorithm [6] indicates that \(Q_{i} \left( {\tau^{i} ,a^{i} } \right)\) has a nonlinear monotonic relationship with \(Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right)\), so a mixing network containing hypernetworks [30] is added to the network structure to enhance the ability of representing \(Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right)\). The loss calculation functions of the QMIX algorithm are given by Eqs. (8)–(10), where \(y_{t}^{QMIX - tot}\) represents the updating target of the JAVF, and \(Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right),s_{t} ;\theta_{t}\) is the joint action value of the currently selected action.

$$ \frac{{\partial Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right)}}{{\partial Q_{i} \left( {\tau^{i} ,a^{i} } \right)}} \ge g_{i} \ge 0,\forall i \in n $$
(7)
$$ L\left( {\uptheta } \right) = E\left[ {\left( {y_{t}^{QMIX - tot} - Q_{tot} \left( {\overrightarrow {{{\varvec{\tau}}_{t} }} ,\overrightarrow {{{\varvec{a}}_{t} }} ,s_{t} ;{\uptheta }_{t} } \right)} \right)^{2} } \right] $$
(8)
$$ Q_{tot} \left( {\overrightarrow {{{\varvec{\tau}}_{t} }} ,\overrightarrow {{{\varvec{a}}_{t} }} ,s_{t} ;{\uptheta }_{t} } \right) = f_{Mixer} \left( {\left[ {\begin{array}{*{20}c} {Q_{1} \left( {\tau_{t}^{1} ,a_{t}^{1} ; \theta_{t}^{1} } \right)} \\ \cdots \\ {Q_{n} \left( {\tau_{t}^{n} ,a_{t}^{n} ;\theta_{t}^{n} } \right)} \\ \end{array} } \right];\theta_{t}^{Mixer} } \right) $$
(9)
$$ \begin{aligned} y_{t}^{QMIX - tot} &= Q_{tot}^{\max } \left( {\overrightarrow {{{\varvec{\tau}}_{t} }} ,\overrightarrow {{{\varvec{a}}_{t} }} ,s_{t} ;{\uptheta }_{t}^{ - } } \right) = r_{t + 1} + \gamma Q_{tot}^{\max } \left( {\overrightarrow {{{\varvec{\tau}}_{t + 1} }} ,\overrightarrow {{{\varvec{a}}_{t + 1} }} ,s_{t + 1} ;{\uptheta }_{t}^{ - } } \right) \\ &= r_{t + 1} + \gamma \max_{{\overrightarrow {{{\varvec{a}}_{t + 1} }} }} Q_{tot} \left( {\overrightarrow {{{\varvec{\tau}}_{t + 1} }} ,\overrightarrow {{{\varvec{a}}_{t + 1} }} ,s_{t + 1} ;{\uptheta }_{t}^{ - } } \right) \hfill \\ &= r_{t + 1} + \gamma f_{Mixer} \left( {\left[ {\begin{array}{*{20}c} {\max_{{a_{t + 1}^{1} }} Q_{1} \left( {\tau_{t + 1}^{1} ,a_{t + 1}^{1} ;\theta_{t}^{1 - } } \right)} \\ \cdots \\ {\max_{{a_{t + 1}^{n} }} Q_{n} \left( {\tau_{t + 1}^{n} ,a_{t + 1}^{n} ;\theta_{t}^{n - } } \right)} \\ \end{array} } \right];\theta_{t}^{Mixer - } } \right) \hfill \\ \end{aligned} $$
(10)

4 Methods

In this section, first, a theoretical analysis is conducted to determine the cause of significant overestimation that occurs when the DQN algorithm is used to estimate the updating JAVF target in the VFD-based MADRL algorithms represented by the QMIX; then, the method of reducing overestimation in SADRL is applied to the VFD-based MADRL algorithms to obtain an improved MADRL algorithm.

4.1 Formation Mechanism of Overestimation in VFD-Based MADRL

Thrun et al. [31] first investigated the overestimation problem in Q-learning, demonstrating that each target value could be overestimated to \(\gamma \epsilon \left( {{{m - 1} \mathord{\left/ {\vphantom {{m - 1} {m + 1}}} \right. \kern-0pt} {m + 1}}} \right)\) when the estimate of action value contained random errors that were uniformly distributed in the interval of \(\left[ { - \epsilon ,\epsilon } \right]\). Later, under more general conditions (i.e., without assuming that the estimation errors of action value satisfied the independently identical distribution), Hasselt et al. [2] proved that estimation errors from any source could lead to the overestimation problem, which is defined by Theorem 1.

Theorem 1

In SADRL, consider a state \(s\), where exists a state value function \(V^{*} \left( s \right)\) that satisfies all true optimal action values \(Q^{*} \left( {s,a} \right) = V^{*} \left( s \right)\). Next, suppose \(Q_{t}\) is an estimate of an action value that is generally unbiased with respect to \(Q^{*} \left( {s,a} \right)\) but is not identical with \(Q^{*} \left( {s,a} \right)\), that is, \(\sum\nolimits_{a} {\left( {Q_{t} \left( {s,a} \right) - V^{*} \left( s \right)} \right)} = 0\); however, \({\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-0pt} \!\lower0.7ex\hbox{$m$}}\sum\nolimits_{a} {\left( {Q_{t} \left( {s,a} \right) - V^{*} \left( s \right)} \right)^{2} } = C\), where \(C > 0\) and \(m \ge 2\) is the action space of an agent. Under the above conditions, it can be obtained that \(\max_{a} Q_{t} (s,a) = Q_{t} (s,\arg \;\max_{a} Q_{t} (s,a)) \ge V^{*} (s) + \sqrt {C/m - 1}\).

It can be seen that using the greedy policy of maximization operation for action selection and action evaluation can cause the overestimation problem in the SADRL algorithm. The centralized training of VFD-based MADRL algorithms includes the following steps: (1) a set of training data containing information on the environment state, action, next state, reward, and whether the termination state is reached is fetched from the experience replay buffer; (2) using the fetched data as the current training data, the \(Q\)-value network and target network of an agent are used to predict the local individual action value \(Q_{i} \left( {\tau_{t}^{i} ,a_{t}^{i} ;\theta_{t}^{i} } \right)\) of the agent when the action is taken in the current state and the maximum local individual action value \(\max_{{a_{t + 1}^{i} }} Q_{i} \left( {\tau_{t + 1}^{i} ,a_{t + 1}^{i} ;\theta_{t}^{i - } } \right)\) among all actions of the agents in the next state. Then, a first- or multi-order hybrid network [32] based on the global state and its corresponding target hybrid network are used to calculate the weighted sum of the local individual action value \(Q_{i} \left( {\tau_{t}^{i} ,a_{t}^{i} ;\theta_{t}^{i} } \right)\) in the current state and the maximum local individual action value \(\max_{{a_{t + 1}^{i} }} Q_{i} \left( {\tau_{t + 1}^{i} ,a_{t + 1}^{i} ;\theta_{t}^{i - } } \right)\) in the next state, thus obtaining the global predicted joint action value \(Q_{tot} \left( {\overrightarrow {{\tau_{t} }} \varvec{,}\overrightarrow {{{\varvec{a}}_{t} }} ;{\uptheta }} \right)\) and the global target joint action value \(Q_{tot}^{\max } \left( {\overrightarrow {{\tau_{t} }} \varvec{,}\overrightarrow {{{\varvec{a}}_{t} }} ;{\uptheta }^{ - } } \right)\) in the current state; (3) the optimizer is used to minimize the mean square error between the global predicted joint action value and the global target joint action value; also, the backpropagation algorithm is employed to update the sub-network parameters in the algorithm model to make the predicted value as close to the true value as possible, thus realizing the cooperative decision-making of multiple agents. The above training process includes the maximization operation that causes the overestimation error in Theorem 1, so this operation will inevitably cause the overestimation problem in the VFD-based MADRL algorithms. Next, Theorem 1 is extended to the VFD-based QMIX algorithm to obtain Lemma 1, and the corresponding proof is provided.

Lemma 1

In MADRL, consider the local action–observation history \(\tau_{t}^{i}\) of an agent \(i\) in a fully cooperative multi-agent system at a moment \(t\). For each agent, there exists \(V_{i}^{*} \left( {\tau^{i} } \right)\) that satisfies the optimal AVFs \(Q_{i}^{*} \left( {\tau^{i} ,a^{i} } \right) = V_{i}^{*} \left( {\tau^{i} } \right)\) of all real individuals, and the real unbiased optimal JAVF \(Q_{tot}^{*} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right)\) can be decomposed into a combination of real individual optimal AVFs \(Q_{i}^{*} \left( {\tau^{i} ,a^{i} } \right)\) of all agents. Next, suppose \(Q_{i} \left( {\tau^{i} ,a^{i} } \right)\) is an estimate of an individual AVF that is generally unbiased with respect to \(Q_{i}^{*} \left( {\tau^{i} ,a^{i} } \right)\) but is not identical with \(Q_{i}^{*} \left( {\tau^{i} ,a^{i} } \right)\), that is, \(\sum\nolimits_{{a^{i} }} {\left( {Q_{i} \left( {\tau^{i} ,a^{i} } \right) - V_{i}^{*} \left( {\tau^{i} } \right)} \right)} = 0\), but \(\sum\nolimits_{{a^{i} }} {\left( {Q_{i} \left( {\tau^{i} ,a^{i} } \right) - V_{i}^{*} \left( {\tau^{i} } \right)} \right)^{2} } = m_{i} C_{i}\), where, \(C_{i} > 0\), \(m_{i} \ge 2\) is the action space of each agent. Under the above conditions, \(Q_{tot}^{\max } \left( {\vec{\varvec{\tau }},\vec{\varvec{a}};{\uptheta }^{ - } } \right) \ge Q_{tot}^{*} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right) + \sum\nolimits_{i = 1}^{N} {\gamma g\sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}} } \ge 0\), where \(\gamma\) is the discount factor, \(N\) is the number of agents, \(g = \min_{i \in N} g_{i}\) is the lower bound of the gradient \(g_{i}\), and \({\uptheta }^{ - }\) is the parameter of the target network in the QMIX algorithm, respectively.

Proof

The estimation error \(\Delta_{t}\) of the JAVF in the VFD-based QMIX algorithm is defined as a difference between the true unbiased optimal JAVF \(Q_{tot}^{*} \left( {\overrightarrow {{\tau_{t} }} \varvec{,}\overrightarrow {{{\varvec{a}}_{t} }} } \right)\) and the global target JAVF \(Q_{tot}^{\max } \left( {\overrightarrow {{{\varvec{\tau}}_{t} }} \varvec{,}\overrightarrow {{{\varvec{a}}_{t} }} ;{\uptheta }_{t}^{ - } } \right)\) estimated using the neural network, that is:

$$ \begin{aligned} \Delta_{t} & = Q_{tot}^{\max } \left( {\overrightarrow {{{\varvec{\tau}}_{t} }} \varvec{,}\overrightarrow {{{\varvec{a}}_{t} }} ;{\uptheta }_{t}^{ - } } \right) - Q_{tot}^{*} \left( {\overrightarrow {{{\varvec{\tau}}_{t} }} \varvec{,}\overrightarrow {{{\varvec{a}}_{t} }} } \right) = \left( {r_{t + 1} + \gamma Q_{tot}^{\max } \left( {\overrightarrow {{{\varvec{\tau}}_{t + 1} }} \varvec{,}\overrightarrow {{{\varvec{a}}_{t + 1} }} ;{\uptheta }_{t}^{ - } } \right)} \right) - Q_{tot}^{*} \left( {\overrightarrow {{{\varvec{\tau}}_{t} }} \varvec{,}\overrightarrow {{{\varvec{a}}_{t} }} } \right) \\ & = \left( {r_{t + 1} + \gamma f_{Mixer} \left( {\left[ {\begin{array}{*{20}c} {\max_{{a_{t + 1}^{1} }} Q_{1} \left( {\tau_{t + 1}^{1} ,a_{t + 1}^{1} ;\theta_{t}^{1 - } } \right)} \\ \cdots \\ {\max_{{a_{t + 1}^{n} }} Q_{n} \left( {\tau_{t + 1}^{n} ,a_{t + 1}^{n} ;\theta_{t}^{n - } } \right)} \\ \end{array} } \right];\theta_{t}^{Mixer - } } \right)} \right)\\ &\quad - \left( {r_{t + 1} + \gamma f_{Mixer} \left( {\left[ {\begin{array}{*{20}c} {Q_{1}^{*} \left( {\tau_{t + 1}^{1} ,a_{t + 1}^{1} } \right)} \\ \cdots \\ {Q_{n}^{*} \left( {\tau_{t + 1}^{n} ,a_{t + 1}^{n} } \right)} \\ \end{array} } \right];\theta_{t}^{Mixer - } } \right)} \right) \\ & = \gamma f_{Mixer} \left( {\left[ {\begin{array}{*{20}c} {\max_{{a_{t + 1}^{1} }} Q_{1} \left( {\tau_{t + 1}^{1} ,a_{t + 1}^{1} ;\theta_{t}^{1 - } } \right) - Q_{1}^{*} \left( {\tau_{t + 1}^{1} ,a_{t + 1}^{1} } \right)} \\ \cdots \\ {\max_{{a_{t + 1}^{n} }} Q_{n} \left( {\tau_{t + 1}^{n} ,a_{t + 1}^{n} ;\theta_{t}^{n - } } \right) - Q_{n}^{*} \left( {\tau_{t + 1}^{n} ,a_{t + 1}^{n} } \right)} \\ \end{array} } \right];\theta_{t}^{Mixer - } } \right) \\ & = \gamma f_{Mixer} \left( {\left[ {\begin{array}{*{20}c} {\max_{{a_{t + 1}^{1} }} Q_{1} \left( {\tau_{t + 1}^{1} ,a_{t + 1}^{1} ;\theta_{t}^{1 - } } \right) - V_{1}^{*} \left( {\tau_{t + 1}^{1} } \right)} \\ \cdots \\ {\max_{{a_{t + 1}^{n} }} Q_{n} \left( {\tau_{t + 1}^{n} ,a_{t + 1}^{n} ;\theta_{t}^{n - } } \right) - V_{n}^{*} \left( {\tau_{t + 1}^{n} } \right)} \\ \end{array} } \right];\theta_{t}^{Mixer - } } \right) \\ \end{aligned} $$
(11)

Thus, the JAVF estimation error can be decomposed into the estimation errors of individual AVFs of all agents. The estimation error of an action r of individual AVF of an agent is defined as \(\epsilon_{{a_{t}^{i} }} = Q_{i} \left( {\tau_{t}^{i} ,a_{t}^{i} ;\theta_{t}^{i} } \right) - V_{i}^{*} \left( {\tau_{t}^{i} } \right)\). Assume that there exists a set \(\left\{ {\epsilon_{{a_{t}^{i} }} } \right\}\) that satisfies the condition of \(\max_{{a_{t}^{i} }} \epsilon_{{a_{t}^{i} }} < \sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}}\), where \(\left\{ {\epsilon_{{a_{t}^{i} }}^{ + } } \right\}\) is denoted as a non-negative set in \(\left\{ {\epsilon_{{a_{t}^{i} }} } \right\}\) with a cardinal of \(p_{i}\), and \(\left\{ {\epsilon_{{a_{t}^{i} }}^{ - } } \right\}\) is denoted as a negative set in \(\left\{ {\epsilon_{{a_{t}^{i} }} } \right\}\) with a cardinal of \(m_{i} - p_{i}\), that is, \(\left\{ {\epsilon_{{a_{t}^{i} }} } \right\} = \left\{ {\epsilon_{{a_{t}^{i} }}^{ + } } \right\} \cup \left\{ {\epsilon_{{a_{t}^{i} }}^{ - } } \right\}\).

If \(p_{i} = m_{i}\), that is, \(\epsilon_{{a_{t}^{i} }} = Q_{i} \left( {\tau_{t}^{i} ,a_{t}^{i} ;\theta_{t}^{i} } \right) - V_{i}^{*} \left( {\tau_{t}^{i} } \right) \ge 0\), as the assumption of \(\sum\nolimits_{{a_{t}^{i} }} {\epsilon_{{a_{t}^{i} }} = } 0\) has already been made under the condition, the expression of \(\epsilon_{{a_{t}^{i} }} = 0\) holds for any \(a_{t}^{i}\). However, this conclusion is contradictory with \(\sum\nolimits_{{a_{t}^{i} }} {\left( {\epsilon_{{a_{t}^{i} }} } \right)^{2} = } m_{i} C_{i}\) under the considered condition, so it can be obtained that \(p_{i} \le m_{i} - 1\), and:

$$ \sum\limits_{{a_{t}^{i} = 1}}^{{p_{i} }} {\epsilon_{{a_{t}^{i} }}^{ + } } \le p_{i} \max_{{a_{t}^{i} }} \epsilon_{{a_{t}^{i} }}^{ + } \le p_{i} \sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}} $$
(12)
$$ \sum\limits_{{a_{t}^{i} = 1}}^{{p_{i} }} {\left( {\epsilon_{{a_{t}^{i} }}^{ + } } \right)^{2} } \le p_{i} \left( {\max_{{a_{t}^{i} }} \epsilon_{{a_{t}^{i} }}^{ + } } \right)^{2} \le \frac{{p_{i} C_{i} }}{{m_{i} - 1}} $$
(13)

Under the assumptions of \(\sum\nolimits_{{a_{t}^{i} }} {\epsilon_{{a_{t}^{i} }} = } 0\), it can be obtained that \(\sum\nolimits_{{a_{t}^{i} = 1}}^{{m_{i} - p_{i} }} {\left| {\epsilon_{{a_{t}^{i} }}^{ - } } \right|} \le p_{i} \max_{{a_{t}^{i} }} \epsilon_{{a_{t}^{i} }}^{ + } \le p_{i} \sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}}\), where \(\max_{{a_{t}^{i} }} \left| {\epsilon_{{a_{t}^{i} }}^{ - } } \right| \le p_{i} \sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}}\). Then, according to Hölder’s inequality, it holds that:

$$ \begin{aligned} \sum\limits_{{a_{t}^{i} = 1}}^{{m_{i} - p_{i} }} {\left( {\epsilon_{{a_{t}^{i} }}^{ - } } \right)^{2} } & \le \sum\limits_{{a_{t}^{i} = 1}}^{{m_{i} - p_{i} }} {\left| {\epsilon_{{a_{t}^{i} }}^{ - } } \right|} \cdot \max_{{a_{t}^{i} }} \left| {\epsilon_{{a_{t}^{i} }}^{ - } } \right| \\ & \le p_{i} \sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}} \cdot p_{i} \sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}} \\ & = \frac{{p_{i}^{2} C_{i} }}{{m_{i} - 1}} \\ \end{aligned} $$
(14)

The above relationship can be used to calculate the square and upper bound of all \(\epsilon_{{a_{t}^{i} }}\) as follows:

$$ \begin{aligned} \sum\limits_{{a_{t}^{i} = 1}}^{{m_{i} }} {\left( {\epsilon_{{a_{t}^{i} }} } \right)^{2} } & = \sum\limits_{{a_{t}^{i} = 1}}^{{p_{i} }} {\left( {\epsilon_{{a_{t}^{i} }}^{ + } } \right)^{2} } + \sum\limits_{{a_{t}^{i} = 1}}^{{m_{i} - p_{i} }} {\left( {\epsilon_{{a_{t}^{i} }}^{ - } } \right)^{2} } \\ & \le \frac{{p_{i} C_{i} }}{{m_{i} - 1}} + \frac{{p_{i}^{2} C_{i} }}{{m_{i} - 1}} \\ & = \frac{{p_{i} \left( {p_{i} + 1} \right)}}{{m_{i} - 1}}C_{i} \\ & \le m_{i} C_{i} \\ \end{aligned} $$
(15)

This conclusion is also contradictory to the condition of \(\sum\nolimits_{{a_{t}^{i} }} {\left( {\epsilon_{{a_{t}^{i} }} } \right)^{2} = } m_{i} C_{i}\), so there exists a set \(\left\{ {\epsilon_{{a_{t}^{i} }} } \right\}\) that makes the assumption \(\max_{{a_{t}^{i} }} \epsilon_{{a_{t}^{i} }} < \sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}}\) invalid. Therefore, for all \(\left\{ {\epsilon_{{a_{t}^{i} }} } \right\}\) sets that satisfy the constraints in Lemma 1, the expression of \(\max_{{a_{t}^{i} }} \epsilon_{{a_{t}^{i} }} \ge \sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}}\) holds, that is, the actual maximum local individual action value \(\max_{{a^{i} }} Q_{i} \left( {\tau^{i} ,a^{i} ;\theta^{i - } } \right)\) estimated by an agent is larger than or equal to the true unbiased individual action value \(Q_{i}^{*} \left( {\tau^{i} ,a^{i} } \right)\). Next, assume that \(g\) is the lower bound of the monotonicity constraint gradient \(g_{i}\) in the QMIX algorithm, that is, \(g = \min_{i \in N} g_{i}\); then, the lower bound of the estimation error \(\Delta_{t}\) of the JAVF in the VDF-based QMIX algorithm is obtained by:

$$ \begin{aligned} \Delta_{t} & = \gamma f_{Mixer} \left( {\left[ {\begin{array}{*{20}c} {\max_{{a_{t + 1}^{1} }} Q_{1} \left( {\tau_{t + 1}^{1} ,a_{t + 1}^{1} ;\theta_{t}^{1 - } } \right) - V_{1}^{*} \left( {\tau_{t + 1}^{1} } \right)} \\ \cdots \\ {\max_{{a_{t + 1}^{n} }} Q_{n} \left( {\tau_{t + 1}^{n} ,a_{t + 1}^{n} ;\theta_{t}^{n - } } \right) - V_{n}^{*} \left( {\tau_{t + 1}^{n} } \right)} \\ \end{array} } \right];\theta_{t}^{Mixer - } } \right) \\ & \ge \gamma f_{Mixer} \left( {\left[ {\begin{array}{*{20}c} {\sqrt {{{C_{1} } \mathord{\left/ {\vphantom {{C_{1} } {m_{1} - 1}}} \right. \kern-0pt} {m_{1} - 1}}} } \\ \cdots \\ {\sqrt {{{C_{n} } \mathord{\left/ {\vphantom {{C_{n} } {m_{n} - 1}}} \right. \kern-0pt} {m_{n} - 1}}} } \\ \end{array} } \right];\theta_{t}^{Mixer - } } \right) \\ & \ge \sum\limits_{i = 1}^{N} {\gamma g_{i} \sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}} } \\ & \ge \sum\limits_{i = 1}^{N} {\gamma g\sqrt {{{C_{i} } \mathord{\left/ {\vphantom {{C_{i} } {m_{i} - 1}}} \right. \kern-0pt} {m_{i} - 1}}} } \\ \end{aligned} $$
(16)

End of proof

Based on the aforementioned proof, the overestimation error will certainly be introduced when the maximization operation is used to estimate the global target JAVF in the VFD-based MADRL algorithm. However, the overestimation problem can be mitigated by effectively reducing the overestimation error in the local target individual action values.

4.2 Overestimation Reduction Method Based on Multi-step Weighted Double Estimation

4.2.1 Estimation Bias Correction Based on Weighted Double Estimation

Based on the updating target calculation formulas of the value functions of the Double Q-Learning [1] and Double DQN algorithms [2], the main objective of overestimation reduction is to decouple the action selection and action evaluation tasks in the target update process by maintaining two relatively independent value functions. For instance, in the Double DQN, a greedy policy is adopted to perform action selection in the current Q-value network using the current Q-value network and the target network in the DQN algorithm, that is, \(a_{t + 1}^{*} = \arg \max_{{a_{t + 1} }} Q\left( {s_{t + 1} ,a_{t + 1} ;\theta_{t} } \right)\), and the target network is employed to evaluate the selected action \(a_{t + 1}^{*}\), that is, \(y_{t} = r_{t + 1} + \gamma Q\left( {s_{t + 1} ,a_{t + 1}^{*} ;\theta_{t}^{ - } } \right)\). Since the parameter \(\theta_{t}^{ - }\) of the target network is copied from the current Q-value network at fixed intervals, the fact that an action \(a_{t + 1}\) is regarded as a greedy action in the current Q-value network does not necessarily guarantee that it continues to be a greedy action in the target network. In addition, the current Q-value network and the target network have the same definition, that is, the condition of \(E\left[ Q \right] = E\left[ {Q^{ - } } \right]\) holds in the training process, and both networks are updated in the \(Q^{*}\) direction, so the accuracy of the update is guaranteed. However, since \(Q\left( {s_{t + 1} ,\arg \max_{{a_{t + 1} }} Q\left( {s_{t + 1} ,a_{t + 1} ;\theta_{t} } \right);\theta_{t}^{ - } } \right) \le \max_{{a_{t + 1} }} Q\left( {s_{t + 1} ,a_{t + 1} ;\theta_{t} } \right)\), which means that the Double DQN tends to use another action value instead of the maximum value to obtain a lower updating target, the updating target may be lower than the true value, thus resulting in an underestimation error.

Commonly, it has been considered that underestimation in SADRL can reduce the impact of over-exploration and accumulation of overestimation errors and motivate agents to improve the value function by exploring other unknown states and actions, thus improving training stability. However, in the centralized training process of the VFD-based MADRL algorithms, it is necessary to fuse the individual AVFs into the JAVF using a hybrid network or a linear summation. In this fusion process, the estimation errors of individuals are not equal, but all of them affect the estimation of the individual value functions of the other agents and the JAVF, which impacts the training stability and makes the learned policy deviate from the optimal solution.

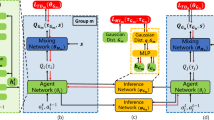
Inspired by the Weighted Double Q-Learning algorithm proposed by Zhang et al. [33], this study incorporates this algorithm into the DRQN [29] algorithm and uses the modified DRQN algorithm to update the local target individual AVFs in the QMIX algorithm to counterbalance the overestimation in the DQN algorithm and the underestimation in the Double DQN algorithm, thus reducing the overestimation error of the JAVF. Particularly, in this study, the target estimate of local individual AVFs is represented as a linear combination of the estimates obtained by the DQN and Double DQN, as shown in Eqs. (17) and (18), where \(\beta \in \left( {0,1} \right]\) is the adjustment coefficient controlled by \(c\), and \(c \ge 0\). The larger the value of \(c\) is, the closer the combined estimate is to the estimate of the Double DQN.

$$ \begin{aligned} y_{t}^{i - WD} & = r_{t + 1} + \gamma Q_{i}^{WD} \left( {\tau_{t + 1}^{i} ,a_{t + 1}^{i} } \right) \\ & = r_{t + 1} + \gamma \left[ \beta Q_{i} \left( {\tau_{t + 1}^{i} ,\arg \max_{{a_{t + 1}^{i} }} Q\left( {\tau_{t + 1}^{i} ,a_{t + 1}^{i} ;\theta_{t}^{i - } } \right);\theta_{t}^{i - } } \right)\right.\\ &\quad\left. + \left( {1 - \beta } \right)Q_{i} \left( {\tau_{t + 1}^{i} ,\arg \max_{{a_{t + 1}^{i} }} Q \left( {\tau_{t + 1}^{i} ,a_{t + 1}^{i} ;\theta_{t}^{i} } \right);\theta_{t}^{i - } } \right) \right] \\ \end{aligned} $$
(17)
$$ \beta = \frac{{\left| {Q_{i} \left( {\tau_{t + 1}^{i} ,\arg \max_{{a_{t + 1}^{i} }} Q\left( {\tau_{t + 1}^{i} ,a_{t + 1}^{i} ;\theta_{t}^{i} } \right);\theta_{t}^{i - } } \right) - Q_{i} \left( {\tau_{t + 1}^{i} ,\arg \min_{{a_{t + 1}^{i} }} Q\left( {\tau_{t + 1}^{i} ,a_{t + 1}^{i} ;\theta_{t}^{i} } \right);\theta_{t}^{i - } } \right)} \right|}}{{c + \left| {Q_{i} \left( {\tau_{t + 1}^{i} ,\arg \max_{{a_{t + 1}^{i} }} Q\left( {\tau_{t + 1}^{i} ,a_{t + 1}^{i} ;\theta_{t}^{i} } \right);\theta_{t}^{i - } } \right) - Q_{i} \left( {\tau_{t + 1}^{i} ,\arg \min_{{a_{t + 1}^{i} }} Q\left( {\tau_{t + 1}^{i} ,a_{t + 1}^{i} ;\theta_{t}^{i} } \right);\theta_{t}^{i - } } \right)} \right|}} $$
(18)
$$ y_{t}^{WD - tot} = r_{t + 1} + \gamma f_{Mixer} \left( {\left[ {\begin{array}{*{20}c} {Q_{1}^{WD} \left( {\tau_{t + 1}^{1} ,a_{t + 1}^{1} } \right)} \\ \cdots \\ {Q_{n}^{WD} \left( {\tau_{t + 1}^{n} ,a_{t + 1}^{n} } \right)} \\ \end{array} } \right];\theta_{t}^{Mixer - } } \right) $$
(19)

Compared with the JAVF updating target calculation method used in the QMIX algorithm, the method defined by Eq. (19) uses a different action selection method, thus shifting from using the greedy policy of maximization operation to selecting an action only in the target network, which is used in the QMIX, performing the action selection partly in the target network and partly in the current Q-value network. In this way, more accurate value estimates can be obtained when the target network is used for evaluation.

4.2.2 Target Value Updating Based on Eligibility Trace Backup

In the QMIX algorithm, the updating target of the JAVF is calculated using the value bootstrapping (VB) method with one-step TD based on the estimated value of the JAVF at the next time step according to a single immediate joint reward. Without sufficient training, the prediction of \(Q_{tot} \left( {\vec{\varvec{\tau }},\vec{\varvec{a}}} \right)\) usually generates a large bias, which severely affects the bootstrapping reward. In addition, due to the influence of the timing credit assignment, this method updates only the previous state while the other previous states and actions are not updated, so the updating speed is slow. Recently, many return-based (RB) multi-step updating methods have been developed for SADRL [34,35,36]. These methods can accelerate information spreading and enhance immediate sensitivity to future rewards by using trajectories with a longer time span for updating the target value. This arrangement can effectively reduce bias, improve learning efficiency, increase the effectiveness of timing credit assignments, and achieve significantly better control performance than one-step updating algorithms in various reinforcement learning tasks. However, these methods can introduce a large variance, especially when sampling samples are insufficient, which may cause instability in the estimation of updating target [37,38,39,40]. Particularly, the updating target of the n-step TD is given by:

$$ G_{t:t + n} = r_{t + 1} + \gamma r_{t + 2} + \cdots + \gamma^{n - 1} r_{t + n} + \gamma^{n} V\left( {s_{t + n} } \right) $$
(20)

Eligibility trace methods, such as \(TD\left( \lambda \right)\), \(TB\left( \lambda \right)\) [41], and Peng’s \(Q\left( \lambda \right)\) [42, 43], can effectively reduce the estimation error and improve the convergence speed of DRL by performing interpolation between the TD method, which is characterized by a small variance, and the Monte Carlo method, which is characterized by a small bias. The Monte Carlo method can be regarded as a special case of the RB method, and its updating target represents the sum of discounted cumulative rewards. According to the error reduction effect of the n-step return given in Eq. (21), if the expected value of the n-step return is used as the maximum error in the estimation of \(V^{\pi } \left( s \right)\), this maximum error will not be \(\gamma^{n}\) times larger than the maximum error created when the pre-update value function \(V_{t + n - 1} \left( s \right)\) is used for the same estimation [24]. Similarly, composite returns, such as eligibility trace, have an error reduction effect similar to that of the independent n-step return shown in Eq. (21), which ensures convergence of updating.

$$ \max_{s} \left| {E_{\pi } \left[ {G_{t:t + n} |s_{t} = s} \right] - V^{\pi } \left( s \right)} \right| \le \gamma^{n} \max_{s} \left| {V_{t + n - 1} \left( s \right) - V^{\pi } \left( s \right)} \right| $$
(21)

In summary, this study uses Peng's \(Q\left( \lambda \right)\) method based on the off-policy eligibility trace to estimate the JAVF updating target. The calculation formula in SADRL is given by Eq. (22), which calculates the exponential mean of all n-step returns, where, \(\lambda \in \left[ {0,1} \right]\) is the hyperparameter controlling the decay rate, and \(T\) is the trajectory length. When \(\lambda = 1\), the weights of \(Q_{t:T}\) are equal to one, and the weights of all other returns are zeros, thus Eq. (22) becomes the Monte Carlo method. When \(\lambda = 0\), Eq. (22) becomes the one-step TD algorithm. It is worth noting that regardless of the maximization operation adopted in the action policy of an agent, Eq. (23) uses the maximization operation to make a backup of each n-step return.

$$ Q_{t}^{\lambda } = \left( {1 - \lambda } \right)\sum\limits_{n = 1}^{\infty } {\lambda^{n - 1} Q_{t:t + n} } = \left( {1 - \lambda } \right)\sum\limits_{n = 1}^{T - t - 1} {\lambda^{n - 1} Q_{t:t + n} } + \lambda^{T - t - 1} Q_{t:T} $$
(22)
$$ Q_{t:t + n} = r_{t + 1} + \gamma r_{t + 2} + \cdots + \gamma^{n - 1} r_{t + n} + \gamma^{n} \max_{{a_{t + n} }} Q\left( {s_{t + n} ,a_{t + n} } \right) $$
(23)

From the perspective of optimization, the essence of Peng’s \(Q\left( \lambda \right)\) method is a fine-tuning process of the overall gradient update direction by continuously accumulating the gradient update direction of the sampled state at the current moment in the historical gradient update direction. That is, this method preserves historical trajectory information to a certain extent through a smooth decaying transition while focusing more on the impact of the latest state and action on the updating target instead of directly ignoring previously visited states. This arrangement provides short-term memory about the obtained trajectory and thus accelerates the algorithm convergence. For the convenience of calculation, in estimating the updating target of the JAVF using Peng’s \(Q\left( \lambda \right)\) method, Eq. (22) is changed into a recursive form, and \(Q_{i}^{WD} \left( {\tau_{t + 1}^{i} ,a_{t + 1}^{i} } \right)\) is used instead of Q-Learning to make backup of each n-step return, forming the updating target estimated using the multi-step weighted double estimation method. In addition, when \(t = T - 1\), then \(Q_{t + 1}^{\lambda - WD - tot} = 0\).

$$ Q_{t}^{\lambda WD - tot} = r_{t + 1} + \gamma \left[ {\lambda Q_{t + 1}^{\lambda - WD - tot} + \left( {1 - \lambda } \right)f_{Mixer} \left( {\left[ {\begin{array}{*{20}c} {Q_{1}^{WD} \left( {\tau_{t + 1}^{1} ,a_{t + 1}^{1} } \right)} \\ \cdots \\ {Q_{n}^{WD} \left( {\tau_{t + 1}^{n} ,a_{t + 1}^{n} } \right)} \\ \end{array} } \right];\theta_{t}^{Mixer - } } \right)} \right] $$
(24)

4.3 λWD QMIX Algorithm

The aforementioned method of reducing overestimation in SADRL is applied to the VFD-based QMIX algorithm, resulting in an improved MADRL algorithm (λWD QMIX) based on the multi-step weighted double estimation. In the algorithm name, λ represents the operation of performing multi-step estimation on the updating target of the JAVF using Peng’s \(Q\left( \lambda \right)\) method based on the eligibility trace, which can counterbalance the VB estimation bias and variance of return-based estimation, thus reducing the estimation error and accelerating the algorithm’s convergence; WD represents the operation of updating the target value of a local individual AVF using the weighted double estimation method, which can counterbalance the overestimation in Q-Learning algorithm and the underestimation in Double Q-Learning, thus reducing the overestimation error of the JAVF. The loss calculation and training process of the λWD QMIX algorithm are shown in Eq. (25) and Algorithm 1, respectively. As the λWD QMIX uses the same network structure and parameters as the QMIX and only employs a different calculation method of the JAVF updating target, its training process is almost the same as that of the QMIX.

$$ L\left( {\uptheta } \right) = E\left[ {\left( {Q_{t}^{{{\uplambda }WD - tot}} - Q_{tot} \left( {\overrightarrow {{{\varvec{\tau}}_{t} }} ,\overrightarrow {{{\varvec{a}}_{t} }} ,s_{t} ;{\uptheta }_{t} } \right)} \right)^{2} } \right] $$
(25)
Algorithm 1
figure a

The pseudocode of the λWD QMIX training process

Full size image

5 Experimental Results

5.1 Experimental Parameter Settings

The proposed algorithm was tested in a SMAC environment [44], which has been a widely used environment for evaluating the MADRL algorithms. The SMAC consisted of a series of StarCraft II (a real-time policy game) micromanagement scenarios encompassing the easy, hard and super-hard levels. The selection of scenarios emphasized the fine-grained distributed micro-manipulation of multiple agents and aimed to evaluate the ability of multiple independent agents to perform complex tasks by learning cooperative actions. The settings of the action space, state features, and reward functions were set as given in [44]. In the experiment, hard and super-hard scenarios in SMAC were mainly selected to test the algorithms under the same environment parameter settings as those used in [45].

The λWD QMIX algorithm was constructed based on the PyMARL framework [44]. The fully-connected layer and GRU hidden layer in the agent network structure had a size of 64 dimensions, and the weighted network and embedding layer of the mixing network used for centralized training were set to 64 dimensions and 32 dimensions, respectively. Four NVIDIA GTX 2080 Ti GPUs were used for training, and the training duration of each scenario was roughly 10–28 h due to the constraints on the number of agents in the scenario and the episode length. During the training, exploration was performed using a \(\epsilon -\) greedy policy; the exploration rate \(\epsilon\) was linearly decreased from 1.0 to 0.05 in the first 0.5M time step and kept constant during subsequent learning; the reward discount factor was set to \(\gamma = 0.99\). Further, the data bits of the latest 5000 episodes were stored in a replay buffer \(D\), the model was saved, and the target network and replay buffer \(D\) were updated upon the completion of each training session of 200 episodes. The network parameters of the model were updated using the Adam optimizer; the learning rate was set to \(lr = 0.001\); the training batch size was set to 128, the test batch size was set to eight; the decay index of \(Q^{\lambda - WD - tot}\) was set to \(\lambda = 0.6\); finally, the weighted adjustment factor was set to \(c = 100\). After each training iteration, the agent performed the selection action using a decentralized greedy policy, evaluated the algorithm performance based on the test win rates obtained in 32 independently run episodes, and took the median of the last 10 tested win rate values as the final performance of the algorithm. Five random seeds were used in each round of the experiment, and the results indicated 95% confidence intervals.

5.2 Comparative Analysis of Experimental Results

In the experiment, four asymmetric hard and super hard scenarios, namely 5m_vs_6m, 6h_vs_8z, 3s5z_vs_3s6z, and corridor, were selected for testing the algorithm. The Sub-AVG algorithm used in the experiment adopted the code provided by the authors, and the number of target neural networks was set to \(K_{s} = 5\). The Double QMIX and MC-QMIX algorithms were designed based on the PyMARL framework, and the number of integrated models in the MC-QMIX algorithm was set to \(K_{m} = 5\). All algorithms used the Adam optimizer to update the network parameters, and the learning rate was set to \(lr = 0.001\). The experimental results are shown in Fig. 1 and Table 1.

Fig. 1
figure 1

The test win rates obtained by different methods in four SMAC scenarios

Full size image
Table 1 The average test win rate and standard deviation after the last 10 training iterations on the SMAC maps for different methods, using 10M training timesteps
Full size table

The experimental results show that the proposed λWD QMIX algorithm achieved the best performance in all four homogeneous or heterogeneous asymmetric scenarios. In particular, the λWD QMIX achieved an 18% higher test win rate than the second-best-performing algorithm MC-QMIX in the hardest task of 6h_vs_8z. The QMIX algorithm achieved the worst performance among all the tested algorithms, which clearly indicated that the final performance of the algorithm could be significantly improved by effectively reducing the overestimation error of JAVF in the VFD-based MADRL algorithms. The Double QMIX and QMIX algorithms can be regarded as two special cases of the λWD QMIX algorithm, that is, the λWD QMIX algorithm was equivalent to the QMIX algorithm when \(c = 0\) and \(\lambda = 0\), but was equivalent to the Double QMIX algorithm when \(c = \infty\) and \(\lambda = 0\). In the Double QMIX algorithm, the DQN algorithm in the QMIX algorithm was replaced by the Double DQN algorithm. Although this was only a small change, it successfully avoided the overestimation problem caused by the maximization operation in calculating the JAVF updating target, which was reflected by the 27% improvement in the average win rate in the four tasks. The Sub-AVG algorithm maintained a faster learning speed under three tasks other than corridor. The main reason for this could be that the Sub-AVG algorithm accelerated the learning efficiency by maintaining multiple target neural networks and averaging the previously learned JAVs. The basis of this arrangement was to enhance the prediction of future rewards using a longer time trajectory when updating the target, which had a certain acceleration effect on the learning speed. The MC-QMIX algorithm could be regarded as a variant of the Double QMIX algorithm. It generated reasonable weights for the multiple maintained action estimators through learning, so it could provide a JAVF estimate that was closer to the true JAVF compared to that provided by the Double QMIX algorithm, indicating that the MC-QMIX algorithm could achieve higher performance. Compared to the Sub-AVG and MC-QMIX algorithms, the λWD QMIX algorithm could achieve a higher accuracy level in the estimation and multi-step prediction of the updating target of JAVF by using the weighted double estimation and eligibility trace methods without requiring augmentation of the network structure. Since the λWD QMIX algorithm combined the advantages of the Sub-AVG and MC-QMIX algorithms, it excelled in both learning efficiency and algorithm performance.

5.3 Ablation Experiment

To investigate the influence of decay index \(\lambda\) and weighted adjustment coefficient \(c\) on the final performance of the proposed algorithm further, this study conducted a series of ablation experiments with different \(\lambda\) and \(c\) settings. The experimental results are shown in Fig. 2 and Table 2, where it can be seen that when \(\lambda\) was fixed to 0.6, the final test win rate increased continuously with the value of \(c\), indicating that the accurate estimation of the true target value played an important role in improving the algorithm’s performance. When c was fixed to 100 and \(\lambda\) changed, the test result of the λWD QMIX algorithm varied significantly among task scenarios. The test results of the λWD QMIX algorithm can be summarized as follows:

  1. (1)

    When \(c = 100\) and \(\lambda = 0.9\), the final performance of the λWD QMIX algorithm was the worst and the learning efficiency was the lowest among all methods. The main reasons were as follows. First, when \(\lambda\) was excessively large, the algorithm overly focused on and relied on past rewards, so it would take more rounds to update the algorithm to achieve the expected result, which indicated a low learning efficiency. Second, when \(\lambda\) was excessively large, the algorithm was too conservative, and the range of exploration was small, which would make it impossible to update the target value effectively, thus downgrading the algorithm performance, as evidenced by the low final win rates of 3.1% and 11.5% achieved in the exploration-intensive tasks of 6h_vs_8z and 3s5z_vs_3s6z, respectively;

  2. (2)

    In the 3s5z_vs_3s6z task, the final performance of the λWD QMIX algorithm was the best among all methods, and a high learning efficiency was maintained when \(c = 100\) and \(\lambda = 0.3\). In other tasks, the final performance of the λWD QMIX algorithm was the best among all methods when \(c = 100\) and \(\lambda = 0.6\). The main reason was as follows. In the 3s5z_vs_3s6z task, the policy the agent needed to learn circuitous tactics, that is, the allied zealots needed to learn to surround the enemy stalkers, while the allied stalkers needed to master kitting and to spread out their positions to avoid enemy attacks. In such a task, the λWD QMIX algorithm had to pay more attention to exploration to discover new and excellent joint state action pairs, so the λWD QMIX algorithm performed better when \(\lambda\) was set to a relatively small value of 0.3. Furthermore, the results indicated that in exploration-intensive task of 6h_vs_8z, the final performance of the λWD QMIX algorithm when \(c = 100\) and \(\lambda = 0.3\) was almost the same as its performance when \(c = 100\) and \(\lambda = 0.6\);

  3. (3)

    When \(c = 100\) and \(\lambda = 0.0\), the λWD QMIX algorithm used only the weighted double estimation method for correcting the estimated value of JAVF. Compared with the Double QMIX algorithm, the λWD QMIX algorithm could better reduce the impact of the inconsistency in the estimation of individual AVFs on the JAVF estimation result, which was reflected by a 9.5% improvement in the average win rate of the λWD QMIX algorithm in the four tasks;

  4. (4)

    When \(c = 0\) and \(\lambda = 0.6\), the λWD QMIX algorithm used only Peng’s \(Q\left( \lambda \right)\) method based on the eligibility trace backup for the multi-step estimation of JAVF. Different from the QMIX algorithm, which used the one-step bootstrapping updating method, the λWD QMIX algorithm used the long-horizon trajectory and thus could better help the agent to explore better policies, which was reflected by a 23.9% improvement in the average win rate in the four tasks.

Fig. 2
figure 2

The ablation experiment’s results of the λWD QMIX algorithm obtained under different hyperparameter settings

Full size image
Table 2 The average test win rate and standard deviation after the last 10 training iterations on the SMAC maps of the λWD QMIX algorithm for different hyperparameter combinations using 10M training timesteps
Full size table

Further, the estimated JAVF updating targets obtained by the λWD QMIX algorithm in exploration-intensive tasks of 3s5z_vs_3s6z and 6h_vs_8z under different hyperparameter settings are shown in Fig. 3, where it can be seen that in both tasks, the JAVF obtained by the λWD QMIX algorithm was not effectively updated and always had a relatively low value when \(c = 100\) and \(\lambda = 0.9\). In the 6h_vs_8z task, most of the policies learned under different hyperparameter combinations were ineffective and could not gain a large reward in the task, so the final JAVF estimates responsible for obtaining the optimal and suboptimal hyperparameter combinations were significantly higher than the other hyperparameter combinations. In the 3s5z_vs_3s6z task, most of the hyperparameter combinations could yield an algorithm performance level higher than 50%, so the policies with an excessively large JAVF value performed poorly under the influence of the overestimation problem.

Fig. 3
figure 3

The JAVF updating targets obtained by the λWD QMIX algorithm in two exploration-intensive tasks under different hyperparameter settings

Full size image

5.4 Proposed Method in MADRL Algorithms Application

Currently, most of the widely-used MADRL algorithms based on communication learning use the VFD method with concealed communication [46, 47]. Particularly, the communication policy network is embedded into the action policy network of individual agents for making decisions based on the information transferred from other agents in the explicit mode. However, this type of method still uses the hybrid networks of QMIX and other methods to perform centralized training on the individual utility function \(Q_{i} \left( {\tau^{i} ,c^{i} ,a^{i} } \right)\) of each agent, where \(c^{i}\) represents the aggregated communication information received by an agent i for making the final action decision. The MADRL algorithms based on communication learning increase learning complexity and usually have better algorithm performance, but they do not change any training process and thus face the problem of JAVF overestimation.

In this section, the λWD QMIX method is applied to the VBC [48] and SCTC algorithms [49], which are two typical MADRL algorithms based on communication learning, to obtain two new algorithms named the λWD VBC and λWD SCTC, respectively; these algorithms are then used to verify the extendibility of the λWD QMIX method. The experimental results of the λWD VBC and λWD SCTC methods under the hyperparameter combination of \(c = 100\) and \(\lambda = 0.6\) are presented in Fig. 4 and Table 3. In addition to the aforementioned four task scenarios, two more communication task scenarios of 1o_10b_vs_1r and 1o_2r_vs_4r were used in the comparative experiment. The experimental results showed that the λWD QMIX method could significantly improve the final performance and learning speed of the VBC and SCTC algorithms, achieving the 33% and 19.1% improvements on average in the final test win rate in the six tasks, respectively.

Fig. 4
figure 4

The test win rates obtained by the f λWD VBC and λWD SCTC algorithms in six SMAC scenarios

Full size image
Table 3 The average test win rate and standard deviation after the last 10 training iterations on the SMAC maps of the λWD VBC and λWD SCTC algorithms using 10M training timesteps
Full size table

6 Conclusion

In this study, it is shown that the estimation bias in the VFD-based MADRL algorithms can cause the overestimation of the JAVF updating target. To address this problem, an improved MADRL algorithm based on the multi-step weighted double estimation named λWD QMIX is proposed. The proposed algorithm can provide a stable and accurate estimation of JAVF through the mechanisms of bias correction based on the weighted double estimation and multi-step updating based on the eligibility trace backup, thus effectively reducing the overestimation error. The extendibility of the proposed method is verified by combining it with the MADRL algorithms based on communication learning. The results of the comparative and ablation experiments conducted on the Starcraft II micro-management benchmark demonstrate the effectiveness of the proposed method. Since the proposed λWD QMIX algorithm only changes the computation of the JAVF updating target, without additionally adding or changing any network structure of the baseline algorithm, it can in principle be combined with any VFD-based MADRL algorithms. And in future work, the core idea of the proposed method could be extended to the MADRL algorithms based on a centralized value function to improve the accuracy of value of the Critic.

7 Code or Data Availability

Data sets generated during the current study are available from the corresponding author on reasonable request.