Abstract
Without altering the inertial system into the two first-order differential systems, this paper primarily works over the global exponential dissipativity (GED) of memristive inertial competitive neural networks (MICNNs) with mixed delays. For this purpose, a novel differential inequality is primarily established around the discussed system. Then, by applying the founded inequality and constructing some novel Lyapunov functionals, the GED criteria in the algebraic form and the linear matrix inequality (LMI) form are given, respectively. Furthermore, the estimation of the global exponential attractive set (GEAS) is furnished. Finally, a specific illustrative example is analyzed to check the correctness and feasibility of the obtained findings.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Competitive neural networks (CNNs) with input layer and competitive layer were proposed primarily by Meyer-B\({\ddot{a}}\)se et al. [1] in 1996, which contain two different kinds of state variables: the long-term memory (LTM) picturing the slow changes of synapses in response to external stimuli and the short-term memory (STM) picturing the rapid neural activity. Different from the double-layer structure BAMNNs, the neurons of CNNs have not only vertical links between the competitive layer and the input layer, but horizontal links between neurons of the parallel layer. This distinct two-layer structure makes that CNNs have been extensively concerned and applied in palmprint recognition [2], optimal estimation [3], chemical engineering [4], image classification [5], geological identification [6] and so on. Consequently, it is meaningful to analyze the dynamic behaviors of CNNs and many successful discoveries have been produced, such as synchronization [7, 8], periodic solutions [9,10,11,12], stability [13,14,15], passivity [16], stabilization [17, 18] and so on.
In 2008, HP team [19] created a memristor device with memory characteristics. Memristor can better connect large circuits than ordinary resistors in NNs, thereby improving the computing power, parallel ability and adaptive ability of NNs. Therefore, an increasing number of academics have begun to introduce memristors into CNNs to form memristive CNNs (MCNNs) [20,21,22]. Besides, because the speed of signal transmission between neurons in NNs is constrained, time delay exists inevitably in NNs [22,23,24]. And studies have shown that time delay can perturb the balance of the system and produce some intricate dynamic characteristics, such as chaos or bifurcation [25]. So, NNs with delays can describe practical problems more realistically and objectively. Since in lots of practical situations, the change of the present state of the system might be associated not only with the present concrete state, but the change of the historical state and the change rate of the historical state, for instance, the equivalent circuit of some components [26]. As a result, neutral-type delay existing in the derivative of the state function was introduced into NNs [27, 28].
Meanwhile, with the rapid development of science and technology, ordinary first-order NNs can no longer meet the actual needs. In 1986, Westervelt and Babcock [29] brought in inertial terms into NNs to obtain inertial NNs (INNs). Inertia terms can not only promote the disordered search performance of NNs, but also are used in inductor circuits in practice to simulate the semicircular capillary cell membrane of animals [30]. In recent years, the dynamics of various INNs [31,32,33,34] have been broadly studied from many scholars. Peng and Jian [31] studied the synchronization of fractional-order INNs in the global Mittag-Leffler sense. The author [32] was dedicated to the fixed-time synchronization of complex-valued INNs. Duan and Du [33] investigated the positive periodic solution for INNs and the author [34] researched the global exponential stabilization of memristive INNs (MINNs). However, the above results all adopt the reduced order method to analyze the inertial item, which causes the increase of the system dimension and the complication of theoretical research. As a result, several scholars [27, 35, 36] have attempted to investigate straightway the dynamic behaviors of INNs via non-reduced order strategy.
As a generalization of Lyapunov stability, the dissipativity was first proposed by Willems [37, 38]. To date, the dissipativity that concentrates on the stability of the whole system has been applied to chaos [39], stability theory [40], robust control [41] and state estimation [42]. Meanwhile, the existing research [43] shows that the dissipativity can be used to determine the attractive set of the system and there is no equilibrium state, periodic state and chaos attractors outside the attractive set [44]. Accordingly, dissipativity analysis has received more and more attention from researchers. Aouiti et al. [45] were dedicated to the global dissipativity of high-order Hopfield BAMNNs. The author [46] used matrix measure theory to discuss the global dissipativity of complex-valued BAMNNs. Ali et al. [47] worked over the global dissipativity of fractional-order quaternion-valued NNs. The dissipativity of uncertain INNs was investigated [48] based on matrix measure. By reduced order ways, Zhang et al. [49] and Duan et al. [28] discussed the GED of MINNs and BAM INNs (BAMINNs) with neutral-type delay, respectively. Using non-reduced order ways, the scholars investigated the dissipativity of MINNs [27] and the GED of uncertain BAMINNs [50]. But, there hardly any paper that concerned with the GED of MICNNs.
Considering the above analysis, this article will work on the GED of MICNNs with mixed delays via non-reduced order strategy. The highlights of this article are as follows: (1) A new differential inequality is firstly established. (2) Adopting non-reduced order approach, the GED of MICNNs is straightway studied by presenting some novel Lyapunov functionals and using the proposed inequality. (3) The criteria in algebraic form and LMI form are supplied to ensure the GED of the studied system. Besides, the framework of the GEAS is also furnished.
The rest part of this article is structured as below: Part 2 supplies the preliminaries and model description. Part 3 provides the main results. Part 4 checks the correctness and effectiveness of the obtained results through a concrete illustrative example. Finally, Part 5 provides a brief summary.
2 Preliminaries and Model Description
Let \( \Re \), \(\Re ^{\ell \times \ell }\) and \(\Re ^\ell \) signify the set of numbers, \(\ell \times \ell \) matrices and \(\ell \)-dimensional vectors in the real number field, respectively. For \(\Upsilon \in \Re ^{\ell \times \ell }\), \(\Upsilon ^{-1}\), \(\Upsilon ^T\), \(\lambda _{\min }(\Upsilon )(\lambda _{\max }(\Upsilon ))\) denote the inverse, transpose, minimal (maximal) eigenvalue of \(\Upsilon \), respectively. \(\Upsilon <0\) shows matrix \(\Upsilon \) is symmetric negative definite, \(*\) shows the symmetric elements in the matrix. \(\aleph =\left\{ 1,2,\ldots ,\ell \right\} \). For \(\jmath =(\jmath _1,\jmath _2,\ldots ,\jmath _\ell )^T\in \Re ^\ell \), the norm is defined by \(\Vert \jmath \Vert = \root \of {\sum \limits _{f\in \aleph } |\jmath _f|^2}\).
Take into account the following MICNNs with mixed time delays for \(f\in \aleph \)
where
the second derivatives are referred to as an inertial term of system (1), \(\Xi _f(t)\) represents the current activity level of the fth neuron, \(\beta > 0\) is a rapid timescale determined by STM, \(\psi _f>0\) is the variable coefficient, \(\pounds _g (\cdot )\) is activation function, \(\gimel _g(t)\ge 0\), \(\daleth _g(t)\ge 0\) and \(\epsilon _g(t)\ge 0\) represent discrete, neutral-type and distributed time-varying delays, respectively. \(h_f>0\) means the strength of the external stimulation, \(b_{f g}(t)\) denotes the synaptic efficiency. \(\varphi _f(\Xi _f(t))\), \(w_{f g}(\Xi _f(t))\), \(x_{f g}(\Xi _f(t))\), \(y_{f g}(\Xi _f(t))\), \(z_{f g}(\Xi _f(t))\) and \(\breve{ \varphi } _f(b _{f g}(t))\) refer to the linked weights of a memristor that vary depending on the properties of current–voltage feature and memristor. \(\breve{\psi }_f>0 \) and \(d_g \) are some constants, external input \(L_f(t)\) satisfies \(|L_f(t)|\le L_f \) with constant \(L_f>0\).
Remark 1
If \(\varphi _f(\Xi _f(t))\), \(w_{fg }(\Xi _f(t))\), \(x_{fg }(\Xi _f(t))\) are constants, \(\beta =\breve{\varphi } _f(b _{f g}(t))=\breve{\psi }_f =1\) and \(y_{fg }(\Xi _f(t))=z_{fg }(\Xi _f(t))=0\), then system (1) can be simplified as the model in [15]. If \(y_{fg }(\Xi _f(t))=z_{fg }(\Xi _f(t))=0, \beta =1\) and \(\ddot{b }_{f g}(t)\) is not considered, then system (1) is the model in [11] and system (1) with \(L_f(t){=0}\) can be reduced to the model (2.4) in [12], respectively. So, the model (1) here is more common.
Remark 2
If \(y_{f g}(\Xi _f(t))=0\), then system (1) can be translated into
If \(z_{f g}(\Xi _f(t))=0\), then system (1) can be expressed as
For simplicity, let \(c_f(t)=\sum \limits _{g\in \aleph }d_g b_{f g}(t)\) and \(\sum \limits _{g \in \aleph }d^2_g=\gamma \), then system (1) can be rewritten as
The state-related parameters in (4) meet
where \(\phi _f >0 \) and \(\breve{\phi }_f > 0\) denote the switching jump, \(\varphi _f^\bullet >0\), \(\breve{\varphi } _f^\bullet >0\), \(\varphi _f^\star >0\), \(\breve{\varphi } _f^\star >0\), \(w _{f g}^\bullet ,w_{f g}^\star ,y _{f g}^\bullet ,y_{f g}^\star ,x _{f g}^\bullet ,x _{f g}^\star \), \(z _{f g}^\bullet ,z _{f g}^\star \in \Re \) are known constants for \(f,g\in \aleph \). In addition, let
It follows from the set-valued map and differential inclusion theory [51] that there are contants \(\varphi _f \in co(\varphi _f(\Xi _f(t)))=[\varphi _f^-, \varphi _f^+]\), \(w_{f g}\in co(w_{f g}(\Xi _f(t)))=[w _{f g}^-,w_{f g}^+]\), \(x_{f g}\in co(x_{f g}(\Xi _f(t)))=[x _{f g}^-,x_{f g}^+]\), \(y_{f g}\in co(y_{f g}(\Xi _f(t)))=[y _{f g}^-,y_{f g}^+]\), \(z_{f g}\in co(z_{f g}(\Xi _f(t)))=[z _{f g}^-,z_{f g}^+]\), \(\breve{\varphi }_f\in co(\breve{\varphi }_f(c_f(t)))=[\breve{\varphi } _f^-, \breve{\varphi } _f^+]\) such that
Hypothesis 1
For \(\forall \imath ,\jmath \in \Re \), there are constants \(\Theta _f^-\) and \(\Theta _f^+ \) such that \(\Theta _f^- \le \frac{\pounds _f(\imath )-\pounds _f(\jmath )}{\imath -\jmath }\le \Theta _f^+\), i.e.,
where \(\Theta ^+=\textrm{diag}\{\Theta _1^+,\Theta _ 2^+,\ldots ,\Theta _ \ell ^+ \}\), \(\Theta =\textrm{diag}\{\Theta _1,\Theta _ 2,\ldots ,\Theta _ \ell \}\), \(\Theta ^-=\textrm{diag}\{\Theta _1^-,\Theta _ 2^-,\ldots ,\Theta _ \ell ^- \}\), \(\Gamma =\Theta ^-\Theta ^+\), \(\Theta _f=\max \{|\Theta _f^-|,|\Theta _f^+|\}\), \(\breve{\Gamma }=\frac{1}{2}(\Theta ^-+\Theta ^+)\).
Remark 3
Compared with the activation functions in [45,46,47, 49], the activation function satisfying Hypothesis 1 here is better and more common, because the constants \(\Theta _f^- \) and \(\Theta _f^+ \) in Hypothesis 1 can be positive, negative or zero. If \(\Theta _f^- = \Theta _f^+ \), the activation function belongs to the Lipschitz-type [27, 36, 48].
Hypothesis 2
Time-varying delays \(\daleth _g(t), \gimel _g(t) \) and \(\epsilon _g(t)\) are differential and bounded and satisfy \(0 \le \daleth _g(t) \le \daleth \), \(0 \le \gimel _g(t) \le \gimel \), \( 0 \le \epsilon _g(t)\le \epsilon \), \(\dot{\daleth }_g(t) \le \daleth _0 <1 \), \(\dot{\gimel }_g(t) \le \gimel _0 < 1 \), \(\dot{\epsilon }_g(t) \le \epsilon _0 < 1\).
The initial conditions of system (5) are
where \( l_f(\breve{\theta }),{\bar{l}}_f(\breve{\theta }),{\mathfrak {T}}_f(\breve{\theta }),\bar{{\mathfrak {T}}}_f(\breve{\theta }) \in C([-\varsigma ,0],\Re )\), \(\varsigma ={\max }\{\gimel ,\daleth ,\epsilon \}\). Assume that system (5) has at least one solution through \((t_0,F,G)\) denoted by \((\Xi ^T(t,F,G),c^T(t,F,G))^T\) and simply expressed as \(H(t)=(\Xi ^T(t),c^T(t))^T\), where
In addition, denote
Then, the matrix form of system (5) is
Based on [28, 50], the following definition can be derived.
Definition 1
System (1) is said to be a globally exponentially dissipative system (GEDS), if there exist positive constant \({\mathfrak {B}}\) for the compact set \(\mho =\big \{H(t)\big |\Vert H(t)\Vert \le {\mathfrak {B}}\big \}\subset \Re ^{2\ell }\) and every solution \(H(t) \subseteq \Re ^{2\ell } -\mho \) with \(\forall \) \(({l^T(\breve{\theta }),{\mathfrak {T}}^T(\breve{\theta })})^T \in \Re ^{2\ell } \) for \(\breve{\theta }\in [t_o-\varsigma ,t_0]\), there is positive numbers \(\kappa =\kappa (\Vert F\Vert ,\Vert G\Vert )\) and \(\delta \) such that
and the set \(\mho \) is called to be a GEAS of system (1).
Lemma 1
[52] For \(x,y\in \Re \) with \( x<y\), integrable vector function \(\pounds (\varpi ):[x,y]\rightarrow \Re ^\ell \) and matrix \({\mathfrak {O}}>0\), then
Lemma 2
Based on Hypothesis 2, let \(\Xi (t)\) and c(t) represent the solution of system (7), \(\Upsilon _f\in \Re ^{\ell \times \ell }(f=1,2,\ldots ,7)\) be positive definite matrices and Lyapunov functional is described as
If there are positive numbers \(k_1,k_2,k_3,k_4,k_5,k_6\) and \( {\mathcal {E}} \) such that
then the following inequality holds
where constant \(\delta >0\) meets
Proof
Choosing a function as \({\mathfrak {S}}(t)=e^{\delta t}({\mathcal {F}}(t)-\frac{ {\mathcal {E}} }{\delta })\), then
Two sides of (10) are integrated from 0 to \(t_1\), then
The double-integral term in (11) can be written as
Identically,
Next, calculating the triple integral in (11), one can get
According to (11)–(14), one can get
that is
Since \(t_1\) is arbitrary, then
\(\square \)
Remark 4
The CNN model (7) here is different from BAMNNs in [28, 50], the result of Lemma 2 here is also different from those in [28, 50] and they do not include each other. Thus, Lemma 2 here and the results in [28, 50] will complement and enrich each other.
3 Main Results
For convenience, the following notations are provided:
Theorem 1
Under Hypotheses 1–2, there are constants \(\delta _f>0\), \(\Im _f>0\), \(\zeta _f>0\), \(\chi _f\wp _f>0\) and \(\xi _f\varepsilon _f>0\) such that
then system (1) is a GEDS and the set
is a GEAS of system (1).
Proof
Introducing a Lyapunov functional as
where
Computing the derivations of \({\mathcal {F}}_f(t)(f=1,2,3,4)\) along system (5), one can have
According to the inequality \(m^2+n^2\ge 2mn\), one can obtain
Identically
Substituting (18)–(24) into (17), then
Combining (25)–(28), one can obtain
for \(\Vert H(t)\Vert ^2 >{\frac{{\mathcal {I}}}{{\mathcal {J}}}}\), i.e. \(H(t) \notin \mho _1\). It follows from (29) that \({\mathcal {F}}(t)\le {\mathcal {F}}(t_0)\), then
where \(\delta =\min \limits _{f\in \aleph }\{\delta _f\}\), and let \(U=\min \limits _{ f\in \aleph }\{\Im _f, \zeta _f\}>0,~~{\mathfrak {M}}=\sqrt{\frac{2}{U}\sup \limits _{ \breve{\theta } \in [t_0-\varsigma ,t_0]}{\mathcal {F}}(\breve{\theta })}\), then
and
On the basis of Definition 1, one can know that system (5) is a GEDS and the set \(\mho _1\) is a GEAS of system (5). Accordingly, system (1) is a GEDS and \(\mho _1\) is a GEAS of system (1). \(\square \)
Remark 5
The results in Theorem 1 are delay-dependent. The proposed Lyapunov-krasovski functionals (16) refers to not only the states and the derivatives of the states of the system but also discrete, neutral-type and distributed time-varying delays, which can further reduce conservativeness.
Remark 6
When \(\delta =\delta _f=0\) for \(f\in \aleph \) in Theorem 1, then the above results in Theorem 1 can be used to investigate global dissipativity of MICNNs with mixed delays.
Corollary 1
If \(\pounds _f(0)=0\), under Hypotheses 1–2, there are constants \(\delta _f>0\), \(\Im _f>0\), \(\zeta _f>0\), \(\chi _f\wp _f>0\) and \(\xi _f\varepsilon _f>0\) such that \( \mathcal { \breve{A} } _f<0,~4 \mathcal { \breve{A} } _f \mathcal { \breve{B} } _f> \mathcal { \breve{C} } _f^2, ~\mathcal { \breve{D} } _f<0, ~4 \mathcal { \breve{D} } _f \mathcal { \breve{N} }_f> \mathcal { \breve{L} }_f^2, f\in \aleph ,\) then system (1) is a GEDS and the set
is a GEAS of (1), where \(\mathcal { \breve{A} } _f\), \(\mathcal { \breve{B} } _f\), \(\mathcal { \breve{C} } _f\), \({\mathfrak {U}}\), \({\mathfrak {N}}\), \(\mathcal { \breve{L} } _f\), \(\mathcal { \breve{K} } _f\), \(\mathcal { \breve{S} } _f\), \(\mathcal { \breve{J} } _f\), \({\mathcal {I}}\) and \({\mathcal {J}}\) are the same as Theorem 1 and
Corollary 2
Under Hypotheses 1–2, there are constants \(\delta _f>0\), \(\Im _f>0\), \(\zeta _f>0\), \(\chi _f\wp _f>0\) and \(\xi _f\varepsilon _f>0\) such that \( \mathcal { \breve{A} } _f<0,~4 \mathcal { \breve{A} } _f \mathcal { \breve{B} } _f> \mathcal { \breve{C} } _f^2, ~\mathcal { \breve{D} } _f<0, ~4 \mathcal { \breve{D} } _f \mathcal { \breve{N} }_f> \mathcal { \breve{L} }_f^2, f\in \aleph ,\) then system (2) is a GEDS and the set
is a GEAS of (2), where \(\mathcal { \breve{A} } _f\), \(\mathcal { \breve{B} } _f\), \(\mathcal { \breve{C} } _f\), \({\mathfrak {U}}\), \({\mathfrak {N}}\), \(\mathcal { \breve{N} } _f\), \(\mathcal { \breve{D} } _f\), \(\mathcal { \breve{L} } _f\), \(\mathcal { \breve{K} } _f\), \(\mathcal { \breve{J} } _f\), \({\mathcal {J}}\), \({\mathcal {I}}\) are the same as Theorem 1 and
Corollary 3
Under Hypotheses 1–2, there are constants \(\delta _f>0\), \(\Im _f>0\), \(\zeta _f>0\), \(\chi _f\wp _f>0\) and \(\xi _f\varepsilon _f>0\) such that \( \mathcal { \breve{A} } _f<0,~4 \mathcal { \breve{A} } _f \mathcal { \breve{B} } _f> \mathcal { \breve{C} } _f^2, ~\mathcal { \breve{D} } _f<0, ~4 \mathcal { \breve{D} } _f \mathcal { \breve{N} }_f> \mathcal { \breve{L} }_f^2, f\in \aleph ,\) then system (3) is a GEDS and the set
is a GEAS of (3), where \(\mathcal { \breve{A} } _f\), \(\mathcal { \breve{B} } _f\), \(\mathcal { \breve{C} } _f\), \({\mathfrak {U}}\), \({\mathfrak {N}}\), \(\mathcal { \breve{N} } _f\), \(\mathcal { \breve{D} } _f\), \(\mathcal { \breve{L} } _f\), \(\mathcal { \breve{S} } _f\), \(\mathcal { \breve{J} } _f\), \({\mathcal {J}}\), \({\mathcal {I}}\) are the same as Theorem 1 and
Theorem 2
If \(\pounds (0)=0\), under Hypotheses 1 and 2, there are diagonal matrices \(\breve{{\mathcal {P}}}_1,\breve{{\mathcal {P}}}_2\in \Re _+ ^{\ell \times \ell }\) and positive definite matrices \(\Upsilon _f\in \Re ^{\ell \times \ell }(f=1,2,\ldots ,14)\) such that
then system (1) is a GEDS and the set
is a GEAS of (1), where \( {\mathcal {E}} =L^T\Upsilon _{14}L\) and constant \(\delta >0\) satisfies
Proof
Utilizing the Lyapunov functional in (8) again, then calculating the derivations of \({\mathcal {F}}_f(t)(f=1,2,3,4,5)\) along system (7), one gets
It is known from Lemma 1 and \(0 \le \epsilon _g(t)\le \epsilon \) that
Moreover, it follows from (6) that
Combining (30)–(36), one can get
where \(\eta =\left( \dot{\Xi }^T(t),\Xi ^T(t),{\dot{c}}^T(t),c^T(t),\pounds ^T(\Xi (t)),\pounds ^T(\dot{\Xi }(t)), ~ \pounds ^T(\Xi (t- \right. \)\(\left. \gimel (t))), \pounds ^T(\dot{\Xi }(t-\daleth (t))), L^T(t), \int _{t- \epsilon (t)}^t\pounds ^T(\Xi (\varpi ))d\varpi \right) ^T\). Based on Lemma 2, one can obtain
where \(\alpha \) is shown in (9). From Definition 11, system (7) is a GEDS and \(\mho _2\) is a GEAS of (7). Accordingly, system (1) is a GEDS and \(\mho _2\) is a GEAS of system (1). \(\square \)
Remark 7
Under different conditions, we can obtain Theorems 1 and 2 by utilizing different analysis methods, respectively. The conditions of Theorem 2 need the activation function satisfying \(\pounds _f(0)=0\), but Theorem 1 may not need the condition \(\pounds _f(0)=0\), which will be illustrated by the later example. So, Theorems 1 and 2 will complement and enrich both.
Remark 8
By establishing differential inequalities, Theorem 3 in [28] and Theorem 1 in [50] obtained the GED criteria in the form of LMI for neutral-type BAMINNs and uncertain BAMINNs, respectively. However, the inequalities in [28, 50] are unavailable for MICNNs with mixed delays. So, Theorem 2 complement the prior research for CNNs and suggest that the findings here are novel.
Remark 9
The existing literatures [8, 11, 12] on the dynamics of CNNs often set \(\beta =1\), which will lead to more conservative results. Literatures [7, 13] pointed out that \(\beta \) may affect the dynamics of systems. And Theorems 1–2 manifest also that the estimations of the attractive set are also affected by \(\beta \). Thus, the results here are more appropriate and general.
Remark 10
Up to now, there are many results on the GED for various NNs [45,46,47,48,49,50], but there is almost no literature to be dedicated to the GED of MICNNs with mixed delays, which shows that the findings of this paper are novel. Based on the non-reduced order method, some dynamic behaviors for integer-order INNs [27, 36] and fractional-order INNs [35] have been investigated. Besides, the authors [11, 12] investigated the anti-periodic solutions problem for inertial CNNs via the reduced order method, and yet this paper gets rid of the reduced order method in [11, 12] and directly researches the GED of MICNNs without altering the original system into a first-order one, which avoids additional computation.
4 An Illustrative Example
Consider MICNN (4) with \(\ell = 2\), \(\daleth _g(t) =0.4\sin t+0.6\), \(\gimel _g(t) =0.1 \sin ^2t+0.9\), \(\epsilon _g(t) =0.5 \sin ^2t+0.5\), then Hypothesis 2 holds with \( 0\le \daleth _g (t) \le \daleth =1\), \(0\le \gimel _g (t)\le {\gimel }=1\), \(0\le \epsilon _g(t) \le \epsilon =1\), \( \dot{\gimel }_g (t)\le \gimel _0=0.1<1\), \(\dot{\daleth }_g (t)\le \daleth _0=0.4<1\), \(\dot{\epsilon }_g (t) \le \epsilon _0=0.5<1( g=1,2)\). \(\varrho \) is constant.
Case 1. Let \(\beta =10\), \(\psi _1= \psi _2=1250\), \( \breve{\psi }_1=\breve{\psi }_2=120 \), \(h_1=h_2=100\), \(r=0.5\), \(L_1(t)=135\varrho \cos t\), \(L_2(t)=135 \varrho \sin t\), \(\pounds _f(\Xi _f(t))=8\tanh (\Xi _f(t))+8\Xi _f(t) +10\cos (\Xi _f(t))\), \(f=1,2\), \(\varphi ^\bullet _1=500\), \(\varphi ^\bullet _2=650\), \(\varphi ^\star _1=670\), \(\varphi ^\star _2=720\), \(\breve{\varphi }^\bullet _1=21\), \(\breve{\varphi }^\bullet _2=25\), \(\breve{\varphi }^\star _1=18\), \(\breve{\varphi }^\star _2=13\), \(\phi _1=\phi _2=0.2\), \(\breve{\phi }_1=\breve{\phi }_2=0.3\), other parameters are given in Table 1.
Obviously, \(\pounds _f(\Xi _f(t)) \) meets Hypothesis 1 with \(\Theta _1=\Theta _2=19.79\) and \(\pounds _1(0)=\pounds _2(0)=10 \). Through calculation, one can get \(L_1=L_2=135|\varrho |\), \(\varphi _1^-=500, \breve{\varphi }_1^-=18, \varphi _2^-=650, \breve{\varphi }_2^-=13, {\hat{w}}_{11}=1.2, {\hat{w}}_{12}=2.0, {\hat{w}}_{21}=2.3, {\hat{w}}_{22}=1.1, {\hat{x}}_{11}=1.0,{\hat{x}}_{12}=1.6, {\hat{x}}_{21}=2.1, {\hat{x}}_{22}=3.1, {\hat{y}}_{11}=1.7, {\hat{y}}_{12}=2.13, {\hat{y}}_{21}=2.2, {\hat{y}}_{22}=3.3, {\hat{z}}_{11}=1.7, {\hat{z}}_{12}=3.1, {\hat{z}}_{21}=0.9, {\hat{z}}_{22}=2.5. \)
Choose \(\Im _1=\Im _2=180\), \(\delta _1=\delta _2=0.02\), \(\zeta _1=\zeta _2=100\), \(\chi _1=\chi _2=\wp _1=\wp _2=\xi _1=\xi _2= \varepsilon _1=\varepsilon _2=1\), then the following data can be obtained: \(\mathcal { \breve{A} }_1=-9.2884<0\), \(\mathcal { \breve{B} }_1=-52.8845\), \(\mathcal { \breve{C} }_1=6.0400\), \(\mathcal { \breve{A} }_2=-13.9826<0\), \(\mathcal { \breve{B} }_2= -47.7329\), \(\mathcal { \breve{C} }_2=-8.9600\), \(\mathcal { \breve{D} }_1= -9.5325<0\), \( \mathcal { \breve{N} }_1= \mathcal { \breve{N} }_2= -100.5325\), \( \mathcal { \breve{D} }_2= -4.5325<0\), \(\mathcal { \breve{L} }_1=-36.9600\), \(\mathcal { \breve{L} }_2=-31.9600\), \({\mathcal {I}}_1=1841.9 \), \({\mathcal {I}}_2=1845 \), \({\mathcal {J}}_1=\min \{ 51.9026, 64.7066\}=51.9026\), \({\mathcal {J}}_2=\min \{ 46.2975, 44.1926\}= 44.1926\). Clearly, \(4 \mathcal { \breve{A} } _f \mathcal { \breve{B} } _f> \mathcal { \breve{C} } _f^2\) and \(4 \mathcal { \breve{D} } _f \mathcal { \breve{N} }_f> \mathcal { \breve{L} }_f^2\) hold for \(f=1,2 \) and all the prerequisites in Theorem 1 are satisfied. Accordingly, MICNN (4) is a GEDS and the set
is a GEAS of MICNN (4). Taking the initial values as \(l_1(\breve{\theta })=0.05\), \(l_2(\breve{\theta })=-0.07\), \({\mathfrak {T}}_1(\breve{\theta })=0.03\), \({\mathfrak {T}}_2(\breve{\theta })=-0.04\), \({\bar{l}}_1(\breve{\theta })=0.5\), \({\bar{l}}_2(\breve{\theta })=-0.6\), \(\bar{{\mathfrak {T}}}_1(\breve{\theta })=0.7\), \(\bar{{\mathfrak {T}}}_2(\breve{\theta })=-0.8\). When \(\rho =0\), there exists an equilibrium point \(H^*=(\Xi ^*_1,\Xi ^*_2,c^*_1,c^*_2)=(0.03122,-0.03772,0.03875,0.03875)\in \mho _1\).
Figures 1 and 2 signify the time response in \(\Re ^2\) and phase plot in \(\Re ^3\) of the states \(\Xi _1(t),\Xi _2(t),c_1(t)\), \(c_2(t)\) of system (4) with \(\varrho =1\) for Case 1, respectively. Figure 3 reveals the changes of the states of system (4) with disparate initial values, which means that the equilibrium point \(H^*\) of system (4) with different initial values and no external inputs in Case 1 is globally exponentially attractive.
Case 2. Let \(\beta =0.85\), \(\psi _1=\psi _2=280\), \( \breve{\psi }_1= \breve{\psi }_2=20 \), \(h_1=14,h_2=10\), \(r=9\), \(L_1(t)=-20 \varrho \cos t\), \(L_2(t)=20 \varrho \sin t\), \(\pounds _f(\Xi _f(t))=0.02\tanh (\Xi _f(t))+0.015\sin (\Xi _f(t))+0.065\Xi _f(t)(f=1,2)\), \(\varphi ^\bullet _1=18.1\), \(\varphi ^\bullet _2=15.1\), \(\varphi ^\star _1=\varphi ^\star _2=12.1\), \(\breve{\varphi }^\star _1=8\), \(\breve{\varphi }^\star _2=5\), \(\breve{\varphi }^\bullet _1=\breve{\varphi }^\bullet _2=4\), \(\phi _1=\phi _2=2\), \(\breve{\phi }_1=\breve{\phi }_2=3\), other parameters are given in Table 2.
Clearly, \(\pounds _f(\Xi _f(t)) \) meets Hypothesis 2 with \(\Theta _1^- = \Theta _2 ^-= 0.05 \), \(\Theta _1^+ = \Theta _2 ^+= 0.1 \) and \(\pounds _1(0)=\pounds _2(0)=0 \). Similarly, one can easily get \(L_1=L_2=20|\varrho |,\varphi _1^-= \varphi _2^-=12.1, \breve{\varphi }_1^-=\breve{\varphi }_2^-=4,w^+_{11}=-0.51, w^+_{12}= w^+_{21}=0.21, w^+_{22}=-0.31,x^+_{11}=0.41, x^+_{12}= -0.21, x^+_{21}= 0.31,x^+_{22}=0.21, y^+_{11}=0.51, y^+_{12}= 1.0, y^+_{21}= -1.1,y^+_{22}=0.31,z^+_{11}=z^+_{22}=0.02, z^+_{12}= -0.02, z^+_{21}=0.01\).
Then, the solutions of \(M<0\) are \(\breve{{\mathcal {P}}}_1{=}\textrm{diag}(0.6852,0.6855)\), \(\breve{{\mathcal {P}}}_2=\textrm{diag}(0.5058,0.5058)\),
\(\lambda _{\max }(\Upsilon _1)=0.2558\), \( \lambda _{\max }(\Upsilon _2)=10^{-3}\times 0.7948\), \(\lambda _{\max }(\Upsilon _3)= 0.1997\), \(\lambda _{\max }(\Upsilon _4)= 0.0098\), \(\lambda _{\max }(\Upsilon _5)=0.1804\), \(\lambda _{\max }(\Upsilon _6)=0.2088\), \(\lambda _{\max }(\Upsilon _7)= 0.1741\), \(\lambda _{\min }(\Upsilon _8)=0.0120\), \(\lambda _{\min }(\Upsilon _9)= 0.0075\), \(\lambda _{\min }(\Upsilon _{10})=0.2519\), \(\lambda _{\min }(\Upsilon _{11})=0.1760\), \(\lambda _{\min }(\Upsilon _{12})= 0.1360\), \(\lambda _{\min }(\Upsilon _{13})=0.1462\).
Then all the conditions in Theorem 2 are satisfied with \(\delta \in (0, 0.2877)\) and \( {\mathcal {E}} = 191.4249\). Therefore, MICNN (4) is a GEDS and the set
is a GEAS of MICNN (4). Let the initial values as \(l_1(\breve{\theta })=0.01 \), \(l_2(\breve{\theta })=-0.01\), \({\mathfrak {T}}_1(\breve{\theta })=0.02\), \({\mathfrak {T}}_2(\breve{\theta })=-0.02\), \({\bar{l}}_1(\breve{\theta })=0.22\), \({\bar{l}}_2(\breve{\theta })=-0.13\), \(\bar{{\mathfrak {T}}}_1(\breve{\theta })=0.23\), \(\bar{{\mathfrak {T}}}_2(\breve{\theta })=-0.18\).
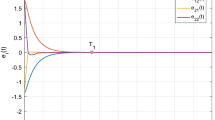
Figures 4 and 5 signify the time response in \(\Re ^2\) and phase plot in \(\Re ^3\) of the states \(\Xi _1(t),\Xi _2(t),c_1(t)\), \(c_2(t)\) of system (4) with \(\varrho =1\) for Case 2, respectively. Figure 6 confirms the changes of the states of system (4) with time under disparate initial conditions, which certifies that the zero solution of system (4) with disparate initial values and no external inputs in Case 2 is globally exponentially attractive.
Remark 11
For inputs \(L_1(t)=L_2(t)=0\), Case 1 with \(\pounds _f(0)\ne 0\) and Case 2 with \(\pounds _f(0)=0\) confirmed that the nonzero solution and the zero solution are globally exponentially attractive based on Theorems 1 and 2, respectively. Two cases have further illustrated the validity of the obtained results.
5 Conclusions
By establishing a novel differential inequality and introducing Lyapunov functionals, some new criteria in the form of LMIs and algebraic inequalities are supplied to guarantee the GED of MICNNs with mixed delays via non-reduced order strategy. Meanwhile, the detailed framework of the GEAS is also provided simultaneously. Numerical examples suggest the validity of the acquired findings in the end. In future research, we will be dedicated to the predefined-time synchronization and fixed-time synchronization for fractional-order CNNs or inertial-type CNNs.
References
Meyer-Bäse A, Ohl F, Scheich H (1996) Singular perturbation analysis of competitive neural networks with different time scales. Neural Comput 8:1731–1742
Liang X, Yang JY, Lu GM, Zhang D (2021) CompNet: competitive neural network for palmprint recognition using learnable gabor kernels. IEEE Signal Process Lett 28:1739–1743
Shi ZC, Yang YQ, Chang Q, Xu XY (2020) The optimal state estimation for competitive neural network with time-varying delay using local search algorithm. Phys A 540:123102
Gavrilescu M, Floria SA, Leon F, Curteanu S (2022) A hybrid competitive evolutionary neural network optimization algorithm for a regression problem in chemical engineering. Mathematics 10:3581
Muhammad SH, Muhammad B (2020) Competitive residual neural network for image classification. ICT Express 6:28–37
Thales Luiz Pinheiro A, Bruno Andrey Fonseca P, Jéssica Lia Santos C, André José Neves A (2021) Identifying clay mineral using angular competitive neural network: a machine learning application for porosity estimative. J Petrol Sci Eng 200:108303
Yang W, Wang YW, Morrescu IC, Liu XK, Huang YH (2022) Fixed-time synchronization of competitive neural networks with multiple time scales. IEEE Trans Neural Netw Learn Syst 33:4133–4138
Chen C, Mi L, Liu ZQ, Qiu BL, Zhao H, Xu LJ (2021) Predefined-time synchronization of competitive neural networks. Neural Netw 142:492–499
Arbi A, Cao JD (2017) Pseudo-almost periodic solution on time-space scales for a novel class of competitive neutral-type neural networks with mixed time-varying delays and leakage delays. Neural Process Lett 46:719–745
Wang DS, Luo DZ (2015) Multiple periodic solutions of delayed competitive neural networks via functional differential inclusions. Neurocomputing 168:777–789
Li YK, Qin JL (2020) Existence and global exponential stability of anti-periodic solutions for generalised inertial competitive neural networks with time-varying delays. J Exp Theor Artif Intell 32:291–307
Du B (2019) Anti-periodic solutions problem for inertial competitive neutral-type neural networks via Wirtinger inequality. J Inequal Appl 2019:1–15
Liu XM, Yang CY, Zhou LN (2018) Global asymptotic stability analysis of two-time-scale competitive neural networks with time-varying delays. Neurocomputing 273:357–366
Liu PP, Nie XB, Liang JL, Cao JD (2018) Multiple Mittag–Leffler stability of fractional-order competitive neural networks with Gaussian activation functions. Neural Netw 108:452–465
Shi M, Guo J, Fang XW, Huang CX (2020) Global exponential stability of delayed inertial competitive neural networks. Adv Differ Equ 2020:1–12
Rajchakit G, Chanthorn P, Niezabitowski M, Raja R, Baleanu D, Pratap A (2020) Impulsive effects on stability and passivity analysis of memristor-based fractional-order competitive neural networks. Neurocomputing 417:290–301
Wang LM, He HB, Zeng ZG (2021) Intermittent stabilization of fuzzy competitive neural networks with reaction diffusions. IEEE Trans Fuzzy Syst 29:2361–2372
Sheng Y, Zeng ZG, Huang TW (2022) Finite-time stabilization of competitive neural networks with time-varying delays. IEEE Trans Cybern 52:11325–11334
Strukov DB, Snider GS, Stewart DR, Williams RS (2008) The missing memristor found. Nature 453:80–83
Zhao Y, Ren SS, Kurths J (2021) Synchronization of coupled memristive competitive BAM neural networks with different time scales. Neurocomputing 427:110–117
Zhao Y, Ren SS, Kurths J (2021) Finite-time and fixed-time synchronization for a class of memristor-based competitive neural networks with different time scales. Chaos Solitons Fractals 148:111033
Gong SQ, Guo ZY, Wen SP, Huang TW (2019) Synchronization control for memristive high-order competitive neural networks with time-varying delay. Neurocomputing 363:295–305
Rakkiyappan R, Chandrasekar A, Cao JD (2015) Passivity and passification of memristor-based recurrent neural networks with additive time-varying delays. IEEE Trans Neural Netw Learn Syst 26:2043–2057
Rakkiyappan R, Premalatha S, Chandrasekar A, Cao JD (2016) Stability and synchronization analysis of inertial memristive neural networks with time delays. Cogn Neurodyn 10:437–451
Mendonca JP, Gleria I, Lyra ML (2019) Delay-induced bifurcations and chaos in a two-dimensional model for the immune response. Phys A 517:484–490
Zhang XM, Han QL (2009) A new stability criterion for a partial element equivalent circuit model of neutral type. IEEE Trans Circuits Syst-II: Exp Briefs 56:798–802
Wu K, Jian JG (2021) Non-reduced order strategies for global dissipativity of memristive neutral-type inertial neural networks with mixed time-varying delays. Neurocomputing 436:174–183
Duan LY, Jian JG, Wang BX (2020) Global exponential dissipativity of neutral-type BAM inertial neural networks with mixed time-varying delays. Neurocomputing 378:399–412
Babcock KL, Westervelt RM (1986) Stability and dynamics of simple electronic neural networks with added inertia. Phys D 23:464–469
Angelaki DE, Correia MJ (1991) Models of membrane resonance in pigeon semicircular canal type II hair cells. Biol Cybern 65:1–10
Peng Q, Jian JG (2023) Synchronization analysis of fractional-order inertial-type neural networks with time delays. Math Comput Simul 205:62–77
Guo RN, Lu JW, Li YM, Lv WS (2021) Fixed-time synchronization of inertial complex-valued neural networks with time delays. Nonlinear Dyn 105:1643–1656
Duan F, Du B (2021) Positive periodic solution for inertial neural networks with time-varying delays. Int J Nonlinear Sci Numer Simul 22:861–871
Sheng Y, Huang TW, Zeng ZG, Li P (2021) Exponential stabilization of inertial memristive neural networks with multiple time delays. IEEE Trans Cybern 51:579–588
Peng Q, Jian JG (2023) Asymptotic synchronization of second-fractional-order fuzzy neural networks with impulsive effects. Chaos Solitons Fractals 168:113150
Li XY, Li XT, Hu C (2017) Some new results on stability and synchronization for delayed inertial neural networks based on non-reduced order method. Neural Netw 96:91–100
Willems JC (1972) Dissipative dynamical systems-Part I: general theory. Arch Ration Mech Anal 45:321–351
Willems JC (1972) Dissipative dynamical systems-Part II: linear systems with quadratic supply rates. Arch Ration Mech Anal 45:352–393
Adéchinan AJ, Kpomahou YJF, Hinvi LA, Miwadinou CH (2022) Chaos, coexisting attractors and chaos control in a nonlinear dissipative chemical oscillator. Chin J Phys 77:2684–2697
Romanovskii VR (2020) Features of the thermal stabilization theory of composite superconductors: The nonlinear description of the dissipative states. Cryogenics 111:103163
Yan YT, Wang RG, Bao J, Zheng CX (2019) Robust distributed control of plantwide processes based on dissipativity. J Process Control 77:48–60
Tavasolipour E, Poshtan J, Shamaghdari S (2021) A new approach for robust fault estimation in nonlinear systems with state-coupled disturbances using dissipativity theory. ISA Trans 114:31–43
Hien LV, Son DT, Trinh H (2018) On global dissipativity of nonautonomous neural networks with multiple proportional delays. IEEE Trans Neural Netw Learn Syst 29:225–231
Liao XX, Luo Q, Zeng ZG (2008) Positive invariant and global exponential attractive sets of neural networks with time-varying delays. Neurocomputing 71:513–518
Aouiti C, Sakthivel R, Touati F (2020) Global dissipativity of high-order Hopfield bidirectional associative memory neural networks with mixed delays. Neural Comput Appl 32:10183–10197
Rajivganthi C, Rihan FA, Lakshmanan S (2019) Dissipativity analysis of complex-valued BAM neural networks with time delay. Neural Comput Appl 31:127–137
Ali MS, Narayanan G, Nahavandi S, Wang JL, Cao JD (2022) Global dissipativity analysis and stability analysis for fractional-order quaternion-valued neural networks with time delays. IEEE Trans Syst Man Cybern Syst 52:4046–4056
Tu ZW, Cao JD, Hayat T (2016) Matrix measure based dissipativity analysis for inertial delayed uncertain neural networks. Neural Netw 75:47–55
Zhang GD, Zeng ZG, Hu JH (2018) New results on global exponential dissipativity analysis of memristive inertial neural networks with distributed time-varying delays. Neural Netw 97:183–191
Wu K, Jian JG (2021) Global robust exponential dissipativity of uncertain second-order BAM neural networks with mixed time-varying delays. IEEE Trans Neural Netw Learn Syst 32:5675–5687
Filippov AF (1988) Differential equations with discontinous right-hand sides. Kluwer, Dordrecht
Gu K, Kharitonov VL, Chen J (2003) Stability of time-delay system. Birkhaser, Boston
Acknowledgements
The authors appreciate the support of the National Natural Science Foundation of China (62273200).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, J., Jian, J. Dissipativity Analysis of Memristive Inertial Competitive Neural Networks with Mixed Delays. Neural Process Lett 56, 151 (2024). https://doi.org/10.1007/s11063-024-11610-3
Accepted:
Published:
DOI: https://doi.org/10.1007/s11063-024-11610-3