New Insights on Bidirectional Associative Memory Neural Networks with Leakage Delay Components and Time-Varying Delays Using Sampled-Data Control

Abstract

The sampling data control of bidirectional associative memory (BAM) neural network with leakage delay is considered in this article. The BAM model is viewed as a mixed delay that combines a distributed delay, a discrete delay that varies over time, and a delay in the leaking period. The sampling system is then converted to a continuous time-delay system using an input delay method. In order to get adequate conditions in the form of linear matrix inequalities(LMIs), we build a new Lyapunov-Krasovskii Functional (LKF) in conjunction with the free weight matrix approach. Finally, a simulation results are given to show the efficiency of the theoretical approach.

1 Introduction

A neural network is a processing device, whose design was inspired by the design and functioning of human brain and their components. There is no idle memory containing data and programmed, but each neuron is programmed and continuously active. Neural network has many applications. The most likely applications for the neural networks are (i) Classification (ii) Association and (iii) Reasoning. One of the applications of neural networks with time delays are unavoidable in many practical systems such as biology systems and artificial neural networks [4,5,6]. Recently, the stability analysis of dynamical systems are greatly focused and has become an emerging area of research due to the fact that it has most successful applications such as image processing, optimization, pattern recognition and other areas [7,8,9]. Various types of time-delay systems and delay dynamical networks have been investigated, and many significant results have been reported [10,11,12,13,14,15]. From the point of view of nonlinear dynamics, the study of neural networks with delays is useful and important to solve problems both theoretically and practically.

An extension of the unidirectional auto associator of Hopfield neural network is called bidirectional associative memory (BAM) neural networks, which was first introduced by kosko [16]. Then, BAM neural networks with delays have attracted considerable attention and have been widely investigated. It is composed of neurons arranged in two layers: the X-layer and the Y-layer. The neurons in one layer are fully interconnected to the neurons in the other layer, while there are no interconnection among neurons in the same layer. Through iterations of forward and backward propagation information flows between the two layers, it performs a two-way associative search for stored bipolar vector pairs and generalize the single-layer auto-associative Hebbian correlation to a two-layer pattern-matched hetero associative circuits. Therefore, it possesses good applications in the field of pattern recognition and artificial intelligence [17,18,19,20,21]. In addition, the addressable memories or patterns of BAM neural networks can be stored with a two-way associative search. Accordingly, the BAM neural network has been widely studied both in theory and applications. In practical applications, the BAM neural network has been successfully applied to image processing, pattern recognition, automatic control, associative memory, parallel computation, and optimization problems. Therefore, it is interesting and important to study the stability of BAM neural network, which has been widely investigated [22,23,24,25,26,27,28,29,30].

Recently, Gopalsamy [31] initially introduced the delays in the ”forgetting” or leakage terms, and some results have been obtained, (see for example [32,33,34,35,36] and the references cited therein). Unfortunately, the delays in the leakage terms of neural networks in most literatures listed above are constants, and few authors have considered the dynamics of BAM neural networks with time-varying delays in the leakage terms [31]. Therefore, it is important and interesting to further investigate the dynamical behaviors of the BAM neural networks with time-varying leakage delays.

Up to now, various control approaches have been adopted to stabilize those instable systems. Controls such as dynamic feedback control, fuzzy logical control, impulsive control, $H_\infty$ control, sliding mode control and sampled-data control are adopted by many authors [37,38,39,40,41,42]. The sampled-data control deals with continuous system by sampling the data at discrete time based on the computer, sensors, filters and network communication. Hence it is more preferable to use digital controllers instead of analogue circuits. This drastically reduces the amount of the transmitted information and improve the control efficiency. Compared with continuous control, the sampled-data control is more efficient, secure and useful [43,44,45,46,47,48,49]. In [50], the author considered the synchronization problem of coupled chaotic neural networks with time delay in the leakage term using sampled-data control. R. Sakthivel et al. [36] established a state estimator for BAM neural networks with leakage delays with the help of Lyapunov technique and LMI framework.

However to the best of our knowledge, the sampled-data control design of BAM neural network with time delay in the leakage term has not been investigated until now. This motivates our work.

The main contribution of this paper lies in three aspects:

• (i). It is the first attempt to study the sampled-data control of delayed BAM neural networks. An efficient approach is presented to deal with it.

• (ii). Based on the Lyapunov-Krasovskii theory and LMI framework, a new set of sufficient conditions is obtained to ensure that the dynamical system is globally asymptotically stable.

• (iii). It is worth pointing that a novel Lyapunov–Krasovskii functional (LKF) is constructed with augmented terms

$$\begin{aligned}&\sum \limits _{i=0}^{1}\tau _{(3-i)}\int _{-\tau _{(3-i)}}^{0}\int _{t+\theta }^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)}\\ \maltese &{} Z_{(3-2i)} \end{array}\right] \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] dsd\theta ,\\&\sum \limits _{i=1}^{2}\tau _{(2i-1)}\int _{-\tau _{(2i-1)}}^{0}\int _{t+\theta }^{t} \left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(2i)} &{} Y_{(2i)}\\ \maltese &{} Z_{(2i)} \end{array}\right] \left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] dsd\theta . \end{aligned}$$

The main objective of this paper is to study the sampled-data control for bidirectional associate memory neural networks with leakage delay components. By constructing suitable triple integral LKF, by utilizing the free-weighting matrix method and reciprocal convex method, a unified linear matrix inequality (LMI) approach is developed to establish sufficient conditions for leakage BAM neural network is globally stable. Finally a numerical example is given to illustrate the usefulness and effectiveness of the proposed method (Table 1).

Notations: Throughout the paper, we have used the standard notations in [36].

Table 1 Comparison with existing results on BAM neural networks (BAMNNs)

2 Problem description and Introductory

We investigated the sampled-data stabilization of a BAM neural networks with leaky delays. The following BAM neural network with leaking delay components is considered:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}^{(1)}_i(t)=-a_ix^{(1)}_i(t-\delta _1)+\sum \limits _{j=1}^{n}{{w}^{(1)}_{ij}}\tilde{f}^{(1)}_j(y^{(1)}_j(t-\tau _1(t)))\\ +\sum \limits _{j=1}^{n}{{w}^{(2)}_{ij}}\int _{t-\tau _1}^{t}\tilde{f}^{(2)}_j(y^{(1)}_j(s))ds+J^{(1)}_i,\\ \dot{y}^{(1)}_j(t)=-b_jy^{(1)}_j(t-\delta _2)+\sum \limits _{i=1}^{n}{{v}^{(1)}_{ij}}\tilde{g}^{(1)}_i(x^{(1)}_i(t-\tau _2(t)))\\ +\sum \limits _{i=1}^{n}{{v}^{(2)}_{ij}}\int _{t-\tau _2}^{t}\tilde{g}^{(2)}_i(x^{(1)}_i(s))ds+J^{(2)}_j. \end{array} \right. \end{aligned}$$

(1)

Here $x^{(1)}_i(t)$ and $y^{(1)}_j(t)$ are the state variables representing the neuron’s of state at time t, respectively. $a_i>0$ and $b_j>0$ are constants, and signify the time scales for the relevant network layers. ${{w}^{(1)}_{ij}},{{w}^{(2)}_{ij}},{{v}^{(1)}_{ij}}$ and ${{v}^{(2)}_{ij}}$ are the synaptic connection weights. The external inputs are represented by $J^{(1)}_i$ and $J^{(2)}_j$; $\ \delta _1$ and $\ \delta _2$ are leakage delays; Time-varying delay components are $\tau _1(t)>0$ and $\tau _2(t)>0$; Neuron activation functions $\tilde{f}^{(1)}_j(\cdot ),\ \tilde{f}^{(2)}_j(\cdot ),\ \tilde{g}^{(1)}_i(\cdot )$ and $\tilde{g}^{(2)}_i(\cdot )$, $\tau _1(t)>0$ and $\tau _2(t)>0$ are differentiable, bounded and satisfies

$$\begin{aligned} 0\le \tau _1(t)\le \tau _1, \quad {\dot{\tau }}_1(t)\le \mu _1,\ 0\le \tau _2(t)\le \tau _2, \quad {\dot{\tau }}_2(t)\le \mu _2, \end{aligned}$$

(2)

where $\tau _1,\ \tau _2,\ \delta _1,\ \delta _2,\ \mu _1$ and $\mu _2$ are positive constants.

Let $(x^{(1)^*},y^{(1)^*})^T$ be an equilibrium point of equation (1). Then, $(x^{(1)^*},y^{(1)^*})^T$ satisfies the following equations:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}0=-a_ix^{(1)^*}_i+\sum \limits _{j=1}^{n}{{w}^{(1)}_{ij}}\tilde{f}^{(1)}_j(y_j^{(1)^{(1)^*}}) +\sum \limits _{j=1}^{n}{{w}^{(2)}_{ij}}\tilde{f}^{(2)}_jy_j^{(1)^*}+J^{(1)}_i,\\ &{}0=-b_jy^{(1)^*}_j+\sum \limits _{i=1}^{n}{{v}^{(1)}_{ij}}\tilde{g}^{(1)}_i(x_i^{(1)^*}) +\sum \limits _{i=1}^{n}{{v}^{(2)}_{ij}}\tilde{g}^{(2)}_ix_i^{(1)^*}+J^{(2)}_j. \end{array} \right. \end{aligned}$$

(3)

By shifting the equilibrium point $(x^{(1)^*},y^{(1)^*})^T$ to the origin using transformation $x_{i}(t)=x^{(1)}_i(t)-x^{(1)^*}_i,\ y_{i}(t)=y^{(1)}_i(t)-y^{(1)^*}_i$ the system (1) can be written as:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\dot{x}(t)=-Ax(t-\delta _1)+W_1f_1(y(t-\tau _1(t))) +W_2\int _{t-\tau _1}^{t}f_2(y(s))ds,\\ &{}\dot{y}(t)=-By(t-\delta _2)+V_1g_1(x(t-\tau _2(t))) +V_2\int _{t-\tau _2}^{t}g_2(x(s))ds, \end{array} \right. \end{aligned}$$

(4)

where $A=diag\{a_1,...,a_n\}>0,\ B=diag\{b_1,...,b_n\}>0,\ W_1=(w^{(1)}_{ij})_{n\times n}\in R^{n\times n},\ W_2=(w^{(2)}_{ij})_{n\times n}\in R^{n\times n},\ V_1=(v^{(1)}_{ij})_{n\times n}\in R^{n\times n},\ V_2=(v^{(2)}_{ij})_{n\times n}\in R^{n\times n},\ f_1(y(t))=\tilde{f}_1(y(t)-y^{(1)^*}),\ f_2(y(t))=\tilde{f}_2(y(t)-y^{(1)^*}),\ g_1(x(t))=\tilde{g}_1(x(t)-x^{(1)^*})$ and $g_2(x(t))=\tilde{g}_2(x(t)-x^{(1)^*})$ with $f_1(0)=f_2(0)=g_1(0)=g_2(0)=0$.

Assumption (A). The neuron activation functions $f_{ki}(\cdot ),\ g_{kj}(\cdot )$ in (4) are non-decreasing, limited, and there exist constants $F^{-}_{ki},\ F^{+}_{ki},\ G^{-}_{kj},\ G^{+}_{kj}$ such that

$$\begin{aligned} F^{-}_{ki}\le \dfrac{f_{ki}(\alpha )-f_{ki}(\beta )}{\alpha -\beta }\le F^{+}_{ki} ,\ i=1,2,..,m,\nonumber \\ G^{-}_{kj}\le \dfrac{g_{kj}(\alpha )-g_{kj}(\beta )}{\alpha -\beta }\le G^{+}_{kj} ,\ j=1,2,..,n. \end{aligned}$$

(5)

Here $k=1,2$ and $\alpha ,\beta \in \mathbb {R}$ are both equal to $\beta$. We define the following matrices for ease of notation:

$$\begin{aligned}&F_{k1}=diag\Big \{F^{-}_{k1}F^{+}_{k1},F^{-}_{k2}F^{+}_{k2},...,F^{-}_{km}F^{+}_{km}\Big \},\\&F_{k2}=diag\bigg \{\frac{F^{-}_{k1}+F^{+}_{k1}}{2},\frac{F^{-}_{k2}+F^{+}_{k2}}{2},..., \frac{F^{-}_{km}+F^{+}_{km}}{2}\bigg \},\\&G_{k1}=diag\Big \{G^{-}_{k1}G^{+}_{k1},G^{-}_{k2}G^{+}_{k2},...,G^{-}_{kn}G^{+}_{kn}\Big \},\\&G_{k2}=diag\bigg \{\frac{G^{-}_{k1}+G^{+}_{k1}}{2},\frac{G^{-}_{k2}+G^{+}_{k2}}{2},..., \frac{G^{-}_{kn}+G^{+}_{kn}}{2}\bigg \}. \end{aligned}$$

The system (4) with control is given by

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\dot{x}(t)=-Ax(t-\delta _1)+W_1f_1(y(t-\tau _1(t))) +W_2\int _{t-\tau _1}^{t}f_2(y(s))ds+u(t),\\ &{}\dot{y}(t)=-By(t-\delta _2)+V_1g_1(x(t-\tau _2(t))) +V_2\int _{t-\tau _2}^{t}g_2(x(s))ds+v(t), \end{array} \right. \end{aligned}$$

(6)

where the output measurements are u(t) and v(t). We define the sampled-data control as:

$$\begin{aligned} u(t)=\mathcal {K}x(t_k),\ v(t)=\mathcal {M}y(t_k), \end{aligned}$$

(7)

where the sampled-data gain matrices are $\mathcal {K},\mathcal {M}\in \mathcal {R}^{n\times n}$. The sample time point, $t_k$, meets the conditions $0=t_0<t_1,...,<t_k<...,$ and $\lim \limits _{k\rightarrow \infty }t_k=+\infty .$ Additionally, there is a positive constant $\tau _3$ such that $t_{k+1}-t_k\le \tau _3,\ \forall k\in {\textbf {N}},$. If $\tau _3(t)=t-t_k,$ for $t\in [t_k,t_{k+1}),$ then $t_k=t-\tau _3(t)$ with $0\le \tau _3(t)\le \tau _3$. The delayed BAM networks with leakage delay (6) may be rebuilt as follows in accordance with the control law:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\dot{x}(t)=-Ax(t-\delta _1)+W_1f_1(y(t-\tau _1(t))) +W_2\int _{t-\tau _1}^{t}f_2(y(s))ds+\mathcal {K}x(t-\tau _3(t)),\\ &{}\dot{y}(t)=-By(t-\delta _2)+V_1g_1(x(t-\tau _2(t))) +V_2\int _{t-\tau _2}^{t}g_2(x(s))ds+\mathcal {M}y(t-\tau _3(t)). \end{array} \right. \end{aligned}$$

(8)

We present the following lemmas, which will be employed in the main theorems.

Lemma 2.1

[51] If the following integrations are defined well, for every positive definite matrix $N>0$ and scalars $\beta>\alpha >0$, we have

$$\begin{aligned}&-(\alpha -\beta )\int _{\beta }^{\alpha }e^T(s)Ne(s) ds\le -\int _{\beta }^{\alpha }e^T(s)ds\ N \int _{\beta }^{\alpha }e(s)ds,\\&-\frac{\beta ^2}{2!}\int _{-\beta }^{0}\int _{t+\delta }^{t}e^T(s)Ne(s)dsd\delta \le -\Big (\int _{\beta }^{0}\int _{t+\delta }^{t}e(s)dsd\delta \Big )^T\ N\ \Big (\int _{\beta }^{0}\int _{t+\delta }^{t}e^T(s)dsd\delta \Big ). \end{aligned}$$

Lemma 2.2

[52] For every constant matrix $R\in R^{n \times n},\ R=R^T>0,$, and $\dot{e}:[-\tau _M,0]\rightarrow R^n$, respectively. The integrations listed below are satisfy

$$\begin{aligned}&-\tau _M\int _{t-\tau _M}^{t} \dot{e}^T(s)N \dot{e}(s)dsd\theta \le \left[ \begin{array} {cc} e(t)\\ e(t-\tau _M) \end{array}\right] ^T \left[ \begin{array} {cc} -R &{} R\\ R &{} -R \end{array}\right] \ \left[ \begin{array} {cc} e(t)\\ e(t-\tau _M) \end{array}\right] . \end{aligned}$$

Lemma 2.3

[53] Let an open subset D of $R^m$ have positive values for $f_1,f_2,...,f_N:R^m\mapsto R$. When $f_i$ over D is reciprocally convex, it is satisfied that,

$$\begin{aligned} \min _{\{\alpha _i|\alpha _i>0,\sum _{i}\alpha _i=1\}} \sum \limits _{i}\frac{1}{\alpha _i}f_i(t)=\sum \limits _{i}f_i(t)+ \max _{g_{ij}(t)}\sum \limits _{i\ne j}g_{i,j}(t) \end{aligned}$$

subject to

$$\begin{aligned} \bigg \{g_{i,j}(t):R^m\mapsto R,g_{i,j}(t)\triangleq g_{i,j}(t), \left[ \begin{array}{cc} f_i(t) &{} g_{i,j}(t) \\ g_{i,j}(t) &{} f_j(t) \end{array}\right] \ge 0 \bigg \}. \end{aligned}$$

3 Main results

This section examines the system stability (8) and derives the necessary requirements while maintaining system stability.

Theorem 3.1

Under Assumption (A), for given gain matrices $\mathcal {K},\ \mathcal {M}$ and scalars $\tau _1$, $\tau _2$, $\tau _3$, $\delta _1$, $\delta _2$, $\mu _1$, and $\mu _2$, the equilibrium point of system (8) is stable if there exist matrices $\mathcal {P}>0$, $\mathcal {Q}>0$, $P_i>0$, $(i=1,2,...,8)$, $Q_j>0$, $R_j>0$, $\left[ \begin{array} {cc} X_{j} &{} Y_{j}\\ \maltese &{} Z_{j} \end{array}\right] >0,$ positive-definite diagonal matrices $U_{j},\ J_{j},$ and any matrices $\left[ \begin{array} {cc} M_{j} &{} N_{j}\\ H_{j} &{} T_{j} \end{array}\right] ,\ (j=1,2,...,4), {\tilde{R}}_1,\ {\tilde{R}}_2, S_1$ and $S_2$ such that the following LMIs hold:

$$\begin{aligned}&\left[ \begin{array}{c|c} \left[ \begin{array} {cc} X_{k} &{} Y_{k} \\ \maltese &{} Z_{k} \end{array}\right] &{} \left[ \begin{array}{cc} M_{k} &{} N_{k} \\ H_{k} &{} T_{k} \end{array}\right] \\ \hline \maltese &{} \left[ \begin{array} {cc} X_{k} &{} Y_{k} \\ \maltese &{} Z_{k} \end{array}\right] \end{array} \right]>0,\ \left[ \begin{array} {cc} R_l &{} {\tilde{R}}_l\\ \maltese &{} R_l \end{array}\right] >0,\ k=1,...,4,\ l=1,2, \end{aligned}$$

(9)

$$\begin{aligned}&\Omega =\left[ \begin{array}{c|c} \left[ \begin{array} {cc} \Omega _{11} &{} [0]_{11n\times 11n} \\ \maltese &{} \Omega _{22} \end{array}\right] &{} [0]_{24n\times 24n} \\ \hline \maltese &{} \left[ \begin{array} {cc} \Omega _{33} &{} [0]_{11n\times 11n}\\ \maltese &{} \Omega _{44} \end{array}\right] \end{array} \right] <0, \end{aligned}$$

(10)

where

$$\begin{aligned} \Omega _{11}&=\left[ \begin{array}{cccccccccccc} (1,1) &{} (1,2) &{} -S_1A &{} Q_1 &{} 0 &{} Q_3+S_1\mathcal {K} &{} 0 &{} G_{12}J_1 &{} S_1W_1 &{} G_{22}J_2 &{} 0 &{} S_1W_2\\ \maltese &{} (2,2) &{} -S_1A &{} 0 &{} 0 &{} S_1\mathcal {K} &{} 0 &{} 0 &{} S_1W_1 &{} 0 &{} 0 &{} S_1W_2 \\ \maltese &{} \maltese &{} -\delta _1P_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{} (4,4) &{} Q_1 &{} 0 &{} 0 &{} 0 &{} G_{32}J_3 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{}\maltese &{} (5,5) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -2Q_3 &{} Q_3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} (7,7) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -J_1 &{} 0&{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -J_3 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} (10,10) &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -J_4 &{} 0 \end{array}\right] ,\\ \Omega _{22}&=\left[ \begin{array}{cccccccccccccc} -R_4 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} -X_1 &{} -Y_1 &{} -M_1 &{} -N_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} -Z_1 &{} -H_1 &{} -T_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} -X_1 &{} -Y_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -R_1 &{} -\tilde{R_1} &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -R_1 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -X_3 &{} -Y_3 &{} -M_3 &{} -N_3 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_3 &{} -H_3 &{} -T_3 \\ \maltese &{}\maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -X_3 &{} -Y_3 \\ \maltese &{}\maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_3 \end{array}\right] ,\\ \Omega _{33}&=\left[ \begin{array}{cccccccccccc} (1,1)^* &{} (1,2)^* &{} -S_2B &{} Q_2 &{} 0 &{} Q_4+S_2\mathcal {M} &{} 0 &{} F_{12}U_1 &{} S_2V_1 &{} F_{22}U_2 &{} 0 &{} S_2V_2\\ \maltese &{} (2,2)^* &{} -S_2B &{} 0 &{} 0 &{} S_2\mathcal {M} &{} 0 &{} 0 &{} S_2V_1 &{} 0 &{} 0 &{} S_2V_2 \\ \maltese &{} \maltese &{} -\delta _2P_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{} (4,4)^* &{} Q_2 &{} 0 &{} 0 &{} 0 &{} F_{32}U_3 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{}\maltese &{} (5,5)^* &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -2Q_4 &{} Q_4 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} (7,7)^* &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -U_1 &{} 0&{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -U_3 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} (10,10)^* &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -U_4 &{} 0 \end{array}\right] ,\\ \Omega _{44}&=\left[ \begin{array}{cccccccccccccc} -R_3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} -X_2 &{} -Y_2 &{} -M_2 &{} -N_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} -Z_2 &{} -H_2 &{} -T_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} -X_2 &{} -Y_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -R_2 &{} -\tilde{R_2} &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -R_2 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -X_4 &{} -Y_4 &{} -M_4 &{} -N_4 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_4 &{} -H_4 &{} -T_3 \\ \maltese &{}\maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -X_4 &{} -Y_4 \\ \maltese &{}\maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_4 \end{array}\right] , \end{aligned}$$

$$\begin{aligned}&(1,1)=\delta _1P_1+P_3+P_5+P_7-Q_1-Q_3+\tau _2^2X_1+\tau _3^2X_3-G_{11}J_1-G_{21}J_2,\\&(1,1)^*=\delta _2P_2+P_4+P_5+P_8-Q_2-Q_3+\tau _1^2X_2+\tau _3^2X_4-F_{11}U_1-F_{21}U_2,\\&(1,2)=\mathcal {P}+\tau _2^2Y_1+\tau _3^2Y_3-S_1,\ (1,2)^*=\mathcal {Q}+\tau _1^2Y_2+\tau _3^2Y_4-S_2,\\&(2,2)=\tau _2^2Q_1+\tau _3^2Q_3+\tau _2^2Z_1+\tau _3^2Z_3+\bigg (\frac{\tau _2^2}{2!}\bigg )^2R_1-S_1-S_1^T,\\&(2,2)^*=\tau _1^2Q_2+\tau _3^2Q_4+\tau _1^2Z_2+\tau _3^2Z_4+\bigg (\frac{\tau _1^2}{2!}\bigg )^2R_2-S_2-S_2^T,\\&(4,4)=-(1-\mu _2)P_3-2Q_1-G_{31} J_3-G_{41} J_4,\\&(4,4)^*=-(1-\mu _1)P_4-2Q_2-F_{31}U_3-F_{41}U_4,\\&(5,5)=-P_5-Q_1,\ (7,7)=-Q_3-P_7, \ (10,10)=-J_2+\tau ^2_2R_4,\\&(5,5)^*=-P_6-Q_2,\ (7,7)^*=-Q_4-P_8, \ (10,10)^*=-U_2+\tau ^2_1R_3, \end{aligned}$$

Proof

We construct the Lyapunov Krasovskii functional as:

$$\begin{aligned} V(x_{t},y_{t},t)=\sum \limits _{i=1}^{7} V_{i}(x_{t},y_{t},t), \end{aligned}$$

(11)

where

$$\begin{aligned} V_1(x_{t},y_{t},t)=&x^T(t)\mathcal {P}x(t)+y^T(t)\mathcal {Q}y(t),\\ V_2(x_{t},y_{t},t)=&\delta _1\int _{t-\delta _1}^{t}x^T(s)P_1x(s)ds +\delta _2\int _{t-\delta _2}^{t}y^T(s)P_2y(s)ds,\\ V_3(x_{t},y_{t},t)=&\int _{t-\tau _2(t)}^{t}x^T(s)P_3x(s)ds +\int _{t-\tau _1(t)}^{t}y^T(s)P_4y(s)ds+\int _{t-\tau _2}^{t}x^T(s)P_5x(s)ds\\&+ \int _{t-\tau _1}^{t}y^T(s)P_6y(s)ds+\int _{t-\tau _3}^{t}x^T(s)P_7x(s)ds+\int _{t-\tau _3}^{t}y^T(s)P_8y(s)ds, \\ V_4(x_{t},y_{t},t)=&\tau _2\int _{-\tau _2}^{0}\int _{t+\theta }^{t}\dot{x}^T(s)Q_1\dot{x}(s)dsd\theta + \tau _1\int _{-\tau _1}^{0}\int _{t+\theta }^{t}\dot{y}^T(s)Q_2\dot{y}(s)dsd\theta \\&+ \tau _3\int _{-\tau _3}^{0}\int _{t+\theta }^{t}\dot{x}^T(s)Q_3\dot{x}(s)dsd\theta + \tau _3\int _{-\tau _3}^{0}\int _{t+\theta }^{t}\dot{y}^T(s)Q_4\dot{y}(s)dsd\theta ,\\ V_5(x_{t},y_{t},t)=&\sum \limits _{i=0}^{1}\tau _{(3-i)}\int _{-\tau _{(3-i)}}^{0}\int _{t+\theta }^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)}\\ \maltese &{} Z_{(3-2i)} \end{array}\right] \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] dsd\theta \\+&\sum \limits _{i=1}^{2}\tau _{(2i-1)}\int _{-\tau _{(2i-1)}}^{0}\int _{t+\theta }^{t} \left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(2i)} &{} Y_{(2i)}\\ \maltese &{} Z_{(2i)} \end{array}\right] \left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] dsd\theta ,\\ V_6(x_{t},y_{t},t)=&\frac{\tau _2^2}{2!}\int _{-\tau _2}^{0}\int _{\theta }^{0}\int _{t+\vartheta }^{t} \dot{x}^T(s) R_1\dot{x}(s)dsd\vartheta d\theta \\&+\frac{\tau _1^2}{2!}\int _{-\tau _1}^{0}\int _{\theta }^{0} \int _{t+\vartheta }^{t}\dot{y}^T(s) R_2\dot{y}(s)dsd\vartheta d\theta ,\\ V_7(x_{t},y_{t},t)=&\tau _1\int _{-\tau _1}^{0}\int _{t+\theta }^{t}f^T_2(y(s))R_3f_2(y(s))dsd\theta \\&+ \tau _2\int _{-\tau _2}^{0}\int _{t+\theta }^{t}g^T_2(x(s))R_4g_2(x(s))dsd\theta . \end{aligned}$$

We calculate the derivatives $\dot{V}_i(x_{t},y_{t},t),\ i=1,2,...,7$ along the trajectories of the system (8) gives,

$$\begin{aligned} \dot{V}_1(x_{t},y_{t},t)=&2x^T(t)\mathcal {P}\dot{x}(t)+2y^T(t)\mathcal {Q}\dot{y}(t),\end{aligned}$$

(12)

$$\begin{aligned} \dot{V}_2(x_{t},y_{t},t)=&\delta _1[x^T(t)P_1x(t)-x^T(t-\delta _1)P_1x(t-\delta _1)] +\delta _2[y^T(t)P_2y(t)-y^T(t-\delta _2)P_2y(t-\delta _2)],\end{aligned}$$

(13)

$$\begin{aligned} \dot{V}_3(x_{t},y_{t},t)\le&x^T(t)[P_3+P_5+P_7]x(t)+y^T(t)[P_4+P_6+P_8]y(t) -(1-\mu _2)x^T(t-\tau _2(t))P_3x(t-\tau _2(t))\nonumber \\&-(1-\mu _1)y^T(t-\tau _1(t))P_4y(t-\tau _1(t))-x^T(t-\tau _2)P_5x(t-\tau _2)-y^T(t-\tau _1) P_6y(t-\tau _1)\nonumber \\&-x^T(t-\tau _3)P_7x(t-\tau _3)-y^T(t-\tau _3)P_8y(t-\tau _3),\end{aligned}$$

(14)

$$\begin{aligned} \dot{V}_4(x_{t},y_{t},t)=&\dot{x}^T(t)[\tau _2^2Q_1+\tau _3^2Q_3]\dot{x}(t)+ \dot{y}^T(t)[\tau _1^2Q_2+\tau _3^2Q_4]\dot{y}(t)-\tau _2\int _{t-\tau _2}^{t}\dot{x}^T(s)Q_1\dot{x}(s)ds\nonumber \\&-\tau _1\int _{t-\tau _1}^{t}\dot{y}^T(s)Q_2\dot{y}(s)ds-\tau _3\int _{t-\tau _3}^{t}\dot{x}^T(s)Q_3\dot{x}(s)ds -\tau _3\int _{t-\tau _3}^{t}\dot{y}^T(s)Q_4\dot{y}(s)ds,\end{aligned}$$

(15)

$$\begin{aligned} \dot{V}_5(x_{t},y_{t},t)=&\sum \limits _{i=0}^{1}\tau ^2_{(3-i)} \left[ \begin{array} {cc} x(t)\\ \dot{x}(t) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)}\\ \maltese &{} Z_{(3-2i)} \end{array}\right] \left[ \begin{array} {cc} x(t)\\ \dot{x}(t) \end{array}\right] \nonumber \\ +&\sum \limits _{i=1}^{2}\tau ^2_{(2i-1)} \left[ \begin{array} {cc} y(t)\\ \dot{y}(t) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(2i)} &{} Y_{(2i)}\\ \maltese &{} Z_{(2i)} \end{array}\right] \left[ \begin{array} {cc} y(t)\\ \dot{y}(t) \end{array}\right] \nonumber \\ -&\sum \limits _{i=0}^{1}\tau _{(3-i)}\int _{t-\tau _{(3-i)}}^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)}\\ \maltese &{} Z_{(3-2i)} \end{array}\right] \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\nonumber \\ -&\sum \limits _{i=1}^{2}\tau _{(2i-1)}\int _{t-\tau _{(2i-1)}}^{t} \left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(2i)} &{} Y_{(2i)}\\ \maltese &{} Z_{(2i)} \end{array}\right] \left[ \begin{array} {cc} y(s)\\ \dot{y}(s), \end{array}\right] ds\end{aligned}$$

(16)

$$\begin{aligned} \dot{V}_6(x_{t},y_{t},t)=&\bigg (\frac{\tau _2^2}{2!}\bigg )^2\dot{x}^T(t)R_1\dot{x}(t) +\bigg (\frac{\tau _1^2}{2!}\bigg )^2\dot{y}^T(t)R_2\dot{y}(t) -\frac{\tau _2^2}{2!}\int _{-\tau _1}^{0}\int _{t+\theta }^{t}\dot{x}^T(s)R_1\dot{x}(s)dsd\theta \nonumber \\&-\frac{\tau _1^2}{2!}\int _{-\tau _1}^{0}\int _{t+\theta }^{t}\dot{y}^T(s)R_2\dot{y}(s)dsd\theta ,\end{aligned}$$

(17)

$$\begin{aligned} \dot{V}_7(x_{t},y_{t},t)=&f_2^T(y(t))\tau _1^2R_3 f_2(y(t))+g_2^T(x(t))\tau _2^2R_4 g_2(x(t))\nonumber \\&-\tau _1\int _{t-\tau _1}^{t}f_2^T(y(s))R_3 f_2(y(s))ds-\tau _2\int _{t-\tau _2}^{t}g_2^T(x(s))R_4 g_2(x(s))ds, \end{aligned}$$

(18)

The integral terms in (15) can be expressed as following

$$\begin{aligned} -\tau _2\int _{t-\tau _2}^{t}\dot{x}^T(s)Q_1\dot{x}(s)ds=&-\tau _2 \int _{t-\tau _2}^{t-\tau _2(t)}\dot{x}^T(s)Q_1\dot{x}(s)ds- \tau _2\int _{t-\tau _2(t)}^{t}\dot{x}^T(s)Q_1\dot{x}(s)ds,\\ -\tau _1\int _{t-\tau _1}^{t}\dot{y}^T(s)Q_2\dot{y}(s)ds=&- \tau _1\int _{t-\tau _1}^{t-\tau _1(t)}\dot{y}^T(s)Q_2\dot{y}(s)ds-\tau _1\int _{t-\tau _1(t)}^{t}\dot{y}^T(s)Q_2\dot{y}(s)ds,\\ -\tau _3\int _{t-\tau _3}^{t}\dot{x}^T(s)Q_3\dot{x}(s)ds=&- \tau _3\int _{t-\tau _3}^{t-\tau _3(t)}\dot{x}^T(s)Q_3\dot{x}(s)ds-\tau _3\int _{t-\tau _3(t)}^{t}\dot{x}^T(s)Q_3\dot{x}(s)ds,\\ -\tau _3\int _{t-\tau _3}^{t}\dot{y}^T(s)Q_4\dot{y}(s)ds=&- \tau _3\int _{t-\tau _2}^{t-\tau _3(t)}\dot{y}^T(s)Q_4\dot{y}(s)ds-\tau _3\int _{t-\tau _3(t)}^{t}\dot{y}^T(s)Q_4\dot{y}(s)ds. \end{aligned}$$

By applying Lemma 2.2, we obtain

$$\begin{aligned}&-\tau _2\int _{t-\tau _2}^{t-\tau _2(t)}\dot{x}^T(s)Q_1\dot{x}(s)ds\le&\left[ \begin{array} {cc} x(t-\tau _2(t))\\ x(t-\tau _2) \end{array}\right] ^T \left[ \begin{array} {cc} -Q_1 &{} Q_1\\ \maltese &{} -Q_1 \end{array}\right] \left[ \begin{array} {cc} x(t-\tau _2(t))\\ x(t-\tau _2) \end{array}\right] , \end{aligned}$$

(19)

$$\begin{aligned}&-\tau _2\int _{t-\tau _2(t)}^{t}\dot{x}^T(s)Q_1\dot{x}(s)ds\le&\left[ \begin{array} {cc} x(t)\\ x(t-\tau _2(t)) \end{array}\right] ^T \left[ \begin{array} {cc} -Q_1 &{} Q_1\\ \maltese &{} -Q_1 \end{array}\right] \left[ \begin{array} {cc} x(t)\\ x(t-\tau _2(t)) \end{array}\right] ,\end{aligned}$$

(20)

$$\begin{aligned}&-\tau _1\int _{t-\tau _1}^{t-\tau _1(t)}\dot{y}^T(s)Q_2\dot{y}(s)ds\le&\left[ \begin{array} {cc} y(t-\tau _1(t))\\ y(t-\tau _1) \end{array}\right] ^T \left[ \begin{array} {cc} -Q_2 &{} Q_2\\ \maltese &{} -Q_2 \end{array}\right] \left[ \begin{array} {cc} y(t-\tau _1(t))\\ y(t-\tau _1) \end{array}\right] ,\end{aligned}$$

(21)

$$\begin{aligned}&-\tau _1\int _{t-\tau _1(t)}^{t}\dot{y}^T(s)Q_2\dot{y}(s)ds\le&\left[ \begin{array} {cc} y(t)\\ y(t-\tau _1(t)) \end{array}\right] ^T \left[ \begin{array} {cc} -Q_2 &{} Q_2\\ \maltese &{} -Q_2 \end{array}\right] \left[ \begin{array} {cc} y(t)\\ y(t-\tau _1(t)) \end{array}\right] ,\end{aligned}$$

(22)

$$\begin{aligned}&-\tau _3\int _{t-\tau _3}^{t-\tau _3(t)}\dot{x}^T(s)Q_3\dot{x}(s)ds\le&\left[ \begin{array} {cc} x(t-\tau _3(t))\\ x(t-\tau _3) \end{array}\right] ^T \left[ \begin{array} {cc} -Q_3 &{} Q_3\\ \maltese &{} -Q_3 \end{array}\right] \left[ \begin{array} {cc} x(t-\tau _3(t))\\ x(t-\tau _3) \end{array}\right] ,\end{aligned}$$

(23)

$$\begin{aligned}&-\tau _3\int _{t-\tau _3(t)}^{t}\dot{x}^T(s)Q_3\dot{x}(s)ds\le&\left[ \begin{array} {cc} x(t)\\ x(t-\tau _3(t)) \end{array}\right] ^T \left[ \begin{array} {cc} -Q_3 &{} Q_3\\ \maltese &{} -Q_3 \end{array}\right] \left[ \begin{array} {cc} x(t)\\ x(t-\tau _3(t)) \end{array}\right] ,\end{aligned}$$

(24)

$$\begin{aligned}&-\tau _3\int _{t-\tau _3}^{t-\tau _3(t)}\dot{y}^T(s)Q_4\dot{y}(s)ds\le&\left[ \begin{array} {cc} y(t-\tau _3(t))\\ y(t-\tau _3) \end{array}\right] ^T \left[ \begin{array} {cc} -Q_4 &{} Q_4\\ \maltese &{} -Q_4 \end{array}\right] \left[ \begin{array} {cc} y(t-\tau _3(t))\\ y(t-\tau _3) \end{array}\right] ,\end{aligned}$$

(25)

$$\begin{aligned}&-\tau _3\int _{t-\tau _3(t)}^{t}\dot{y}^T(s)Q_4\dot{y}(s)ds\le&\left[ \begin{array} {cc} y(t)\\ y(t-\tau _3(t)) \end{array}\right] ^T \left[ \begin{array} {cc} -Q_4 &{} Q_4\\ \maltese &{} -Q_4 \end{array}\right] \left[ \begin{array} {cc} y(t)\\ y(t-\tau _3(t)) \end{array}\right] . \end{aligned}$$

(26)

By applying the Lemmas 2.1 and 2.3 in $\dot{V}_5(x_{t},y_{t},t)$, we obtain the following results

$$\begin{aligned}&-\sum \limits _{i=0}^{1}\tau _{(3-i)}\int _{t-\tau _{(3-i)}}^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)}\\ \maltese &{} Z_{(3-2i)} \end{array}\right] \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\\&\quad =-\sum \limits _{i=0}^{1}\tau _{(3-i)}\Bigg [\int _{t-\tau _{(3-i)}(t)}^{t} +\int _{t-\tau _{(3-i)}}^{t-\tau _{(3-i)}(t)}\Bigg ] \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds,\\&\quad =-\sum \limits _{i=0}^{1}\tau _{(3-i)}\Biggl [-\tau _{(3-i)}\int _{t-\tau _{(3-i)}(t)}^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\\&\qquad -\tau _{(3-i)}\int _{t-\tau _{(3-i)}}^{t-\tau _{(3-i)}(t)} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\Biggl ],\\&\quad =-\sum \limits _{i=0}^{1}\tau _{(3-i)}\Biggl [\frac{\tau _{(3-i)}}{\tau _{(3-i)}(t)}\times \tau _{(3-i)}(t)\int _{t-\tau _{(3-i)}(t)}^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\\&\qquad -\frac{\tau _{(3-i)}(\tau _{(3-i)}-\tau _{(3-i)}(t))}{(\tau _{(3-i)}-\tau _{(3-i)}(t))}\times \int _{t-\tau _{(3-i)}}^{t-\tau _{(3-i)}(t)} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\Biggl ],\\&\quad \le -\sum \limits _{i=0}^{1}\tau _{(3-i)}\Biggl [\frac{\tau _{(3-i)}}{\tau _{(3-i)}(t)}\int _{t-\tau _{(3-i)}(t)}^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T ds \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] \int _{t-\tau _{(3-i)}(t)}^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\\&\qquad -\frac{\tau _{(3-i)}}{(\tau _1-\tau _{(3-i)}(t))}\int _{t-\tau _{(3-i)}}^{t-\tau _{(3-i)}(t)} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T ds \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] \int _{t-\tau _{(3-i)}}^{t-\tau _{(3-i)}(t)} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\Biggl ],\\&\qquad \le -\sum \limits _{i=0}^{1}\tau _{(3-i)}\Biggl [\int _{t-\tau _{(3-i)}(t)}^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T ds \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] \int _{t-\tau _{(3-i)}(t)}^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\\&\qquad -2\int _{t-\tau _{(3-i)}(t)}^{t} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T ds \left[ \begin{array} {cc} M_{(3-2i)} &{} N_{(3-2i)}\\ H_{(3-2i)} &{} T_{(3-2i)} \end{array}\right] \int _{t-\tau _{(3-i)}}^{t-\tau _{(3-i)}(t)} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\\&\qquad -\int _{t-\tau _{(3-i)}}^{t-\tau _{(3-i)}(t)} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ^T ds \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] \int _{t-\tau _{(3-i)}}^{t-\tau _{(3-i)}(t)} \left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\Biggl ], \end{aligned}$$

$$\begin{aligned} =-\sum \limits _{i=0}^{1}\tau _{(3-i)}\left[ \begin{array}{c} \begin{array}{c} \int _{t-\tau _{(3-i)}(t)}^{t}\left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\\ \hline -\int _{t-\tau _{(3-i)}}^{t-\tau _{(3-i)}(t)}\left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds \end{array} \\ \end{array} \right] ^T&\left[ \begin{array}{c|c} \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] &{} \left[ \begin{array}{cc} M_{(3-2i)} &{} N_{(3-2i)} \\ H_{(3-2i)} &{} T_{(3-2i)} \end{array}\right] \\ \hline \maltese &{} \left[ \begin{array} {cc} X_{(3-2i)} &{} Y_{(3-2i)} \\ \maltese &{} Z_{(3-2i)} \end{array}\right] \end{array} \right] \nonumber \\ {}&\times \left[ \begin{array}{c} \begin{array}{c} \int _{t-\tau _{(3-i)}(t)}^{t}\left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds\\ \hline -\int _{t-\tau _{(3-i)}}^{t-\tau _{(3-i)}(t)}\left[ \begin{array} {cc} x(s)\\ \dot{x}(s) \end{array}\right] ds \end{array} \\ \end{array} \right] . \end{aligned}$$

(27)

We can estimate the three terms in inequality (16) in a similar way to (27) as

$$\begin{aligned}&-\sum \limits _{i=1}^{2}\tau _{(2i-1)}\int _{t-\tau _{(2i-1)}}^{t} \left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] ^T \left[ \begin{array} {cc} X_{2i} &{} Y_{2i}\\ \maltese &{} Z_{2i} \end{array}\right] \left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] ds\nonumber \\ {}&\le -\sum \limits _{i=1}^{2}\tau _{(2i-1)} \left[ \begin{array}{c} \begin{array}{c} \int _{t-\tau _{(2i-1)}(t)}^{t}\left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] ds\\ \hline \int _{t-\tau _{(2i-1)}}^{t-\tau _{(2i-1)}(t)}\left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] ds \end{array} \\ \end{array} \right] ^T \left[ \begin{array}{c|c} \left[ \begin{array} {cc} X_{(2i)} &{} Y_{(2i)} \\ \maltese &{} Z_{(2i)} \end{array}\right] &{} \left[ \begin{array}{cc} M_{(2i)} &{} N_{(2i)} \\ H_{(2i)} &{} T_{(2i)} \end{array}\right] \\ \hline \maltese &{} \left[ \begin{array} {cc} X_{(2i)} &{} Y_{(2i)} \\ \maltese &{} Z_{(2i)} \end{array}\right] \end{array} \right] \nonumber \\ {}&\hspace{2cm}\times \left[ \begin{array}{c} \begin{array}{c} \int _{t-\tau _{(2i-1)}(t)}^{t}\left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] ds\\ \hline \int _{t-\tau _{(2i-1)}}^{t-\tau _{(2i-1)}(t)}\left[ \begin{array} {cc} y(s)\\ \dot{y}(s) \end{array}\right] ds \end{array} \\ \end{array} \right] . \end{aligned}$$

(28)

The upper bound of the reciprocally convex combination in $\dot{V}_6(x_{t},y_{t},t)$ can be obtained as

$$\begin{aligned}&-\frac{\tau _2^2}{2!}\int _{-\tau _2}^{0}\int _{t+\theta }^{t}\dot{x}^T(s)R_1\dot{x}(s)dsd\theta \nonumber \\&\quad \le \left[ \begin{array} {cc} \int _{-\tau _2(t)}^{0}\int _{t+\theta }^{t}\dot{x}^T(s)ds\\ \int _{-\tau _2}^{-\tau _2(t)}\int _{t+\theta }^{t}\dot{x}^T(s)ds \end{array}\right] ^T \left[ \begin{array} {cc} -R_1 &{} -{\tilde{R}}_1\\ \maltese &{} -R_1 \end{array}\right] \left[ \begin{array} {cc} \int _{-\tau _2(t)}^{0}\int _{t+\theta }^{t}\dot{x}^T(s)ds\\ \int _{-\tau _2}^{-\tau _2(t)}\int _{t+\theta }^{t}\dot{x}^T(s)ds \end{array}\right] ,\end{aligned}$$

(29)

$$\begin{aligned}&-\frac{\tau _1^2}{2!}\int _{-\tau _1}^{0}\int _{t+\theta }^{t}\dot{y}^T(s)R_2\dot{y}(s)dsd\theta \nonumber \\&\quad \le \left[ \begin{array} {cc} \int _{-\tau _1(t)}^{0}\int _{t+\theta }^{t}\dot{y}^T(s)ds\\ \int _{-\tau _1}^{-\tau _1(t)}\int _{t+\theta }^{t}\dot{y}^T(s)ds \end{array}\right] ^T \left[ \begin{array} {cc} -R_2 &{} -{\tilde{R}}_2\\ \maltese &{} -R_2 \end{array}\right] \left[ \begin{array} {cc} \int _{-\tau _1(t)}^{0}\int _{t+\theta }^{t}\dot{y}^T(s)ds\\ \int _{-\tau _1}^{-\tau _1(t)}\int _{t+\theta }^{t}\dot{y}^T(s)ds \end{array}\right] . \end{aligned}$$

(30)

According to Lemma 2.1 the following inequality’s are hold:

$$\begin{aligned}&-\tau _1\int _{t-\tau _1}^{t}f_2^T(y(s))R_3 f_2(y(s))ds\le - \Bigg (\int _{t-\tau _1}^{t}f_2(y(s))ds\Bigg )^T R_3\Bigg (\int _{t-\tau _1}^{t}f_2(y(s))ds\Bigg ),\end{aligned}$$

(31)

$$\begin{aligned}&-\tau _2\int _{t-\tau _2}^{t}g_2^T(x(s))R_4 g_2(x(s))ds\le - \Bigg (\int _{t-\tau _2}^{t}g_2(x(s))ds\Bigg )^T R_4\Bigg (\int _{t-\tau _2}^{t}g_2(x(s))ds\Bigg ). \end{aligned}$$

(32)

On the other hand, for any matrices $S_1$ and $S_2$ with appropriate dimensions the following equations holds:

$$\begin{aligned}&0=[x(t)+\dot{x}(t)] S_1[-\dot{x}(t)+\dot{x}(t)],\nonumber \\&0=[x(t)+\dot{x}(t)] S_1[-\dot{x}(t)-Ax(t-\delta _1)+W_1f_1(y(t-\tau _1(t))) +W_2\int _{t-\tau _1}^{t}f_2(y(s))ds+\mathcal {K}x(t-\tau _3(t))],\end{aligned}$$

(33)

$$\begin{aligned}&0=[y(t)+\dot{y}(t)]S_2[-\dot{y}(t)+\dot{y}(t)],\nonumber \\&0=[y(t)+\dot{y}(t)]S_2[-\dot{y}(t)-By(t-\delta _2)+V_1g_1(x(t-\tau _2(t))) +V_2\int _{t-\tau _2}^{t}g_2(x(s))ds+\mathcal {M}y(t-\tau _3(t))]. \end{aligned}$$

(34)

Furthermore, based on Assumption (A), we have

$$\begin{aligned}&\Big [f_{ki}(y_i(t))-F_{ki}^{-}y_i(t)\Big ]^T\Big [f_{ki}(y_i(t))-F_{ki}^{+}y_i(t)\Big ]\le 0,\ i=1,2,...,n,\\&\Big [g_{kj}(x_j(t))-G_{kj}^{-}x_j(t)\Big ]^T\Big [g_{kj}(x_i(t))-G_{kj}^{+}x_j(t)\Big ]\le 0,\ j=1,2,...,n, \end{aligned}$$

where $k=1,2,$

which is equivalent to

$$\begin{aligned}&\left[ \begin{array} {cc} y(t)\\ f_{k}(y(t)) \end{array}\right] ^T \left[ \begin{array} {cc} F_{ki}^{-}F_{ki}^{+}y_iy_i^T &{} -\frac{F_{ki}^{-}+F_{ki}^{+}}{2}y_iy_i^T\\ -\frac{F_{ki}^{-}+F_{ki}^{+}}{2}y_iy_i^T &{} y_iy_i^T \end{array}\right] \left[ \begin{array} {cc} y(t)\\ f_{k}(y(t)) \end{array}\right] \le 0,\\&\left[ \begin{array} {cc} x(t)\\ g_{k}(x(t)) \end{array}\right] ^T \left[ \begin{array} {cc} G_{kj}^{-}G_{kj}^{+}x_jx_j^T &{} -\frac{G_{kj}^{-}+G_{kj}^{+}}{2}x_jx_j^T\\ -\frac{G_{kj}^{-}+G_{kj}^{+}}{2}x_jx_j^T &{} x_jx_j^T \end{array}\right] \left[ \begin{array} {cc} x(t)\\ g_{k}(x(t)) \end{array}\right] \le 0. \end{aligned}$$

where $x_i$ and $y_j$ denotes the units column vector having element 1 on its $i^{th}$ row, $j^{th}$ row, and zeros elsewhere. Let $U_k=diag\{u^k_{11},u^k_{12},...,u^k_{1n}\}>0,$ $J_k=diag\{{\overline{j}}^k_{11},{\overline{j}}^k_{12},...,{\overline{j}}^k_{1n}\}>0,$. Here $x_i$ and $y_j$ stand for the units column vector, which has zeros on the other rows and element 1 on the $i^{th}$ row, $j^{th}$ rows. It is simple to observe that if $U_k=diag\{u^k_{11},u^k_{12},...,u^k_{1n}\}>0,$ $J_k=diag\{{\overline{j}}^k_{11},{\overline{j}}^k_{12},...,{\overline{j}}^k_{1n}\}>0,$

$$\begin{aligned}&\sum \limits _{i=1}^{n}u^k_{1i} \left[ \begin{array} {cc} y(t)\\ f_{k}(y(t)) \end{array}\right] ^T \left[ \begin{array} {cc} F_{ki}^{-}F_{ki}^{+}y_iy_i^T &{} -\frac{F_{ki}^{-}+F_{ki}^{+}}{2}y_iy_i^T\\ -\frac{F_{ki}^{-}+F_{ki}^{+}}{2}y_iy_i^T &{} y_iy_i^T \end{array}\right] \left[ \begin{array} {cc} y(t)\\ f_{k}(y(t)) \end{array}\right] \le 0,\\&\sum \limits _{j=1}^{n}{\overline{j}}^k_{1j} \left[ \begin{array} {cc} x(t)\\ g_{k}(x(t)) \end{array}\right] ^T \left[ \begin{array} {cc} G_{kj}^{-}G_{kj}^{+}x_jx_j^T &{} -\frac{G_{kj}^{-}+G_{kj}^{+}}{2}x_jx_j^T\\ -\frac{G_{kj}^{-}+G_{kj}^{+}}{2}x_jx_j^T &{} x_jx_j^T \end{array}\right] \left[ \begin{array} {cc} x(t)\\ g_{k}(x(t)) \end{array}\right] \le 0, \end{aligned}$$

That is,

$$\begin{aligned}&\left[ \begin{array} {cc} y(t)\\ f_{k}(y(t)) \end{array}\right] ^T \left[ \begin{array} {cc} -F_{k1}U_{k} &{} F_{k2}U_{k}\\ F_{k2}U_{k} &{} -U_{k} \end{array}\right] \left[ \begin{array} {cc} y(t)\\ f_{k}(y(t)) \end{array}\right] \ge 0,\end{aligned}$$

(35)

$$\begin{aligned}&\left[ \begin{array} {cc} x(t)\\ g_{k}(x(t)) \end{array}\right] ^T \left[ \begin{array} {cc} -G_{k1}J_{k} &{} G_{k2}J_{k}\\ G_{k2}J_{k} &{} -J_{k} \end{array}\right] \left[ \begin{array} {cc} x(t)\\ g_{k}(x(t)) \end{array}\right] \ge 0. \end{aligned}$$

(36)

Similar to above, for $U_{k+2}=diag\{u^{k+2}_{11},u^{k+2}_{12},...,u^{k+2}_{1n}\}>0$, $J_{k+2}=diag\{{\overline{j}}^{k+2}_{11},{\overline{j}}^{k+2}_{12},...,{\overline{j}}^{k+2}_{1n}\}>0,$ we can obtain the following inequalities:

$$\begin{aligned}&\left[ \begin{array} {cc} y(t-\tau _1(t))\\ f_{k}(y(t-\tau _1(t))) \end{array}\right] ^T \left[ \begin{array} {cc} -F_{k1}U_{k+2} &{} F_{k2}U_{k+2}\\ F_{k2}U_{k+2} &{} -U_{k+2} \end{array}\right] \left[ \begin{array} {cc} y(t-\tau _1(t))\\ f_{k}(y(t-\tau _1(t))) \end{array}\right] \ge 0,\end{aligned}$$

(37)

$$\begin{aligned}&\left[ \begin{array} {cc} x(t-\tau _2(t))\\ g_{k}(x(t-\tau _2(t))) \end{array}\right] ^T \left[ \begin{array} {cc} -G_{k1}J_{k+2} &{} G_{k2}J_{k+2}\\ G_{k2}J_{k+2} &{} -J_{k+2} \end{array}\right] \left[ \begin{array} {cc} x(t-\tau _2(t))\\ g_{k}(x(t-\tau _2(t))) \end{array}\right] \ge 0. \end{aligned}$$

(38)

Now, combining (12)–(38), we have

$$\begin{aligned} \dot{V}(x_{t},y_{t},t)\le -\zeta ^T(t)\Omega \zeta (t), \end{aligned}$$

(39)

where

$$\begin{aligned} \zeta ^T(t)=&[\zeta _1^T(t)\ \zeta _2^T(t)],\\ \zeta _1^T(t)=&\bigg [x^T(t)\quad \dot{x}^T(t)\\ {}&\quad x^T(t-\delta _1)\quad x^T(t-\tau _2(t))\quad x^T(t-\tau _2)\quad x^T(t-\tau _3(t))\quad x^T(t-\tau _3)\quad g^T_1(x(t)\\ {}&g^T_1(x(t-\tau _2(t)) \quad g^T_2(x(t)\quad g^T_2(x(t-\tau _2(t))\\ {}&\quad \int _{t-\tau _2}^{t}g^T_2(x(s)ds\quad \int _{t-\tau _2(t)}^{t}x^T(s)ds\quad \int _{t-\tau _2(t)}^{t}\dot{x}^T(s)ds\\&\int _{t-\tau _2}^{t-\tau _2(t)} x^T(s)ds\quad \int _{t-\tau _2}^{t-\tau _2(t)} \dot{x}^T(s)ds\quad \int _{-\tau _2(t)}^{0}\int _{t+\theta }^{t}\dot{x}^T(s)ds \\ {}&\quad \int _{-\tau _2}^{-\tau _2(t)}\int _{t+\theta }^{t}\dot{x}^T(s)ds\quad \int _{t-\tau _3(t)}^{t}x^T(s)ds\\&\int _{t-\tau _3(t)}^{t}\dot{x}^T(s)ds\quad \int _{t-\tau _3}^{t-\tau _3(t)} x^T(s)ds\quad \int _{t-\tau _3}^{t-\tau _3(t)}\dot{x}^T(s)ds\bigg ],\\ \zeta _2^T(t)=&\bigg [y^T(t)\quad \dot{y}^T(t)\\ {}&\quad y^T(t-\delta _2)\ y^T(t-\tau _1(t))\ y^T(t-\tau _1)\quad y^T(t-\tau _3(t))\quad y^T(t-\tau _3) \quad f^T_1(y(t)\\ {}&f^T_1(y(t-\tau _1(t))\\ {}&\quad f^T_2(y(t)\quad f^T_2(y(t-\tau _1(t))\ \int _{t-\tau _1}^{t}f^T_2(y(s)ds\quad \int _{t-\tau _1(t)}^{t}y^T(s)ds\quad \int _{t-\tau _1(t)}^{t}\dot{y}^T(s)ds\\ {}&\int _{t-\tau _1}^{t-\tau _1(t)} y^T(s)ds\quad \int _{t-\tau _1}^{t-\tau _1(t)}\dot{y}^T(s)ds\ \int _{-\tau _1(t)}^{0}\int _{t+\theta }^{t}\dot{y}^T(s)ds \ \int _{-\tau _1}^{-\tau _1(t)}\int _{t+\theta }^{t}\dot{y}^T(s)ds\\&\int _{t-\tau _3(t)}^{t}y^T(s)ds \int _{t-\tau _3(t)}^{t}\dot{y}^T(s)ds\\ {}&\quad \int _{t-\tau _3}^{t-\tau _3(t)} y^T(s)ds\ \int _{t-\tau _3}^{t-\tau _3(t)}\dot{y}^T(s)ds\bigg ], \end{aligned}$$

and $\Omega$ is defined as in (10).

Thus, the equilibrium point of (8) is globally asymptotically stable. It may be inferred from the inequality (39) that,

$$\begin{aligned} V(x_{t},y_{t},t)+\int _{0}^{t}\zeta ^T(s)\Omega \zeta (s)ds\le V(0)<\infty , \end{aligned}$$

(40)

where

$$\begin{aligned} V(0)\le \big [&\lambda _{max}(\mathcal {P})+\delta _1\lambda _{max}(P_1)+\tau _2\lambda _{max}(P_3)+\tau _2\lambda _{max}(P_5) +\tau _3\lambda _{max}(P_7)+\frac{\tau _2^2}{2!}\lambda _{max}(Q_1)\\ +&\frac{\tau _3^2}{2!}\lambda _{max}(Q_3)+\sum \limits _{i=0}^{1}\frac{\tau _{(3-i)}^2}{2!}\lambda _{max}\left[ \begin{array} {cc} X_{(2i+1)} &{} Y_{(2i+1)}\\ \maltese &{} Z_{(2i+1)} \end{array}\right] + \frac{\tau _2^3}{3!}\lambda _{max}(R_1)+\frac{\tau _2^2}{2!}\lambda _{max}(R_3)\big ] \mathbf \Psi _{x_t}^2\\+&\big [\lambda _{max}(\mathcal {Q})+\delta _2\lambda _{max}(P_2)+\tau _1\lambda _{max}(P_4) +\tau _1\lambda _{max}(P_6)+\tau _3\lambda _{max}(P_8)+\frac{\tau _1^2}{2!}\lambda _{max}(Q_2)\\ +&\frac{\tau _3^2}{2!}\lambda _{max}(Q_4)+\sum \limits _{i=1}^{2}\frac{\tau _{(2i-1)}^2}{2!}\lambda _{max}\left[ \begin{array} {cc} X_{(2i)} &{} Y_{(2i)}\\ \maltese &{} Z_{(2i)} \end{array}\right] +\frac{\tau _1^3}{3!}\lambda _{max}(R_2)+ \frac{\tau _1^2}{2!}\lambda _{max}(R_4)\big ]\mathbf \Psi _{y_t}^2, \end{aligned}$$

$$\begin{aligned} =\varSigma _1\mathbf \Psi _{x_t}^2+\varSigma _2\mathbf \Psi _{y_t}^2, \end{aligned}$$

(41)

where

$$\begin{aligned}&\mathbf \Psi _{x_t}=max\{\sup \limits _{\theta \in [-\upsilon _{x_t},0]}\Vert \psi _{x_t} (\theta )\Vert ,\ \sup \limits _{\theta \in [-\upsilon _2,0]}\Vert {\dot{\psi }}_{x_t}(\theta )\Vert \},\\ {}&\mathbf \Psi _{y_t} =max\{\sup \limits _{\theta \in [-\upsilon _{y_t},0]}\Vert \psi _{y_t} (\theta )\Vert ,\ \sup \limits _{\theta \in [-\upsilon _2,0]}\Vert {\dot{\psi }}_{y_t}(\theta )\Vert \}. \end{aligned}$$

On the other hand, by the definition of $V(x_{t},y_{t},t)$, we get

$$\begin{aligned} V(x_{t},y_{t},t)\ge&x^T(t)\mathcal {P}x(t)+y^T(t)\mathcal {Q}y(t),\nonumber \\ \ge&\lambda _{min}\mathcal {P}x^T(t)x(t)+\lambda _{min}\mathcal {Q}y^T(t)y(t),\nonumber \\ =&\lambda _{min}\mathcal {P}\Vert x(t)\Vert ^2+\lambda _{min}\mathcal {Q}\Vert y(t)\Vert ^2,\nonumber \\ =&\min \{\lambda _{min}\mathcal {P},\lambda _{min}\mathcal {Q}\}\big (\Vert x(t)\Vert ^2+\Vert y(t)\Vert ^2\big ), \end{aligned}$$

(42)

Then, combining (41) and (42), we obtain

$$\begin{aligned} \Vert x(t)\Vert ^2+\Vert y(t)\Vert ^2\le \frac{V(0)}{\min \{\lambda _{min}\mathcal {P},\lambda _{min}\mathcal {Q}\}}. \end{aligned}$$

(43)

It is clear that the system (8) is globally asymptotic stable for $\Omega <0$, by Lyapunov stability theory. This completes the proof. $\square$

4 Sampled-Data Stabilization

Theorem 4.1

Under Assumption (A), for given scalars $\tau _1,\ \tau _2,\ \tau _3,\ \delta _1,\ \delta _2,\ \mu _1$, and $\mu _2$, the equilibrium point of system (8) is stable if there exist matrices $\mathcal {P}>0,\ \mathcal {Q}>0,\ P_i>0,\ (i=1,2,...,8), \ Q_j>0,\ R_j>0,\ \left[ \begin{array} {cc} X_{j} &{} Y_{j}\\ \maltese &{} Z_{j} \end{array}\right] >0,$ positive-definite diagonal matrices $U_{j},\ J_{j}$ and any matrices $\left[ \begin{array} {cc} M_{j} &{} N_{j}\\ H_{j} &{} T_{j} \end{array}\right] ,\ (j=1,2,...,4), {\tilde{R}}_1,\ {\tilde{R}}_2, {L_1}, {L_2}$ such that the following LMIs hold:

$$\begin{aligned} \left[ \begin{array}{c|c} \left[ \begin{array} {cc} X_{k} &{} Y_{k} \\ \maltese &{} Z_{k} \end{array}\right] &{} \left[ \begin{array}{cc} M_{k} &{} N_{k} \\ H_{k} &{} T_{k} \end{array}\right] \\ \hline \maltese &{} \left[ \begin{array} {cc} X_{k} &{} Y_{k} \\ \maltese &{} Z_{k} \end{array}\right] \end{array} \right]>0,\ \left[ \begin{array} {cc} R_l &{} {\tilde{R}}_l\\ \maltese &{} R_l \end{array}\right] >0,\ k=1,...,4,\ l=1,2, \end{aligned}$$

(44)

$$\begin{aligned} {\overline{\Omega }}=\left[ \begin{array}{c|c} \left[ \begin{array} {cc} {\overline{\Omega }}_{11} &{} [0]_{11n\times 11n} \\ \maltese &{} {\overline{\Omega }}_{22} \end{array}\right] &{} [0]_{24n\times 24n} \\ \hline \maltese &{} \left[ \begin{array} {cc} {\overline{\Omega }}_{33} &{} [0]_{11n\times 11n}\\ \maltese &{} {\overline{\Omega }}_{44} \end{array}\right] \end{array} \right] <0, \end{aligned}$$

(45)

where

$$\begin{aligned} {\overline{\Omega }}_{11}&=\left[ \begin{array}{cccccccccccc} (1,1)^{\diamond } &{} (1,2)^\diamond &{} -S_1A &{} Q_1 &{} 0 &{} Q_3+{L_1} &{} 0 &{} G_{12}J_1 &{} S_1W_1 &{} G_{22}J_2 &{} 0 &{} S_1W_2\\ \maltese &{} (2,2)^\diamond &{} -S_1A &{} 0 &{} 0 &{} {L_1} &{} 0 &{} 0 &{} S_1W_1 &{} 0 &{} 0 &{} S_1W_2 \\ \maltese &{} \maltese &{} -\delta _1P_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{} (4,4)^\diamond &{} Q_1 &{} 0 &{} 0 &{} 0 &{} G_{32}J_3 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{}\maltese &{} (5,5)^\diamond &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -2Q_3 &{} Q_3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} (7,7)^\diamond &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -J_1 &{} 0&{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -J_3 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} (10,10)^\diamond &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -J_4 &{} 0 \end{array}\right] ,\\ {\overline{\Omega }}_{22}&=\left[ \begin{array}{cccccccccccccc} -R_4 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} -X_1 &{} -Y_1 &{} -M_1 &{} -N_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} -Z_1 &{} -H_1 &{} -T_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} -X_1 &{} -Y_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -R_1 &{} -\tilde{R_1} &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -R_1 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -X_3 &{} -Y_3 &{} -M_3 &{} -N_3 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_3 &{} -H_3 &{} -T_3 \\ \maltese &{}\maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -X_3 &{} -Y_3 \\ \maltese &{}\maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_3 \end{array}\right] ,\\ \Omega _{33}&=\left[ \begin{array}{cccccccccccc} (1,1)^\dag &{} (1,2)^\dag &{} -S_2B &{} Q_2 &{} 0 &{} Q_4+{L_2} &{} 0 &{} F_{12}U_1 &{} S_2V_1 &{} F_{22}U_2 &{} 0 &{} S_2V_2\\ \maltese &{} (2,2)^\dag &{} -S_2B &{} 0 &{} 0 &{} {L_2} &{} 0 &{} 0 &{} S_2V_1 &{} 0 &{} 0 &{} S_2V_2 \\ \maltese &{} \maltese &{} -\delta _2P_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{} (4,4)^\dag &{} Q_2 &{} 0 &{} 0 &{} 0 &{} F_{32}U_3 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{}\maltese &{} (5,5)^\dag &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -2Q_4 &{} Q_4 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} (7,7)^\dag &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -U_1 &{} 0&{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -U_3 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} (10,10)^\dag &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -U_4 &{} 0 \end{array}\right] ,\\ {\overline{\Omega }}_{44}&=\left[ \begin{array}{cccccccccccccc} -R_3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} -X_2 &{} -Y_2 &{} -M_2 &{} -N_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} -Z_2 &{} -H_2 &{} -T_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} -X_2 &{} -Y_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -R_2 &{} -\tilde{R_2} &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -R_2 &{} 0 &{} 0 &{} 0 &{} 0 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -X_4 &{} -Y_4 &{} -M_4 &{} -N_4 \\ \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_4 &{} -H_4 &{} -T_3 \\ \maltese &{}\maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -X_4 &{} -Y_4 \\ \maltese &{}\maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} \maltese &{} -Z_4 \end{array}\right] , \end{aligned}$$

$$\begin{aligned}&(1,1)^\diamond =\delta _1P_1+P_3+P_5+P_7-Q_1-Q_3+\tau _2^2X_1+\tau _3^2X_3-G_{11}J_1-G_{21}J_2,\\&(1,1)^\dag =\delta _2P_2+P_4+P_5+P_8-Q_2-Q_3+\tau _1^2X_2+\tau _3^2X_4-F_{11}U_1-F_{21}U_2,\\&(1,2)^\diamond =\mathcal {P}+\tau _2^2Y_1+\tau _3^2Y_3-S_1,\ (1,2)^\dag =\mathcal {Q}+\tau _1^2Y_2+\tau _3^2Y_4-S_2,\\&(2,2)^\diamond =\tau _2^2Q_1+\tau _3^2Q_3+\tau _2^2Z_1+\tau _3^2Z_3+\bigg (\frac{\tau _2^2}{2!}\bigg )^2R_1-S_1-S_1^T,\\&(2,2)^\dag =\tau _1^2Q_2+\tau _3^2Q_4+\tau _1^2Z_2+\tau _3^2Z_4+\bigg (\frac{\tau _1^2}{2!}\bigg )^2R_2-S_2-S_2^T,\\&(4,4)^\diamond =-(1-\mu _2)P_3-2Q_1-G_{31} J_3-G_{41} J_4,\\&(4,4)^\dag =-(1-\mu _1)P_4-2Q_2-F_{31}U_3-F_{41}U_4,\\&(5,5)^\diamond =-P_5-Q_1,\ (7,7)^\diamond =-Q_3-P_7, \ (10,10)^\diamond =-J_2+\tau ^2_2R_4,\\&(5,5)^\dag =-P_6-Q_2,\ (7,7)^\dag =-Q_4-P_8, \ (10,10)^\dag =-U_2+\tau ^2_1R_3, \end{aligned}$$

Moreover, desired controller gain matrix are given by

$$\begin{aligned} \mathcal {K}=S_1^{-1}{L_1},\ \mathcal {M}=S_2^{-1}{L_2}. \end{aligned}$$

(46)

Proof

The proof is similar to that of Theorem 3.1. Because it is not included here. $\square$

Remark 4.2

By adopting the input delay approach, the proposed model can be transformed into continuous system. Because of the sampled-data control strategy deals with continuous system by sampling data at discrete time, we make the first attempt to address the sampled-data synchronization control problem for the presented model. A novel sampled-data control strategy was adopted to ensure that the drive system could achieve synchronization with the response system. To be noted that the sampled-data control drastically reduces the amount of transmitted information and increases the efficiency of bandwidth usage, because its’ control signals are kept constant during the sampling period and are allowed to change only at the sampling instant. On the other hand, due to the rapid growth of the digital hardware technologies, the sampled-data control method is more efficient, secure and useful. Thus, in this research area, a great deal of remarkable research investigations have been made and it can be found in [54,55,56,57].

Remark 4.3

The leakage delay, in particular, which exists in the negative feedback term of BAM, has recently emerged as a research topic of great significance. In [58] Gopalsamy was the first who investigated the stability of the BAM neural networks with constant leakage delays. He was surprised to launched that time delays in leakage terms has an essential impact on the dynamical performances, and the stability issue has been destabilized by leakage term for NN model. Hence, it is clear that, dynamic behaviours of system including leakage/forgetting term, that can be construct in the negative feedback term in the system model, which has been sketched back to 1992 Later on, a substantial achievements have been reached regarding the dynamics of BAM with delay in the leakage term [59,60,61,62]. On the other hand, it is natural that the BAM contains certain information about the derivative of the past state. This is expressed via the encompass of delay in the neutral derivative of BAM which often appears in the study of automatic control, population dynamics and vibrating masses attached to an elastic bar; the reader may consult the papers [63,64,65,66] for more details.

Table 2 Example 5.1. Calculated upper bound of $\tau _1=\tau _2$ for different $\delta _1,\ \delta _2$ and $\tau _3$ and $\mu _1,\ \mu _2=1$

5 Numerical Examples

The usefulness of the theoretical methods proposed is demonstrated in this section by numerical examples.

Example 5.1

We consider the following BAM neural networks with leakage delays:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\dot{x}(t)=-Ax(t-\delta _1)+W_1f_1(y(t-\tau _1(t))) +W_2\int _{t-\tau _1}^{t}f_2(y(s))ds+\mathcal {K}x(t-\tau _3(t)),\\ &{}\dot{y}(t)=-By(t-\delta _2)+V_1g_1(x(t-\tau _2(t))) +V_2\int _{t-\tau _2}^{t}g_2(x(s))ds+\mathcal {M}y(t-\tau _3(t)), \end{array} \right. \end{aligned}$$

(47)

with the following parameters:

$$\begin{aligned}&A= \left[ \begin{array}{cc} 5 &{} 0 \\ 0 &{} 5 \end{array}\right] ,\ W_1= \left[ \begin{array}{cc} 0.03 &{} 0.02 \\ 0.02 &{} 0.01 \end{array}\right] ,\ W_2= \left[ \begin{array}{cc} 0.09 &{} 0.02 \\ 0.02 &{} 0.01 \end{array}\right] ,\\&B= \left[ \begin{array}{cc} 4 &{} 0 \\ 0 &{} 5 \end{array}\right] ,\ V_1= \left[ \begin{array}{cc} 0.1 &{} 0.2 \\ 0.2 &{} 0.2 \end{array}\right] ,\ V_2= \left[ \begin{array}{cc} 0.03 &{} 0.05 \\ 0.02 &{} 0.04 \end{array}\right] . \end{aligned}$$

Let the activation functions as $f_1(x)=f_2(x)=g_1(x)=g_2(x)=tanh(x).$ It is obvious that Assumption (A) is satisfied, and we obtain

$$\begin{aligned} F_{11}=F_{21}=G_{11}=G_{21}=0,\ F_{12}=F_{22}=G_{12}=G_{22}=0.4I. \end{aligned}$$

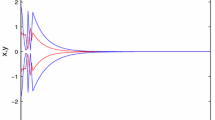
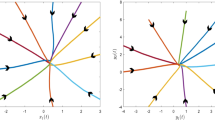
The allowable new upper bounds of $\tau _1,\ \tau _2$ and the corresponding new gain matrices for various values of $\mu _1,\ \mu _2$ and leakage delays $\delta _1,\ \delta _2$ are obtained by solving the LMIs in (45) with the aforementioned new parameter values using the LMI control toolbox. These results are listed in Table 2. Let $\tau _1=\tau _2=0.5746,\ \mu _1=\mu _2=1$ the dynamical analysis of BAM neural framework (1) is stable. The feasible solutions are shown below.

$$\begin{aligned}&\mathcal {P}=10^{-03}\times \left[ \begin{array}{cc} 0.9842 &{} -0.0028\\ -0.0028 &{} 0.9901 \end{array}\right] ,\ \mathcal {Q}=\left[ \begin{array}{cc} 0.0009 &{} 0.0000\\ 0.0000 &{} 0.0012 \end{array}\right] ,\ P_1=\left[ \begin{array}{cc} 0.0592 &{} -0.0001\\ -0.0001 &{} 0.0595 \end{array}\right] ,\\&P_2=\left[ \begin{array}{cc} 0.0489 &{} 0.0034\\ 0.0034 &{} 0.0746 \end{array}\right] ,\ P_3=10^{-05}\times \left[ \begin{array}{cc} 0.9160 &{} -0.0427\\ -0.0427 &{} 0.9800 \end{array}\right] ,\ P_4=10^{-04}\times \left[ \begin{array}{cc} 0.1719 &{} -0.0596\\ -0.0596 &{} 0.0207 \end{array}\right] ,\\&Q_1=10^{-05}\times \left[ \begin{array}{cc} 0.4919 &{} 0.0387\\ 0.0387 &{} 0.4522 \end{array}\right] ,\ Q_2=10^{-04}\times \left[ \begin{array}{cc} 0.3667 &{} 0.0561\\ 0.0561 &{} 0.1904 \end{array}\right] ,\\\&R_1=10^{-04}\times \left[ \begin{array}{cc} 0.7117 &{} -0.0382\\ -0.0382 &{} 0.7690 \end{array}\right] ,\\&R_2=10^{-03}\times \left[ \begin{array}{cc} 0.1542 &{} -0.0535\\ -0.0535 &{} 0.0186 \end{array}\right] ,\ R_3=10^{-04}\times \left[ \begin{array}{cc} 0.8700 &{} -0.0032\\ -0.0032 &{} 0.5637 \end{array}\right] ,\\\&U_1=10^{-06}\times \left[ \begin{array}{cc} 0.3773 &{} 0\\ 0 &{} 0.0455 \end{array}\right] ,\\&J_1=10^{-03}\times \left[ \begin{array}{cc} 0.1113 &{} 0\\ 0 &{} 0.1189 \end{array}\right] ,\ L_1=\left[ \begin{array}{cc} -0.0010 &{} 0.0000\\ 0.0000 &{} -0.0010 \end{array}\right] ,\ L_2=\left[ \begin{array}{cc} -0.0009 &{} -0.0000\\ -0.0000 &{} -0.0012 \end{array}\right] ,\\&S_1=10^{-04}\times \left[ \begin{array}{cc} 0.6801 &{} -0.0043\\ -0.0043 &{} 0.6882 \end{array}\right] ,\ S_2=10^{-04}\times \left[ \begin{array}{cc} 0.7692 &{} -0.0034\\ -0.0034 &{} 0.7825 \end{array}\right] . \end{aligned}$$

The following gain matrices are obtained by taking the sample time points $t_k=0.01k, k=1,2,...,$ and the sampling period $\tau _3=0.03$, respectively.

$$\begin{aligned} \mathcal {K}=S_1^{-1} L_1= \left[ \begin{array}{cc} -15.1595 &{} -0.0495\\ -0.0494 &{} -15.0783 \end{array}\right] ,\ \mathcal {M}=S_2^{-1} L_2= \left[ \begin{array}{cc} -12.3263 &{} -0.3975\\ -0.3764 &{} -15.6087 \end{array}\right] . \end{aligned}$$

Thus every requirement in Theorem 4.1 has been satisfies and system (47) is stable under the specified sampled-data feedback control, according to Theorem 4.1.

6 Conclusion

In order to regulate BAM neurons with leakage delays, a novel sampled-data control approach and its stability analysis are investigated in this research. We started by looking at instability events brought on by leakage delays. After that, we used a sampled-data control approach to bring the unstable systems under control. To determine the gain matrix for the planned sampled-data controllers, certain LMIs were generated. Finally, to demonstrate the efficiency of our theoretical findings, a numerical example and accompanying computational models have been provided. Future planning will take into account the intricacy of some control systems.Our future study will also focus on some systems biology with leakage delays as a key field of research such as Event triggered control and bifurcation analysis.