1 Introduction

Most of the industrial processes are nonlinear dynamical systems. The control of these systems requires a robust controller, which can handle the systems uncertainties, load change, disturbances, and interference noises [1,2,3,4,5]. Conventional PID controller is still widely used in industry on account of its simpler structure. Furthermore, the three terms of the PID controller perform an interpreted and clear action on the system response. Unfortunately, most of the tuning methods of conventional PID parameters require known model parameters and fixed operating points [1, 3, 6]. Therefore, the conventional PID controller fails when it faces a variation in the system parameters, a sudden load change, an external disturbance, a set-point change [2, 6, 7]. For these drawbacks of the conventional PID controller, the researchers worked seriously to find suitable controllers to control such complex nonlinear dynamical systems [8, 9].

In [6], a fuzzy-back propagation (fuzzy- BP) neural network PID was introduced to control a tracking system of a wheeled mobile robot. In [10], the authors presented a single output adaptive PID controller to govern the DC side voltage of a Vienna rectifier. Three training algorithms were used in [8], for an artificial neural network-based PID controller to flight control of quadcopter using at least three input neurons, three hidden neurons and three output neurons, i.e., (3–3-3) neural network structure. The time delay temperature system was controlled using adaptive PID with Lyapunov function in [11]. The level in a tank was governed using (8–4-3) structure PID based on neural network as mentioned in [7]. A radial basis function (RBF) neural network was used to tune the PID controller parameters for DC motor position control in [12]. In [13], a PID controller with (4-5-3) BP neural network structure was applied to an experimental model. An electric-heating reactor was controlled using an RBF neural networks-based PID controller as introduced in [14]. Dynamical systems were controlled using a neural network-based PID controller with (3-20-1) structure and tangent hyperbolic activation function was used as mentioned in [15].

In addition, a PID controller based on general dynamic neural networks (GDNN) with (2-4-3) structure was introduced in [16] to control an inverted pendulum. A liquid in a surge tank was controlled using (3-30-3) neural structure-based PID controller, which is highlighted in [17]. Furthermore, [18] proposed a multiple-input-multiple-output adaptive neural-based PID controller (MIMO-AN-PID) to control a hexacopter, i.e., unmanned aerial vehicles. Recently, in 2018, a contour error identifier based on a neural network is constructed to adapt the three parameters of the PID controller (PID-NNEI) using (15-15-1) neural structure and a hyperbolic tangent activation function that used to control three axes of a computer numerical control (CNC) machine as presented in [19]. In 2020, a PID controller based on an RBF neural network (PID-RBFNN) was introduced for a speed profile control of a subway train using (3-5-3) neural network structure [20]. In 2020, a neural network-based PID controller using Levenberg–Marquardt identifier (NNPID-LM) was introduced in [21]. The NNPID-LM controller, which was optimized by using an LM learning algorithm and an adaptive learning rate, used a neural network structure (2-5-1) and a 'log-sigmoid' activation function and it was used to control nonlinear dynamical systems. Moreover, in 2021, a smart optimized PID controller based on neural networks (SOPIDNN) with (4-18-3) structure using 'tan sigmoid' activation function was introduced to control the two-wheeled differential mobile robot [22]. The neural network of SOPIDNN was trained using the BP algorithm and the weights were adjusted using gradient descent manner. The main challenge faced the previous researchers is the large number of tunable parameters that need a large computation time. On the other hand, the BP algorithm, which converges along the mean square error (MSE) gradient descent has drawbacks such as falling in local minima and convergence rate is slow.

Early, a polynomial recurrent neural network (PRNN) based identification and control is proposed using a smaller number of tunable parameters (12 parameters) with gradient descent training algorithm and fixed learning rate [23]. PRNN is still suffering from slow convergence speed and a relatively large number of the adjusted input weights, which depends on the number of external inputs and the number of neurons in the hidden layer. Therefore, the motivation of the proposed work is to overcome the mentioned challenges and drawbacks.

In this paper, a novel structure of a polynomial weighted output recurrent neural network (PWORNN) is introduced. To guarantee the stability and speed up the convergence of the weights of the PWORNN, Lyapunov criteria-based adaptive learning rate is developed to update the weights. Furthermore, a Lyapunov criterion is used for optimizing the parameters of the controller and eliminating the problem of gradient descent besides guaranteeing the controller stability. Then, the proposed neural network structure is used to obtain the controller parameters of the PID controller. The proposed adaptive PID controller structure based on a PWORNN (APID-PWORNN) is designed for controlling nonlinear systems to reduce the effect of system uncertainties and external disturbances. The contributions of this paper can be summarized as follows:

  • This paper presents an adaptive PID controller based on a novel PWORNN structure with only 6 tunable parameters.

  • A stable learning algorithm is proposed in this work by deriving a new weight update rule based on the Lyapunov stability criterion to overcome the drawbacks of the gradient descent learning algorithm and prevent the proposed learning algorithm from falling in local minima.

  • Deriving a new adaptation rule for the learning rate based on the Lyapunov stability criterion to guarantee the optimal convergence speed to prevent the proposed learning algorithm from slow convergence speed as in the case of using gradient descent learning algorithm.

  • Two cases are studied and comparisons among the six controllers' performance show that the proposed APID-PWORNN controller has a robust performance and it is superior to other existing controllers.

The remainder of this paper is organized as follows: the structure of the polynomial recurrent neural network is described in Sect. 2. Sequentially, the proposed structure is explained in Sect. 3. Section 4 presents Lyapunov stability criteria for deriving a new weight update rule and adaptive learning rate formula following that, simulation results of a two cases studies considering, the system parameters uncertainties, disturbances, sensor measurement uncertainty, noise in the control signal, and set-point change and comparisons are introduced in Sect. 5. Finally, the conclusions are summarized in Sect. 6.

2 Polynomial Recurrent Neural Network Controller (PRNNC) Structure

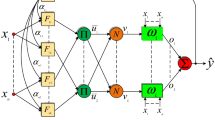
This section describes the structure of PRNNC [23]. PRNNC consists of three layers; the input layer, the hidden layer and the output layer. The input layer receives the recurrent network inputs; these inputs are weighted then transmitted to the hidden layer. The hidden neurons sum the weighted inputs then send them to the output layer. The output neurons multiply all the outputs coming from the hidden neurons then send them to the output of the network as shown in Fig. 1. In the structure shown below in Fig. 1, the output of the \({j}^{th}\) hidden neuron; (\({S}_{j}(k)\)) is given as:

$$ S_{j} \left( k \right) = \mathop \sum \limits_{i = 0}^{N} w_{ij} \left( k \right)X_{i} \left( k \right) $$
(1)

where \(k\) is the sample number, \({w}_{ij}\) is the connection weight between \({i}^{th}\) input neuron to \({j}^{th}\) hidden neuron, N is the number of input neurons and \({X}_{i}\left(k\right)=[1,r\left(k\right),r\left(k-1\right),u\left(k-1\right),y\left(k-1\right),y\left(k-2\right)]\); is the input vector, i.e., online training data set. Basically, \({S}_{j}(k)\) changes its value based on the weights updating and the input vector. The output of the network is given as:

$$ u\left( k \right) = \mathop \prod \limits_{j = 1}^{M} S_{j} \left( k \right) $$
(2)

where \(u(k)\) is the control signal and M is the number of the hidden neurons. Now, \(u(k)\) is expressed as the result of multiplication of aggregated terms (product of sum) operation that means polynomial function.

Fig. 1
figure 1

Structure of PRNNC [23]

Full size image

For the control purpose, the squared error is used as a cost function, and the gradient descent is applied to minimize the accumulative sum of the cost function as follows:

$$ E\left( k \right) = \frac{1}{2}\left( {r\left( k \right) - y\left( k \right)} \right)^{2} $$
(3)

where \(E\left( k \right)\) is the cost function, \({ }r\left( k \right)\) is the reference input, \(y\left( k \right)\) is the plant output. This method produces the following update rule:

$$ w_{ij} \left( k \right) = h\left( {r\left( k \right) - y\left( k \right)} \right)\frac{\partial y\left( k \right)}{{\partial u\left( k \right)}}\frac{\partial u\left( k \right)}{{\partial w_{ij} \left( k \right)}} $$
(4)

where \(h\) is the fixed learning rate.

3 Proposed APID-PWORNN Controller Structure

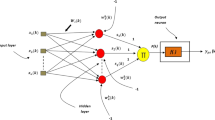
The structure of the proposed APID-PWORNN controller is highlighted in Fig. 2. The proposed adaptive PID controller is constructed based on a polynomial network with weighted outputs. The input layer receives the recurrent input vector. Every hidden neuron sums the incoming inputs and then generates an output to the output layer. The output layer consists of three neurons, each output neuron products all the weighted outputs coming from the hidden neurons and then generates its own output. The three outputs coming from the output layer represent the three adaptive PID controller parameters,\( K_{P} \left( k \right)\), \(K_{I} \left( k \right)\), and \(K_{D} \left( k \right)\).

Fig. 2
figure 2

Structure of the proposed APID-PWORN controller

Full size image

The inputs and outputs of each layer are given as follows:

Input layer: The input vector to this layer is set as; \(X_{i} \left( k \right) = \left[ {e\left( k \right),u\left( {k - 1} \right),y\left( {k - 1} \right)} \right]\), i.e., online training data set, where\(, y\left( {k - 1} \right),{ }u\left( {k - 1} \right)\), and \(e\left( k \right)\) are the recurrent plant output, the recurrent control signal, and the error signal between the reference input and the plant output, respectively.

Hidden layer: The inputs of each neuron in this layer are the elements of the input vector\(; X_{i} \left( k \right)\). While the output of the \(jth\) hidden neuron is given as:

$$ F_{j} \left( k \right) = \mathop \sum \limits_{i = 1}^{N} X_{i} \left( k \right) $$
(5)

where N is the number of input neurons and \(F_{j} \left( k \right)\) is the hidden neuron output.

Output layer: The inputs to the output neuron are \( F_{j} \left( k \right)\). While the three outputs of the output layer are defined as follows:

$$ K_{P} \left( k \right) = \mathop \prod \limits_{j = 1}^{M} w_{jP} \left( k \right)F_{j} \left( k \right) $$
(6)
$$ K_{I} \left( k \right) = \mathop \prod \limits_{j = 1}^{M} w_{jI} \left( k \right)F_{j} \left( k \right) $$
(7)
$$ K_{D} \left( k \right) = \mathop \prod \limits_{j = 1}^{M} w_{jD} \left( k \right)F_{j} \left( k \right) $$
(8)

where M is the number of the hidden neurons, and \( w_{jP}\),\( w_{jI}\), \(w_{jD}\) are the connection weights between the \(jth\) hidden neuron and the proportional output neuron (P node), integral output neuron (I node), and the derivative output neuron (D node), respectively.

Obviously, in this simple structure, the number of the tunable parameters (adjustable weights) doesn’t depend on the number of inputs neurons (N) but only it depends on the number of the hidden neurons (M). Accordingly, the number of the tunable parameters always equals 3 M. In this work (3-2-3) structure is used, which results in 6 tunable parameters. Therefore, the proposed structure aims to reduce the number of the tunable parameters, which leads to a reduction of the computation time.

Figure 3 describes the block diagram of the closed loop control system based on the proposed APID-PWORNN controller. In this block diagram, an incremental PID controller based on discrete-time form is used as follows:

$$ \Delta u\left( k \right) = K_{P} \left( k \right)e_{1} \left( k \right) + K_{I} \left( k \right)e_{2} \left( k \right) + K_{D} \left( k \right)e_{3} \left( k \right) $$
(9)
$$ u\left( k \right) = \Delta u\left( k \right) + u\left( {k - 1} \right) $$
(10)

where \({ }K_{P} \left( k \right)\),\( K_{I} \left( k \right)\),\( K_{D} \left( k \right)\) are the adaptive PID controller parameters,\({ }e_{1} \left( k \right) = e\left( k \right) - e\left( {k - 1} \right)\),\({ }e_{2} \left( k \right) = e\left( k \right)\),\( e_{3} \left( k \right) = e\left( k \right) - 2e\left( {k - 1} \right) + e\left( {k - 2} \right)\),\({ }\Delta u\left( k \right) = u\left( k \right) - u\left( {k - 1} \right)\), \(u\left( k \right)\) is the control signal, and \(e\left( k \right) = r\left( k \right) - y\left( k \right)\) is the error signal between the reference input and the plant output.

Fig. 3
figure 3

Block diagram of the proposed controller

Full size image

4 Lyapunov Stability Analysis

In this section, the Lyapunov stability analysis-based updating parameters and learning rate is presented to overcome the shortcomings of the gradient descent learning algorithm, which are mentioned above in the introduction section. The first part of this section explains the deriving of a new update rule for the adjusted weights of the proposed structure based on the Lyapunov stability criterion. This solution aims to prevent the proposed learning algorithm from falling in local minima. The other part explains the deriving of a new adaptation rule for the learning rate based on the Lyapunov stability criterion. This solution guarantees the optimal convergence speed and the stability for the proposed learning algorithm.

4.1 Update Rule Based on the Lyapunov Stability Criterion

For deriving a new update rule, a more flexible positive definite Lyapunov function is chosen as in [24]:

$$ V_{L} \left( k \right) = ax_{v}^{2} \left( k \right) + 2bx_{v} \left( k \right)y_{v} \left( k \right) + cy_{v}^{2} \left( k \right) $$
(11)

with these constrains;\( a > 0 {\text{and}} ac - b^{2} > 0.\)

In this work, the parameters of Eq. (11) are replaced by the error signal; \(e\left( k \right), \) and the connection weights vector; \(w\left( k \right) = \left[ {w_{1P } , w_{2P } , w_{1I} , w_{2I} , w_{1D} ,w_{2D} } \right]{ }^{T}\), where \(x_{v} \left( k \right) = e\left( k \right), y_{v} \left( k \right) = w\left( k \right).\) Therefore, the Lyapunov function can be rewritten as:

$$ V_{L} \left( k \right) = ae^{2} \left( k \right) + 2be\left( k \right)w\left( k \right) + cw^{2} \left( k \right) $$
(12)

The Lyapunov stability criterion states that the controlled system is asymptotically stable if the following condition is satisfied as [24]:

$$ \Delta V_{L} \left( k \right) = V_{L} \left( {k + 1} \right) - V_{L} \left( k \right) \le 0 $$
(13)

Then:

$$ \Delta V_{L} \left( k \right) = \left[ {ae^{2} \left( {k + 1} \right) + 2be\left( {k + 1} \right)w\left( {k + 1} \right) + cw^{2} \left( {k + 1} \right)} \right] - \left[ { ae^{2} \left( k \right) + 2be\left( k \right)w\left( k \right) + cw^{2} \left( k \right)} \right] \le 0 $$
(14)

Substituting \(\Delta e\left( k \right) = e\left( {k + 1} \right) - e\left( k \right),{\text{and}} \Delta w\left( k \right) = w\left( {k + 1} \right) - w\left( k \right)\) in Eq. (14) and performing some simple mathematical operations those lead to:

$$ \Delta V_{L} \left( k \right) = c\left[ {\Delta w\left( k \right)} \right]^{2} + \Delta w\left( k \right)\left[ {2b\Delta e\left( k \right) + 2be\left( k \right) + 2cw\left( k \right)} \right] + a [\Delta e\left( k \right)]^{2} + \Delta e\left( k \right)\left[ {2ae\left( k \right) + 2bw\left( k \right)} \right] \le 0 $$
(15)

Equating Eq. (15) by zero and dividing both sides by \(\Delta w\left( k \right)\) that gives:

$$ { }\Delta V_{L} \left( k \right) = c\Delta w\left( k \right) + \left[ {2b\Delta e\left( k \right) + 2be\left( k \right) + 2cw\left( k \right)} \right] + a\frac{{\left[ {\Delta e\left( k \right)} \right]^{2} }}{\Delta w\left( k \right)} + \frac{\Delta e\left( k \right)}{{\Delta w\left( k \right)}}\left[ {2ae\left( k \right) + 2bw\left( k \right)} \right] = 0 $$
(16)

At small change, \(\frac{\Delta e\left( k \right)}{{\Delta w\left( k \right)}}\) can be replaced by \(\frac{\partial e\left( k \right)}{{\partial w\left( k \right)}}\) in Eq. (16); Then:

$$ \Delta w\left( k \right) = - \frac{1}{c} \left[ {\left( {2b\Delta e\left( k \right) + 2be\left( k \right) + 2cw\left( k \right)} \right) + \frac{\partial e\left( k \right)}{{\partial w\left( k \right)}}\left( {2a\Delta e\left( k \right) + 2ae\left( k \right) + 2bw\left( k \right)} \right)} \right] $$
(17)

For simplifying the incremental term form in Eq. (17), let:

$$ L_{1} = \left( {2b\Delta e\left( k \right) + 2be\left( k \right) + 2cw\left( k \right)} \right){\text{ and }}L_{2} = \left( {2a\Delta e\left( k \right) + 2ae\left( k \right) + 2bw\left( k \right)} \right) $$

Then Eq. (17) can be rewritten as follows:

$$ { }\Delta w\left( k \right) = - \frac{1}{c}\left[ {L_{1} + \frac{\partial e\left( k \right)}{{\partial w\left( k \right)}}L_{2} } \right] $$
(18)

Now Eq. (18) guarantees the convergence stability. Moreover, to satisfy the optimization, the main formula of weight update, which minimizes the cost function that defined in Eq. (12), is given as:

$$ w\left( {k + 1} \right) = w\left( k \right) + h\left( k \right) \Delta w\left( k \right) $$
(19)

where \(h\left( k \right)\) is the adaptive learning rate, and \(\Delta w\left( k \right)\) is the incremental term, which is given in Eq. (18), and the last term (\(h\left( k \right) \Delta w\left( k \right)\)) in Eq. (19) can be called the updating term. Using the chain rule, the term \(\frac{\partial e\left( k \right)}{{\partial w\left( k \right)}}\) in Eq. (18) can be replaced by \( \frac{\partial e\left( k \right)}{{\partial w\left( k \right)}} = \frac{ - \partial y\left( k \right)}{{\partial w\left( k \right)}} = \frac{ - \partial y\left( k \right)}{{\partial u\left( k \right)}}\frac{\partial u\left( k \right)}{{\partial w\left( k \right)}}\). Then, the six adjusted weights (connecting weights from the hidden layer to the output layer) of the proposed APID-PWORNN controller can be updated using Eq. (19) as follows:

$$ w_{1P} \left( {k + 1} \right) = w_{1P} \left( k \right) - h\left( k \right)\frac{1}{c}\left[ {L_{11P} - \frac{\partial y\left( k \right)}{{\partial u\left( k \right)}}\frac{\partial u\left( k \right)}{{\partial w_{1P} \left( k \right)}}L_{21P} } \right] $$
(20)
$$ w_{2P} \left( {k + 1} \right) = w_{2P} \left( k \right) - h\left( k \right)\frac{1}{c}\left[ {L_{12P} - \frac{\partial y\left( k \right)}{{\partial u\left( k \right)}}\frac{\partial u\left( k \right)}{{\partial w_{2P} \left( k \right)}}L_{22P} } \right] $$
(21)
$$ w_{1I} \left( {k + 1} \right) = w_{1I} \left( k \right) - h\left( k \right)\frac{1}{c} \left[ {L_{11I} - \frac{\partial y\left( k \right)}{{\partial u\left( k \right)}} \frac{\partial u\left( k \right)}{{\partial w_{1I} \left( k \right)}} L_{21I} } \right] $$
(22)
$$ w_{2I} \left( {k + 1} \right) = w_{2I} \left( k \right) - h\left( k \right)\frac{1}{c} \left[ {L_{12I} - \frac{\partial y\left( k \right)}{{\partial u\left( k \right)}} \frac{\partial u\left( k \right)}{{\partial w_{2I} \left( k \right)}} L_{22I} } \right] $$
(23)
$$ w_{1D} \left( {k + 1} \right) = w_{1D} \left( k \right) - h\left( k \right)\frac{1}{c} \left[ {L_{11D} - \frac{\partial y\left( k \right)}{{\partial u\left( k \right)}} \frac{\partial u\left( k \right)}{{\partial w_{1D} \left( k \right)}} L_{21D} } \right] $$
(24)
$$ w_{2D} \left( {k + 1} \right) = w_{2D} \left( k \right) - h\left( k \right)\frac{1}{c} \left[ {L_{12D} - \frac{\partial y\left( k \right)}{{\partial u\left( k \right)}} \frac{\partial u\left( k \right)}{{\partial w_{2D} \left( k \right)}} L_{22D} } \right] $$
(25)

where \(L_{11P} , L_{21P} , L_{12P} , L_{22P} ,L_{11I} , L_{21I} , L_{12I} , L_{22I} , L_{11D} , L_{21D}\),\(L_{12D} {\text{and}} L_{22D}\) are given in Appendix.

The value of the partial derivative; \(\frac{\partial y\left( k \right)}{{\partial u\left( k \right)}}\) has no major effect on the learning algorithm in Eqs. (20–25) because it can be absorbed by the learning rate; \(h\left( k \right) \)[23]. Therefore, it is considered a constant value in this work, while \(\frac{\partial u\left( k \right)}{{\partial w\left( k \right)}}\) can be calculated as the following remark:

Remark: For deriving the formulas of \(\frac{\partial u\left( k \right)}{{\partial w\left( k \right)}}\) in Eqs. (20–25), since the two hidden neurons used in this structure generate the same output value from Eq. (5), and then, let, \(F_{j} \left( k \right) = F\), accordingly Eqs. (6–8) can be rewritten in the following form:

$$ K_{P} \left( k \right) = F^{2} w_{1P} \left( k \right)w_{2P } \left( k \right) $$
(26)
$$ K_{I} \left( k \right) = F^{2} w_{1I} \left( k \right)w_{2I } \left( k \right) $$
(27)
$$ K_{D} \left( k \right) = F^{2} w_{1D} \left( k \right)w_{2D } \left( k \right) $$
(28)

Substituting Eqs. (26–28) in Eq. (9) and Eq. (10) and performing the partial differentiation on Eq. (10), the required formulas of \(\frac{\partial u\left( k \right)}{{\partial w\left( k \right)}}\) for the six adjusted weights can easily derived as follows:

$$ \frac{\partial u\left( k \right)}{{\partial w_{1P} \left( k \right)}} = \frac{\partial u\left( k \right)}{{\partial K_{P} \left( k \right)}}\frac{{\partial K_{P} \left( k \right)}}{{\partial w_{1P} \left( k \right)}} = e_{1} \left( k \right)F^{2} w_{2P } \left( k \right) + \frac{{\partial u\left( {k - 1} \right)}}{{\partial w_{1P} \left( {k - 1} \right)}} $$
(29)
$$ \frac{\partial u\left( k \right)}{{\partial w_{2P} \left( k \right)}} = \frac{\partial u\left( k \right)}{{\partial K_{P} \left( k \right)}}\frac{{\partial K_{P} \left( k \right)}}{{\partial w_{2P} \left( k \right)}} = e_{1} \left( k \right)F^{2} w_{1P } \left( k \right) + \frac{{\partial u\left( {k - 1} \right)}}{{\partial w_{2P} \left( {k - 1} \right)}} $$
(30)
$$ \frac{\partial u\left( k \right)}{{\partial w_{1I} \left( k \right)}} = \frac{\partial u\left( k \right)}{{\partial K_{I} \left( k \right)}}\frac{{\partial K_{I} \left( k \right)}}{{\partial w_{1I} \left( k \right)}} = e_{2} \left( k \right)F^{2} w_{2I } \left( k \right) + \frac{{\partial u\left( {k - 1} \right)}}{{\partial w_{1I} \left( {k - 1} \right)}} $$
(31)
$$ \frac{\partial u\left( k \right)}{{\partial w_{2I} \left( k \right)}} = \frac{\partial u\left( k \right)}{{\partial K_{I} \left( k \right)}}\frac{{\partial K_{I} \left( k \right)}}{{\partial w_{2I} \left( k \right)}} = e_{2} \left( k \right)F^{2} w_{1I } \left( k \right) + \frac{{\partial u\left( {k - 1} \right)}}{{\partial w_{2I} \left( {k - 1} \right)}} $$
(32)
$$ \frac{\partial u\left( k \right)}{{\partial w_{1D} \left( k \right)}} = \frac{\partial u\left( k \right)}{{\partial K_{D} \left( k \right)}}\frac{{\partial K_{D} \left( k \right)}}{{\partial w_{1D} \left( k \right)}} = e_{3} \left( k \right)F^{2} w_{2D } \left( k \right) + \frac{{\partial u\left( {k - 1} \right)}}{{\partial w_{1D} \left( {k - 1} \right)}} $$
(33)
$$ \frac{\partial u\left( k \right)}{{\partial w_{2D} \left( k \right)}} = \frac{\partial u\left( k \right)}{{\partial K_{D} \left( k \right)}}\frac{{\partial K_{D} \left( k \right)}}{{\partial w_{2D} \left( k \right)}} = e_{3} \left( k \right)F^{2} w_{1D } \left( k \right) + \frac{{\partial u\left( {k - 1} \right)}}{{\partial w_{2D} \left( {k - 1} \right)}} $$
(34)

Sequentially, the proposed APID-PWORNN controller parameters given by Eqs. (26–28) can be updated directly by inserting the updated weights Eqs. (20–25) into Eqs. (26–28).

4.2 Adaptation of the Learning Rate Based on the Lyapunov Stability Criterion

To guarantee the optimization of the convergence speed and the convergence stability that may be lost when using the gradient descent learning algorithm. An adaption rule for the learning rate based on the Lyapunov function is derived for the proposed learning algorithm in this subsection. Following the same manner used in [25,26,27,28] an adaptation rule can be obtained as follows:

Let the Lyapunov function is as follows:

$$ L_{v} \left( k \right) = \frac{1}{2}e^{2} \left( k \right) $$
(35)

where \(L_{v} \left( k \right)\) is a Lyapunov function, \(e\left( k \right)\) is the error signal. To guarantee the stability, the following condition should be achieved:

$$ \Delta L_{v} \left( k \right) = L_{v} \left( {k + 1} \right) - L_{v} \left( k \right) \le 0 $$
(36)

Then,

$$ \Delta L_{v} \left( k \right) = \frac{1}{2}\left[ {e^{2} \left( {k + 1} \right) - e^{2} \left( k \right)} \right] $$
(37)

Equation (37) can be rewritten as:

$$ \Delta L_{v} \left( k \right) = \frac{1}{2}\left[ {e\left( {k + 1} \right) + e\left( k \right)} \right]\left[ {e\left( {k + 1} \right) - e\left( k \right)} \right] $$
(38)

Since \(\Delta e\left( k \right) = e\left( {k + 1} \right) - e\left( k \right)\), then Eq. (38) can be rewritten as:

$$ \Delta L_{v} \left( k \right) = \Delta e\left( k \right)\left[ {\frac{1}{2}\left( {\Delta e\left( k \right)} \right) + e\left( k \right)} \right] \le 0 $$
(39)

Now Tayler series expansion is used to express \(e\left( {k + 1} \right)\) as:

$$ e\left( {k + 1} \right) = e\left( k \right) + \frac{\partial e\left( k \right)}{{\partial Q\left( k \right)}}\Delta Q\left( k \right) + h_{ot} $$
(40)

where \(Q\left( k \right)\) is any tuned parameter in PWORNN, which can be considered the output weight vector; \(w\left( k \right)\), and \(h_{ot}\) is the higher order terms that can be neglected. So, \(\Delta e\left( k \right)\) can be written as:

$$ \Delta e\left( k \right) = \frac{\partial e\left( k \right)}{{\partial Q\left( k \right)}}\Delta Q\left( k \right) = \frac{\partial e\left( k \right)}{{\partial w\left( k \right)}}\;\Delta w\left( k \right) = \frac{{\partial \left( {r\left( k \right) - y\left( k \right)} \right)}}{\partial w\left( k \right)}\;\Delta w\left( k \right) = \frac{ - \partial y\left( k \right)}{{\partial w\left( k \right)}}\Delta w\left( k \right) $$
(41)

Now, for guaranteeing the weight updating stability, \(\Delta w\left( k \right)\) in Eq. (41) can be considered the updating term (\(h\left( k \right)\Delta w\left( k \right)\)) from the update rule; Eq. (19). Then, replacing \(\Delta e\left( k \right) \) in Eq. (39) by \(\Delta e\left( k \right) = \frac{ - \;\partial y\left( k \right)}{{\partial w\left( k \right)}}\Delta w\left( k \right)h\left( k \right)\), which yields that:

$$ \Delta L_{v} \left( k \right) = \frac{1}{2}h\left( k \right)\Delta w\left( k \right)\frac{\partial y\left( k \right)}{{\partial w\left( k \right)}}\left[ {h\left( k \right)\Delta w\left( k \right)\frac{\partial y\left( k \right)}{{\partial w\left( k \right)}} - 2e\left( k \right)} \right] \le 0 $$
(42)

Then, replacing \(\Delta e\left( k \right) \) in Eq. (17) by \(\Delta e\left( k \right) = \frac{ - \partial y\left( k \right)}{{\partial w\left( k \right)}}\Delta w\left( k \right)h\left( k \right)\), which gives \(\Delta w\left( k \right)\) as follows:

$$ \Delta w\left( k \right) = - \frac{1}{c} \frac{{\left[ {\frac{\partial y\left( k \right)}{{\partial w\left( k \right)}}\left[ { - 2bw\left( k \right) - 2ae\left( k \right)} \right] + 2be\left( k \right) + 2cw\left( k \right)} \right]}}{{\left[ {1 - \frac{2h\left( k \right)}{c}\frac{\partial y\left( k \right)}{{\partial w\left( k \right)}}\left[ {b - a\frac{\partial y\left( k \right)}{{\partial w\left( k \right)}}} \right]} \right]}} $$
(43)

Finally, substituting Eq. (43) in Eq. (42) that leads to:

$$ 0 \le h\left( k \right) \le \frac{ce\left( k \right)}{{\left[ {\left[ {\frac{\partial y\left( k \right)}{{\partial w\left( k \right)}}} \right]^{2} \left( {bw\left( k \right) - ae\left( k \right)} \right) + \frac{\partial y\left( k \right)}{{\partial w\left( k \right)}}(be\left( k \right) - cw\left( k \right)} \right]}} $$
(44)

Taking the Euclidean norm, the adaptive learning rate, which guarantees the learning stability is given as:

$$ { }0 \le h\left( k \right) \le \frac{ce\left( k \right)}{{\left[ {\left[ {\frac{\partial y\left( k \right)}{{\partial w\left( k \right)}}} \right]^{2} \left( {bw\left( k \right) - ae\left( k \right)} \right) + \frac{\partial y\left( k \right)}{{\partial w\left( k \right)}}(be\left( k \right) - cw\left( k \right)} \right]}} $$
(45)

The adaptation of the learning rate; \(h\left( k \right) \) can be performed by using the Euclidean norm of the previous equation, which mainly depends on the weight updating and the error signal (\(e\left( k \right))\).

5 Simulation Results

This section presents the MATLAB simulation results and the comparisons among the performance of the proposed APID-PWORNN controller, and four previous published neural network PID controllers that are pre-described in the introduction section such as the PID-NNEI controller [19], the PID-RBFNN controller [20], the NNPID-LM controller [21], which is optimized by the LM learning algorithm and an adaptive learning rate, and the SOPIDNN controller [22]. In addition, an improved particle swarm-based PID (IPSO-PID) controller [29], is added to the comparisons. All these algorithms are programmed using MATLAB R2017b scripts. The neural structure of the PID-NNEI controller [19] is (5-5-1) with biases in the hidden and output neurons for the error identifier, in addition three adjusted parameters of the PID controller that totally yields 39 tunable parameters. The used NN structure of the PID-RBFNN controller [20] is (3-5-3) with two adjusted parameters for each RBF hidden neuron (i.e., center and radius), which yields 25 tunable parameters. Moreover, an (2-5-1) NN structure with neurons biases for plant identifier is used for the NNPID-LM controller [21]; in addition to the three adjusted parameters of the PID controller, which totally yields 24 tunable parameters. In addition, a (2-18-3) neural structure that used to control single–input–single–output systems (SISO systems), which yields 90 tunable parameters is used for SOPIDNN controller [22].

Furthermore, to judge the superiority of the performance of the proposed controller, two indices are considered; the integral absolute error (IAE) and the mean absolute error (MAE). Several simulation tasks are preceded on the six controllers to investigate the robustness of the proposed controller performance such as unit step response, set-point change, system parameters uncertainty, system disturbance, and actuator noise. All these simulation tasks are applied through two cases studies that are explained in details in the following subsections. For fairness, the learning rate is unified for all five NN controllers to be \(h = 0.001\). Furthermore, all initial weights values are unified and chosen as random numbers in [− 0.5, 0.5]. For the proposed APID-PWORNN controller; the coefficients of the Lyapunov function in Eq. (12) are chosen as; \( a = 1, b = 0.2,c = 2\); and the initial value of the learning rate is \(h\left( k \right) = 0.001\). In addition, the total number, which is used for the particles for the IPSO-PID controller, is 25 particles. The optimized IPSO-PID controller parameters are \(K_{P} = 39.45 \times 10^{ - 3} , K_{I} = 58.4 \times 10^{ - 3} , K_{D} = 154.3 \times 10^{ - 3}\) for the case study 1, and \(K_{P} = - 9.875 \times 10^{ - 3} , K_{I} = - 1.575 \times 10^{ - 3} , K_{D} = - 2.225 \times 10^{ - 3}\) for the case study 2. Moreover, the two indices, which are measured for all controllers, are given as:

$$ IAE = T\mathop \sum \limits_{k = 1}^{n} \left| {e\left( k \right)} \right| $$
(46)
$$ MAE = \frac{1}{n}\mathop \sum \limits_{k = 1}^{n} \left| {e\left( k \right)} \right| $$
(47)

where T is the sampling time and n is the total number of the iteration.

5.1 Case Study 1

Consider the mathematical nonlinear dynamical system described as [23]:

$$ y_{p} \left( {k + 1} \right) = \frac{{P_{1} y_{p} \left( k \right)}}{{1 + y_{p}^{2} \left( k \right) + y_{p}^{2} \left( {k - 1} \right)}} + \frac{{P_{2} }}{{1 + e^{{ - P_{3} \left[ {y_{p} \left( k \right) + y_{p} \left( {k - 1} \right)} \right]}} }} + P_{4} u\left( k \right) + P_{5} u\left( {k - 1} \right) + d_{p} $$
(48)

where \(y_{p} \left( k \right)\) is the system output, \(u\left( k \right)\) is the control input (control signal), and the system parameters set as \(P_{1} = 1, P_{2} = 0.1, P_{3} = 1, P_{4} = 1, P_{5} = 0.4, d_{p} = 0.\)

5.1.1 Task 1: Unit Step Response

The control scheme is built as in Fig. 3. A unit step input is applied to the closed-loop system to depict the system response for the six controllers. Figure 4 shows the system response for the proposed APID-PWORNN controller and other controllers. It’s clear that the proposed controller, which is indicated with the red curve, reaches to the set-point faster than the other controllers. Furthermore, Fig. 5 shows the control signal of all controllers.

Fig. 4
figure 4

System output (Task 1)

Full size image
Fig. 5
figure 5

Control Signal (Task 1)

Full size image

5.1.2 Task 2: Set-Point Change

Figure 6 presents the behavior of the six controllers when the set-point is changed. Obviously, the proposed APID-PWORNN controller has more convergence speed and accuracy than the other controllers. NNPID-LM controller causes some overshoot in the beginning and it is relative slow convergence. SOPIDNN and PID-RBFNN controllers are slowed down at the last stage of the learning (from k = 2000 to k = 2500). PID-NNEI controller is slowed down at stage (from k = 1500 to k = 2000). Figure 7 shows the control signal for all controllers. Moreover, Fig. 8 shows the adaptation of the APID-PWORNN controller parameters.

Fig. 6
figure 6

System output (Task 2)

Full size image
Fig. 7
figure 7

Control Signal (Task 2)

Full size image
Fig. 8
figure 8

APID-PWORNN controller parameters (Task 2)

Full size image

5.1.3 Task 3: System Parameters Uncertainty

In this task, all system parameters are decreased to 80% as parameters uncertainty. Figure 9 depicts the unit step response with the effect of this uncertainty. The proposed APID-PWORNN controller is still the superior controller. It is the least affected and faster retraced the reference input. Furthermore, the control signal is presented in Fig. 10 for all controllers.

Fig. 9
figure 9

System output (Task 3)

Full size image
Fig. 10
figure 10

Control Signal (Task 3)

Full size image

5.1.4 Task 4: Disturbance Model

A disturbance signal is added to Eq. (48) as \({d}_{p}\left(k\right)=0.7\) (70% of the reference input) at iteration number k = 500. Figure 11 shows how each controller handles the system with this disturbance model. Here, the six controllers proved the robust performance but still the proposed APID-PWORNN controller is the fastest controller for handling this disturbance and the least affected one. Figure 12 shows the control signal for all controllers. Figure 13 indicates the changing of the APID-PWORNN controller parameters along the time in particular during applying the disturbance.

Fig. 11
figure 11

System output (Task 4)

Full size image
Fig. 12
figure 12

Control Signal (Task 4)

Full size image
Fig.13
figure 13

APID-PWORNN controller parameters (Task 4)

Full size image

The IAE and MAE are listed in Tables 1 and 2, respectively for the five neural controllers and the IPSO-PID controller that are used in this work. Moreover, to investigate the powerful computation of the proposed neural structure (3-2-3), which yields only 6 tunable parameters, the neural structure of the SOPIDNN and PID-RBFNN controllers are unified to be (3-2-3) i.e., SOPIDNN (3-2-3), which results in 12 tunable parameters and PID-RBFNN (3-2-3), which results in 10 tunable parameters. In addition, the conventional PID controller is performed for purpose of comparison.

Table 1 Values of IAE
Full size table
Table 2 Values of MAE
Full size table

Tables 1 and 2 show that the proposed APID-PWORNN controller has the least values of IAE and MAE in all tasks. Furthermore, the proposed controller with an adaptive learning rate (APID-PWORNN-AL) recorded fewer values of the proposed controller with a fixed learning rate (APID-PWORNN-FL). It’s clear that the proposed controller has a simple structure with fewer parameters and a good robustness compared with other controllers. Moreover, the robustness performance is proved through the above tests.

5.2 Case Study 2

Consider the heat exchanger system described in [30]. This system aims to raise the temperature of the process water; \(y\left( k \right) \) by steam flow rate. The system has two inputs and one output and classified from the control view point as a temperature control system. The first input is the steam flow rate, which is a fixed rate and another is the water flow rate; \(u\left( k \right)\), which is controlled by the control signal of the APID-PWORNN controller and other controllers in the simulations. The two inputs can be controlled using pneumatic control valves as shown in Fig. 14. Temperature is the output of this system, which has a nonlinear behavior. The dynamics of the steam-heat exchanger are given as:

$$ y\left( k \right) = q_{1} y\left( {k - 1} \right) + q_{2} y\left( {k - 2} \right) + q_{3} z\left( {k - 1} \right) + q_{4} z\left( {k - 2} \right) + d_{q} \left( k \right) $$
(49)
$$ z\left( k \right) = u\left( k \right) + q_{5} u^{2} \left( k \right) + q_{6} u^{3} \left( k \right) + q_{7} u^{4} \left( k \right) $$
(50)

where \(y\left( k \right)\) is the plant output (process temperature),\({ }u\left( k \right)\) is the control input (input water flow rate), and the system parameters are set as; \( q_{1} = 1.608, q_{2} = - 0.6385, q_{3} = - 6.5306, q_{4} = 5.5652, q_{5} = - 1.3228, q_{6} = 0.767, q_{7} = - 2.1755,\) \(d_{q} \left( k \right) = 0\). These parameters values are derived from real data for a practical system as explained in [31,32,33]. So, the model given by Eqs. (49) and (50) represents a real system.

Fig. 14
figure 14

Heat Exchanger System [30]

Full size image

5.2.1 Task 1: STEP Response

Figure 15 shows the heat exchanger response of a unit step input signal. The proposed APID-PWORNN controller based on adaptive learning rate has more convergence speed than other controllers. NNPID-LM and PID-NNEI controllers caused some overshoots in the transient period. The PID-RBFNN controller showed the least convergence speed in this task. Figure 16 presents the control signals of all controllers.

Fig. 15
figure 15

Heat exchanger output (Task 1)

Full size image
Fig. 16
figure 16

Control signal for heat exchanger (Task 1)

Full size image

5.2.2 Task 2: Set-Point Change

Figure 17 depicts the response of the heat exchanger system when the reference input is changed. From the figure, the superiority (more accurate, and more convergence speed) of the proposed APID-PWORNN controller compared with other controllers is shown. The control signals for all controllers are shown in Fig. 18. The adapting of the APID-PWORN controller parameters is depicted in Fig. 19.

Fig. 17
figure 17

Heat exchanger output (Task 2)

Full size image
Fig. 18
figure 18

Control signal for heat exchanger (Task 2)

Full size image
Fig. 19
figure 19

Changing the APID-PWORNN controller parameters (Task 2)

Full size image

5.2.3 Task 3: Heat Exchanger System Uncertainty

All the parameters of the heat exchanger have acquired an uncertainty by adding them with 80% at the 500th instant. The adaptation of the learning rate of the APID-PWORNN controller increased the convergence speed and accordingly minimized the effect of the uncertainty in the response that is shown in Fig. 20. Moreover, the control signal is depicted in Fig. 21 for all controllers.

Fig. 20
figure 20

Heat exchanger output (Task 3)

Full size image
Fig. 21
figure 21

Control signal for heat exchanger (Task 3)

Full size image

5.2.4 Task 4: Heat Exchanger With an External Disturbance Model

This disturbance in the output measurements can be caused by the sensor uncertainty. This task is performed by substituting \(d_{q} \left( k \right) = - \;0.284\sin \left( {0.1{\text{y}}\left( {\text{k}} \right)} \right)\) in Eq. (49). Figure 22 shows the simulated heat exchanger response for all controllers due to this disturbance model. The proposed controller is the least affected controller. Figure 23 shows the control signal for all controllers. Furthermore, the self-changing of the APID-PWORNN controller parameters to eliminate the effect of the external disturbance is shown in Fig. 24.

Fig. 22
figure 22

Heat exchanger output (Task 4)

Full size image
Fig. 23
figure 23

Control signal for heat exchanger (Task 4)

Full size image
Fig. 24
figure 24

Adapting the APID-PWORNN controller parameters (Task 4)

Full size image

5.2.5 Task 5: Actuator Noise

Actuator noise can be expressed by adding a noise signal to the plant output at the 500th instant. So, in this work, a noise signal with -0.05 rand (1) is added to the heat exchanger output in Eq. (49). Figure 25 shows the superiority of the proposed APID-PWORNN controller compared with other controllers. Furthermore, the control signal is presented in Fig. 26 for all controllers.

Fig. 25
figure 25

Heat exchanger output (Task 5)

Full size image
Fig. 26
figure 26

Control signal for heat exchanger (Task 5)

Full size image

For any nonlinear system, the stability and the limit cycle can be defined as follows:

Stability: the dynamical system is stable if all state variables of it are converged to the equilibrium point after the internal or external perturbation is applied to the dynamical system. And the system is called unstable if at least one of its state variables has diverged in an oscillatory or exponential manner [34].

A limit cycle: is a closed trajectory in phase space having a property that at least one other trajectory spirals into it [34].

Based on the above definitions, the stability and limit cycles (i.e., phase portrait) for the open-loop system and closed-loop system of the heat exchanger system are highlighted in Fig. 27 (a, b), respectively.

Fig. 27
figure 27

Phase portrait of heat exchanger system a Open loop. b Closed loop

Full size image

Figure 27a shows the phase portrait between the heat exchanger output; \(\left( {Y = y\left( k \right)} \right)\) on the horizontal axis, and the derivative of the output \({\text{Ydot}} = \frac{{y\left( k \right) - y\left( {k - 1} \right)}}{T}\) on the vertical axis at input changes such as \(u\left( k \right) = 1,{ }0.75,{ }1,{ }0.75,{\text{ and }}1{ }\) without controller (i.e., open-loop), while Fig. 27b shows the phase portrait at a set-point change such as \(r\left( k \right) = 1, 0.75, 1, 0.75, {\text{and}} 1\) with the proposed controller (i.e., closed-loop). Clearly, the proposed controller rapidly attracted the state variables of the heat exchanger to the equilibrium point and stabilizes the system.

Finally, in this subsection, the comparisons of the performance for all six algorithms are introduced considering again the IAE, MAE. Tables 3 and 4 list the IAE and MAE, respectively for all controllers. The proposed algorithm has fewer values of IAE and MAE than other algorithms. Table 5 lists the computation time, NN structure and number of parameters for NN algorithms and only the computation time of the IPSO-PID controller. It’ is clear that the computation time for the proposed controller is lower than other NN algorithms. On the other hand, the number of parameters for the proposed NN structure is smaller than those parameters for other NN algorithms. All simulations are performed by MATLAB scripts on a PC with a processor Intel (R) Core (TM) i3 CPU M350 @ 2.27 GHz, RAM 6.0 GB, 64-bit operating system, and Windows 7.

Table 3 Values of IAE
Full size table
Table 4 Values of MAE
Full size table
Table 5 Computation time, NN structure and number of parameters for all algorithms
Full size table

The main advantages of the proposed APID-PWORNN controller over other controllers are summarized as:

  • It possesses a stable learning algorithm because the learning algorithm is developed based on the Lyapunov stability criteria.

  • It has less computation time and less number of tunable parameters as shown in Table 5, and simple structure as shown in Fig. 2.

  • Moreover, the proposed controller recorded the minimum values of the performance indices such as IAE and MAE as indicated by Tables 1, 2, 3, and 4 that explore its computation accuracy compared to the existing controllers published previously.

6 Conclusions

In this paper, a novel structure of an adaptive PID controller based on a polynomial weighted output recurrent neural network and an adaptive learning rate algorithm is introduced. The simulation results proved that the proposed controller has the superiority for controlling the complex nonlinear dynamical systems and the robustness performance is examined through five tasks with two case studies (mathematical nonlinear system and heat exchanger system). Moreover, the optimization, the stability and the convergence speed are achieved by deriving parameters update rule and adaptation formula of the learning rate using a Lyapunov function. The proposed APID-PWORNN structure with a fewer number of tunable parameters, i.e., 6 weights, considered as a simple NN structure that reduced the computation time and it is applicable for microcontrollers with low-speed processors.