Introduction

Groundwater is one of a nation's important natural resources but its incorporation with level in terms of groundwater table (GWT) dedicates a nonlinear time-dependent concern in many geo-engineering projects (Hu & Jiao, 2010; Parry et al., 2014; Tang et al., 2017; Salvo et al., 2020). Modeling of GWT is applied to conceptualize and integrate knowledge on the natural and engineering disciplines to address a range of issues in different spatial and temporal scales (Mohammadi, 2009; Yeh et al., 2015; Bizhanimanzar et al., 2019). However, due to several embedded nonlinear complexities in the system, modeling of GWT is an inherently difficult task. Moreover, the sources of uncertainties related to model parameters, underlying conceptual assumptions, structure of model, geological conditions, observed spatial data (i.e., lack of data on natural variability), and steady-state GWT should be considered (Beven & Binley, 1992; Stedinger et al., 2008; Yeh et al., 2015; Hauser et al., 2017). As a result, computer code models have primarily been developed over simplified assumptions using long-term time series through different approaches, such as statistical techniques, approximation methods and numerical analyses (Rushton, 2003; Yan et al., 2018). Therefore, evaluating the robustness and accuracy performance of a predictive GWT model using uncertainty quantification (UQ) analysis is often required. Nowadays, alternative modern computational artificial intelligent techniques (AIT) lead to systematic UQ analysis that can be applied effectively to generate a GWT model (Guillaume et al., 2016; Sahoo & Russo, 2017; Chen et al., 2020; Wunsch et al., 2020; Yin et al., 2021).

Uncertainty can simply be described as knowledge situations involving imperfect or unknown information (Gärdenfors & Sahlin, 1982). To quantify uncertainty, three sources including physical variability of equipment, data, and model error should be considered (Barford, 1985; Kennedy & O'Hagan, 2001). In the modeling process, methods UQ are described in the context of different factors, such as input variabilities, assumptions and approximations, measurement errors, and sparse and imprecise data (Yan et al., 2015). In the literature, statistical techniques, sensitivity analyses, Taylor series approximation, Monte Carlo simulation, numerical estimation, and probability distributions are the most commonly used methods for UQ (e.g., Cox & Baybutt, 1981; Glimm & Sharp, 1999; Bárdossy & Fodor, 2001; Uusitalo et al., 2015; Elam & Rearden, 2017; Asheghi et al., 2020). However, when using these techniques for value-based judgements, all sources of uncertainty may not be quantifiable (Morgan & Henrion, 1990). The taxonomy of different methods applied to UQ are given in Figure 1.

Figure 1
figure 1

Taxonomy of UQ methods

Full size image

In statistical techniques, UQ is based usually on the estimated variance and determined confidence limits by assuming normally distributed error (e.g., Eisenhart et al., 1983; Cacuci & Ionescu-Bujor, 2004; Jiang et al., 2018; Zhang et al., 2020). Because quantification is most often based on statistical indices (e.g., mean, median, population quantiles) due to limited sample size, estimations must be provided with the associated confidence intervals (Geffray et al., 2019). Therefore, due to underlying foundations, such as measurement errors, material properties, unknown design demand models, and stochastic environments, the applicability of statistical techniques is limited (Taper & Ponciano, 2016). The Taylor series approximation can be used to determine theoretical error bounds but is very complex to derive and it tends to increase quickly the risk of error (Barrio et al., 2011). Monte Carlo is applied mainly to explain the probability density function but it is a complex process and requires several simulations and computational resources when the dataset is large. Therefore, it only provides statistical estimates of results, not exact figures (Atanassov & Dimov, 2008). Results of numerical methods of UQ, which are simulated by computer codes, inherently involve error or uncertainty. Such drawbacks can be addressed in part by defining the error magnitude or bound the error in a given simulation (Freitas, 2002). By using probability distributions, accurate information on the uncertainty can be achieved, but infinite extension along either side of the most probable region creates a sophisticated situation that is difficult to interpret (Kabir et al., 2018). Moreover, quantitative measures may bias the description of uncertainty towards the more computational components of the assessment (Bárdossy & Fodor, 2001). Therefore, the concepts and methods used for UQ make it difficult to communicate the results effectively. This implies that the analysis for UQ through ensemble methods is one of the main benchmarks to assess the performance of complex systems (Vrugt & Robinson, 2007; Zhang et al., 2021), especially in geo-engineering and GWT predictive modeling, which often suffer from inadequate experimental or data (e.g., Whitman, 2000; Wu & Zeng, 2013; Sepulveda & Doherty, 2015; Huber, 2016; Li et al., 2018; Chahbaz et al., 2019). Furthermore, computing the contribution of each error component on total uncertainty is difficult and it leads to extreme weighting schemes with applicability that is often questionable. Therefore, no unified applicable methodology exists for combining uncertainties. Because these methods typically yield an estimate of the total variance of measurement values, reliance on statistical variance can produce misleading results that are not readily applicable (e.g., Goodman, 1960; Yager, 1996; Borgonovo, 2006; Farrance & Frenkel, 2012).

Due to the revolution of different types of AITs in recent years, and deep neural networks (DNNs) in particular, these mechanisms have shown impressive state-of-the-art performance on a wide variety of engineering tasks dealing with challenging scientific data analysis and UQ problems (e.g., Vrugt & Robinson, 2007; Chahbaz et al., 2019; Abbaszadeh et al., 2020; Hernandez & Lopez, 2020). However, despite the rapid emergence of AIT and the subsequent DNN-based UQ (e.g., Krzywinski & Altman, 2013; Gal & Ghahramani, 2016; Zhu et al., 2019), the performance of these methods may suffer from a series of shortcomings, such as complexities arising from topology and hyperparameter choices (Asheghi et al., 2020), computational cost for multiple trainings, and weak performance due to model instabilities (Foong et al., 2019). Moreover, because DNNs tend to produce overconfident predictions, accurate outcome, especially in out-of-domain data, is an important issue (Loquerico et al., 2020; Klotz et al., 2021). Moreover, current DNN-based methods of UQ, such as Monte Carlo dropout (MCD) (Gal & Ghahramani, 2016) or quantile regression (QR) (Weerts et al., 2011), behave differently at training and inference time due to implemented changes in topology and optimization processes.

When using the MCD, UQ is performed through a set of trained topologies, which are subjected to randomly removed neurons, while in the QR, UQ is based on a conditional quantile of a dependent variable without assuming any specific conditional distribution. However, these methods typically ignore prior knowledge about the data and consequently tend to make assumptions that lead to oversimplification and thus underestimate uncertainty (Waldmann, 2018). Such concerns imply that developing new schemes or approaches to present robust UQ is still a crucial challenge with a tremendous potential for application in complex geo-engineering problems, particularly for GWT pattern modeling.

In Sweden, the GWT is an important part of sustainable ecosystems and for human water consumption. However, the GWT pattern can be affected by geo-engineering projects in combination with changes in the natural variability and the climate. Due to the significant benefits offered by an adequately accurate predictive model and the approved efficiency of AIT in providing more precise solution than many simulation processes, this paper addresses and then examines a new approach of systematic analysis for UQ through the development of an automated procedure.

Therefore, a novel state-of-the-art ensemble automated random deactivating connective weights approach (ARDCW) is proposed herein. In this framework, instead of dropping neurons, the connective weights between layers of the identified optimum topology are deactivated randomly. To overcome the problem of overfitting and to avoid being trapped in local minima, the ARDCW uses several embedded internal and nested loops to monitor all the topologies based on different hyperparameters. This approach was then applied experimentally to 244 sets of GWT geolocation data in an urbanized area of Stockholm. Due to the use of the optimum topology, ARDCW led to a state-of-the-art performance of UQ whereby the produced multiple predictions can be interpreted in terms of average errors. In comparison to other methodologies such as MCD and QR, the evaluated and compared performance of ARDCW showed superior capability in the spatial prediction of GWT.

Study Area and Data Source

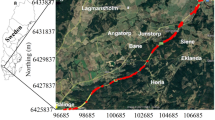
The study area, which contained 357 investigated GWT wells, encompasses 20 km of an ongoing highway project in south Stockholm, Sweden. Among the monitored GWT data, 244 points were screened and compiled from continuous recorded intervals from 19 to 25 September 2020. The location of the study area with respect to the generated long-term map of spatial monitored GWTs for the entirety of Sweden is presented in Figure 2a, which was retrieved from Geological Survey of Sweden. As shown in Figure 2b, in the northwest of the study area, Mälaren Lake controls the GWT toward the downstream, while the coverage in the northeast consists of bedrock outcrop incorporated with intermediate soil-filled valleys. This implies that the topographical variation in the surface of the bedrock dominantly controls the groundwater flows. The GWT in the high terrain Masmo hills, located in the middle of the study area (Fig. 2b), mostly follows the surface topography, but without connecting to any nearby aquifers. To the southwest (Fig. 2b), homogenous bedrock and a uniform GWT pattern can be observed. However, in the southeast of study area, the bedrock is highly heterogenic without uniform GWT levels due to the influence of cracking on hydraulic connectivity. An integrated spatial distribution of groundwater aquifers with the GWT data over the entire study area is presented in Figure 2c.

Figure 2
figure 2

(a) Distribution of GWT in Sweden. (b) Digital elevation map overlaid on a satellite image of the study area. c Mapped aquifers and monitored GWT data in the area. (a) and (c) were retrieved from Geological Survey of Sweden

Full size image

A Summary of UQ Analysis Using AIT

UQ, as one of the main challenges in AIT, needs extensive exploration. However, currently, the focus is often on giving a best estimate as defined by a loss function. Referring to Figure 1, Bayesian techniques (MacKay, 1992) are the main AIT-based framework for UQ. However, they are often computationally slow and difficult to train because they are traditionally formalized through parametric probability distributions of network activations and weights (Hernandez-Lobato & Adams, 2015). Sampling technique (Gal & Ghahramani, 2016) is another method used for UQ, but due to inability, explicitly modeling generates overconfident predictions (Hernandez & Lopez, 2020). Because an input with large noise provides wider model uncertainty than the same input with lower noise, the risk of underestimated uncertainties is increased because sampling-based methods generally disregard the relationship between data and model uncertainty (Bárdossy & Fodor, 2001; Gal & Ghahramani, 2016; Kabir et al., 2018).

Despite the significant performance of the Markov chain Monte Carlo (MCMC) in UQ, it is mostly appropriate for small networks and thus computationally expensive for large DNNs (Quinonero-Candela et al., 2006). However, this shortcoming can be overcome using stochastic gradient MCMC (Chen et al., 2014), which only needs to estimate the gradient on small sets of mini batches. Because MCMC requires a significant amount of time to converge on a desired distribution, the sufficient number of iterations is unknown (Neal, 2012). Therefore, to provide a relatively faster approximate Bayesian solution, different methods such as variational inferences, assumed density filtering, expectation propagation and the stochastic gradient Langevin diffusion technique have been introduced (Lakshminarayanan et al., 2017). However, the posterior UQ in the variational method is typically underestimated rather than overestimated in the expectation propagation technique.

QR is a type of powerful regression analysis that estimates the conditional median (or other quantiles) of the response predicted values, where the quantile itself is a parameter for the loss function. This implies that for each quantile, the training process should be analyzed through individual asymmetric weighting (Yang et al., 2016). Accordingly, a trained model, when subjected to different quantiles, generates different bounds that picks out the conditional quantiles away from the median, that is, the 95% prediction intervals can be found when subjected to the quantiles 0.025 and 0.975. The mean square error, as the most commonly used loss function, would then correspond to the Gaussian distribution. Accordingly, the mode (peak) of this distribution corresponds to the mean parameter, and DNNs predict the mean value of the output, which may have been noisy in the training set. Moreover, the dependency of the quality of prediction on computational complexity, degree of approximation and correctness of the prior distribution implies that UQ using these methods cannot be guaranteed to provide underlying beliefs (Hirschefeld et al., 2020).

UQ can be performed using ensemble-based methods, whereby inputs are trained and passed through multiple networks (Fig. 3a). Greater accuracy can be achieved by using such methods than any individual model because the predictions vary across multiple runs of a set of models M = {M1, M2, …, Mn} rather than training a single Mi. However, the primary drawback of any ensemble-based method of UQ is the increased training time, depending on the size of the ensembles. As presented in Figure 3, in addition to ensemble methods, the UQ can be based on mean–variance, distance-based strategies and union-based strategies (Angiulli & Fassetti, 2020; Hirschefeld et al., 2020; Zhang et al., 2020). The problem with training Bayesian neural networks for large data sets can be solved by using mean–variance estimation, where the output layer is modified and trained using a negative log likelihood loss to predict both the mean and variance of the interested input (Hirschefeld et al., 2020). Through distance-based methods, the minimum distance between each interested prediction from its nearest neighbors in the training set is interpreted as uncertainty. The larger the distance between the training sets and predictions, the higher the error and thus the greater the uncertainty (Angiulli & Fassetti, 2020). However, significant sensitivity of the calculated distance to outliers is the major drawback of this estimator in UQ. The union-based method (Huang et al., 2015) is a combined confidence estimator, where the output of the trained neural network is fed to another model to provide an ensemble model and thus calculate uncertainty into the task-specific latent space.

Figure 3
figure 3

Simplified schematic of different strategies for UQ: (a) ensemble-based, (b) distance-based, (c) mean variance and (d) union-based. PE = predicted error. PV = predicted variance

Full size image

The MCD (Gal & Ghahramani, 2016) is one of the most widely used methods for UQ and it can even be implemented on an already trained model. In this procedure, any trained topology with dropouts is used to prevent overfitting and can thus be interpreted as an approximate inference of the posterior weights. Accordingly, the average of multiple predictions for the analysis of distributions is considered to calculate meaningful variance. In a fixed topology during the MCD process, all in/out connective weights and biases of dropped neurons are ignored. This implies that in each dropout, the data are trained using a different topology, while none of these connectives participate in the prediction process nor will they be updated. Therefore, the dependency of UQ on the dropped neuron and internal hyperparameters is the main drawback of MCD. Moreover, due to the training of several topologies, the produced approximations can be categorized in ensemble techniques, which significantly enable improved overall performance (Dietterich, 2000). In comparison to the Bayesian approach (MacKay, 1992), which attempts to average and thus find the single best model (or parameters), ensembles combine the topologies to obtain a more powerful model. Therefore, ensembles potentially provide a complementary source for predictive UQ. Referring to Figure 4, UQ through the MCD is performed over multiple networks at the test time, where a model with n neuron can provide a collection of 2n possible topologies as an ensemble combination (Srivastava et al., 2014).

Figure 4
figure 4

Overview of MCD modeling process mimicking ensemble-based method (highlighted and dash lines correspond to dropped neurons and weights)

Full size image

Proposed UQ Approach

In recent years, UQ using different AITs has increased because the provided models can offer simple but precise solutions in many engineering simulation problems. Systematic UQ can be applied by considering a combination of several components, including data, model structure and parameter values. This implies that UQ should be conceptualized in a concrete mathematical sense and thus be amenable for programming. Because noise will be produced in each random dropping, which will affect results, therefore, mathematically, the performance and predictability of the DNN structure should always be evaluated with the original optimum model. By using the dropout concept integrated with the optimum topology, the ensemble automated random deactivating connective weights (ARDCW) approach was proposed. The ARDCW is focused solely on randomly switched off weights, not neurons, where the remaining weights are forced to participate in learning processes and assist in decreasing the overfitting. Accordingly, this approach uses an optimum trained topology capable of performing a given task even when the weights are randomly sampled. This implies that the training of multiple different topologies is avoided, as the uncertainty will be estimated by changing the internal assigned weights of a fixed optimum model.

In a DNN topology, all m neurons of a layer are associated with probability p, otherwise they are dropped (set to zero), with probability 1- p (Hinton et al., 2012). According to probability theory, the expected value of a random variable (E[X]) is a generalization of the weighted average with probabilities of pi as:

$$E\left[X\right]=\sum_{i=1}^{n}{x}_{i}{p}_{i} \;\mathrm{where} \; \sum_{i=1}^{n}{p}_{i}=1$$
(1)

Mathematically, for a constant random variable, E[X = c] = c. Therefore, E[X] with equiprobable outcomes {c1, c2, …, cn} expresses the arithmetic mean of the terms with probabilities P(X = ci). Using this concept, the impact of dropped weights (ŵij) in UQ can be described with mean field theory (Kadanoff, 2009) as:

$$\hat{w} _{ij}=\left\{\begin{array}{c}{w}_{ij \;{\rm with}\; p(c)}\\ 0 \;{\rm otherwise}\end{array}\right.$$
(2)

where P(c) denotes the probability of keeping a weight, whereby the implemented neurons are kept with the probability p and otherwise will drop (0) with probability 1-p. This implies that the UQ can be generalized by dropping the connective weights with probability 1-p rather than the neurons (Wan et al., 2013). Consequently, in a topology with h hidden layers, where Z(l) and y(l) denote the vector of inputs into and output from layer l ϵ {1, 2, …, h}, the feed-forward process is described as:

$${z}_{i}^{(l+1)}={w}_{i}^{(l+1)}{y}^{l}+{b}_{i}^{(l+1)}$$
(3)
$${y}_{i}^{(l+1)}=f\left({z}_{i}^{(l+1)}\right)$$
(4)

where \({w}_{i}^{(l+1)}\), \({b}_{i}^{(l+1)}\) and f denote the weight, bias and applied activation function, respectively. Referring to neural network topology, the activity of dropout weight of the ith neuron in hth hidden layer (\({a}_{i}^{h}\)), and consequently the corresponding output (\({O}_{i}^{h}\)), can be expressed as:

$${a}_{i}^{h}=\sum_{l<h}{\sum }_{j}{w}_{ij}^{hl}{{\delta }_{ij}^{l}a}_{j}^{l} \;\mathrm{with} \;{a}_{j}^{0}={X}_{j}$$
(5)
$${O}_{i}^{h}=f\left({a}_{i}^{h}\right)=f\left(\sum_{X<h}{\sum }_{j}{w}_{ij}^{hl}{{\delta }_{ij}^{l}a}_{j}^{l}\right) \;\mathrm{with} \;{O}_{j}^{0}={X}_{j}$$
(6)

where \({\delta }_{ij}^{l}\) is a gating 0-1 Bernoulli variable with P(\({\delta }_{ij}^{l}\)=1) = \({p}_{j}^{l}\). Therefore, in dropout, the output of layer l using element-wise product (*) is then presented as:

$${z}_{i}^{(l+1)}={w}_{i}^{(l+1)}\left({p}_{i}^{l}*{y}^{l}\right)+{b}_{i}^{(l+1)}$$
(7)

Accordingly, the expectation of the activity of all neurons for a fixed input vector taken over all possible \({\delta }_{ij}^{l}\) variables, and thus the possible ensemble models, can be achieved as:

$${E(a}_{i}^{h})=\sum_{l<h}{\sum }_{j}{w}_{ij}^{hl}{{p}_{j}^{l}E(a}_{j}^{l}) \;\mathrm{for} \;h>0$$
(8)

The dropout is not applied on a fixed input that produces a constant output in the lth layer (\({O}_{j}^{l}\)); thus, the dropout on the hth hidden layer is then presented as:

$$Var\left({a}_{i}^{h}\right)=\sum_{l<h}{\left({w}_{ij}^{hl}\right)}^{2}{\left({O}_{j}^{l}\right)}^{2}{p}_{j}^{l}(1-{p}_{j}^{l})$$
(9)

where Var is the variance. Therefore, the expectation of dropout gradient as a random variable is the regularized ensemble error associated with all possible models (Eens) and is expressed as:

$$E\left( {\frac{{\partial E_{D} }}{{\partial w_{i} }}} \right) = \frac{{\overbrace {{\partial (0.5(t - \sum\nolimits_{{i = 1}}^{n} {p_{i} w_{i} X_{i} } )^{2} )}}^{{{\text{regularized}}\;E_{{{\text{ens}}}} }}}}{{\partial w_{i} }} + w_{i} p_{i} (1 - p_{i} )X_{i}^{2} \frac{{\overbrace {{\partial (0.5(t - \sum\nolimits_{{i = 1}}^{n} {p_{i} w_{i} X_{i} } )^{2} )}}^{{{\text{regularized}}\;E_{{{\text{ens}}}} }}}}{{\partial w_{i} }} + w_{i} X_{i}^{2} Var(\delta _{i} )$$
(10)
$$E[\mathrm{dropout gradient}]={E}_{ens}+0.5\sum_{i=1}^{n}{w}_{i}^{2}{X}_{i}^{2}Var({\delta }_{i})$$
(11)

where t is the target value of input Xj and ED denotes the error of the network with dropout. With recourse to Eqs. 8 and 11, additional layers corresponding to real-valued output for error or variance can be attached to the optimum topology. This implies producing a multi-objective model, where the output of error and variance are also predicted using the same fixed optimum DNN with an added layer(s).

Referring to presented block procedure of the proposed ARDCW (Fig. 5), it does not require any changes in optimum topology and thus can even be used for already trained models. In this process, the optimum topology was captured through the proposed automated strategy by Abbaszadeh et al. (2021b). The performance of the optimum model is then monitored through the randomly sampled deactivated weights using an automated dropout procedure for the achieved database. Since all deactivations occur for the one optimum topology, the ARDCW captures different models and, as shown in Figure 3a, it can be interpreted as an ensemble-based Bayesian approximation of the Gaussian process probabilistic model. Accordingly, the inadvertent tuning on the model is addressed through a regularization strategy, which needs a robust implementation that accounts for floating-point stability and reproducibility in geo-engineering-related problems. The minimum number of sampled weights in this study is 1, while the maximum number of desired droppings was set at 50% of the whole connective weights. Although selecting this rate for dropout is flexible and user defined, the dependency on the topology and network type (shallow or deep) that overfits the training data should be considered. Moreover, the greater the number of deactivations, the more examined ensembles, which thus requires more analysis time.

Figure 5
figure 5

Block diagram of the proposed ARDCW approach for UQ modeling (n: number of weights, Wi: weight components, J: number of models, m: number of randomly sampled weights)

Full size image

As an advantage, in each examination, the model is trained using a constant topology but with a different set of randomly deactivated weights in the layers. Therefore, the outcome can be considered as an averaging ensemble of many different models trained on one batch of data only. The ARDCW can be regularized to calculate the mean and variance of randomized data and can then predict unlabeled data. Moreover, using the optimum model will minimize the problem of overfitting, while the overall performance of the DNN topology due to randomly switched off weights in each layer becomes less sensitive.

Results of Experimental Application

The randomization process increases the predictability skill of system in training and dedicate more generalize findings. It then leads to more powerful developed predictive systems in evaluating the unseen data. This implies that, through random shuffling, the chances of last few batches being disproportionately noisy will reduce. Because there are no special rules in percentage of randomizations, 65, 20 and 15% for training, testing and validation were used (e.g., Xu & Goodacre, 2018; Ghaderi et al., 2019). In configuring the optimum model, the regularization and tuning of hyperparameters (e.g., training algorithm, number neurons, layer arrangements, learning rate, activation function and architecture) played a significant rule to overcome trapping in local minima, overfitting and early convergence. Therefore, the automated approach proposed by Abbaszadeh et al. (2021a) as presented in Figure 5 was employed to capture the optimum model. This system using several inner nested loops integrated with constructive technique can automatically monitor the different combinations of hyperparameters and thus provide faster learning procedure. According to Figure 5, by applying 65% of the 244 compiled GWT data, a 3-32-8 topology subjected to hyperbolic tangent activation function trained with quasi-Newton algorithm was considered as the optimum, which was then retrained using two extra predicted outputs, including the error and variance. Considering the y and ŷ as the target and model output, respectively, the error and variance were predicted through (y − ŷ) and (y − ŷ)2. Referring to Figure 4, a series of models was retrained using the updated dropout weights database (Fig. 5) subjected to the fixed defined custom loss function in optimum topology for each mini batch. To visualize the range of predicted distribution, the results of the randomly deactivated weight using K-fold validation for a series of dropout test sets are presented in Figures 6 and 7. Accordingly, Figure 6a shows the variation of the predicted GWT from all the K-fold validations using ARDCW, and uncertainties at each point can be estimated from these outcomes. Subsequently, the errors between the observed and predicted GWT in each K-fold validation are reflected in Figure 6b, which shows high error values and thus high uncertainties at data points. Figure 6c depicts the variance of errors as described where uncertainties are high. According to these outcomes, PE and PV derived from UQ, when subjected to different random dropouts are more preferred due to lower variance estimators. Proper experimental measurement associated with an estimated level of confidence not only allows a scientific hypothesis to be confirmed or refuted, but also facilitates the judgments on the quality of the data and leads to meaningful comparisons with other similar values or predictive models. Accordingly, 95% prediction interval (PI), which is often used in regression analysis, shows the certain probability of an estimation of future observation (Fig. 8).

Figure 6
figure 6

Predictability of the optimum model subjected to applied dropouts in training and testing stages for GWT (a) data, (b) mean and (c) variance

Full size image
Figure 7
figure 7

Comparison of distributions of optimum and dropout models for (a) training and (b) testing data sets

Full size image
Figure 8
figure 8

Calculated PI using the optimum model for GWT (a) data, (b) predicted mean and (c) predicted variance

Full size image

Due to the dynamic nature of areas without data, creating a 3D visual perspective depicting the predictive spatial distribution of the GWT levels is a challenging task, but this can provide more utility in interpreting the subsurface characterization (Abbaszadeh et al., 2020, 2021a). However, the level of accuracy and the confidence of the model can vary depending on the quality of available data and the approach. This is the reason why pseudo data can therefore play an important role in building knowledge for unsampled locations (Tacher et al., 2006; Cruzes & Dyba, 2011; Abbaszadeh Shahri et al., 2020). Figure 9 shows the step-by-step creation of the 3D model of the study area depicting the retrieved outlines of the uncertainties. In this process, the produced digital elevation model of the area (Fig. 9a) was incorporated with the 3D spatial distribution of acquired GWT (Fig. 9b) and corresponding results of the automated predictive optimum topology (Fig. 9c). The estimated uncertainties of the optimum topology in the level of 95% using the proposed ARDCW were then added (Fig. 9d, e). Referring to the estimated uncertainties, more comprehensive spatial GWT patterns can be realized to avoid the relevant risk of facing aquifers during geo-engineering projects. Due to the ease of updating with new data, the flexibility of such models provides a preferred tool for geo-engineers and decision planners in the observation and analysis of geo-environmental engineering issues within a project.

Figure 9
figure 9

Incorporating results of predictive optimum topology and the proposed ARDCW in visualizing the estimated uncertainty: (a) surface of the area, (b) measured GWT, (c) predicted GWT, (d) upper and lower limits of estimated uncertainties, and (e) overlay of supplementary perspective for the entire study area

Full size image

Discussion and Validation

Predictive AIT-based models are indispensable tools in geo-engineering applications, not only to ensure the function in labeled variables but also to estimate uncertainty in unlabeled data. In recent years, several studies have been dedicated to the importance of UQ in GWT modeling and decision-making at different scales (WWAP, 2012; Middlemis & Peeters, 2018). However, from geo-engineering point of view, each parameter of a geologic object can be a source of uncertainty and, thus, in practice, the number of involved sources can be innumerable. To evaluate the robustness and accuracy of the predictive spatial pattern of GWT, UQ is often required. Because standard AIT-based procedures of UQ are still limited, developing an efficient method that uses DNN predictive models in particular is of great interest for industrial-scale and real-world applications. In the current paper, the presented UQ approach, ARDCW, is discussed and validated using contour maps of predicted error in different dropouts, accuracy metrics and success rate, and by comparison with MCD and QR.

Effects of Dropout on Estimated Uncertainty

This concern was monitored by comparing variations of captured distributions in post and prior predictions with respect to the optimum topology. These variations are referred to in the ARDCW by using the saved updated database for each examined model (Fig. 5). The comparison of different post distributions and the corresponding residual contour map of the area are given in Figure 10 to show how the dropped weights can influence on the variation of the captured functions in the optimum topology. Therefore, the uncertainty of the optimum model can be evaluated through the sampled weights, where each plot depicts a single draw from the prior functions. Accordingly, multiple repetition of ARDCW can inspire an idea of the prior functions and weight matrices over the fed inputs, which help to find a function to fit variational objective data with the minimum penalty with respect to the prior distribution in the optimum model. This implies that in case of a lack of observations, the uncertainty can be interpreted through the interpolation of unlabeled predictions.

Figure 10
figure 10

Contour maps of residuals for different results of ARDCW

Full size image

Uncertainty is generally evaluated from data and models due to the presence of noise and an imbalanced training data distribution (Loquerico et al., 2020). In AIT-based models, the source of uncertainty occurs when the feed data are mismatched, where smaller differences between the observed GWT and those predicted by ARDCW show a higher degree of safety in the prediction process (Fig. 11a, b). Subsequently, stronger differences can be interpreted as higher uncertainties in prediction. Accordingly, the performance of the optimum and examined GWT models using ARDCW, as well as error for the measured and unlabeled prediction datasets, are given in Figure 11c and d.

Figure 11
figure 11

Variations of predicted GWT and error for (a), (c) validation data and (b), (d) unlabeled data

Full size image

Comparing Different Uncertainty Models

Statistical Metrics

The coefficient of efficiency (Ec) (Nash & Sutcliffe, 1970) is one of the most widely used metrics for evaluating the performance of hydrologic models, thus:

$${E}_{c}=1.0-\frac{\sum_{i=1}^{N}{\left({O}_{i}-{P}_{i}\right)}^{2}}{\sum_{i=1}^{N}{\left({O}_{i}-\overline{O }\right)}^{2}}\; \overline{O }: \mathrm{observed} \mathrm{mean}$$
(12)

where N is the total number of GWT data, Oi and Pi denote observed and predicted data, Ecϵ is interval (− ∞, 1.0] in which the value of 1.0 expresses perfect fit. Ec = 0 reflects large variability in the observed data, while Ec < 0 indicates that the \(\overline{O }\) would have been a better predictor than the model. Further, Ec is the ratio of mean square error (MSE), thus:

$$MSE={N}^{-1}\sum_{i=1}^{N}{\left({O}_{i}-{P}_{i}\right)}^{2}$$
(13)

Therefore, Ec represents an improvement over the coefficient of determination for model evaluation purposes in that it is sensitive to differences in the observed and model simulated means and variance (Leavesley et al., 1983; Wilcox et al., 1990).

To cover the lack and insensitivity of Ec and R2 in considering the calculated square differences between the observed and predicted means and variances (Legates & McCabe, 1999), the index of agreement (Willmott, 1984), which is the ratio of mean square and potential errors is defined as:

$$IA=1-\frac{\sum_{i=1}^{N}{\left({O}_{i}-{P}_{i}\right)}^{2}}{\sum_{i=1}^{N}{\left(\left|{P}_{i}-\overline{O }\right|-\left|{P}_{i}-\overline{O }\right|\right)}^{2}}$$
(14)

The percentage of observed GWT (NGWT) bracketed by confidence interval (CI) in the 95% level (\({P}_{CI}^{95\%}\)) is defined as:

$${P}_{CI}^{95\%}=\frac{{N}_{GWT}}{N}\times 100$$
(15)

whereby the properly modeled uncertainty is justified based on the closeness to 100%.

Referring to Jin et al. (2010), the quality of the predicted uncertainty can be assessed using the average relative interval of the CI (ARIL), thus:

$${ARIL}_{CI}^{\%95}=\frac{1}{n}\sum_{i}^{n}\frac{{UCL}_{pred, i}^{GWT}-{LCL}_{pred, i}^{GWT}}{{GWT}_{i}^{obs}}$$
(16)

where \({UCL}_{pred, i}^{GWT}\) and \({LCL}_{pred, i}^{GWT}\) express the calculated upper and lower CI of the ith predicted GWT, and n is the number of total observations; thus, a lower \({ARIL}_{CI}^{\%95}\) value represents better performance.

A comparison of the above indices in evaluating the predicted uncertainty using three different methods, namely ARDCW, QR and MCD, is given in Figure 12 and Table 1. Referring to \({P}_{CI}^{95\%}\), although both ARDCW and QR showed competitive coverages of the true GWT levels (95%) with respect to MCD (68%), the ranking score of ARDCW was superior to those of the other methods. The closeness statistics of the ARDCW and QR methods can be interpreted as similar properties of posterior distribution of predicted GWT for these methods.

Table 1 Comparison and rankings of the UQ models through statistical metrics
Full size table
Fig. 12
figure 12

Comparison of \({P}_{CI}^{95\%}\) of the three models based on the validation dataset

Full size image

Success Rate Using Confusion Matrix

A confusion matrix can intuitively describe the performance of a model based on a set of data using the true labeled instances (Asheghi et al., 2019). This concept conceptualizes the error probabilities of developed models in assigning the individual predicted outputs into the classified input. The best performance is defined by zeroes, except on diagonals. Referring to obtained confusion matrix (Table 2), ARDCW and QR methods provide more true predicted instances (33 and 29 out of 37) compared to MCD. As presented in Table 3, the performance of ARDCW in terms of classification accuracy and misclassification error at an 89% correct classification showed 22 and 14% improvement in estimated uncertainty over those by MCD and QR, respectively.

Table 2 Comparison of success rates of different UQ methods for GWT data
Full size table
Table 3 Improvement of ARDCW in UQ compared to MCD and QR
Full size table

Uncertainty Intervals in Studied Area

Sufficiently accurate modeling procedures are essential tools in subsurface geo-engineering disciplines to reflect fidelity between the real and counterparts. However, despite enhanced computational power, different sources such as modeling errors in describing the real system, numerical errors generated by mathematical equations, and data errors caused by uncertainties can cause the appearance of differences. A critical part of prediction is assessment of how much a predicted value will fluctuate due to noise or variations in the data. Figure 13 shows the 95% uncertainty intervals estimated using ARDCW for the studied area. It can provide the distribution of different uncertainty levels and it gives an indication of the reason for high uncertainties; for example, if uncertainty arises from lack of observed data or from sudden big changes in the groundwater levels. This map can also help in the planning of future data collection and determining where to drill more groundwater boreholes to reduce high uncertainties in estimating the groundwater surface.

Figure 13
figure 13

Estimated uncertainty intervals using GWT data (black dots) in the entirety of the study area

Full size image

Comparison of CI and PI

Due to the dynamic nature and time-dependent behavior, the exact modeling of GWT problems is a complex issue to resolve. The time-dependent GWT data points over an interval can benefit from outlier removal to present an overall perspective of variation in the study area as well as a better analysis and understanding and thus uncover patterns in datasets for future forecasting (Shumway, 1988; Keogh & Kasetty, 2003). However, the problems regarding generalization from a single study, difficulty in obtaining appropriate measures, and accurately identifying the correct model to represent the data should be considered.

Therefore, the bias and discrepancy of the applied models can be interpreted through comparison of the estimated uncertainty. Statistically, a predictive model is stable and under control if most of the predictions fall within the range of the CI. This range refers to the long-term success rate of the method in capturing the predicted output, whereby the wider the CI, the greater the instability. The CI level of 95% reflects a range of values where 5% can contain the false mean of the population. Due to lack of knowledge, observation error (variability of experimental measurements) and the underlying physics in GWT problems, such a comparison (Fig. 14) can show how accurately a mathematical model describes the true system in a real-life situation. Mathematically, the variations in predicted uncertainty come from the adjusted model parameters and, correspondingly, the implemented algorithm as well as feed input variables whose exact values are unknown or cannot be inferred by statistical methods (Kennedy & O'Hagan, 2001). Therefore, the dimensionality of an engineering problem would cause variability in its performance, whereby the implemented algorithm can provide discrete numerical uncertainty.

Figure 14
figure 14

Comparative plots of the methods applied in UQ at 95% level for both CI and PI

Full size image

Concluding Remarks

AI-based models are becoming a standard computational and decision-making tool in civil and construction industries. However, due to inherent complexities, computational costs and poor performance, most of the AI-based methods of UQ rarely make the leap from research to production. Therefore, in this context the need for a validated coding procedure able to meet the regulatory requirements was highlighted in this paper. In order to gain insight into the predictability level of the complex AIT-based predictive subsurface geo-engineering model, an evaluation of the estimated uncertainty using simulation codes with iterative analyses is required. Moreover, because a model or method can be adjusted using a wide range of internal characteristics, subsequently presenting reliable but robust uncertainty estimates presents a significant challenge. Therefore, if AI systems could reliably identify unlabeled data, they could be deployed with a greater degree of certainty. This concern is especially vital for geo-engineering applications, where the expectation is to achieve the same distribution for observations and the training data.

In response to greater demand for DNN-based methods of UQ, the ARDCW, as a new state-of-the-art approach that applies randomly weighted components that dropout at test time, was introduced and developed. Using ARDCW, the estimated uncertainty was visualized using the average results of many ensembled predictive models derived from a demonstrated learned optimum automated DNN topology through K-fold validation and randomly deactivated weights. The issue of underestimated uncertainty, which is usually observed in most AIT-based methods of UQ, originates from changes in model and optimization process. In this point of view, the ARDCW approach does not require any changes in the topology and can be applied on already trained models. Because the ARDCW is built on a weight database, it does not have restrictions in application on time-dependent data such as GWT with sequences of seasonal fluctuations in monitored data over different intervals of the year. However, presenting a seasonal time-dependent GWT model was beyond the scope of this paper.

An experimental application of the proposed ARDCW was applied to 244 measured GWTs from a geo-engineering project in Stockholm, Sweden. The 3-32-8-1 predictive DNN topology, as the characterized optimum model, showed significant competence in comparison with MCD and QR. The results showed that due to the use of different topologies, the MCD can behave differently at training and inference time, while for assured dropout creating a custom layer with predefined training parameters for regular dropout should be employed.

Using the ARDCW, the estimated uncertainty boundaries with 95% level of CI were visualized and presented on the generated 3D predictive spatial pattern of subsurface GWT data. This cost-effective and adequately accurate tool can reflect the potential risks associated with the distributed spatial aquifers, thus preventing water inrush, or facing underground geo-structures. The validity of most analyzed GWTs with respect to both engineering and societal challenges is limited in the findings as it is often not included in uncertainty assessment. This implies that uncertainty should be estimated in many previously presented GWT models, which are intended for efficient decision support. Using the created 3D predictive model, the geospatial distribution of GWT and corresponding variations within subsurface geo-formations can be pursued. This concern can significantly influence the design of underground transport infrastructures for the city of Stockholm, where, in geo-engineering perspective the drainage of the GWT through tunnelling can cause ground settlements in the surrounding buildings. This phenomenon can be particularly problematic in weak soil/rock formations and manifest as a defective injection process. Moreover, the created model can decrease the risk of water inrush from excavation. By adding more geological data, the ability to recognize swelling clayey material which is a major threat in tunnelling projects can also be achieved. This implies that the presented GWT model is an indispensable tool for decision makers in urban development projects (e.g., building detached homes, roads, railways and bridges), where substantial land surface processes can be imposed.