Introduction

Magnetically targeted drugs (MTD) are a method for orienting and delivering drugs to a specific target using an external magnetic field produced by a permanent magnet [1,2,3,4,5,6]. The idea of magnetically targeted drugs arose from the use of erythrocytes loaded with magnetic particles or magnetic microspheres as carriers [7]. Studies, such as the one presented by Senyei et al. [7], have indicated the need for a systemic dose that is 100 times lower than the non-target drug in order to achieve the same local concentration in the tumor tissue. Experimental studies in animals and preclinical studies in human patients have shown promising results for the future [8, 9].

Fig. 1
figure 1

Diagram of NP Transport in Blood Vessel

Full size image

MDT techniques are advancing due to the rapid progress in the growth of functionalized magnetic nanoparticles, which are used in chemotherapy, radiotherapy, and gene therapy directly in the tumor [2, 10, 11]. They also have the potential for combined therapy, where they can be used with multiple drugs and types of therapy such as hyperthermia [12], radiotherapy, photodynamic therapy [13], and chemoembolization (where blood flow to a certain part of the body is interrupted) [14]. Various studies have shown that MDT is a relatively safe and effective method for directing drugs to specific sites [14]. This technique can significantly increase the specificity of certain medical treatments.

Due to the difficulty of real-time control over the trajectory of magnetic nanoparticles in the bloodstream, it is necessary to characterize the trajectories using analytical and computational methods. Several works have been developed with this approach. Simulations of particle movement in the bifurcation of the carotid artery were developed by Bharai and Vajy [15] and Palmen et al. [16], where significant potential was found for their application in the treatment of arteriosclerosis [11, 17]. Havekort et al. studied the left coronary and the carotid arteries, finding the efficiency of particle capture favorable. The simulation showed that approximately a quarter of the inserted 4 \(\mu m\) particles are captured by the blood flow of the left coronary artery when the magnetic field is located at a distance of 4.25 cm, and if the distance is changed to 1 cm, all particles are captured by the magnetic field [18].

Simulation studies of NP-red blood cell interactions in capillaries of 11 \(\mu m\) and 20 \(\mu m\), as well as NPs ranging from 10 to 200 nm, have revealed that the increased dispersion of NPs and their binding to red blood cells is not solely due to a volume exclusion effect. The rate of NP binding is higher when mixed with red blood cells at the same dose and concentration compared to when NPs are in pure form. This is because of the higher concentration of NPs near the vessel wall, indicating that NPs originally located in the center of blood vessels migrate toward the edge during collisions with red blood cells. The rotational motion of red blood cells enhances the dispersion of NPs [19]. Riaño et al. developed a kinetic model of the interaction between NPs and a red blood cell (RC) that considered an elastic collision. They calculated the scattering angle as a function of the impact parameter with respect to the symmetry axis of the RC. They found that in frontal collisions with values close to the center of the symmetry axis, the NP follows the same incident trajectory, with a zero scattering angle [20]. On the other hand, Roa et al. demonstrated in [21] how different phases of the blood pulse modify the trajectories of NPs through molecular dynamics.

Despite the different advances, there is still a lack of understanding about the dynamics of NPs. In this work, the targeting efficiency of magnetic NPs subjected to a constant magnetic field was estimated by simulating the interaction processes of NPs with the hemodynamic system using the finite element technique.

Methods

The topology of the blood vessels surrounding a breast cancer tumor was determined using the lighting adjustment technique. The mammograms were obtained from the publicly available database of the University of South Florida, USA. Based on this, a 3D model was developed, which served as the basis for modeling the blood vessels [22].

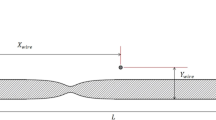
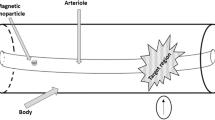
The magnetic NPs were simulated to be injected into the blood vessel in the direction of flow (direction of the blood vessel that irrigates the tumor in the breast, in the \({\textbf {z}}\) -direction) and directed by the application of a constant external magnetic field generated by a cylindrical magnet placed outside the body at a distance \({\textbf {d}}\) that will be estimated as the object of study of this article. The magnet is oriented perpendicular to the blood flow direction (in the \(\varrho \) - direction). Figure 1 shows the diagram of the transport of NPs, with blood vessels assumed to be cylindrical tubes with laminar flow.

The efficiency of targeting was established as the number of NPs attracted by the magnetic field that reach the target (Eq. 1):

$$\begin{aligned} CE = \frac{\text {Number of NPs in the tumor}}{\text {Number of NPs that enter}} \times 100 \end{aligned}$$
(1)

The equation of motion for NPs in the fluid is considered as (Eq. 2)

$$\begin{aligned} \dfrac{{\textbf {d}} (\textit{m}_p {\textbf {v}})}{{\textbf {d}} t} = \overrightarrow{{\textbf {F}}}_D + \overrightarrow{{\textbf {F}}}_{m} \end{aligned}$$
(2)

where, \({\textbf {m}}_p\) is the mass of the particle, \(\varvec{v}\) is the velocity of the particle, \(\overrightarrow{{\textbf {F}}}_D\) is the drag force and \(\overrightarrow{{\textbf {F}}}_{m}\) is the magnetic force. \(\overrightarrow{{\textbf {F}}}_D\) is defined as (Eq. 3) [23]:

$$\begin{aligned} \overrightarrow{{\textbf {F}}}_D = \dfrac{1}{\tau _p} {{\textbf {m}}_p} {({\textbf {u}}- {\textbf {v}})} \end{aligned}$$
(3)

where, \(\tau _p\) is the response time of the particle velocity, \({\textbf {u}}\) s the fluid velocity, and v es la velocidad de las partículas. Taking into account that the flow is laminar, the response time of the particle velocity is (Eq. 4) [23]:

$$\begin{aligned} \tau _p = \dfrac{\rho _p {D}^{2}}{18 \eta } \end{aligned}$$
(4)

where \(\tau \) is the relaxation time for dynamic viscosity, D is the diameter of the blood vessel, and \(\rho \) is the density.

As properties of NPs, they are considered as solid spheres of \(FeO_3\), which have high magnetic susceptibility and high saturation magnetization; these particles have a density of approximately \(\rho _{p}\) = 6450 \(Kg \cdot m^{-3}\) [18] and hydrodynamic diameters of 50, 100, and 200 nm.

At the initial position, 700 particles were introduced, with input conditions including 10 particles per release, \({\textbf {q}} = {\textbf {q}}_o\), where \({\textbf {q}}\) is the position of the particle, \({\textbf {v}} = {\textbf {v}}_o\).

Magnetic force, Kelvin or magnetomotive force, causes the movement of particles towards regions where the magnetic field is stronger. The magnetophoretic force is applied to particles with neutral charge and relative permeability different from the fluid, and is given by [24]:

$$\begin{aligned} \overrightarrow{{\textbf {F}}}_{mp} = 2\pi r^{3}_p \mu _o \mu _r K \nabla \overrightarrow{{\textbf {H}}}^{2} \end{aligned}$$
(5)

where \(\vec {{\textbf {H}}}\) is the magnetic field and \(\mu _{r}\) is the relative permeability of the fluid, assumed to be 1 and K is defined as:

$$\begin{aligned} {\textbf {K}} =\dfrac{\mu _{r,p}- \mu _{r}}{\mu _{r,p} + 2\mu _{r}} \end{aligned}$$
(6)

where \(\mu _{r,p}\) is the relative permeability of the particle, assumed to be 4000.

The distribution of the magnetic field around the magnet is calculated from [25]:

$$\begin{aligned} \overrightarrow{B} = u_{0} (\overrightarrow{H} + \overrightarrow{M}) \end{aligned}$$
(7)

where \(\overrightarrow{B}\) is the magnetic flux density (T), \(\mu _{0}\) is the vacuum permeability = \(4 \pi x 10 ^{-7}NA ^{-2}\), \(\overrightarrow{H}\) is the magnetic field strength (\(A \cdot m^{-1}\)), and \(\overrightarrow{M}\) is magnetization (A/m).

$$\begin{aligned} \overrightarrow{H} = - \nabla V_{m} \end{aligned}$$
(8)
$$\begin{aligned} \nabla \cdot \overrightarrow{B} = 0 \end{aligned}$$
(9)

The magnetic force acting on the particles is expressed as [26]:

$$\begin{aligned} \overrightarrow{F}m = \mu _{0} V_{p} (\overrightarrow{M} \cdot \nabla ) \overrightarrow{H} \end{aligned}$$
(10)

\(V_{p}\)= \(\dfrac{4}{3} \pi {r}^{3}\) is the volume of the particle. The influence of the external magnetic field causes magnetic NPs to magnetize, generating a variation in their trajectory and allowing their alignment in the direction of the field [27, 28]. Equations  (11) and (12) correspond to the components of the magnetic field, where the field \(\vec {H}(\rho ,z)=H_{\rho }(\rho ,z)\hat{\rho }+H_z(\rho ,z) \hat{z}\).

$$\begin{aligned} H_{\rho }(\rho ,z)=\frac{m_m r_m^2\ }{2}\left[ \frac{\left( \rho +d\right) ^2-z^2}{\left[ \left( \rho +d\right) ^2+z^2\right] ^2}\right] \end{aligned}$$
(11)
$$\begin{aligned} H_{z}(\rho ,z)=\frac{m_m r_m^2\ }{2}\left[ \frac{2\left( \rho +d\right) z}{\left[ \left( \rho +d\right) ^2+z^2\right] ^2}\right] \end{aligned}$$
(12)

where \(H_{\rho }\) and \(H_{z}\) are the magnetic field intensity of the magnet in the \(\rho \) and z axes respectively, \(m_{m}\) is the magnetization of the magnet, \(r_{m}\) is the magnet’s radius and d is the distance between the center of the magnet and the z axis.

The motion of magnetic NPs is described by the second law of Newton as:

$$\begin{aligned} m_{p}\frac{du_{p}}{dt}=\sum {\overrightarrow{F}}_{ext} \end{aligned}$$
(13)

where \(m_p\) is the mass and \(u_{p}\) is the velocity of the magnetic particles, and \(\sum \overrightarrow{F}{ext}\) is the sum of all external forces acting on the particle. The inertial term \(m_p \dfrac{du{p}}{dt}\) is very small and can be ignored. For the magnetic field, the properties of a cylindrical superconducting magnet with a height of 100mm, thickness of 50mm and a maximum field intensity of \(\overrightarrow{B} \approx 120 mT\) were used.

One strategy to analyze fluid and particle flow is by using finite element software, such as COMSOL and ANSYS, Inc., to solve finite volumes [18, 26].

The numerical simulation requires a computational domain of arteries, blood flow, and surrounding tissue [29]. To verify the application, the simulation results are compared with the results of equal simulations that use a fluid [18]. Simulating characteristics based on fluid flow in general geometries, and implementing the model of viscosity and magnetization of particles will contribute to the design of specific treatments for each individual.

The finite element method is a numerical analysis technique used to approximate solutions to partial differential equations. The method divides a large problem into smaller parts, called finite elements. It then seeks a solution to each of the differential equations that models those small parts and assembles the solutions to model the original problem in its entirety. The use of finite element analysis allows for a more detailed representation of the object being analyzed, enables the integration of different materials, facilitates the observation of local effects, and ultimately yields a more comprehensive solution.

The equations of fluid and particle flow were solved using finite elements using COMSOL Multiphysics software (version 5.2), [24], which facilitates the steps in the process of modeling and simulating physics problems through an interface that allows combining various physical phenomena, modeling the object to be analyzed, specifying the type of physical analysis to be performed (heat transfer, electrostatics, mechanics, etc.), and enables the type of solution and visualization of results.

The blood dynamics near Newtonian flow was simulated using the finite element method implemented by the modeling tool. The generated topology was exported to COMSOL considering the initial arterial pressure as \(p = 20 Pa\) [30]. The simulation was performed in a three-dimensional computational space, with an approximation of laminar flow, as the velocity in the arterioles does not exceed 5cm/s [30]. The density was set as \(1060 Kg \cdot m^{-3}\) and the dynamic viscosity as 0.004 \(Pa \cdot s\) [31].

Essentially, the solution to a problem can be divided into three parts: first, the model description involving the definition of the geometry or object to analyze; second, the simulation process in which the model and the type of physical analysis are specified; and finally, the visualization of the results.

The model was simulated with quadratic geometric shape order, considering the magnetic field, laminar flow, and particle tracking, with the first two being stationary and the third being temporal. The degrees of freedom for the numerical convergence analysis were 293437 for the magnetic field and 46620 for the laminar flow, with 700 magnetite NPs with a density of \(\rho _{p}\) 6450 \(\mathrm {Kg \cdot m^{-3}}\), subjected to Neodymium (NdFeB) magnets with a magnetic field magnitude of 0.12 T (see Table 1), relative permeability of 4000, and then the number of NPs that reach the tumor was evaluated.

Table 1 Simulation parameters used in the analysis
Full size table
Table 2 Efficiency percentage of magnetic NPs with different distances from the magnet and different NP sizes
Full size table

Results

The results obtained from the simulation process allowed us to obtain the topology of the blood vessel and evaluate the effect of the simulated magnetic field. Without a magnetic field acting on the NPs, 47 % of them, both for 50 nm, 100 nm, and 200 nm, reach the tumor as shown in Table 2. The remaining percentage of NPs is distributed to other blood vessels that do not irrigate the tumor, as shown in Figure 2.

Fig. 2
figure 2

Trajectory of 50 nm particles when they are not subjected to a magnetic field. Time: 3200 s. Velocity magnitude (m/s)

Full size image

Next, the trajectory of the simulated NPs along the blood vessels is presented. Figure 3 shows the laminar flow.

Fig. 3
figure 3

NP trajectory

Full size image

Particles of 50 nm, 100 nm, and 200 nm exhibit similar behavior with the different distances evaluated from the magnet at 2.5 cm. In this case, the particles are attracted to the magnet, and they cluster near the wall of the blood vessel, not continuing their trajectory to the tumor, as shown in Figure 5. This could have adverse effects on the endothelial cells or even affect the blood flow at this point, as shown in Figure 4. These findings are similar to those found for 200 nm particles with a magnetic field located at 5 cm [6].

Fig. 4
figure 4

Detail of the trajectory of 50 nm particles with a magnetic field located at 2.5 cm. Time: 400 s, Magnetic field strength (T), Velocity magnitude (m/s)

Full size image

Ninety-seven percent of 50 nm particles reached the tumor with a magnetic field located at 5 and 15 cm, and 94 % when the magnetic field was at 7.5 cm from the tumor (see table 2).

For 100 nm particles, 94 % reached the tumor with a magnetic field located at 5 cm and 15 cm, and 15 cm. The targeting efficiency of these NPs is shown in Table 2.

The targeting efficiency for 200 nm particles improves with the increase in the magnet’s distance, as shown in Figure 7. When the magnet is too close, at 2.5 and 5 cm, the NPs cluster near the wall of the blood vessel. As the magnet moves further away, the targeting efficiency increases from 13 % to 94 % (Fig. 5). Figure 6 shows 200 nm particles at 7.5 cm from the magnetic field.

Fig. 5
figure 5

Trajectory of 50 nm particles with a magnetic field located at 5 cm. Time: 400 s, Magnetic field strength (T), Velocity magnitude (m/s)

Full size image
Fig. 6
figure 6

Trajectory of 200 nm NPs, magnetic field located at 7.5 cm. Time: 400 s, Magnetic field strength (T), Velocity magnitude (m/s)

Full size image

The size of NPs and the distance from the magnet play a very important role in targeting efficiency. Haverkort et al., found in simulations that approximately one quarter of 4 \(\mu m\) particles inserted can be captured from the left coronary artery bloodstream when the magnet is placed at a distance of 4.25 cm. When the same magnet is placed 1 cm away from a carotid artery, almost all of the inserted 4 \(\mu m\) particles are captured [18]. These findings suggest that for NPs of this size, capture is increased by decreasing the distance from the magnet to the tumor. Zhang et al., found that as particle size increases from 300 to 500 nm, delivery efficiency improves by nearly 9.3 % or 18.1 %, respectively [34]. In this study, NPs of 50, 100, and 200 nm were evaluated, considering that particles between 10 nm and 200 nm have higher capture by the magnetic field within the bloodstream [23].

Larimi et al., modeled the fluid flow and behavior of magnetic nanoparticles under the influence of an external magnetic field and found that the number of particles delivered to the target region decreases as nanoparticle diameter decreases [35]. In the present study, the magnetic field was kept constant and a decrease in the efficiency of particles reaching the tumor was observed for 200 nm diameter NPs when the magnet was placed at 5 and 7.5 cm from the tumor, compared to 50 and 100 nm NPs.

Furthermore, it was found that when the magnetic field was at 2.5 cm from the tumor, the NPs agglomerated on the blood vessel wall, which prevented them from reaching the tumor. This characteristic could be used in the future by employing thrombolytic agents attached to magnetic NPs to dissolve plaque deposited on arterial walls.

The study also showed that the forces created by the magnetic push at 15 cm are sufficient to move particles of 50, 100, and 200 nm in the blood vessels (Fig. 7).

Table 2 summarizes the results of the study with the sizes of NPs and distance of the magnet evaluated, which correspond to NPs of 50 nm, 100 nm, and 200 nm. Particles smaller than 50 nm are eliminated by the liver, while particles larger than 200 nm in diameter are retained in the spleen. Additionally, particles between 20 nm and 200 nm in diameter are more effectively absorbed by most non-phagocytic cells. The majority of commercially available magnetic particles approved by the Food and Drug Administration (FDA) for imaging applications are within this range of 20 to 200 nm. Particles of 100 nm can have long circulation times in the blood [36, 37].

Fig. 7
figure 7

Percentage of 200 nm NPs that reach the target with a magnetic field located at 2.5, 5, 7.5, and 15 cm from the tumor and without a magnetic field

Full size image

It should be noted that the magnitude of the force behaves inversely proportional to the distance between the magnet and the NPs, and this force is closely related to the size of the NPs. When the generated force magnetic significantly exceeds the drag force of the blood plasma, a clustering phenomenon is manifested, illustrated in Fig. 4. For example, this process occurs at a distance of 2.5 cm for all nanoparticle scales.

In addition, the size of the nanoparticles determines the magnetic force, which is cubed with respect to its diameter, following the relationship \(V = \frac{4}{3} \pi (\frac{d}{2})^3\) (see eq. 10). In this way, the clustering phenomenon is more intense in larger NPs, due to their greater amount of material. It is relevant to note that, at a separation of 15 cm between the magnet and the nanoparticles (NPs), the clustering phenomenon does not occur, regardless of the size of the NPs. In the case of 200 nm NPs, it is observed that at a distance of 7.5 cm, clustering still occurs, although not as intensely as at distances less than 5 cm.

In the scenario where the magnetic force fails to induce clustering, it is observed that the nanoparticles tend to move near the wall of the blood vessels adjacent to the tumor. In this case, the dynamics of the nanoparticles is dominated by the drag force of the blood flow, as reflected in Fig. 6. Under these circumstances, the efficiency approaches 100% as can be seen in Table 2.

Conclusion

The numerical model for the kinetics of magnetic nanoparticles (MNPs) of 50, 100, and 200 nm in size subjected to a constant magnetic field of 0.12 T was developed. The magnetic field was placed at distances of 2.5 cm, 5 cm, 7.5 cm, and 15 cm from the tumor in a breast cancer case. The results indicate that MNPs subjected to a constant magnetic field located 2.5 cm away adhere to the vessel wall, preventing NPs from reaching the target. This behavior is also observed in 200 nm nanoparticles subjected to magnetic fields located 2.5 and 5 cm away. The targeting efficiency of 200 nm magnetic nanoparticles subjected to a constant magnetic field increases when the magnet is placed 5 to 15 cm away from the tumor. In the case of 50 and 100 nm NPs, the targeting efficiency is \(> 90 \%\) when the magnet is placed at 5, 7.5, and 15 cm away from the target.

Computational simulations are a crucial tool for assessing the feasibility and practicality of magnetic drug targeting (MDT) before clinical trials. By enabling the investigation of various factors independently and for optimization, they also offer valuable insights for the design of MDT systems. Our simulation results suggest that particles ranging from microns to nanometers in size, including paramagnetic particles, can be effectively captured by cancer tumors. These findings underscore the importance of further research in MDT. Future studies should involve experimental investigations of MDT in artificial arteries to validate and confirm the results presented here.