Abstract
Analyses of truncation patterns (e.g. Rob, from Robert) have traditionally focused on the templatic shape of such forms, while less attention has been paid to the question of which parts of the base word may survive in the truncatum. This feature of truncation, usually referred to as ‘anchoring,’ is investigated in the present paper. On the empirical basis of the generalizations emerging from an extensive database of truncation patterns in the world’s languages, a formal typology of anchoring in the framework of Optimality Theory is constructed and its defining ranking conditions (its ‘typological properties’) are extracted. The typological properties reveal the grammatical forces shaping the various classes of truncation patterns. They show that anchoring constraints must indeed form an integral part of any model of morphological truncation since—in interaction with templatic size-restrictor constraints—they determine whether truncation occurs at all and whether output forms vary in size or are of a fixed templatic shape. A thorough analysis of anchoring thus also provides evidence for templatic shapes emerging from constraint interaction and against an approach in terms of fixed, language-specific templates.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Truncation patterns are described in the literature as arising through the truncation of a base word down to a predictable form which can be defined in terms of prosodic categories. For instance in English, one pattern of name truncation shortens base names such as Robert to the form of a heavy syllable (Rob), which at the same time represents the smallest possible foot in the language (Alber and Arndt-Lappe 2012, to appear; Bat-El 2019). With respect to the general process of realizing a predictable form filled with material from a base, truncation is similar to partial reduplication (see McCarthy and Prince 1986, 1998 for discussion of both word-formation processes in similar terms). A main difference between the two word-formation processes is that reduplication usually generates affixes, while the outputs of truncation are free-standing forms.
Analyses of the output form of truncation patterns have traditionally focused on the templatic shape of such forms, which is often taken to be invariant for a given truncation pattern (mostly within the framework of Prosodic Morphology, McCarthy and Prince 1986 et seq.; for case studies cf. e.g. Piñeros 2000; Wiese 2001; Bat-El 2005). For example, Italian has a productive name truncation pattern that is invariably disyllabic (Alber 2010). The most productive English pattern of name truncation, by contrast, produces truncated forms that are invariably monosyllabic. Examples of these patterns are given in (1) and (2). We call the underived form the ‘base’ of truncation, the derived form the ‘truncatum,’ and we use the symbol (⧫) as a symbol to indicate morphological relatedness (cf. Bauer et al. 2013 for discussion), spelling out the related pairs as Truncatum ⧫ Base.
-
(1)

-
(2)

The present paper is concerned with the question which parts of the base survive in the truncated form, a question that has received less attention than templatic shape in the literature. For example, all truncated names in (1) preserve a string of sounds starting with the first sound of the base name. By contrast, among the truncated names in (2) only Pat (⧫ Patrícia) unambiguously shows this pattern; Trish (⧫ Patrícia) preserves a string of sounds starting with the main-stressed syllable in the base name. Al (⧫ Álfred) could belong to either of the two patterns, since it preserves the first part of the base, which, at the same time, is its stressed syllable. Looking at more English data, we find that both patterns are robustly attested in the language. Examples of monosyllables starting from the initial segment of the base are Cass (⧫ Cassándra) and Nat (⧫ Nathániel); examples of monosyllables starting from the stressed syllable of the base are Kye (⧫ Hezekíah), Vest (⧫ Sylvéster), Lige (⧫ Elíjah). In this paper we use the term ‘anchoring’ to refer to the phenomenon by which truncation patterns preserve segments of particular base positions—the left and the right edge, and the stressed syllable of the base. Note that our usage of the term ‘anchoring’ hence deviates from the use of the term found in some of the formal literature, where it has often been used to refer to edges of strings only, not to segments (McCarthy and Prince 1995).
Especially theoretically oriented accounts of truncation have tended to focus on explaining the templatic shape of the truncation rather than anchoring. One reason is that much pertinent work has been set within the research program of Prosodic Morphology (McCarthy and Prince 1986 et seq.), where the templatic shape of truncations has served as key evidence for the motivation of metrical constituents (in particular, the metrical foot). The question as to which material from the base survives within that templatic shape is, thus, not of principal interest in that research program. Another reason why anchoring in truncation has received little attention in the literature is that it is often assumed that, even though there may be certain crosslinguistic tendencies, there are no principled restrictions as to which parts of the base may survive in the truncation. It is hence concluded that anchoring is not of interest to a grammatical model of truncation (e.g. Scullen 1997; Bat-El 2005).
Contrary to this view, a growing number of studies have argued that, among productive truncation processes, anchoring patterns are clearly regular (e.g. Piñeros 2000; Nelson 2003; Alber 2010; Alber and Arndt-Lappe 2012; Hashimoto 2015; Arndt-Lappe 2018), and that the variation which is observed among productive formations is systematic, not random. Typically, productive anchoring patterns have been argued to preserve those parts of their bases that are prominent, with ‘prominence’ referring to phonetic prominence (i.e. stressed material in stress languages) and psycholinguistic prominence (i.e. word beginnings and endings, which play an important role in word recognition and lexical access; cf. esp. Beckman 1998). Languages may have several productive truncation patterns, which are distinguished by different templatic shapes and/or by different anchoring patterns. Sometimes these patterns have different functions (cf. e.g. Lappe 2007 on truncated names and non-names in English).
Furthermore, there is evidence that both metrical constituency and anchoring patterns are fundamental to understanding the shape of truncations. Such evidence comes from patterns in which the shape of truncations can only be explained as resulting from the interaction of templatic requirements and requirements on anchoring. In optimality-theoretic terms this means that constraints governing word shapes are violable, and that dominant anchoring constraints can be the reason for such violations. The examples given in (3) and (4), for instance, show simultaneous anchoring to the initial and the stressed syllable (cf. also van de Vijver 1997 for a related pattern in Dutch).
-
(3)

-
(4)

The word shape of the truncated forms in (3) and (4) corresponds to the stretch of material from the beginning of the base to its stressed syllable. As we will show in this paper, both the left edge and the stressed material of the base form are protected by anchoring constraints. These constraints are satisfied at the expense of whatever constraint(s) call(s) for (in these cases, monosyllabic) templatic shape. Violation of templatic constraint(s) is, however, minimal, as can be seen from the fact that material beyond the stressed syllable is truncated in these forms.
The theoretical implication of the existence of patterns like those in (3) and (4) is that anchoring is a fundamental property of truncation patterns without which we cannot fully understand such patterns. This crucially includes their shape, as templatic constraints calling for a particular word shape are violable and interact with anchoring constraints. This insight, however, raises important questions about the typological predictions that such an approach is making, as well as about the empirical adequacy of such predictions. Both issues have hitherto remained largely unexplored.
The present paper takes a first step towards remedying this situation. It is a first step in the sense that exploring the complexities involved in the interaction of anchoring and templatic constraints exhaustively is beyond the scope of this paper. We will instead focus on a detailed account of the anchoring side, and make only basic assumptions about the forces determining templatic word shape. In particular, we will not explore the full range of interactions of the constraints that impose size restrictions on truncated forms as proposed by the literature set within Prosodic Morphology (following Generalized Template Theory, McCarthy and Prince 1999). Based on the evidence from doubly anchored patterns illustrated in (3) and (4) above, however, we do assume that violation of templatic constraints is gradient, in the sense that whenever higher ranking constraints (in our case: anchoring constraints) lead to templatic shapes being abandoned, nevertheless the resulting output forms come as close as possible, in terms of number of syllables, to some template. This means that our analysis provides arguments against the existence of inviolable truncation templates, at least in some languages. Templatic behavior arises from constraint interaction; hence, truncatum shape cannot always be explained by template shape alone.
The aims of the paper with respect to anchoring in truncation are twofold. The first aim is to guarantee satisfactory empirical coverage of this fundamental feature of truncation; the second aim is to propose an analysis of the interaction of constraints responsible for anchoring with constraints favoring templatic shape of the truncatum. On the basis of a large database of truncation patterns compiled from the literature and our own empirical work, we first provide an overview of what systematic anchoring patterns we find documented crosslinguistically. The empirical findings are then taken as the basis of a formal typological model of truncation in the framework of Optimality Theory. We will compare the predictions of the formal model, which we call Basic Truncation Typology (BTT), to the patterns attested in the world’s languages. An in-depth analysis of BTT will, in a final step, allow us to understand the grammatical forces determining the various traits characterizing the classes of languages populating the typology. This analysis will go beyond the investigation of simple ranking permutations, as we will use Property Theory (Alber and Prince 2015, 2017, in prep.) to extract the key ranking conditions generating the whole typological system. This will not only help us to determine the appropriateness of the mapping between empirical facts and theoretical predictions, but also enable us to understand how the theory of anchoring forms an integral part of any model of morphological truncation. This means that we cannot understand truncation if we do not understand anchoring.
The paper is structured as follows. Sect. 2 will deal with the empirical facts, and Sect. 3 will motivate our set of anchoring constraints. The typological analysis will be presented in Sect. 4. The paper ends with a concluding discussion of our findings and the theoretical model (Sect. 5).
2 The database
In order to get an overview of which patterns are attested crosslinguistically, we created a database of truncation patterns and classified them with respect to observable templatic shapes and anchoring. The data comprise patterns that have been reported in the literature as well as patterns that we have investigated in our own research. As we will see, the truncation patterns emerging from the database as most typical are those in which the truncatum realizes a monosyllabic or disyllabic template and preserves word-initial, stressed or word-final segments of the base. In what follows, we first explain our methodology in compiling the database, and then explain what types of patterns we find.
2.1 Methodology
One principled restriction that we implemented in the database is that we excluded patterns which take morphologically or syntactically complex expressions as their input (e.g. clipped compounds or abbreviations of syntactic phrases).Footnote 1 Our final database comprises 154 truncation patterns from 43 different languages. All patterns and their codings are listed in Appendix 1 to this paper. The list also includes the literature on which our coding is based. When citing a pattern in the text, we will henceforth use the pattern ID given in the Appendix for reference. For Amharic, Armenian, Oromo and for Tongan no published documentation is available. This data is based on our own fieldwork, for which we conducted in-depth interviews with speakers.Footnote 2
We base our classification of truncation patterns on two central ideas. One is that truncation patterns are regular morphological patterns and, hence, involve predictable forms. The second is that languages can (and in fact, most often do) have multiple truncation patterns.Footnote 3 Following Alber and Arndt-Lappe (2012), we define a ‘predictable form’ in terms of its word structure and anchoring pattern. ‘Word structure’ is often referred to as a ‘template’ in the literature; we will use ‘template’ as a convenient label, in spite of the fact that, as we will see, some truncation patterns are not templatic in a strict sense because they yield outputs of variable shape. In addition, there may be a predictable fixed segment or affix (to be discussed below).
An obvious challenge in setting up the database is to determine which empirical conditions must be met for us to say that word structure and anchoring should count as predictable, and how to distinguish regular and predictable patterns from idiosyncratic forms or exceptions. Our approach to answering this question is the same as in standard fieldwork analyses of morphological systems, which tells us that regular patterns are characterised by occurring in many different word types (cf. esp. Baayen 1992 et seq.). We thus considered a pattern to be regular and predictable if it is supported by a substantial number of different words in the literature consulted and/or in our own research. In cases in which we had no access to primary data and thus had to rely on small numbers of examples cited in relevant publications, we assumed a predictable pattern if a configuration of word structure, anchoring, and fixed segment/affix was unambiguously represented by at least four different examples in the publication concerned.Footnote 4
By contrast, forms were considered to be exceptional and, hence, not representative of a regular pattern, if we found them represented by only very few different forms, or if these forms could convincingly be explained by other factors which are well known to shape the structure of truncations. Among these are, for example, phonological markedness of corresponding regular forms (cf. Sect. 3.1 for examples), or the etymology of a truncated form, as existing short forms sometimes become associated with other base forms (cf. Sundén 1904:146ff. for a comprehensive, empirically founded discussion of this phenomenon). As a consequence, we sometimes come to an assessment of the status of forms that is different from that in the published literature.
As an illustration of the frequency criterion, consider the English form Beth (⧫ Elizabeth). In spite of its high token frequency (Beth is a common form), the existence of a form like Beth does not comprise convincing evidence that there is a name truncation pattern in English that anchors to the word-final syllable of their base names. The reason is that in English there are very few different truncated names that unambiguously anchor to the final syllable of their bases (cf. Lappe 2007 for a quantitative study of this). Our classification of Russian hypocoristic patterns ending in -a illustrates another type of exceptionality. Based on Soglasnova’s (2003) substantial empirical study of Russian truncation patterns, we classify Russian -a suffixed hypocoristics into three patterns, one anchoring to the initial syllable (e.g. Svét-a ⧫ Svetlána, Russian01), one anchoring to the final or stressed syllable (e.g. Ménj-a ⧫ Pimén, Russian04), and one anchoring to both initial and final material, gapping intervening material (e.g. Sím-a ⧫ Serafíma, Russian05). Unlike Soglasnova, however, we do not interpret examples which anchor to a medial, unstressed syllable of their bases as evidence for yet another pattern (or, in the author’s interpretation, for the absence of restrictions on anchoring). Such examples are: Lím-a ⧫ Olimpjáda, Dím-a ⧫ Radimír, Tón-a ⧫ Platonída. A systematic analysis of all forms showing medial anchoring that were extracted from two onomastic dictionaries (Superanskaya 2004; Petrovskij 2005; our interpretation of the data follows Stroganova 2016) shows that virtually all of these forms (102 out of 106) can be explained by one of two common mechanisms observed in truncation. Thus, they systematically occur with vowel-initial bases (Lím-a ⧫ Olimpjáda), suggesting that their anchoring behavior is conditioned by phonological markedness (cf. Sect. 3.1 for details). Forms derived from consonant-initial bases, by contrast, are systematically related to other base names or alternative forms of the same base name (e.g. Tón-a ⧫ Platonída, Platón’a; Dím-a ⧫ Radimír, Dimítrij, Nikodím, Vladímir, among others). Note that for all truncation patterns we provide the sources on which we base our classification in the Appendices to this paper, inviting interested readers to draw their own conclusions.
Furthermore, we distinguish patterns that involve prespecified material from those that do not. An example of a pattern involving prespecified material is again Russian name truncations ending in -a (e.g. Menj-a ⧫ Pimén, Russian04). As in the Russian example, prespecified material often adds a syllable to the template. Prespecified material is treated inconsistently in the literature, where it is sometimes considered part of the template, and other times it is not. 86 of our 154 patterns involve prespecified material. For example, German i-formations (Gabi ⧫ Gabriele, German01) have often been described in terms of a disyllabic template (Féry 1997; Wiese 2001). By contrast, the template in Japanese name truncations like Riko-chaN ⧫ Mariko, which end in the suffix -chan (Japanese03; our orthographic representation follows Ito 1990), has traditionally been analysed under the assumption that the suffix is outside the template (Poser 1984a, 1984b, 1990; Ito 1990). In our database we consistently treat prespecified material as being outside the template proper. The rationale here is that, even though this strategy in some rare cases leads to codings that may seem unexpected given the literature on templates, it enables us to use one single consistent coding for all data, without making any a priori assumptions about the nature of templates (e.g. assumptions about the metrical foot being the preferred templatic shape, which has often lead researchers to integrate prespecified material fulfilling what is thought to be a well formed foot in the investigated language). Since the focus of the present study is on anchoring, a detailed investigation of the relation between template size and prespecification/affixation is not intended in this paper. In examples cited in the text of this paper, prespecified material will be marked by a hyphen (-).
2.2 Overview of the data
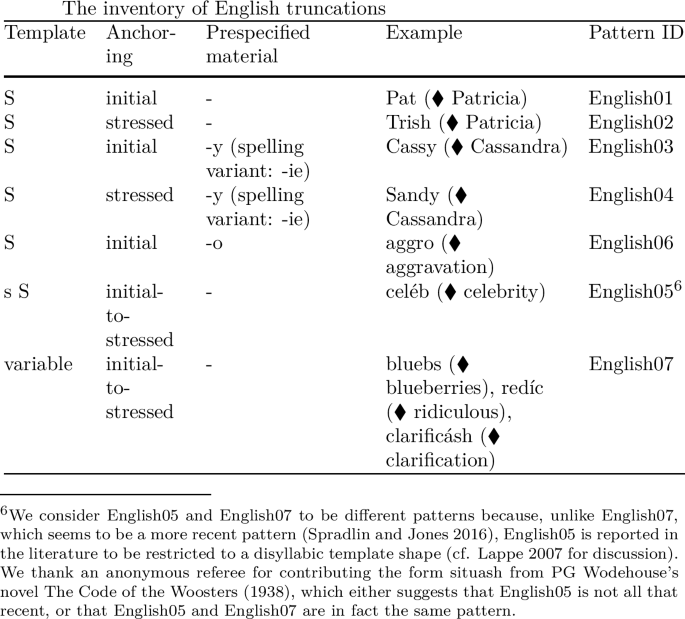
As an example, the inventory of English truncations as represented in our database is given in (5). ‘S’ stands for a stressed syllable, ‘s’ stands for an unstressed syllable and ‘variable’ is the tagging used for patterns which derive forms of variable length.Footnote 5
-
(5)
An overview of the types of templates attested in our database is provided in (6).
-
(6)
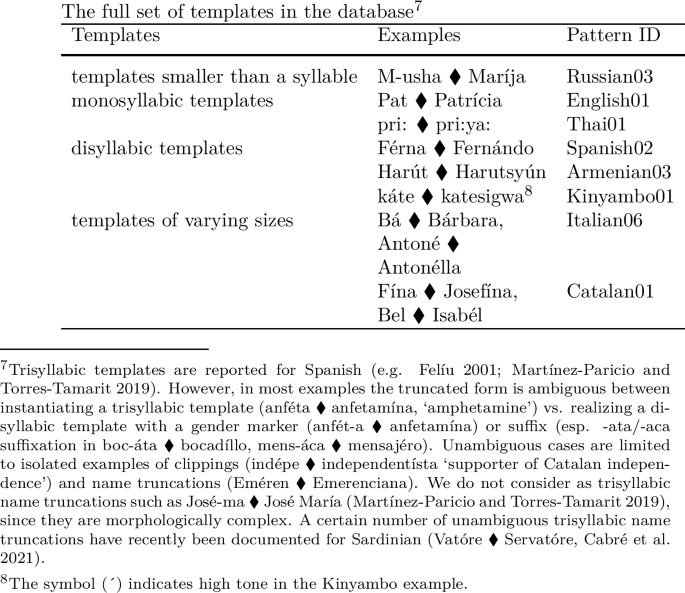
Most templates in our database are invariably monosyllabic (96 of our 154 patterns). The second most frequent template is a disyllabic, trochaic template (27 patterns); iambic patterns are considerably less frequent (9 patterns). There are 10 patterns in our database that have a varying templatic shape.
In the database, anchoring is coded as follows. For each pattern, we determine the position of the anchoring point(s) in the base form. The following categories are used: ‘initial position,’ ‘stressed position,’ ‘final position,’ ‘other.’ Stress anchoring always means that the main-stressed vowel in the base corresponds to the main-stressed vowel in the truncated form. Anchoring is classified as ‘initial’ if the leftmost segment of the template corresponds to the leftmost segment in the base.Footnote 6 Anchoring is classified as ‘final’ if the rightmost segment of the template corresponds to the rightmost segment in the base. In the overwhelming majority of cases, the segments in the truncated form comprise a contiguous string both in the base form and in the truncated from. In most of these cases, one anchoring point suffices to describe the anchoring pattern. For example, Albanian has a disyllabic truncation pattern that anchors to the initial syllable of its bases, as in the examples Ásqe (⧫ Asqerí) and Dóni (⧫ Doníka, Albanian01). Greek has a pattern that anchors to the main-stressed syllable, as in the example Mítr-os (⧫ Dhimítris, Greek02). Finally, Malay has a monosyllabic pattern that anchors to the final syllable, as in Rin (⧫ Ásrin) or Zul (⧫ Hafízul, Malay01).
There are, however, two types of cases where specifying one anchoring point does not suffice to describe the anchoring pattern. The first are cases in which the segments that survive in the truncated form do not form a contiguous string in the base. For example, Japanese has a pattern which anchors to the initial and the final syllable of the base, as in Mako-chaN (⧫ Mariko, Japanese04); medieval Italian had a pattern which anchors to the initial segment and the stressed vowel of the base, as in Bíce (⧫ Beatríce, Italian07; cf. footnote 18 below for discussion that this pattern may even be anchored to three prominent positions: the leftmost segment, the stressed vowel, and the rightmost segment). The second type of pattern with more than one anchoring point is comprised of patterns that vary in templatic shape, depending on the location of the two anchoring points in the base form. This is attested, for example, for a (Central/Southern) Italian vocative pattern, according to which Páola is truncated to Pá, Francésca is truncated to Francé, and Antonélla is truncated to Antoné (Italian06).
Another complication is that some patterns are ambiguous between different anchoring patterns. For example, in languages which have consistent initial stress, it is impossible to distinguish between initial anchoring and stress anchoring. Hungarian is a case in point (e.g. Féri ⧫ Férencz, Hungarian01). Likewise, in languages with consistent final or penult stress, stress anchoring is often indistinguishable from final anchoring. This is the case, for example, for French patterns like the one that derives Zabét from Elisabéth (French10). Ambiguous patterns were coded for both possible anchoring points. (7) provides an overview of which anchoring patterns are attested in our database.
-
(7)

(7) suggests that truncation patterns typically anchor to prominent material in the base form. These are initial material, the main-stressed vowel, and final material (cf. esp. Beckman 1998).
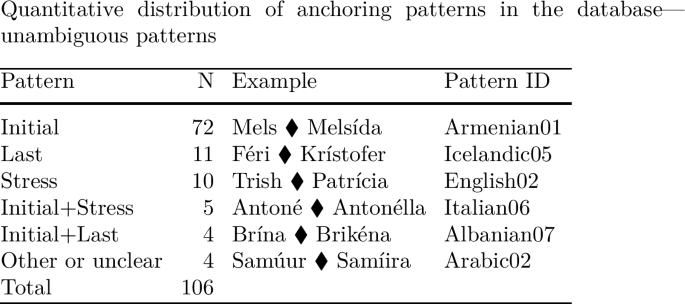
The most typical truncation pattern thus is one in which the truncation has a clear templatic shape (monosyllabic or disyllabic), and in which the truncation preserves either initial or stressed or final material from the base. In our database, 131 patterns conform to this generalization. Among the main anchoring patterns, initial anchoring is most frequent; 74 patterns in our database display a clear (i.e. unambiguous) initial anchoring pattern. Furthermore, with the exception of Indonesian, there is no language in our database for which no pattern with initial anchoring is documented. One anchoring pattern that is controversial in the literature is the pattern that we call ‘Final’ in (7). The observation that right anchoring seems to be rarer than other anchoring patterns in reduplication, truncation and infixation leads Nelson (2003) to posit that, across languages, there is no genuine right anchoring, but that cases of apparent right anchoring are due to higher-ranked constraints prohibiting anchoring to initial or stressed material. The truncation patterns that we classified as ‘Final’ in our database, however, do not allow us to reanalyze them as being conditioned by other factors. For example, the work on which our pattern Icelandic05 in (7) is based reports that among 800 Icelandic names collected in a survey, 250 correspond to the Icelandic05 pattern, and that for 60 base names both a truncation based on the final syllable (our Icelandic05) and a truncation based on the initial syllable (our pattern Icelandic02) were found (Willson 2007:216).
The table in (7) also shows that anchoring to a single prominent segment is not the only option available, as there are also patterns that multiply anchor to two (or potentially even more, cf. (14a) below) prominent positions in the base. There are two principled types of such patterns. One type is clearly templatic, in the sense that the output always corresponds to a disyllabic template; in these patterns, both multiple anchoring and faithfulness to the template restriction are achieved by gapping intervening material (cf. e.g. Korean03 ju ce ⧫ ju joŋ ce in (7)). The other type varies in word structure, so that the length of the truncatum is determined by the number of syllables between the leftmost and the rightmost anchoring point (cf. e.g. English07, redíc ⧫ ridículous in (7); cf. (5) above for more examples that show that word structure varies in this pattern).
Interestingly, our database provides evidence for the existence of all logically possible combinations of multiple anchoring points, with, possibly, one exception. This exception is a pattern that anchors to both the main-stressed vowel and the word-final segment. We have attestations of single truncated forms of this type in our datasets, such as Ménico ⧫ Doménico, Níbale ⧫ Anníbale (Italian). However, the evidence does not meet our criteria to claim that this is a productive pattern (cf. the beginning of this section, above, for discussion). There are, however, patterns in the database which are ambiguous between an interpretation of double anchoring to stressed and final material and an interpretation in terms of employing a single anchor. These are cases like Italian09, Bérto ⧫ Robérto or French10, Zabét ⧫ Elisabéth, which could be analyzed as anchoring to both the stressed vowel and the final segment (which, in the case of French, coincide in the same syllable), but also as realizing a disyllabic template while anchoring to either of the two anchor points.
The absence of clear patterns anchored both to stress and the right edge might be an accidental gap, considering the relatively small number of unambiguously right- and unambiguously stress-anchored patterns and the even smaller overall number of cases of (unambiguous) multiple anchoring. A further reason that patterns of this type are rare might be that in order to be unambiguous, the truncatum has to be derived from bases with a very specific structure, where stress falls at least three syllables from the right edge (but not on the first syllable). Base forms of this type, with antepenultimate stress, are themselves rare.
In the database there are 17 multiply anchored patterns. Of these, four show variable template structures. The only case of variable template length that cannot be accounted for in terms of multiple anchoring is a Japanese pattern (Japanese09) documented in Labrune (2002). In her account of the pattern, the first anchoring point is always initial, but the length of the truncated form is determined by the location of pitch accent in the base. Instead of preserving the pitch-accented syllable like the other variable patterns in our database, the truncation ends just before the pitch-accented syllable. Examples are: sando ⧫ sandoítti, kosume ⧫ kosumetíkku, irasuto ⧫ irasutoréesyon. Note, however, that Labrune’s generalization about the role of pitch accent location in delimiting Japanese loanword truncations is not uncontroversial (cf. e.g. Ito and Mester 2016 for recent discussion). The implications of the pattern for a general typology of anchoring in truncation are hence unclear and must be left to future research.
Two other patterns that are not readily captured by our description of anchoring patterns are two Arabic patterns, one (Arabic01) described in McCarthy and Prince (1990; the language is simply classified as ‘Arabic’), and one Jordanian Arabic pattern of hypocoristic formation (Arabic02) described in Zawaydeh and Davis (1999). Both patterns have a clear disyllabic template and are discussed in the context of the Prosodic Morphology framework, which is why they were included in the database. However, both patterns straddle the boundary between properties typically associated with truncation and those associated with Semitic Root-and-Pattern morphology. They may hence provide an interesting window into what these two types of processes have in common (cf. Bat-El 2019 for an insightful recent discussion). It is, however, unclear how to best conceptualize the notion of anchoring in such a system.
The tables in (8) and (9) provide an overview of the quantitative distributions of the different anchoring patterns in our database. Note, however, that numbers are clearly not representative of the typological distributions amongst languages. The reason is that some languages are overrepresented, as we have evidence for many different patterns in that language, whereas for others we do not (e.g. Albanian: 13 patterns vs. Tongan: 1 pattern). The table in (8) lists those patterns that can be unambiguously assigned to one single anchoring pattern. For multiply anchored patterns all anchoring points are given and connected by (+). The table in (9) lists those patterns in which anchoring is ambiguous; the reason for ambiguity is always that stress in pertinent languages coincides with either of the edges, so that it is not possible to unambiguously distinguish edge anchoring from stress anchoring. The two alternatives are separated by (/) in the table.
-
(8)
-
(9)

After this overview of the empirical facts, we now turn to the question of how the typology as observed in our database can be modelled in an OT typology. We will first motivate the relevant constraints on the basis of the properties of truncation patterns as observed in our database (Sect. 3). We will then study the ranking typology that results from these constraints.
3 Anchoring constraints
In the Prosodic Morphology literature, specific Anchor constraints have been proposed since McCarthy and Prince (1995) to account for the fact that reduplication and truncation morphemes copy prominent positions from their bases. The definition of anchoring constraints often integrates two crucial aspects of the phenomenon: faithfulness (the prominent position of the base has to be present in the truncation) and alignment (prominent positions in the truncatum have to be ‘close’ to prominent positions in the base).Footnote 7 We will follow Alber (2010) and Alber and Arndt-Lappe (2012) here in proposing that while the definition of anchoring to the left and the right edge of the base has to integrate the basic format of alignment constraints, anchoring to stress has to be defined as faithfulness to the stressed vowel. We will discuss the two cases in turn.
3.1 Edge anchoring
Alber (2010) and Alber and Arndt-Lappe (2012) propose to define Anchor constraints referring to the edges of the base as faithfulness constraints which—crucially—incorporate the concept of gradience known from alignment constraints, as defined in the theory of Generalized Alignment (McCarthy and Prince 1993a).Footnote 8 This is implemented in the definitions in (10), which differ from Nelson’s earlier (2003) formal account of anchoring patterns in two important ways. One is that we assume that anchoring is symmetric (cf. Sect. 2.2 for discussion and justification). The second is that we assume that violations are gradient; we discuss the evidence for this assumption below.
-
(10)

AnchL and AnchR return violation marks for base material not realized in the truncatum and therefore belong to the family of faithfulness constraints. However, they assign penalties for each base segment missing between the first/last syllable of the truncatum and the specified edge and this means that their definition incorporates the sensitivity to edge distance typical of alignment constraints (see McCarthy and Prince 1993a and Hyde 2012 for discussion). In this sense, they can be interpreted as a gradient version of the prominence sensitive Max constraints proposed e.g. in Beckman (1998).
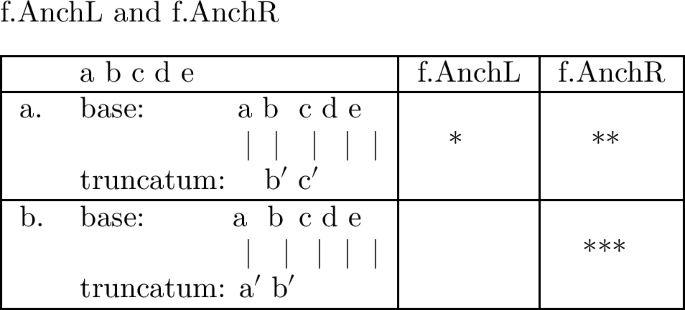
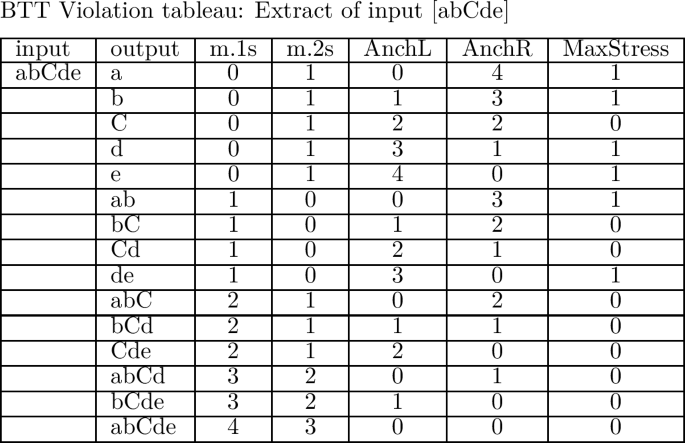
The following tableau illustrates the violations assigned by AnchL and AnchR to two candidates realizing an abstract base of five segments, /abcde/:Footnote 9
-
Candidate a. collects one violation for AnchL, since /b/, the base correspondent of the leftmost truncatum segment [b′], is preceded by segment /a/, not realized in the truncatum. The same candidate exhibits two violations for AnchR, since segments /d/ and /e/ intervene between /c/, the base correspondent of the last truncatum segment, and the right edge of the base.
-
Candidate b. exhibits perfect anchoring to the left edge, but accumulates three violations on AnchR because of /c, d, e/, intervening between /b/, the base-correspondent of final [b′] in the truncatum, and the right edge of the base.
-
(11)
There are two key arguments for defining the Anchor constraints specified for edges in this way, one based on the observation of certain attested truncation patterns, the other related to the predictions different definitions of constraints make for the overall typology.
From an empirical point of view, we observe that in several languages edge-anchored truncation patterns display a gradience effect (see Bat-El 2014 for a detailed discussion of Hebrew). For instance, in Russian there is a left-anchored monosyllabic truncation template, augmented by the suffix -a and, usually, characterized by palatalization of the final consonant of the truncatum (data from Soglasnova 2003 and Stroganova 2016; see also discussion in Sect. 2.1).Footnote 10 The interesting fact about this truncation pattern is that while a consonant-initial base gives rise to the usual left-anchored monosyllabic template (12a-d), in vowel-initial bases the first syllable is skipped and the truncation morpheme is anchored to the second syllable of the base (12e-h):
-
(12)

We interpret patterns like these as being subject to anchoring in a gradient fashion: if other restrictions (such as here, a requirement to obey the constraint Onset) inhibit perfect edge-anchoring, the truncation morpheme is anchored as close as possible to the relevant edge. If, on the other hand, edge-anchoring was defined in a ‘categorical’ fashion, failure to satisfy the anchor constraint would pass the decision to a lower ranked constraint. We would then expect the truncation morpheme to select another prominent position as an anchoring point, e.g. the stressed syllable. Consonant-initial Stanisláv would then still be truncated to Stán’-a, but vowel-initial Afanásij would be realized as *Nas’-a via anchoring to the stressed syllable of the base.
Russian is not the only language displaying gradient anchoring. Patterns of this type are also attested for Bernese Swiss German01 ( ⧫ Ánton, Grueter 2002, 2003), Hungarian01 (Bér-ci ⧫ Álbert, van de Weijer 1989; Rebrus and Szigetvari 2016), French06 (Zazá ⧫ Isabélle, Mazzola 2017)Footnote 11 and Czech02 (Tónda ⧫ Ántonin, Alber 2010; see also examples in Bethin 2003); single examples occur in descriptions of truncation patterns of Icelandic05 (Túr-i ⧫ Ártur, Willson 2007), Bavarian dialects like Tyrolean01 (Gust-l ⧫ Áugustin, Tscholl 2001) and Brazilian Portuguese04 (Dri ⧫ Adriána, our own data).
⧫ Ánton, Grueter 2002, 2003), Hungarian01 (Bér-ci ⧫ Álbert, van de Weijer 1989; Rebrus and Szigetvari 2016), French06 (Zazá ⧫ Isabélle, Mazzola 2017)Footnote 11 and Czech02 (Tónda ⧫ Ántonin, Alber 2010; see also examples in Bethin 2003); single examples occur in descriptions of truncation patterns of Icelandic05 (Túr-i ⧫ Ártur, Willson 2007), Bavarian dialects like Tyrolean01 (Gust-l ⧫ Áugustin, Tscholl 2001) and Brazilian Portuguese04 (Dri ⧫ Adriána, our own data).
Typically, gradient violations of anchoring occur with vowel initial bases in order to guarantee that the truncated form be realized with an onset consonant. A particularly interesting and complex case is attested for Fon (Gbe, Ewe02), where French names are the basis of a monosyllabic, reduplicating truncation pattern as in dʒódʒō ⧫ Joseph.Footnote 12 The pattern is left-anchored, but the first syllable is skipped if the base starts with a vowel (dede ⧫ Adeline), a rhotic (gaga ⧫ Rogatien) or a consonant cluster (vivi ⧫ Flavien). If both the first and the second syllable exhibit one of the marked contexts, the base is scanned rightward until a suitable anchor point is found as e.g. in  (the first syllable has a complex onset, the second a rhotic, anchoring takes place to the third) or kiki⧫ Erik (the first syllable has no onset, the second starts with a rhotic, anchoring takes place to the last segment, to which an epenthetic [i] is attached). Patterns such as that of Fon show beyond doubt that edge-anchoring is a gradient phenomenon and that anchoring constraints referring to edges have to be defined accordingly.
(the first syllable has a complex onset, the second a rhotic, anchoring takes place to the third) or kiki⧫ Erik (the first syllable has no onset, the second starts with a rhotic, anchoring takes place to the last segment, to which an epenthetic [i] is attached). Patterns such as that of Fon show beyond doubt that edge-anchoring is a gradient phenomenon and that anchoring constraints referring to edges have to be defined accordingly.
Gradience of edge anchoring as evoked here for truncation also has an interesting parallel among reduplication patterns. In Timugon Murut reduplication (McCarthy and Prince 1986, 1993a, 1993b; data from Prentice 1971), the monosyllabic reduplicant is anchored to the left edge of the base (bu-bulud, ‘ridge’), but if the base starts with a vowel, the reduplicant is infixed and anchored to the second syllable (om-po-podon, ‘always flatter’). McCarthy and Prince (1993a, 1993b) analyze the pattern as the result of the constraint Onset dominating an alignment constraint requiring the reduplicant to align to the left edge of the base. The only difference with respect to the truncation patterns described above is that a syntagmatically operating alignment constraint can account for gradient affixation in reduplication, while in truncation edge-anchoring constraints have to be defined paradigmatically, as above, requiring alignment between an (input) base and an (output) truncatum.
The second argument in favor of a definition of edge-anchoring as above is that it makes the assumption of a Max constraint requiring maximal realization of base material in the truncation morpheme superfluous. Max constraints relating the base and the truncatum have figured prominently in the truncation literature to account for the fact that the template is maximally filled with base material. Thus, German Sylvia is truncated to Sylv-i (German02), not to *Syl-i, because the monosyllabic template has to be filled to the brim with base material, suggesting activity of a Max(base-truncatum) constraint. However, the interaction of Max(base-truncatum) with the Anchor constraints (however defined) leads to some unwelcome predictions for the overall typology of truncation. As Alber (2010) and Alber and Arndt-Lappe (2012) observe, under a ranking where Max(base-truncatum) dominates the Anchor constraints, we predict patterns where anchoring is sacrificed to maximal copying from the base. This would mean, for instance, that the base was scanned for the highest possible number of segments fitting into a template—without any regard for prominent anchor points. We could then imagine a hypothetical language where the name Carméla was truncated to Carm, totaling four segments copied from the base, while in the same language the name Petrosílla was truncated to Tros, since cutting out a medial slice of the base would fare better in terms of base copying (four segments) than, for instance, copying the initial part Pet (three segments). Effects of this type are not attested in our database of truncation patterns.
AnchL and AnchR, as defined above, on the other hand, can also account for the effect of maximal copying in truncation. As we will see more clearly in the typological model in Sect. 4, it is the subordinate edge-anchor constraint which guarantees maximal copying. Consider again the example of German Sylvia, truncated to Sylv-i. In left-anchored truncation patterns like these, AnchL must dominate AnchR. But AnchR, even though dominated, guarantees that Sylv-i is preferred over *Syl-i, since in Sylv- there is less base material (precisely, [i, a]) between the correspondent of the last segment of the truncatum in the base and the right edge of the base. Under this view, the maximality effect in truncation is not so much an effect of maximal copying as an effect of maximal stretching towards the opposite edge as the one specified by the dominant Anchor constraint. Stretching, however, excludes the possibility of just cutting out a conveniently large slice of the base (as predicted by Max), since stretching is limited in range by attachment to the dominant anchor point (and by the size restrictor constraints defining the template).
3.2 Stress anchoring
We assume that stress anchoring, unlike left and right edge anchoring, is an effect of a faithfulness constraint calling for the main-stressed vowel in the base form to correspond to the main-stressed vowel in the derived form. The definition of our constraint is provided in (13). The format of the constraint is the format of well-known Max constraints (McCarthy and Prince 1995).
-
(13)

Three assumptions are in need of justification here. The first is that the relevant constraint is a correspondence constraint, not an alignment constraint, which means that stress anchoring is of a conceptually different nature than edge anchoring. The second regards the fact that the relevant correspondent constraint belongs to the family of Max constraints and not to that of Ident constraints. The third is that the stressed vowel (rather than e.g. the foot or the syllable or the vowel only) is the relevant scope of the constraint.
The idea that stress anchoring is an instance of faithfulness to prosodic information in the base is well-established in the literature on Prosodic Morphology (cf. esp. Beckman 1998). There is, indeed, evidence also that stress anchoring is of a conceptually different nature than edge anchoring. In stress-anchored patterns, we do not find the gradient alignment effects that we find in edge anchoring (cf. Sect. 3.1). Whereas, for example, there is ample evidence for the relevance of markedness constraints on segmental and syllabic structure in stress-anchored truncation patterns, repair strategies involve substitution or deletion in all documented cases; minimal skipping of syllables, by contrast, is unattested. A well-known group of patterns that exhibits segmental markedness effects is Spanish stress-anchored nicknames (Spanish03, cf. e.g. Piñeros 2000; Sanz Álvarez 2015 and references therein). A marked consonant that is systematically avoided in such forms is [ θ]; repair, however, systematically involves substitution by [tʃ]. For example, the truncated form of Asun[ θ]ión is [tʃ]óna. The form substitutes marked [ θ] by another, less marked consonant, but still retains the stressed vowel from the base. A form like *Súna, in which the anchoring point is minimally shifted (here: to the left) to avoid marked material, is unattested.
With respect to the second issue, we propose that the relevant correspondence constraint has to be of the Max rather than the Ident type. Ident constraints require that corresponding segments have identical values with respect to some feature x (McCarthy and Prince 1995:370). This definition makes the constraint inadequate for the cases observed here since, first of all, stress cannot be interpreted as a feature linked to some segment (Liberman and Prince 1977). Secondly, Ident constraints are satisfied vacuously if the targeted segment is deleted, but we never find deletion as a strategy to guarantee stress preservation in truncation. Rather, constraints of the Max family seem to be at play, requiring both that the base vowel be realized in the output and that it be realized as stressed. MaxStress thus conflates two requirements, that of preserving the stressed vowel of the input and to maintain it as stressed. In this sense, the constraint is similar to the prominence maximization constraints proposed in Beckman (1998), which are Max constraints specified for prominent positions.
The third issue is the domain targeted by the faithfulness constraint. Our evidence that this domain is the stressed vowel (and not e.g. the foot or the stressed syllable) comes from the fact that all truncation patterns in our database that display stress anchoring retain the stressed vowel and keep it as a stressed vowel in the truncated form.
Evidence that the targeted domain is not larger than the stressed vowel comes from the multiply anchored patterns described in Sect. 2. The patterns exemplified in (14a) preserve initial and main-stressed material from the base forms but assume an invariant disyllabic templatic shape, by ‘gapping’ base material.Footnote 13 The patterns exemplified in (14b) also preserve both initial and main-stressed material from the bases but violate the template. For reasons of clarity, segments in the base that have a correspondent in the truncated form are underlined.Footnote 14
-
(14)

A property that all multiply anchored gapping patterns like those in (14a) have in common is that they preserve the initial consonant of the base and the vowel of the main-stressed syllable. Forms that (also) preserve the onset of the stressed syllable (such as e.g., *Bríce ⧫  or *Frínda ⧫
or *Frínda ⧫  ) are unattested. We conclude from this that the onset of the stressed syllable is not protected by the stress anchoring constraint.Footnote 15 Furthermore, note in (14a) that the vowel of the stressed syllable is always preserved. The fact that we don’t find forms like *Béce (⧫
) are unattested. We conclude from this that the onset of the stressed syllable is not protected by the stress anchoring constraint.Footnote 15 Furthermore, note in (14a) that the vowel of the stressed syllable is always preserved. The fact that we don’t find forms like *Béce (⧫  ) or *Flónda (⧫
) or *Flónda (⧫  ), which preserve both the onset and the nucleus of the initial syllable and part of the head foot of their bases, suggests that the stressed vowel, rather than the head foot, is the domain of the anchoring constraint.
), which preserve both the onset and the nucleus of the initial syllable and part of the head foot of their bases, suggests that the stressed vowel, rather than the head foot, is the domain of the anchoring constraint.
Forms like those in (14b) provide evidence that stress anchoring is not foot preservation. For example, the head foot of the English truncated form celéb ⧫ celébrity is a heavy monosyllabic foot (leb); this is not the shape of the head foot in the base, which is probably a disyllabic foot (lé.bri). The same holds for the Italian example in (14b). Salvató ends in a degenerate monosyllabic foot (tó); the full foot (tó.re) is not preserved. In fact, as noted in Kenstowicz (2019), Central/Southern Italian vocatives do not necessarily preserve the whole nucleus of the stressed syllable of the base, since only the stressed element of diphthongs in the base name is preserved (see Páo.la ⧫ Pá; *Páo).
3.3 Contiguity of copying
All anchoring constraints that we propose in this section are quite narrow in scope: both edge anchoring constraints, AnchL and AnchR, only protect word edges, i.e. the leftmost or the rightmost segments of the base word. Similarly, the scope of MaxStress is restricted to a single, stressed vowel. The approach thus raises two questions. The first is how we explain that truncations usually copy more material from their bases than only those sounds that are protected by these constraints. The second question is how we explain which material that is not protected by anchoring constraints is copied in truncation.
With regard to the first issue, we assume that the subordinate anchor constraint (e.g. AnchR) has a stretching effect, which favors copying beyond the anchoring point demanded by the dominant Anchor constraint (e.g. AnchorL; see the discussion of gradient edge-anchoring in Sect. 3.1, above). The minimal size of truncations, on the other hand, is the effect of a set of templatic constraints, which can be conceived of as markedness constraints on minimal word structure, along the lines proposed in Generalized Template Theory (McCarthy and Prince 1999; cf. Alber and Arndt-Lappe 2012 for discussion).
The second issue that calls for an explanation is that, as it stands, our account predicts that the optimal way for truncations to satisfy anchoring constraints while at the same time adhering to all templatic constraints should be to satisfy them all at the same time, at the expense of gapping intervening material. We already saw in (7) and (8) in Sect. 2.2 that gapping patterns are indeed attested. This is the case, for example, in Spanish forms like Fínda (Spanish07), which preserve the initial and the main-stressed and/or final part of its base  (cf. also our discussion of (14a)). However, as is clear from our database, such patterns are certainly not very frequent. We therefore assume that such formations are often ruled out because the constraint Contiguity (McCarthy and Prince 1995) is dominant, defined in (15) below.
(cf. also our discussion of (14a)). However, as is clear from our database, such patterns are certainly not very frequent. We therefore assume that such formations are often ruled out because the constraint Contiguity (McCarthy and Prince 1995) is dominant, defined in (15) below.
-
(15)

Truncation patterns violating Contiguity certainly deserve further exploration. However, given their rarity among documented truncation patterns we cannot be sure that the typology of anchoring patterns for which we currently have evidence exhausts all the possibilities or whether some observed gaps are accidental. For instance, we did not find productive patterns in which the stressed vowel and the last segments of the base are preserved to the exclusion of other segments. More empirical research is needed, for instance eliciting such patterns from speakers in an experimental setting. We therefore will not integrate gapping patterns, nor the constraint Contiguity, in our formal model in Sect. 4.
4 A typological analysis of anchoring
With constraint definitions determining anchoring to edges and to stress in place we can now turn to the construction and analysis of a formal typological model of truncation in the framework of Optimality Theory. The goal of constructing a formal model is twofold. First, it allows us to test the predictions in terms of sets of languages generated by the modelFootnote 16 and to compare this factorial typology to the patterns that we find among the natural languages of the world. By and large, the predictions made by the formal typology should be borne out by what we find in the typology of anchoring in natural languages, though some discrepancies may arise, if only due to the higher frequency of some patterns with respect to others (see the discussion in Sect. 2 on the possibility of an accidental gap with respect to languages anchoring unambiguously to the stressed and the last syllable). Second, and, we maintain, even more interestingly, the analysis of the formal typology allows us to reach a higher level of understanding of its inner workings by uncovering the grammatical forces, in the form of ranking conditions, which determine the various classes of truncation patterns.
The formal typology is generated with the help of OTWorkplace (Prince et al. 2007-2021), an open-source software suite which also provides the essential tools for its analysis.Footnote 17 The analysis of anchoring in this section follows Property Theory, as developed in Alber and Prince (2015, 2017, in prep.).Footnote 18 Property Theory aims to uncover the meaningful ranking relations in a linguistic typology in the form of ‘typological properties.’ Typological properties, in the sense of Alber and Prince (2015, 2017, in prep.), are the defining ranking conditions of a typology. They take the form of a binary choice between two logically opposite ranking conditions, X > Y and Y > X, summarized as X < > Y, where X and Y represent single constraints, or sets of constraints. The two choices offered by a typological property are called its ‘values.’ Each language in the typology is defined by a specific set of property values and groups of languages share certain property values. Thus, typological properties provide a classification of the typology according to intensional principles, in the form of ranking conditions shared by the grammars of groups of languages. This intensional classification can then be used to explain how the extensional traits of a typology, i.e. the surface patterns that we observe, come about. In the extensional domain, we may find right-anchored, left-anchored or stress-anchored truncation patterns in the typology, but only the typological properties will tell us which ranking conditions are responsible for generating them and whether, for instance, right-anchored and left-anchored patterns are characterized by ranking conditions (i.e. intensional properties) which exclude stress-anchored patterns.
The classification of languages according to typological properties may also lead to results which are otherwise easily overlooked or simply never discovered. Thus, we will for instance see that ranking conditions involving the constraints AnchL and AnchR play a crucial role in determining whether truncation can occur at all, in any given language. If, in the grammar of a language, both AnchL and AnchR dominate the constraints favoring a templatic shape of the truncatum, copying will take place from the left to the right edge and no truncation will occur. The antagonism between anchor constraints referring to edges and constraints favoring templatic structure therefore partitions the typology into two classes of languages: those where truncation occurs, and those where it doesn’t (the latter consisting of a single language).Footnote 19
In the remainder of this section we will first define the set of candidates evaluated in our typology and the set of constraints evaluating them (4.1). We will then present the factorial typology which is generated and discuss its extensional traits (4.2). In Sect. 4.3. we propose an analysis of the typological properties defining the typology and show how they generate the extensional traits characterizing it.
4.1 BTT.Gen and BTT.Con
The formal typology we present here is basic in its nature (we call it the Basic Truncation Typology, BTT, for short), since we focus on the basic interactions between constraints referring to anchor points and constraints referring to templatic shape. We therefore need to devise an abstract representation of truncation patterns which preserves the necessary information on anchor points and templatic shape, but at the same time ignores other features of no concern to the present discussion, such as e.g. segmental changes. To guarantee this focus we choose an abstract representation of the bases and outputs of truncation as strings of syllables. We represent these strings of syllables as strings of ordered letters where capitalized letters indicate syllables bearing main stress. A base like Patrícia will thus be represented as /aBc/, a trisyllabic string with penultimate main stress. A truncated form like Trish, derived from Patrícia, will be represented as [B], a monosyllable preserving the main stressed syllable of the base. A truncated form like Pat will be represented as [a], a monosyllable preserving the initial, unstressed syllable of the base. Stress is annotated in output forms only where it is preserved from the base of truncation (e.g. [B]), and output forms not preserving base stress like [a] are assumed to receive the language’s default stress (see also discussion in 4.1.1).
Choosing the syllable as a unit of representation may seem surprising, given that, as we saw in Sect. 3 above, none of our anchoring constraints do formally refer to the syllable as a unit. Reference to the syllable (or to a higher-level unit of prosodic organisation such as the foot) is, however, an indispensable property of any plausible definition of templatic constraints. Representing both bases and truncated forms in terms of syllables will allow us to refer to the anchor points of a pattern (in the example Pat ⧫ Patrícia, the left edge, represented by the syllable /a/ in the base /aBc/) as well as to the template of the output (monosyllabic [a]). Refraining from inserting more variables into the system will allow us an unobstructed, clear view of the basic interactions. Building on the insights obtained by our basic typology BTT, future research may then aim at constructing more complex formal typologies.
4.1.1 BTT.Gen
We define BTT.Gen, the set of candidates evaluated by the constraints of BTT, as the set of all mappings from an input prosodic word (PrWd), consisting of any number of syllables and headed by a single stressed syllable, to all logically possible contiguous substrings of it.Footnote 20
-
(16)

The input represents the base of truncation, the output the truncatum. There are no restrictions on the position of the stressed syllable in the input PrWd. There are, however, restrictions on the position of the stressed syllable in the output truncated form. Since the output consists of a contiguous substring of the input, it will either preserve a substring containing the stressed syllable of the input (as in the case of Trish ⧫ Patrícia, i.e. [aBc] → [B]), or a string not containing the stressed syllable of the base (as in Pat ⧫ Patrícia, i.e. [aBc] → [a]). In the former case, stress in the output form is determined by stress in the base. In the latter case, we assume that the unstressed output form will receive the default stress of the language.
The reason why stress-bearing input strings are assumed is that truncation patterns often do preserve the stress of their input bases and hence clearly make reference to stressed base forms, a phenomenon described in the literature as base-truncatum (= output-output) correspondence. It is well-known, however, that truncation patterns sometimes do make reference to the underlying form of their bases as well (input-truncatum-, or input-output-correspondence; see Alber and Arndt-Lappe 2012 for discussion). Since we are explicitly interested in stress-anchoring and its interaction with constraints favoring other anchor-points, we put this possibility of referring to unstressed input forms aside in this paper.
The assumed set of inputs, where stress can fall on any syllable in the string, finds its closest match among truncation patterns in languages with lexical stress, such as Russian. These are languages where indeed stress can fall on any syllable of the base. Many of the languages in our database are not of this type. Rather, they exhibit regular initial, final, penultimate or antepenultimate stress in the words which form the input for truncation. We have calculated the various formal typologies resulting from inputs with consistent regular stress (e.g. only antepenultimate stress). The resulting typologies were in each case subsets of the more comprehensive typology presented in this paper. For this reason we assume inputs with stress in any position, keeping in mind that not all inputs will be available for every natural language, hence not every language will have the potential to exhibit all truncation patterns predicted by BTT.
From the set of possible candidates defined by BTT.Gen we hypothesize a typological support, i.e. a set of candidates sufficient to generate the whole typology (see Alber et al. 2016 for the definition of typological support and proof of its sufficiency in the case of the stress typology nGX). The support we select from the possibilities of BTT.Gen comprises input PrWds of two to five syllables, with stress falling on any syllable in the PrWd, as defined by BTT.Gen. Possible inputs thus include forms such as [Ab], a two-syllable input with initial stress, [abC], a trisyllabic input with final stress or [abCde], a five-syllable string with antepenultimate stress. Output strings consist of all possible contiguous nonempty substrings of these input strings:
-
(17)

-
(18)

The rationale behind the choice of strings from two to five syllables is that the set of five-syllable inputs contains, among others, the input string /abCde/, which is ‘long enough’ to allow for unambiguous mappings to disyllabic left-anchored ([ab]), right-anchored ([de]) or stress-anchored (e.g., [Cd]) patterns. Shorter forms are often ambiguous in their mappings. For instance, the mapping /abCd/ → [Cd] can be interpreted as the realization of a disyllabic, stress-anchored pattern, or a disyllabic, right-anchored pattern, or even as a pattern which is both stress- and right-anchored, but only by accident conforms to a particular templatic shape.
Inputs which are longer than five syllables repeat mappings which are ambiguous in their interpretation, and others which are not, but do not add any new information.Footnote 21 The lower minimum of two input syllables excludes monosyllabic inputs such as [A], which, trivially, can be mapped only to themselves.
The set of candidates which form the support of BTT.Gen by no means contains only expected outputs, such as [ab], or [C], but also unattested patterns, such as [bCd], which should not emerge in a factorial typology matching the patterns observed in the real world.
4.1.2 BTT.Con
BTT.Con contains the following set of five constraints, with Anchor constraints and MaxStress adapted to the abstract notation of the formal typology:Footnote 22
-
(19)

By defining the violations of m.1s and m.2s in terms of numbers of syllables, we are able to abstract away from the rhythmic properties of truncations. As a welcome result, the resulting typology is independent of the specific metrical system of the languages modelled. It is however clear that the TMPL constraints m.1s and m.2s, as defined above, are placeholders for a more complex set of markedness constraints responsible for the templatic shapes that we find in the world’s languages. In line with Generalized Template Theory (McCarthy and Prince 1999; see also discussion in Alber and Arndt-Lappe 2012) we believe that the size of truncations is not an effect of idiosyncratic templatic constraints, but of (sets of) markedness constraints that are active in the language.Footnote 23 Such constraints pertain to prosodic and phonological word structure, to syllable structure, and to segmental markedness, all of which play a role in truncation (see e.g. McCarthy and Prince’s 1994 analysis of Diyari).
The anchor constraints specified for edges, AnchL and AnchR, have been defined in the terms discussed in Sect. 3. They can be understood as prominence sensitive faithfulness constraints, in the sense that they assign violation marks when input syllables close to a prominent (left or right) edge are not realized in the output. They share with alignment constraints the feature that every prosodic constituent (in this case, every syllable) intervening between two designated edges returns a violation mark. In the property analysis below they are grouped into the class of EDGE constraints.
MaxStress, as discussed in Sect. 3, is a faithfulness constraint returning a violation mark whenever the stressed syllable of the base is not realized as a stressed syllable in the output. Together with the EDGE constraints, MaxStress forms the class of PROM constraints (for ‘prominence’) in the analysis below. Since BTT.Gen does not include destressed outputs, or outputs where stress has shifted with respect to stress in the input, a violation of MaxStress is equivalent to deletion of the input stressed vowel in the output.
There are no additional constraints in BTT.Con assigning stress to the output. We assume that, in this basic truncation typology, the stress pattern constraints active in the language assign default stress to the output, in case the output does not preserve the stressed syllable of the input. As in the case of the definition of the TMPL constraints, this assumption allows us to abstract away from language specific rhythmic patterns. In future typological analyses, however, it might be interesting to investigate the interaction of stress pattern constraints with stress-preserving constraints such as f.MaxStress. This would make it possible to examine the patterns of stress-preservation vs. imposition of default stress, depending on whether MaxStress or (some) stress pattern constraints are dominant.
4.2 The factorial typology of BTT and its extensional classification
The full set of candidates and their evaluation are made available in the BTT violation tableau in Appendix 2. Here we show an extract of the violation tableau, limited to the input [abCde], and all its possible mappings. The input [abCde] and its mappings will be useful in classifying the languages of BTT into extensional classes.
-
(20)
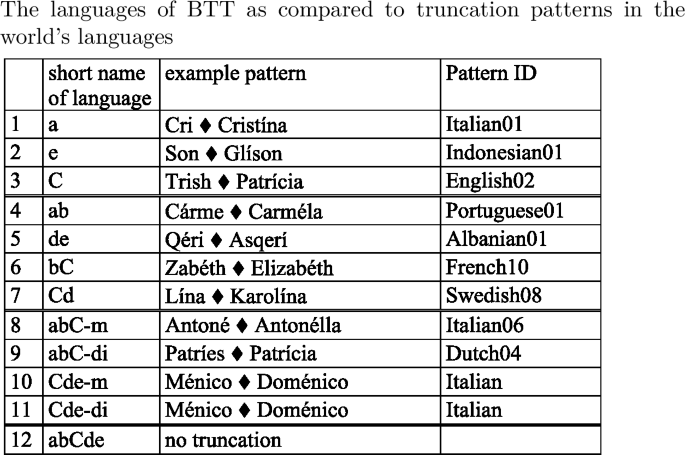
From the violation tableau we generate the factorial typology of BTT, which contains 12 distinct languages.
-
(21)
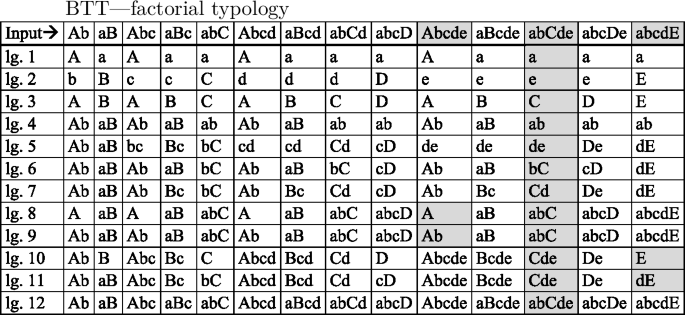
The factorial typology, as generated by OTWorkplace, shows each language’s inventory of output forms as generated for various input forms. In order to understand the extensional classes characterizing BTT we single out the output forms generated for the input /abCde/, which are shaded in (21). These output forms distinguish unambiguously almost all languages of BTT. To distinguish the two cases where /abCde/ yields identical output forms—[abC] for lgs. 8 and 9 and [Cde] for lgs. 10 and 11—we add an initially stressed input such as /Abcde/ and a finally stressed input, /abcdE/ to our set of maximally distinguishing input forms. This allows us to differentiate the [abC] languages 8 and 9 into one with a monosyllabic output and one with a disyllabic output for initially stressed inputs. Similarly, the [Cde] languages 10 and 11 are distinguished by the outputs they realize for finally stressed inputs.
With these maximally distinguishing inputs at hand it is now possible to reduce the factorial typology to a format in which it is easier to discern the classes of languages of BTT.
-
(22)
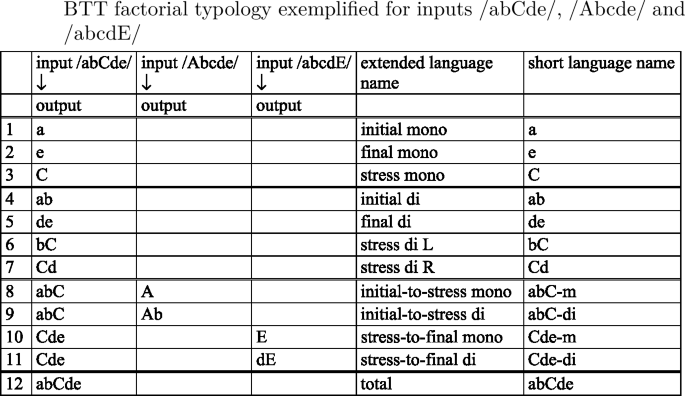
Throughout the paper we will use the short language names in the last column of the above table, which reflect the output form realized by a language for input /abCde/, as well as the ‘m(ono)’ or ‘di’ (syllabic) outputs realized for initially and finally stressed inputs. This naming convention allows us to codify the relevant features distinguishing the languages of BTT: the anchor points realized (initial, final or stress), the templates realized for some or all outputs (mono or di), whether base material is preserved from the initial to the stressed or from the stressed to the final syllable, and left or right orientation in preservation of base material.
The factorial typology of truncation patterns falls broadly into four groups of languages. We recognize the familiar monosyllabic and disyllabic patterns, with the first, the last or the stressed syllable used as anchor points. Languages 8–11, where a contiguous input string from the initial to the stressed [abC] or from the stressed to the final syllable [Cde] is preserved, do not realize a templatic form for the input /abCde/. However, they do map some inputs to templatic outputs. Thus, an initially stressed input such as [Abcde] gives rise to two possible outputs, [A] and [Ab], which both conform to the description that the input string from the first to the stressed syllable—in this case trivially coinciding with [A]—be preserved. The two outputs [A] and [Ab] contrast as to whether they realize a mono- or a disyllabic template. Once the initial-to-stress requirement is fulfilled, these mappings still have room for a choice between the two template types. The two [abC] languages are therefore languages where outputs are generally atemplatic, but—given specific structural features of the input (i.e. ‘initially stressed’)—templates do emerge. We hence distinguish between two [abC] languages, [abC-m] and [abC-di], according to the template they realize for initially stressed outputs. The same is true for languages [Cde-m] and [Cde-di], when finally stressed inputs are concerned. We call these patterns ‘long,’ or ‘atemplatic,’ to distinguish them from ‘short,’ ‘templatic’ patterns, which realize templatic forms for all inputs, abstracting away from the fact that they, as well, have templatic forms in their inventory. Language 12 forms a class by itself as the language where no truncation occurs.
On the basis of the factorial typology it is now possible to propose an extensional classification of BTT, based on the surface traits exhibited by the groups of languages populating it. We group languages according to extensional traits that they share, such as the length of truncation, whether they make use of a monosyllabic or disyllabic template, whether they preserve the stress of the base and whether their anchoring is oriented towards the left or the right edge of the word.
-
(23)
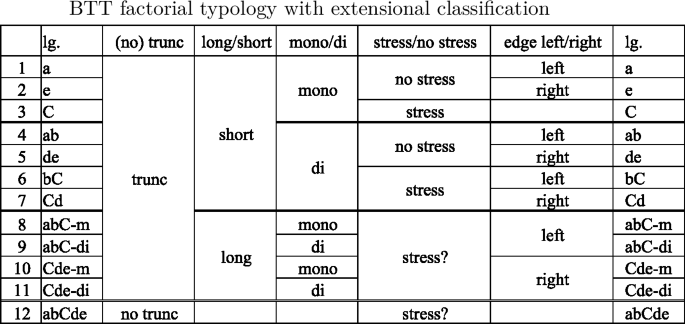
In the extensional domain of the truncation typology we distinguish classes of languages according to the degree of truncation they undergo as well as to their anchoring properties. In one language, lg. 12 [abCde], no truncation occurs at all, while in all other languages some truncation does occur. There is a set of languages which can be characterized as ‘short’ truncations, in the sense that they consistently truncate the base down to a templatic mono- or disyllable, as opposed to ‘long’ truncations, which copy from the initial to the stressed [abC-m/di] or from the stressed to the final syllable [Cde-m/di]. Both short and long truncation patterns furthermore fall into two groups contrasted by whether they choose a mono- or a disyllabic template. With respect to the preservation of anchor points, there are truncation patterns preserving the stressed syllable, such as [C, bC, Cd] and others that don’t, such as [a, e, ab]. Finally, we can distinguish between patterns anchoring to the left edge [a, ab, abC-m/di], or ‘stretching’ towards the left [bC] and patterns that anchor or ‘stretch’ towards the right [e, de, Cde-m/di, Cd].
An extensional classification of this type, based on the features of output forms alone, cannot tell us anything about the forces shaping the different classes, which are hidden in the interactions of the constraints generating the typology. Note, in fact, that there may be more than one plausible extensional classification. Thus, it is not completely clear which languages should fall into the category of stress anchoring languages. Should we classify as such only the templatic truncation patterns [C, bC] and [Cd], where stress-anchoring is in clear contrast to left and right anchoring? Or should we include also the long truncations [abC-m/di] and [Cde-m/di], which always include the stressed syllable, and hence do not create any contrast with other anchoring patterns? And what about [abCde]? Is this a stress-preserving pattern ([C] is mapped faithfully, after all), or is the presence of [C] in the output only a by-product of full mapping of the input to the output? The question marks in the column referring to stress preservation express this indeterminacy. It will be resolved by the property analysis of BTT, which will reveal that preservation of [C] in lgs. 8–12 has a different grammatical source than preservation of the stressed syllable in all other languages. Copying of [C] in these patterns is triggered by different ranking conditions, defining the length of truncation, not the choice of a prominent anchor point. In intensional terms, it is therefore not appropriate to classify languages 8–12 together with other stress-preserving languages, since the grammatical forces leading to stress-preservation are not the same. The intensional analysis of the ranking conditions defining the extensional traits can thus resolve indeterminacies in the extensional classification.
A comparison of the set of languages of BTT with attestations of truncation patterns in the world’s languages reveals that all patterns are attested, though some of them are represented in our database only by ambiguous patterns or occur as single attestations.Footnote 24
-
(24)
Atemplatic truncation patterns of the type 8–11 are rare in general, and it is rare that enough data is available to distinguish patterns parsing monosyllabic outputs for initially or finally stressed inputs ([abC/Cde-m]) from patterns realizing a disyllabic output for the same inputs. Italian06 must be classified as [abC-m], since—in this particular vocative pattern—initially stressed names such as Bárbara are truncated to Bá (and not to Bárba). A candidate example of the [abC-di] pattern is Dutch04. The generalisation described in van de Vijver (1997) is that the pattern showing initial-to-stress anchoring is restricted to bases that are stressed on the second syllable (Patríes ⧫ Patrícia), and that truncations for bases with initial stress are generally disyllabic (Górba ⧫ Górbasjov, classified as Dutch02 in our database). More research is needed, though, as Dutch has a monosyllabic pattern as well and the generalisations cited by van de Vijver are not without exceptions.
4.3 BTT—property analysis
In order to arrive at an intensional classification of BTT we examine the grammars of its languages and extract its typological properties. By typological properties we mean the ranking conditions defining a formal typology. They correspond to the grammatical forces which determine the whole of the typology.
To give a basic example of a typological property, let us reduce the typological space of BTT to disyllabic, stressless inputs and monosyllabic outputs. Let us call the typology inhabiting this world ETT, for Elementary Truncation Typology.Footnote 25 Let us then posit as ETT.Gen a single input /ab/ mapped to one of two possible output forms, [a] or [b]. Assume, finally, that this reduced candidate set is evaluated by the five constraints defined above for BTT.Con.
-
(25)
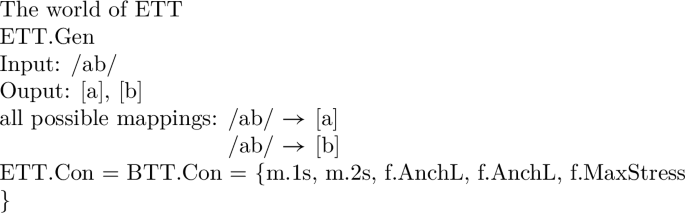
The factorial typology of ETT contains exactly two input-output mappings, language /ab/ → [a] and language /ab/ → [b]. Let us now examine the grammars of ETT. By ‘grammar of a language’ we mean the set of linear orders of constraints defining the language, represented either as a set of Elementary Ranking Conditions in a comparative tableau (ERCs, Prince 2002a, 2002b; and seq.), or as a set of Hasse diagrams.Footnote 26
The grammars of the two languages /ab/ → [a] and /ab/ → [b] differ with respect to the ranking of the two constraints AnchL and AnchR. The first dominates the latter in language /ab/ → [a], as the preference of AnchL for output [a] over [b] (a ∼ b) shows, while the opposite ranking holds in the grammar of /ab/ → [b], where output [b] is preferred by AnchR over [a].
-
(26)
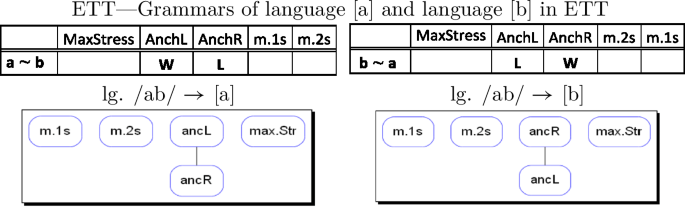
All other constraints do not play any role in ETT. MaxStress is satisfied vacuously by each candidate (there is no input stress which could be preserved), m.1s is satisfied by both candidates and m.2s by neither. We then have exactly two ranking conditions, AnchL > AnchR and AnchR > AnchL, determining the whole of ETT. Following Alber and Prince (2015, 2017, in prep.), we recognize one typological property for ETT, AnchL < > AnchR, which we may call Edge.L/R, with two logically opposite values, L and R, defining all classes of languages in ETT, of which there are exactly two, /ab/ → [a] and /ab/ → [b]. Nothing more is needed to define the rankings determining the languages populating the universe of ETT.
-
(27)

BTT, which aims at coming closer to the empirical reality of truncation patterns than ETT, has a more complex structure with respect to its typological properties. The table in (28) gives an overview of the five typological properties of BTT, the contrasts between the languages of BTT that they implement, and the constraint classes playing a role in the definition of the properties. The details of each property will be discussed extensively in the following sections, but presenting the results of the analysis beforehand in this reference table should make it easier for the reader to follow the discussion.
Following Alber and Prince (2015, 2017, in prep.), we use the suffixes ‘.dom’ and ‘.sub’ to refer to the highest-ranked or lowest-ranked constraints within a constraint class (see Sect. 4.3.2 for detailed discussion). For names of properties we use the following convention: Name.valueA/valueB, where value A and B correspond to the two logically opposite values expressed by the ranking conditions defining the property. Thus, Edge.L/R represents the property Edge, which comes with the values L and R, where L corresponds to the ranking condition AnchL > AnchR and R to the ranking condition AnchR > AnchL. The symbol (< >) conveniently summarizes both ranking conditions in the definition of the property. Classes of constraints are represented in caps (TMPL, EDGE, PROM), to distinguish them from property names. They are described in the last rows of the table.
-
(28)
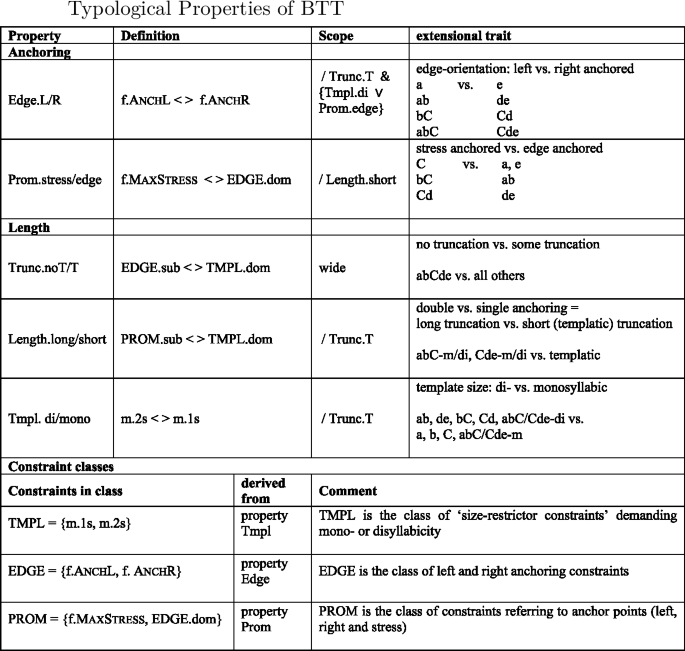
Before the properties are discussed one by one in the remainder of this section, it is useful to give an overall idea of the meaning of the five properties characterizing BTT and the role that constraint classes play in them.
There are two classes of properties defining BTT, one related to anchor points, and one to the length of truncation patterns. With respect to the former we recognize the property Edge.L/R, which is defined as in our example of ETT above, in terms of an antagonism between the constraints AnchL and AnchR deciding whether to anchor a truncatum to the left or the right of its base. These two constraints form a class, the class of EDGE constraints, which plays an important role in the property Prom.stress/edge, the second property concerned with anchor points. In this property, the EDGE constraints are antagonistic to MaxStress, the constraint favoring anchoring to the stressed syllable of the base.
The length of truncation patterns is determined by the properties Trunc.noT/T, Length.long/short and Tmpl.di/mono. The ranking conditions defining the property Trunc.noT/T decide whether we have any truncation at all. The antagonists here are the EDGE constraints on one side and the class of TMPL constraints, m.1s and m.2s, on the other. While the former favor anchoring to both edges, hence copying from one edge to the other of the base, the latter would favor any truncation which brings the truncatum closer to a mono- or disyllabic template. The property Length.long/short decides whether the truncatum is always templatic, hence ‘short,’ or whether it may be ‘long,’ i.e. of the [abC/Cde] type. Here the class of PROM constraints, which includes the EDGE constraints (AnchL and AnchR) as well as MaxStress, comes into play. They prefer anchoring to multiple anchor points, while their antagonists, the TMPL constraints, favor short, templatic copying. Finally, the property Tmpl.di/mono decides whether templatic truncation is of the mono- or disyllabic type.
Note that not every property plays a role in every class of grammars in the system. This fact is expressed by the concepts of mootness and scope, developed in Alber and Prince (2015, 2017, in prep.). If we consider, for instance, the property Tmpl.di/mono, it is clear that this property plays a role only among languages that do have some degree of truncation, i.e. languages that are specified for the value Trunc.T. In languages without truncation (i.e. the single lg. 12, [abCde]), the question of whether the truncatum should realize a mono- or disyllabic template has no meaning. We say that the property Tmpl.di/mono is moot with respect to the property value Trunc.noT and has scope over Trunc.T. Similarly, the issue of deciding between long and short truncations decided by the property Length.long/short arises only in Trunc.T languages. The property Trunc.noT/T, on the other hand, has wide scope, i.e. all grammars in the typological system have to satisfy one or the other of its values.
In Property Theory, relationships of mootness and scope receive a precise definition in terms of ranking conditions and their satisfaction by (classes of) grammars. Thus mootness of the property Tmpl.di/mono with respect to the value Trunc.noT means that the ranking conditions expressed by Tmpl.di/mono (m.2s < > m.1) are satisfied by the grammars defined by the property value Trunc.noT. In other words, both values of Tmpl.di/mono, m.2s > m.1s and m.1s > m.2s, are compatible with the grammar of the single Trunc.noT language, lg. 12. That this is indeed the case becomes evident from a brief examination of the grammar of lg. 12 represented as a Hasse diagram:
-
(29)

Since m.1s and m.2s are not ranked with respect to each other, one value of the property Tmpl.di/mono (e.g. m.2s > m.1s) will be satisfied by some linear orders of constraints compatible with the grammar of lg. 2, while the opposite value (m.1s > m.2s) will be satisfied by others. Tmpl.di/mono hence is moot with respect to the property value Trunc.noT and has scope only over the property value Trunc.T.
In the presentation of properties in the next sections we will discuss in detail both the ranking conditions defining each property as well as their scope.
4.3.1 Property: Edge.L/R—edge orientation
The property Edge.L/R distinguishes between languages which are left anchored and languages which are right anchored (see table in (23) above). In what follows, we give the ERC (Elementary Ranking Conditions; Prince 2002a, 2002b, et seq.) representation of the property and illustrate each property value by means of Hasse diagrams of examples of languages instantiating this value. The property Edge.L/R is exemplified by the Edge.L language [bC] and the Edge.R language [Cd].Footnote 27
-
(30)
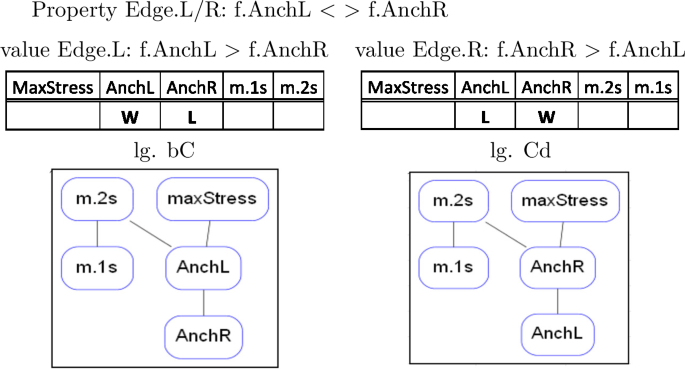
While the grammar of [bC], with AnchL dominating AnchR, satisfies the ranking condition of the property value Edge.L, the opposite ranking holds in [Cd]. The grammars of the two languages are otherwise identical. In a similar fashion, the grammars of lg.s [ab], [a] and [abC-m/di] satisfy the value Edge.L, while lg.s [de], [e] and [Cde-m/di] are defined by the opposite ranking of the value Edge.R (see Appendix 3 for all grammars of BTT).
There are only two languages where the Edge.L/R contrast does not play any role and AnchL and AnchR are not ranked with respect to each other. These are the monosyllabic language [C] and the language without truncation, [abCde]. In both cases it is clear why edge orientation should not play any role. A monosyllabic, stress-anchored truncation like [C] does not distinguish between left and right edge orientation. It is too small to stretch towards one edge or the other. Similarly, a language which copies the whole input faithfully does not express a preference for the left or the right edge. It is too large to express such a preference. In languages [C] and [abCde], therefore, the property Edge.L/R is moot—it does not instantiate any contrasts. This implies that the property Edge.L/R has scope over the properties defining the grammars of all languages other than [C] or [abCde]. This straightforward fact can be expressed positively only by a series of restrictions. In order to exclude [abCde] we can say that the property Edge.L/R is limited to grammars which do exhibit truncation, i.e. satisfy property Trunc.T. The grammar of [C] is excluded if we state that the scope of the property Edge.L/R extends only to grammars which either satisfy the property value Tmpl.di, i.e. realize a disyllabic template, or are of the Prom.edge type, i.e. are edge-, not stress-anchored. This includes all disyllabic languages, but, among the monosyllabic, only those which are either left- or right-anchored.
4.3.2 Property: Prom.stress/edge—stress-anchoring or edge-anchoring
The property Prom.stress/edge determines whether a language is stress-anchored or edge-anchored. In order for a language to be stress-anchored, the constraint MaxStress has to dominate the class of EDGE constraints, AnchL and AnchR, which are competing with it for anchor positions. This is expressed by the ranking MaxStress > EDGE.dom, where the operator .dom in EDGE.dom calls up whichever of the two EDGE constraints is dominant. Under the opposite ranking, EDGE.dom > MaxStress, edge-anchoring will be favored over stress-anchoring.Footnote 28 As will become clear when discussing the property Length.long/short (see Sect. 4.3.4), the property Prom.stress/edge is active only among short, templatic truncation patterns.
The operator .dom is used here to specify the interaction between classes of constraints. If MaxStress dominates the dominant EDGE constraint, it will dominate both EDGE constraints. The logically opposite ranking, EDGE.dom > MaxStress, entails that at least one of the EDGE constraints dominates MaxStress. This is true if the constraint dominating MaxStress happens to be the dominant EDGE constraint alone, but it is also true if the subordinate EDGE constraint (and hence both EDGE constraints) dominates MaxStress. Thus the .dom operator is useful in defining ranking relations involving classes of constraints and specifying whether, in any given constraint interaction, all or some constraints of a class dominate or are dominated. Of similar usefulness is the variable .sub, which denotes the subordinate, i.e. lowest ranked constraint, of a constraint class. This operator will be crucial in the definition of the properties Length.long/short and Trunc.noT/T, below.
We give the ERC representations of the two values of the property Prom and Hasse diagrams of example languages satisfying them. In the example languages the dominant EDGE constraint is AnchL.
-
(31)
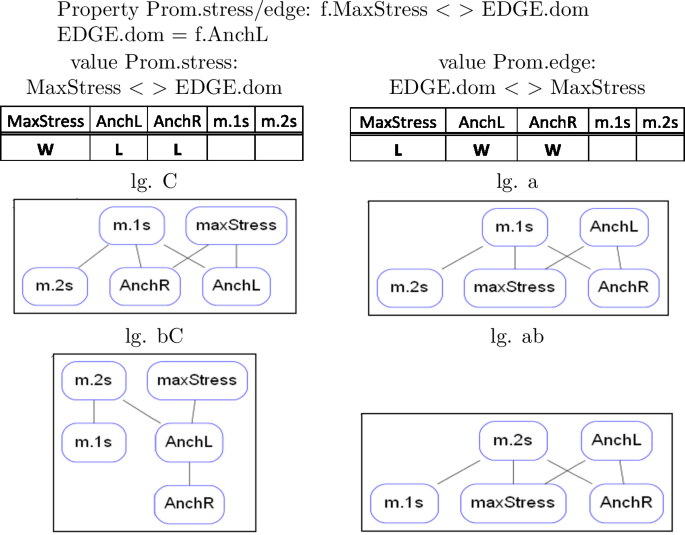
In languages [C] and [bC] MaxStress dominates both EDGE constraints. In [C], the EDGE constraints are not ranked with respect to each other; but in every possible linear order consistent with this grammar, MaxStress will dominate the dominant of the two EDGE constraints, whichever that might be. In languages [a] and [ab] the property value Prom.edge is satisfied, since the dominant of the two EDGE constraints (here: AnchL) dominates MaxStress.
The property value Prom.stress is satisfied in languages [C], [bC] and [Cd]. The opposite value, Prom.edge, is satisfied in languages [a], [ab], and also in [e] and [de], where AnchR acts as the dominant EDGE constraint (see Appendix 3 for all grammars).
The antagonism between MaxStress on the one hand and the class of EDGE constraints on the other plays out only in the realm of short, mono- or disyllabic truncation patterns. As soon as we add long patterns of the [abC, Cde] type to the picture, this clear antagonism breaks down. As we will see when discussing the property Length.long/short, which distinguishes short from long truncation patterns, MaxStress and one of the EDGE constraints can actually join forces to antagonize the TMPL constraints in their strive for short patterns and thus lead to the generation of long patterns, doubly anchored to one edge and the stressed syllable. With respect to scopal issues this means that the property Prom.stress/edge is limited in its scope to grammars satisfying the property Length.short and is moot in the grammars characterizing Length.long languages.
4.3.3 Property: Trunc.noT/T—truncation yes or no
The length of truncation patterns is determined by the interaction of the PROM constraints AnchL, AnchR and MaxStress with the TMPL constraints m.1s and m.2s, and by the interaction of the TMPL constraints among themselves. A first distinction is made by the property Trunc.noT/T between the single language that does not allow for any truncation and all other languages, which do allow for some truncation of the input material.
In BTT, truncation is blocked whenever both EDGE constraints dominate both TMPL constraints. In this typological system, anchoring to both edges necessarily requires full copying, from the first to the last segment.Footnote 29 This requirement is expressed by the property value Trunc.noT, satisfied in the no-truncation language [abCde]:
-
(32)
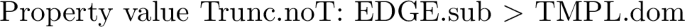
EDGE.sub, via its suffix .sub, demands that the subordinate EDGE constraint dominate TMPL.dom, hence that both EDGE constraints do. They will dominate the dominant TMPL constraint, which means that they will dominate both TMPL constraints, in whichever order they might occur.
The opposite property value, Trunc.T, instantiated by the ranking condition TMPL.dom > EDGE.sub, holds in every language exhibiting some degree of truncation. In every one of these 11 languages, some TMPL constraint (m.1s or m.2s) dominates at least one of the EDGE constraints.
The two languages [abCde] and [abC-m] illustrate the rankings defining the property Trunc.noT/T, where [abC-m] is taken as a representative for forms where some truncation occurs. In [abC-m] the subordinate EDGE constraint is AnchR and the dominant TMPL constraint is m.1s, since [abC-m] copies input material from the first to the stressed syllable and realizes monosyllabic templates for initially stressed inputs.
-
(33)

For [abCde] to win, both EDGE constraints have to dominate both TMPL constraints, as is apparent in the Hasse diagrams. The opposite value of the property Trunc is satisfied by the ranking condition TMPL.dom > EDGE.sub, telling us that the dominant TMPL constraint (= at least one TMPL constraint) must dominate the subordinate (= at least one) EDGE constraint. We find this value realized in the Hasse diagram of language [abC-m], where m.1s dominates the subordinate EDGE constraint AnchR. In the grammar of [abC-m], m.1s is the dominant TMPL constraint, since—if given a choice—the output will be monosyllabic, not disyllabic. It is therefore m.1s which dominates the subordinate EDGE constraint, AnchR, in the Hasse diagram.
Note that which constraint plays the role of EDGE.sub and which constraint plays the role of TMPL.dom in a certain grammar, is decided by other properties satisfied by these grammars. These are the properties Edge.L/R and Tmpl.di/mono. Thus, EDGE.sub may be incarnated by AnchR, as in the example of lg. [abC-m], or its role may be played by AnchL, as in lg. [Cde-m], which is a right-aligning language. Similarly, the dominant TMPL constraint may be m.1s, as in this example, or it may be m.2s. But for all languages other than [abCde] (i.e. languages that exhibit some truncation) it holds that one of the TMPL constraints must dominate at least one of the EDGE constraints. This can be verified in the grammars given in Appendix 3.
4.3.4 Property: Length.long/short—long truncation or short (templatic) truncation
Among languages that exhibit some truncation, there are those that contain forms which may be ‘long’ and atemplatic [abC, Cde], and others which are consistently ‘short’ and templatic, i.e. mono- or disyllabic.Footnote 30 The distinction between these two classes of languages is made by the property Length.long/short, which takes scope over languages of the Trunc.T type, which allow for truncation of input material.
The distinction between the two groups of languages is brought about by the interaction of the class of PROM constraints on the one hand, which include MaxStress and the EDGE constraints, and the class of TMPL constraints on the other. The property is defined as follows:
-
(34)
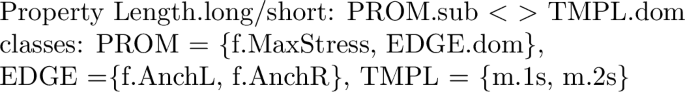
The sense of the property value Length.long is straightforward: in order to obtain a long, atemplatic truncation (as opposed to a short, templatic one), two PROM constraints (PROM.sub) must join forces and dominate the TMPL constraints, which seek to impose a templatic length. One of the two PROM constraints has to be MaxStress,Footnote 31 the other one is whichever EDGE constraint happens to be dominant. Thus the essence of long truncations is their demand for double anchoring.
Under the opposite property value Length.short, generating templatic truncation patterns, TMPL.dom forces weighing one of these anchors: either the anchor to stress or the anchor referring to the dominant edge is abandoned. We obtain an edge-anchored pattern in the former case and a stress-anchored pattern in the latter.
The logic of the ranking conditions for the value Length.long (both MaxStress and the dominant EDGE constraint over both TMPL constraints) and those for the value Length.short (dominant TMPL over either MaxStress or both EDGE constraints) is made explicit in what follows:
-
(35)

The ERC representations of the two property values are given below. The Hasse diagrams in (36) represent example languages where EDGE.dom is ANCHL and TMPL.dom is m.2s. The Hasse diagram for the language [abC-di] instantiates the value Length.long, while the Hasse diagrams for the languages [ab] and [bC] instantiate the two disjuncts of the value Length.short.
-
(36)
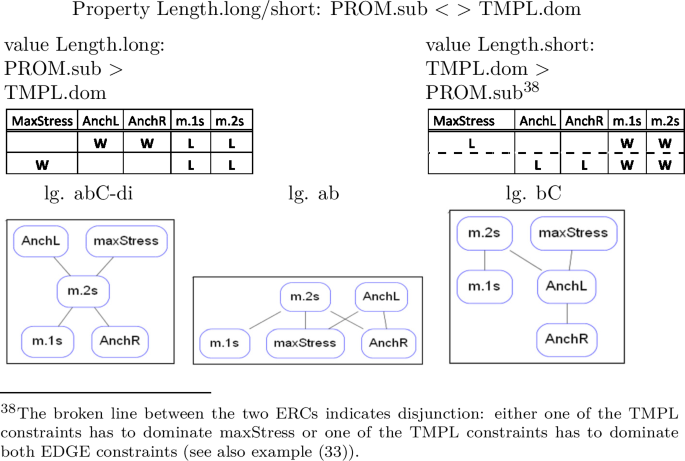
In the grammar of [abC-di], the property value Length.long is realized since MaxStress and the dominant EDGE constraint dominate both TMPL constraints. In the grammars of languages [ab] and [bC] we see the logically opposite property value Length.short (TMPL.dom > PROM.sub). In the Hasse diagram of [ab], the dominant TMPL constraint m.2s dominates MaxStress. In the grammar of language [bC], the dominant TMPL constraint m.2s dominates the dominant EDGE constraint AnchL, thus fulfilling the second disjunct of Length.short = TMPL.dom > EDGE.dom, via the domination relation [m.2s > AnchL] and [m.2s > AnchR].
The same contrast of property values can be seen in the grammars of languages [abC-m] and [Cde-m/di] when compared to all other languages with mono- or disyllabic outputs, as can be verified by consulting the grammars in Appendix 3. What may change, of course, is which of the TMPL constraints assumes the role of TMPL.dom and which constraints incarnate PROM.sub.
4.3.5 Property: Tmpl.di/mono—di- or mono-syllabic templates
The last property defining BTT is again an elementary property, involving two single constraints as antagonists. The size of templates is decided by the property Tmpl.di/mono = m.2s < > m.1s:
-
(37)
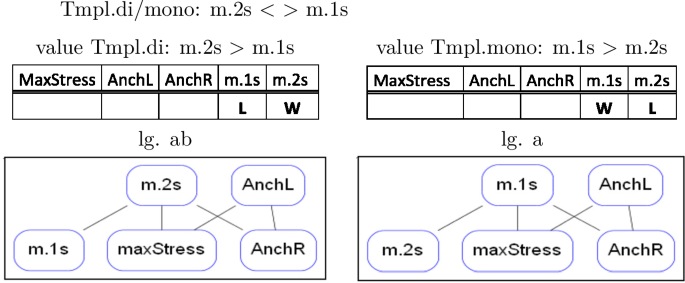
The Hasse diagrams of the example languages [ab] and [a] show that they differ in the ranking of m.1s and m.2s. As can be verified in the grammars of Appendix 3, the former ranking distinguishes all monosyllabic truncation patterns, the latter all disyllabic patterns. Furthermore, the property Tmpl.di/mono distinguishes the two pairs of long truncation patterns, [abC-m] vs. [abC-di], and [Cde-m] vs. [Cde-di]. Although these patterns do not yield a templatic form for longer inputs with medial stress, such as the input base [abCde], templates do emerge for input forms with initial or final stress (see discussion in Sect. 4.2).
Property Tmpl.di/mono has scope over languages where some truncation occurs and is moot in the Trunc.noT language 12, which faithfully preserves all input material.
4.4 Intensional classification of BTT
The five typological properties extracted from the grammars allow us to classify the languages of BTT intensionally, i.e. according to the ranking conditions that define the whole of the typology. The intensional classification of BTT is represented in the following property table, where grey cells instantiate one property value and white cells the other:
-
(38)
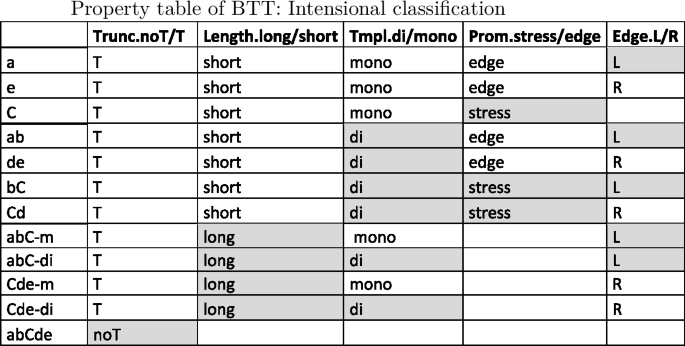
A property table should show that the combination of all values of all properties yields exactly the twelve languages of BTT, thus validating the analysis of this specific typological system (see also Appendix 4 for a property table of BTT verified with the property-checker of OTWorkplace). This is in fact the case, within the limits of mootness relationships, indicated by blank cells.
Thus, we see that there are only two languages—the monosyllabic, stress-anchoring language [C] and the language without truncation [abCde]—which are moot with respect to the property Edge.L/R: their grammars do not rank the constraints AnchL and AnchR with respect to each other. Mootness entails that the property Edge.L/R does not take scope over these two languages. Mootness is also evident for the properties Tmpl.di/mono and Length.long/short, which play out only in languages exhibiting some truncation.
The property of Prom.stress/edge is distinctive only among short patterns, distinguishing [C] from the other monosyllablic truncation patterns, and [bC] and [Cd] from other disyllabic patterns. Interestingly, the property Prom.stress/edge is not expressed in the grammars of the languages [abC-m/di] and [Cde-m/di], even though these languages do preserve the stressed syllable C. The reason is that preservation of C in the stress-anchoring patterns of languages [C], [bC] and [Cd] and preservation of C in languages [abC-m/di] and [Cde-m/di] have different sources, in terms of constraint interaction. In [C], [bC] and [Cd], preservation of the stressed syllable is obtained by the interaction of MaxStress with the EDGE constraints AnchL and AnchR, via the property Prom.stress/edge. In languages [abC-m/di] and [Cde-m/di], preservation of the stressed syllable is the result of the interaction of MaxStress (and one of the EDGE constraints) with the TMPL constraints m.1s, m.2s, via the property Length.long/short (compare the columns of properties Prom.stress/edge and Length.long/short in the property table above). In the case of the property Prom.stress/edge, the ranking decides to which of the prominent positions the truncatum should be anchored: whether to the stressed, the leftmost or the rightmost syllable. In the case of the property Length.long/short, the question is not so much as to which position should be favored in anchoring as to how many prominent positions should be involved in anchoring. The TMPL constraints favor anchoring to a single position; their domination by MaxStress and the dominant EDGE constraint makes double anchoring possible. And double anchoring leads to preservation of the stressed syllable C. The two reasons to preserve C are illustrated here by the respective properties involved:
-
(39)

The property analysis here reveals a feature of the typology of anchoring which is not at all visible in the extensional description of the factorial typology alone. The presence of C in a pattern can be either due to the internal conflict among the PROM constraints (MaxStress, AnchL and AnchR), or it can be the result of the group of PROM constraints battling the class of TMPL constraints in their quest for double anchoring. In other words, having C or not in a truncation pattern can either be due to a choice of short patterns to anchor to stress, instead of anchoring to an edge, or it can be due to choosing a doubly anchored pattern over a templatic pattern.
In a similar fashion, the property Trunc.noT/T, which decides on whether we have truncation or we don’t, is really about double anchoring to edges, since it sees the EDGE constraints joining forces against the size-restricting TMPL constraints in generating the no-truncation language [abCde]. Only once the demand of double edge anchoring is lifted can real truncation begin to exist. In this case, of course, the presence of C in the language [abCde] is not linked to activity of the constraint MaxStress at all, but rather is the by-product of full copying.
Property analysis thus allows us to resolve the question marks present in the extensional classification of the typology in (23), where we asked ourselves whether languages of the [abC] or [Cde] type and the no-truncation language [abCde] should be classified as stress-anchoring. Since the property Prom.stress/edge is moot in languages [abC, Cde, abCde], it is not possible to classify them together intensionally (i.e. as classes defined by typological properties) with the Prom.stress languages [C, bC, Cd]. The reason is that the former are generated through interaction of MaxStress with AnchL and AnchR, while the latter are the result of the interaction of MaxStress with the TMPL constraints m.1s and m.2s or, in the case of [abCde], of the interaction of the class of EDGE constraints with the size-restricting TMPL constraints. Thus the intensional classification, based on the grammatical forces generating the surface patterns can resolve indeterminacies and arbitrariness present in a classification based on surface patterns alone.
There is a final feature of the analysis of BTT which deserves comment, because of its interest for Property Theory in general. The analysis of BTT relies heavily on the use of the constraint classes EDGE, PROM and TMPL. While it may seem obvious that the anchor constraints AnchL and AnchR should form a class of EDGE constraints, and m.1s and m.2s the class TMPL, the definition of PROM as including MaxStress and EDGE.dom goes beyond pure and immediate intuition. We start understanding why the constraint classes in BTT are defined in a certain way once we realize that each of them can be derived from specific properties. Thus, the constraint class EDGE contains the antagonists which define the property Edge.L/R: AnchL and AnchR. TMPL contains the antagonists defining the property Tmpl.di/mono. And the class PROM includes those constraints and constraint classes, MaxStress and EDGE.dom, which are direct antagonists in the property Prom.stress/edge, defined as MaxStress < > EDGE.dom. It seems thus to be a common (if maybe not exclusive) feature of typological properties that they make use of constraint classes which are based on the antagonists of other properties. This is not too surprising, since constraints antagonizing each other in some property are sensitive to similar structures, and hence may behave as a class in some other context.
Also of interest is the fact that the derivation of constraint classes in BTT is recursive in one instance: the property Edge.L/R generates the class of EDGE constraints, which are involved in the definition of the property Prom.stress/edge as MaxStress < > EDGE.dom. The property Prom, itself, generates the constraint class PROM {MaxStress, EDGE.dom}, which plays a role in the definition of the property Length.long/short as PROM.sub < > TMPL.dom.
Summarizing, we see that of the five properties of BTT, four classify the systems according to the number and type of anchors:
-
(40)
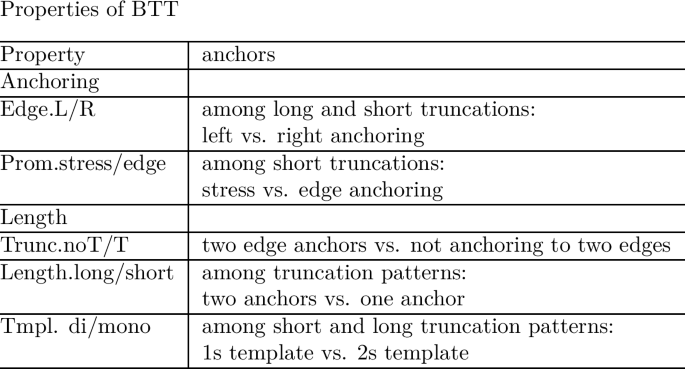
Truncation thus is, to a large extent, about anchoring. This insight is not something a superficial scrutiny of the factorial typology can bring about. Only once we understand how the different rankings generating the typology cluster into properties will we truly understand how to classify the typology intensionally, i.e. according to the grammatical forces that determine it. While the factorial typology tells us what our analysis predicts, full understanding of the typology will only set in once we understand which properties have generated it.
5 Conclusion
This paper makes a twofold contribution to existing research on the structure of truncations in the world’s languages. On an empirical level, we presented a systematic overview of attested anchoring patterns. On a theoretical level, we showed that property analysis can be fruitfully applied not only to model the existing typology of anchoring, but also to yield new insights into what grammatical factors are constitutive of truncation. Crucially, we saw that an adequate grammatical model of truncation needs to be based on a theory of anchoring.
Our findings have several important theoretical implications. First of all, they contribute a new rationale for the classification of truncation patterns into different types, an issue that has been the subject of much debate in the literature (cf. e.g. Manova 2016 for a recent summary).
Secondly, they provide interesting new evidence for the gradient nature of templates, in that they show that truncated forms do not always correspond to an invariant word shape. Instead, the word structure of truncated forms often crucially depends on the ranking of prominence-preserving anchoring constraints (see the discussion of [abC] and [Cde] languages in Sect. 4). This fact poses a challenge to accounts of morphological truncation that account for templates as fixed shapes, assuming that truncation shapes always correspond to metrical constituents. For analyses which use templates to argue for the existence of certain types of feet (e.g. Martínez-Paricio and Torres-Tamarit 2019), this means that they have to take into account possible anchoring effects as well.
Given the important role that anchoring seems to play in truncation, the question arises whether template-generating constraints, in the spirit of Generalized Template Theory (McCarthy and Prince 1999), should play a role in truncation at all. At first glance it would seem that even in our model the effect of m.1s and m.2s does not go much beyond demanding outputs to ‘be shorter.’ It seems that disyllables are an exception here, though, as they also preserve non-prominent material. The interaction between template-generating sets of constraints, which are more complex than m.1s and m.2s used here, remains therefore an interesting field for future explorations.
With respect to a deeper understanding of the phenomenon of anchoring, we have shown that the definition of edge-anchoring constraints as faithfulness constraints which are sensitive to the distance of the anchoring point to the edge of the prosodic word accounts for gradience effects in anchoring observed in certain languages where initial marked segments are skipped and anchoring occurs to the leftmost unmarked segment. The same definition of edge-anchoring constraints also avoids the unwarranted predictions that Max constraints make, when used to model maximal copying from the base. The use of edge-anchor constraints defined this way in our formal model BTT furthermore shows that they lead to the generation of languages which in fact appear to be attested in the world’s languages.
Our formal model of truncation, BTT, contains a set of 12 languages which by and large cover the typologies of truncation patterns in the world’s languages, both with respect to their size and their anchoring behavior. Comparison of the factorial typology with the patterns attested in natural languages also makes clear that any typological investigation of truncation has to contend with the fact that some patterns are ambiguous in their classification and that, for other patterns (e.g. the [Cde] patterns discussed in Sect. 4), only single attestations can be found. The generation of a complete formal typology has the merit of making the predictions of the model explicit and to stimulate investigation of the question of why certain patterns might be rarer than others.
The property analysis of BTT reveals five typological properties, in the form of ranking conditions, which determine the size and the anchoring behavior of the various truncation patterns. The output of the analysis is an intensional classification of the typology, which is based on the grammatical principles determining it, and is thus void of the potential arbitrariness of classifications based on extensional traits alone.
Note also that while the five properties defining BTT bear a superficial resemblance to parameters proposed in work outside of Optimality Theory (for stress typologies, see e.g. Halle and Idsardi 1995 et seq.), what sets them apart from such approaches is that they are not hypothesized by the analyst, but emerge independently, from the interaction of primitive constraints or classes of constraints. Once Gen and Con are defined, the typological properties of a typological system are an inevitable prediction of the theory, not something imposed on it.
Finally, the property analysis makes us understand the crucial role that anchoring plays in truncation: constraints referring to anchor points do not simply guarantee anchoring to these specific points, but—in interaction with template constraints—also decide on the size of a given truncation pattern.
Notes
Examples of English clipped compounds include op art (⧫ optical art) or scigov (⧫ science government) (cf. Bauer 2006; Beliaeva 2014). Spanish examples are clipped complex names like Joséma (⧫ José María) or Maribél (⧫ María Isabél) (Martínez-Paricio and Torres-Tamarit 2019). Examples of abbreviations of syntactic expressions can be found among secret languages (e.g. Boontling, Weeda 1992). Complex expressions were excluded because very often such forms seem to anchor to morphological constituents within the expression (e.g. to the compound constituents science and government) rather than to phonologically prominent material. Given that the number of pertinent forms that are reported in the literature are generally very low, it is often hard to distinguish between phonological and morphological anchoring domains.
Thanks to Tekabe Legesse Feleke, Haykanush Barseghyan, Frunze Hovhannisyan and Mele Taimoipeau for sharing name truncations with us.
Note that following standard methodologies in morphological analysis, we should consider not only predictability of form, but predictability of mappings of form and meaning or function, and we should assume that different formal patterns should correspond to different meanings or functions. We focus on formal aspects here only. Very little is known about the meaning of truncations. Most existing accounts assume that the function of many truncation patterns is a morpho-pragmatic one (e.g. Schneider 2003; Barbaresi and Dressler 2020), similar to that of diminutives, but little is known about functional differences between formally different patterns (cf. Arndt-Lappe 2018; Alber and Kokkelmans, to appear, for some initial evidence; cf. Alber and Arndt-Lappe, to appear, for discussion).
We say here that a configuration must be ‘unambiguously’ attested because forms may (and in fact often are) ambiguous between patterns. For example, the form bluebs (⧫ blúeberries, cf. (4) above) is ambiguous between at least three different English patterns: the pattern for which the form is documented in Spradlin and Jones 2016, which preserves the stretch from the beginning of its base to the stressed syllable (English07, cf. the discussion of the data in (4)); the monosyllabic pattern which anchors to the initial syllable of the base (English01); the monosyllabic pattern which anchors to the main-stressed syllable of the base (English02).
Note also that, as this paper is concerned with purely formal and not with semantic properties of truncation, we do not distinguish between name truncations and the truncation of non-names (cf. e.g. Lappe 2007; Berg 2011; Arndt-Lappe 2018 for discussion of why this distinction is important from a morphological perspective).
In some initially anchored patterns anchoring to the left edge of the word might be gradient, though. In these patterns the anchor point is as close as possible to the left edge of the base, but not in absolute initial position, if restrictions on markedness exclude the initial position as a suitable anchor point (see discussion of Russian and Fon in Sect. 3.1).
We thank Alan Prince for suggesting this line of thought.
We use slashes (/ /) and brackets ([ ]) here to refer to input bases and output truncated forms, respectively. We do so to enhance readability, without a theoretical commitment to what kind of representations (underlying or surface representation) is relevant. Cf. Lappe (2007:Chap. 2.5) for arguments why both types of representation matter.
Patterns such as these correspond to the monosyllabic, left-anchoring pattern [a] in the formal typology in Sect. 4. See (31) and Appendix 3 for the grammar of [a] patterns represented in a comparative tableau and as a Hasse diagram. For analysis including violation tableaux of patterns such as (12) see also Alber and Arndt-Lappe (2012).
For French reduplicating patterns derived from vowel-initial bases see also Nelson (1998, 2003). Nelson, however, considers only examples interpretable as stress-anchored (Titín ⧫ Ernestín), for which she argues that, indeed, the form is stress-anchored because initial anchoring is ruled out by the Onset requirement. However, Mazzola (2017) shows that French has an initial-anchoring and a stress-anchoring pattern, and that the edge-anchoring pattern displays gradience effects of the type described here. Zazá ⧫ Isabélle is an example.
Note that all patterns in (14a) are actually ambiguous between stress anchoring and final anchoring (cf. our coding of these patterns in the Appendices). The reason is that all our examples for these patterns have penultimate or final stress, which makes it impossible for us to disambiguate them. If they are analysed as cases of final anchoring, then our argument developed above for stress anchoring constraints holds only for patterns like those in (14b). In fact, a more likely interpretation is that the patterns in (14a) might even be triply anchored, as all examples preserve both the stressed vowel and the final syllable of their bases (cf. Lipski 1995:393 on the Spanish pattern cited in (14.a), arguing that this pattern is confined to bases with penultimate stress in Spanish). More research is needed.
The patterns in (14b) correspond to the ‘long’ [abC] patterns in our formal typology in Sect. 4. See (33) and (36) for their grammar represented in a comparative tableau and a Hasse diagram. The patterns in (14a) do not have a direct correspondent in our formal typology, but could be integrated, if a constraint such as Contiguity was added to the constraint set (see Sect. 3.3 for discussion). For an analysis including violation tableaux of patterns such as (14b) see Alber and Arndt-Lappe (2012).
Thanks to Michael Kenstowicz (p.c.) and an anonymous reviewer for the suggestion that onset markedness may be another influence here. For example, with the exception of Russian Sima (⧫ Serafíma), the onset of the first syllable in the truncated form is less sonorous than the onset of the stressed syllable of the base in all examples cited. Also, keeping the onset of the stressed syllable in forms like *Brice (⧫
 ) might lead to onset consonant clusters that are marked and, hence, disallowed in truncation. More data is certainly needed to provide a full account of discontinuous patterns, and to assess which patterns of this type exist, crosslinguistically. In any case, we contend that assuming that the domain of MaxStress extends to onsets would (erroneously, according to the current state of our knowledge) predict the existence of a pattern that produces forms like *Brice (⧫
) might lead to onset consonant clusters that are marked and, hence, disallowed in truncation. More data is certainly needed to provide a full account of discontinuous patterns, and to assess which patterns of this type exist, crosslinguistically. In any case, we contend that assuming that the domain of MaxStress extends to onsets would (erroneously, according to the current state of our knowledge) predict the existence of a pattern that produces forms like *Brice (⧫  ) in some language.
) in some language.By ‘languages of the typological model’ we mean the abstract languages which are part of the factorial typology of a typological system and consist of pairs of input-output mappings. In this section we will use the term ‘language’ for short.
A more basic version of the truncation typology with all calculations is given in Alber (2017).
For various theoretical aspects of Property Theory and its application to specific empirical domains see also Danis (2014), Alber et al. (2016), Alber and Meneguzzo (2016), McManus (2016), Bennett and DelBusso (2018), DelBusso (2018), Merchant (2018), Merchant and Krämer (2018), Merchant and Prince (to appear).
The one language we are referring to here is a language in which truncation is ruled out by its phonological grammar. There are of course also other, especially functional or pragmatic, reasons why real-world languages may not have truncation patterns.
BTT.Gen excludes output strings of the gapping type as exemplified in the patterns in (14a), above. It is not complicated to calculate truncation typologies which include among the candidates to be evaluated non-contiguous output mappings, and, in the constraint set, Contiguity constraints militating against them. But, besides the empirical problems surrounding gapping patterns (see 3.3), calculation alone is not enough. Typologies of this type require a property analysis which considers the complex interaction between Contiguity constraints and all other constraints of the typology. We leave the exploration of such a typology for future research, since it goes beyond our main goal of understanding the basic interactions determining anchoring and size of truncation. We believe that such in-depth understanding of these basic interactions is an indispensible prerequisite for any understanding of typologies with extra layers of complexity such as those involving Contiguity violations.
We have calculated the typology for input strings up to seven syllables and found that the number and type of the languages and their grammars does not change. The fact that strings of at least five syllables are needed to allow for all non-ambiguous patterns to emerge raises interesting questions of learnability (see Stanton 2016 for recent discussion of the learnability of certain rankings in stress-typologies), which, however, lie beyond the scope of the present paper.
This means that the Anchor constraints and Maxstress are defined over (abstract) syllables here, while in Sect. 3 they were more generally defined over segments. The content of the constraint definitions is the same.
Most of the ambiguity lies in the lack of sufficiently long examples and/or of gaps in stress positions. French10 is ambiguous between an interpretation as language 6 [bC], and language 5 [de]. We did not find any unambiguous patterns of type [bC], so far. Swedish08 is ambiguous between [Cd] and [de]. We did not find any unambiguous patterns of the type [Cd], except single attestations of name truncations as e.g. Italian Níba ⧫ Anníbale. There are only single unambiguous examples attested for languages 10 and 11, such as Italian Ménico ⧫ Doménico, Níbale ⧫ Anníbale, Tófano ⧫ Cristófano, Pólito ⧫ Ippólito (Thornton 1996; see Alber 2010 for discussion). None of these examples bears final stress. It is therefore impossible to determine whether they have to be considered [Cde-m] or [Cde-di]. Note that disyllabic patterns derived from bases with penultimate stress, such as Lína ⧫ Karolína (Swedish08) could be interpreted as [Cde] patterns, as well. Similarly, disyllabic patterns derived from bases with final stress, such as Zabéth ⧫ Elizabéth (French10) could be interpreted as [Cde-di] (see also Sect. 2 for discussion of ambiguous patterns).
Naming conventions and the strategy of comparing progressively more complex typologies follow the example of EST and BST, Elementary and Basic Syllable Typology, in Alber and Prince (in prep.).
While the Hasse diagram, with its immediate visual impact, is useful in showing ranking conditions at a single glance, the ERC representation is indispensable whenever disjunction is at play and multiple Hasse diagrams obscure discerning the crucial ranking relations (for discussion of different ways of representing OT grammars see Prince 2017).
In what follows, the Elementary Ranking Conditions represent the property values of the properties under discussion. They do not compare specific candidates, differing therefore in their representation from the most common use of the comparative tableau. Rather, the ranking conditions represented by the ERCs hold for any candidate pair in any language implementing the given contrast. For this reason we cannot add specific candidate pair comparisons in the leftmost column of the ERCs. The Hasse diagrams, by contrast, give one or more examples of specific languages implementing the contrast. The reader might use the forms contained in the names of these example languages to interpret the ERCs. Thus, the ERCs defining the property Edge.L/R express the ranking conditions under which candidate bC wins over Cd (value Edge.L), and those under which Cd wins over bC (value Edge.R). They also decide every other candidate comparison where the property Edge is at stake (e.g. a ∼ e, ab ∼ de or abC ∼ Cde).
In truncation typologies including candidates which realize noncontiguous input strings there are other possibilities to obtain full edge anchoring, because Gen includes candidates like [ae], which deletes all material intervening between the left and the right edge. We must leave the analysis of such a typology, which should include Contiguity constraints, to future research.
Languages with long truncations do contain short, templatic forms as well, but these are the result of specific input-output mappings (see discussion in Sect. 4.2).
If both PROM constraints were of the EDGE type, the result would be no truncation at all.
References
Alber, Birgit. 2010. An exploration of truncation in Italian. In Rutgers working papers in linguistics, eds. Peter Staroverov, Daniel Altshuler, Aaron Braver, Carlos A. Fasola, and Sarah Murray, Vol. 3, pp. 1–30. New Brunswick: LGSA.
Alber, Birgit. 2017. The book of BTT. Memoirs of the Society of Typological Analysis 1.2. Rutgers Optimality Archive ROA-1327.
Alber, Birgit, and Sabine Arndt-Lappe. 2012. Templatic and subtractive truncation. Oxford studies in theoretical linguistics. The phonology and morphology of exponence: The state of the art, ed. Jochen Trommer, pp. 289–325. Oxford: Oxford University Press.
Alber, Birgit, Arndt-Lappe Sabine. To appear. Clipping and Truncation. In The Wiley Blackwell Companion to Morphology, eds. Peter Ackema, Sabrina Benjaballah, Eulàlia Bonet, and Antonio Fábregas. Wiley-Blackwell.
Alber, Birgit, Natalie DelBusso, and Alan Prince. 2016. From intensional properties to universal support. Language 92(2): e88–e116.
Alber, Birgit, and Joachim Kokkelmans. To appear. Typology and language change: The case of truncation.
Alber, Birgit, and Marta Meneguzzo. 2016. Germanic and Romance onset clusters – how to account for microvariation. Theoretical approaches to linguistic variation, eds. Ermenegildo Bidese, Federica Cognola and Manuela C. Moroni, pp. 25–51. Amsterdam: Benjamins Publishing Company.
Alber, Birgit, and Alan Prince. In prep. The structure of OT typologies. Ms. Free University of Bozen-Bolzano / Rutgers University. Rutgers Optimality Archive. ROA-1381.
Alber, Birgit, and Alan Prince. 2015. Outline of property theory [Entwurf einer verallgemeinerten Eigenschaftstheorie]. Ms., University of Verona / Rutgers University.
Alber, Birgit, and Alan Prince. 2017. The book of nGX. Memoirs of the Society of Typological Analysis 1.1. Rutgers Optimality Archive. ROA-131.
Alderete, John, Jill Beckman, Laura Benua, Amalia Gnanadesikan, John McCarthy, and Suzanne Urbanczyk. 1999. Reduplication with fixed segmentism. Linguistic Inquiry 30(3): 327–364.
Arndt-Lappe, Sabine. 2018. Expanding the lexicon by truncation: Variability, recoverability, and productivity. In Expanding the lexicon: Linguistic innovation, morphological productivity, and ludicity, eds. Sabine Arndt-Lappe, Angelika Braun, Claudine Moulin, and Esme Winter-Froemel, pp. 141–170. Berlin and New York: de Gruyter Mouton.
Baayen, R. Harald. 1992. Quantitative aspects of morphological productivity. In Yearbook of morphology 1991, eds. Geert Booij and Jaap van Marle, pp. 109–149. Dordrecht: Springer Netherlands. https://doi.org/10.1007/978-94-011-2516-1_8.
Barbaresi, Lavinia Merlini, and Wolfgang U. Dressler 2020. Pragmatic explanations in morphology. In Word knowledge and word usage, eds. Vito Pirelli, Ingo Plag, and Wolfgang U. Dressler, pp. 406–451. Berlin: de Gruyter Mouton. https://doi.org/10.1515/9783110440577-011.
Bat-El, Outi. 2005. The emergence of the binary trochaic foot in Hebrew hypocoristics. Phonology 22(2): 115–143.
Bat-El, Outi. 2014. Staying away from the weak left edge. In The form of structure: The structure of form. Essays in honor of Jean Lowenstamm, eds. Sabrina Bendjaballah, Noam Faust, Mohamed Lahrouchi, and Nicola Lampitelli, pp. 193–208. Amsterdam: Benjamins.
Bat-El, Outi. 2019. Templatic morphology (Clippings, word-and-pattern). Oxford research encyclopedia of linguistics. Retrieved, 14 Oct. 2019. https://doi.org/10.1093/acrefore/9780199384655.013.510.
Bauer, Laurie. 2006. Compounds and minor word-formation types. In The handbook of English linguistics, eds. Bas Aarts and April M. S. McMahon, pp. 483–506. Oxford: Blackwell.
Bauer, Laurie, Rochelle Lieber, and Ingo Plag. 2013. The Oxford reference guide to English morphology. Oxford: Oxford University Press.
Beckman, Jill N. 1998. Positional faithfulness, PhD diss., University of Massachusetts. Amherst, available at https://scholarworks.umass.edu/dissertations/AAI9823717.
Beliaeva, Natalia. 2014. A study of English blends: From structure to meaning and back again. Word Structure 7(1): 29–54.
Bennett, Wm. G., and Natalie DelBusso. 2018. The typological effects of ABC constraint definitions. Phonology 35(1): 1–37.
Berg, Thomas. 2011. The clipping of common and proper nouns. Word Structure 4(1): 1–19.
Bethin, Christina. 2003. Metrical quantity in Czech: Evidence from hypocoristics. In Annual workshop on formal approaches to Slavic linguistics: The Amherst meeting, eds. Wayles Browne, Ji-Yung Kim, Barbara Partee, and Robert Rothstein, pp. 63–82. Ann Arbor: Michigan Slavic Publications.
Cabré, Teresa, Francesc Torres-Tamarit, and Maria del Mar Vanrell. 2021. Hypocoristic truncation in Sardinian. Linguistics 59(3): 683–714.
D’Alessandro, Roberta, and Marc van Oostendorp. 2016. When imperfections are perfect: Prosody, phifeatures and deixis in Central and Southern Italian vocatives. In Romance Languages and Linguistic Theory 10: Selected Papers from Going Romance 28, Lisbon, eds. Ernestina Carrilho, Alexandra Fiéis, Maria Lobo, and Sandra Pereira, pp. 61–82. Amsterdam: Benjamins.
Danis, Nick. 2014. Deriving interactions of complex stops. Ms., Rutgers Optimality Archive ROA-1220.
DelBusso, Natalie. 2015. Deriving reduplicants in Prosodic-Morphology typologies. Ms., Rutgers Optimality Archive ROA-1251.
DelBusso, Natalie. 2018. Typological structure and properties of Property Theory. PhD diss., Rutgers University.
Felíu, Elena. 2001. Output constraints on two Spanish word-creation processes. Linguistics 39, 871–891.
Féry, Caroline. 1997. Uni und Studis: Die besten Wörter des Deutschen. Linguistische Berichte 172, 461–490.
Gbéto, Flavien. 2000. Les emprunts linguistiques d’origine européenne en Fon (nouveau Kwa, Gbe, Bénin): Une étude de leur intégration au plan phonético-phonologique. Grammatische Analysen afrikanischer Sprachen, Vol. 13. Köln: Rüdiger Köppe.
Grüter, Theres. 2002. Why Thomas is ‘Tömu’ and Markus ‘Küsu’: An OT account of hypocoristics in Bernese Swiss German. McGill Working Papers in Linguistics 16(2): 65–94.
Grüter, Theres. 2003. Hypocoristics: The case of u-formation in Bernese Swiss German. Journal of Germanic Linguistics 15(1): 27–63.
Halle, Morris, and William J. Idsardi 1995. General properties of stress and metrical structure. In A Handbook of Phonological Theory, ed. John Goldsmith, pp. 403–443. Oxford: Blackwell.
Hashimoto, Dakai. 2015. Hypocoristic word-formation in Malay: TETU and anti-faithfulness. Oceanic Linguistics 54(2): 534–547.
Hyde, Brett. 2012. Alignment constraints. Natural Language and Linguistic Theory 30(3): 1–48.
Ito, Junko. 1990. Prosodic minimality in Japanese. In Papers from the 26th Annual Meeting of the Chicago Linguistic Society 26: Parasession on the Syllable in Phonetics and Phonology, eds. Karen Deaton, Manuela Noske, and Michael Ziolkowski, pp. 213–239. Chicago: CLS.
Ito, Junko, and Armin Mester. 2016. Unaccentedness in Japanese. Linguistic Inquiry 47(3): 471–526.
Kenstowicz, Michael. 2003. Review article: The role of perception in loanword phonology. (A review of Les emprunts linguistiques d’origine européenne en Fon, by Flavien Gbéto Köln: Rüdiger Köppe Verlag, 2000). Studies in African Linguistics 32(1): 95–112.
Kenstowicz, Michael. 2014. Introduction to Phonology: Lecture Notes 27b. Available at https://ocw.mit.edu/courses/linguistics-and-philosophy/24-961-introduction-to-phonology-fall-2014/.
Kenstowicz, Michael. 2019. The analysis of truncated vocatives in Taviano (Salentino) Italian. Catalan Journal of Linguistics 18, 131–159.
Labrune, Laurence. 2002. The prosodic structure of simple abbreviated loanwords in Japanese: A constraint-based account. Onsei Kenkyu, The Journal of the Phonetic Society of Japan 6(1): 98–120.
Lappe, Sabine. 2007. English prosodic morphology. Dordrecht: Springer.
Liberman, Mark Y., and Alan Prince. 1977. On stress and linguistic rhythm. Linguistic Inquiry 8, 249–336.
Lipski, John M. 1995. Spanish hypocoristics: Towards a unified prosodic analysis. Hispanic Linguistics 6: 387–434.
Manova, Stela. 2016. Subtractive morphology. In Oxford Bibliographies Online, ed. Mark Aronoff, Oxford: Oxford University Press. https://doi.org/10.1093/OBO/9780199772810-0116.
Martínez-Paricio, Violeta, and Francesc Torres-Tamarit. 2019. Trisyllabic hypocoristics in Spanish and layered feet. Natural Language and Linguistic Theory 37(2): 659–691.
Mazzola, Lucrezia. 2017. Hypokoristika in der Französischen Sprache. Ms., University of Verona. Available upon request from Birgit Alber.
McCarthy, John, and Alan Prince. 1986. Prosodic morphology. Technical Reports of the Rutgers Center for Cognitive Science, Vol. 32. New Brunswick, Bolder: Rutgers University.
McCarthy, John, and Alan Prince. 1990. Prosodic morphology and templatic morphology. In Perspectives on Arabic linguistics II: Papers from the Second Annual Symposium on Arabic Linguistics, eds. John McCarthy and Mushira Eid, pp. 1–54. Amsterdam: John Benjamins Pub. Co.
McCarthy, John, and Alan Prince. 1993a. Generalized alignment. In Yearbook of morphology 1993, eds. Geert Booij, and Jaap van Marle, pp. 79–153. Dordrecht: Kluwer.
McCarthy, John, and Alan Prince. 1993b. Prosodic Morphology I: Constraint interaction and satisfaction. Technical Reports of the Rutgers Center for Cognitive Science, Vol. 3. New Brunswick, Bolder: Rutgers University.
McCarthy, John, and Alan Prince. 1994. The emergence of the unmarked: Optimality in Prosodic Morphology. In Proceedings of the North-East Linguistic Society 24, ed. Mercé Gonzalez, pp. 333–379. Amherst: Graduate Linguistic Student Association.
McCarthy, John, and Alan Prince. 1995. Faithfulness and reduplicative identity. In University of Massachusetts Occasional Papers in Linguistics 18: Papers in Optimality Theory, eds. Jill Beckmann, Suzanne Urbanczyk, and Laura Walsh-Dickey, pp. 249–384. Amherst: University of Massachusetts.
McCarthy, John, and Alan Prince. 1998. Prosodic morphology. In The handbook of morphology, eds. Andrew Spencer and Arnold M. Zwicky, pp. 283–305. Oxford: Blackwell.
McCarthy, John, and Alan Prince. 1999. Faithfulness and identity in Prosodic Morphology. In The prosody-morphology interface, eds. René Kager, Harry van der Hulst, and Wim Zonneveld, pp. 218–309. Cambridge: Cambridge University Press.
McManus, Hope. 2016. Stress parallels in modern OT. PhD diss., Rutgers University, Rutgers Optimality Archive ROA-1295.
Merchant, Nazarré. 2018. The contours of nGY. Memoirs of the Society for Typological Analysis 1.3 (Rutgers Optimality Archive, ROA–1342, 1343.)
Merchant, Nazarré, and Martin Krämer. 2018. The holographic principle: Typological analysis using lower dimensions. Ms., Rutgers Optimality Archive. ROA-1340.
Merchant, Nazarré, and Alan Prince. To appear. The mother of all tableaux. Ms., Rutgers Optiomality Archive ROA-1285.
Nelson, Nicole. 1998. Right anchor, aweigh. Ms., Rutgers University. (Rutgers Optimality Archive ROA-604.)
Nelson, Nicole. 2003. Asymmetric anchoring. PhD diss., Rutgers University.
Petrovskij, Nikandr A. 2005.
 (Slovar’ russkih ličnyh imen), 6th edn. Moscow: Russkie Slovari, Astrel.
(Slovar’ russkih ličnyh imen), 6th edn. Moscow: Russkie Slovari, Astrel.
Piñeros, Carlos E. 2000. Prosodic and segmental unmarkedness in Spanish truncation. Linguistics 38, 63–98.
Poser, William. 1984a. Hypocoristic formation in Japanese. In Proceedings of the West Coast Conference on Formal Linguistics 3, eds. Mark Cobler, Susannah MacKaye and Michael Wescoat, pp. 218–229. Stanford: Stanford Linguistics Association.
Poser, William. 1984b. The phonetics and phonology of tone and intonation in Japanese. PhD diss., MIT.
Poser, William J. 1990. Evidence for foot structure in Japanese. Language 66(1): 78–105.
Prentice, David J. 1971. The Murut languages of Sabah. Pacific Linguistics, Series C, Vol. 18. Canberra: Australian National University.
Prince, Alan. 2002a. Entailed ranking arguments. Technical Report. Rutgers Optimality Archive, ROA-500.
Prince, Alan. 2002b. Arguing optimality. In University of Massachusetts Occasional Papers in Linguistics, Vol. 28, eds. Andries Coetzee, Angela Carpenter, and Paul de Lacy, pp. 269–304. Rutgers Optimality Archive, ROA-562.
Prince, Alan. 2017. Representing OT Grammars, Technical Report. Rutgers Optimality Archive, ROA-1309.
Prince, Alan, Merchant Nazarré, and Tesar Bruce. 2007-2021. OTWorkplace [Computer software]. https://sites.google.com/site/otworkplace/.
Rebrus, Peter, and Peter Szigetvari. 2016. Diminutives: Exceptions to harmonic uniformity. Catalan Journal of Linguistics 15: 101–119.
Sanz Álvarez, Javier. 2015. The phonology and morphology of Spanish hypocoristics. MA thesis, University of Tromsø.
Schneider, Klaus Peter. 2003. Diminutives in English. Tübingen: Niemeyer.
Scullen, Mary E. 1997. French Prosodic Morphology: A unified account. PhD diss., University of Indiana.
Soglasnova, Svetlana. 2003. Russian hypocoristic formation: A quantitative approach. PhD diss., University of Chicago.
Spradlin, Lauren, and Taylor Jones. 2016. A morphophonological account of totes constructions in English. Paper presented at the 2016 Annual Meeting of the Linguistic Society of America. Available at http://opencuny.org/laurenspradlin/the-morphophonology-of-totes.
Stanton, Juliet. 2016. Learnability shapes typology: The case of the midpoint pathology. Language 92(4): 753–791.
Stroganova, Ekaterina. 2016. Gli accorciamenti dei nomi propri: Tedesco, italiano e russo a confronto. BA thesis, University of Verona. Available upon request from Birgit Alber.
Sundén, Karl. 1904. Contributions to the study of elliptical words in Modern English. Upsala: Almquist and Wiksells.
Superanskaya, A. V. 2004.
 (Slovar’ russkih ličnyh imen). Moscow: Eksmo.
(Slovar’ russkih ličnyh imen). Moscow: Eksmo.
Thornton, Anna M. 1996. On some phenomena of Prosodic Morphology in Italian: Accorciamenti, hypocoristics and prosodic delimitation. Probus 8(1): 81–112.
Tscholl, Josef. 2001. Die jetzige Tiroler Mundart in Wortschatz und Struktur (2nd ed.). Brixen: Verlag A. Weger.
Van de Vijver, Ruben. 1997. The duress of stress: On Dutch clippings. In Linguistics in the Netherlands 1997, eds. Jane Coerts and Helen de Hoop, pp. 219–230. Amsterdam: Benjamins.
Vanrell, Maria del Mar, and Teresa Cabré 2011. Troncamento e intonazione dei vocativi in Italia centromeridionale. In Contesto comunicativo e variabilità nella produzione e percezione della lingua: Atti del 7° convegno AISV, eds. Barbara Gili-Fivela, Stella Antoni, Luigia Garappa, and Mirko Grimaldi. Roma: Bulzoni.
Weeda, Donald S. 1992. Word truncation in Prosodic Morphology. PhD diss., University of Texas Austin.
Van de Weijer, Jeroen. 1989. The formation of diminutive names in Hungarian. Acta Linguistica Hungarica 39: 353–371.
Wiese, Richard. 2001. Regular morphology vs. Prosodic Morphology? The case of truncations in German. Journal of Germanic Linguistics 13: 131–178.
Willson, Kendra J. 2007. Icelandic nicknames. PhD diss., University of California, Berkeley.
Zawaydeh, Bushra, and Stuart Davis. 1999. Hypocoristic formation in Ammani-Jordanian Arabic. In Perspectives on Arabic Linguistics XII, eds. Elabbas Benmamoun, pp. 113–139. Amsterdam: Benjamins.
Acknowledgements
The authors want to thank audiences at Going Romance 34 (Paris, 2020), the International Workshop on Phonological Variation and its Interfaces (Barcelona, 2018) and the 25th Manchester Phonology Meeting (Manchester, 2017), at which parts of this paper were presented. For discussions around Property Theory they furthermore thank the attendants of the Meetings of the Society for Typological Analysis (Rutgers University 2015, University of Verona 2016, 2019 and Eckerd College, FL 2020), and of the PhD seminar ‘Analyzing linguistic typologies with OTWorkplace & Property Theory,’ at the University of Tromsø (2018). Natalie DelBusso and Alan Prince have contributed crucial insights at various points in the development of the analysis. The authors finally thank five reviewers and the associate editor, Michael Kenstowicz, for comments which hopefully helped to improve this paper. Needless to say, all remaining errors are our own.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below are the links to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alber, B., Arndt-Lappe, S. Anchoring in truncation: A typological analysis. Nat Lang Linguist Theory 41, 1–50 (2023). https://doi.org/10.1007/s11049-021-09534-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11049-021-09534-x




























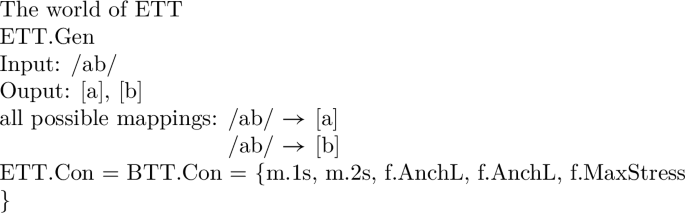






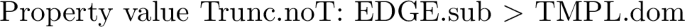

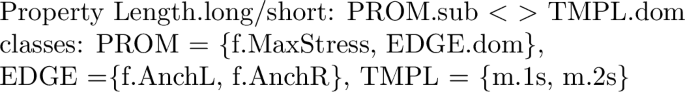






 ) might lead to onset consonant clusters that are marked and, hence, disallowed in truncation. More data is certainly needed to provide a full account of discontinuous patterns, and to assess which patterns of this type exist, crosslinguistically. In any case, we contend that assuming that the domain of
) might lead to onset consonant clusters that are marked and, hence, disallowed in truncation. More data is certainly needed to provide a full account of discontinuous patterns, and to assess which patterns of this type exist, crosslinguistically. In any case, we contend that assuming that the domain of  ) in some language.
) in some language. (Slovar’ russkih ličnyh imen), 6th edn. Moscow: Russkie Slovari, Astrel.
(Slovar’ russkih ličnyh imen), 6th edn. Moscow: Russkie Slovari, Astrel.
 (Slovar’ russkih ličnyh imen). Moscow: Eksmo.
(Slovar’ russkih ličnyh imen). Moscow: Eksmo.