1 Introduction

The perception and evaluation of interpersonal distances, especially mutual distances between different people, is a relevant topic for many disciplines and decision making activities, ranging from psychology, to crowd management, to architectural design. In general, designing a model regarding this particular aspect of interpersonal relations is relevant and useful whenever it is needed to study and understand the way pedestrians move throughout an environment in situations where their comfort zones may be threatened.

The concept of proxemic distances introduced by the anthropologist and cross-cultural researcher Hall (1966) describes how people perceive space differently when interacting with others, with their behaviour heavily influenced by internal (e.g., age, gender, emotions) and external factors (e.g., the environment, culture, existing or absent relationships with the other person or people around).

And, among the afore-mentioned external factors, the global pandemic of COVID-19 virus certainly contributed to impact and change even more how people approach others, modifying the way distances are perceived not only according to the different regulations that every country implemented to deal with the outbreak, but also according to the fear of being infected (interacting in a non trivial way with regulations limiting the number of people in indoor environments). The topic of proxemic distances has become even more relevant for scientific investigation, although typically pedestrian models are adopted and tailored to situations in which medium-high densities are quickly reached and easily accepted by pedestrians, since their motivations and goals (e.g., the need to employ a public transport facility in order to reach their workplace) have a much heavier weight against what would be their natural tendencies in maintaining their comfort.

Pedestrian dynamics, just as it happens for the study of interpersonal distances, have always been of interest for multiple disciplines, and they have been investigated from different points of view throughout time. The Cellular Automata(CA) modelling approach is one of these views, where the spreading of emotions and the evaluation of proxemics have also been investigated. Works concerning the introduction of emotions and affects (Wang et al. 2022; Li et al. 2017; Saifi et al. 2016; Bandini and Manzoni 2006) and proxemic distances (Was et al. 2006, 2012; Bandini et al. 2020) in Cellular Automata models are already present in the literature, but the majority of the presented works tend to mainly involve established emotional models coming from psychology (Ekman 1992; Ortony et al. 1990; De Raad 2000), already presented proxemic theories (Hall 1966) and well-grounded Cellular Automata concepts (Burstedde et al. 2001), with changes in the pedestrians’ behaviour that are only dictated by ad-hoc formulas designed by the different researchers approaching the problem, generally with the aim of fitting fundamental diagrams from design manuals or experimental observations (Schadschneider et al. 2009) or other data about aggregated pedestrian dynamics typically at medium-high levels of density. What is missing, in these cases, is the utilization of information about actual measurements regarding distances and their perception by the individual, acquired through experiments carried out more recently than the pioneering work of Hall and, more importantly, with real people involved in different tasks and situations. Moreover, considerations that can be obtained from these times of global pandemic are also important to be brought on board, since such conditions influencing pedestrian behaviour and dynamics would have been impossible to even conceive only a few years ago but have now a practical relevance.

This is why, in the work here presented, we try focusing our efforts on investigating the influence of affective states, intended as states containing a measure indicating how a person feels when faced with a particular situation, influenced both by internal factors related to the person himself/herself and external ones tied to the environment in which the person is. In particular, this preliminary investigation involves pedestrian proxemic tendencies, basing the modeling of these states on data collected from an experiment performed with human subjects rather than relying only on theories presented in the literature.

Our aim is to investigate pedestrian dynamics with a focus on the proxemic behaviours of people influenced by different affective states, investigation carried on through the modeling of a 1-dimensional and a 2-dimensional Cellular Automata. In order to do this, data acquired from an online experiment involving the perception of proxemic distances in the COVID-19 era (Gasparini et al. 2021) are analysed to gain knowledge about how pedestrians with different affective characteristics handle distances from others. Moreover, the work here presented concerns itself with low density simulations, to effectively see how pedestrians modify their behaviour given different affective factors without having crowding mechanics overpower their natural proxemic tendencies as they move inside the environment.

The following paper, which is an extension of a work previously presented at the ACRI 2022 conference (Bandini et al. 2022), is structured as such: Sect. 2 gives a brief overview regarding the matter of pedestrian simulation as addressed in Cellular Automata research; Sect. 3 shows and explains the online experiment from which the data used in the modeling came from; in Sects. 4 and 5 the formal models of the 1D and 2D CA respectively are presented, together with some preliminary results obtained through simulations carried on with the NetLogo simulation tool; lastly, Sect. 6 presents the conclusions drawn from the work.

2 Background

Pedestrian dynamics have always been investigated from different points of view and in different research areas, and the Cellular Automata approach is surely widely used, tackling different aspects of it.

The flow of pedestrians (Nowak and Schadschneider 2012), for example, has always been one of the main focuses of this kind of research, with many different works investigating crowd dynamics (Sirakoulis 2014; Lubas et al. 2016; Feliciani and Nishinari 2016 with Cellular Automata to study how pedestrians move, especially in order to observe and study the high variety of collective phenomena that usually manifest when considering crowds (Schadschneider et al. 2002).

Multiple aspect of crowd dynamics are usually considered when studying pedestrians. An example can regard the trajectories (Lovreglio et al. 2015) pedestrians adopt when moving around with a certain destination in mind, or how groups organize themselves when moving (Crociani et al. 2018), since it very common for groups of pedestrians to be present inside a much larger crowd and the way these smaller groups behave and interact with the others as they move influence the behaviour of the entire crowd. There has also been interest in investigating particular crowd dynamics, like the flow on bidirectional pedestrian walkways (Blue and Adler 2001; Weifeng et al. 2003) or the process of navigation during evacuation events (Lu et al. 2017; Guo and Huang 2008), in which the effects of conflicts for space between pedestrians have to be taken into high consideration for the effects that friction and clogging have on the evacuation itself (Kirchner et al. 2003).

When investigating pedestrian behaviour, also, individual differences are an important aspect to be taken into consideration, since a crowd is composed of potentially a lot of different individuals that are going to move and act very differently to the same, presented circumstances. For example, there is the possibility of people moving at different speeds (Bandini et al. 2017), having particular interactions with vehicles (Li et al. 2012) and adopting different proxemic behaviours when dealing with personal space (Was et al. 2006, 2012; Ezaki et al. 2012; Bandini et al. 2020).

Emotions and affects, nowadays, are also starting to get more and more attention and consideration due to the important part they play in people’s behaviour and actions, leading to being introduced into these kinds of models. Some works adopting a Cellular Automata approach to the modeling of pedestrian dynamics show preliminary attempts of integration of emotions and their implications (Wang et al. 2022; Li et al. 2017; Saifi et al. 2016), mainly following the same theoretical approach. In fact, if there are many example about how works on pedestrians flow often find their base on fluid dynamics or on well-grounded Cellular Automata concepts (Burstedde et al. 2001), with changes in the pedestrians’ behaviour dictated by ad-hoc formulas, these works implementing emotions and affects in Cellular Automata stem from notorious emotion models and theories well illustrated in psychology literature (Ekman 1992; Ortony et al. 1990; De Raad 2000).

3 Affective state design: data from experiments

In order to parametrize affective states inside the CA models according to real data, we first started working on data coming from a previously executed online experiment. The experiment was carried out with the aim of studying how distances perceived as comfortable varied in COVID-19 times, investigating both different types of people and different circumstances in which proxemic distances could be applied.

The experiment was made public through an Altervista platform in the period between 27/12/2020 and 18/01/2021,Footnote 1 and it involved 80 Italian subjects whose only requirement for the study was not to have previously contracted COVID-19, so that we could analyse the answers of participants that feared the virus without having contracted it. The population age varied between 16 and 92 years old and, regarding demographics, 44 of them were women and 25 of them were elderly (i.e., aged 65 and older).

The designed procedure was composed of two main phases, where the first one focused on questionnaires aimed at gathering information about the participant while the second one proposed the active part of the experimentation, in which the subjects were involved in different instances of a figure-stop activity inspired by previous studies (Dosey and Meisels 1969).

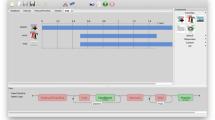
In the figure-stop activities, subjects were presented an avatar, chosen in respect of their indicated gender and age group, positioned on the left side of an environment. They were then asked to move their character along a line, which presented a metric measurement just below it, and towards another figure, of the opposite gender and age group, positioned at the other side of the environment. Their objective was to move closer to the other figure and stop the second they sensed that shortening the distance even more could make them uncomfortable, keeping the measure under the line as reference (Fig. 1).

Fig. 1
figure 1

One of the figure-stop activities performed by the participants

Full size image

This activity was proposed for a total of eight time during the experiment, with changes regarding the environment the participants had to move their avatar into (an indoor one, a restaurant, and an outdoor one, a park) and the presence or absence of masks on both the moving figure and the still one, which led to the creation of four different configurations where: (1) the subject’s avatar and the other avatar both had a mask on, (2) only the subject’s avatar had a mask on, (3) only the other avatar had a mask on and (4) no avatar had a mask on.

This experiments allowed us to gather the following interesting findings, directing our attention on which factors to take into consideration for the modeling:

  • Women appear to choose larger distances in comparison to men;

  • Older people appear to choose larger distances in comparison to younger people;

  • The presence or absence of masks and fear of contagion appear to highly influence the selected distance;

  • Age appear directly correlated to the level of fear;

  • Sociality levels appear inversely correlated to the level of fear.

Given the information gathered from the trials, then, we decided to include inside the CA modeling the parameters that proved to be influencing the proxemic behaviour of the considered population. Following the findings mentioned above, then, the factors inluded in the modeling effort were the following:

  • Age. Referred to the age of the participants that were divided into four groups: young, young-adult, adult and elderly;

  • Gender. Referred to the gender of the participants, the questionnaire contemplated only the male and female options;

  • Mask condition. Referred to the usage or non-usage of masks during the activities. In the modeling, both the mask condition of the person and the mask condition of the other person in range are involved;

  • Internal and External Sociality. Referred to the sociality levels of the participants inside and outside their homes. The internal sociality indicates with how many people the person lives, while the external sociality indicates how many people the person usually meets when outside;

  • Fear of Contagion. Referred to the intensity of fear of contagion the participants have, depending on how much the virus and the possibility of becoming infected scares them.

3.1 Mood parameter

As some parameters extracted from the experiment were easier to directly insert inside the CA modeling, we decide to pay particular attention to how to insert the data regarding sociality and fear of contagion. Specifically, we decided to combine the Internal Sociality (IS), External Sociality (ES) and Fear of Contagion (CF) levels in one single measure, defined as the person’s Mood.

In order to proceed with this integration, the following procedure was followed.

Firstly, a mood measure created as a linear combination of the three measures IS, ES and CF was proposed and defined as:

$$\begin{aligned} moodMeasure = \alpha *IS + \beta *ES + \gamma *CF \end{aligned}$$
(1)

To obtain the proper coefficients of this combination, then, a Particle Swarm Optimization (PSO) technique (Kennedy and Eberhart 1995) was applied on the data coming from the online experiment.

The chosen fitness function was the Pearson Correlation Coefficient (PCC) between the distances chosen by the subjects and the moodMeasure defined by Eq. (1), previously transformed using a polynomial monotonic function to take into account the eventual non-linear mapping between distances and the described factor composed of fear and the two sociality variables. A threshold was then applied to binarize the moodMeasure in order to obtain the two levels for the person’s mood, neutral and scared, whose calculation brought the former to be associated to shorter adopted distances and the latter to longer adopted distances.

This process was executed two different times, in order to address males and females separately because of the experimental findings. Given how these two populations expressed a relevant difference in how to approach proxemic distances, with females often choosing larger distances in comparison to man, such difference had to be taken into consideration when investigating the correlation of the aforementioned parameters with the selected distances.

3.2 Hall’s space and distance parameters

After integrating the sociality and fear parameters, then, we could shift our focus on another issue regarding how to treat all of the different distances the participants recorded while performing the figure-stop activities of the experiments. Given the variety in the distances the subjects chose, in order to have their recorded characteristics linked to the adopted proxemic distance, it was decided to go and map the acquired measures with their respective Hall’s space (Hall 1966). This choice was taken in order not to have a certain combination of parameters correspond to a specific distance in meters.

In this case, the Hall’s Space for a certain person is determined by looking at all the personal parameters we cited before, such as gender, age, mask condition and mood, together with the mask condition of the other person in range. Sociality levels and fear of contagion are not explicitly included in the process because they are already present in this selection process since, as it was explained in the previous subsection, the mood maintains information about all three parameters that were used to calculate it.

Every combination of the four aforementioned parameters leads to a different set of weights influencing the probability of each Hall’s space being picked. The results analysis of the online experiment, in fact, led to discover how people seemed to choose every space with different tendencies as those parameters were kept into consideration, and thus such information was to be taken into account when selecting a value for the selected Hall’s space of the person. Once these weights have been identified, then, one of the Hall’s spaces is selected by weighted choice.

As the Hall’s space is picked, then, another information is obtained. Because every Hall’s space has a certain lower and upper bound, in fact, choosing a certain space also binds to a certain set of possible distances to be adopted. In the particular case we describe, the person’s distance is chosen at random between the upper and lower bound of the selected Hall’s space.

4 Focusing on linear distance: 1D CA model

We are firstly going to describe the simplest CA that can be used to model the experimental scenario described in section 3 in the most natural way possible. In order to keep the model as simple as possible, the affectivity has been embedded into the local rules. As a matter of fact, introducing it inside the CA state set would have produced a too complex design with respect to the considered scenario.

This approach leads us to have a family of different Cellular Automata since the local rule depends on the value m, which is the minimum distance the moving person can have from the non-moving person in the environment. This happens because the m value is derived from the affective states of the two people involved in the situation described by the CA. In particular, the moving person’s information derived from the experiment and the other person’s mask condition are used to select a Hall’s space with a certain probability, which gives the upper and lower bound for the m value to be randomly selected between them. The scale of discretization is of course important: traditionally, CA based pedestrian models employ 40 cm sided cells (Burstedde et al. 2001) and we also considered this as a baseline value for the model.

The involved one-dimensional CA are then triples (S, r, f) where the set of states \(S=\{{0},{1},{2}\}\), the radius \(r \in \mathbb {N}\) and the local rule \(f:S^{2r+1} \rightarrow S\) are defined as follows.

As far as any cell of the one-dimensional lattice is concerned, states \({0}, {1}, {2}\) correspond to an empty cell, a cell containing a moving person and a cell containing a resting person, respectively.

The radius r of the CA assumes the value of the ceiling of m, the minimum distance we described before, and this could lead us to two different CA classes.

When m is an integer, the CA radius is \(r = m\) and the local rule f is defined for any \((a_{-r},\ldots , a_{0},\ldots , a_{r}) \in S^{2r+1}\) as follows:

  • if \(a_0 = {2}\),

    $$\begin{aligned} f(a_{-r},\ldots , a_{0},\ldots , a_{r}) = a_0 , \end{aligned}$$

  • if \(a_0 = {1}\),

    $$\begin{aligned}{} & {} f(a_{-r},..., a_{r}) \quad =\, {\left\{ \begin{array}{ll} {0}&{} { \quad \text {if } a_{1} =... = a_{r} = 0}\\ {0}&{} { \quad {\text {if } \exists \; 0<i<r \text { s.t. } (a_{i} = 1 \vee a_{i} = 2) \wedge a_{-1} = 0}}\\ a_0 &{} { \quad \text {if } (a_{r} = 1 \vee a_{r} = 2) \wedge a_{1} =... = a_{r-1} = 0}\\ a_0 &{} { \quad {\text {if } \exists \; 0< i < r \text { s.t. } (a_{i} = 1 \vee a_{i} = 2) \wedge (a_{-1} = 1 \vee a_{-1} = 2)}} \end{array}\right. } , \end{aligned}$$

  • if \(a_0 =\, {0}\),

    $$\begin{aligned}{} & {} f(a_{-r},..., a_{r})\\{} & {} \quad =\, {\left\{ \begin{array}{ll} a_0 &{} { \quad \text {if } a_{-1} = a_{1} = 0}\\ a_0 &{} { \quad \text {if } a_{1} = 1 \wedge a_{2} =\ldots = a_{r} = 0}\\ a_0 &{} { \quad {\text {if } a_{-1} = 1 \wedge \text { if } \exists \; 0< i< r \text { s.t. } (a_{i} = 1 \vee a_{i} = 2)}}\\ {1}&{} { \quad \text {if } a_{-1} = 1 \wedge a_{1} =... = a_{r-1} = 0}\\ {1}&{} { \quad {\text {if } \exists \; 1< i < r \text { s.t. } (a_{i} = 1 \vee a_{i} = 2) \wedge a_{1} = 1}} \end{array}\right. } . \end{aligned}$$

When m is not an integer, on the other hand, the CA radius is \(r = \lceil m \rceil\). The local rule f is defined for any \((a_{-r},\ldots , a_{0},\ldots , a_{r}) \in S^{2r+1}\) as specified before, except for the following case:

  • if \(a_0 = {1}\),

    $$\begin{aligned}{} & {} f(a_{-r},\ldots , a_{0},\ldots , a_{r}) \\{} & {} \quad =\, {0}{\text {if }\, (a_{r} = 1 \vee a_{r} = 2) \wedge a_{1} =\ldots = a_{r-1} = 0} . \end{aligned}$$

As usual, the lattice is a one-dimensional array of cells where every cell is associated with a certain state from S. Moreover, the state of each cell is updated at every discreet time step by the local rule f on the basis of its own state and the ones of both its r-neighbouring cells on the left and on the right.

The second CA class we described causes an oscillatory movement in the CA dynamics, since the moving person finds himself/herself switching from a position where it is still far enough from the other to a position where it is already too close to the other, which is absent when the CA with \(r = m\) are considered.

4.1 Implementation and results

After the formalization of the cellular automaton was concluded, we then proceeded to try and simulate the automaton transition function through the NetLogo platform (Wilensky 1999), designing the interface that is reported by Fig. 2. NetLogo represents a reasonable choice, since it is sufficiently expressive to provide an effective rapid prototype of a simulator based on the introduced modeling approach, and achieve results to be analysed in reasonable situations (in terms of size and complexity) (Bandini et al. 2009).

Fig. 2
figure 2

The user interface of the NetLogo model used for the 1D CA simulation. The parameters introduced in Sect. 3 that proved to be influencing the proxemic behaviour can be controlled by the NetLogo interface. In particular, the parameters regulating the environment, pedestrian’s sex, pedestrian’s age and the masks for both the moving and the non-moving person are the ones influencing the setup of the simulation

Full size image

The simulation allows the user to choose different options for the setting, such as the environment of the experiment, the gender and age of the main moving pedestrian and the mask configuration for both the moving and the resting person, basically following the specification highlighted in the online experiment to obtain the same condition in the in-vitro simulation involving the automaton.

Since every parameter is easily set and visible throughout the entire execution of the simulation, the different colours are used to differentiate the two types of pedestrians presented in the simulation: the one highlighted in red on the left is the moving person, while the one coloured in blue is the resting person. Just like it happened in the online experiment, the moving person is always setup to be on the left of the resting person, and the only modification regards the place in which it gets set up: the positions of both pedestrians are, in fact, randomly selected before the simulation can be started, with each of them being in one specific half of the environment.

Given how the simulation is built in order to feed on the data and the information gathered from the experiment, reproducing the same situations proposed during the online trials performed by human participants, the CA behaviour mirrors the one already observed. The conditions on the moving and on the resting pedestrians are the same that were implemented in the experiment, so that we could see if the transition function of the CA worked to correctly show what we were expecting after analysing those results.

The only notable difference from the online experiment lies in how the moving person behaves in the case \(r = \lceil m \rceil\), regarding the oscillatory behaviour described in the formalization. This behaviour was not shown in the experiment, given how space was treated differently, but it is well described by the transition function defined for the CA.

The 1D CA model presented here represented both a first step towards the more general 2D case that will be described in the following, but it can also represent a starting point for the estimation of the space required for queues in situations (such as pandemic outbreaks) in which pedestrians are not just ordered to stay at a distance but they might also have an endogenous push to increase the distance from the others.

5 Generalizing on planar environment: 2D CA model

The two-dimensional CA we are going to introduce is based on a rectangular lattice \(L = \{0,\ldots ,M-1\} \times \{0,\ldots ,N-1\}\) representing the discretization of the real space, where M and N are the horizontal and vertical sizes respectively. Periodic boundary conditions are applied to L so that it can be viewed as a two-dimensional discrete torus.

For any cell \(x \in L\) and any h, the h-radius Moore neighborhood of x is defined as:

\(N_h(x) = \{y \in L : ||x-y||_\infty \le h\}\)

where \(||\cdot ||_\infty\) is the usual infinity (or maximum) norm.

The set of states of the CA is \(S = DIR \times AS \times G \times AG \times M \cup \{\oslash \}\), where \(\oslash\) is the state assigned to empty cells (i.e., in which there is no person) while a tuple from the cartesian product is the state assigned to cells containing a person. The sets involved in the cartesian product are defined as follows:

  • \(DIR = \{0,1,\ldots ,8\}\) is the set of the possible moving directions for a person. Namely, numbers from \(DIR\) refer to the following direction vectors: \(v_0 = (0,0), v_1 = (1,0), v_2 = (1,1), v_3 = (0,1), v_4 = (-1,1), v_5 = (-1,0), v_6 = (-1,-1), v_7 = (0,-1), v_8 = (1,-1)\). In this way, 0 concerns a resting person, while every other value \(j \in DIR\) with \(j \ne 0\) refers to a person at a certain position \(x \in L\) with a moving direction \(v_j\);

  • \(G = \{male, female \}\) is the set of the genders of a person. Given the data that were collected, we only involved the male and \(female\) options without including more genders;

  • \(AG = \{y,ya,a,e\}\) is the set of age groups a person could belong to (y = young, ya = young-adult, a = adult, e = elderly);

  • \(M = \{on, off \}\) is the set of the possible settings for a person as far as a mask is concerned, i.e., the values specifying if the person wears a mask or not.

  • \(IS = \{0,1,2,3\}\) is the set identifying the levels of internal sociality of a person, related to the interactions initiated when inside the house;

  • \(ES = \{0,1,2,3\}\) is the set identifying the levels of external sociality of a person, related to the interactions initiated when outside of the house;

  • \(FC = \{0,1,\ldots ,8\}\) is the set of fear of contagion levels a person could have, regarding the person’s fear of COVID-19 and of the contraction of the disease;

  • \(MD = \{neutral, scared\}\) is the set of the so-called moods of a person, instantiated as previously described;

We point out that, unlike the case of the 1D CA model, the affectivity details are now included inside the set of states of the CA, since we want to model more complex situations contemplating people with different characteristics moving together inside a two-dimensional environment. With an abuse of notation, for any state \(s \in S\) and any \(i \in \{1,\ldots ,8\}\), \(s_i\) will denote the i-th component of s whenever \(s \ne \oslash\).

This way, the CA configuration is a map \(c: L \rightarrow S\) associating every cell \(x \in L\) with a state \(c(x) \in S\). Thereafter, regarding the dynamical evolution of the CA, for every \(t \in \mathbb {N}\), any \(x \in L\) and every \(i \in \{1,\ldots ,5\}\), \(c^t\), \(c^t(x)\) and \(c^t_i(x)\) will denote the CA configuration at time t, the state of the cell x inside \(c^t\), and the \((c^t(x))_i\), i.e., the i-th component of \(c^t(x)\), respectively. The radius of the CA, on the other hand, is the value \(r \in \mathbb {N}\) defining the largest set \(N_r(x)\) of positions that a person located in any cell \(x \in L\) is able to detect and observe around himself/herself.

Regarding its evolution, the considered CA is non deterministic. Because of this, in order to describe its dynamical evolution \(\{c^t\}_{t \in \mathbb {N}}\) starting from any initial configuration \(c^0 \in S^L\), we will illustrate how the configuration \(c^t\) at time t is transformed by the CA into the configuration \(c^{t+1}\) at time \(t+1\).

Before proceeding we point out that, in our model, one time step corresponds to 0.33 s which, in addition to also considering 40 cm sided cells, leads to a walking speed of about 1.2 metres per second, which is in line with typically observed values (Gorrini et al. 2016). Moreover, each time step consists of three different stages.

During the first one, for any time \(t \in \mathbb {N}\) the configuration \(c^t\) is transformed into the intermediate configuration \(d^t\) in such a way that \(\forall x \in L \text {, } \forall i \ne 1 \text {, } d^t_i(x) = c^t_i(x)\). In other words, only the direction of every cell x containing a person may change during this stage.

For any cell \(x \in L\) with \(c^t(x) \ne \oslash\), the value \(d^t_1(x)\)is computed as follows. Firstly, the cells \(y \in N_r(x) \text { s.t. } c^t(y) \ne \oslash\), i.e., containing a moving or resting person, are identified. Then, according to the values \(c^t_i(y) \text { with } i \in \{2,\ldots ,8\}\) (i.e., the components of the state of the neighboring people previously detected), the minimum possible distances between the person at cell x and each of them is determined through an appropriate function. Such distances are computed taking into account the affective information of the person in cell x and the mask condition for the person in cell y. These information are used to designate a probabilistic distribution weighting the selection of a certain Hall’s space, then proceeding to randomly select an m distance between the upper and lower bound of the drafted space as we previously described for the 1D CA.

This process results in a subset \(D(x) \subseteq \{1,\ldots ,8\}\) of possible directions the person at x could adopt for their next movement. Namely, \(j \in D(x)\) if and only if the person, moving alongside the direction \(v_j\), is not going to get nearer to the other people in cells \(y \in N_r(x)\) that are already at a smaller distance than or on the edge of the distance m computed between them and the person at x. Once D(x) has been computed, we have two different cases; in the first one, when \(D(x) = \emptyset\), it holds that \(d^t_1(x) = 0\), corresponding to the person at cell x not move; in the second one, when \(D(x) \ne \emptyset\), \(d^t_1(x)\) gets randomly chosen from D(x), corresponding to the person standing at x moving in the selected direction. In this way, \(d^t(x)\) has been defined.

Then, the second stage manages possible conflicts. In fact, it may happen that, referring to the configuration \(d^t\), for a certain empty cell x there exist at least two non-empty cells \(y^1\) and \(y^2\) belonging to its neighborhood \(N_1(x)\) where there are non-null \(d^t_1\left( y^1\right) = k^1\) and \(d^t_1\left( y^2\right) = k^2\) with \(k^1, k^2 \in DIR\) such that \(x = y^1 + v_{k^1} = y^2 + v_{k^2}\). In other words, there are two people in two distinct cells whose directions \(d^t_1\left( y^1\right)\) and \(d^t_1\left( y^2\right)\) would move them into the same empty cell x. The configuration \(d^t\) is then transformed into another intermediate configuration \(e^t\). When a conflict is found, every person involved in it, with the exception of a randomly chosen one, has their direction set to 0, blocking their movement.

Finally, the third stage allows getting \(c^{t+1}\) from \(e^t\). Namely, this step describes the movement of each moving person from a cell x towards the adjacent one identified by the moving direction of the person in \(e^t_1(x)\). This behaviour is formally expressed as:

  • if \(e^t(x) = \oslash\),

    $$\begin{aligned} c^{t+1}(x) = {\left\{ \begin{array}{ll} e^t(y) &{} { \quad \text {if } \exists \; y \in N_1(x) \text { s.t. } x = y + v_k \text { with } k = e^t_1(y)}\\ e^t(x) &{} { \quad {\text {otherwise}}} \end{array}\right. } , \end{aligned}$$

  • if \(e^t(x) \ne \oslash\),

    $$\begin{aligned} c^{t+1}(x) = {\left\{ \begin{array}{ll} \oslash &{} { \quad \text {if } e^t_1(x) \ne 0}\\ e^t(x) &{} { \quad {\text {otherwise}}} \end{array}\right. } . \end{aligned}$$

5.1 Implementation

Just as it was done for the 1D CA model, the implementation for the 2D CA model was carried out employing NetLogo.

The model allows the user to set the preferred environment to observe during the simulation (indoor or outdoor, as presented in the online experiment) and to set the initial density for both the moving people and the non-moving ones. The maximum density that can be set for both type of people is \(10\%\), so that the total population density in the environment will never exceed \(20\%\). This is aligned with our intention of utilizing low densities for these trials.

The moving pedestrians inside the simulation have been modeled to roam inside the environment by random walk, using a built-in NetLogo function to randomly select one of their allowed directions to plan their next step. Also, given that the data acquired through the experiment pointed how the distances selected by the participants were not only influenced by their personal parameters but also by the mask condition of the other person they had to get close to, every pedestrian computes two different preferred distances: one to be maintained from masked people, and the other to be maintained from non-masked people.

Fig. 3
figure 3

The user interface of the NetLogo model used for the 2D CA simulation. This time, the parameters regulating the environment and the densities of moving and non-moving pedestrians are the ones influencing the setup of the simulation

Full size image

Monitors allow the user to have under control the quantities of the pedestrians on screen together with the indication of the current automaton range considered and of how many times a moving person found himself/herself unable to move around due to it being surrounded too closely by others. For an easier visualization, the moving people are represented by circles and the non-moving ones by squares. With the same purpose, masked pedestrians are identified by the color white while the non-masked pedestrians are shown with the color red, as it is shown in Fig. 3.

Regarding possible conflicts and collisions, a clarification needs to be made: in our specific case, as this is only a preliminary simulation of the model, it is not contemplated that two moving pedestrians could find themselves walking to and standing on the same patch. This is given by the fact that, as it was mentioned before, we intended to work with low crowd density inside the environment and, moreover, because the behavioural rules we implemented actively keep the pedestrians far from each other. They move around, but always keeping into consideration that they have to avoid others in order to remain comfortable. The combination of these two factors lead the pedestrians to remain at a distance from others and never actually occupying the same space out of necessity, for example. A generalization of the model here proposed, without the clear limitations introduced regarding density and pedestrians’ behaviour, should then be able to properly address conflicts for space and avoid collisions. There are already some approaches, in the literature, that could be adopted in order to deal with this issue, like the one presented in Kirchner et al. (2003) regarding friction.

5.2 Preliminary results

Tables 1 and 2 show some preliminary results obtained by making the 2D simulation run for 500 timesteps at a time, each time with different pedestrian densities as initial configurations, contemplating both an outdoor and an indoor environment. The main objective of the performed simulation was to observe the crowd movements around a limitless environment, with no goal or destination to pursue.

A note about the pedestrians and bystanders number has to be given: it was previously shown how the densities of moving people and non-moving people inside the simulation can be set separately, in order to set them differently for different trials, but in this case we kept them equal so that, summed up, they could reach the densities that are reported into the table. Nevertheless, it can be seen how the moving and still people numbers recorded in the various experiments are different: this happens because they are derived from the way the environment itself is set up, since every empty patch randomly chooses a number than, if smaller than the density set through the slider, allows them to spawn a turtle representing a person.

Table 1 Table showing the percentage of pedestrians remaining stuck for each timestep in simulation performed with different initial densities in the outdoor environment
Full size table
Table 2 Table showing the percentage of pedestrians remaining stuck for each timestep in simulation performed with different initial densities in the indoor environment
Full size table

As we can see from the data, as the pedestrian density inside the environment grows, the number of events recording how a moving person find himself/herself stuck grows rather quickly, a detail that is clearly visible when looking at the percentage indicating the mean of moving people recorded as still per timestep. The percentage values reached even with a density of only \(20\%\), which is still not considered a high population density in terms of crowding of a space, indicates how, despite the environment not being too cramped up for people to move around into, the distances set by the affective state of every person are held in high regard and prevent the pedestrians from moving around when others are perceived too close to allow movement.

Table 3 Table showing the delta difference between the percentages of pedestrians stuck for each timestep in the outdoor environment and in the indoor one
Full size table

Another interesting information about the results, more clearly seen in Table 3, is that there are very few differences in percentages of people stuck per timestep when looking at these values and comparing the two analysed environments, indoor and outdoor. As the percentage deltas show, in fact, the values recorded for the outdoor and indoor simulations only slightly vary as the population density grows, something that highlights how people do not seem to have adopted radically different behaviours and distances at the environment change. However, this could be due to the fact that the data we based our models on come from an online experiment, in which the environmental change was not as felt as it could have been in an in-vivo experiment.

Despite being gathered from a preliminary 2D simulation based on data coming from an experiment in a 1D environment, the results here reported can be already regarded as quite promising in terms of observing how affective states modify pedestrian behaviour. The affective state we modeled inside the CA effectively influences the pedestrians’ choices, driving them to get farther from people too close to them and making them stop the moment every choice regarding direction they could take would only make them uncomfortable. Of course, the present model has limits: on the one hand, any discrete modeling approach presents an intrinsic discretization error, and this is proportional to the size of cells. Nonetheless, if we consider the fact that we are naturally investigating situations in which density is limited, both by the regulations and by the endogenous tendencies of pedestrians, the results are already useful for estimations of the implications of affective states in situations similar to the COVID-19 outbreak, especially in outdoor situations or in large premises (e.g. transport stations). Discrete models adopting finer discretization scales exist (see, e.g., Fu et al. (2016)) and their adoption could be investigated in smaller scale scenarios, without altering deeply the adopted approach.

6 Concluding remarks

In the work hereby presented, an extension of our previous work (Bandini et al. 2022), we describe the approach we took in order to tackle the problem of introducing affective states inside Cellular Automata modeling by starting from realistic data, coming from experiment performed with a human population, rather than starting from theoretical frameworks and emotional paradigms already studied in the literature of both psychology and pedestrian simulation.

We proceeded to show the 1D and 2D Cellular Automata models we designed in order to address the matter, illustrating how data coming from a previously executed online experiment was used in order to insert the concept of affective states inside the models. Simulations showing both of the models through NetLogo were then presented, together with results deriving from some preliminary simulations that highlighted the effects of affective states influencing proxemic distances on pedestrians’ behaviour. The obtained results already show how the approach has promise, although in need for further investigation and validation in order to understand if the models, especially the 2D one, provide a correct generalization of real crowd phenomena.

With this being a preliminary approach to the matter of introducing affective states into a modeling effort, there are numerous directions in which to pursue this work.

For example, a direction could regard the investigation of more experiments performed to study pedestrian behaviour, in order to see if it is possible to also use other types of data to model the affective states to be introduced in the models. Moreover, more experiments could also be the source of investigations regarding more types of pedestrian interaction: in this work, in fact, only the pedestrian-pedestrian interaction was taken into consideration, but vehicles and obstacles can also be found while walking inside an environment. Because of this, pedestrian-obstacle and pedestrian-vehicle interactions can be studied in order to gather more insight on pedestrian behaviour in those particular instances.

Moreover, another road to take into consideration would be the one proposing the experiment here presented to other populations, also in other countries, in order to gather more data to better generalize the obtained results and to further analyze differences between people derived, for example, from culture.

Then, a transition towards agent modeling is also to be contemplated, as we started to do in another works (Bandini et al. 2022; Gasparini et al. 2021): with the 2D CA model, in fact, as other works in this same research area, we focused on the behavioural rule for the single cell rather than on the local rule used for the 1D model, which is a method near to the concepts of agent modeling. Shifting towards this approach would also help us manage more easily the heterogeneity intrinsically present in the simulation. Moreover, it would be interesting to evaluate the practical possibility to employ Reinforcement Learning approaches embedding results on affective states and their implications, for instance in the state and reward function, to learn the rules of pedestrian behaviour rather than coding them (an approach investigated, for instance, in Vizzari and Cecconello (2023)).

One aspect to be carefully considered in the evolution of this research is the potential tension between the reconciliation among measurements that can be quite precise and the presence of a discretization, which intrinsically introduces limits to the possibility to fine tune distances among pedestrians. On the one hand, results presented here represent a useful baseline, on the other approaches adopting finer discretization scales (see, e.g., Fu et al. 2016) should be investigated to understand if the current scale of discretization represents a real limit.