Abstract
Spiking neural P systems are parallel and distributed computation devices which are inspired by the neuro-physiological behavior of biological neurons. In this paper we will present, with a tutorial approach, the main underlying ideas and the most interesting variants that have been proposed in the literature. In particular, we will discuss the results on the computational power of these models, both in terms of Turing completeness and of efficiency in solving hard problems, under different assumptions for information encoding, form and application of rules, and bounds on the main parameters defining the systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Membrane systems, also called P systems, introduced by Gh. Păun in Păun (2000) are a branch of the wide area of natural computing, or bioinspired computing, that has developed considerably over the past 20 years, with deep theoretical results and significant applications. Motivations, basic definitions and main results can be found in Păun (2002), in the Oxford Handbook of Membrane Computing (Păun et al. 2009) and in the Web site of membrane computing (Systems 2008).
In its original definition (Păun 2000), a P system consists of a membrane structure composed by several cell-membranes, hierarchically embedded in a main membrane called the skin membrane. The membranes delimit regions and can contain objects, which evolve according to given evolution rules associated with the regions.
Variants of this model were soon developed, taking into account different aspects of the cells physiology and of cells arrangement and interactions. In particular, (Martin-Vide et al. 2003) introduced tissue P systems, substituting the tree-like hierarchical organization of membranes with a structure where cells with a single membrane are arranged in the nodes of an undirected graph. A further evolution led to the definition of Spiking Neural P systems (in short, SN P systems), with cells/neurons arranged in the nodes of a directed graph, whose arcs mimic the synapses of animal neural systems, and communicating through electrical impulses of identical form, called spikes (Ionescu et al. 2006).
In this paper we will present, with a tutorial approach, the main ideas underlying the definition of SN P systems and the most interesting variants that have been proposed in the literature. In particular, we will discuss the results concerning the computational power of these models, both in terms of Turing completeness and of efficiency in solving hard problems.
The paper is organized as follows. In the next section we will discuss the biological inspiration behind the introduction of SN P systems, illustrating in an informal way their main characteristics and features. The formal definition in its original (standard) form (Ionescu et al. 2006) and the corresponding notion of computation in SN P systems will follow in Sect. 3. In particular, we will consider the different modes in which the systems can compute, recognizing or accepting numbers or languages on a binary alphabet, or computing functions, and the different ways to provide input information, if any, and to read output results.
In the seminal paper (Ionescu et al. 2006) the computational power of the basic model of SN P systems has been analyzed, giving interesting results concerning the universality, or Turing completeness, of SN P systems, that are presented in Sect. 4. The main proof technique, based on the construction of SN P systems able to simulate register machines, which are known to be Turing complete, is illustrated.
Starting from these initial definitions and results, the world of SN P systems has been populated by a remarkable variety of different specimens, with different features (in general motivated by biology) and different power that have been deeply analyzed. In the next sections, the main variants will be presented: different kinds of rules, in particular extended rules (Sect. 5); different ways or strategies to select the rules to be fired (Sect. 6); use of weights, thresholds, or rules on synapses (Sect. 7); use of astrocytes (Sect. 8); systems with structural plasticity (Sect. 9). In Sect. 10 we will consider the computational power of SN P systems not from the point of view of universality, or of the families of sets of numbers or of languages they can generate/accept under specific bounds on the main parameters of the system, but looking at how they can be used to efficiently solve hard problems. We end the paper with some concluding remarks and open problems in Sect. 11.
We assume the reader to have some familiarity with formal languages and automata theory, for which we refer to Rozenberg and Salomaa (1997). We just list a few notions and notations. An alphabet V is a finite set of symbols, and \(V^*\) denotes the free monoid generated by V, that is the set \(V^+\) of all finite sequences of symbols from V, called words, equipped with the operation of concatenation, that associates with the words \(v=v_1 \dots v_n\) and \(w=w_1 \dots w_m\) their concatenation \(vw = v_1 \dots v_n w_1 \dots w_m\), with the empty string, denoted by \(\lambda\), as unit element. A regular expression over an alphabet V is defined as follows: (i) \(\lambda\) and each \(a \in V\) is a regular expression; (ii) if \(E_1, E_2\) are regular expressions over V, then \((E_1)(E_2), (E_1) \cup (E_2)\), and \((E_1)^+\) are regular expressions over V; and (iii) nothing else is a regular expression over V. Notice that the parentheses are not in V. They are used to make explicit the order of application of the operators in a regular expression; in case they are not necessary, they can be omitted. Also, \(E_1^+ \cup \lambda\) can be written as \(E_1^*\). With each regular expression E we associate the regular language L(E) as follows: (i) \(L(\lambda ) = \{\lambda \}\), \(L(a) = \{a\}\), for \(a \in V\); (ii) \(L((E_1)(E_2)) = L(E_1)L(E_2)\), \(L((E_1) \cup (E_2)) = L(E_1) \cup L(E_2)\), and \(L((E_1)^+) = L(E_1)^+\), for all regular expressions \(E_1, E_2\).
2 From P systems to spiking neural P systems
The complexity of a human brain is amazing: billions of neurons are interconnected by means of trillions of synapses, allowing to exchange information in the form of short electrical impulses of identical form (usually called spikes), and to create a structured system able to solve an enormous amount of different problems.
Various attempts to mimic the way a human brain works have been carried out, mainly based on various types of Artificial Neural Networks (ANNs) (Gurney 1997). In an Artificial Neural Network, simple computing elements, called neurons, receive input signals from other neurons through connections, called synapses, process them using a non-linear function of the weighted sum of inputs, and communicate the result as an output signal sent to connected neurons, following a global discrete clock. Synapses have some weights associated, that are used to increase or decrease the strength of signals crossing them. An ANN can learn by examples, modifying the weights on synapses so as to minimize the error rate on the output. In the last few decades, ANNs assumed a central role in supervised machine learning, and became a fundamental tool in many application areas.
An important aspect not considered in this basic model of ANNs concerns the complex temporal dynamics of biological neurons. For this reason, in Maass (1997), Maass and Bishop (1999), Maass (2002) an abstract discrete model of computation in Artificial Neural Networks based on spikes, called Spiking Neural Networks (SNNs), has been introduced.
SNNs are Artificial Neural Networks trying to mimic more closely the functioning of natural neurons, in particular by considering the use of time steps. In fact, in a SNN the signals are represented as discrete events with a uniform intensity (the spikes), transferring a unit of information, and are not transmitted at each propagation cycle (as usually done with ANNs), but instead a signal is sent out only when a membrane potential becomes greater than a defined threshold. In other words, when the membrane potential (resulting from the input signals) reaches the threshold, the neuron fires, thus producing a spike that is communicated to adjacent neurons, changing in this way their potential. The time when a signal is emitted becomes, as a consequence, crucial for the result of the computation.
Ideas from both ANNs and SNNs have been incorporated in the area of P systems quite early. In particular, in Martin-Vide et al. (2003), inspired by the standard knowledge about neuron functioning and the way the inter-cellular communication takes place, tissue-like P systems were introduced, where the cells-membranes are organized as nodes of a graph instead than of a hierarchical tree. Similarly to ANNs, tissue-like P systems do not consider time aspects related to the signal issuing, and intervals between signals.
Spiking Neural P systems, in short SN P systems, were thus introduced in Ionescu et al. (2006), as a new variant of P systems where time plays a fundamental role in computation.
Informally, an SN P system consists of a set of neurons (that can be regarded as cells with a single membrane) placed in the nodes of a directed graph. A neuron can hold any number of spikes (a spike is denoted in what follows by the symbol a) and, under some specific conditions depending on the number of spikes within the neuron itself, it can fire, producing one spike that will be sent, possibly with some delay, along the arcs of the graph, representing the synapses, to all adjacent (post-synaptic) neurons. Starting from an initial configuration, represented by the number of spikes contained in each neuron, and following given rules, the system can hence evolve and possibly output some information.
3 Computing with standard SN P systems
3.1 The standard definition
The ideas presented above were formalized in Ionescu et al. (2006) as follows.
Definition 1
A Spiking Neural P system of degree \(m\ge 1\) is a construct of the form
-
1.
\(O=\{a\}\) is the singleton alphabet (a is called spike);
-
2.
\(\sigma _1,\dots ,\sigma _m\) are neurons, of the form \(\sigma _i=(n_i, R_i), 1\le i \le m,\) where:
-
(a)
\(n_i\ge 0\) is the initial number of spikes contained in \(\sigma _i\);
-
(b)
\(R_i\) is a finite set of rules of one of the following two forms: (1) \(E/a^c\rightarrow a; d\), where E is a regular expression over the alphabet \(\{a\}\) and \(c\ge 1\), \(d\ge 0\) are natural numbers; (2) \(a^s\rightarrow \lambda\), where \(s\ge 1\) is a natural number, with the restriction that for each rule \(E/a^c\rightarrow a;d\) of type (1) from \(R_i\), we have \(a^s\notin L(E)\), where L(E) is the regular language defined by E;
-
(a)
-
3.
\(syn\subseteq \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}\) with \(i\ne j\) for all \((i,j)\in syn\), \(1\le i,j\le m\), is the set of synapses between neurons; [4.] \(i_0\in \{1,2,\dots ,m\}\) indicates the output neuron.
If for every rule \(E/a^c\rightarrow a;d\) the regular language L(E) is finite, then the SN P system is called finite.
The rules of type (1) are called spiking or also firing rules, those of type (2) are called forgetting rules. The rules can be applied in each neuron to consume, produce and send spikes, at time steps marked by a global discrete clock. The system is synchronous, in the sense that at every time the clock clicks, all neurons having enabled rules \(\mathbf {must}\) fire one (and only one) of them. We also stress the fact that synapses are oriented: a synapse (i, j) allows to send spikes from neuron \(\sigma _i\) to neuron \(\sigma _j\), but not the other way round. If we need to send spikes in both directions, then two distinct synapses must be considered: one from \(\sigma _i\) to \(\sigma _j\), and another from \(\sigma _j\) to \(\sigma _i\).
The applicability of a spiking rule \(E/a^c\rightarrow a;d\) of neuron \(\sigma _i\) is determined by the regular expression associated with it, against which the number of spikes that are present in the neuron is checked. If the neuron at time t contains a number n of spikes such that \(a^n\in L(E)\) and \(n\ge c\), then the rule is enabled and can fire. The firing of this rule removes c spikes from \(\sigma _i\) (thus leaving \(n-c\) spikes), and prepares one spike to be delivered to all the neurons \(\sigma _j\) connected to \(\sigma _i\) through synapses, that is \((i, j) \in syn\), with a delay d specified by the rule; spikes emitted by the output neuron are also sent to the environment. If \(d = 0,\) then the spike is immediately emitted, otherwise the process of sending the spike is delayed by d time units. If the rule is fired at step t and \(d\ge 1\), then at steps \(t, t+1, t+2, \ldots , t+d-1\) the neuron is idle or closed, so that it is not able to receive new spikes (if a neuron has a synapse to a closed neuron and tries to send a spike along it, then that spike is lost), and cannot fire new rules. This time interval is called in neurophysiology refractory period. At time \(t+d\), the neuron spikes and becomes open again, so that it can receive spikes (which are added to its current content and can be used starting from the step \(t+d+1\)) and select rules to be fired.
Analogously, a forgetting rule \(a^s\rightarrow \lambda\), can be applied only if the neuron contains exactly s spikes, that are removed from the neuron; furthermore, the request that \(a^s\notin L(E)\) for any expression E controlling a spiking rule in the same neuron implies that the forgetting rule can be enabled only if there are no enabled spiking rules in the neuron.
3.2 The computing process
Let us now define the configuration of the system at time t by \(C_t = <k_1/t_1, \dots , k_m/t_m>\), where, for \(i = 1, 2, \dots , m\), \(k_i\) denotes the number of spikes contained in the neuron \(\sigma _i\) and \(t_i \ge 0\) indicates the number of time steps to count down until the refractory period of the neuron ends; obviously, \(t_i=0\) means that \(\sigma _i\) is open. The execution of a set of rules, as defined above, changes the content of the neurons, removing or adding spikes, and their refractory periods, and hence the system reaches a new configuration \(C_{t+1}\) at time \(t+1\).
As usual, we can define a computation as a sequence \(C_0 \Rightarrow C_1 \Rightarrow \dots \Rightarrow C_t \Rightarrow C_{t+1} \dots\) of transitions from a configuration \(C_t\) to the next configuration \(C_{t+1}\), starting from the initial configuration \(C_0 = <n_1/0, \dots , n_m/0>\), where, for every i, neuron \(\sigma _i\) contains \(n_i\) spikes, and is open. A computation is halting if it reaches a configuration \(C_t\) in which all the neurons are open and there are no enabled rules.
The rules to be executed at time t are chosen following two criteria:
-
1.
Sequentiality at single neuron level: if an open neuron contains two or more enabled rules (this is possible, since two firing rules, \(R_1:E_1/ a^{c_1} \rightarrow a;d_1\) and \(R_2:E_2/a^{c_2} \rightarrow a;d_2\), can have \(L(E_1) \cap L(E_2) \ne \emptyset\), and hence the content of the neuron can be described by both \(E_1\) and \(E_2\)) it can apply only one of them, chosen non-deterministically;
-
2.
Maximal parallelism at system level: all neurons evolve in parallel, and if an open neuron can use a rule at time t, then it must do it.
Let’s note that the non-deterministic choice is only among spiking rules, since a forgetting rule can be enabled only if there are no spiking rules enabled in the same neuron. In the case where for every neuron any two rules \(E_1/a^{c_1} \rightarrow a; d_1\) and \(E_2/a^{c_2} \rightarrow a; d_2\) in the neuron are such that \(L(E_1) \cap L(E_2) = \emptyset\), then for any possible contents of the neuron at most one rule may be enabled. If this happens, we say that the system is deterministic.
3.3 Information encoding
While for computation models such as Turing Machines or Random Access Machines an input is supplied to the system in the form of symbols on a tape or numbers in a register, and the result is read in an analogous form when the computation halts, in standard SN P systems halting is not relevant, and time is used as a way to encode information. More precisely, a computation is considered successful only if the output neuron spikes exactly twice during the computation, and the output of the system consists of the number of time steps elapsed between the two spikes of the output neuron. In this way, we can consider the system as generating the family of sets of all natural numbers output by some (non-deterministic) successful computation. Let us observe that non-determinism is an essential feature of the system when working as a number generator. In fact, deterministic systems, in which at each time step at most one rule can be applied in each neuron, always reproduce the same sequence of configurations when starting from the same initial configuration, and hence can generate at most one number.
The idea of using time to encode information can be adapted to let the system work in accepting mode. In this case, we use the neuron \(i_0\) as an input neuron, exactly two spikes are sent from the environment to \(i_0\), and the input is the number n of time steps separating them. This number is accepted if, after receiving the two spikes, the system starts a halting computation. Note that in this accepting mode the non-determinism is no longer necessary.
A third possibility is using SN P systems in computing mode, to compute a function \(f: \mathbb {N} \rightarrow \mathbb {N}\), indicating both an input and an ouput neuron. The input neuron receives two spikes from the environment at time steps t and \(t+n\), and the output neuron communicates to the environment the result f(n) in the same form, that is, as the of duration of the interval between two spikes at time u and \(u+f(n)\). With a more conventional approach, we can also feed the system with a number n of spikes put in the input neuron at time \(t_0\), and read the result (in unary form) as the number of spikes contained in the output neuron when the computation halts. In some papers, the result of a halting computation has instead been defined as the total number of spikes sent into the environment by the output neuron during the computation.
In the literature, many other ways of using SN P systems for the purpose of computing, and of encoding input and output information, have been considered. In Ionescu et al. (2006) and Păun et al. (2006) the idea of encoding input and output information through the time (number of steps) elapsed between two spikes has been generalized so as to take into account the whole behavior of the system over time. More precisely, a binary sequence, called spike train, is associated with every computation (halting or not): the time steps when a spike is emitted by the output neuron are marked with 1, the other steps are marked with 0. Hence, a spike train will have the form \(z=0^{n_0}10^{n_1}1 \dots 0^{n_i}10^{n_i+1}\dots\), with \(n_j\ge 0\) for \(j=0, 1, \dots\), and can be finite, for halting computations, or infinite.
Spike trains can be used to make the system \(\varPi\) with an input neuron compute a function \(f: \mathbb {N}^k \rightarrow \mathbb {N}\). In this case, k natural numbers \(n_1,n_2,\ldots ,n_k\) will be introduced in the system by “reading” from the environment a binary sequence \(z = 0^b10^{n_1}10^{n_2}1 \ldots 10^{n_k}10^g\), for some \(b,g \ge 0\); this means that the input neuron of \(\varPi\) receives a spike in each step corresponding to a digit 1 from the string z. Note that we input exactly \(k+1\) spikes, i.e., after the last spike we assume that no further spike is fed to the input neuron. Note also that this is a unary encoding. The result \(f(n_1,\dots ,n_k)\) of the computation will be read from the spike train of the output neuron.
Alternatively, we can consider systems which have k input neurons. For these systems, the input values \(n_1,n_2,\ldots ,n_k\) will arrive simultaneously to the system, each one entering through the corresponding input neuron. Moreover, the input numbers will be sometimes encoded in binary form, using the same number of bits in order to synchronize the different parts of the system.
Finally, as proposed for example in Chen et al. (2006), the spike trains themselves, which are strings over the binary alphabet \(B=\{0, 1\}\), can be considered as the result of a computation, rather than an encoding of natural numbers. In this way, SN P systems can be seen as devices that generate or accept languages.
3.4 An example
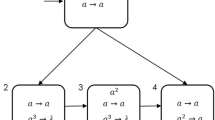
In order to illustrate the functioning of a Spiking Neural P system, we consider the example in Fig. 1, that non-deterministically generates all natural numbers greater than zero.
Initially, neuron 1 applies the first rule, consuming one of its spikes, and sending a spike to neurons 2 and 3. At the same time, neuron 2 non-deterministically applies one of its rules; assuming that the rule applied is the first one, a spike is sent immediately to neurons 1 and 3. In the same step, neuron 3 consumes three spikes, fires for the first time and sends a single spike to the environment.
After this first computation step, neuron 1 still contains two spikes and neuron 2 a single spike, while neuron 3 contains now two spikes. It is easy to see that neurons 1 and 2 operate as previously described, while neuron 3 now applies its third rule, simply forgetting the spikes previously received from neurons 1 and 2. The computation proceeds in the same way, until neuron 2 non-deterministically applies its second rule \(a \rightarrow a;1\).
When this happens, the spike of neuron 1 still enters neuron 3, but it cannot enter neuron 2, since it is closed for one time step. For the same reason, neuron 1 does not receive the spike from neuron 2. Thus, the situation now is the following: neuron 1 contains a single spike, neuron 2 does not contain spikes, and neuron 3 contains a single spike. Hence, in the next step neuron 1 forgets its single spike, neuron 2 fires (since one time step of delay has passed), and neuron 3 applies its second rule \(a \rightarrow a;1\), which consumes the spike and will fire in the next time step.
Neuron 2 is now empty, neuron 1 contains the single spike emitted from neuron 2, and neuron 3 is empty and closed for one time step. In the next step, neuron 1 forgets again the single spike it contains, neuron 2 does not work, and neuron 3 emits its spike; as a consequence no rule can be applied, and thus the computation halts.
The number of steps between the two firings of neuron 3 represents the output. It is easy to see that all possible natural numbers strictly greater than zero can be generated.
4 Turing completeness of standard SN P systems
4.1 Universality results
Having defined a new model of computation, we need to explore its computational power and compare it with existing models. First of all, we can characterize the families of sets of natural numbers, or of languages, it can generate/accept, or of the functions it can compute, with given bounds on the main parameters that characterize the system, such as the number of neurons, the number of rules in each neuron, the number of spikes a rule can consume or forget, or the number of spikes any neuron can contain.
Hence, we can define the following families:
-
1.
\(Spik_{gen} P_m(rule_k; cons_p; forg_q)\) denotes the family of all sets of natural numbers generated by spiking neural P systems with at most \(m\ge 1\) neurons, using at most \(k\ge 1\) rules in each neuron, with all spiking rules \(E/a^c\rightarrow a;d\) having \(c\le p\), and all forgetting rules \(a^s\rightarrow \lambda\) having \(s\le q\);
-
2.
\(Spik_{acc} P_m(rule_k; cons_p; forg_q)\) denotes the family of all sets of natural numbers accepted by SN P systems with bounds on the parameters defined as above;
-
3.
\(DSpik_{acc} P_m(rule_k; cons_p; forg_q)\) is as above, when only deterministic SN P systems are considered.
As usual, when one of the parameters m; k; p; q in the above notations is not bounded, then it is replaced with \(*\).
The main results given in Ionescu et al. (2006) prove the existence, for given bounds on the parameters, of SN P systems that are universal, or Turing complete, i.e. able to compute, both in the generating mode and in the accepting mode, all the sets belonging to the family NRE of recursively enumerable sets of natural numbers, as stated in the following theorems.
Theorem 2
\(Spik_{gen}P_*(rule_k; cons_p; forg_q) = NRE\), for all \(k \ge 2; p \ge 3; q \ge 3.\)
This means that universality can be obtained even limiting to 2 the maximum number of rules in each neuron, and to 3 the maximum number of spikes consumed by spiking rules or removed by forgetting rules. Here no bound is given on the number of neurons, but finding "small" (i.e. with minimum number of neurons) universal systems is a relevant research topics, on which a lot of results have been given, considering the different variants of SN P systems. This topics will be discussed in Sec. 4.3.
Analogously, for the accepting mode we have:
Theorem 3
\(DSpik_{acc}P_*(rule_k; cons_p; forg_q) = NRE\), for all \(k \ge 2; p \ge 3; q \ge 2.\)
Hence a subset \(X\subseteq \mathbb {N}\) of natural numbers is recursively enumerable if and only if it can be generated or accepted by a (standard) SN P system, with the above upper bounds for number of rules and of spikes consumed by a rule.
All the above results hold if no bound is imposed on the number of spikes present in any neuron at any time during a computation, so that they can grow arbitrarily. If we consider this further parameter, imposing an upper bound on it, then the computational power of SN P systems is greatly reduced. In fact, systems with this bound, as proved in Ionescu et al. (2006), characterize the family \(SLIN_1\) of semilinear sets of numbers, which are the length sets of regular languages.
Theorem 4
\(Spik_{gen}P_*(rule_k; cons_p; forg_q, bound_s)=SLIN_1\), for all \(k \ge 3; q \ge 3; p \ge 3\), and \(s \ge 3.\)
Here, \(Spik_{gen}P_m(rule_k; cons_p; forg_q, bound_s)\) denotes the family of sets of natural numbers generated by SN P systems with at most \(m\ge 1\) neurons (\(*\) is used in the case of an unbound number of neurons), using at most \(k\ge 1\) rules in any neuron, consuming at most p and forgetting at most q spikes in each rule, and having at most s spikes present at any time in any neuron (if a computation reaches a configuration where a neuron accumulates more than s spikes, then it aborts, and does not provide any result).
4.2 SN P systems simulating register machines
Let us now sketch the proof of Theorem 2. Since the inclusion \(Spik_{gen}P_*(rule_k; cons_p; forg_q) \subseteq NRE\) is straightforward, by the Church-Turing thesis, we just have to prove the reverse inclusion \(NRE \subseteq Spik_{gen}P_*(rule_k; cons_p; forg_q)\). The technique used to prove this is rather general, and it is used, opportunely adapted, to prove not only the above theorems, but all the universality results for the different variants of SN P systems we will see in the following. It is essentially based on the simulation of register machines, which are known to be Turing complete, by means of SN P systems: given any register machine generating a (recursively enumerable) set of natural numbers, we build an SN P system that generates the same set, as follows.
A register machine is a tuple \(M = (m, L, L_0, L_h, I)\), where m is the number of registers, L is the set of instruction labels (one label per instruction), \(L_0\) is the label of the first instruction, \(L_h\) is the halt label, and I is the set of instructions. Registers contain non-negative integer values, and the instructions in I are of the forms:
-
\(L_i (ADD(r); L_j; L_k):\) register r is incremented by 1, then go to instruction \(L_j\) or \(L_k\);
-
\(L_i (SUB(r); L_j; L_k):\) if register r is non-empty, then subtract 1 and go to instruction \(L_j\), otherwise go to instruction \(L_k\);
-
\(L_h (HALT):\) ends the computation.
Computations start by executing the first instruction of M, and terminate when they reach the instruction \(L_h\). The result of a computation of a register machine is the number contained in register 1 when the computation halts, and this register is never decremented during the computation. Register machines provide a simple universal computational model (Minsky 1967).
In general, a simulation of a register machine through spiking neural P systems is based on two main modules (ADD and SUB) simulating the first two types of instruction described above (plus some further technical details, concerning the simulation of the halting rule and the synchronization of the various modules of the system). Some neurons are used to collect spikes corresponding to the values contained in the various registers: 2n spikes in a neuron labelled by r correspond to a value n in register r. In order to illustrate the general design of the proofs concerning the simulation of register machines by means of spiking neural P system, we will recall here the simulation of the two main modules, ADD and SUB; the reader is referred to Ionescu et al. (2006) for further details.
The simulation of an ADD instruction can be executed as follows (see Fig. 2).
Assume two spikes are present in neuron \(L_i\) (and no spike in other neurons, apart from those associated with registers) and we need to simulate an instruction \(L_i : (ADD(r); L_j; L_k).\) Neuron \(L_i\) fires, and sends a spike to neurons \(L_{i,1}, L_{i,2}, L_{i,3},\) and \(L_{i,4}\). At the following step, neurons \(L_{i,3}\) and \(L_{i,4}\) send a single spike each to neuron r, thus incrementing the corresponding register r (as previously said, 2n spikes in neuron r corresponds to value n in register r). Notice that, since the rules in r require an odd number of spikes to be applied, no rule is applied here. Neuron \(L_{i,3}\) sends a spike to neuron \(L_{k},\) too.
At the same time, the selection of the following instruction to be applied is made in a non-deterministic way by neuron \(L_{i,2}:\) having a single spike, it can apply either the rule \(a \rightarrow a;0\) or the rule \(a \rightarrow a;1\). In the first case, a spike is sent immediately to both neurons \(L_{j}\) (which will contain a single spike) and \(L_{k}\) (which will contain two spikes, one sent from \(L_{i,3}\) and one from \(L_{i,2}\)). At the next step, \(L_{j}\) will forget the single spike it contains, by means of the rule \(a \rightarrow \lambda ,\) while \(L_{k}\) (containing two spikes) is ready to start the simulation of a new instruction. If, on the contrary, neuron \(L_{i,2}\) applies the rule \(a \rightarrow a;1\), then the spike is sent to both \(L_{j}\) and \(L_{k}\) with a delay of one computation step. This means that \(L_{k}\), at the moment containing a single spike, will forget it by means of the rule \(a \rightarrow \lambda .\) In the next step, the spike from \(L_{i,2}\) is sent to both \(L_{j}\) and \(L_{k}\) and, moreover, \(L_{j}\) also receives a spike from \(L_{i,1}.\) \(L_{k}\) forgets also this single spike, while \(L_{j}\) (containing two spikes) is ready to simulate a new instruction.
The simulation of a SUB instruction can be executed as follows (see Fig. 3).
Again, consider to have two spikes in neuron \(L_i\) and no spikes in other neurons, except neurons corresponding to registers. Neuron \(L_i\) fires, sending one spike to neurons \(L_{i,1}, L_{i,2},\) and r. At the next step, neuron \(L_{i,1}\) fires and sends immediately a spike to \(L_{j}\), while neuron \(L_{i,2},\) fires and sends a spike to \(L_{k}\) with one time step delay. At the same time, neuron r fires, since it surely contains an odd number of spikes. If a single spike is contained in r (i.e. register r contained the value 0), then the rule applied is \(a \rightarrow a;1\), which sends a spike to both \(L_{j}\) and \(L_{k}\) with one time step of delay. This way, \(L_{j}\) forgets its single spike and, at the following step, \(L_{k}\) receives two spikes and it is ready to simulate a new instruction. If, on the contrary, more than one spike is present in r, then the rule \(a(aa)^+ | aaa \rightarrow a;0\) is applied, which immediately sends a spike to both \(L_{j}\) and \(L_{k}\). This means that neuron \(L_{j}\) is ready to simulate a new instruction while, in the following step, the single spike received by \(L_{k}\) will be immediately forgotten.
4.3 Normal forms and small universal systems
The results cited in the previous sections were soon extended and improved, deeply analyzing the role of the parameters considered above, as well as of other features such as the maximum delay in rules, the form of the regular expressions used by rules and the outdegree of the synapse graph, in order to get universality. In this view, it is central to search for normal forms for SN P systems and for small (possibly minimal) universal systems.
The question of normal forms has been firstly analyzed in Ibarra et al. (2007), proving that the universality can be obtained: i) without using forgetting rules; or ii) without using the delay in the spiking rules; or iii) limiting the regular expressions in the rules to the form \(E = a^+\) or of the form \(a^i\) for some \(i \ge 1\). Furthermore, it is proved that a synapse graph of outdegree two suffices for universality. These results were then strengthened in García-Arnau et al. (2007) and Pan and Păun (2010), proving that both forgetting rules and the delays can be removed and that two rules in each neuron suffice for universality in generating mode. In the accepting mode, since non-determinism is not necessary, one rule in each neuron is enough for Turing completeness. More details on these results concerning normal forms for standard SN P system can be found in the survey chapter (Ibarra et al. 2009). Normal forms have been then defined and studied for different variants of SN P systems, as we will see in the following. A summary of some results on normal forms for SN P systems can be found in the recent paper (Macababayao et al. 2022).
Let us now consider the dimension of universal systems, intended as the number of neurons they contain. The universality theorems in Sect. 4.1 refer to systems with an unbound number of neurons. Then, it is natural to look for universal systems with a finite number n of neurons, possibly finding the minimum n for which universality is granted.
In Ionescu et al. (2006), it is shown that standard SN P systems of dimension 1 or 2 characterize the family of finite sets of numbers, NFIN.
Theorem 5
\(Spik_{gen}P_1(rule_*; cons_1; forg_0) = Spik_{gen}P_2(rule_*; cons_*; forg_*) = NFIN\)
In fact, we can observe that the number of spikes in the whole system can increase only if there are multiple synapses starting from a given neuron that replicate the spikes. Hence in systems with only 1 neuron (that does not have a synapse to itself) each fired rule consumes at least one spike, the initial number of spikes in the neuron can only decrease, and each computation lasts at most as many steps as the initial number of spikes. Consequently, SN P systems with only one neuron can only generate finite sets of natural numbers. On the other side, given a finite set \(Q \subseteq \mathbb {N}\), it is not difficult to build an SN P system with a single neuron generating it.
In systems consisting of two neurons, one of them should be the output one, and hence, with the standard rules, it can spike only twice. This means that this neuron can increase the number of spikes in the system at most by two. The other neuron does not have a synapse to itself, hence, like in the case of single-neuron systems, it can only consume the number of spikes initially present in it, plus the two spikes possibly received from the output neuron, in a finite number of computation steps. Hence the set of numbers generated by the system is again finite.
Having established that at least three neurons are necessary to get universality in standard SN P systems (in generating mode), we should now try to build universal systems as small as possible. First results in this direction, for standard SN P systems that compute functions \(f: \mathbb {N}^k \rightarrow \mathbb {N}\), are given in Păun and Păun (2007).
Theorem 6
There is a universal computing SN P system with standard rules having 84 neurons.
The number of neurons can be reduced for SN P systems generating sets of numbers:
Theorem 7
There is a universal number generating SN P system with standard rules having 76 neurons.
In Zhang et al. (2008), these results were improved: 67 neurons in the case of computing functions, and 63 neurons in the case of generating sets of numbers are sufficient to get universality.
4.4 SN P systems as language generators
If we look at SN P systems as generators of string languages, we cannot obtain analogous universality results. In fact, as shown in Chen et al. (2006), there are strong restrictions on their computing power: on one hand some very simple languages cannot be generated, while on the other hand it is possible to build systems that generate “hard” languages.
Let’s recall from Chen et al. (2006) that, given an SN P system \(\varPi\), the language \(L(\varPi )\) generated by it is the set of binary strings describing the spike trains of all the (non-deterministic) halting computations of \(\varPi\). As done for number generating systems, we can define families of languages generated by systems with given bounds on the number of neurons, of rules, of consumed or forgotten spikes, maximum delay, and so on. In particular, we denote by \(LSNP_m(rule_k, cons_p, forg_q)\) the family of languages \(L(\varPi )\), generated by systems \(\varPi\) with at most m neurons, each neuron having at most k rules, each of the spiking rules consuming at most p spikes, and each forgetting rule removing at most q spikes. As usual, the values m, k, p, q are replaced with \(*\) if the corresponding parameter is unbound. If the underlying SN P systems are finite, we denote the corresponding families of languages by \(LFSNP_m(rule_k, cons_p, forg_q)\).
The restrictions on the use of rules given in the standard definition of SN P systems lead to a very simple proof of the following theorem (Chen et al. 2006).
Theorem 8
There are finite languages, for instance \(L_{k,j} = \{0^k, 10^j\}\), for any \(k \ge 1, j \ge 0\), which cannot be generated by any SN P system.
Note that the very simple language \(L_{1,0}=\{0, 1\}\) belongs to this class, hence \(L_{1,0} \notin LSNP_* (rule_*, cons_*, forg_*)\). In Chen et al. (2006) some other examples are given of finite languages that can be generated by SN P systems, and the relationships with the family of regular languages are investigated.
Theorem 9
The family of languages generated by finite SN P systems is strictly included in the family of regular languages over the binary alphabet.
Furthermore, it is shown that some “hard” languages can also be generated, and recursively enumerable languages can be characterized as projections of inverse-morphic images of languages generated by SN P systems.
A survey on SN P systems as language generators can be found in Ibarra et al. (2009).
5 SN P systems with extended rules
Let us now look at some of the most interesting variants of SN P systems that have been considered.
A first generalization of the “standard” rules was introduced in Ionescu et al. (2006) and Păun and Păun (2007) as a way to reduce the dimension (number of neurons) of an universal SN P system, and then more precisely presented in Chen et al. (2008) under the name of extended rules. The corresponding systems were defined as follows:
Definition 10
An extended spiking neural P system of degree \(m\ge 1\) is a construct of the form \(\varPi =(O,\sigma _1,\dots ,\sigma _m, syn, i_0), \text{ where: }\)
-
1.
\(O=\{a\}\) is the singleton alphabet (a is called spike);
-
2.
\(\sigma _1,\dots ,\sigma _m\) are neurons, of the form \(\sigma _i=(n_i, R_i), 1\le i \le m,\) where:
-
(a)
\(n_i\ge 0\) is the initial number of spikes contained in \(\sigma _i\);
-
(b)
\(R_i\) is a finite set of rules of the form \(E/a^c\rightarrow a^p\), where E is a regular expression over a and \(c\ge 1\), \(p\ge 0\) are natural numbers, with the restriction \(c\ge p\);
-
(a)
-
3.
\(syn\subseteq \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}\) with \(i\ne j\) for all \((i,j)\in syn\), \(1\le i,j\le m\) is the set of synapses between neurons;
-
4.
\(i_0\in \{1,2,\dots ,m\}\) indicates the output neuron.
Using criteria similar to the standard ones, a rule \(E/a^c\rightarrow a^p\) is enabled if the associated neuron contains \(k \ge c\) spikes, and \(a^k \in L(E)\). While a standard rule, when applied, consumes c spikes and produces exactly one spike (spiking rules) or no spikes (forgetting rules), extended rules can produce any number \(p\ge 0\) of spikes, consuming c spikes. Being \(p \ge 0\), we obtain a generalization of both standard spiking and forgetting rules, with the additional feature of having the forgetting rules also controlled by regular expressions. Moreover, forgetting rules are now allowed to compete in a non-deterministic way with spiking rules. Note that with this definitions there are no delays between firing and spiking, hence the produced spikes are immediately delivered.
Possible ways to encode information, non-deterministic choice among two or more enabled rules in a neuron, configurations, transitions, computations, generation or acceptance of numbers are defined just as in standard SN P systems.
Spike trains can be defined in two different ways. Following the standard definition, if the output neuron spikes, then we write 1, independently of the number p of spikes emitted, otherwise we write 0. Alternatively, we can also consider spike trains as encoding words on an arbitrary alphabet, associating the symbol \(b_i\) with a step when the output neuron emits \(i\ge 1\) spikes. Steps when no spikes are emitted can be associated to a symbol \(b_0\) in the alphabet or to the empty string \(\lambda\). In the first case we denote the language generated by a system \(\varPi\) by \(L_{res}(\varPi )\) (with” res” coming from “restricted”), in the latter one we write \(L_\lambda (\varPi )\).
The universality of extended SN P systems (\(SN^eP\) systems) as number generators can be proved as usual through simulation of register machines, in a simpler way Chen et al. (2008):
Theorem 11
\(Spik_{gen}SN^eP_*(rule_4; cons_5; prod_2) = NRE\).
This means that the family of recursively enumerable sets of natural numbers can be generated by extended SN P systems with unbound number of neurons, at most 4 rules in each neuron, at most 5 spikes consumed and at most 2 spikes produced by any rule.
If we look at the minimal number of neurons needed to obtain universality, extended rules give some advantage with respect to standard ones (Păun and Păun 2007).
Theorem 12
There is a universal number generating SN P system with extended rules (without delay) having 50 neurons
In a similar way, the results on minimal universal computing SN P systems can be improved if extended rules are used:
Theorem 13
There is a universal computing SN P system with extended rules (without delay) which has 49 neurons.
The proofs are based on simulating a small universal register machine from Korec (1996), with a fine tuning of the number of used neurons.
6 Different strategies of using rules
Let’s now focus on a second relevant feature of SN P systems, that is the way rules to be executed in a given computation step are selected. As described in Sect. 3, in standard SN P systems all neurons evolve in parallel, synchronized by a global clock, but inside each neuron only at most one rule can be applied at each computation step, non-deterministically selected among all enabled rules. This type of application of rules is usually defined as sequential, at single neuron level.
Various works have appeared that consider different strategies, or different semantics, for the application of the rules inside the neurons.
A first alternative strategy, that has been considered in Leporati et al. (2007), is the maximally parallel semantics, intended exactly as in cell-like P systems. Let us denote by k the number of spikes contained in a neuron at time t. We can ideally divide the computation step in two parts. We first select, in a non-deterministic way, one rule of the neuron to be applied. If such a rule consumes c spikes, after (ideally) removing these spikes from the neuron, the rule selection process is repeated, considering the remaining \(k-c\) spikes, until no further rule can be applied. In this way, a rule may be chosen many times to be applied, and thus at the end of the process we will have a multiset of rules that will be simultaneously fired. A little technical difficulty is given by the fact that the chosen rules may have different delays; hence, we define the delay associated with a multiset of rules as the maximum of the delays that appear in the rules. As we will better discuss in Sect. 10, dedicated to the efficiency of SN P systems in solving hard problems, this strategy has been considered in order to enhance this efficiency. In fact, we will see that NP-complete problems can be solved by SN P systems in polynomial time (and exponential space), by exploiting the intrinsic parallelism of such systems. Nonetheless, the systems must be initialized with an exponential amount of spikes. In particular, in Leporati et al. (2007) it was proved that, by using maximal parallelism, any integer number in the usual binary notation, received as an input by a SN P system, can be translated to the unary form in polynomial time, by producing a corresponding amount of spikes. As a consequence, we can build a system that is able to first generate the required amount of spikes, and then to solve the considered NP-complete problem. In the same paper, it was also proved that the conversion from binary to unary notation cannot be performed in polynomial time when the use of maximal parallelism is forbidden.
Another kind of semantics that has been considered is the exhaustive mode (Ionescu et al. 2007), assuming extended rules. In this case, at every step of computation one of the enabled rules in each neuron is non-deterministically chosen, and then applied as many times as possible, on the basis of the amount of spikes in the neuron. Hence, the number of spikes produced in that neuron in a computation step can be arbitrarily large. Note that the enabling condition is checked only on the total number of spikes in the neuron, and not on the ‘ideal’ number of spikes remaining at each substep of the selection phase. Similar results as in the case of sequential application of rules are obtained, in particular concerning computational completeness, both for number generating mode and for number accepting mode. Nonetheless, the systems required to obtain such results are, in general, significantly more complex than systems that use sequential semantics. As stated by the authors of the paper, the main reason of this complexity is related to the difficulty of simulating intrinsically sequential devices such as register machines by using a parallel application of rules. In Zhang et al. (2010) a small universal system of this type with 125 neurons, using standard rules without delays and encoding the output as length of the interval between two spikes of the output neuron, was shown. One extra neuron (126 in total) is needed if the result of the computation is given by the total number of spikes of the output neuron. The result has been improved in Pan and Zeng (2011), where a universal system with exhaustive use of rules, using only 36 neurons, has been obtained.
A semantics in between the sequential and the exhaustive mode, called generalized use of rules, was considered in Zhang et al. (2014): in each neuron, one of the applicable rules is chosen in a non-deterministic way, and then applied for a number of times also non-deterministically chosen. In this case, the authors proved that the number of neurons is fundamental to achieve a desired computational power. In fact, SN P systems using rules according to this semantics and consisting of one neuron characterize finite sets of natural numbers. When exactly two neurons are used, then the computational power of the systems is improved, but limited to the possibility to generate semilinear sets of numbers. When three neurons can be used, then at least a non-semilinear set of numbers can be generated. If no bound on the number of neuron is set, then SN P systems using this semantics are computationally complete. In Jiang et al. (2019) an improved universal system of this type was obtained, where each neuron contains at most 5 rules, each spiking rule consumes at most 4 spikes, and each forgetting rule deletes at most 4 spikes.
Yet another possibility, based on the ideas used in tissue-like P systems, is to apply rules according to a so-called flat maximal parallelism (Pan et al. 2016): at every computation step, the rules chosen to be executed in each neuron form a maximal set, to which no further applicable rule can be added; nonetheless, each rule in the set is applied only once. In Wu and Jiang (2021) authors show that SN P systems working in the flat maximally parallel mode are Turing universal as number generating devices. Moreover, it is proved that 68 neurons are sufficient to construct a universal SN P system working in the flat maximally parallel mode.
A more restrictive strategy that has been proposed in Ibarra et al. (2006) extends sequentiality also at system level: we will call this the strong sequential mode. In this mode, at every step of the computation, if there is at least one neuron with at least one rule that is enabled, we only allow one such neuron and one such rule (both chosen non-deterministically) to be fired. It was shown in Ibarra et al. (2006) that certain classes of strongly sequential SN P systems are equivalent to partially blind counter machines (see Greibach (1978) for definitions), while others are universal.
Finally, in Cavaliere et al. (2008) and Cavaliere et al. (2009), based on the observation that our biological neural systems are not synchronized, the synchronization between neurons is removed, and the power of asynchronous spiking neural P systems is investigated. More precisely, in such systems, a global clock is still present, but neurons work asynchronously in the sense that the execution of rules in each neuron is not forced to happen at a specific time instant. At each time step instead any neuron containing enabled rules may (non-deterministically) choose whether or not to fire (at most) one of them. If the content of the neuron is not changed, a rule which was enabled, and not fired, at step t can fire later. If new spikes are received, then it is possible that the unfired rule is no more enabled, while other rules will be enabled - and can be applied or not. Since the asynchronicity applies also to the output neuron, the distance in time between the first two spikes sent out by the system has now elements of randomness, and cannot be used as the result of the computation. Hence, for non-synchronized SN P systems, we will assume as the result of the computation the total number of spikes sent out to the environment. This makes it necessary to consider only halting computations. The synchronization is in general a powerful feature, and removing it seems to cause a significant reduction in computational power of asynchronous standard SN P systems, whose universality has not been proved: it remains an open problem, with a feeling in favour of non-universality. However, it turns out that the loss in power entailed by removing the synchronization is compensated by the use of extended rules. In fact, in the above papers it has been proved that a set \(Q \subseteq \mathbb {N}\) of natural numbers is recursively enumerable (i.e. \(Q \in NRE\)) if and only if it can be generated by an asynchronous SN P system with extended rules, with or without delays, with an unbound number of neurons. Moreover, finite languages and recursively enumerable languages were shown to be characterized by asynchronous SN P systems in Zhang et al. (2009).
The asynchronous operating mode has been considered for most of the variants we will discuss here: asynchronous SN P systems with structural plasticity in Cabarle et al. (2015); asynchronous extended SN P systems with astrocytes in Pan et al. (2012); asynchronous SN P systems with rules on synapses in Song et al. (2015). Furthermore, the notion of local synchronization was introduced in Song et al. (2013), and the constructed systems were proved to be computationally complete in the generating case.
7 SN P systems with weights or active synapses
7.1 Weighted SN P systems
Two key features in Artificial Neural Networks are the threshold associated with each neuron and the weight associated with each synapse (Gurney 1997). Assuming the simplest model, the binary threshold neuron, a neuron \(\sigma _i\) spikes at time \(t+1\) if the following holds: \(\sum w_{j,i} \sigma _j(t) \ge \theta _i\), where \(w_{j,i}\) is the weight associated with the synapse (j, i), \(\sigma _j(t)\) is the state (1 for spiking, 0 otherwise) of the neuron \(\sigma _j\) at time t, and \(\theta _i\) is the threshold associated with neuron \(\sigma _i\). This means that a neuron spikes if and only if the sum of spikes coming from its input neurons, weighted through the synapses, at least equals the given threshold, and that synapses are not passive crossing points in the network topology, but have an active role in systems evolution. In both cases, whether the total input signal reaches the threshold or not, it vanishes. Furthermore, a fundamental aspect in ANNs is that the weights on synapses are modified during the training phase by learning algorithms.
Hence, it was rather natural to introduce similar elements in SN P systems, as done in Wang et al. (2010), where SN P systems with weights are defined. In the following definition, \(\mathbb {R}_c\) indicates the set of computable real numbers.
Definition 14
A Spiking Neural P system with weights (WSN P system for brevity) of degree \(m\ge 1\) is a construct of the form
-
1.
\(\sigma _1,\dots ,\sigma _m\) are neurons, of the form \(\sigma _i=(p_i, R_i), 1\le i \le m,\) where:
-
a)
\(p_i \in \mathbb {R}_c\) is the initial potential in neuron \(\sigma _i\);
-
b)
\(R_i\) is a finite set of spiking rules of the form \(T_i /d_s \rightarrow 1, s = 1, 2, . . . , n_i\) for some \(n_i \ge 1\), where \(T_i \in \mathbb {R}_c, T_i \ge 1\), is the firing threshold potential of neuron \(\sigma _i\), and \(d_s \in \mathbb {R}_c\) with the restriction \(0 < d_s \le T_i\).
-
a)
-
2.
\(syn\subseteq \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}\times \mathbb {R}_c\) is the set of synapses between neurons, with \(i\ne j\), \(r \ne 0\) for all \((i,j,r)\in syn\), and for each \((i,j) \in \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}\) there is at most one synapse (i, j, r) in syn;
-
3.
\(in, out\in \{1,2,\dots ,m\}\) indicate the input and output neuron, respectively.
In this definition, the content of neurons is not an integer number of spikes, but it is a potential represented by a computable real number. At time t each neuron \(\sigma _i\), containing \(n_i\) rules of the form \(T_i /d_s \rightarrow 1\), compares its current potential p with its threshold \(T_i\) (note that the threshold is common to all the rules in the neuron). There are three cases: i) if \(p < T_i\), then the neuron \(\sigma _i\) returns to the resting potential 0; ii) if \(p > T_i\), then the potential p remains unchanged; iii) if \(p = T_i\), then a rule \(T_i /d_s \rightarrow 1 \in R_i\) is non-deterministically chosen and applied: the potential is reduced to \(T_i-d_s\) and a spike (unit potential) is emitted. The spike is immediately delivered to all the neurons \(\sigma _j\) such that \((i, j, r) \in syn\); r is the weight of the synapse, and neuron \(\sigma _j\) receives a quantity of potential equal to r, which is added to its current potential and can be used at time \(t+1\). Since r can be positive or negative, the potential of the receiving neuron is increased or decreased.
As you can see, this definition is radically different from the standard one, from the conceptual point of view. However, we can define computations and their results, in generating mode, as usual:
-
a global clock is assumed, marking the time for the whole system and synchronizing the system;
-
rules are executed sequentially at neuron level (each neuron uses at most one rule in each step, non-deterministically chosen among its rules), and in a maximally parallel way at system level (all neurons that have enabled rules at time t must choose and apply a rule);
-
the configuration \(C_t\) of the system at time t consists of the distribution of potentials in neurons at time t. The initial configuration of the system is the tuple \(C_0 = <p_1, \dots , p_m>\);
-
applying the rules as explained above, we obtain transitions \(C_t \Rightarrow C_{t+1}\) among configurations;
-
a computation is any sequence \(C_0 \Rightarrow C_1 \Rightarrow \dots C_t \Rightarrow C_{t+1} \dots\) of transitions starting from the initial configuration. It is halting if it reaches a configuration where no rule can be used;
-
with any computation, halting or not, we associate a spike train, the binary sequence with occurrences of 1 indicating time steps when the output neuron spikes;
-
the number generated by a computation is the number of steps elapsed between the first two spikes of the output neuron.
The set of all numbers generated by the system \(\varPi\) is denoted by \(N_{gen}(\varPi )\). We can consider also \(\varPi\) working in accepting mode: after starting the computation from the initial configuration, we send from outside to the input neuron two spikes at steps \(t_1\) and \(t_2\); the number \(n = t_2 - t_1\) is accepted if the computation eventually halts. The set of numbers accepted by \(\varPi\) is denoted by \(N_{acc}(\varPi )\).
7.2 Universality results
In Wang et al. (2010) the computational power of WSN P systems (in both generating and accepting mode) has been investigated, considering limitations on the main parameters characterizing the system: number of neurons, class of numbers used for weights, thresholds and potentials (i.e. natural numbers \(\mathbb {N}\), integers \(\mathbb {Z}\), rational numbers \(\mathbb {Q}\), real computable numbers \(\mathbb {R}_c\)). The family of all sets \(N_\alpha (\varPi ), \alpha \in \{gen, acc\}\) of natural numbers generated/accepted by WSN P systems with at most \(m \ge 1\) neurons (\(*\) is used for an unbound number of neurons), using weights, thresholds, and potentials in the rules taken from the set X, for \(X \in \{\mathbb {N}, \mathbb {Z}, \mathbb {Q}, \mathbb {R}_c \}\), is denoted by \(N_\alpha W_XSNP_m\).
The following theorem shows that universality, in both generating and accepting mode, can be obtained using only integers (both positive and negative) for weights, thresholds and potentials.
Theorem 15
\(N_\alpha W_ \mathbb {Z}SNP_* = NRE\) for \(\alpha \in \{gen, acc\}\).
From the proof, based as usual on the characterization of NRE by means of register machines, it is also possible to conclude that the universality of WSN P systems in generating mode is preserved if we use only: (i) weights 1 and \(-1\) for synapses; (ii) at most two rules per neuron; and (iii) all rules are of one of the following three forms: \(1/1 \rightarrow 1, 2/2 \rightarrow 1,\) and \(2/1 \rightarrow 1\). Obviously, in generating mode at least two rules in at least one neuron are needed to grant non-determinism. This is not the case for accepting mode: in this case, one rule in each neuron is sufficient.
The further restriction that weights, thresholds and potential are limited to be natural numbers, so excluding negative values, limits to semilinear sets of natural numbers the generating power of the systems.
Theorem 16
\(N_ {gen}W_ \mathbb {N}SNP_* = SLIN\).
In Pan et al. (2012) weights on synapses are introduced without radically modifying the basic idea of spikes as units of information. Simply, multiple synapses between neurons are allowed, and the connection between two neurons \(\sigma _i\) and \(\sigma _j\) is endowed with an integer weight denoting the number of synapses connecting them. Hence, when \(\sigma _i\) spikes, the number of spikes that reach \(\sigma _j\) is a multiple of the number of spikes emitted by \(\sigma _i\). It is proved that the use of weights on synapses allows to construct small universal spiking neural P systems. Specifically, a universal spiking neural P system with standard rules and weights having 38 neurons is produced as device of computing functions; as generator of sets of numbers, we find a universal system with standard rules and weights having 36 neurons.
7.3 The language generation power of WSN P systems
As done for standard SN P systems, we can now look at the power of WSN P systems in generating languages (Zeng et al. 2014). For a WSN P system \(\varPi\), the language \(L(\varPi )\) generated by \(\varPi\) is defined as the set of spike trains associated with any halting computation, and \(LW_XSNP_m\) denotes the family of all languages generated by WSN P systems with at most \(m \ge 1\) neurons, using weights, thresholds, and amounts of consumed potentials in the rules taken from the set X, for \(X \in \{\mathbb {N}; \mathbb {Z}; \mathbb {Q}; \mathbb {R}_c\}\). When the number of neurons is not bounded, the subscript m is replaced with \(*\).
It is immediate to prove that, with the usual encoding of the output result, there are very simple languages that cannot be generated.
Theorem 17
There is no WSN P system that can generate a language of the form \(\{0x; 1y\}\), where x and y are arbitrary strings over \(\{0, 1\}\).
In fact, a string 1y can be generated only if the output neuron can (and hence must) spike in the initial configuration. But in this case it will be impossible to generate a string of the form 0x. So, the languages of the form \(\{0x; 1y\}\) do not belong to \(LW_{\mathbb {R}_c}SNP_*\).
In order to avoid this problem, in Zeng et al. (2014), a slightly modified definition of strings generated by \(\varPi\) is given.
Definition 18
Let \(\varPi\) be a WSN P system; a string x over \(\{0, 1\}\) is generated by \(\varPi\) if there is a computation with spike train of the form \(0^b1x, b \ge 0\).
Hence, only computations that send at least one spike to the environment are considered, and the prefix \(0^b1\) of the spike train, including the first 1, is discarded. The language generated by \(\varPi\) under this definition is denoted by \(L_{dis}(\varPi )\), and the family of languages generated by WSN P systems is denoted by \(L_{dis}W_XSNP_m\), where X and m have the same meaning as above.
We first consider the language generation power of WSN P systems with natural numbers as synapse weights, thresholds, and potentials. In this case, the family of generated languages is a proper subset of regular languages.
Theorem 19
\(L_{dis}W_\mathbb {N}SNP \subset REG\).
If synapse weights, thresholds, and potentials of WSN P systems are integers, then the language generation power of WSN P systems strictly increases.
Theorem 20
There exists a language \(L \in L_{dis}W_\mathbb {Z}SNP_*\) such that \(L \notin REG\).
Finally, an indirect characterization of recursively enumerable languages can be given by projections of inverse-morphic images of languages generated by WSN P systems.
Theorem 21
For an alphabet \(V = \{e_1, e_2, \dots , e_k\}\), and any language \(L \subseteq V^*, L \in RE\), there are a morphism \(h_1 : (V\cup \{y, z\}^*) \rightarrow \{0, 1\}^*\), and a projection \(h_2 : (V\cup \{y, z\}^*) \rightarrow V^*\) such that there is a WSN P system \(\varPi\) with integer weights such that \(L = h_2(h_1^{-1} (L_{dis}(\varPi )))\).
7.4 “Variants of the variant”
WSN P systems, as defined above, use weights and thresholds in a rather different way than ANNs. In particular, the neuron spikes when the weighted sum of incoming potentials is exactly equal to the threshold, while in ANNs the spike is produced if the total input signal is at least equal to the threshold. For this reason, in Zeng et al. (2014) spiking neural P systems with thresholds (SNPT systems) are considered such that a neuron fires when its potential is equal or higher than the threshold. Two possible alternatives for the use of the potential, when the neuron fires, are considered: i) the potential is reduced by the amount established by the fired rule; or ii) the potential vanishes i.e., it is reset to zero. In Zeng et al. (2014) it is proved that the systems of the former type can compute all Turing computable sets of numbers and the systems of the latter type characterize the family of semilinear sets of natural numbers. The results show that the firing mechanism of neurons has a crucial influence on the computation power of the SNPT systems.
Another variant, weighted spiking neural P systems with anti-spikes (AWSN P systems) is defined in Ren et al. (2020), adding anti-spikes to spiking neural P systems with weighted synapses. Anti-spikes act as inhibitors of communication between neurons. Turing universality of AWSN P systems as number generating and accepting devices is proved. In the same paper, considering the dimension of universal AWSN P systems using standard rules, it is shown that 34 neurons are sufficient to generate recursively enumerable sets of natural numbers, and 34 to compute recursive functions.
As said before, the success of ANNs in many application areas is based on their ability to learn from examples, by modifying synaptic weights so as to strengthen or weaken connections among neurons during the computation. In Gutiérrez-Naranjo et al. (2009), a variant of WSN P systems with Hebbian learning has been considered, and more recently in Song et al. (2019) a class of specific SN P systems with simple Hebbian learning function has been constructed to recognize English letters. The experimental results are very promising, and open interesting perspectives for applications of WSN P systems in pattern recognition.
7.5 Rules on synapses
A different way to give synapses an active role is proposed by Song et al. (2014), were a new class of SN P systems, with extended rules (spiking or forgetting) placed on synapses, is introduced as follows.
Definition 22
A SN P system with extended rules on synapses and with delay (in the general form, for computing functions) of degree \(m\ge 1\) is a construct of the form \(\varPi =(O,\sigma _1,\dots ,\sigma _m,syn,in,out)\), where:
-
1.
\(O=\{a\}\) is the singleton alphabet (a is called spike);
-
2.
\(\sigma _1,\dots ,\sigma _m\) are neurons, of the form \(\sigma _i=(n_i), 1\le i \le m\), where \(n_i\ge 0\) is the initial number of spikes contained in \(\sigma _i\);
-
3.
syn is the set of synapses; each element in syn is a pair of the form \(((i, j), R_{(i, j)})\), where (i, j) indicates that there is a synapse connecting neurons \(\sigma _i\) and \(\sigma _j\), with \(i, j \in {1, 2,..., m}\), \(i \ne j\), and \(R_{(i, j)}\) is a finite set of rules of one of the following two forms:
-
(1)
\(E/a^c\rightarrow a^p;d\), where E is a regular expression over O, \(c\ge p \ge 1\), \(d\ge 0\) are natural numbers;
-
(2)
\(a^s\rightarrow \lambda\), where \(s\ge 1\) is a natural number, with the restriction that \(a^s\notin L(E)\) for any rule \(E/a^c\rightarrow a^p;d\) from any \(R_{(i,j)}\), where L(E) is the regular language defined by E;
-
(1)
-
4.
\(in, out\in \{1,2,\dots ,m\}\) indicate the input and output neuron, respectively.
In SN P systems of this type, the neurons contain only spikes, while the rules are moved on the synapses. As in the standard case, a rule \(r=E/a^c\rightarrow a^p;d \in R_{(i,j)}\) is enabled at time t if \(n_i \in L(E)\), where \(n_i\) is the current number of spikes in the neuron \(\sigma _i\). If multiple rules in the set \(R_{(i,j)}\) are enabled, then one of them is non-deterministically chosen to be fired. In fact, the system works sequentially on each synapse (at most one rule from each set \(R_{(i, j)}\) can be used), and in parallel at the level of the system (if a synapse has at least one rule enabled, then it has to use a rule).
Firing the rule \(r=E/a^c\rightarrow a^p;d \in R_{(i,j)}\) means consuming c spikes from \(\sigma _i\) and sending (with delay d) p spikes only to \(\sigma _j\), and not to all the neurons connected to \(\sigma _i\) as in the standard systems. Forgetting rules are treated in a similar way; note that a forgetting rule can be enabled only if there are no enabled spiking rules in any synapse. An immediate problem arises when several synapses starting from \(\sigma _i\) have enabled rules, each one of them requiring to consume a certain number of spikes. In order to avoid conflicts on the use of resources (spikes), the following restriction is introduced: all rules consume the same number c of spikes, and c spikes are removed from \(\sigma _i\), regardless of the number of fired rules (if higher than 1). Apart from these differences, all the other notions such as configuration, transition, computation, input and output encoding and so on are as in the standard case.
In Song et al. (2014) it is shown that placing the rules on synapses allows to give simpler universality proofs and to obtain smaller universal systems in comparison with the case when the rules are placed in the neurons.
With the usual technique of simulation of register machines, it is possible to prove that SN P systems with extended rules on synapses, with the result of a computation being defined as the number of spikes sent to the environment, can generate all recursively enumerable sets of numbers.
Theorem 23
\(NsSN_*^2P=NRE\).
where \(NsSN_*^2P\) denotes the family of sets of natural numbers generated by SN P systems with an unbound number of neurons and at most 2 rules associated with a synapse.
As a further result, two small universal SN P systems with rules on synapses for computing functions are constructed, using standard or extended spiking rules
Theorem 24
There is a universal SN P system with standard spiking rules (with delay) on synapses having 39 neurons for computing functions.
The use of extended rules allows to reduce the number of neurons.
Theorem 25
There is a universal SN P system with extended spiking rules (with delay) on synapses having 30 neurons for computing functions.
More recently, in Song et al. (2021) it is proposed to associate delays to synapses, so that the spiking neuron immediately sends its spike, that is delivered to different receiving neurons at different instants, depending on the delay time on the synapses connecting them. It is proved that the Spiking Neural P systems with Delay on Synapses (SNP-DS systems) are universal as number generators. Two small universal SNP-DS systems, with standard or extended rules, are constructed to compute functions, using 56 and 36 neurons, respectively.
8 SN P systems with astrocytes
In Binder et al. (2007) it was observed that in animal nervous system an important role in modulating synaptic transmission is played by astrocytes. Astrocytes are star-shaped glial cells in the brain and spinal cord that perform many functions, including biochemical control of endothelial cells that form the blood-brain barrier, regulation of cerebral blood flow, provision of nutrients to the nervous tissue, maintenance of extracellular ion balance, modulation of neuronal excitability and synaptic transmission, with both an excitatory and an inhibitory action. Hence, in Binder et al. (2007) and Păun (2007) the SN P systems with astrocytes (SNPA systems) were proposed to take into account the joint action of the two interacting networks of neurons and astrocytes.
While (Binder et al. 2007) introduces two kinds of astrocytes, excitatory and inhibitory, Păun (2007) considers a much simplified version of SNPAs, with only inhibitory astrocytes. The basic idea is adding to the system a set of astrocytes, each one of them controlling a subset of synapses. If at computation step t two or more spikes are transmitted along the synapses controlled by the astrocyte x, then exactly one spike is selected, non-deterministically, to reach the destination neuron, while all others are removed (obviously, in the case of 0 or 1 transmitted spikes x does not intervene). Hence a new degree of non-determinism is added to the functioning of the system by the branching due to the non-deterministic choice of the surviving spike. A second relevant observation is that, since the same synapse can be controlled by several astrocytes, it is possible that their action is contradictory, with a resulting deadlock of the system: in fact an astrocyte could decide to suppress a spike on the common synapse, and another to let it survive. A simple example of deadlock can be found in the paper Păun (2007), that focuses on the deadlock decidability problem, proving that it is undecidable whether an arbitrary SN P system with (at least three) astrocytes reaches a deadlock. On the other side, any SN P system with astrocytes controlling several synapses, without forgetting rules, can be reduced to an equivalent system in normal form with each astrocyte controlling only two synapses.
In Pan et al. (2012), starting from the observation that, in a biological nervous system, the same astrocyte can have an excitatory or inhibitory role, depending on the spike traffic along the supervised synapses, a slightly different definition is given. In the following we will refer to this definition.
Definition 26
A Spiking Neural P system with Astrocytes (SNPA system) of degree \(m\ge 1\), \(l\ge 1\) is a construct of the form \(\varPi =(O,\sigma _1,\dots ,\sigma _m,syn, ast_1,\dots , ast _l,in,out)\), where:
-
1.
\(O=\{a\}\) is the singleton alphabet (a is called spike);
-
2.
\(\sigma _1,\dots ,\sigma _m\) are neurons, of the form \(\sigma _i=(n_i, R_i), 1\le i \le m,\) where: [a)] \(n_i\ge 0\) is the initial number of spikes contained in \(\sigma _i\); [b)] \(R_i\) is a finite set of rules of one of the following two forms:
-
(1)
\(E/a^c\rightarrow a;d\), where E is a regular expression over the alphabet \(\{a\}\) and \(c\ge 1\), \(d\ge 0\) are natural numbers;
-
(2)
\(a^s\rightarrow \lambda\), where \(s\ge 1\) is a natural number, with the restriction that for each rule \(E/a^c\rightarrow a;d\) of type (1) from \(R_i\), we have \(a^s\notin L(E)\);
-
(1)
-
3.
\(syn\subseteq \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}\) with \(i\ne j\) for all \((i,j)\in syn\), \(1\le i,j\le m\) is the set of synapses between neurons;
-
4.
\(ast_1,\dots , ast_l\) are astrocytes, of the form \(ast_i = (syn_{ast_i}, t_i)\), where \(1 \le i \le l, syn_{ast_i} \subseteq syn\) is the set of synapses controlled by the astrocyte \(ast_1\), \(t_i \in \mathbb {N}\) is the threshold of the astrocyte \(ast_1\);
-
5.
\(in, out \in \{1,2,\dots ,m\}\) indicate the input and output neuron, respectively.
In SNPA systems, the neurons execute the rules as in standard SN P systems at each time step, then astrocytes intervene, exercising their function of spike traffic control. Each astrocyte \(ast_i\) counts the number k of neurons that are requesting to cross the synapses in the set \(syn_{ast_i}\), then uses its threshold \(t_i\) to decide its role:
-
1.
If \(k > t_i\), then it will have an inhibitory role, removing all the k spikes from the system;
-
2.
If \(k < t_i\), then it will have an excitatory role, and all the k spikes will reach the target neurons;
-
3.
If \(k = t_i\), then it will non-deterministically choose an inhibitory or an excitatory role.
Even with this definition the deadlock problem must be addressed, since it is possible that two or more astrocytes control the same synapse. In this case, if all these astrocytes have an excitatory role, then the spike along this synapse, if any, will pass to the destination neuron; if at least one of these astrocytes has an inhibitory role, then the spike will be suppressed.
8.1 Universality results
In order to prove universality of SNPA systems, in both generating and accepting mode of sets of natural numbers, it is sufficient to consider the class SHSNPA of simple homogeneous SNPA system. In these systems each neuron has only the very simple spiking rule \(a^*/a \rightarrow a\) (simplicity), the same for all neurons (homogeneity). Note that this implies that the behavior of neurons is deterministic, hence the non-determinism of the system, necessary for the universality in number generating mode, depends only on the non-determinism of astrocytes.
Now, denoting by \(N_{gen}SHSNPA\) the family of sets of natural numbers generated by SHSNPA systems, with the usual technique of building SNPA systems simulating register machines we can prove our universality result.
Theorem 27
\(N_{gen}SHSNPA = NRE\)
This result can be easily extended to the accepting mode, using an input neuron that will receive two spikes from outside; the input is the length n of the time interval between these two spikes, and it is accepted if the related computation will halt.
Theorem 28
\(N_{acc}SHSNPA = NRE\)
As in the case of standard SN P systems, imposing a bound on the number of spikes present in any neuron during any computation reduces the generating power of SNPA systems to the family of linear sets of natural numbers.
Theorem 29
\(N_{gen}SHSNPA(bound_*) = SLIN\)
with the obvious meaning of the notation.
Small universal SNPA systems (without delay and forgetting rules) were investigated in Kong et al. (2014), through simulation of the small register machine described in Korec (1996). It is proved that that 57 neurons and 19 astrocytes are sufficient to compute any Turing computable function, and that 54 neurons and 17 astrocytes are sufficient to generate any Turing computable set of natural numbers.
9 SN P systems with structural plasticity
9.1 The definition
Another relevant feature of the animal nervous system is its structural plasticity, that is its capability to modify the synapse graph through synapse creation and deletion. This feature is added to SN P systems in Cabarle et al. (2015), where SN P systems with structural plasticity are defined. A slightly different definition is given in Macababayao et al. (2022), but we will refer to the original one.
Definition 30
A Spiking Neural P system with Structural Plasticity (SNPSP system) of degree \(m\ge 1\) is a construct of the form \(\varPi =(O,\sigma _1,\dots ,\sigma _m, syn, in, out)\) where:
-
1.
\(O=\{a\}\) is the singleton alphabet (a is called spike);
-
2.
\(\sigma _1,\dots ,\sigma _m\) are neurons, of the form \(\sigma _i=(n_i, R_i), 1\le i \le m,\) where:
-
(a)
\(n_i\ge 0\) is the initial number of spikes contained in \(\sigma _i\);
-
(b)
\(R_i\) is a finite set of rules of one of the following two forms: [(1)] Spiking rule: \(E/a^c\rightarrow a\), where E is a regular expression over the alphabet \(\{a\}\) and \(c\ge 1\) is a natural number; [(2)] Plasticity rule: \(E/a^c\rightarrow \alpha k(i, N_j)\), where \(c\ge 1\), \(\alpha \in \{+,-, \pm , \mp \}\), \(k\ge 1\), \(1 \le j \le |R_i|\) and \(N_j \subseteq \{1, \dots , m\}\);
-
(a)
-
3.
\(syn\subseteq \{1,2,\dots ,m\}\times \{1,2,\dots ,m\}\) with \(i\ne j\) for all \((i,j)\in syn\), \(1\le i,j\le m\) is the set of synapses between neurons;
-
4.
\(in, out \in \{1,2,\dots ,m\}\) indicate the input and output neurons, respectively.
Hence SNPSP systems do not have delays nor forgetting rules. In the following, given a neuron \(\sigma _i\), \(pres(i) = \{j|(i,j) \in syn\}\) denotes the set of neurons that can receive spikes from \(\sigma _i\). Similarly, \(pos(i) = \{j|(j,i) \in syn\}\) denotes the set of neurons that can send spikes to \(\sigma _i\).
Spiking rules are applied as in standard SN P systems. A plasticity rule \(E/a^c\rightarrow \alpha k(i, N) \in R_i\) can be applied at time t if the neuron \(\sigma _i\) contains \(b \ge c\) spikes and \(a^b \in L(E)\). Its application consumes c spikes and has effects on the synapses that depend on the value of the parameter \(\alpha\).
-
1.
If \(\alpha =+\) and \(N - pres(i)=\emptyset\), or if \(\alpha = -\) and \(pres(i)=\emptyset\), then no synapse is created or removed;
-
2.
If \(\alpha =+\) and \(|N - pres(i)| \le k\), then a synapse (i, l) is deterministically created for every \(l \in N-pres(i)\), and a spike is immediately sent from \(\sigma _i\) to \(\sigma _l\);
-
3.
If \(\alpha =+\) and \(N - |pres(i)| > k\), then k neurons are non-deterministically selected in \(N - pres(i)\), a synapse (i, l) is created for every selected neuron \(\sigma _l\) and a spike is immediately sent from \(\sigma _i\) to \(\sigma _l\);
-
4.
If \(\alpha =-\) and \(|pres(i)| \le k\), then all the synapses in pres(i) are deterministically deleted;
-
5.
If \(\alpha =-\) and \(|pres(i)| > k\), then k neurons are non-deterministically selected in pres(i) and synapses to the selected neurons are deleted;
-
6.
If \(\alpha \in \{\pm , \mp \}\) then create (respectively, delete) synapses at time t and then delete (respectively, create) synapses at time \(t+1\). Only the priority of application of synapse creation or deletion is changed, but the application is similar to \(\alpha \in \{+, -\}\). The neuron is always open from time t until \(t+1\), i.e., the neuron can continue receiving spikes. However, the neuron can only apply another rule at time \(t+2\). Furthermore, creating a synapse (i, j) implies immediately sending a spike from \(\sigma _i\) to \(\sigma _j\).
Creating or deleting synapses modifies the synapse graph, and hence the configuration of the system at time t must include the structure of the graph, in addition to the number of spikes contained in any neuron. Transitions, computation, generating and accepting mode are then defined as in standard SN P systems.
9.2 Universality results
For both the accepting and generating modes of sets of natural numbers, SNPSP systems are proved to be universal. In fact, indicating with \(N_{gen}SNPSP\) (resp., \(N_{acc}SNPSP\)) the family of sets of natural numbers generated (resp., accepted) by SNPSP systems, we have:
Theorem 31
\(N_{gen}SNPSP = N_{acc}SNPSP = NRE\)
Let us consider the generating case. The difficult part is to prove the inclusion \(NRE \subseteq N_{gen}SNPSP\). As usual, given any set \(Q \in NRE\), the proof is based on the construction of a SNPSP system that simulates a register machine M that generates Q. The construction given in Cabarle et al. (2015) uses SNPSP systems with neurons that contain only a spiking rule of the simple form \(a \rightarrow a\), together with fewer neurons that have plasticity rules. Hence in this case the universality is granted by the non-determinism introduced by plasticity rules, while spiking rules are used in a deterministic way. In the accepting case non-determinism is not relevant, hence the SNPSP system simulating M is therefore simpler.
In Cabarle et al. (2015) a variant of the SNPSP systems semantics is also introduced, called saving mode. In this mode, when no synapses are created or removed, then no spikes are consumed. It is proved that even in this mode universality is maintained. However, deadlock situations can arise, and undecidability of deadlock states is proved.
Interesting results are also given in Macababayao et al. (2022), concerning normal forms for standard SN P systems, for SN P systems with structural plasticity and for SN P systems with rules on synapses. In fact, it is proved that universal standard SN P systems with only two rules per neuron and one kind of regular expression can be built, while in the case of SNPSP systems and of SN P systems with rules of synapses the number of rules per neuron can be reduced to only one.
10 Approaching computationally hard problems
The computational power of SN P systems can also be considered from a different point of view, their capability to efficiently solve computationally hard problems. This point of view has been assumed for example in Chen et al. (2006), where a variant of spiking neural P systems which have, in their initial configuration, an arbitrarily large number of inactive neurons which can be activated (in an exponential number) in polynomial time. Using this model of P systems we can deterministically solve the satisfiability problem (SAT) in constant time, so trading space for time.
In Leporati et al. (2007), a solution for the NP-complete problem Subset Sum in a constant number of computation steps was proposed, by means of a non-deterministic SN P system with extended rules.
The Subset Sum problem can be defined as follows. Problem: Subset Sum.
-
Instance: a (multi)set \(V = \{v_1, v_2, \ldots , v_n\}\) of positive integer numbers, and a positive integer number S.
-
Question: is there a sub(multi)set \(B \subseteq V\) such that \(\sum \limits _{b \in B} b = S\)?
When we allow to non-deterministically choose the rules to be applied within a neuron, then we are able to define an SN P system like the one depicted in Fig. 4 that is able to solve any given instance of Subset Sum in a constant number of steps.
Consider the following instance of Subset Sum to be solved: \(V = (\{v_1,v_2,\ldots ,v_n\}, S).\) In the initial configuration, the leftmost neurons contain (starting from the top to bottom) \(v_1,v_2,\ldots ,v_n\) spikes, while the rightmost neurons do not contain spikes.
When the computation starts, each leftmost neuron non-deterministically applies one of its rules, thus including or not the corresponding value \(v_i\) in the (candidate) solution \(B \subseteq V\). The spikes emitted by all neurons applying a firing rule are collected in the rightmost neurons (let us denote by N the total amount of spikes collected).
We have now three possible cases:
-
\(N < S\): in this case, no rule in the rightmost neurons can be applied, and thus no spike is emitted to the environment;
-
\(N = S\): only the first rightmost neuron fires, emitting a spike to the environment;
-
\(N > S\): both neurons fire; a spike is emitted immediately to the environment from the first neuron, while a second one is emitted with a time step delay by the second neuron.
The given instance of Subset Sum has a positive answer if and only if a single spike is emitted during the computation.
As pointed out in Leporati et al. (2007), a problem related to the SN P system described above is that the rules of the neurons are checking for the existence of a number of spikes which may be of an exponential size with respect to the usually agreed instance size of Subset Sum. Moreover, the system may require, to be initialized, a number of spikes which could also be exponential.
Nonetheless, in the same paper it was shown that the numbers occurring in the instance of Subset Sum in input, namely \(v_1, v_2,\ldots , v_n\), can be also inserted in the system in binary form, and a Spiking Neural P sub-system is able to convert such binary encoding in a unary encoding in polynomial time. In this way, it was proved that the possibility to efficiently solve Subset Sum by means of an SN P system like the one described before does not require an exponential effort to initialize the system, but depends only on the non-deterministic application of the rules.
A question that arises immediately concerns the possibility to obtain similar results by deterministic systems, possibly by considering added features to increase their efficiency. In many variants of standard P systems, an interesting feature that is commonly considered to improve efficiency of deterministic systems is the possibility to give an active role to membranes. In particular, P systems with active membranes are able to create new membranes during the computation by division, budding, or separation of existing membranes, allowing in this way to obtain a trade off between time and space resources that allows to attack NP–complete (or even harder) problems in polynomial time and exponential space (see, e.g., Păun (2001), Krishna and Rama (1999), Sosík (2019), Zandron et al. (2000)).
Concerning SN P systems, it is known that their ability to evaluate in a constant time the applicability of the rules, according to the associated regular expressions, can be exploited to deterministically solve computationally hard problems in polynomial time. In fact, in Leporati et al. (2009) it was proved that, by using regular expressions in a succinct form over a singleton alphabet, the membership problem is equivalent to NP-complete problems like Subset Sum. In the same paper, it was also proved that when we consider regular expressions of a certain restricted form, then it is possible to simulate SN P systems by a deterministic Turing machine with a polynomial slowdown.
As a consequence, in order to get enough computational power to solve, in polynomial time, computationally hard problems, we could either use complex regular expressions, or we need to consider ideas similar to those exploited for standard P systems, that allow to produce an exponential space in a polynomial number of steps.
A first solution of this type for SN P systems was considered in Pan et al. (2011), where neuron division and budding was allowed (operations inspired from recent discoveries concerning the neural stem cells). By means of these types of rules, a parent neuron can be replaced by two offsprings. In case of neuron division, both the new neurons have the same synapses connections (both coming-in and going-out) as the parent neuron. When a neuron budding rule is applied, instead, one of the two neurons inherits the coming-in synapses connection of the parent neuron, while the other inherits its going-out synapses. Moreover, a synapse from the first to the second new neuron is created.
It was proved that uniform families of SN P systems of this type are able to solve the NP-complete problem SAT in polynomial time (Leporati et al. 2009). An improved solution, obtained by also considering the possibility to dissolve neurons when they are no more necessary to the computation, was proposed in Zhao et al. (2016). In Wang et al. (2010) authors proved that budding of neurons is not strictly necessary: a uniform family of SN P systems with neuron division only can solve the SAT problem in a polynomial number of steps. The system proposed has another very interesting feature: the initial size of the system is limited to a constant number of neurons, differently from the original solution, where a number of neurons that is linear with respect to the dimension of the input SAT formula is required.
Another possibility that has been considered to approach complex problems within the framework of SN P systems was to use pre-computed resources, as proposed in Chen et al. (2006). Instances of a decision problem were encoded in a number of spikes, and then placed, at the beginning of the computation, in an (arbitrarily large) pre-computed system, that has an exponentially large workspace available, in the form of an exponentially large number of inactive neurons, which will be activated and used in constant time in our computation. A constant-time solution for the problem SAT was described in Chen et al. (2006). The assumption of pre-computed resources was used in Ishdorj and Leporati (2008) to build uniform families of spiking neural P systems that solve in deterministic polynomial time instances of the problems SAT and 3-SAT. Similarly, in Ishdorj et al. (2010) solutions for the PSPACE-complete problems QSAT and Q3SAT in polynomial time were proposed, showing in this way that problems in the class PSPACE can be efficiently solved by SN P systems.
11 Concluding remarks
In the above sections, we have presented the basic ideas and the main theoretical results concerning Spiking Neural P systems, and only a few of the many variants that have been proposed since the first definition of standard SN P systems in Ionescu et al. (2006). Other variants, trying to incorporate in the computational model different aspects suggested by the biological background, include: SN P systems with anti-spikes, that have an inhibitory function, introduced in Pan and Păun (2009), and in a slightly different form in Song et al. (2012); SN P systems with polarizations (Wu et al. 2018); axon P systems (Zhang et al. 2015), proved to be universal as both function computing devices and number generator devices; SN P systems with communication on request (Pan et al. 2017); and many other variants, variants of the variants and combinations of different features.
The main theoretical issues to be investigated are the same for all these variants. The first question concerns the optimal combination of features and of values of different parameters, needed to obtain computationally complete systems, able to generate/accept recursively enumerable sets of numbers, or to compute recursive functions. This implies the definition of normal forms, the study of the trade-off between different parameters, while maintaining the same computational power, the search for minimal universal systems, the study of relations with other standard and non-standard computing models. In the same vein, various limits and restrictions to the definition of the basic model have been considered, aiming at the definition of variants that are not Turing universal. This would allow to define specific computational classes, possibly having some peculiar decidable properties. The computational power of SN P systems as language generators or acceptors has also been deeply investigated.
Another relevant research direction concerns the efficiency of SN P systems in solving computationally hard problems, such as NP-complete or PSPACE-complete problems. In this respect, there are some intriguing points, concerning unary representations vs binary representations, use of pre-computed resources, uniform solutions vs non-uniform or semi-uniform solutions, which are worthy of further study. An interesting research topic is also to study what restrictions can be considered to obtain systems characterizing specific complexity classes between NP and PSPACE.
In this paper we focussed on theoretical aspects and results, but, of course, the use of these computation models in solving problems related to real-life applications is a topic of great interest: function approximation, pattern recognition, fault diagnosis of power systems, computational biology, biochip design, vehicle routing, cryptography, clustering, or decision making are all possible applications of the model. A recent survey can be found in Fan et al. (2020).
References
Binder A, Freund R, Oswald M (2007) Extended Spiking Neural P systems with Excitatory and Inhibitory Astrocytes. In: Proc 5th Brainstorming Week on Membrane Computing, 63-72
Cabarle FGC, Adorna HN, Pérez-Jiménez MJ, Song T (2015) Spiking neural P systems with structural plasticity. Neural Comput Appl 26(8):1905–1917
Cabarle FGC, Adorna HN, Pérez-Jiménez MJ (2015) Asynchronous spiking neural P systems with structural plasticity. UCNC 2015 ( Calude CS, Dinneen MJ, eds.), LNCS 9252, Springer, 132-143
Cavaliere M, Egecioglu O, Ibarra OH, Ionescu M, Păun G, Woodworth S (2008) Asynchronous spiking neural P systems; decidability and undecidability. In: Garzon MH, Yan H (eds) DNA13, \(13^{\rm th}\) International Meeting on DNA Computing. Revised Selected Papers, LNCS 4848, Springer, pp 246–255
Cavaliere M, Egecioglu E, Ibarra OH, Ionescu M, Păun Gh, Woodworth S (2009) Asynchronous spiking neural P systems. Theor Comput Sci 410(24–25):2352–2364
Chen H, Ionescu M, Ishdorj T-O (2006) On the efficiency of spiking neural P systems. In: Gutierrez-Naranjo MA , Păun G, Riscos-Nuñez A, Romero-Campero FJ (Eds) Proc Fourth Brainstorming Week on Membrane Computing, Fenix Editora, Sevilla, vol I, 195-206
Chen H, Freund R, Ionescu M, Păun Gh, Pérez-Jiménez MJ (2006) On string languages generated by spiking neural P systems. In: Proc Fourth Brainstorming Week on Membrane Computing (Gutierrez-Naranjo MA, Păun Gh, Riscos-Nuñez, Romero-Campero FJ, eds), Fenix Editora, vol I, 169-193
Chen H, Ionescu M, Ishdorj T-O, Păun A, Păun Gh, Pérez-Jiménez MJ (2008) Spiking neural P systems with extended rules: universality and languages. Natural Comput 7:147–166
Fan S, Paul P, Wu T, Rong H, Zhang G (2020) On Applications of Spiking Neural P Systems. Appl Sci 10: Art. 7011
García-Arnau M, Pérez D, Rodríguez-Patón A, Sosík P (2007) Spiking neural P systems: Stronger normal forms. In: Proc Fifth Brainstorming Week on Membrane Computing, Fenix Editora, Sevilla, 157-178
Greibach SA (1978) Remarks on blind and partially blind one-way multicounter machines. Theor Comput Sci 7:311–324
Gurney K (1997) An introduction to neural networks. CRC Press
Gutiérrez-Naranjo MA, Pérez-Jiménez MJ (2009) Hebbian learning from spiking neural P systems view. In: Proc 9th Int Workshop on Membrane Computing, WMC9, (Corne D et al. eds), LNCS 5391, Springer, 217-230
Ibarra OH, Woodworth S, Yu F, Păun A (2006) On spiking neural P systems and partially blind counter machines. Proc. 5th International Conference on Unconventional Computation, LNCS, vol 4135, Springer, Berlin, 113-129
Ibarra OH, Păun A, Păun Gh, Rodríguez-Patón A, Sosik P, Woodworth S (2007) Normal forms for spiking neural P systems. Theor Comput Sci 372:196–217
Ibarra OH, Leporati A, Păun A, Woodworth S (2009) Spiking Neural P Systems. In: "The Oxford Handbook of Membrane Computing", Oxford University Press, 337-362
Ionescu M, Păun G, Yokomori T (2006) Spiking neural P systems. Fundam Inf 71(2–3):279–308
Ionescu M, Păun A, Păun G, Pérez-Jiménez MJ (2006) Computing with spiking neural P systems: traces and small universal systems. In: Mao C, Yokomori T, Zhang B-T (eds) DNA12, \(12^{\rm th}\) International Meeting on DNA Computing. Revised Selected Papers, LNCS, vol 4287, Springer, Berlin, 1–16
Ionescu M, Păun Gh, Yokomori T (2007) Spiking neural P systems with an exhaustive use of rules. Intern J Unconv Comput 3:135–153
Ishdorj T-O, Leporati A (2008) Uniform solutions to SAT and 3-SAT by spiking neural P systems with pre-computed resources. Nat Comput 7(4):519–534
Ishdorj T-O, Leporati A, Pan L, Zeng X, Zhang X (2010) Deterministic solutions to QSAT and Q3SAT by spiking neural P systems with pre-computed resources. Theor Comput Sci 411(25):2345–2358
Jiang Y, Su Y, Luo F (2019) An improved universal spiking neural P system with generalized use of rules. J Membr Comput 1:270–278
Kong Y, Jiang K, Chen Z, Xu J (2014) Small universal spiking neural P systems with astrocytes. Rom J Inf Sci Technol 17(1):19–32
Korec I (1996) Small universal register machines. Theor Comput Sci 168:267–301
Krishna SN, Rama R (1999) A variant of P-systems with active membranes: solving NP-complete problems. Rom J Inf Sci Tech, 2(4)
Leporati A, Zandron C, Ferretti C, Mauri G (2007) Solving Numerical NP-complete Problems with Spiking Neural P Systems. In: Eighth International Workshop on Membrane Computing, WMC8, Selected Invited Papers, LNCS 4860, Springer-Verlag, Berlin, 336-352. https://doi.org/10.1007/978-3-540-77312-2-21
Leporati A, Zandron C, Ferretti C, Mauri G (2009) On the computational power of spiking neural P systems. Int J Unconv Comput 5(5):459–473
Leporati A, Mauri G, Zandron C, Păun Gh, Pérez-Jiménez MJ (2009) Uniform solutions to SAT and subset sum by spiking neural P systems. Nat Comput 8(4):681–702
Maass W (1997) Networks of spiking neurons: the third generation of neural network models. Neural Netw 10(9):1659–1671
Maass W, Bishop C (eds) (1999) Pulsed Neural Networks. MIT Press, Cambridge
Maass W (2002) Computing with spikes. Special Issue on Foundations of Information Processing of TELEMATIK 8(1):32–36
Macababayao ICH, Cabarle FGC, de la Cruz RTA, Zeng X (2022) Normal forms for spiking neural P systems and some of its variants. Inf Sci 595:344–363
Martin-Vide C, Păun G, Pazos J, Rodríguez-Patón A (2003) Tissue P systems. Theor Comput Sci 296(2):295–326
Minsky ML (1967) Finite and Infinite Machines. Prentice Hall, Englewood Cliffs, New Jersey
Pan L, Păun Gh (2009) Spiking neural P systems with anti-spikes. Int J Comput Commun Control 4(3):273–282
Pan L, Păun G (2010) Spiking neural P systems: an improved normal form. Theor Comput Sci 411:906–918
Pan L, Zeng X (2011) Small universal spiking neural P systems working in exhaustive mode. IEEE Trans NanoBiosci 10(2):99–105. https://doi.org/10.1109/TNB.2011.2160281
Pan L, Păun G, Pérez-Jiménez MJ (2011) Spiking neural P systems with neuron division and budding. Sci China Inf Sci 54(8):1596–1607. https://doi.org/10.1007/s11432-011-4303-y
Pan L, Zeng X, Zhang X, Jiang Y (2012) Spiking neural P systems with weighted synapses. Neural Process Lett 35(1):13–27
Pan L, Wang J, Hoogeboom HJ (2012) Spiking neural P systems with astrocytes. Neural Comput 24(3):805–25
Pan L, Wang J, Hoogeboom HJ (2012) Asynchronous extended spiking neural P systems with astrocytes. In: Gheorghe V et al. (eds) Proc 12th International Conference on Membrane Computing, LNCS 7184, Springer, 243-256
Pan L, Păun Gh, Song B (2016) Flat maximal parallelism in P systems with promoters. Theor Comput Sci 623:83–91
Pan L, Păun G, Zhang G, Neri F (2017) Spiking neural P systems with communication on request. Int J Neural Syst 27(8):1–13
Păun G (2000) Computing with membranes. J Comput Syst Sci 61(1):108-143, and TUCS Research Report 208, 1998 (http://www.tucs.fi)
Păun G (2001) P systems with active membranes: attacking NP-complete problems. J Autom Lang Comb 6(1):75–90
Păun Gh (2002) Membrane Computing - An Introduction. Springer, Berlin
Păun G, Pérez-Jiménez MJ, Rozenberg G (2006) Spike trains in spiking neural P systems. Intern J Found. Comput Sci 17(4):975–1002
Păun A, Păun Gh (2007) Small universal spiking neural P systems. BioSystems 90(1):48–60
Păun Gh (2007) Spiking neural P systems with astrocyte-like control. J Univ Comput Sci 13(11):1707–1721
Păun G, Rozenberg G, Salomaa A (2009) eds. The Oxford Handbook of Membrane Computing, Oxford University Press
Ren Q, Liu X, Sun M (2020) Turing Universality of Weighted Spiking Neural P Systems with Anti-spikes. Computational Intelligence and Neuroscience, 2020, 8892240
Rozenberg G, Salomaa A (eds) (1997) Handbook of Formal Languages. Springer-Verlag, Berlin
Song T, Pan L, Wang J, Venkat I, Subramanian KG, Abdullah R (2012) Normal forms of spiking neural P systems with anti-spikes. IEEE Trans Nanobiosci 11(4):352–359
Song T, Pan L, Păun Gh (2013) Asynchronous spiking neural P systems with local synchronization. Inf Sci 219:197–207
Song T, Pan L, Păun G (2014) Spiking neural P systems with rules on synapses. Theor Comput Sci 529:888–895
Song T, Zou Q, Liu X, Zeng X (2015) Asynchronous spiking neural P systems with rules on synapses. Neurocomputing 151:1439–1445
Song T, Pan L, Wu T, Zheng P, Wong MLD, Rodríguez-Patón A (2019) Spiking neural P systems with learning functions. IEEE Trans Nanobiosci 18(2):176–190
Song X, Valencia-Cabrera L, Peng H, Wang J, Pérez-Jiménez MJ (2021) Spiking neural P systems with delay on synapses. Int J Neural Syst 31(1):2050042
Sosík P (2019) P systems attacking hard problems beyond NP: a survey. J Membr Comput 1:198–208
The P Systems Web Page: http://ppage.psystems.eu
Wang J, Hoogeboom HJ, Pan L, Păun Gh, Pérez-Jiménez MJ (2010) Spiking neural P systems with weights. Neural Comput 22(10):2615–2646
Wang J, Hoogeboom HJ, Pan L (2010) Spiking Neural P Systems with Neuron Division. In: Gheorghe M, Hinze T, Păun Gh, Rozenberg G, Salomaa A eds (Eds) 11th Int. Conf. on Membrane Computing, CMC11, LNCS 6501, Springer, Berlin, Heidelberg, 361-376. https://doi.org/10.1007/978-3-642-18123-8-28
Wu T, Păun A, Zhang Z, Pan L (2018) Spiking neural P systems with polarizations. IEEE Trans Neural Netw Learn Syst 29(8):3349–3360
Wu T, Jiang S (2021) Spiking neural P systems with a flat maximally parallel use of rules. J Membr Comput 3:221–231
Zandron C, Ferretti C, Mauri G (2000) Solving NP-complete problems using P systems with active membranes. In: Antoniou I, Calude CS, Dinneen MJ (eds) Unconventional Models of Computation. Springer-Verlag, London, pp 289–301
Zeng X, Xu L, Liu X, Pan L (2014) On languages generated by spiking neural P systems with weights. Inf Sci 278:423–433
Zeng X, Zhang X, Song T, Pan L (2014) Spiking neural P systems with thresholds. Neural Comput 26(7):1340–1361
Zhang X, Zeng X, Pan L (2008) Smaller universal spiking neural P systems. Fundam Inf 87:117–136
Zhang X, Zeng X, Pan L (2009) On languages generated by asynchronous spiking neural P systems. Theor Comput Sci 410:2478–2488
Zhang X, Jiang Y, Pan L (2010) Small universal spiking neural P systems with exhaustive use of rule. J Comput Theor Nanos 7(5):890–899
Zhang X, Wang B, Pan L (2014) Spiking Neural P Systems with a Generalized Use of Rules. Neural Comput 26:2925–2943
Zhang X, Pan L, Păun A (2015) On the universality of axon P systems. IEEE Trans Neural Netw Learn Syst 26(11):2816–2829
Zhao Y, Liu X, Wang W (2016) Spiking neural P systems with neuron division and dissolution. PLoS ONE 11(9):e0162882. https://doi.org/10.1371/journal.pone.0162882
Funding
Open access funding provided by Università degli Studi di Milano - Bicocca within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Leporati, A., Mauri, G. & Zandron, C. Spiking neural P systems: main ideas and results. Nat Comput 21, 629–649 (2022). https://doi.org/10.1007/s11047-022-09917-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11047-022-09917-y