1 Introduction

Spatially interconnected systems arise in a number of areas (D’Andrea and Dullerud 2003) (as one possible starting point for the literature) including electrical ladder networks/circuits, mechanical systems, composed, e.g, of masses and springs and heat transfer problems. For these systems, time and spatial dynamics can arise. Hence they can be treated as two dimensional, or 2-D, systems, which is the setting used in this paper.

In many cases, these systems are composed of a finite number of blocks or cells. Hence, for analysis, there is the option to embed the spatial dynamics into the system variables using a form of lifting based on the discrete (finite) spatial variable and obtain a system where time is the independent variable, referred to as a 1D system in some of the 2-D systems literature, see, e.g. Sulikowski et al. (2015). One drawback of this approach, for systems composed of a large number of cells, is the need to compute with matrices that have very large dimensions and hence possible computational issues. The 2-D systems setting does not involve increasing the dimensions of the matrices used to represent the dynamics.

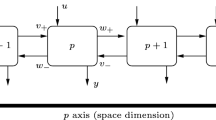
As one class, this paper considers electrical ladder networks or circuits, which are formed as a chain of blocks/cells that are identical in their structure. The passive parts of these cells are realized by longitudinal and transversal resistances, reactances, or, in general, impedances and the active parts by the addition of autonomous or controlled current and voltage sources. Application areas for ladder circuits include filter analysis and design, the modeling of delay lines and equivalent circuits for transmission lines, chains of transmission gates or long wire interconnections, e.g. Alioto et al. (2004), the approximation of distributed parameter systems, e.g. Schanbacher (1989) and in the simulation of physical systems. A representative example is shown in Fig. 1, where the upper diagram shows the overall system structure and the bottom the structure of an individual cell.

Fig. 1
figure 1

Ladder circuit as a spatially interconnected system

Full size image

The dynamics of 2-D systems are characterized by information propagation in two independent directions and the independent variables can both be discrete, both continuous or mixed, i.e. one continuous and one discrete. Spatially interconnected systems, including ladder circuits, can be considered as a class of 2-D systems where the independent variables are the time, which can be continuous or discrete and the node/cell number, which has to be discrete. However, left–right and right–left dependence between neighboring cells are often needed. Such systems are not causal along the spatial axis, i.e. along the node/cell direction. Hence, they cannot be modeled by the standard and extensively investigated 2-D (Roesser 1975a) and (Fornasini and Marchesini 1976) state-space models. Also the well known stability analysis methods for these systems are not applicable.

Repetitive processes are another class of 2-D dynamics that arise in the modeling of physical systems. These processes operate over a finite time duration and the 2-D structure arises as repeated passes are made through the dynamics and the output on any pass explicitly contributes to the dynamics produced on the next one. Background on these processes and the control problems they pose can be found in Rogers et al. (2007).

The links between linear repetitive processes and the Roesser and Fornasini–Marchesini state-space models has been investigated in previous research. For example, in Galkowski et al. (1998) the conditions for local controllability of linear repetitive processes have been derived via their transformation into the singular 2-D Roesser or Fornasini–Marchesini form and in Galkowski et al. (1999), building on previous work cited in this reference, the equivalence of their stability properties was investigated. This previous research established stability tests can, in some but not all, cases be interchanged. This is true for one class of repetitive processes but other classes can exhibit dynamics that have no Roesser or Fornasini–Marchesini state-space model representation. More recent work in this general area includes (Boudellioua et al. 2016, 2017; Galkowski et al. 2017) where new results on system equivalence are reported.

It is to be expected that at least some of these results would apply to spatially interconnected systems whose dynamics are written as 2-D linear systems. This is the motivation for the current paper where system equivalence between the state-space models of ladder circuits and those for the singular 2-D Roesser or Fornasini–Marchesini systems. The problem of reducing by equivalence a general 2-D polynomial matrix to the singular Roesser form has been considered previously, e.g. Pugh et al. (2005) developed a method for reducing a general 2-D polynomial matrix to such a form. Their method uses a two-step algorithm which is then adapted to the case of a general polynomial system matrix. In this paper, a direct method is developed to reduce a 2-D polynomial system matrix arising from a class of ladder circuit systems to an equivalent singular 2-D Fornasini–Marchesini or Roesser state-space model. The transformation used is shown to be zero coprime system equivalence of the two system matrices. This type of equivalence has previously been considered in the literature, e.g. Levy (1981), Johnson (1993), Boudellioua (2012), Pugh et al. (1996) and Pugh et al. (1998).

2 State-space models and associated transfer functions

In this paper, the general problem considered is the equivalence between ladder circuits and commonly used Roesser and Fornasini–Marchesini models for 2-D linear systems. In the remainder of this section, the relevant state-space models are introduced.

2.1 Ladder circuits

Applying Kirchhoff’s laws, the dynamics of ladder circuits, see Fig. 2 for the configuration and layout, can be written in the form of a 2-D differential-discrete linear systems state-space model, see Sulikowski et al. (2015), where the independent variables are time and the node numbers \(p=0,1,\ldots , \alpha -1.\) The resulting model is

$$\begin{aligned} \frac{d}{dt}x(p,t)= & {} {\mathcal {A}}_{1}x(p-1,t) + {\mathcal {A}}_2x(p,t) + {\mathcal {A}}_3x(p+1,t)\nonumber \\&\quad + {\mathcal {B}}u(p,t), \end{aligned}$$
(1)

where x(p, t) and u(p, t),  respectively, denote the state and input vectors. In this paper, the particular case of an active ladder circuit of the from of Fig. 1 is considered, which for onward analysis is considered in the form of Fig. 2, where the controlled sources \(i(p,t)=\gamma U_c(p-1,t)\) and \(E(p,t)=u(p,t)\) have been added to the nodes as possible control input variables but could also be an intrinsic part of a particular circuit.

Fig. 2
figure 2

A ladder chain

Full size image

In this paper, the state vector for node p in Fig. 2 is defined as

$$\begin{aligned} x(p,t)= \begin{bmatrix} U_C(p,t)\\ i_L(p,t) \\ \end{bmatrix} \end{aligned}$$
(2)

and then the matrices in (1) are

$$\begin{aligned}&{\mathcal {A}}_{1}= \begin{bmatrix} \frac{\gamma }{C}&0 \\ \frac{1}{L}&0 \\ \end{bmatrix} ,\;\;\; {\mathcal {A}}_2= \begin{bmatrix} -\frac{1}{R_2 C}&\frac{1}{C} \\ -\frac{1}{L}&-\frac{R_1}{L} \\ \end{bmatrix} ,\;\;\; {\mathcal {A}}_3 = \begin{bmatrix} 0&-\frac{1}{C} \\ 0&0 \\ \end{bmatrix},\nonumber \\&\quad {\mathcal {B}} = \begin{bmatrix} 0\\ -\frac{1}{L} \end{bmatrix}. \end{aligned}$$
(3)

The output equation is

$$\begin{aligned} y(p,t)&= {\mathcal {C}} x(p,t), \end{aligned}$$
(4)

where the matrix \({\mathcal {C}}\) depends on which signals are chosen as output variables. To complete the description, the following boundary conditions are assumed

$$\begin{aligned} \begin{aligned} x(-1,t)&= \begin{bmatrix} U(t) \\ 0 \\ \end{bmatrix} ,\; x(\alpha ,t) = \begin{bmatrix} 0 \\ i (t) \\ \end{bmatrix},\\ x(p,0)&= 0,\;0\le p\le \alpha -1. \end{aligned} \end{aligned}$$
(5)

Introduce the following differential and discrete, respectively, shift operators

$$\begin{aligned} z_1x(p,t)=\dfrac{dx(p,t)}{dt},\;\;z_2x(p,t)=x(p+1,t). \end{aligned}$$
(6)

Then the resulting transfer-function matrix under zero boundary conditions is

$$\begin{aligned} G_{LC}(z_1,z_2)={\mathcal {C}} \left( z_1I_n-z_2{\mathcal {A}}_3-{\mathcal {A}}_2-z_2^{-1}{\mathcal {A}}_{1} \right) ^{-1} {\mathcal {B}}, \end{aligned}$$
(7)

provided the inverse of the matrix \(z_1I_n-z_2{\mathcal {A}}_3-{\mathcal {A}}_2-z_2^{-1}{\mathcal {A}}_{1}\) exists.

2.2 2-D singular Fornasini–Marchesini model

A singular version of the 2-D Fornasini–Marchesini state-space model (Fornasini and Marchesini 1976) for discrete linear dynamics is

$$\begin{aligned} Ex(i+1,j+1)= & {} A_{1}x(i+1,j)+A_{2}x(i,j+1)\nonumber \\&+ A_{0}x(i,j)+Bu(i,j)\nonumber \\ y(i,j)= & {} Cx(i,j)+Du(i,j), \end{aligned}$$
(8)

where x(i, j) is the state vector, u(i, j) is the input vector, y(i, j) is the output vector, E, \(A_{0}\), \(A_{1}\), \(A_{2}\), B, C and D are constant real matrices of compatible dimensions and E is a singular matrix. In this paper, the model (1) is continuous in time t and therefore the differential version of singular 2-D Fornasini–Marchesini state-space model, is required, i.e.

$$\begin{aligned} {\mathbf {E}}\dfrac{d{\mathbf {x}}(p+1,t)}{dt}= & {} {\mathbf {A}}_{1}\dfrac{d\mathbf {{\mathbf {x}}}(p,t)}{dt}+{\mathbf {A}}_{2}{\mathbf {x}}(p+1,t) \nonumber \\&+ {\mathbf {A}}_{0}{\mathbf {x}}(p,t)+{\mathbf {B}}{\mathbf {u}}(p,t), \nonumber \\ {\mathbf {y}}(p,t)= & {} {\mathbf {C}}{\mathbf {x}}(p,t)+{\mathbf {D}}{\mathbf {u}}(p,t), \end{aligned}$$
(9)

where \({\mathbf {x}}(p,t)\) is the state vector, \({\mathbf {u}}(p,t)\) is the input vector, \({\mathbf {y}}(p,t)\) is the output vector, p denotes the node number and the matrices are as in (1). If E is nonsingular in either model then the standard (or nonsingular) model is obtained.

Note 1

In this paper differential dynamics are considered. If, however, the system is sampled then the analysis still applies with the shift operator \(z_{1}\) in (6) defined as a forward shift operator in t.

For systems described by (9), using the operators in (6) gives the transfer-function matrix for zero boundary conditions

$$\begin{aligned} G_{DSFM}(z_1,z_2)={\mathbf {C}}(z_1z_2{\mathbf {E}}-z_1{\mathbf {A}}_{1}-z_2{\mathbf {A}}_{2}-{\mathbf {A}}_{0})^{-1}{\mathbf {B}}+{\mathbf {D}}. \end{aligned}$$
(10)

2.3 2-D singular Roesser model

A discrete singular Roesser state-space model (1975a) is given by

$$\begin{aligned} \begin{aligned} E \left[ \!\!\begin{array}{c} x^{h}(i+1,j)\\ x^{v}(i,j+1) \end{array}\!\right] \! =&\left[ \!\!\begin{array}{cc} A_{11} &{} A_{12}\\ A_{21} &{} A_{22} \end{array}\!\!\right] \!\! \left[ \!\!\begin{array}{c} x^{h}(i,j)\\ x^{v}(i,j) \end{array}\!\!\right] \! +\!\left[ \!\!\begin{array}{c} B_1\\ B_2 \end{array}\!\!\right] u(i,j), \\ y(i,j)=&\left[ \begin{array}{cc} C_{1}&C_{2} \end{array}\right] \left[ \begin{array}{cc} x^{h}(i,j)\\ x^{v}(i,j) \end{array}\right] +Du(i,j), \end{aligned} \end{aligned}$$
(11)

where \(x^{h}(i, j)\in {\mathbb {R}}^{n_1}\) is the horizontal state vector, \(x^{v}(i,j)\in {\mathbb {R}}^{n_2},\) is the vertical state vector, \(y(i,j)\in {\mathbb {R}}^m\) is the output vector, \(u(i,j)\in {\mathbb {R}}^l\) is the input vector and the matrix E is square and singular. In this model, static in both directions i and j links between sub-vectors are allowed. If E is nonsingular then (as in the Fornasini-Marchesini model) the standard model is obtained. The boundary conditions are \(x^h(0,j) = f(j),\, j \ge 0\) and \(x^v(i,0) = d(i),\, i \ge 0,\) where the \(n_1 \times 1\) vector f(j) and the \(n_2 \times 1\) vector d(i) have known constant entries.

This paper requires the differential Roesser model given by

$$\begin{aligned} \begin{aligned} E \left[ \!\!\begin{array}{c} \dfrac{dx^h(p,t)}{dt}\\ x^{v}(p+1,t) \end{array}\!\right] \! =&\left[ \!\!\begin{array}{cc} A_{11} &{} A_{12}\\ A_{21} &{} A_{22} \end{array}\!\!\right] \!\! \left[ \!\!\begin{array}{c} x^{h}(p,t)\\ x^{v}(p,t) \end{array}\!\!\right] \! +\!\left[ \!\!\begin{array}{c} B_1\\ B_2 \end{array}\!\!\right] u(p,t), \\ y(p,t)=&\left[ \begin{array}{cc} C_{1}&C_{2} \end{array}\right] \left[ \begin{array}{cc} x^{h}(p,t)\\ x^{v}(p,t) \end{array}\right] +Du(p,t). \end{aligned} \end{aligned}$$
(12)

Using the shift operators \(z_1\) and \(z_2\) and assuming zero boundary conditions and that the matrix \(z_1E_1+z_2E_2-A\) is invertible, the transfer-function matrix corresponding to (12) is

$$\begin{aligned} G_{DSR}(z_1,z_2)= C(z_1E_1+z_2E_2-A)^{-1}B+D, \end{aligned}$$
(13)

where

$$\begin{aligned} E= & {} \begin{bmatrix} E_{11}&E_{12} \\ E_{21}&E_{22} \end{bmatrix}, E_1=\begin{bmatrix} E_{11}&0 \\ E_{21}&0 \end{bmatrix}, E_2=\begin{bmatrix} 0&E_{12} \\ 0&E_{22} \end{bmatrix}, A=\begin{bmatrix} A_{11}&A_{12} \\ A_{21}&A_{22} \\ \end{bmatrix}, \\ B^T= & {} [B_1^T\;\;B_2^T],\,\, C=[C_1 \;\;C_2]. \end{aligned}$$

3 Polynomial system matrix descriptions and system equivalence

One general description of a 2-D linear system, in common with (Rosenbrock 1970) for the 1-D linear systems case, is the polynomial form

$$\begin{aligned} T(z_1,z_2)x= & {} U(z_1,z_2)u,\nonumber \\ y= & {} V(z_1,z_2)x+W(z_1,z_2)u, \end{aligned}$$
(14)

where \(x\in {\mathbb {R}}^n\) is the state vector, \(u\in {\mathbb {R}}^l\) is the input vector and \(y\in {\mathbb {R}}^m\) is the output vector, T, U, V and W are polynomial matrices with elements in \({\mathbb {R}}[z_1,z_2]\) of dimensions \(n\times n, n\times l, m\times n\) and \(m\times l,\) respectively. The meaning of the operators \(z_1\) and \(z_2\) depend on the case considered as detailed in the previous section.

A system described by (14) can be rewritten as

$$\begin{aligned} P(z_1,z_2)\left[ \begin{array}{r} x\\ -u \end{array} \right] =\left[ \begin{array}{r} 0\\ -y \end{array} \right] , \end{aligned}$$
(15)

where

$$\begin{aligned} P(z_1,z_2)=\left[ \begin{array} [c]{rc} T(z_1,z_2) &{} U(z_1,z_2)\\ -V(z_1,z_2) &{} W(z_1,z_2) \end{array} \right] . \end{aligned}$$
(16)

Assuming that \(T(z_1,z_2)\) is invertible and the system matrix in (16) is regular, the associated transfer-function matrix is

$$\begin{aligned} G(z_1,z_2)=V(z_1,z_2)T^{-1}(z_1,z_2)U(z_1,z_2)+W(z_1,z_2). \end{aligned}$$
(17)

Using \(P(z_{1}, z_{2})\), the equivalence between systems can be studied, where numerous forms of this property are known in n-D systems. One of these for 2-D system matrices is zero coprimeness, see, e.g. Levy (1981), and Johnson (1993). This equivalence may be viewed as an extension of Fuhrmann’s strict system equivalence (Fuhrmann 1977) from 1-D to 2-D systems and is defined as follows.

Definition 1

Let \({\mathbb {P}}(m,l)\) denote the class of \((n+m)\times (n+l)\) with polynomial system matrices in \(z_1\) and \(z_2\) with real coefficients. Two polynomial system matrices \(P_1(z_1,z_2)\) and \(P_2(z_1,z_2)\)\(\in {\mathbb {P}}(m,l)\), are said to be zero coprime system equivalent if they satisfy

$$\begin{aligned}&\underbrace{\left[ \begin{array} [c]{cc} M(z_1,z_2) &{} 0\\ X(z_1,z_2) &{} I_{m} \end{array} \right] }_{S_1(z_1,z_2)} \underbrace{\left[ \begin{array} [c]{cc} T_1(z_1,z_2) &{} U_1(z_1,z_2)\\ -V_1(z_1,z_2) &{} W_1(z_1,z_2) \end{array} \right] }_{P_1(z_1,z_2)} \nonumber \\&\quad =\underbrace{\left[ \begin{array} [c]{cc} T_2(z_1,z_2) &{} U_2(z_1,z_2)\\ -V_2(z_1,z_2) &{} W_2(z_1,z_2) \end{array} \right] }_{P_2(z_1,z_2)} \underbrace{\left[ \begin{array} [c]{cc} N (z_1,z_2)&{} Y(z_1,z_2)\\ 0 &{} I_{l} \end{array} \right] }_{S_2(z_1,z_2)} , \end{aligned}$$
(18)

where \(P_1(z_1,z_2),S_2(z_1,z_2)\) are zero right coprime, \(P_2(z_1,z_2),S_1(z_1,z_2)\) are zero left coprime and \(M(z_1,z_2)\), \(N(z_1,z_2)\), \(X(z_1,z_2)\) and \(Y(z_1,z_2)\) are polynomial matrices of compatible dimensions.

The system matrix can be used to study critical systems properties such as controllability, observability and stability. In the case of 2-D linear systems, the zero structure of their associated system matrices, see, e.g. Zerz (2000), Johnson (1993), Levy (1981), Pugh et al. (1998), and Pugh et al. (1996), is of particular interest. One result is the following.

Lemma 1

(Johnson 1993) Zero coprime system equivalence preserves the transfer-function matrix and the zero structure of the matrices

$$\begin{aligned} T_i(z_1,z_2),\; P_i(z_1,z_2),\; \left[ \begin{array}[c]{cc} T_i(z_1,z_2)&U_i(z_1,z_2) \end{array}\right] , \; \left[ \begin{array}[c]{r} T_i(z_1,z_2) \\ -V_i(z_1,z_2) \end{array}\right] , i=1, 2. \end{aligned}$$

The system matrix associated with the ladder circuit of (1) and (4) is

$$\begin{aligned} P_{LC}(z_1,z_2)=\left[ \begin{array}{c|c} z_1I_n-z_2{\mathcal {A}}_3-{\mathcal {A}}_2-z_2^{-1}{\mathcal {A}} &{} {\mathcal {B}}\\ \hline -{\mathcal {C}} &{} 0_{m,l} \end{array} \right] . \end{aligned}$$
(19)

An alternative description of (1) and (4) is obtained by forward shifting the node number in the state equations, which corresponds to multiplication by the shift operator \(z_2\). This corresponds to multiplying the system matrix \(P_{LC}\) in (19) from the left by the following matrix that preserves the transfer-function matrix

$$\begin{aligned} \left[ \begin{array}{c|c}z_2I_n &{} 0 \\ \hline 0 &{} I_l \end{array} \right] , \end{aligned}$$

resulting in the polynomial system matrix

$$\begin{aligned} {\tilde{P}}_{LC}(z_1,z_2)= & {} \left[ \begin{array}{c|c} z_1z_2I_n-z_2^2{\mathcal {A}}_3-z_2{\mathcal {A}}_2-{\mathcal {A}} &{} z_2{\mathcal {B}}\\ \hline -{\mathcal {C}} &{} 0_{m,l} \end{array} \right] \nonumber \\= & {} \left[ \begin{array}{cc} -{\mathcal {A}} &{} 0\\ -{\mathcal {C}} &{} 0 \end{array} \right] +\left[ \begin{array}{cc} I &{} 0\\ 0 &{} 0 \end{array} \right] z_1z_2+\left[ \begin{array}{cc} -{\mathcal {A}}_2 &{} {\mathcal {B}}\\ 0 &{} 0 \end{array} \right] z_2+\left[ \begin{array}{cc} -{\mathcal {A}}_3 &{} 0\\ 0 &{} 0 \end{array} \right] z_2^2. \end{aligned}$$
(20)

A system described by (9) can be written as

$$\begin{aligned}&P_{a}(z_1,z_2) \left[ \begin{array}[c]{r} {\mathbf {x}}\\ -{\mathbf {u}} \end{array} \right] \nonumber \\&\quad =\left[ \begin{array} [c]{r} 0\\ -{\mathbf {y}} \end{array} \right] , \end{aligned}$$
(21)

with polynomial system matrix

$$\begin{aligned} P_{a}(z_1,z_2)=\left[ \begin{array} [c]{c|c} z_1z_2{\mathbf {E}}-z_1{\mathbf {A}}_{1}-z_2{\mathbf {A}}_{2}-{\mathbf {A}}_{0} &{} {\mathbf {B}}\\ \hline -{\mathbf {C}} &{} {\mathbf {D}} \end{array} \right] . \end{aligned}$$
(22)

Similarly a system described by (12) can be written as

$$\begin{aligned} P_{b}(z_1,z_2)\left[ \begin{array}{r} x_h \\ x_v \\ -u \\ \end{array}\right] =\left[ \begin{array}{r} 0 \\ 0 \\ -y \\ \end{array}\right] , \end{aligned}$$
(23)

with polynomial system matrix

$$\begin{aligned} P_{b}(z_1,z_2)=\left[ \begin{array}{c|c} z_1E_1+z_2E_2-A &{} B\\ \hline -C &{} D \end{array} \right] . \end{aligned}$$
(24)

Next, conditions under which the polynomial system matrix of the ladder circuit is equivalent to (9) are established.

4 Transformation of the ladder circuit model to a differential Fornasini–Marchesini model

The polynomial system matrix of (20) can be written as

$$\begin{aligned} {\tilde{P}}_{LC}(z_1,z_2)={\tilde{P}}_{0,0}+{\tilde{P}}_{1,1}z_1z_2+{\tilde{P}}_{0,1}z_2+{\tilde{P}}_{0,2}z_2^2. \end{aligned}$$
(25)

Also introduce the matrices

$$\begin{aligned} {\tilde{E}}= & {} \left[ \begin{array}{cc} 0_{n+l,n+l} &{} 0_{n+l,n+l} \\ 0_{n+m,n+l} &{} {\tilde{P}}_{1,1} \end{array} \right] ,\nonumber \\ {\tilde{A}}_0= & {} \left[ \begin{array}{cc} -I_{n+l} &{} 0_{n+l,n+l} \\ 0_{n+m,n+l} &{} -{\tilde{P}}_{0,0} \end{array} \right] ,\nonumber \\ {\tilde{A}}_1= & {} 0,\quad {\tilde{A}}_2=\left[ \begin{array}{cc} 0_{n+l,n+l} &{} I_{n+l} \\ -{\tilde{P}}_{0,2} &{} -{\tilde{P}}_{0,1} \end{array} \right] ,\nonumber \\ Y_{m}= & {} \left[ \begin{array}{c} 0_{2n+l,m} \\ I_{m} \end{array} \right] , Z_l=\left[ \begin{array}{cc} 0_{l,2n+l}&I_l \end{array} \right] \end{aligned}$$
(26)

and hence the polynomial system matrix

$$\begin{aligned} P_{DSFM}(z_1,z_2)\equiv \left[ \begin{array}{cc} T_{SFM} &{} U_{SFM}\\ -V_{SFM} &{} 0_{m,l} \end{array} \right] =\left[ \begin{array}{cc|c} z_1z_2{\tilde{E}}-z_2{\tilde{A}}_2-{\tilde{A}}_0 &{} Y_m &{} 0\\ -Z_l &{} 0_{l,m} &{} I_l\\ \hline 0_{m,n+l} &{} -I_m &{} 0_{m,l} \end{array} \right] . \end{aligned}$$
(27)

This matrix corresponds to that of (22) with

$$\begin{aligned} {\mathbf {E}}=\left[ \begin{array}{cc} {\tilde{E}} &{} 0\\ 0 &{} 0 \end{array} \right] ,\; {\mathbf {A}}_0=\left[ \begin{array}{cc} {\tilde{A}}_0 &{} -Y_m\\ Z_l &{} 0 \end{array} \right] ,\;{\mathbf {A}}_2=\left[ \begin{array}{cc} {\tilde{A}}_2 &{} 0\\ 0 &{} 0 \end{array} \right] , \;\;{\mathbf {A}}_1=0. \end{aligned}$$
(28)

Theorem 1

The polynomial system matrices (27) and (20) are zero coprime equivalent i.e.

$$\begin{aligned} S_1{\tilde{P}}_{LC}=P_{DSFM}S_2, \end{aligned}$$
(29)

where

$$\begin{aligned} S_1=\left[ \begin{array}{c|c} 0_{n+l,n} &{} 0_{n+l,m}\\ I_{n} &{} 0_{n,m}\\ 0_{m+l,n} &{} 0_{m+l,m}\\ \hline 0_{m,n} &{} I_{m} \end{array} \right] ,\;\;\; S_2=\left[ \begin{array}{c|c} z_2I_{n} &{} 0_{n,l}\\ 0_{l,n} &{} z_2I_{l}\\ I_{n} &{} 0_{n,l}\\ 0_{l,n} &{} I_l\\ {\mathcal {C}} &{} 0_{m,l}\\ \hline 0_{l,n} &{} I_l \end{array} \right] . \end{aligned}$$
(30)

Proof

The matrix of (27) can be written as

$$\begin{aligned} \left[ \begin{array}{ccc|c} I_{n+l} &{} -z_2I_{n+l} &{} 0 &{} 0\\ z_2{\tilde{P}}_{0,2} &{} z_1z_2{\tilde{P}}_{1,1}+z_1{\tilde{P}}_{0,1}+z_2{\tilde{P}}_{0,1}+{\tilde{P}}_{0,0} &{} {\mathcal {F}}^T_m &{} 0\\ 0 &{} -{\mathcal {F}}_l &{} 0 &{} I_l\\ \hline 0 &{} 0 &{} -I_m &{} 0\\ \end{array} \right] , \end{aligned}$$
(31)

where \({\mathcal {F}}_k=\left[ \begin{array}{cc}0_{k,n}&I_k\end{array}\right] \) and hence (29) holds, i.e.

$$\begin{aligned} \begin{array}{c} S_1{\tilde{P}}_{LC}=P_{DSFM}S_2= \left[ \begin{array}{cc} 0_{n+l,n} &{} 0_{n+l,l}\\ z_1z_2I_n-z_2^2{\mathcal {A}}_3-z_2{\mathcal {A}}_2-{\mathcal {A}} &{} z_2{\mathcal {B}}\\ 0_{m+l,n} &{} 0_{m+l,l}\\ -{\mathcal {C}} &{} 0_{m,l} \end{array} \right] . \end{array} \end{aligned}$$
(32)

Finally, zero right coprimeness of the two matrices follows since the matrix

$$\begin{aligned} \left[ \begin{array}{c} {\tilde{P}}_{LC}\\ S_2 \end{array} \right] =\left[ \begin{array}{cc} z_1z_2I_n-z_2^2{\mathcal {A}}_3-z_2{\mathcal {A}}_2-{\mathcal {A}} &{} {\tilde{z}}_2{\mathcal {B}}\\ -{\mathcal {C}} &{} 0_{m,l}\\ \hline z_2I_{n} &{} 0_{l,l}\\ 0 &{} z_2I_n\\ I_{n} &{} 0_{n,l}\\ 0_{l,n} &{} I_l\\ {\mathcal {C}} &{} 0_{m,l}\\ 0_{l,n} &{} I_l \end{array} \right] , \end{aligned}$$
(33)

contains a minor of order \(n+l\) (the identity submatrix). Similarly, zero left coprimeness of the two matrices follows immediately since

$$\begin{aligned} \left[ \begin{array}{cc} P_{DSFM}&S_1 \end{array} \right] =\begin{bmatrix} X_{11}&X_{12} \\ X_{21}&X_{22} \\ \end{bmatrix}, \end{aligned}$$
(34)

where

$$\begin{aligned} X_{11} = \left[ \begin{array}{cccc} I_{n+l} &{} -z_2I_{n+l} &{} 0 &{} 0 \\ z_2{\tilde{P}}_{0,2} &{} z_1z_2{\tilde{P}}_{1,1}+z_1{\tilde{P}}_{0,1}+z_2{\tilde{P}}_{0,1}+{\tilde{P}}_{0,0} &{} {\mathcal {F}}_m^T &{} 0\\ 0 &{} -{\mathcal {F}}_l &{} 0 &{} I_l \\ \end{array}\right] \end{aligned}$$

and

$$\begin{aligned} X_{12}= & {} \left[ \begin{array}{cc} 0 &{} 0\\ I_n &{} 0\\ 0 &{} 0\\ \end{array}\right] , \\ X_{21}= & {} \left[ \begin{array}{cccc} 0 &{} 0 &{} -I_m &{} 0 \\ \end{array}\right] ,\;\; X_{22}=\left[ \begin{array}{cc} 0 &{} I_m\\ \end{array}\right] , \end{aligned}$$

has a highest order minor equal to 1 obtained by deleting the columns \(n+l+1,\ldots ,2(n+l)\) from the matrix in (34). \(\square \)

5 Equivalence of the ladder circuit and the differential singular Roesser model

The polynomial system matrix (20) can be written as

$$\begin{aligned} {\tilde{P}}_{LC}(z_1,z_2)={\tilde{P}}_{0,0}+{\tilde{P}}_{1,1}z_1z_2+{\tilde{P}}_{0,1}z_2+{\tilde{P}}_{0,2}z_2^2. \end{aligned}$$
(35)

Introduce the matrices

$$\begin{aligned}&{\tilde{E}}=\left[ \begin{array}{ccc} 0_{n+l,n+l} &{} 0_{n+l,n+l} &{} 0\\ 0_{n+m,n+l} &{} {\tilde{P}}_{1,1} &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right] ,\; {\tilde{A}}_0=\left[ \begin{array}{ccc} -I_{n+l} &{} 0_{n+l,n+l} &{} 0\\ 0_{n+m,n+l} &{} -{\tilde{P}}_{0,0} &{} -{\mathcal {F}}_{m,n+m}^T\\ 0 &{} {\mathcal {F}}_{l,n+l} &{} 0 \end{array} \right] ,\nonumber \\&\quad {\tilde{A}}_2=\left[ \begin{array}{ccc} 0_{n+l,n+l} &{} 0_{n+l,n+l} &{} 0\\ -{\tilde{P}}_{0,2} &{} -{\tilde{P}}_{0,1} &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right] . \end{aligned}$$
(36)

Then the polynomial system matrix in singular differential Roesser form is given by

$$\begin{aligned}&P_{SR}(z_1,z_2)\equiv \left[ \begin{array}{cc} T_{SR} &{} U_{SR}\\ -V_{SR} &{} 0_{m,l} \end{array} \right] \nonumber \\&\quad =\left[ \begin{array}{cccc|c} I_{2(n+l)+m} &{} -z_1I_{2(n+l)+m} &{} 0_{2(n+l)+l,l} &{} 0_{2(n+l)+l,m} &{} 0_{2(n+l)+l,l}\\ z_2{\tilde{E}} &{} -z_2{\tilde{A}}_2-{\tilde{A}}_0 &{} {\mathcal {F}}^T_{2(n+l)+m,l} &{} 0_{2(n+l)+m,m} &{} 0_{2(n+l)+m,l}\\ 0_{m,2(n+l)+m} &{} -{\mathcal {F}}_{m,2(n+l)+m} &{} 0_{m,l} &{} I_m &{} 0_{m,l}\\ 0_{l,2(n+l)+m} &{} 0_{l,2(n+l)+m} &{} -I_l &{} 0_{l,m} &{} I_l\\ \hline 0_{m,2(n+l)+m} &{} 0_{m,2(n+l)+m} &{} 0_{m,l} &{} -I_m &{} 0_{m,l} \end{array} \right] , \end{aligned}$$
(37)

where \({\mathcal {F}}_{r,k}=[0_{r,k-r}\;I_r]\).

Theorem 2

The system matrices (37) and (20) are zero coprime system equivalent, i.e.

$$\begin{aligned} S_1 {\tilde{P}}_{LC}=P_{SR}S_2, \end{aligned}$$
(38)

where

$$\begin{aligned} S_1=\left[ \begin{array}{c|c} 0_{} &{} 0_{}\\ I_{t} &{} 0_{}\\ 0_{} &{} 0_{}\\ 0_{} &{} 0_{}\\ \hline 0_{} &{} I_{m} \end{array} \right] ,\quad S_2=\left[ \begin{array}{c|c} z_1z_2I_{n} &{} 0_{}\\ 0 &{} z_1z_2I_{l}\\ z_1I_{n} &{} 0_{}\\ 0 &{} z_1I_{l}\\ z_1{\mathcal {F}}_{m,t} &{} 0\\ z_2I_{n} &{} 0_{}\\ 0 &{} z_2I_{l}\\ I_{n} &{} 0_{}\\ 0 &{} I_{l}\\ {\mathcal {F}}_{m,n} &{} 0_{m,l}\\ 0 &{} I_l\\ {\mathcal {F}}_{l,n} &{} 0\\ \hline 0_{} &{} I_l \end{array} \right] . \end{aligned}$$
(39)

Proof

It can be verified that

$$\begin{aligned} S_1{\tilde{P}}_{LC}=P_{SR}S_2=\left[ \begin{array}{cc} 0 &{} 0\\ {\tilde{T}}_{LC} &{} {\tilde{U}}_{LC}\\ 0 &{} 0\\ 0 &{} 0\\ {\tilde{V}}_{LC} &{} 0_{m,l} \end{array} \right] \end{aligned}$$
(40)

and it remains to establish the zero coprimeness of the matrices, where zero right coprimeness of \({\tilde{P}}_{LC}\) and \(S_2\) follows from the fact that the matrix \(\left[ \begin{array}{c} {\tilde{P}}_{LC}\\ S_2 \end{array} \right] \) contains a highest order minor of order \(n+l\) which is equal to 1. The zero left coprimeness of \(P_{SR}\) and \(S_1\) follows since the matrix

$$\begin{aligned} \left[ \begin{array}{cc} P_{SR}&S_1 \end{array} \right] = \left[ \begin{array}{ccccc|cc} I_{2(n+l)+m} &{} -z_1I_{2(n+l)+m} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ z_2{\tilde{E}} &{} -z_2{\tilde{A}}_2-{\tilde{A}}_0 &{} {\mathcal {F}}^T_{2(n+l)+m,l} &{} 0 &{} 0 &{} I_{2(n+l)+m} &{} 0\\ 0 &{} -{\mathcal {F}}_{m,2(n+l)+m} &{} 0 &{} I_m &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} -I_l &{} 0 &{} I_l &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -I_m &{} 0 &{} 0 &{} I_m \end{array} \right] , \end{aligned}$$
(41)

has a highest order minor of order \(2[2(n+l)+l+m]+m\) which is equal to \(\pm 1\), obtained by deleting the second and third block columns of the matrix in (41). \(\square \)

6 Conclusions

In this paper, an equivalent representation is obtained in the form of 2-D Fornasini–Marchesini and Roesser singular state-space models for a given system matrix arising from a hybrid linear ladder circuit system. The exact connections between the original system matrix with its corresponding 2-D singular forms have been developed and shown to be zero coprime system equivalence. Also the zero structure of the original polynomial system matrix is preserved, making it possible to analyze the polynomial system matrix in terms of its associated 2-D singular form. Moreover, the transformation matrices include identity sub-matrices and this suggests that these transformations can be generated by finite sequences of elementary row/column operations together with trivial inflation/deflation of the polynomial system matrices. This area is the subject of ongoing research. Also the implications of these results in terms of the structure and design of control laws is also under investigation.