1 Introduction

Friction is a reaction behavior that always occurs whenever two or more bodies get into contact with each other. It has a dissipative character and removes energy from the system [1, p. 2]. Friction is therefore an ubiquitous phenomenon in moving mechanical systems and can have a major impact on their dynamic behavior. For the dynamics of multibody systems, a large number of different friction models are presented and studied in the current literature.

Coulomb’s law states that the friction force is proportional to the normal force and opposes relative motion. Stribeck’s research demonstrated that the transition from static to dynamic friction is a gradual process. The generalized Stribeck curve, as shown in [2], categorizes friction into four regimes. Regime 1 is characterized by elastic deformation without sliding. Regime 2 is named “boundary lubrication” and refers to the area where the coefficient of static friction is still almost fully effective and there is hardly any lubrication. Regime 3, named “partial fluid lubrication”, is where the coefficient of friction in the contact area decreases rapidly with increased lubrication. Finally, Regime 4 represents “full fluid lubrication”. However, the phenomenon of friction is very complex, and a great deal of research was done on this topic in the twentieth century. Armstrong et al. [3] summarized the findings on a large number of friction phenomena, especially stiction state.

Numerous models have been developed to describe friction in dynamic systems. The main challenge is to numerically represent the nonlinear friction characteristic in the stiction region. Therefore, models typically differ in their advantages and disadvantages regarding performance and the reproducibility of friction properties.

In [4–6] it is pointed out that friction models are usually divided into “static” and “dynamic” friction models. Unfortunately, these terms are also used to refer to friction at zero sliding velocity as “static friction” or “stiction” and to Coulomb friction as “dynamic friction”. Typically, “static friction models” describe the steady-state behavior of the friction force as a function of sliding velocity, and “dynamic friction models” are characterized by the use of internal states [6].

The studies by [6–10] discuss, among others, discontinuous static models such as the general Coulomb and Stribeck approach and the Karnopp model [11] as well as regularized static friction models like Threlfall [12], Bengisu and Akay [13], and more advanced static models as the Ambrósio [14] or Awrejcewicz [15] model. In addition, numerous dynamic models are also discussed, such as the Dahl model [16], the bristle model [17], the reset integrator model [17], LuGre [18], and the generalized Maxwell slip model [19].

In general, static friction models incorporate a regularization that transforms a Coulomb-like discontinuous approximation into a continuous function of the sliding velocity. Unlike regularized static friction models, dynamic friction models can maintain long-term stick. However, they can produce dynamic break-away effects, overshoots, and even unrealistic drifts [20, 21].

The study by [22] shows that static models can also adequately reproduce experimental measurements. There, a hyperbolic tangent function is used to approximate the Coulomb friction model, which is very similar to the regularization approach of RecurDyn or Threlfall.

Today, commercial multibody simulation (MBS) packages such as Adams, RecurDyn, or Simpack offer a limited choice of specific friction models, in particular specific stick-slip approaches for joint friction [23–25]. The specific stick-slip models are rarely mentioned in the literature. All three MBS packages provide a regularized static friction model by default. In addition, Adams users can choose between the dynamic LuGre model and an Adams specific friction model to describe stick-slip [23]. RecurDyn users can select a specific friction model [25], which is very similar to the Adams stick-slip model. Simpack offers also a specific stick-slip model [24], which is different from the Adams and RecurDyn specific approach. These specific friction models are presumably designed to provide a more reliable friction behavior than the static regularization, especially for stick-slip effects and long-term stiction.

Despite the availability of a large number of friction models, the commercial multibody simulation packages Adams, RecurDyn, and Simpack have recently developed their own stick-slip friction models. Only Adams offers the LuGre model. Therefore, the purpose of this paper is to investigate the behavior and potential drawbacks of these specific stick-slip models.

This paper focuses on the friction models provided by these commercial MBS software packages. In particular, it focuses on their specific stick-slip models. After describing the different approaches, this paper uses a simple test model and a practical example to assess the reproducibility of friction phenomena and user-friendliness of these models.

2 General friction characteristics

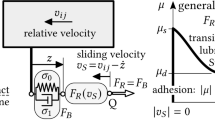
In general, the frictional force has a static and a dynamic part. According to Coulomb, a critical static friction force must be exceeded to set a frictional body in motion. If this body is in motion, a dynamic friction force acts [1, p. 156f]. Figure 1 shows a general friction characteristics that is often the basis for numerical models such as those mentioned above. Here, the friction force \(F_{\mathrm{R}} \) is proportional to the normal force via the friction coefficient \(\mu \), see Fig. 1. According to Stribeck, hydrodynamic friction also shows a velocity dependent friction force [1, p. 235].

Fig. 1
figure 1

General friction characteristics with discontinuity at \(|v|=0 \)

Full size image

Therefore, friction characteristics are usually considered as a function of velocity. Figure 1 shows this behavior, where \(\mu _{\mathrm{s}}\) describes the coefficient of static friction and \(\mu _{\mathrm{d}}\) the coefficient of dynamic friction. For static friction (“stiction”, at \(v=0\)), this function is ambiguous since the actual friction force acting in this case depends on the external force. To set the body in motion, the static friction level must be exceeded. For \(|v|>0\), a velocity-dependent friction coefficient generally applies. The stick-slip models of Adams, RecurDyn, and Simpack approximate the stiction region by using an additional displacement state.

3 Friction models in commercial multibody simulation packages

The simplest model provided by these MBS packages is a piecewise defined regularization between friction regimes. A standard regularization approximates stiction behavior by slow joint creep. To achieve long-term stiction, MBS package specific friction models are provided. These models switch between stick and slip. Each algorithm uses relative velocity to distinguish between different states to maintain long-term stick [23–25]. Adams also offers the LuGre model as a dynamic friction model. However, as illustrated in [20], this model exhibits severe drawbacks.

3.1 Standard regularizations of Adams, RecurDyn, and Simpack

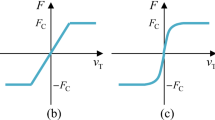
A regularized friction model \(\mu =\mu (|v|)\) is usually defined by three characteristic points: \((\mu (|v|=0)=0)\), (\(\mu (|v|=v_{ \mathrm{s}})=\mu _{\mathrm{s}}\)), and (\(\mu (|v|=v_{\mathrm{d}})=\mu _{ \mathrm{d}}\)), where \(\mu _{\mathrm{s}}\) and \(\mu _{\mathrm{d}}\) specify the static and dynamic friction coefficient and the velocities \(v_{\mathrm{s}}\) and \(v_{\mathrm{d}}\) model the regularization and the attenuation pattern.

In friction regularization, the friction coefficient \(\mu \) is calculated by a piecewise defined function, depending on the relative velocity \(v\). In the first section, for \(|v| \leq v_{\mathrm{s}}\), the friction coefficient \(\mu (|v|)\) increases from \(\mu (0)=0\) to the stiction coefficient \(\mu (v_{\mathrm{s}})=\mu _{\mathrm{s}}\). In the second section, for \(v_{\mathrm{s}} < |v| \leq v_{\mathrm{d}}\), \(\mu (|v|)\) decreases from \(\mu (v_{\mathrm{s}})=\mu _{\mathrm{s}}\) to the dynamic coefficient \(\mu (v_{\mathrm{d}})=\mu _{\mathrm{d}}\), and in the third section, for \(|v| > v_{\mathrm{d}}\), the friction coefficient applies to \(\mu (|v|)=\mu _{\mathrm{d}}=\mathrm{const}\). The standard regularization is typically defined as follows:

$$ \mu _{\mathrm{sr}}(|v|)= \textstyle\begin{cases} \mu _{\mathrm{\text{0} \rightarrow \mu _{\mathrm{s}}}}(|v|), & |v| \leq v_{\mathrm{s}} \\ \mu _{\mathrm{\mu _{\mathrm{s}} \rightarrow \mu _{\mathrm{d}} }}(|v|), & v_{\mathrm{s}} < |v| \leq v_{\mathrm{d}} \\ \frac{v}{|v|}\mu _{\mathrm{d}}, & |v| > v_{\mathrm{d}}. \end{cases} $$
(1)

To approximate the friction characteristics, see Fig. 1, the best possible way, \(v_{\mathrm{s}}\rightarrow 0\) and therefore has a very small value. To generate a frictional force, the body needs a relative velocity.

All three MBS packages offer a regularization of the friction characteristic shown in Fig. 2. Adams regularizes similarly as described in Eq. (1) [23]. RecurDyn, on the other hand, neglects the static friction coefficient in its regularized friction model and transitions directly to \(\mu _{\mathrm{d}} \) [25]. Simpack models its regularization with trigonometric functions in the same scheme as Eq. (1). The mathematical approach is completely described in [24]. Adams and RecurDyn have not described in detail the transition function used to transfer the coefficient of friction between \(\mu _{s} \) and \(\mu _{d} \). Adams states in its user manual that “a STEP function” [23, p. 144] is used for the transition between the friction coefficients [23, p. 144]. Tests have shown that Adams and RecurDyn use a fifth-order polynomial (STEP5 function) to describe the smooth transition between the friction coefficients [23, 25]. Figure 2 shows a general plot comparing the regularizations. For Adams and RecurDyn, a STEP5 function is assumed to be a transition function between the friction coefficients. The steady-state friction characteristics, as implemented in Adams [23, p. 145], are calculated by the equation

$$ \mu _{\mathrm{LG}}(|v|)=\mu _{\mathrm{d}}+(\mu _{\mathrm{s}}-\mu _{ \mathrm{d}})e^{-(|v|/v_{\mathrm{a}})^{\alpha}} $$
(2)

with a decay exponent of \(\alpha = 2 \).

Fig. 2
figure 2

Regularized friction characteristics \(\mu =\mu (|v|) \) and the LuGre steady-state characteristics

Full size image

The \(\mathrm{STEP5}\) function is described in its typical syntax as used in the MBS packages. For example, \(\mathrm{STEP5}(x,x_{\mathrm{0}},y_{\mathrm{0}},x_{\mathrm{1}},y_{ \mathrm{1}})\) is a fifth-order polynomial that smoothly changes the value \(y_{0} \) to \(y_{1} \) in the interval \(x_{0} \le x \le x_{1} \).

3.2 LuGre model as implemented in Adams

The LuGre model is a dynamic friction model that is often described in the literature. It is based on a bristle model, which describes dynamic friction force [18]. Adams has implemented the LuGre model, while RecurDyn and Simpack only provide their own stick-slip models. The Adams implementation also takes a normal force dependency into account [23]. The advantages and disadvantages of this description are well known and can be found in Åström et al. [26], Marques et al. [6], and Rill et al. [20], among others.

The main disadvantages are the drift during pulse-like excitation and the undefined frictional characteristics caused by the bristle dynamics and the discontinuous steady-state friction characteristics.

The LuGre model as implemented in Adams [23, p. 145] determines the friction force by

$$ F_{\mathrm{R}} = \sigma _{0} z + \sigma _{1} \dot{z} + \sigma _{2} v, $$
(3)

where \(\sigma _{0} \) is the bristle stiffness coefficient, \(\sigma _{1} \) is the bristle damping coefficient, and \(\sigma _{2} \) is the viscous damping coefficient. \(z \) is the average bristle deflection and \(\dot{z} \) denotes its time derivative, \(v \) is the relative velocity of the contact bodies. The dynamics of the bristle is described using the normal contact force \(F_{\mathrm{N}} \) and Eq. (2) by the differential equation

$$ \dot{z} = v - \sigma _{0} \frac{| v |}{F_{\mathrm{N}}\mu _{\mathrm{LG}}(v)} z. $$
(4)

3.3 Stick-slip models of Adams and RecurDyn

The specific stick-slip model of Adams and RecurDyn can be separated into \(\mu _{\mathrm{stick}}(x,v)\) and \(\mu _{\mathrm{slip}}(v)\). \(\mu _{\mathrm{slip}}\) regularizes the transition from \(\mu _{\mathrm{s}}\) to \(\mu _{\mathrm{d}}\) in \(|v| > v_{\mathrm{s}} \) by a fifth-order polynomial (STEP5 function) and depends only on the relative velocity \(v\) [23, 25]. In addition to the standard regularization, the friction coefficient is calculated using a multidimensional function that also takes into account the relative displacement \(x\) as an internal state. The right two plots in Fig. 3a show the limits of this approach, where the model parameter \(x_{\mathrm{s}}\) describes the maximum displacement until the coefficient of friction increases to the static coefficient of friction \(\mu _{\mathrm{s}}\). The exact implementation of the model in the software is not disclosed. It is therefore not possible to say with certainty how the displacement state \(x \) is determined in detail. As with the standard regularization, the transition functions are not explained in detail in the manuals. Various tests have shown that a STEP5 function is probably used as well. The left plot in Fig. 3a shows the function of the static friction coefficient \(\mu _{\mathrm{stick}}(x,v)\). The mathematical model in Adams and RecurDyn follows the equation

$$ \mu _{\mathrm{ss}}(x,v)= \textstyle\begin{cases} \mu _{\mathrm{stick}}(x,v), & |v|\leq v_{\mathrm{s}} \\ \mu _{\mathrm{slip}}(v)=\pm \textstyle\begin{cases} \frac{v}{|v|} \cdot \mathrm{STEP5}(|v|,v_{\mathrm{s}},\mu _{ \mathrm{s}},v_{\mathrm{d}},\mu _{\mathrm{d}}), \\ \quad v_{\mathrm{s}}< |v| \leq v_{\mathrm{d}} \\ \frac{v}{|v|} \cdot \mu _{\mathrm{d}} \\ \quad |v| > v_{\mathrm{d}} \end{cases}\displaystyle & |v| > v_{\mathrm{s}} \end{cases} $$
(5)

Subsequently, the friction force is defined by

$$ F_{\mathrm{R}}=\pm \mu (x,v) \cdot F_{\mathrm{N}}. $$
(6)

In Adams [23, p. 145] the stiction characteristics is implemented as

$$ \mu ^{\mathrm{A}}_{\mathrm{stick}}(x,v) = (1-\beta (|v|)) \mu _{ \mathrm{1}}(|x|) \cdot \mathrm{sgn}(|x|) + \mu _{\mathrm{s}}\beta (|v|) \cdot \mathrm{sgn}(|v|), $$
(7)

and in difference to this the stiction characteristics in RecurDyn [25] is implemented by

$$ \mu ^{\mathrm{R}}_{\mathrm{stick}}(x,v)= -(1-\beta (|v|)) \mu _{ \mathrm{1}}(x) - \mu _{\mathrm{v}}(v), $$
(8)

where the last term \(\mu _{\mathrm{v}}(v)=\mu _{\mathrm{s}}\beta (v)\). The value \(\beta (|v|) = \mathrm{STEP5}(|v|,-v_{\mathrm{s}},-1,v_{\mathrm{s}},1)\) and \(\mu _{\mathrm{1}}(|x|)=\mathrm{STEP5}(|x|,-x_{\mathrm{s}},-\mu _{ \mathrm{s}},x_{\mathrm{s}},\mu _{\mathrm{s}})\) are nonlinear STEP5 transfer functions, see Fig. 3b. The first and the second terms in Eq. (7) and Eq. (8) are identical in both implementations. The difference is the sign definition, which means that the ± character in Eq. (5) and Eq. (6) must be adapted to the respective MBS package.

Fig. 3
figure 3

a) Stiction region of the stick-slip model of Adams and RecurDyn b) Parameters \(\beta \) and \(\mu _{\mathrm{1}}\)

Full size image

The description of stiction over displacement and velocity is shown in Fig. 3a. The upper right plot of Fig. 3a shows the standard regularization for \(x=0\). In the case of \(v=0\), the friction value is determined by the displacement \(x\), as shown in the lower right plot in Fig. 3a.

The first terms of Eqs. (7) and (8) are significantly influenced by the relative displacement \(x\), and the second terms are influenced by the relative velocity \(v\). Due to \((1-\beta (|v|)) \mu _{\mathrm{1}}(x) \), a coefficient of friction \(\mu \) can be maintained even without of relative velocity. The term \((1-\beta (|v|))\) ensures that \(\mu _{\mathrm{stick}} \leq \mu _{\mathrm{s}}\). In case of “slip to stick” the relative displacement will reset to \(x=0\).

In contrast to the standard regularization, this description makes it possible to create long-term stiction without slipping of the contact bodies. The necessary frictional force is achieved by a small deflection of the bodies.

To parameterize this model, four or five parameters are required in Adams and RecurDyn, respectively: the friction coefficients \(\mu _{\mathrm{s}}\) and \(\mu _{\mathrm{d}}\), the static model parameter \(x_{\mathrm{s}}\), the static regularization velocity \(v_{\mathrm{s}}\), and in Adams a transition coefficient \(\lambda \) to describe the dynamic regularization velocity \(v_{\mathrm{d}}=\lambda v_{\mathrm{s}}\). By default, \(\lambda =1.5\) in Adams and in RecurDyn \(\lambda =1.5\) is a fixed value that cannot be changed by the user.

3.4 Stick-slip model of Simpack

The stick-slip model of Simpack is shown in Fig. 4. The static friction force

$$ F_{\mathrm{R,stick}} = c_{\mathrm{f}} \cdot \Delta x_{\mathrm{c_{f}}} + d_{\mathrm{f}} \cdot v $$
(9)

is modeled by a spring-damper element with a stiffness coefficient \(c_{\mathrm{f}}\) and a damping coefficient \(d_{\mathrm{f}}\). The stiffness component \(F_{\mathrm{c_{f}}} = c_{\mathrm{f}} \cdot \Delta x_{\mathrm{c_{f}}} \) is calculated by the relative displacement \(\Delta x_{\mathrm{c_{\mathrm{f}}}} = x - \Delta x_{\mathrm{0}} \). The displacement at the time of transition from slip to stick is represented by \(\Delta x_{\mathrm{0}} \). The dynamic friction force

$$ F_{\mathrm{R,dyn}} = -\mu _{\mathrm{d}} F_{\mathrm{N}} \frac{v}{|v|} $$
(10)

is the dynamic Coulomb friction force [24].

Fig. 4
figure 4

Calculation scheme of the Simpack stick-slip model (refers to [24])

Full size image

Simpack distinguishes between stick and slip in the stick to slip direction by the condition \(F_{\mathrm{c_{f}}}>\mu _{\mathrm{s}}F_{\mathrm{N}}\) and in the slip to stick direction by the condition \(v=0\). This approach is discontinuous due to the direct transition between the stick and slip states. In case of slip to stick the spring displacement \(\Delta x_{\mathrm{c_{\mathrm{f}}}}\) can be reset to zero or preloaded with the sliding force.

The friction coefficients \(\mu _{\mathrm{s}}\) and \(\mu _{\mathrm{d}}\), the stiffness \(c_{\mathrm{f}}\) and the damping \(d_{\mathrm{f}}\) are to be defined by the user. The latter two are part of the mathematical model corresponding to a classic penalty approach. The dimensions of \(c_{\mathrm{f}}\) and \(d_{\mathrm{f}} \) are the reason why they are not comparable to real physical values of stiffness and damping.

For nonexpert users it is difficult to define the parameters \(c_{\mathrm{f}}\) and \(d_{\mathrm{f}}\) correctly. Following the approach outlined in [21], an empirical method for estimating the stiffness

$$ c_{\mathrm{f}}=\frac{\bar{F}_{\mathrm{s}}}{x_{\mathrm{s}}}= \frac{\mu _{\mathrm{s}}\bar{F}_{\mathrm{N}}}{x_{\mathrm{s}}} $$
(11)

is to use a reference static friction force \(\bar{F}_{\mathrm{s}}\) and a fictitious maximum displacement \(x_{\mathrm{s}}\). In addition, the friction damping parameter \(d_{\mathrm{f}}\) can be calculated by

d f =2D c f ⋅ m f with m f = F ¯ N g
(12)

using the damping ratio \(D\), and \(m_{\mathrm{f}}\) is an approximated fictitious mass calculated by the estimated reference normal force \(\bar{F}_{\mathrm{n}}\) and the gravity \(g\).

It should be noted that the normal force in multibody systems generally does not have a constant value. For example, \(\bar{F}_{\mathrm{N}}\) can be estimated by a static equilibrium or from a dynamic simulation.

The stiffness \(c_{\mathrm{f}}\) can also be calculated using the rise time \(t_{\mathrm{rt}}\) needed for the stiffness force \(F_{\mathrm{c_{f}}}\) to rise to a constant impulse load. According to [27, p. 316], the rise time

$$ t_{\mathrm{rt}}= \frac{\pi -\arccos (D)}{\omega _{\mathrm{0}}\sqrt{1-D^{2}}} $$
(13)

can be calculated for a second-order dynamic system with stepwise excitation. From this, a stiffness

$$ c_{\mathrm{f}} = m_{\mathrm{f}}\left ( \frac{\pi -\arccos (D)}{t_{\mathrm{rt}}\sqrt{1-D^{2}}}\right )^{2} $$
(14)

can be estimated using the natural frequency \(\omega _{\mathrm{0}}=\sqrt{c_{\mathrm{f}}/m_{\mathrm{f}}}\).

In the case of dynamically oscillating frictional forces, the stiffness and damping ratio must be adapted accordingly to the respective system. For this purpose, reasonable parameters for \(t_{\mathrm{rt}}\) and \(D\) must be selected. For a rise time \(t_{\mathrm{rt}} \) significantly below the oscillation time of the acting force, a limited overshoot and oscillation of the stiffness force, a damping ratio of \(0.3< D<0.7\) has proven itself.

According to Eq. (11) the stiffness coefficient \(c_{\mathrm{f}}\) is determined by a fictitious displacement \(x_{\mathrm{s}}\), equivalent to the Adams and RecurDyn approach. In Eq. (14) the rise time \(t_{\mathrm{rt}}\) of the stiffness force \(F_{\mathrm{c_{f}}}\) is used to determine \(c_{\mathrm{f}}\).

4 Pulse load

Some friction models, such as the standard regularization or the LuGre model, drift at pulse-like excitation as investigated by Rill et al. [20], among others. To examine the presented friction models for drift, the simple test model of [20] is used. Figure 5 shows the test model and its parameters. A series of three pulse-loads with an amplitude \(F_{\mathrm{i}}=0.8 \cdot F_{\mathrm{s}}\) is applied to the mass. To make the different approaches comparable, it was necessary to increase the interval from \(\tau =0.1\,\mathrm{s} \) to \(\tau =1.0\,\mathrm{s} \). The friction models are simulated with the standard parameters of the MBS package, as shown in Fig. 5. Table 1 provides information on the software version and solver used. The relative small maximum step size of \(h_{\mathrm{max}} = 5 \cdot 10^{-6} \, \mathrm{s} \) was selected to achieve a high resolution of the stick-slip events.

Fig. 5
figure 5

Simple test model with model parameters and standard friction model parameters of the corresponding MBS package. In Adams and RecurDyn, \(\lambda =1.5 \) is used to adjust the velocity \(v_{\mathrm{d}} \) to \(v_{\mathrm{s}} \) (as described in Sect. 3.3). In contrast, Simpack does not use either the \(v_{\mathrm{s}} \) or \(v_{\mathrm{d}} \) parameter

Full size image
Table 1 Software versions and solver parameters
Full size table

4.1 Standard regularization and LuGre

Figure 6a shows that the LuGre model drifts as expected. The static friction force is not reached and the LuGre model breaks too early, see Fig. 6c. Figure 6a also shows the result of regularization according to \(\mu _{\mathrm{d}}\) in RecurDyn. Due to \(F_{\mathrm{i}} > F_{\mathrm{d}}\), the sliding friction level is exceeded and the mass starts to accelerate. With regularization to \(\mu _{\mathrm{s}}\), only a very small drift occurs, which depends on the regularization velocity \(v_{\mathrm{s}}\), see Fig. 6b. The regularization in Adams, which includes both \(\mu _{\mathrm{s}}\) and \(\mu _{\mathrm{d}}\), shows the same result, because a STEP5 function is used for the transition to \(\mu _{\mathrm{s}}\), also. In Fig. 6b it can be seen that the Simpack regularization absolutely drifts a little further (\(\Delta x=0.25 \cdot 10^{-4} \, \mathrm{m}\)) than the STEP5 function in Adams or RecurDyn. This is due to the different slopes of the two regularizations. They are slightly higher for the STEP5 function than for the sin function, as can be seen in Fig. 2. Therefore, the friction force is generated at a lower relative velocity.

Fig. 6
figure 6

Simulation results for standard regularizations a) Displacement of LuGre model and RecurDyn regularization \(\mu _{\mathrm{d}}\) b) Displacement of Adams, Simpack and RecurDyn regularization \(\mu _{\mathrm{s}} \) c) Friction force

Full size image

4.2 Stick-slip models

Figure 7 shows the results of the stick-slip models. There is no drift in all three models. The displacement in Fig. 7a and the force curve in Fig. 7c show no difference between Adams and RecurDyn. The maximum displacement \(x^{\mathrm{A,R}}_{\mathrm{max}} = 5.1 \cdot 10^{-6} \, \mathrm{m}< x_{ \mathrm{s}}\) is smaller than the model parameter \(x_{\mathrm{s}} \). It can also be seen that this stick-slip model requires about \(0.25 \, \mathrm{s}\) to reach its maximum deflection and about \(0.5 \, \mathrm{s}\) to return to its initial position without excitation. This nonlinear “time constant” can only be influenced indirectly by the model parameters \(v_{\mathrm{s}}, x_{\mathrm{s}} \). There is a significantly lower deflection of \(x^{\mathrm{S}}_{\mathrm{max}} = 4.7 \cdot 10^{-8} \, \mathrm{m}\) with pulse-like excitation in Simpack, see Fig. 7b. The significantly lower displacement is due to the different standard parameters. Compared to Adams parameters, Simpack’s stiffness results in a maximum displacement \(x_{\mathrm{s}}=F_{\mathrm{s}} / c_{\mathrm{f}} = 5.886 \cdot 10^{-5} \,\mathrm{mm} \) at the static friction force. If the model parameter \(x_{\mathrm{s}} \) is significantly reduced in Adams and RecurDyn, a very stiff characteristic curve is generated. This can lead to difficulties for the solver.

Fig. 7
figure 7

Simulation results for the stick-slip models a) Displacement of Adams and RecurDyn b) Displacement of Simpack c) Friction forces

Full size image

4.3 Adams and RecurDyn in detail

A different set of friction model parameters created from a practical approach shows a different implementation of the stick-slip model in Adams and RecurDyn. To investigate long-term stiction, Rill et al. [21] estimated a reference friction force \(F_{\mathrm{Rref}} \) and a reference deflection \(x_{\mathrm{sref}} \). These were adjusted to the body and the friction parameters to parameterize its friction model. For the simple test model (Fig. 5), the regularization velocity is set to \(v_{\mathrm{s}} = 1.0 \, \mathrm{mm/s} \) and the model parameter \(x_{\mathrm{s}} \) is set to \(x_{\mathrm{s}} = x_{\mathrm{sref}} = 1.0 \cdot 10^{-3} \, \mathrm{mm} \), according to [21]. The amplitude of the impulse force is \(F_{\mathrm{i}}=0.95 \cdot F_{\mathrm{s}}=5.5917 \, \mathrm{N} \).

4.3.1 Drift based on excitation force

Figure 8 shows the displacement and the friction force resulting from the adjusted parameters. After removing the excitation force (\(t>3.0\,\mathrm{s}\)) Adams remains with a constant drift of \(\Delta x = 5.0\cdot 10^{-7} \, \mathrm{m} \). In contrast to Adams, RecurDyn shows no drift, which indicates that the implementation of this stick-slip approach is different in these two MBS software packages. Adams allows access to the internal displacement state of the friction model \(z \) (Fig. 8a, dashed line). It can be seen that the internal state \(z \) is limited to the model parameter \(x_{\mathrm{s}} \) (\(z\leq x_{\mathrm{s}} \)). It returns to its initial value if the excitation force is removed. Figure 8b shows the friction force in general and Fig. 8c in detail for the pulse-like excitation. The friction force is identical in both models except after the pulse. RecurDyn drops about \(0.01\,\mathrm{s} \) later than Adams.

Fig. 8
figure 8

Simulation results for the stick-slip models with adjusted friction parameters a) Displacements and internal state b) Friction forces in general c) Friction forces in detail

Full size image

Another example illustrates this behavior even better. As described in Rill et al. [21], the simple test model (Fig. 5) is now excited by a force, generated by a STEP function (a third-order polynomial) in a time interval of \(\tau =0.001 \, \mathrm{s} \). Due to the constant external force \(F_{\mathrm{e}}=0.95 \cdot F_{\mathrm{s}} \) for \(t>0.001 \, \mathrm{s} \), the friction coefficient of \(\mu _{\mathrm{st}}=0.95 \cdot \mu _{\mathrm{s}} \) results in a steady state. Equation (5) is simplified by \(v=0 \) to

$$ \mu _{\mathrm{st}} = \mu ^{\mathrm{A}}_{ss}(x^{\mathrm{A}}_{ \mathrm{st}}, 0) = (1 - \beta (|v|)) \mu _{1}(|(x^{\mathrm{A}}_{ \mathrm{st}}|) \cdot \mathrm{sgn}(x^{\mathrm{A}}_{\mathrm{st}}) + \mu _{s}\beta (|0|) \cdot \mathrm{sgn}(0) = \mu _{1}(|x^{\mathrm{A}}_{ \mathrm{st}}|), $$
(15)

and the inverse function of \(\mu ^{-1}_{1}(|(x^{\mathrm{A}}_{\mathrm{st}}|) \) results in the steady state displacement of

$$ x^{\mathrm{A}}_{\mathrm{st}}=\mu _{1}^{-1}(\mu _{\mathrm{st}})=0.71 \cdot 10^{-6} \, \mathrm{m}. $$
(16)

After the first overshoot the displacement of RecurDyn, \(x^{\mathrm{R}} \) and the internal state displacement \(z^{\mathrm{A}} \) of Adams converge to \(x^{\mathrm{A}}_{\mathrm{st}} \), see Fig. 9a. The displacement of Adams \(x^{\mathrm{A}} \) converges to \(x^{\mathrm{A}}_{\mathrm{st}}=0.83\cdot 10^{-6} \, \mathrm{m} \), and an offset of \(u= x^{\mathrm{A}}_{\mathrm{st}} - z^{\mathrm{A}}_{\mathrm{st}}=0.12 \cdot 10^{-6} \, \text{m}\) remains.

Fig. 9
figure 9

Simulation results for a excitation with a step function a) Displacements and internal state b) Internal state and velocity in detail

Full size image

The internal state \(z^{\mathrm{A}} \) of Adams is identical to the displacement \(x^{\mathrm{A}} \) and to the displacement of RecurDyn \(x^{\mathrm{R}} \) until the model parameter \(x_{\mathrm{s}} \) is reached. After that, the internal state \(z^{\mathrm{A}} \) remains constant. It also decreases and converges to \(x_{\mathrm{st}} \) once the inflection point of the displacement has been reached. Figure 9 shows the corresponding zero crossing of the velocity of the mass.

RecurDyn does not provide access to the internal state \(x^{\mathrm{R}} \). The reason for the drift in Adams seems to be the limitation of the internal state \(z^{\mathrm{A}} \) to the regularization parameter \(x_{\mathrm{s}} \) (\(z^{\mathrm{A}} \leq x_{\mathrm{s}} \)). This limitation leads to an offset between the displacement \(x^{\mathrm{A}} \) and the internal state \(z^{\mathrm{A}} \). As soon as \(z^{\mathrm{A}} \) is in steady state, the friction force equals the external force \(F_{\mathrm{e}} \) and the displacement \(x^{\mathrm{A}} \) remains constant with the existing offset.

4.3.2 Drift based on regularization parameters

Unlike overshoot drift, which is caused by the excitation force, a drift may also occur due to an inadequate selection of model parameters, specifically \(v_{\mathrm{s}}\) and \(x_{\mathrm{s}}\).

Another simulation was performed using the model shown in Fig. 5 with a time interval \(\tau =0.001 \, \mathrm{s} \). The model parameter \(x_{\mathrm{s}}=(10.0, 1.0, 0.1, 0.01)\cdot 10^{-3} \, \mathrm{m} \) was varied and the results simulated with Adams are shown in Fig. 10. Additionally, one simulation with the standard regularization is displayed as a solid black line. The stick-slip model approximates the standard regularization as the model parameter \(x_{\mathrm{s}} \) increases.

Fig. 10
figure 10

Behavior of Adams and RecurDyn stick-slip model with varying \(x_{\mathrm{s}} \) a) Displacements b) Extract of excitation and friction force (color figure online)

Full size image

Equation (5) corresponds to a fifth-order polynomial in both the x and y direction. As can be shown, the partial derivatives at the origin are given by

$$\begin{aligned} \frac{\partial \mu _{\mathrm{ss}}(x,v)}{\partial x} \bigg|_{x=0,v=0} &= \frac{15}{8}\mu _{\mathrm{s}} \cdot \frac{1}{x_{\mathrm{s}}} \end{aligned}$$
(17)

and

$$\begin{aligned} \frac{\partial \mu _{\mathrm{ss}}(x,v)}{\partial v} \bigg|_{x=0,v=0} &= \frac{15}{8}\mu _{\mathrm{s}} \cdot \frac{1}{v_{\mathrm{s}}} . \end{aligned}$$
(18)

When the regularization parameters \(x_{\mathrm{s}} \) and \(v_{\mathrm{s}} \) have a similar order of magnitude, both directions have the same gradients. Due to the dynamics, the velocity state \(v \) is more sensitive than its integration into the position state \(x \). As a result, the stick-slip model \(\mu _{\mathrm{ss}}(x,v) \) approximates the regularized friction model \(\mu _{\mathrm{sr}}(v) \) in the stiction range \(|v| < v_{\mathrm{s}} \).

$$\begin{aligned} \mu _{\mathrm{ss}}(x,v\rightarrow 0) \approx \mu _{\mathrm{sr}}(v). \end{aligned}$$
(19)

However, the displacement of the box is still taken into account, and \(\mu _{\mathrm{ss}} \) is only an approximation of \(\mu _{\mathrm{sr}} \). Figure 11 illustrates that the drift decreases over an extended simulation period. It takes about \(6 \, \mathrm{s} \), which is equivalent to approximately 6000 times the excitation time \(\tau \). Figure 10 shows that the “time constant” of the model depends on the ratio of the regularization parameters

$$\begin{aligned} \kappa = \frac{\partial \mu _{\mathrm{ss}}(x,v)}{\partial x} \bigg|_{x=0,v=0} \bigg( \frac{\partial \mu _{\mathrm{ss}}(x,v)}{\partial v} \bigg|_{x=0,v=0} \bigg)^{-1} = \frac{v_{\mathrm{s}}}{x_{\mathrm{s}}}. \end{aligned}$$
(20)

A higher ratio of \(\kappa \) results in a quicker reduction of the drift.

Fig. 11
figure 11

Long-term simulation of the Adams standard regularization and the stick-slip friction models

Full size image

5 Crane festoon model

The crane festoon model (Fig. 12) used by Rill et al. [20] is a useful practical application because it combines a variety of friction phenomena into a general multibody system. This model allows us to investigate breakaway behavior at different pulse loads and the stick-slip effect. Additionally, when cable trolleys are moved in positive and negative directions, the friction model must dynamically change the sign of the friction force as a result.

Fig. 12
figure 12

a) Crane Festoon model used by Rill et al. [20] and its parameters b) Excitation \(u_{\mathrm{TT}}(t)\) and \(\dot{u}_{\mathrm{TT}}(t)\)

Full size image

The model consists of a rail on which cable trolleys (T) can move in x-direction. The trolleys are connected by a cable, modeled by lumped masses (C1-C3) and spring-damper elements. The towing trolley is driven (rehonom) by the predefined function \(u_{\mathrm{TT}}=u_{\mathrm{TT}}(t) \). The other trolleys are free in x-motion. The parameter \(l_{\mathrm{0}}\) defines the unloaded length, \(c^{\mathrm{+}}\) defines the stiffness, and \(d^{\mathrm{+}} \) defines the damping of the cable.

Figure 12b shows the motion specification and its time derivative. The first second ensures a quasi-static state. From \(1\,\mathrm{s}\) to \(15\,\mathrm{s}\), the towing trolley is moved slowly to and fro. As a result, only trolley 2 is set in motion, but not trolley 1. After \(15\,\mathrm{s}\), a fast expansion occurs, which leads to oscillations in the movement of the trolleys. The crane festoon model shown in Fig. 12 was used for the following studies. The friction models were simulated using the default parameters of the MBS package, as shown in Fig. 5a. Table 1 provides information on the software version and solver used.

5.1 Friction in general

The displacement and velocity of the trolleys and the frictional forces between the cable trolleys and the rail are each calculated by the corresponding MBS package. Only the specific stick-slip models of the packages will be discussed here. The LuGre model and a regularized friction model have already been discussed on the festoon model in detail in Rill et al. [20].

Figure 13 shows the simulation results of trolley 2 (T2). There is no significant difference between Adams and RecurDyn observed, only minor inconsistencies, which could be due to the different solvers. In addition, the position and velocity curve for Simpack does not show any significant differences to Adams and RecurDyn. In the transitions from sliding to sticking (\(t \approx 4.5 \, \mathrm{s} \), \(t \approx 12.6 \, \mathrm{s} \), \(t \approx 19.9 \, \mathrm{s} \),…), the static friction peak is missing in Simpack. The sliding friction is modeled by the dynamic Coulomb friction force and switched to the static friction force by the condition \(v=0\).

Fig. 13
figure 13

Trolley 2 results a) Displacement b) Velocity c) Friction force

Full size image

5.2 Friction in detail

Figure 14a shows the time history of the friction coefficient \(\mu (t) = F_{\mathrm{R}} / F_{\mathrm{N}} \) at the second transition from sliding to sticking (\(t\approx 20.6 \, \mathrm{s} \)) at the extension maneuver. Adams and RecurDyn keep the regularization as defined and reach the maximum static friction value of \(\mu _{\mathrm{s}}=0.08 \). For Simpack, the maximum static friction value \(\mu _{\mathrm{s}}\) exceeds by \(\Delta \mu = 2.3 \cdot 10^{-3} \). According to the definition of the switching condition \(F_{\mathrm{c_{f}}}>F_{\mathrm{s}} \), the actually acting friction \(F_{\mathrm{R}}=F_{\mathrm{c_{f}}}+F_{\mathrm{d_{f}}} \) exceeds the specification by the damping component \(F_{\mathrm{d_{f}}} \).

Fig. 14
figure 14

Detailed results of trolley 2 a) Dynamic overshoot at stick to slip b) Friction force at slip to stick transition c) velocity at slip to stick transition

Full size image

Figure 14b shows the frictional force during the transition from sliding to sticking at \(t\approx 22.39\,\mathrm{s} \). A time offset in the force curves of the three MBS packages can be seen. This is \(\Delta t_{\mathrm{1}}=0.4\,\mathrm{ms} \) between Adams and RecurDyn and \(\Delta t_{\mathrm{2}}=7.3\,\mathrm{ms} \) between RecurDyn and Simpack. The difference between Adams and RecurDyn may arise because of the different solvers applied as standard in the MBS packages. The qualitative behavior is comparable except for the time offset. The larger time offset to Simpack results on the one hand from the switching condition \(v=0\), which occurs slightly later than the peak of Adams and RecurDyn at \(v=v_{\mathrm{s}}\) (Fig. 14c), and on the other hand from the slightly higher friction accumulated in the system due to the overshoots. At \(t=22.3942\,\mathrm{s} \) a step in the Simpack friction force can be seen. Before \(t=22.3942\,\mathrm{s} \), the Simpack model is in sliding mode. In the next time step, the switching condition \(v=0 \) gets triggered and the model changes to sticking mode. The default setting “unloaded stiffness” sets the relative displacement \(x=0 \) at this time. At the point of switching, the static friction force \(F_{\mathrm{R}}=c_{\mathrm{f}}x+d_{\mathrm{f}}v=0 \) and must therefore be built up first. Figure 14c shows the velocity during the transition from sliding to sticking at \(t\approx 22.39\,\mathrm{s} \). At \(v=0\) (\(t=22.3942\,\mathrm{s}\)), a bent can be seen in the velocity curve of Simpack. This is caused by the step in the friction force curve. Since the step in the friction force curve is generated by the friction model and not by the actual force or velocity acting on trolley 2, a step occurs. That results in a bent in the velocity curve.

Figure 15a shows the characteristics of the Simpack model. To improve the resolution, only the first \(12.5\,\mathrm{s} \) were plotted. A square is used to represent the output values during switching, and no other values were calculated between these points. Ideally, switching would occur at \(v=0 \). At \(v \approx 0 \) the friction force is \(F_{\mathrm{R}}=c_{\mathrm{f}}x+d_{\mathrm{f}}v=0 \), and for \(|v|>0 \) the friction force is \(F_{\mathrm{R}}=-(v / |v|) \mu _{\mathrm{d}}F_{\mathrm{N}} \). Due to the resolution of \(\Delta t_{\mathrm{step}}=5\cdot 10^{-6}\,\mathrm{s} \), the velocity jumps at the transition from \(F_{\mathrm{R,stick}} \) to \(F_{\mathrm{R,slip}} \) or from \(F_{\mathrm{R,slip}} \) and \(F_{\mathrm{R,stick}} \). At the transition from \(F_{\mathrm{R,slip}} \) to \(F_{\mathrm{R,sick}} \) the static friction force oscillates. This is therefore in the dissipative quadrants. In the first \(12.5\,\mathrm{s}\), the system transits from sticking to sliding in both positive and negative directions. During the slowly to and fro motion, the friction force is built quasi-statically, and no dynamic overshoot occurs. The static friction coefficient of \(\mu =0.08\) is maintained.

Fig. 15
figure 15

Friction characteristics \(\mu (v) \) simulated with the festoon model a) Simpack stick-slip model b) Adams and RecurDyn stick-slip model

Full size image

Figure 15b shows the friction characteristics \(\mu (v)\) of the stick-slip model from Adams and RecurDyn during the entire \(25\,\mathrm{s} \). The static friction coefficient \(\mu _{\mathrm{s}}\) is maintained. Ambiguities occur for \(-v_{\mathrm{s}}< v< v_{\mathrm{s}}\) due to additional determination of \(\mu \) by the displacement \(x\). For \(|v|>v_{\mathrm{s}}\), the friction coefficient is transitioned to the dynamic friction coefficient \(\mu _{\mathrm{d}}\) by the STEP5 function. Figure 16 shows the general stiction characteristics \(\mu _{\mathrm{stick}}(v,x)\) of Adams and RecurDyn and the simulated friction coefficients, respectively. Both the Simpack and the Adams or RecurDyn models deviate from the respective theoretically ideal friction characteristic \(\mu =\mu (v) \), as seen in Fig. 1.

Fig. 16
figure 16

In detail, the coefficient of friction \(\mu (x,v) \), as well as the stiction region \(\mu _{\mathrm{stick}}(x,v) \) of Adams and RecurDyn

Full size image

6 Conclusions

This paper clarifies and compares the standard friction models of Adams, RecurDyn, and Simpack. First, the standard regularizations are considered. These regularize the ambiguous friction curve over velocity into a continuous curve. This has the disadvantage that no long-term stiction is possible since a relative velocity must be present to generate a friction force. Therefore, second, the focus is on the specific stick-slip models using two different approaches. Adams and RecurDyn enhance the standard regularization by a regularization over the displacement. Simpack models sticking by a spring-damper element and switches to dynamic Coulomb friction in sliding cases. Both approaches allow long-term stiction.

Adams and RecurDyn show a strongly coupled influence of the model parameters. Moreover, the simple test model indicates a difference in the implementation between the respective software. Notably, the model simulated using Adams drifts during high-frequency excitation with a magnitude, almost equal to the static friction force, whereas RecurDyn and Simpack do not show any drift in any of the simulations.

The comparison with the festoon model shows no significant differences in the results. However, a closer look reveals specific differences. In both approaches, a function \(F_{\mathrm{R}}(x,v) \), which also takes displacement into account, replaces the friction characteristics \(F_{\mathrm{R}}(v) \), in the stiction region. As a consequence, the ideal friction characteristics is not fulfilled in this region. Simpack exhibits undesired overshoots in friction force during the transition from stick to slip and neglects the Stribeck effect.

This paper does not include a performance analysis of the friction models due to the significant differences between the model parameters and the unknown influence of the different software, solvers, and implementations.

From a practical point of view, the main studies were carried out using the default parameters of the MBS packages. The default parameters have only been modified to highlight the drift behavior of RecurDyn and Adams.

At first glance, the models generated the expected results and the stick-slip models should be suitable for many practical use cases. However, upon closer inspection, differences became apparent and strange effects were observed. Therefore, further studies are necessary to determine the sensitivity or robustness of the friction model parameters to the simulation results.