1 Introduction

Bearings are key components in many mechanical systems, in particular rotary machinery, making the relative motion between stationary and moving parts possible, allowing an efficient and smooth operation [1]. Accordingly, they also constitute one of the most recurrent causes of failure in rotating machinery. Some reports detail that nearly half of the failures related to motors are due to bearing malfunctions [2]. These elements are responsible for 40% to 50% of all breakdowns in rotating machinery [3], this percentage increases to 70% in gearbox issues within wind turbine systems [4]. A failure of a bearing often involves the full shutdown of the machine to inspect the system in order to find the failure’s sources and, eventually, to replace the element. These maintenance procedures alter the normal operation of those mechanical systems and result in significant costs in terms of both downtime and resources. Most of these fault-related breakdowns can be prevented if the local defects that trigger them are detected at the earliest stage possible [5].

The development and utilisation of computational modelling techniques for rolling contact bearings within the context of predictive maintenance approaches have demonstrated their potential over the last few decades [6–18]. Simulations of these machine components have become a powerful tool for understanding their dynamic behaviour under different operating conditions. To that end, the definition of reliable and efficient numerical models is of utmost importance; it involves the detailed description of the bodies’ geometry and their material properties, the interactions established between the elements and the operating environment [19–22]. Besides this, the dynamic modelling of rolling bearings aims at two main goals: (i) the improvement of the design and the performance of these components; and (ii) the simulation of the irregular behaviours associated with defective elements through their virtual twins in order to identify potential issues and improve their reliability [23]. The computational modelling of rolling element bearings for predictive maintenance purposes has experienced significant developments within the context of Industry 4.0 [24], driven by the advancements in information and communication technologies. Nowadays, in this data-driven environment, heavily influenced by the use of smart sensors and devices, real-time data can be collected and fed into the computational models, and their smart exploitation provides multiple advantages in terms of productivity, efficiency and competitiveness. Special attention is paid to those methodologies that reduce shutdown times and cut costs down, namely condition monitoring [25], digital twins [26], artificial intelligence [27] or virtual sensors [28].

Multibody dynamics is a methodology that stands out for its versatility, thus being suitable for a wide range of applications [29–34], and can be an interesting and powerful tool to implement in these new techniques. Within its framework, contact/impact events are usually modelled using two alternative approaches: non-smooth methods (also called impulse-momentum-based approaches) and contact-force-based models [35, 36]. The former considers contact interactions as almost instantaneous events [37], which makes it possible to achieve simple, computationally efficient models. However, some issues arise when dealing with certain scenarios such as permanent or intermittent contacts [36, 38, 39]. On the other hand, contact-force-based models, also known as compliant models, characterise contact events through forces defined as continuous functions of the relative penetration (and its temporal derivative) of the contacting bodies [40, 41]. Thus, the contact/impact process is not an instantaneous event and can be fully monitored. The contact regions of each body are modelled as a set of spring-damper elements scattered over their surfaces. Still, they present some drawbacks, mainly the proper choice of the parameters associated with the definitions of the forces [42]. In these systems, the right detection of the initial instant of contact is critical to obtaining accurate results [34, 43].

The main purpose of this work is to propose and develop several geometrical-based methodologies that allow the simulation of the behaviour of these critical components successfully with a balance between computational efficiency and result consistency. The presented approaches stand out for their straightforward definition and the application of general-use contact detection algorithms. The possibility of including defects on different bearing elements in future research has been considered during the development. Among the presented solutions, various choices are recommended according to the complexity of the system in which the bearings are included. A special focus has been given to the cage modelling and its interaction with the rolling elements. In this study, the assumption of a 2D environment will be considered, and its advantages and shortcomings will be subsequently discussed. However, this premise does not affect the consistency of the results and contributes to the models’ efficiency. The equations of motion have been implemented in an in-house-developed MATLAB code conceived to perform and solve forward dynamic analysis, which allows multiple customisation choices as well as good control of the integration process and provides accurate results at a reasonable computational cost. The computational models of rolling element bearings proposed in the present work are a solid base for future research on this topic since they can be further enhanced with the inclusion of different types of defects, either by changing the parts’ geometries or their contact properties.

The rest of the paper is structured as follows. Section 2 makes an introduction to the fundamental aspects of the bearings’ operation, particularly ball bearings. In Sect. 3, the planar multibody system formulation utilised in the context of this work is revised. Section 4 provides the details of the contact modelling methodology for different types of interaction, both in terms of contact detection and force estimation. Section 5 includes the description of several approaches, with various levels of complexity, to model a deep groove ball bearing and their corresponding dynamics responses. In Sect. 6, a critical discussion of the results is developed, comparing the computational efficiency of the models. Finally, in Sect. 7, the main conclusions are drawn.

2 Bearings: overview

A bearing is usually defined as a mechanical element that allows a relative, rotary motion between two parts, namely the shaft and the housing [44]. It must serve three functions: (i) to allow a free rotation of the shaft with minimum friction, (ii) to support and keep it in its right position and (iii) to withstand the acting loads on the shaft, transmitting them to the foundation of the machine they are part of.

As a result of their variety, bearings can be classified according to different criteria, namely the geometry of their surfaces, the direction of the supporting load or the principle of operation. Among these, the main criterion for bearings’ classification is based on their working principle and holds two distinct groups: contact bearings and non-contact bearings, which can subsequently be divided into smaller types [45]. The first includes those cases where mechanical contact among their elements happens in the form of sliding, rolling or flexing, hence identifying three subtypes (sliding contact, rolling contact or flexure bearings, respectively), whereas the second group encompasses those bearings in which their elements do not hold direct contact among the elements and the supporting load is transmitted through an intermediate fluid or by magnetic forces, which are not in the scope of this work.

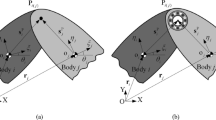
This work will focus on the modelling of bearings based on the rolling contact mechanism, where rolling elements with varied geometries are introduced between two rings or washers, as shown in Fig. 1(a). These elements serve two functions: (i) to transmit the load from one element of the bearing (shaft or housing) to the other; and (ii) to transform the sliding motion endured in the plain bearings into rolling motion, so the friction resistance is reduced [46]. A cage, also known as separator, retainer or crown, is included, so the rolling elements are equally distributed, keeping them separated and allowing a uniform distribution of the loads. These rolling elements can have different geometries depending on the application of the bearing, as represented in Fig. 2, being mainly divided into ball and roller bearings. Ball bearings, which contain spherical rolling elements, are the most used ones. They can be divided into three classes according to the nature of the dominant load that must withstand, namely deep groove (radial loads), thrust (axial load) and angular contact bearings (both types). Although deep groove ones can experience axial loads, their load capacity is lower when compared with angular contact bearings [44]. Ball bearings also stand out for generating low noise during their operation, therefore making them appropriate for high-speed applications [44, 47–49]. A typical issue of both deep groove and thrust bearings is the lack of self-alignment, which can greatly affect their performance in certain applications. In order to overcome this problem, self-aligning ball bearings are used, which consist of two rows of rolling elements with a common spherical outer race. They are suitable for those applications where slight misalignments can come up during the assembly or because of a deflection of the shaft. Compared to deep groove ball bearings, cylindrical roller ones allow a higher radial load capacity because of the greater contact area, which results in lower friction losses under high-speed requirements. However, they are not suitable to withstand thrust loads nor tolerate misalignments. This drawback is overcome by using taper roller bearings, in which both raceways and rollers have a conical geometry so the projections of their axes meet at a common point. They are able to support both types of loads, normally at low and moderated velocities [50, 51]. Needle roller bearings are a variation of cylindrical roller ones, with a length/diameter ratio greater than four [44]. They stand out for their load capacity/size ratio, although the existing limitations during their manufacturing limit their accuracy, leading to higher friction. Spherical roller bearings are also included in this second group with a similar working principle to that of self-aligning ball bearings, which allows them to compensate for misalignment and shock loads. They can withstand higher loads than their ball-based counterparts.

Fig. 1
figure 1

Description of the geometry of a rolling contact bearing

Full size image
Fig. 2
figure 2

Representation of rolling contact bearing models

Full size image

In what concerns the numerical modelling of rolling elements bearing, there has been an extensive amount of work during the last decades, in which most of the modelling approaches proposed by different authors can be classified into two groups, namely static/quasi-static and dynamic models [46]. The first type of solution makes use of static equilibrium equations to provide the initial conditions for the differential equations of motion that define the dynamic behaviour of bearings. Stribeck developed what is considered the first proper works on rolling contact bearings based on the static approach [52, 53]. In [52], he applied the Hertzian equations to the study of deformation, contact dimension and contact pressure in the ball-bearing geometry. He defined a model with zero clearance and subjected to simple radial loads. Results are applicable to all types of concentrated Hertzian contacts. In [53], he carried out the first study on the values of friction coefficient for different lubrication regimes, comparing different bearing geometries. However, the main figure of this group is Jones, who proposed the first computer code to perform analyses on this type of bearings [54]. In the same work, he proposed, based on Hertzian contact theory, a quasi-static model considering centrifugal force and gyroscopic effect. Jones also proposed the so-called “race control hypothesis”, which can be summarised in two points [54, 55]: (i) a ball rolls without spinning on one race, which is defined as the controlling race, while rolls and spins on the other race; and (ii) the gyroscopic moment on a certain ball is only counteracted by the friction force associated with the ball-controlling-race contact without slippage, whereas the other raceway-ball contact has no contribution to the resistant gyroscopic moment. Thus, there is no spin motion between the rolling element and the race that provides the larger friction torque, therefore defining uniquely the angular velocity of the rolling elements. In parallel to Jones’ work, Harris developed dynamic models and discussed different issues regarding geometry, elasticity, statics, dynamics and heat transfer of rolling bearings. He took Jones’ model one step forward, applying it to a variety of loading conditions and bearings, resulting in the generally known Jones–Harris Method (JHM), which is widely used in the determination of bearing deflection [56]. Static/quasi-static solutions provide fairly good results in terms of load distribution in the rolling elements, bearing stiffness and fatigue life [57–59].

Until the 1970s, most of the analytical simulations of rolling-element bearings were based on quasi-static models. However, the development of computing technology allowed the proposal of dynamic models, especially suited for high-speed applications. In this alternative approach, differential equations of motion for each bearing component, based on Newton’s second law of motion, are used instead. One of the most prolific authors regarding this type of solution is Gupta, who is responsible for some of the greatest breakthroughs in this research field. He proposed, in a four-part work [7–10], a generalised dynamic model, for both cylindrical roller and ball bearings, that considered all relevant interactions between the different elements. Gupta’s work set a milestone in the dynamic modelling of rolling contact bearings, replacing the race control hypothesis with the dynamic equilibrium of each element of the system, thus providing a time-domain transient simulation of the response of all of them. Other authors distinguished by their contributions based on dynamic approaches are Walters [6], Meeks [11], Tiwari [20], Harsha [60], and Xu [16–18], just to name a few [61–63]. The models proposed in this work will be focused on dynamic simulations of deep groove ball bearings, although most of the conclusions obtained could be extended to other types of rolling elements such as cylindrical roller bearings.

3 Multibody systems formulation

The formulation adopted in this work to construct the equations of motion for constrained multibody systems follows closely the work developed by Nikravesh for planar systems, who used absolute or generalised Cartesian coordinates to describe the configuration of any multibody system [64, 65]. As the name implies, a general multibody system is constituted by several rigid and/or flexible bodies that can describe large translations and rotations. If only rigid bodies are considered, the position of the mass centre of a body \(i\) is defined as

$$ \mathbf{r}_{i} = \left \{ \textstyle\begin{array}{c@{\quad}c} x_{i} & y_{i} \end{array}\displaystyle \right \}^{\mathrm{T}} $$
(3.1)

where \(x_{i}\) and \(y_{i}\) are the Cartesian coordinates of the centre of mass of body \(i\) with respect to the global reference system. Furthermore, the location of any point \(P\) of body \(i\) can be determined following its position in relation to the local body reference frame as follows:

$$ \mathbf{r}_{i}^{P} = \mathbf{r}_{i} + \mathbf{A}_{i}\mathbf{s}_{i}^{\prime P} $$
(3.2)

in which vector \(\mathbf{s}_{i}^{\prime P}\) defines the location of point \(P\) with respect to body \(i\) mass centre in local-system coordinates, being this vector constant in rigid bodies. \(\mathbf{A}_{i}\) represents the transformation matrix of body \(i\), which describes the orientation of the local coordinate frame with respect to the global one. This transformation matrix is a function of angle \(\phi _{i}\), which defines the rotation state of body \(i\) in relation to the global coordinate system. Thus, this angle, along with the two Cartesian coordinates that locate the position of the mass centre, form the coordinate vector of body \(i\), which describes uniquely its position and orientation

$$ \mathbf{q}_{i} = \left \{ \textstyle\begin{array}{c@{\quad}c} \mathbf{r}_{i} & \phi _{i} \end{array}\displaystyle \right \}^{\mathrm{T}} = \left \{ \textstyle\begin{array}{c@{\quad}c@{\quad}c} x_{i} & y_{i} & \phi _{i} \end{array}\displaystyle \right \}^{\mathrm{T}} $$
(3.3)

The motion of the bodies is typically constrained by making use of mechanical joints between them. The function of these mechanical components can be represented by kinematic holonomic constraints, which are defined through a set of algebraic equations in the following form:

$$ \boldsymbol{\Phi} \equiv \boldsymbol{\Phi} (\mathbf{q}) = \mathbf{0} $$
(3.4)

The first derivative of Equation (3.4) with respect to time yields the velocity constraint equations, whereas the second one leads to the acceleration constraint equations

$$ \ddot{\boldsymbol{\Phi}} \equiv \mathbf{D}\ddot{\mathbf{q}} + \dot{\mathbf{D}}\dot{\mathbf{q}} = \mathbf{0} $$
(3.5)

where \(\dot{\mathbf{q}}\) and \(\ddot{\mathbf{q}}\) denote the generalised velocities and acceleration vectors, respectively, and \(\mathbf{D}\) is the Jacobian matrix of dimension \(k\cdot m\), in which \(k\) represents the total number of constraints of the system and \(m\) defines the number of coordinates (i.e. three per body). This set of equations is typically rewritten as

$$ \mathbf{D}\ddot{\mathbf{q}} = \boldsymbol{\upgamma} $$
(3.6)

in which term \(\boldsymbol{\upgamma}\) is usually defined as the right-hand side of the acceleration constraint equations and includes those terms of Equation (3.5) that are explicitly dependent on positions, velocities and time.

On the other hand, equations of motion of a planar constrained multibody system using Newton–Euler formulation are defined as [66]

$$ \mathbf{M}\ddot{\mathbf{q}} + \mathbf{D}^{\mathrm{T}}\boldsymbol{\lambda} = \mathbf{g} $$
(3.7)

where \(\mathbf{M}\) is the system mass matrix, \(\mathbf{g}\) represents the generalised force vector that contains all external forces and moments applied to the system, such as those associated with gravitational field and contact–impact events [67], and the term \(\mathbf{D}^{\mathrm{T}}\boldsymbol{\lambda}\) denotes the reaction forces and moments that act on the bodies due to the kinematic joints, based on the Lagrange multipliers. Gathering Equations (3.6) and (3.7), a system of differential-algebraic equations (DAE) can be obtained in matrix form as

$$ \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{M} & \mathbf{D}^{\mathrm{T}} \\ \mathbf{D} & \mathbf{0} \end{array}\displaystyle \right ]\left \{ \textstyle\begin{array}{c} \ddot{\mathbf{q}} \\ \boldsymbol{\lambda} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \mathbf{g} \\ \boldsymbol{\upgamma} \end{array}\displaystyle \right \} $$
(3.8)

This system of equations governs the dynamics of a constrained multibody system and, knowing the initial conditions, it can be solved for \(\ddot{\mathbf{q}}\) and \(\boldsymbol{\lambda}\) to obtain the dynamic evolution of the system. In each integration time step, the accelerations vector \(\ddot{\mathbf{q}}\), together with the velocities vector \(\dot{\mathbf{q}}\), is integrated to obtain the velocities and positions for the following time step. Figure 3 presents the flowchart that shows the algorithm of the standard solution of the equations of motion. This algorithm is repeated until the final analysis time is reached.

Fig. 3
figure 3

Flowchart of the computational procedure to perform dynamic analysis of multibody systems based on the standard Lagrange multipliers method

Full size image

However, the system described in Equation (3.8), known as the standard Lagrange multipliers method, does not consider explicitly the position and velocity constraint equations. This leads to a violation of the constraint equations when dealing with moderately long simulations, due to the error accumulated over the integration process and/or to inaccurate initial conditions. In order to avoid error propagation and eliminate any slip in the position and velocity constraint equations throughout the analysis or, at least, keep such errors within a defined margin, different methodologies have been proposed. In this work, the Baumgarte stabilisation method has been considered to deal with the violation of the constraint equations [68].

Baumgarte proposed an alternative expression for Equation (3.6), adding two additional control terms [68], which results in a new set of equations of motion written as

$$ \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{M} & \mathbf{D}^{\mathrm{T}} \\ \mathbf{D} & \mathbf{0} \end{array}\displaystyle \right ]\left \{ \textstyle\begin{array}{c} \ddot{\mathbf{q}} \\ \boldsymbol{\lambda} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \mathbf{g} \\ \boldsymbol{\gamma} - 2\alpha \dot{\boldsymbol{\Phi}} - \beta ^{2}\boldsymbol{\Phi} \end{array}\displaystyle \right \} $$
(3.9)

where \(\alpha \) and \(\beta \) are the control parameters that quantify the weight of velocity and position constraint violations, respectively, on the control of the infringement of the acceleration constraints. If both parameters \(\alpha \) and \(\beta \) are chosen as positive constants, the stability of the system is assured. It has been demonstrated that, for a fixed time step, the values \(\alpha = \beta = 5\) lead to a convergence of the integration process without oscillations [69]. These were the values chosen for this work.

4 Contact force modelling

A contact/impact event between two bodies can be characterised using two different approaches: the non-smooth method and smooth formulations [36]. Three elements distinguish these two methods: (i) contact point location; (ii) the equations that define the forces; and (iii) the use of the value of indentation [35, 70]. Non-smooth models consider the contact event as an instantaneous process in which the interaction between the bodies, which are assumed to only withstand deformations very small compared to their geometry, is characterised by an impulse. In contrast to this approach, there are smooth formulations, in which the interactions between the bodies are implemented through contact forces, which are defined as continuous functions of the relative indentation of the contacting bodies, which are assumed to be deformable. These forces are responsible for preventing penetration between the bodies from occurring, making the definition of unilateral constraints unnecessary. Moreover, smooth formulations have proved to deal with multiple-simultaneous impact scenarios successfully [34], making them suitable for systems such as the rolling element bearings described in this work.

In this paper, the contact events between the different elements of the bearing will be modelled using the second approach. Having that in mind, two planar geometrical contact detection algorithms are described in this section, namely circle–plane and circle–circle [71].

4.1 Contact detection algorithms

To define the contact between circular and planar surfaces, consider the system composed of a circle \(i\) with its centre on point \(C\) and with radius \(R\) and an infinite plane defined by its point \(P\), and its normal unit vector \(\mathbf{n}_{j}\), as schematically represented in Fig. 4. Thus, any point \(\mathbf{r}_{j}\) belonging to the plane can be given by the following implicit function:

$$ \mathbf{n}_{j}^{\mathrm{T}}\left ( \mathbf{r}_{j} - \mathbf{r}_{j}^{P} \right ) = 0 $$
(4.1)

The distance from the centre of the circle to the plane, \(d\)sp, represented in Fig. 4, is computed as

$$ d_{\mathrm{sp}} = \mathbf{n}_{j}^{\mathrm{T}}\left ( \mathbf{r}_{i}^{C} - \mathbf{r}_{j}^{P} \right ) $$
(4.2)

which is given in vector form as

$$ \mathbf{d}_{\mathrm{sp}} = d_{\mathrm{sp}}\mathbf{n}_{j} $$
(4.3)

Then, the projection of the mass centre of the circle on the plane defines the potential contact point \(Q\) in the plane, whose coordinates can be determined as follows:

$$ \mathbf{r}_{j}^{Q} = \mathbf{r}_{i}^{C} - \mathbf{d}_{\mathrm{sp}} $$
(4.4)

In turn, the coordinates of the potential contact point \(Q \) on the circle are estimated as follows:

$$ \mathbf{r}_{i}^{Q} = \mathbf{r}_{i}^{C} - R_{i}\mathbf{n}_{j} $$
(4.5)
Fig. 4
figure 4

Contact detection parameters for a circle–plane interaction

Full size image

Hence, the value of the indentation between both surfaces \(\delta \) is calculated using the following expression:

$$ \delta = R_{i} - d_{\mathrm{sp}} $$
(4.6)

in which positive values indicate that there is contact happening between the circle and the plane and, therefore, the relative velocities on the contact must be determined, and the normal and tangential contact force values must be estimated. The initial instant of contact takes place when \(\delta = 0\). It must be noted that this contact case does not require to be applied to a full circle and an infinite plane, it might be employed to model the contact between a partially round surface and a finite planar face.

On the other hand, to establish the contact between two circular surfaces, consider the system presented in Fig. 5, in which two circles \(i\) and \(j\) with centres in \(C_{i}\) and \(C_{j}\) and radii \(R_{i}\) and \(R_{j}\), respectively, come into contact. In this case, two different interactions can take place according to the arrangement of the bodies, namely an external contact (Fig. 5(a)) or an internal one (Fig. 5(b)). The contact points can be determined as

$$\begin{aligned} & \mathbf{r}_{i}^{Q} = \mathbf{r}_{i}^{C} + R_{i}\mathbf{n} \end{aligned}$$
(4.7)
$$\begin{aligned} & \mathbf{r}_{j}^{Q} = \mathbf{r}_{j}^{C} - R_{j}\mathbf{n} \end{aligned}$$
(4.8)

where \(\mathbf{n}\) is the unit normal vector to the contact plane between the surfaces

$$ \mathbf{n} = \frac{\mathbf{d}}{d} $$
(4.9)

where \(d \) and \(\mathbf{d}\) denote the magnitude and vector distance between the centres of the two circles, respectively. The latter can be calculated as

$$ \mathbf{d} = \mathbf{r}_{j}^{C} - \mathbf{r}_{i}^{C} $$
(4.10)
Fig. 5
figure 5

Contact detection parameters for a circle–circle interaction: (a) External contact; (b) Internal contact

Full size image

Finally, the relative penetration between the two bodies can be estimated for both cases as follows:

$$ \delta = \left \{ \textstyle\begin{array}{c@{\quad}c} R_{i} + R_{j} - d & \mathrm{external} \quad \mathrm{contact} \\ R_{i} - R_{j} + d & \mathrm{internal} \quad \mathrm{contact} \end{array}\displaystyle \right . $$
(4.11)

For both interactions, the contact will only occur when the penetration reaches positive values, the start of the interaction being when \(\delta = 0\).

4.2 Contact force models

For each contact interaction established, an appropriate set of both normal and friction forces must be defined. Different aspects such as the geometries and the material properties of the bodies or the characteristics of the contact interaction itself must be taken into account. The reader interested in the quantification of the contact forces can find useful references in [35].

Regarding the normal contact force, a certain amount of energy dissipation was considered along with the Hertzian contact to stabilise the dynamic response of the system. Thus, the total contact force is computed as the sum of the Hertzian term and a dissipative one:

$$\begin{aligned} & f_{\mathrm{n}} = f_{\mathrm{n},\mathrm{hertz}} + f_{\mathrm{n},\mathrm{dis}} \end{aligned}$$
(4.12)
$$\begin{aligned} & f_{\mathrm{n},\mathrm{hertz}} = K\delta ^{n} \end{aligned}$$
(4.13)
$$\begin{aligned} & f_{\mathrm{n},\mathrm{dis}} = \chi \delta ^{n}\dot{\delta} \end{aligned}$$
(4.14)

where \(K\) is the combined stiffness of the contact pair, \(\dot{\delta} \) denotes the relative penetration velocity, \(n\) is the exponent that quantifies the degree of nonlinearity of the force–indentation relation and \(\chi \) is the hysteresis damping factor. Most of the models available in the literature, which are, to some degree, based on the work by Hunt and Crossley [72], include explicitly the normal indentation velocity at the start of the contact, denoted as \(\dot{\delta}^{(-)}\), in the hysteresis term [36]

$$ \chi = a\frac{K}{\dot{\delta}^{( - )}} $$
(4.15)

where \(a\) is usually a function of the coefficient of restitution. This value of the initial velocity at the start of the contact process depends heavily on the accurate detection of that moment [43], which can be a highly time-consuming process, especially in this work, in which multiple contact events take place simultaneously and a variable-step integration algorithm has been used. For the aforementioned reasons, the modified Kelvin–Voigt approach used by Ambrósio in [73] was chosen to characterise all normal interactions, as has proven effective in similar demanding scenarios. Thus, the normal contact force can be evaluated as

$$ f_{\mathrm{n}} = \left \{ \textstyle\begin{array}{c} K\delta ^{n}c_{e} \hfill \\ K\delta ^{n}[c_{e} + (1 - c_{e})(3r^{2} - 2r^{3})] \hfill \\ K\delta ^{n} \hfill \end{array}\displaystyle \right . \textstyle\begin{array}{c} \dot{\delta} \le 0 \hfill \\ 0 < \dot{\delta} < v_{0} \hfill \\ \dot{\delta} \ge v_{0} \hfill \end{array} $$
(4.16)

where \(c_{e}\) is the coefficient of restitution of the contact event and \(v_{0}\) is the penetration velocity tolerance, and \(r\) represents the ratio \({\dot{\delta}} / {v_{0}}\). The substitution of the initial normal velocity \(\dot{\delta}^{(-)}\) for a defined value allows a more efficient contact modelling, which is critical in complex systems such as those described in this work.

The value of the contact stiffness \(K\) can be obtained through different methods, namely numerically [74], from experimental tests [75], or theoretically as a function of the geometries of the contacting bodies. For a contact between two spheres \(i\) and \(j\) with radii \(R_{i}\) and \(R_{j}\), respectively [76]

$$ K = \frac{4}{3\left ( \sigma _{i} + \sigma _{j} \right )\sqrt{\kappa _{i} + \kappa _{j}}} \qquad \kappa _{l} = \frac{1}{R_{l}} \quad \left ( l = i,j \right ) $$
(4.17)

where \(\kappa \) is the local surface curvature of the sphere, i.e. the inverse of its radius. \(R_{i}\) and \(R_{j}\) have the same +/- sign if the contact is external (convex surfaces) and the opposite if it is an internal one. The sphere with the largest radius is a concave surface, thus it has a negative radius value, whereas the other sphere is convex and its radius is positive. \(\sigma _{i}\) and \(\sigma _{j}\) are material parameters given by

$$ \sigma _{l} = \frac{1 - v_{l}^{2}}{E_{l}} \qquad \left ( l = i,j \right ) $$
(4.18)

where \(v_{l}\) and \(E_{l}\) are Poisson’s ratio and Young’s modulus of each sphere, showing the influence of the material properties in the contact event.

However, as the contact interactions implemented in the models described in the following section are far more complex than a sphere–sphere contact, a more detailed analysis of the Hertzian contact approach must be made, specifically for the ball–race contact. Following the geometries described in Fig. 6, the curvature in the lateral and longitudinal directions in both contacting bodies is considered constant, so the distance between the undeformed surfaces in the vicinity of the contact can be approximated using a quadratic function

$$ z(x,y) = Ax^{2} + By^{2} $$
(4.19)

where \(A\) and \(B\) represent the average curvatures of both surfaces in each principal direction, and they can be computed as follows:

$$\begin{aligned} & A = \frac{\kappa _{i,\mathrm{s}} + \kappa _{j,\mathrm{s}}}{2} \end{aligned}$$
(4.20)
$$\begin{aligned} & B = \frac{\kappa _{i,\mathrm{u}} + \kappa _{j,\mathrm{u}}}{2} \end{aligned}$$
(4.21)

where \(\kappa \) represents the local surface curvature of the body in a certain direction (\(\mathrm{s}\) or \(\mathrm{u}\), according to Fig. 6(a)), defined as the inverse of the radius in that direction:

$$\begin{gathered} \kappa _{l,m} = \frac{1}{R_{l,m}}\quad (l = i,j;m = \mathrm{s},\mathrm{u}) \end{gathered}$$
(4.22)
Fig. 6
figure 6

Description of the curvature radii for the ball–race interaction

Full size image

The generalised local stiffness is then computed as

$$ K = \frac{4C_{\delta} \pi}{3(\sigma _{i} + \sigma _{j})\sqrt{A + B}} $$
(4.23)

where the parameter \(C_{\delta}\) is a function of the ratio \(A\)/\(B\), which is tabulated in the literature [76, 77]. In what concerns bearing modelling following Hertzian theory, the common approach was proposed by Harris [78], which considered both races simultaneously in the computation of the contact force between the rolling elements and them. Instead, in the present work, this interaction is developed independently for each race. Furthermore, the interaction between the cage and the rolling elements is thoroughly discussed, and several modelling approaches are tested.

With respect to the friction forces, Coulomb’s law was applied only to the ball–race contacts, using the hyperbolic tangent approximation defined in [79]

$$ f_{\mathrm{f}} = \mu _{\mathrm{k}}\tanh (kv_{\mathrm{T}})f_{\mathrm{n}} $$
(4.24)

where \(\mu _{\mathrm{k}}\) denotes the kinetic coefficient of friction, \(k\) is a value that defines the slope of the curve for nearly null values of velocity and \(v_{\mathrm{T}}\) is the module of the relative tangential velocity. There are other strategies to deal with friction phenomena available in the literature. For example, other models make use of elastohydrodynamic lubrication (EHL) theory to model these interactions [14, 80–82]. However, this is a highly time-consuming approach that can be neglected in this early stage of design and setting [48, 62, 83, 84] by using Coulomb’s approach instead [7, 9, 48, 49].

5 Bearing modelling solutions

In this section, different modelling approaches for deep groove ball bearings are presented and described in the framework of planar multibody systems, recurring to the methodologies described in the previous sections. The primal assumption of a planar environment involves the impossibility of implementing axial loads and the neglection of phenomena between the different elements of the bearing system such as tilting and skewing [85], which are described in Fig. 7, as well as the gyroscopic effects of the rolling elements. However, a planar model can provide conclusions of great value in those scenarios in which no axial motion takes place. Moreover, due to the assumptions considered here, these modelling solutions could be extended to other types of rolling element bearings, such as cylindrical or needle rollers.

Fig. 7
figure 7

Tilting angle \(\eta \) and skewing angle \(\theta \) between the roller and the races in a cylindrical roller bearing

Full size image

Among the several modelling scenarios, the main criterion has been established to divide the proposed designs, which consists of the way in which the cage is modelled, that is, whether the interactions between the cage and the balls are treated with the contact methodologies presented in Sect. 4.1 or not. Thus, on the one hand, those approaches that do not make use of contact interactions regarding the cage are denoted as “non-contact” models and presented in Sect. 5.2, on the other hand, the solutions that do include contact events are named “contact” models and given in Sect. 5.3.

The dimensions of the bearing and its components are based on a real model from which the pitch diameter and the ball diameter are known. The main dimensional parameters are represented in Fig. 8. The value of the clearance has been defined according to those used in similar works [16]. Moreover, the values of the race diameters have been obtained using the following expressions:

$$\begin{aligned} & D_{\mathrm{o}} = D_{\mathrm{m}} + D_{\mathrm{b}} + \frac{1}{2}P_{\mathrm{d}} \end{aligned}$$
(5.1)
$$\begin{aligned} & D_{\mathrm{i}} = D_{\mathrm{m}} - D_{\mathrm{b}} - \frac{1}{2}P_{\mathrm{d}} \end{aligned}$$
(5.2)
Fig. 8
figure 8

Geometrical description of the simulated deep groove ball bearing: (a) Full model; (b) Detail view of the pocket

Full size image

The geometric and material properties for the deep groove ball bearing used in the model are provided in Table 1, whereas the parameters implemented in the normal and friction contact forces and the spring elements are resumed in Table 2. The same value of the coefficient of restitution and friction coefficient has been applied to all the contact events to ensure a suitable comparison of results among the different modelling approaches.

Table 1 Geometric and material properties of the bearing elements
Full size table
Table 2 Force parameters implemented in the models described in this work
Full size table

5.1 Initial conditions

Different simplifications were assumed during the modelling process, most of them for the sake of computational efficiency:

  • The outer race was assumed to be a fixed body since it is connected to the housing.

  • The inner ring is coupled to a shaft; therefore, its inertia considers the shaft’s contribution.

  • No interactions between the cage and the races were considered in this early stage of development.

  • No lubricant effects are included. Friction is implemented using Coulomb’s law.

  • The effects of gravity were implemented in the negative direction of \(y\)-axis.

  • A constant radial working load of 100 N was included in the inner race, in the negative direction of the vertical axis.

The motion was incorporated into the system by giving the inner ring, which is coupled to a shaft, an initial angular velocity of 500 rpm. Some studies have proposed different kinematic relationships to ensure that the rotational velocities of the cage and the balls are equal, thereby preventing contact between them [16, 20, 49, 86]. To smooth the problem in the first steps of the integration process and to avoid a stiff start that could lead to a dramatic increase in computing time, a set of relations among the different elements was defined. The first assumption considers a pure rolling condition; thus, the relative velocities at the contact points between the balls and the outer race were set to be zero at the initial instant, as shown in Fig. 9.

Fig. 9
figure 9

Schematic representation of the kinematic conditions defined for the deep groove ball bearing model

Full size image

Based on [49], the linear velocity of the ball at its mass centre is given by the average velocity at the contact points with the inner and the outer races

$$ v_{\mathrm{b}} = \frac{v_{\mathrm{b}}^{A} + v_{\mathrm{b}}^{C}}{2} = \frac{v_{\mathrm{ir}}^{A} + 0}{2} = \frac{v_{\mathrm{ir}}^{A}}{2} $$
(5.3)

The linear velocity at the contact point between the inner race and the ball is defined as

$$ v_{\mathrm{ir}}^{A} = \omega _{\mathrm{ir}}R_{\mathrm{ir}} $$
(5.4)

where \(R\)ir denotes the radius of the inner ring. The linear velocity of the cage at the centre of the ball can be calculated as follows:

$$\begin{gathered} v_{\mathrm{c}}^{B} = v_{\mathrm{b}}^{B} = \omega _{\mathrm{c}}\left ( \frac{R_{\text{or}} + R_{\mathrm{ir}}}{2} \right ) \end{gathered}$$
(5.5)

where \(R\)or is the radius of the outer ring. Considering Equations (5.3), (5.4) and (5.5), it can be concluded that

$$ \omega _{\mathrm{c}} = \omega _{\mathrm{ir}}\left ( \frac{R_{\mathrm{ir}}}{R_{\text{or}} + R_{\mathrm{ir}}} \right ) $$
(5.6)

A similar approach was applied to the ball, considering that its linear velocity at the contact point with the inner race can be computed as

$$ v_{\mathrm{ir}}^{A} = v_{\mathrm{b}} + \omega _{\mathrm{b}}R_{\mathrm{b}} $$
(5.7)

where \(R_{\mathrm{b}}\) is the radius of the ball. Manipulating Equation (5.7) and considering the expressions defined above,

$$ \omega _{\mathrm{b}} = - \frac{v_{\mathrm{ir}}^{A} - v_{\mathrm{b}}}{R_{\mathrm{b}}} = - \frac{1}{2}\omega _{\mathrm{ir}}\frac{R_{\mathrm{ir}}}{R_{\mathrm{b}}} $$
(5.8)

In Equation (5.8), the appropriate sign has been included to indicate that the ball rotates in the opposite sense to that of the inner ring. The values defined by these kinematic relations were implemented as initial conditions, considering the suitable senses of the vectors to be physically consistent.

All the simulations performed in the scope of this work have been carried out with a variable-step-size integration algorithm, namely the ODE113 available in MATLAB. This solver integrates the velocities and accelerations of the system using a variable order method. The motion of the bearing is simulated for 1 s, which allows the balls to complete around three full orbits around the inner ring.

5.2 “Non-contact cage” models

The first group comprises those approaches that do not use smooth contact formulations to define the interactions between the cage and the balls. In these designs, the primary function of the cage is to keep the rolling elements equally spaced around the inner race, which is done through the utilisation of spring elements or rigid links. These solutions, denoted here as non-contact cage models, do not consider pocket clearance and are preferred when the bearing is part of a more complex system, and no analysis of the bearing’s dynamic behaviour is intended. When using any model of this group, defect characterisation is limited to the races and the rolling elements, since only their geometry and resulting contact interaction are fairly modelled.

The interaction between the balls and the races was implemented through two independent circle–circle interactions, as described in the previous section. An external contact was considered to model the interactions of the balls with the inner ring, and an internal contact represents their interactions with the outer ring. Regarding the cage’s modelling, the first and simplest choice, shown in Fig. 10(a) and referred to as NC1, consists of a rigid octagon whose vertices are connected to the centres of the rolling elements through revolute joints. This is the most straightforward solution and the most efficient in terms of computational cost, although it restricts the relative motion between the rolling elements. Figure 11 illustrates the evolution of the ratio of the angular velocities of the cage and the inner ring during the analysis for all NC-models, which remains approximately constant at about 0.382 throughout the simulation. The theoretical value has been also defined, which according to Equation (5.6) is 0.3813. The obtained values, which are similar to those obtained in previous works from different authors [87, 88], may vary slightly depending on the bearing type and friction coefficient considered, as well as on the result of undesirable phenomena such as skidding [63, 82]. For instance, Deng and his co-authors obtained in [88] a value of about 0.444 for an angular contact ball bearing. Nonetheless, the obtained results confirm the validity of the assumed initial conditions and the model’s ability to quickly reach a steady state. In turn, Fig. 12 displays the values of the magnitudes of the contact force between one of the balls and the inner ring during its second full orbit for all the non-contact cage designs. The values from the first rotation were disregarded as the system did not reach a steady-state condition at that time. As can be seen, the force is nearly zero throughout most of the rotation (i.e. the ball is unloaded) except when it is rolling in the lowest part of the outer race where the contact occurs. The peak is centred about 270°, which corresponds to the lowest point of the orbital rotation, which is consistent with similar works [89].

Fig. 10
figure 10

Non-contact cage proposals

Full size image
Fig. 11
figure 11

Evolution of the ratio between the angular velocities of the cage and the inner ring for all NC-models

Full size image
Fig. 12
figure 12

Normal contact force values of the ball–inner ring interaction for a full orbit of the ball in all NC-models

Full size image

The second approach for modelling the cage without using contact models involved dividing the previous octagon into eight rigid links connecting every two consecutive balls (NC2), as illustrated in Fig. 10(b). This configuration allowed for a certain clearance between the rolling elements. However, treating each part of the cage as a single body made the definition of their inertial properties not physically intuitive. The ratio of the angular velocities kept around the same value for each cage element, as shown in Fig. 11, although the oscillations seem slightly larger, especially during the early stages of the analysis. This can be attributed to the increased accelerations caused by the relative motion between the balls. Regarding the contact forces, the evolution of the value of the normal force, for the same interaction, is represented in Fig. 12. The behaviour is similar to that obtained in the NC1 model, reaching the maximum value of the contact force about 270°.

The inclusion of spring elements was another solution contemplated to allow a greater degree of relative motion between the balls. For the third design, referred to as NC3 and described in Fig. 10(c), one of the rigid links considered in NC2 was replaced with a linear spring element, while the remaining balls were kept connected using rigid elements and revolute joints. The stiffness parameter of this spring was chosen to strike a balance between stability and allowing proper vibration. Based on values used by different authors in previous works, a stiffness of 108 N/m was chosen [82, 90]. Nevertheless, some tests were carried out with lower stiffness values, and it was found that this parameter had a significant impact on the dynamics of the system. Therefore, its definition should be considered when tuning the model. It must be noted that, if this value is too small, then the balls might come too close, or even make contact, during the simulation, which does not represent the function of the cage. Moreover, the free length of the spring was defined in such a way that, when the balls are equally spaced, there is no spring force acting on them. From the obtained results, it was found that, as expected, the system was not symmetric, and the behaviour of each ball depended heavily on its location relative to the spring’s position, as depicted in Fig. 13. The first steps of the simulation, associated with a transient state where high accelerations take place, have been neglected in this plot. The angular velocity ratio values shown in Fig. 11 confirmed once again that the initial conditions assumed were consistent and smoothed the integration process in its early stages.

Fig. 13
figure 13

Linear acceleration of the mass centres of the balls for the NC3 model (one-spring cage)

Full size image

To achieve a more symmetric, dynamic behaviour of the ball bearing, the fourth modelling proposal, referred to as NC4 and presented in Fig. 10(d), considered a linear spring element between every other pair of consecutive balls. In this way, more flexibility was introduced into the system and more uniform values of acceleration were obtained amongst the eight balls when compared to the NC3 model, as can be seen in Fig. 14.

Fig. 14
figure 14

Linear acceleration of the mass centres of the balls for the NC4 model (spring-rigid element cage)

Full size image

The fifth solution, denoted as NC5 and illustrated in Fig. 10(e), aimed at easing the definition of the physical properties by eliminating the need for a cage. Instead, all rolling elements were connected through linear spring elements. However, the value of the spring stiffness had an even greater impact on the obtained results. For the stiffness value considered previously (i.e. 108 N/m), the accelerations obtained were of a much greater scale, as shown in Fig. 15. This problem could be addressed by reducing the stiffness, but that would also increase the maximum values of the contact forces. The evolution of the normal contact force during an orbital rotation of the ball around the inner ring, represented in Fig. 12, exhibited similarities to those observed in the previous designs.

Fig. 15
figure 15

Linear acceleration of the mass centres of the balls for the NC5 model (full-spring cage)

Full size image

A compromise solution between the completely rigid NC1 model and the subsequent spring-based proposals was considered. This final design, referred to as NC6, is shown in Fig. 10(f). Again, the rolling elements are arranged at the vertices of an octagon as in NC1, but, in this design, spring elements are used to connect the rolling elements to the cage, replacing the previously used revolute joints. The main benefit of the NC6 model is that the cage remains as a single body, simplifying the definition of its inertial properties. However, this model also requires a further tuning process of the stiffness parameter during the verification stage. For this preliminary stage, the default value has been set (108 N/m). Both the values of the ratio of the angular velocities and the normal contact force, presented in Fig. 11 and Fig. 12, respectively, are in agreement with the previously described models. It can be observed that, for the contact force, the maximum values occur about 270°, although they are slightly lower than those provided by the NC5 model.

5.3 “Contact-cage” models

While the earlier introduced approaches have shown some consistency for analysis and comparison with a real bearing system, they proved to be inadequate in accurately modelling the free motion of the rolling elements within their pockets. Furthermore, the inclusion of restrictive elements in the form of rigid links or spring elements affected the obtained results and presented some shortcomings, namely limiting the ability to simulate defects in the races and the balls and introducing an additional parameter to be estimated during the dynamic analysis. Bearing that in mind, one of the purposes of this work is to develop a multibody model of a rolling element bearing whose parameters could be experimentally measured or indirectly estimated, and the aforementioned non-contact cage solutions include some parameters that lack of “physical meaning”. For this reason, an alternative methodology that considers a smooth contact characterisation between the cage and the balls was preferred, which allows a free motion of the balls, the implementation of cage defects and a comprehensive monitoring of the contact events. Moreover, this new approach facilitates the future implementation of the cage–race interaction, considered in several works [21, 61, 91, 92], depending on the desired level of complexity. This second group includes six bearing model designs, named contact-cage models, which distinguish themselves from the solutions presented in the previous section by defining the cage as a single body with its own properties (inertia, material and geometry) that interacts with all rolling elements simultaneously, thus resulting in a more complex behaviour.

The first model considering a contacting cage, referred to as C1, utilised the circle–plane interaction methodology described in Sect. 4.1 to define two planes for each pocket within the balls would freely move, while kept separated from the other rolling elements. Figure 16 illustrates a schematic representation of the C1 model. Points PJ1 and PJ2, which define the limits of the cage pocket, were determined by setting a value for the angular amplitude with respect to the central line of the pocket. They, as well as the geometrical centre of the pocket, are set along the pitch circle, and the normal vector for the two cage planes is derived from them. However, this approach presented certain drawbacks. Since no interaction between the cage and the rings had been defined, a revolute joint was necessary to keep the cage centred with respect to the outer ring. Additionally, the circumferential clearance in the external zone of the pockets was found to be unrealistically large. Regarding the dynamic behaviour of this model, the results depicted in Fig. 17 and Fig. 18, respectively, are consistent with those obtained from the non-contact cage models. Both figures exhibit slight vibrations in their magnitudes, reflecting the unrestricted motion of the rolling elements.

Fig. 16
figure 16

First contact-cage model (C1): (a) Normal planes of the cage for each pocket; (b) Complete model

Full size image
Fig. 17
figure 17

Evolution of the ratio between the angular velocities of one of the cage elements and the inner ring for all C-models

Full size image
Fig. 18
figure 18

Normal contact force values of the ball–inner ring interaction for a full orbit of the ball in all C-models

Full size image

To enhance the design and eliminate the need for a revolute joint to hold the cage, more advanced modelling approaches were developed. The two proposed designs, referred to as C2 and C3, are illustrated in Fig. 19. In this case, the planes were defined by establishing a circle within the pocket with a certain clearance with respect to the ball radius. Then an angle of 45° (C2) or 30/60° (C3) was defined to set the points for the additional planes, PJ1 up to PJ5. Thus, the C2 incorporated three planes on each side of the cage, while the C4 utilised five planes. The increased number of planes aimed to maintain the cage in its typical position. However, the greater the number of planes, the larger the number of circle–plane interactions to be defined and solved during the dynamic simulation in each time step. This issue can introduce some numerical inconsistencies if the solver is not precisely set up, and it results in a dramatical increase of the computational time as accurate detection of the contact condition is critical in smooth formulations [34], leading to a significant reduction of the step size to properly identify the contact start. Since multiple interactions are simultaneously taking place, it can become a stiff problem for the integrator. The comparison of the dynamic response obtained for both C2 and C3 approaches is represented in Fig. 20 and Fig. 21. While Fig. 21 shows that the loading of the rolling elements is identical for both models, Fig. 20 demonstrates that a greater number of planes used on the cage definition produced more stable results, reducing the amplitude of the oscillations.

Fig. 19
figure 19

Successive iterations of the first contact-cage model: (a) 3-plane version (C2); (b) 5-plane version (C3)

Full size image
Fig. 20
figure 20

Comparison of the evolution of the ratio between the angular velocities of one of the cage elements and the inner ring for the C2 and C3 models

Full size image
Fig. 21
figure 21

Comparison of the normal contact force values of the ball-inner ring interaction during a full orbit of the ball for the C2 and C3 models

Full size image

The fourth approach of this group, named C4 and illustrated in Fig. 22, is based on the internal circle–circle interaction introduced above. In this model, the radius of the cage pocket was defined with sufficient clearance to allow free movement of the balls while ensuring that the interactions between the balls and races are not compromised. However, it is important to note that if the radial clearance of the bearing is excessively large, the rolling elements may make contact with a non-existent part of the cage pocket instead of the rings, as schematically represented in Fig. 23. Nevertheless, this solution proved to be more computationally attractive since the definition of 2 (C1), 6 (C2) or 10 (C3) plane–circle contacts was replaced for just one circle–circle interaction. Moreover, when using several planes, the contact scenario can change from one plane to the following one, which involves an abrupt variation of the contact location and contact direction. By contrast, the circle–circle interaction ensures a smooth contact evolution in the ball–cage contact. Regarding the consistency of the model, the results presented in Fig. 17 and Fig. 18 were in agreement with those obtained from the non-contact cage designs. The maximum value of the contact force is placed about the same place as in the previous designs.

Fig. 22
figure 22

Circle–circle interaction-based model (C4): (a) Geometrical description; (b) Complete model

Full size image
Fig. 23
figure 23

Undesired contact interaction that can be observed in the C4 model if the pocket clearance is smaller than the radial clearance of the bearing

Full size image

Based on the external circle–circle interaction described in Sect. 4.1, another solution was developed, referred to as C5 and illustrated in Fig. 24. In this design, four circles were considered for each pocket, and their locations and radii were defined to keep the ball contained within the pocket. Similar to the C1 model, an angular amplitude with respect to the central line of the pocket was defined, establishing the centres of the circles in the outer and inner radii. The model exhibited consistent behaviour when compared with the previous solutions, as evidenced by the results depicted in Fig. 17 and Fig. 18. However, a major drawback of this design is the lack of physical intuitiveness when specifying the circles that represent the cage, resulting in a complex geometrical definition.

Fig. 24
figure 24

Cage modelling based on the external circle–circle interaction model (C5): (a) Complete model; (b) Detail view of the definition of the pocket circles

Full size image

The last contact-cage modelling approach combines the models previously described in this section. Starting from the internal circle–circle interaction, the aim was to restrict the interaction to the actual area corresponding to the cage pocket, addressing the main drawback of the C4 model. As clearly demonstrated in Fig. 25, the thickness of the cage is much smaller than the diameter of the rolling element. However, that would result in an abrupt transition between the material area (the cage itself) and the space between the elements, as can be seen in Fig. 25(a). By making use of the external circle–circle interaction implemented in the C5 model, two circles were added to the limit points of the cage, thus obtaining a convex-concave-convex profile, illustrated in Fig. 25(b). To ensure a smooth passage between the external and internal contacts, a suitable transition function was employed to mitigate sudden changes in the contact stiffness between the different parts of the profile. This approach helped to obtain a robust and reliable model. The radii of the limit circles were carefully defined, so the aforementioned transition was as smooth as possible. Regarding consistency, the results obtained from the C6 model slightly differ from those of the previously described proposals, as concluded from the analysis of Fig. 17 and Fig. 18. This discrepancy might be associated with the parameters of the smooth function and the values of the radii of the limit circles, both of which have a crucial influence and require further tuning.

Fig. 25
figure 25

Sixth contact-cage model (C6): (a) Abrupt transition; (b) Concave-convex solution; (c) Full model

Full size image

6 Comparison and discussion

Different solutions to model a radial-loaded deep groove ball bearing using planar multibody models have been presented in the previous section. These approaches can be divided into two main groups according to the way the ball–cage interaction was taken into account. On the one hand, the cage function was replaced with spring elements or rigid links. On the other hand, smooth contact formulations were used to treat that interaction. The choice of the model depends on the specific requirements of the multibody system being developed. If an imperfect kinematic joint between two bodies is sought, as seen in previous works such as [67, 93], the first group of proposals could provide a useful solution at a reasonable computational cost. However, if a deeper understanding of the internal behaviour between the bearing elements is desired, then the second group would be a preferable choice, especially if defect simulation is intended. It is worth noting that this complexification of the modelling approach will consequently involve a noticeable increase in computing time.

The computation time ratio, using the most efficient model (NC1) as the reference, presented in Fig. 26, allows to perform a comparative analysis among all proposed bearing multibody models in terms of their computational cost. The results show that the models within the first group exhibit similar computational times. NC1 and NC5, the simplest designs, are the most efficient options, but they are not suitable for defect implementation, as discussed earlier. Among the contact-cage solutions, the last model (C6) may not be optimum in terms of efficiency, but it offers the advantage of ease of definition since its contact interactions are based on a realistic description of the cage geometry. Furthermore, plane-based designs are the most computationally demanding options. It is important to note that the analysis parameters were kept constant for all models with a 1-second analysis duration and a reporting time step of 10−5 s. It can be observed that, for complex systems as those described in this work, the bottleneck is not the geometry complexity of the contacting bodies but the number of contact interactions that take place simultaneously. For instance, C2 and C3 models are simpler in terms of geometry definition than C6, but they take almost double the time for the same analysis. When using a variable time step integration algorithm, the instant when the contact event begins involves a major change in the numerical stiffness of the equations of motion; therefore, the algorithm needs to reduce the step size to meet the defined tolerances. Thus, when multiple contacts/impacts simultaneously occur, the computational efficiency is largely affected. Having that in mind, if a more complex contact methodology, in which the evolution of contact forces is smoothed, is used instead of other simpler contact models, then the computational time might not be penalized by the increasing complexity.

Fig. 26
figure 26

Computational time ratio for all the models described in this work. NC1 is chosen as the reference model

Full size image

During the design and modelling processes, several aspects were minutely considered. One critical factor is the value of the clearance, both in the pocket and radial direction, which has a significant impact on the results obtained. Excessively large values can smooth the integration process but may distort the results and affect the dynamic behaviour of the system. On the other hand, excessively low clearance values can lead to a significantly higher number of contact/impact events, requiring a greater amount of computation and a reduction of the step size, which results in increased computational time.

Another aspect to consider, particularly in smooth-contact formulation, is the suitable setup of the integration algorithm used to solve the dynamic problem described by the set of ordinary differential equations (ODE) in Equation (3.9). Since the multibody modelling of rolling element bearings presented in this work results in the occurrence of several contact/impact events, which need a proper detection of the start of the contact state, the use of variable step size integration is fully recommended. Thus, the integrator can adapt to the stiffness of the dynamic problem, which tends to increase during contact interactions. The utilisation of the fourth-order Runge–Kutta method with constant step size was also evaluated during the course of this work to avoid the excessive step reduction observed in variable step size algorithms during contact analysis. However, a sensitivity analysis was required to determine the appropriate time-step value to ensure results similar to those obtained with the variable step integrators. Since the dynamic analyses presented in this work were performed in an in-house general planar multibody code developed in MATLAB environment, the ODE solvers provided by MATLAB were used. Two different integrators were employed for the presented solutions. The variable-step-size integrator ODE113 was tested and proved to yield better results than the general-use integrator ODE45 for stiff problems such as viscoelastic contacts. ODE113 is a PECE implementation of Adams–Bashforth–Moulton methods [94] and the “113” makes reference to the fact that it is a variable order solver from order 1 to 13. In PECE implementations (predict-evaluate-correct-evaluate), the second evaluation improves the accuracy of the method, as improved function values are used in the set of backpoints in the subsequent steps [95]. The main advantage of MATLAB default integrators is that they include features to adjust the maximum step size or the precision considered in the solution. For the contact-cage models based on the circle–plane interaction, the solver ODE89 was contemplated. In this case, “89” refers to the 9(8) Runge–Kutta pair from which it is derived [96], where “8” denotes the order method for the error estimate and “9” defines the order of the solution to obtain the next step values. Although this solver performed better in demanding cases such as the C1, C2 and C3 designs, its excessively high computational cost led it to be discarded.

7 Concluding remarks

In the present paper, multiple solutions to model a radial-loaded deep groove ball bearing have been proposed within the framework of multibody system dynamics. During the design process, certain assumptions have been made, namely the neglection of axial motion and cage–race contact. Notably, these models have independently defined the interactions between the different elements (rollers, external and internal races, and cage), which was not previously reported in the open literature. Thus, these interactions consider different modelling characteristics such as normal and friction force models or friction parameters, just to mention a few.

The proposed multibody models of deep groove ball bearings can be categorised into two groups: (i) those based on the definition of rigid links and/or linear spring elements to deal with the ball–cage interaction, suitable for simple models within more complex systems; and (ii) those that make use of smooth contact formulations to simulate the interactions between the rolling elements and the cage. The latter methodology has been proven effective in handling multiple-simultaneous contact scenarios, making it suitable for capturing the internal behaviour of the bearing or incorporating defect modelling. The analysis and comparison of the results obtained for all the presented models show an agreement with those reported in previous works by different authors. These outcomes are promising and set the path for future verification processes.

Since rolling contact bearings are critical components in rotary machinery, this work provides a realistic solution that will be of interest to researchers involved in studies on bearing modelling under the umbrella of multibody system dynamics. Depending on the specific application, different options have been proposed and developed. Furthermore, some of the suggestions discussed here, particularly those concerning contact forces, may also be applicable to other complex systems involving multiple-simultaneous contact/impact scenarios.

While this work provides a comprehensive investigation into the dynamic modelling of deep groove ball bearings, encompassing various approaches considering planar motion, there is still potential for further improvement and exploration. Building upon the findings of this study, several paths for future research emerge. One important direction for future work is the inclusion of the contact interaction between the cage and both the internal and external rings. This aspect, which was not addressed in the current study, would provide a more extensive understanding of the bearing system’s behaviour and enable a more accurate representation of real-world conditions. Additionally, the modelling of contact cases requires the definition of several parameters related to geometry, materials and numerical aspects of the contact models. Therefore, a more refined estimation and tuning of these parameters could enhance the realism and efficiency of the simulation, leading to more accurate predictions of bearing performance. To validate the dynamic response obtained from the modelling approaches, experimental validation becomes crucial. Conducting experiments on actual bearing systems would allow for a better assessment of the modelling options and facilitate the optimisation of selected normal and tangential contact force models. Another area of future investigation lies in the implementation of defects on the rolling elements or raceways. By incorporating such defects, the models can be applied in the context of predictive maintenance and monitoring systems, enabling the detection and evaluation of potential faults or abnormalities in the bearing performance using the model as a digital twin. Finally, while the use of planar formulations allows for the study of certain geometries of radially loaded rolling contact bearings, extending the models to a spatial formulation would broaden the scope of bearings that can be analysed. This extension would make the inclusion of axial loads and misalignments possible, providing a more detailed understanding of the bearing behaviour in various operating conditions. By addressing these areas of further investigation, future research can improve the understanding and application of dynamics modelling approaches for rolling contact bearings, contributing to the advancement of bearing analysis, design and maintenance practices.