1 Introduction

Developing computational models that predict structural failure is of great importance in mechanical systems. By understanding how fracture forms and propagates, proactive measures can be taken to prevent or control mechanical failure. The analysis of the dynamics of a mechanical system and the prediction of failure in a single computational model is a current research topic of interest for different engineering applications. Coupling different formulations and developing reliable computational simulations for such systems are two key challenges.

The analysis of multibody systems involves studying the kinematics and dynamics of mechanical systems or mechanisms, composed of multiple bodies connected by kinematic joints or other types of elements. In these analyses, the bodies can be assumed to be rigid or flexible, depending on the system idealization. The development of formulations to represent the structural flexibility integrated in multibody mechanisms closely follows the developments of the numerical methods aimed at solving the problems of continuum mechanics. Thus, the possibility to simulate large displacements and rotations combined with linear and nonlinear deformations has been achieved by different formulations. The early implementations of the floating reference frame formulation [1] and the absolute nodal coordinate formulation (ANCF) [2, 3] among others make use of the finite element methodology. The problem of dealing with nonlinear material and geometric deformations was first handled by Ambrósio et al. [4–6]. Although plasticity was one of the material nonlinearities modelled in their flexible multibody dynamics approaches, the problems of crack propagation were not included in the formulations.

The drawbacks of methods involving the use of meshes to discretize the domain, including FEM, motivated the use of alternative formulations to simulate certain types of deformable structures without the need for extensive remeshing thus avoiding numerical problems of local singularities. Smoothed particle hydrodynamics (SPH) is one such formulation, originally aimed at solving problems of astrophysics [7, 8], but primarily applied to fluid dynamics [9, 10]. Relevant applications of SPH in the context of multibody systems include the analysis of moving loads in vehicle dynamics [11], as well as fluid-structure interaction [12–14]. The discrete element method (DEM) [15] is a meshless method that is particularly suited for the simulation of mediums characterised by multiple contacts between particles, such as the problem of granular mechanics [11, 16]. The element-free Galerkin method (EFGM) is a meshless approach originally developed to solve PDEs [17]. Examples of the integration of EFGM in multibody systems include the development of flexible joints [18], the simulation of mechanisms with bodies with geometrically nonlinear behaviour [19] and the simulation of granular materials with multiple contacts [20]. It is worth noting that the paradigms of parallel computing create new possibilities for the efficient simulation of very large problems involving the interaction between fluid or granular materials and structures and complex mechanisms that are subjected to large spatial displacements and rotations [14, 21].

The integration of meshless methods in the multibody domain is already established, as the aforementioned examples demonstrate. However, there are still features of the meshless methods that have not been fully explored in a multibody framework. To the knowledge of the authors of this work, the use of meshless methods to simulate the propagation of cracks in the bodies of a multibody system is absent from the literature. In particular, a recent nonlocal approach called peridynamics has shown success dealing with fracture mechanics, retains the advantages of particle methods and has the potential for seamless integration with a multibody systems framework.

Peridynamics (PD) [22, 23] is a theory of continuum mechanics that has attracted the attention of the theoretical and computational mechanics community in the past several years. Its capabilities dealing with discontinuities allows the simulation of complex phenomena such as crack propagation and fragmentation simulations in a mathematically and physically consistent framework. The main reason for that is the fundamental change in the nature of the underlying equations of motion.

The PD equations of motion are at their core a reformulation of the classical continuum mechanics equations of motion, transforming the well-known partial differential equations (PDEs) into integrodifferential equations [22]. The equilibrium of internal forces at each point, usually written as the divergence of its stress state, is modified to an integral of a pairwise force density over a finite distance denominated as the horizon of the point (length scale). Each point is influenced by its neighbour points, inside its horizon, which means that PD is a nonlocal formulation. It quickly becomes evident that discontinuities such as cracks, which lead to singularities in the classical PDEs, do not produce any problems in the PD equations. Moreover, the nonlocal character of the equations provides an adequate setting for the simulation of multiscale phenomena [24].

For clarity, PD models are often classified based on the direction of the force interactions. When the developed forces are aligned with the interaction (bond) direction and have the same magnitude, the model is said to be bond-based. If the developed forces are aligned with the bond direction but do not have the same magnitude, then the model is said to be ordinary state-based. Moreover, their magnitude can depend on the deformation of other bonds in contrast to bond-based, in which the magnitude depends only on the deformation of that particular bond. If the developed forces are not aligned with the bond direction and do not have the same magnitude, then the model is said to be non-ordinary state-based.

In the literature two main PD streams can be found: the native-based modelling approach and the correspondence-based modelling approach [25]. The first approach consists of developing new constitutive models, tailored directly for PD. These models are often bond-based or ordinary state-based. The second approach relies on the correspondence principle, which allows using classical continuum mechanics material models. The correspondence-based models are usually of the non-ordinary state-based type. It should be stressed that each type of modelling approach has its advantages. In the current work we resort to the simplest existing model: the prototype microelastic brittle (PMB) [26], which is a bond-based PD model. It has the advantage of being computationally efficient, easy to model, and crack propagation is achieved easily with this model.

In a general context, as PD is usually discretized as a meshfree method, some similarities can been found between PD and the classical meshfree methods. Particularly, Bessa et al. [27] provided a connection between moving least squares and reproducing kernel approximations and correspondence-based PD. Equivalence with total Lagrangian smoothed particle hydrodynamics has also been shown by Ganzenmuller et al. [28] for correspondence-based PD with nodal integration. Still, as noted in these works, PD provides a more convenient way of making the computations while being based in a more sound continuum mechanics framework for fracture. Regarding native-based PD models, connections with molecular dynamics can also be found in the literature [29, 30], which is expected since native-based modelling relies on defining potentials between particles within the horizon of each point.

Nevertheless, PD has been used to model and analyse diverse material behaviours. Examples of this, which include correspondence-based and native-based models, are models of hyperelasticity [31], viscoelasticity [32], plasticity [33–35] and constitutive models for concrete fracture [25]. PD has also been successfully employed for the modelling of structures. The following works on beams, plate and shell domains [36–39] are good examples of this capacity. Multi-physics modelling with PD has also shown high potential. It is common that multiple fields interact when cracks nucleate and propagate in different material domains. This is the case of thermomechanical coupling where both the thermal and mechanical field interact and have a high influence in the crack near-fields [40–42]. Another example is electromechanical coupling where interactions between electrical and mechanical fields have huge influence both in crack propagation direction and in fracture loads [43, 44]. Fluid structure interaction has also been subject of study, where material failure can be accounted for in the simulations [45–48].

As can be deducted, PD can also be very useful in simulations where multibody interactions are meaningful. This is the case of impact and ballistics simulations, where contact between multiple bodies needs to be accounted for and crack nucleation and propagation and body fragmentation are essential to predict. Indeed, PD has been successfully applied on those domains [36, 49–52], showing high promise in this regard. Another example is the modelling of granular systems, where the interaction of granular media and particle breakage can be predicted [53, 54]. Multibody system dynamics is a complementary field focusing on the analysis of multibody interactions for other types of applications. Within the framework of flexible multibody dynamics, the components can undergo large deformations and even deform permanently [5]. Such cases can lead to fracture and subsequent failure of the mechanical system, for which PD can play a role at predicting such scenarios. Despite this, to the knowledge of the authors, no works to date have addressed these issues, and the potential of the integration of PD in a multibody system dynamics framework has not been explored. To that end, this work aims to propose a methodology that integrates a peridynamics theory with a multibody formulation to describe nonlinear deformations, including crack initiation and propagation. This methodology is described for 2D scenarios and demonstrated via classic and new application cases.

This article is organised as follows: Sect. 2 presents the PD theory employed in this work, Sect. 3 introduces the fundamentals of the planar multibody formulation, Sect. 4 describes the integration between the two methods, Sect. 5 includes the numerical studies and Sect. 6 discloses the conclusions.

2 Peridynamics overview

In this section the bond-based peridynamics formulation is briefly overviewed. Damage and fracture modelling is also addressed. Lastly, a short description on the implemented meshless discretization is given together with its solving scheme.

2.1 Formulation

Peridynamics can be viewed as a reformulation of the classical continuum mechanics theory. The equations of motion in classical continuum mechanics, in the reference configuration, are given as

$$ \rho _{0}\ddot{\textbf{u}} = \nabla \cdot \textbf{P} +\textbf{b}, $$
(1)

where \(\textbf{P}\) is the first Piola–Kirchhoff stress tensor, \(\textbf{b}\) is the body force vector, \(\rho _{0}\) is the undeformed mass density and \(\ddot{\textbf{u}}\) is the acceleration field, expressed as the second derivative of the displacement field. The divergence of the stress tensor (which represents the equilibrium of internal forces) introduces restrictions to a given body deformation, since this deformation should be sufficiently smooth in order for the stress tensor to be differentiable. In the presence of discontinuities, such as cracks, the partial derivatives become undefined and the equations are no longer valid at those points. Several models have been developed in the last century to deal with these shortcomings, e.g. linear elastic fracture mechanics.

In order to overcome these difficulties, in bond-based peridynamics the equilibrium of internal forces is changed from the divergence of the stress tensor to an integral over a horizon of points [22], resulting in

$$ \rho _{0}\ddot{\textbf{u}} = \int _{H_{\textbf{x}}}\mathbf{f}(\boldsymbol{\eta}, \boldsymbol{\xi})dV' + \textbf{b}, $$
(2)

where \(\mathbf{f}\) is the pairwise force function, representing a bond interaction between point \(\textbf{x}\) and a neighbour \(\textbf{x}'\). The pairwise force function depends on the relative position of the pair of points \(\boldsymbol{\xi} = \textbf{x}' - \textbf{x}\), also known as bond vector, and the relative displacement vector \(\boldsymbol{\eta} = \textbf{u}' - \textbf{u}\). Points belonging to the neighbourhood of \(\textbf{x}\) are said to be part of its family \(H_{\textbf{x}}\). The nonlocal character of peridynamics arises from the fact that bond interactions occur beyond nearest neighbours. In this sense, \(H_{\textbf{x}}\) can be defined as a region centred in \(\textbf{x}\) for which any point \(\textbf{x}'\) such that \(|\boldsymbol{\xi}|<\delta \) belongs to \(H_{\textbf{x}}\), where \(\delta \) is a finite distance called horizon. It must be stated that when \(\delta \rightarrow 0\), peridynamics converges to the classical continuum formulation. In Fig. 1 a PD body is shown, illustrating kinematics in the reference and deformed configurations.

Fig. 1
figure 1

Peridynamics kinematics

Full size image

The pairwise force function can be defined for a microelastic material from a scalar micropotential \(w\) as

$$ \mathbf{f}(\boldsymbol{\eta},\boldsymbol{\xi}) = \frac{\partial w}{\partial \boldsymbol{\eta}}( \boldsymbol{\eta},\boldsymbol{\xi}). $$
(3)

In bond-based peridynamics the pairwise force function has the same direction of its associated bond, i.e.

$$ \mathbf{f}(\boldsymbol{\eta},\boldsymbol{\xi}) = f(y,\xi ) \frac{\boldsymbol{\xi}+\boldsymbol{\eta}}{|\boldsymbol{\xi}+\boldsymbol{\eta}|}, $$
(4)

where \(\boldsymbol{\xi}+\boldsymbol{\eta}\) is the current relative position vector, \(\xi = |\boldsymbol{\xi}|\) and \(y = |\boldsymbol{\xi}+\boldsymbol{\eta}|\). If we consider a linear microelastic material such that the micropotential is written as [26]

$$ w(\boldsymbol{\eta},\boldsymbol{\xi}) = \frac{1}{2}c(\xi ) s^{2} \xi , $$
(5)

where \(s\) is the stretch in a bond defined as

$$ s = \frac{|\boldsymbol{\xi}+\boldsymbol{\eta}|-|\boldsymbol{\xi}|}{|\boldsymbol{\xi}|}, $$
(6)

the corresponding pairwise force function can take the following form:

$$ \mathbf{f} = c(\xi )s\frac{\boldsymbol{\xi} + \boldsymbol{\eta}}{|\boldsymbol{\xi} + \boldsymbol{\eta}|}, $$
(7)

where \(c(\xi )\) is called micromodulus function. This function contains the material constant properties, and its value can vary with the bond distance \(\xi \). This allows a given point \(\textbf{x}\) to have higher force contributions from closer neighbours.

To obtain an expression for the micromodulus, the usual approach is matching the strain energy obtained from classical continuum mechanics, for a given homogeneous deformation, with the peridynamic strain energy density, with the same imposed deformation, given as

$$ W(\textbf{x}) = \frac{1}{2} \int _{H_{\textbf{x}}}w(\boldsymbol{\eta},\boldsymbol{\xi})dV'. $$
(8)

Using this approach and assuming a constant micromodulus in this work, it may be written as

$$ c = \textstyle\begin{cases} \frac{6E}{\pi h \delta ^{3} (1-\nu )} & \text{, plane stress} \\ \frac{6E}{\pi h \delta ^{3} (1+\nu )(1-2\nu )} & \text{, plane strain} \end{cases}\displaystyle , $$
(9)

where \(E\) is the Young modulus, \(\nu \) is the Poisson ratio and \(h\) is the thickness of the domain. This form of pairwise potential limits the types of deformation that can be obtained, as explained in [22, 23]. As a result, the Poisson ratio is restricted to \(\nu =1/3\) in plane stress and \(\nu =1/4\) in plane strain and 3D conditions. This limitation is solved in the state-based peridynamics framework as shown in [23].

It is evident that this formulation can be thought of as a system of point masses connected by springs with their corresponding spring constants \(c(\xi )\), with a numerical implementation similar to that of unconstrained multibody systems. In that sense, the extension/integration of this peridynamic formulation in a multibody dynamics framework can be achieved in a straightforward way. Its numerical implementation is similar to that of unconstrained multibody systems.

2.2 Fracture criteria and damage

One of the virtues of peridynamics is the intrinsic way in which fracture is treated. The emergence and propagation of cracks shall be considered a natural part of peridynamic simulations. In opposition to other fracture mechanics approaches, in peridynamics this kind of problems is solved without the need of any ad-hoc treatment. This subsection shows how fracture is treated in an intrinsic way in the context of peridynamics, thus being a natural outcome of simulations.

The starting point of fracture is the recognition that the creation of a crack implies creating a new surface. In peridynamics this is achieved at the expense of breaking bonds. When all the bonds crossing a given surface are broken, a new fracture surface is generated.

The most popular brittle fracture criterion is the critical stretch criterion. This criterion states that once a bond stretch exceeds a given material dependent critical stretch value, the bond is broken. This can be written as

$$ \mu (\xi ,\eta ) = \textstyle\begin{cases} 1 & \text{if } s < s_{c} \\ 0 & \text{otherwise} \end{cases}\displaystyle , $$
(10)

where \(\mu \) is the bond status variable and \(s_{c}\) is the critical stretch. The pairwise force function incorporates the bond status variable in the following manner:

$$ \mathbf{f} = \mu (\xi ,\eta )c(\xi )s \frac{\boldsymbol{\xi} + \boldsymbol{\eta}}{|\boldsymbol{\xi} + \boldsymbol{\eta}|}. $$
(11)

When a bond is broken, it stops bearing force, which is redistributed among the neighbouring bonds.

The critical energy release rate, \(G_{c}\) (a material property), is defined as the energy required to create a new unit fracture area. In a peridynamic domain, computing \(G_{c}\) involves accounting for the energy of all the broken bonds associated with the creation of the unit surface area. This summation is expressed in mathematical terms as the integral of the micropotential of all the bonds, given by

$$ G_{c} = \int _{0}^{\delta }\int _{z}^{\delta }\int _{0}^{\arccos ( \frac{z}{\xi})} w_{c} d\phi d\xi dz \quad \text{(2D)}, $$
(12)

where

$$ w_{c} = \frac{1}{2}c(\xi )s_{c}^{2} \xi . $$
(13)

Figure 2 illustrates the domain of integration to evaluate the fracture energy.

Fig. 2
figure 2

Domain of integration for the evaluation of the fracture energy

Full size image

Finally, by solving equation (12), the critical stretch is expressed in terms of the critical energy release rate \(G_{c}\) of the material as [55]

$$ s_{c} = \textstyle\begin{cases} \sqrt{\frac{4\pi G_{c}}{9E\delta}} & \text{, plane stress} \\ \sqrt{\frac{5\pi G_{c}}{12E\delta}} & \text{, plane strain} \end{cases}\displaystyle . $$
(14)

In peridynamics, the usual indicator of damage at a point is obtained by considering a ratio between the number of remaining unbroken bonds and the total number of initial unbroken bonds with the following expression:

$$ \varphi \left (\textbf{x}\right ) = 1 - \frac{\int _{H_{\textbf{x}}} \mu (\xi ,\eta ) dV'}{\int _{H_{\textbf{x}}} dV'}. $$
(15)

The damage at each point can vary between 0 (undamaged—all the bonds intact) and 1 (fully damaged—all the bonds broken). When \(\varphi =0.5\), half the bonds are broken, which can represent a new surface. In the discrete setting, a crack is usually assumed to exist for values of \(\varphi \) higher than 0.4.

2.3 Numerical implementation

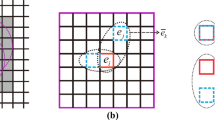
In peridynamics, the most usual discretization of the equations is a straightforward meshless point collocation method, due to its simplicity. The domain is divided in a finite number of points, and to each point is attributed an area/volume, as illustrated in Fig. 3.

Fig. 3
figure 3

Peridynamics meshfree discretization

Full size image

In this work we consider a point \(n\) belonging to the family of point \(j\) if their distance is less than \(\delta \), i.e. \(\xi \le \delta \), as displayed in a darker grey tone in Fig. 3. For the implementation of the PD equations, the integral operations are approximated by sums. Hence, for point \(\textbf{x}_{j}\), the equation of motion is written as

$$ \rho _{j}\ddot{\textbf{u}}^{t}_{j} = \sum _{n=1}^{N} \mathbf{f}(\boldsymbol{\eta}^{t},\boldsymbol{\xi})V_{n} + \textbf{b}_{j} $$
(16)

with \(N\) being the number of points in the family of point \(j\). The time integration of the equations of motion is addressed in Sect. 4.

The imposition of essential boundary conditions can be done with a fictitious layer of points. A layer with thickness \(\delta \) prescribes displacement. While more effective methods have recently emerged [56–58], the presented naive approach is straightforward to implement and yields results with acceptable accuracy. Nonetheless, boundary conditions can be implemented at individual points or layers with thickness smaller than \(\delta \), but one must be aware that close to those locations high oscillations can appear due to the well known skin effect in PD due to incomplete horizons [55].

As loads cannot be enforced along boundary surfaces in the PD equations, these are imposed in the form of body forces in the \(\textbf{b}\) vector. For the load boundary conditions, a single layer of points is used, i.e. a layer of a thickness equal to the grid spacing.

3 Multibody formulation

Multibody simulations allow the study of the kinematics and dynamics of complex mechanical systems that experience large displacements and rotations. A multibody model is commonly defined by a collection of rigid and/or flexible bodies interconnected by kinematic joints and force elements. The subject of this work is how to incorporate the flexible bodies that may develop cracks during the normal or abnormal operation of the system.

The multibody formulation used in this work relies on the use of planar Cartesian coordinates. The position of a body \(i\) relative to the global reference frame is expressed by the vector \(\textbf{r}_{i}\), while the orientation is expressed by the angle \(\theta _{i}\). The position and angular coordinates form the vector of the coordinates of the body \(\textbf{q}_{i}=\left [\textbf{r}^{T} \quad \theta \right ]_{i}^{T}\)

Kinematic joints [59] constrain the relative motion between bodies of a system and are described by algebraic equations, expressed in terms of the coordinates of the rigid bodies. These algebraic constraint equations compose the Jacobian matrix \(\boldsymbol{\Phi}_{q}\) and the vector of the right-hand side of the acceleration equations \(\boldsymbol{\gamma}\). The Lagrange multiplier method is used to add these constraints to the system of equations of motion through the addition of the vector of Lagrange multipliers \(\boldsymbol{\lambda}\) to the vector of the unknowns. Force elements, which represent the internal forces that develop between the bodies due to their relative motion, contribute to the force vector \(\textbf{g}\) by developing forces due to the relative motion between the bodies. External forces may also be applied to the system components as a consequence of their interaction with the surrounding environment. The resulting system of the equations of motion of a rigid multibody system is expressed by

$$ \begin{bmatrix} \textbf{M} & \boldsymbol{\Phi}_{\textbf{q}}^{T} \\ \boldsymbol{\Phi}_{\textbf{q}} & \textbf{0} \end{bmatrix} \begin{Bmatrix} \ddot{\textbf{q}} \\ \boldsymbol{\lambda} \end{Bmatrix} = \begin{Bmatrix} \textbf{g} \\ \boldsymbol{\gamma}^{\ast }\end{Bmatrix} , $$
(17)

where the vector of the system accelerations is

$$ \ddot{\textbf{q}}= \begin{bmatrix} \ddot{\textbf{r}}_{1}^{T} & \ddot{{\theta}}_{1}^{\prime} & \cdots & \ddot{\textbf{r}}_{i}^{T} & \ddot{{\theta}}_{i}^{\prime} \end{bmatrix} . $$
(18)

The vector of the right-hand side of the acceleration constraint equations \(\boldsymbol{\gamma}\) is modified to vector \(\boldsymbol{\gamma}^{\ast}\) to include the contributions associated with the Baumgarte stabilisation [60], to control the drift of the system response due to the numerical violation of the position and velocity constraint equations, expressed as

$$ \boldsymbol{\gamma}^{\ast }= \boldsymbol{\gamma}-2\alpha \dot{\boldsymbol{\Phi}}-\beta ^{2} \boldsymbol{\Phi}, $$
(19)

where \(\alpha \) and \(\beta \) are scalars and \(\boldsymbol{\Phi}\) and \(\dot{\boldsymbol{\Phi}}\) are the position and velocity constraint equations, respectively.

The time integration of vector \(\ddot{\textbf{q}}_{t}\) is performed using an adequate time integration algorithm, as will be shown in Sect. 4.

4 Flexible multibody dynamics with peridynamic bodies

This section presents the coupled multibody peridynamics formulation (MBD-PD) to include peridynamic flexible bodies in a multibody system dynamics framework. In order to leverage the capabilities of PD, its discretization is done at a meshless collocation level. This implies that the integral of the internal forces is taken as a discrete summation of forces between each point and its neighbours. A commonly used analogy is to think about the bond connections between particles as springs. Therefore, in the multibody framework, each PD point can be treated as a rigid body connected to its neighbours by springs.

For simplicity, as this integration is done for the first time, the presented bond-based PD formulation is used. This formulation has the advantages of being easily implemented and bond breaking is straightforward. In the perspective of the multibody framework, the resulting body connecting springs are geometrically nonlinear, with stiffness according to equation (9), since the stretch measure in the present BBPD formulation is nonlinear, as depicted in Fig. 4. Another consequence of this choice is that each PD rigid body has only two displacement degrees of freedom and no rotational degree of freedom. This is in contrast with the non-PD rigid bodies, which generally feature the three degrees of freedom in planar dynamics. In fact, the PD rigid bodies are better labelled as particle masses due to their lack of rotational degrees of freedom.

Fig. 4
figure 4

Equivalences between meshless peridynamics and multibody systems

Full size image

The resulting system of equations for the flexible multibody system is the expansion of the system described by equation (17) with the addition of the contributions associated with peridynamics, given by

$$ \begin{bmatrix} \textbf{M}_{r} & \textbf{0} & \boldsymbol{\Phi}_{\textbf{q}r}^{T} \\ \textbf{0} & \textbf{M}_{f} & \boldsymbol{\Phi}_{\textbf{q}f}^{T} \\ \boldsymbol{\Phi}_{\textbf{q}r} & \boldsymbol{\Phi}_{\textbf{q}f} & \textbf{0} \end{bmatrix} \begin{Bmatrix} \ddot{\textbf{q}}_{r} \\ \ddot{\textbf{q}}_{f} \\ \boldsymbol{\lambda} \end{Bmatrix} = \begin{Bmatrix} \textbf{g}_{r} \\ \textbf{g}_{f} \\ \boldsymbol{\gamma}^{\ast }\end{Bmatrix} , $$
(20)

where \(\ddot{\textbf{q}}_{r}\) and \(\ddot{\textbf{q}}_{f}\) are the acceleration vectors of the standard rigid bodies and PD flexible bodies, respectively. The dimensions of the vector \(\ddot{\textbf{q}}_{r}\) are \(3N_{b}\), where \(N_{b}\) is the number of standard rigid bodies, and the dimensions of the \(\ddot{\textbf{q}}_{f}\) vector are \(2N_{f}\), where \(N_{f}\) is the number of PD particles.

Matrix \(\textbf{M}_{r}\) is the standard mass matrix of the rigid bodies. \(\textbf{M}_{f}\) is the mass matrix of the flexible body, defined as

$$ \textbf{M}_{f} = \begin{bmatrix} \ddots & & & \textbf{0} \\ & \rho _{j} & & \\ & & \rho _{j} & \\ \textbf{0} & & & \ddots \end{bmatrix} , $$
(21)

where the entries for particle \(j\) are highlighted. Notice that only the diagonal is populated with the mass of each individual particle. Consequently, this is a lumped mass matrix with dimensions \(2N_{f} \times 2N_{f}\).

The matrices \(\boldsymbol{\Phi}_{\textbf{q}r}\) and \(\boldsymbol{\Phi}_{\textbf{q}f}\) are the Jacobian matrices accounting for the constraint equations associated with the rigid and flexible bodies degrees of freedom, respectively. The vector of Lagrange multipliers \(\boldsymbol{\lambda}\) has a length equal to the number of kinematic constraint equations of the system.

Vector \(\textbf{g}_{r}\) collects the contributions of the standard rigid bodies. In turn, force vector \(\textbf{g}_{f}\) accounts for the internal forces of the flexible body, in accordance to equation (16), and is expressed as

$$ \textbf{g}_{f} = \begin{Bmatrix} \vdots \\ \sum _{n=1}^{m} {f}_{1j}(\boldsymbol{\eta}^{t},\boldsymbol{\xi})V_{n} + b_{1j} \\ \sum _{n=1}^{m} {f}_{2j}(\boldsymbol{\eta}^{t},\boldsymbol{\xi})V_{n} + b_{2j} \\ \vdots \end{Bmatrix} , $$
(22)

where the entries for particle \(j\) are highlighted. This vector has length \(2N_{f}\). Note that this term, associated with the internal forces, also contains surface and volume correction factors, according to [55], to reduce the well-known skin effect in PD and minimize the quadrature error, respectively.

Notice that, from the expression of the PD pairwise force vector, if the critical stretch of a bond (or spring) exceeds the PD critical stretch, then this bond is eliminated, leading to a spontaneous crack growth. To the best knowledge of the authors, this constitutes a novelty in the context of multibody dynamic simulations.

To account for the coupling between flexible and rigid bodies, a rigid-flexible joint was developed. This joint allows introducing a PD flexible body in the multibody dynamics framework in a consistent manner. The rigid-flexible joint connects a single PD point to a virtual body, which is a standard massless rigid body [61]. Note that the use of the virtual body concept allows not only to use any kinematic joint available for rigid multibody systems without any further implementation, but also to connect different flexible bodies described by different formulations [62]. A set of rigid-flexible joints can be used to define a layer of PD points, of thickness \(\delta \), that establishes an interface between the deformable body defined by PD points and the virtual body, as shown in Fig. 5. The virtual body then can be used to define kinematic joints between the deformable body and other rigid or flexible bodies.

Fig. 5
figure 5

Integration of a PD body into a multibody system using a virtual body

Full size image

The rigid-flexible joint defines a kinematic constraint enforcing the positions of point \(P_{i}\) in the virtual body \(i\) and the position of PD point \(j\) to be equal. Accordingly, the position constraint equations that govern the rigid-flexible joint are

$$ \boldsymbol{\Phi}^{rf} = \textbf{r}_{i} + \textbf{A}_{i}\textbf{s}^{\prime}_{i}{^{P}} - \textbf{y}_{j}, $$
(23)

where \(\textbf{r}_{i}\) is the position of virtual body \(i\) w.r.t. the global reference frame, \(\textbf{s}^{\prime}_{i}{^{P}}\) is the position of point \(P_{i}\) w.r.t. the local reference frame of body \(i\) and \(\textbf{y}_{j}\) is the position of PD point \(j\) w.r.t. the global reference frame. \(\textbf{A}_{i}\) is the transformation matrix from local to global coordinates. The Jacobian matrix contributions associated with the rigid-flexible joint are

$$ \boldsymbol{\Phi}_{\textbf{q}}^{rf} = \begin{bmatrix} \boldsymbol{\Phi}_{\textbf{q}r}^{rf} & \boldsymbol{\Phi}_{\textbf{q}f}^{rf} \end{bmatrix} = \begin{bmatrix} \textbf{I} & \textbf{B}_{i}\textbf{s}^{\prime}_{i}{^{P}} & -\textbf{I} \end{bmatrix} , $$
(24)

where

$$ \textbf{B}_{i} = \begin{bmatrix} -\sin{\phi}_{i} & -\cos{\phi}_{i} \\ \cos{\phi}_{i} & -\sin{\phi}_{i} \end{bmatrix} . $$
(25)

The right-hand side vector of the acceleration constraint equations is

$$ \boldsymbol{\gamma}^{rf} = \textbf{A}_{i}\textbf{s}^{\prime}_{i}{^{P}} \dot{\theta}_{i}, $$
(26)

which contributes to the right-hand side of the system of equations of motion defined in equation (20).

From a PD point of view, this flexible-rigid joint approach allows an easy computation of the reactions by the simple inspection of the resulting joint forces and moments through the Lagrange multipliers method, according to

$$ \textbf{g}^{(c)} = -(\boldsymbol{\Phi}_{\textbf{q}}^{rf})^{T} \boldsymbol{\lambda}, $$
(27)

where \(\textbf{g}_{r}^{(c)}\) contains the joint reaction forces and moments.

Figure 6 shows the standard multibody dynamics simulation algorithm for the solution and integration of the equations of motion, which is described as follows:

  1. (i)

    set the initial time \({t_{0}}\), the vectors of the initial positions of the rigid and flexible bodies \(\textbf{q}_{r,0}\) and \(\textbf{q}_{f,0}\) and the vectors of the initial velocities of the rigid and flexible bodies \(\dot{\textbf{q}}_{r,0}\) and \(\dot{\textbf{q}}_{f,0}\);

  2. (ii)

    assemble the mass matrices of the rigid and flexible bodies \(\textbf{M}_{r}\) and \(\textbf{M}_{f}\), the Jacobian matrices associated with the constraint equations of the rigid and flexible bodies \(\boldsymbol{\Phi}_{\textbf{q}r}\) and \(\boldsymbol{\Phi}_{\textbf{q}f}\), the force vectors of the rigid and flexible bodies \(\textbf{g}_{r}\) and \(\textbf{g}_{f}\) and the vector of the right-hand side of the acceleration constraint equations \(\boldsymbol{\gamma}\);

  3. (iii)

    solve the equations of motion to determine the vectors of the accelerations \(\ddot{\textbf{q}}_{r}\) and \(\ddot{\textbf{q}}_{f}\) and Lagrange multipliers \(\boldsymbol{\lambda}\);

  4. (vi)

    assemble the vector of the global accelerations \(\ddot{\textbf{q}}_{t}=\left [ \ddot{\textbf{q}}_{r} \quad \ddot{\textbf{q}}_{f} \right ]_{t}^{T}\) and the vector of the global velocities \(\dot{\textbf{q}}_{t}=\left [ \dot{\textbf{q}}_{r} \quad \dot{\textbf{q}}_{f} \right ]_{t}^{T}\);

  5. (v)

    integrate vectors \(\ddot{\textbf{q}}_{t}\) and \(\dot{\textbf{q}}_{t}\) to obtain the global vectors of the velocities and positions in the next time step \(\dot{\textbf{q}}_{t+\Delta t}\) and \({\textbf{q}}_{t+\Delta t}\) by using an appropriate ordinary differential equations solver;

  6. (vi)

    update the time variable \({t = t+\Delta t}\);

  7. (vii)

    stop simulation if \({t> t_{end}}\), or else go to step (ii).

Fig. 6
figure 6

Direct dynamics algorithm of the multibody simulation

Full size image

It is common in peridynamics to use explicit dynamic solver schemes due to their simplicity and computational efficiency. This work employs a forward and backward finite difference integration scheme expressed by

$$ \dot{\textbf{q}}_{t+\Delta t} = \ddot{\textbf{q}}_{t}\Delta t + \dot{\textbf{q}}_{t} $$
(28a)
$$ {\textbf{q}}_{t+\Delta t} = \dot{\textbf{q}}_{t+\Delta t}\Delta t + { \textbf{q}}_{t}. $$
(28b)

However, employing explicit dynamic solvers must be taken with care since stability issues may arise. To ensure stability, according to Silling [26], the time step must satisfy

$$ \Delta t < \sqrt{ \frac{2\rho}{\sum _{n} V_{n} C_{j n}} }, $$
(29)

where \(C_{jn} = C(\xi _{jn})\) is the linearized micromodulus function. From a multibody point of view, this upper bound of the time step results from the use of springs with very high stiffness and bodies with low mass, meaning that sufficiently low time step values are required to accurately integrate the resulting equations.

5 Numerical studies

This section presents a set of examples with different levels of complexity that demonstrate the use of the proposed framework to simulate fracture and simple mechanisms.

5.1 Plate with different in-plane loadings

In the computational fracture mechanics literature, the single-edge notched test is a commonly used benchmark where a square plate is subjected to tension and shear in-plane loads [63–66]. Figure 7 shows a simple setup with general boundary conditions and associated virtual bodies and kinematic joints. Depending on the simulation case, different sets of kinematic joints are used, following the imposed boundary conditions. The simulation of the following scenarios demonstrates the accuracy of the present peridynamics methodology to solve fracture problems.

Fig. 7
figure 7

Plate and virtual bodies with applied boundary and initial conditions

Full size image

Layers with thickness \(\delta \) are connected to the virtual bodies through rigid-flexible joints. The virtual bodies are easily constrained with standard multibody joints, such as revolute or translation joints. To enforce deformation in these examples, the virtual bodies are connected to drivers, which can impose horizontal and vertical translation or rotation. The capabilities of the proposed formulation are highlighted by the results of different sets of in-plane loadings and showing crack propagation when critical criteria values are achieved, leading to complete failure.

A short discussion on the definition of the size of the horizon \(\delta \) is due. The selection of \(\delta \) may depend on the goal of the simulation. To analyse the deformations while disregarding crack propagation, a smaller value of \(\delta \) is recommended to approximate the local limit of continuum mechanics. Conversely, to analyse crack propagation, a larger value of \(\delta \) is desired to include the intrinsic nonlocal effects of fracture propagation phenomena. A compromise must be found between the use of larger values of \(\delta \), with the associated increase in computational cost, and smaller values of \(\delta \) that prevent the accurate simulation of crack propagation.

In the following examples, the plate has dimensions \(L \times L\), where \(L\) is equal to 1 mm, with thickness 1 mm, with an initial notch with length \(h = 0.5 \) mm, in plane strain conditions. The mechanical properties are: Young modulus \(E = 206.8\) GPa; Poisson ratio \(\nu = 0.3333\); density \(\rho = 7800\) kg/m3; and critical energy release rate \(G_{c} = 2700\) N/m. The domain is discretized into \(24 \times 24\) points with two additional layers of \(3 \times 24\) points, which is consistent with the size of the horizon used \(\delta = 0.121\) mm. As a result, the horizon size is three times the grid spacing, i.e. \(m = 3\), where \(\delta = m \Delta \textbf{x}\), and \(\Delta \textbf{x}\) is the spacing between two adjacent points. In the following example the time step is selected following equation (29) to guarantee numerical stability. Moreover, the values of the Baumgarte parameters are selected considering the study described in [67].

5.1.1 Plate subject to traction loading

In this subsection numerical results of the plate subjected to traction on both the left and right sides are presented. It is intended to display the behaviour of the peridynamic formulation for fracture prediction. With that in mind, firstly a horizontal velocity \(v = 1 \) m/s is imposed on both sides in order to obtain results that can be compared with quasi-static simulations from the literature for this benchmark. For this numerical simulation, a time step \(\Delta t = 1\times 10^{-9}\) ensures the stability of the simulation, and the Baumgarte parameters used are \(\alpha = 1\times 10^{7}\) and \(\beta = 1.4\times 10^{7}\).

In Fig. 8 the damage plot for the described conditions is shown. The crack propagates in a straight line from the initial crack tip to the bottom of the plate, as expected for such conditions, since the velocity is low enough. Note that the damage scalar values, which vary from 0 to 1, are plotted in a linear scale from 0 to 0.4. This is because the crack face is supposed to emerge when half of the bonds connected to a point are broken. In a discrete setting this value is approximately 0.4. Therefore, it is usually enough and visually clearer to plot the damage up to 0.4.

Fig. 8
figure 8

Damage pattern in tension test (\(v = 1\) m/s)

Full size image

To assess the numerical accuracy of the formulation, Fig. 9 shows the load-displacement curve of the MBD-PD numerical dynamic simulation and a comparison with quasi-static results from the literature [63–66]. As can be observed, the result obtained in the present work is in good agreement with the references. The difference in the curves, in the elastic loading phase, comes from the fact that dynamic effects are considered in the MBD-PD simulations but not considered in the references. These dynamic effects are also present after the crack is fully propagated, as can be observed in the oscillation of the reaction force after 7 ms. Moreover, in terms of critical fracture load, our predictions are also in good agreement with both the phase-field fracture and correspondence-based PD approaches.

Fig. 9
figure 9

Load-displacement curves in tension test (\(v = 1\) m/s)

Full size image

To further display the capabilities of the proposed approach, a numerical simulation with imposed velocity \(v = 15\) m/s is run. In Fig. 10 the resulting damage plot for the described simulation is shown. As can be observed, the crack branching phenomenon is clearly captured in this numerical simulation. The crack branching phenomenon, associated with high imposed velocities, is caused by the reflected incident elastic waves travelling in the direction opposite to the propagation of the initial vertical notch. The results show that the PD model has the capability of capturing this phenomenon, which is characteristic of dynamic fracture [68].

Fig. 10
figure 10

Damage pattern in tension test (\(v = 15\) m/s)

Full size image

5.1.2 Plate subject to shear loading

In this subsection, numerical results of the same plate, now subjected to shear loading, are presented. A vertical velocity \(v = 1 \) m/s is imposed on both sides (downwards on the left side and upwards on the right side) to obtain results comparable with quasi-static simulations from the literature. The numerical parameters used in this test are the same as in the previous section.

In Fig. 11 the damage plot for the described conditions is shown. As can be seen, the initial crack is deflected towards the right side, from the initial crack tip. This result further demonstrates the capability of our PD model to handle crack propagation in any direction in both modes of in-plane loading. The load-displacement curve of our numerical dynamic simulation is shown in Fig. 12 and compared to quasi-static results from the literature.

Fig. 11
figure 11

Damage pattern in shear test (\(v = 1\) m/s)

Full size image
Fig. 12
figure 12

Load-displacement curves in shear test (\(v = 1\) m/s)

Full size image

Again, the result obtained in the present work is in good agreement with the references. The influence of considering dynamic effects is again visible. Besides the good agreement in terms of critical fracture load, it can be also observed from our result that the post peak phase can also be captured.

5.1.3 Plate with different properties subjected to various loadings

In this section numerical simulations of the same benchmark are presented with different geometrical dimensions and material properties. The objective is to display the capabilities of our model regarding large deformations and rotations.

\(L\) is now equal to 1 m with plate thickness 5 mm and an initial notch with length \(h = 0.5 \) m in plane stress conditions. The mechanical properties are of an artificial material and take the following values: Young modulus \(E = 2.068\) MPa; Poisson ratio \(\nu = 0.3333\); density \(\rho = 7800\) kg/m3; and the critical stretch has prescribed value \(s_{c} = 0.45\). The horizon used is \(\delta = 0.121\) m. For this numerical simulation, a time step \(\Delta t = 1\times 10^{-4}\) ensures the stability of the simulation, and the Baumgarte parameters used are \(\alpha = 1000\) and \(\beta = 1400\). The prescribed velocity magnitude on the boundaries is \(v = 1\) m/s.

In Fig. 13 different snapshots of a tension test simulation are shown, each corresponding to a different time instant. As can be clearly observed, the crack propagates downwards from the initial crack tip. A shear test was also repeated with the current conditions, as shown in Fig. 14. The large deformation is visible and the crack starts to propagate only after a large displacement took place. Both aforementioned figures are analogous to Figs. 8 and 11 and can be thought as an amplification of their deformations.

Fig. 13
figure 13

Crack propagation in tension test

Full size image
Fig. 14
figure 14

Crack propagation in shear test

Full size image

A loading case with imposed rotation, which is typically challenging to implement in a PD framework, is also presented. However, in the present framework accounting for large rotations is done in a seamless manner. Note that in this case the centre of rotation of both the left and the right sides is at \(y = 0\). The left side rotates anti-clockwise and the right side rotates clockwise, with a prescribed angular velocity magnitude \(\omega = 6.28\)rad/s, as shown in Fig. 15.

Fig. 15
figure 15

Crack propagation in rotation test

Full size image

This simulation provides a good example of the capabilities of the present model since fracture is obtained in a progressive unguided fashion, while considering geometric nonlinearities without any additional numerical treatment.

5.2 Slider-Crank

This section presents the analysis of a slider-crank mechanism, including a comparison of results against a classical flexible multibody methodology, to demonstrate the accuracy of the proposed framework. This mechanism has been studied by several authors and is widely considered as a benchmark for flexible multibody dynamics [62, 69–72]. The slider-crank mechanism, shown in Fig. 16, features a flexible rod described by the PD formulation and is driven by rotating the crank with a constant angular velocity \(\omega = 2\pi \) rad/s. The initial velocities of the nodes of the flexible rod are consistent with the initial angular velocity of the rod. The length of the crank is 0.0254 m, while the length of the flexible rod is \(L = 0.1524\) m with thickness 1 mm. To establish the connections with the crank on one end and the slider on the other end, two rigid-flexible joints are used to connect a prescribed number of PD points of the rod and two virtual bodies. The remaining kinematic joints of the system are the revolute joint connecting the crank with the ground and the translation joint connecting the slider with the ground. The mechanical properties of the flexible rod are: Young modulus \(E = 2.068\) MPa; Poisson ratio \(\nu = 0.3333\); density \(\rho = 7800\) kg/m3.

Fig. 16
figure 16

Schematic representation of the slider-crank mechanism

Full size image

For the baseline model, a \(3\times 67\) discretization is used with a horizon size \(\delta = 0.004\) m. The time step of the simulation is \(\Delta t = 1\times 10^{-4}\) s, the Baumgarte parameters are \(\alpha = 1000\) and \(\beta = 1400\). The positions of the PD points of the rod and the position and orientation of the crank are presented in Fig. 17 at different time instants for a full revolution of the crank. These results demonstrate the capability of the proposed framework for flexible multibody dynamic analyses. The different time instants demonstrate a deformation coherent with the properties of the rod.

Fig. 17
figure 17

Body positions and deformations at different time instants

Full size image

To assess the accuracy of our model, a comparison against a flexible multibody implementation is made with MUBODyn [62]. The reference model involves a total of 1200 Ansys Shell 181 finite elements. The flexible multibody dynamics methodology uses a floating frame of reference formulation and the component mode synthesis. To this end, the in-plane modes of vibration associated with the first 11 natural frequencies were considered. Moreover, a refinement analysis is also presented to assess the influence of the discretization. Besides the baseline model, two more refined models are used. In the first model, a discretization of \(5\times 104\) points, using a horizon \(\delta = 0.0019\) m and a time step \(\Delta t = 5\times 10^{-5}\) s with Baumgarte parameters \(\alpha = 2000\) and \(\beta = 2800\), is used. The second model uses a discretization of \(9\times 183\) points, using a horizon \(\delta = 0.0.0012\) m and a time step \(\Delta t = 3\times 10^{-5}\) with Baumgarte parameters \(\alpha = 2000\) and \(\beta = 2800\).

Figure 18 shows the results of the rod midpoint displacement for different discretizations and the MUBODyn results. As can be observed, refining the discretizations reduces the differences to the reference result. It should also be noted that peridynamics is a nonlocal reformulation of classical continuum mechanics, and only in the limit \(\delta \rightarrow 0\) the classical local formulation can be recovered. In these results a horizon size corresponding to \(m = 1.5\) is used, which is the minimum that can be used in 2D, so that the PD results approach the reference as much as possible. While not being perfectly coincident with the reference, this was expected, and the results demonstrate the capabilities of PD in approximating local solutions for smaller horizons.

Fig. 18
figure 18

Rod midpoint displacement - refinement effect

Full size image

Other issue in nonlocal formulations is the imposition of boundary conditions. As stated in Sect. 2, boundary conditions are usually imposed through a finite layer of points for accuracy reasons. In the current work we analyse the effect of imposing boundary conditions through single point connections or through a layer of points, as illustrated in Fig. 19.

Fig. 19
figure 19

Connection types (\(i\)) MN - multiple nodes, (\(ii\)) SN - single node

Full size image

In the previous slider-crank simulations, we used one point connections to the virtual bodies. To analyse the effect of using one point connections or connections to a layer of thickness \(\delta \), we present Fig. 20. Results for two different discretizations are shown. From observation, it can be easily concluded that using multiple node connections increases the deviation from the reference results. For each discretization, a small increase in the wavelength, or decrease in the frequency, can be observed. This is probably because of the additional mass in the ends of the flexible rod due to the extra nodes used in the boundary.

Fig. 20
figure 20

Rod midpoint displacement - boundary effect

Full size image

For completeness, we also show the effect of the horizon size in the results, in Fig. 21. Visibly, the horizon also has a large influence on the numerical results. By inspection of the figure, an increase in the horizon size leads to an increase of the wavelength, as well as a clear increase in the wave amplitude. Notably, increasing the horizon size lowers the stiffness of the structure being modelled. The horizon can be used to model materials and structures at multiscale, as referred in [24]. This opens up the possibilities of using the current framework also for modelling mechanisms at any length scale.

Fig. 21
figure 21

Rod midpoint displacement - horizon size effect

Full size image

5.3 Simple pendulum subjected to impact

In this example a simple PD pendulum is analysed. A layer of points of the PD body is connected to a virtual body through a rigid-flexible joint and the virtual body is connected to the ground through a revolute joint. The PD body pendulum starts from a horizontal configuration with an initial angular velocity. On the right side, a rigid-flexible joint connects a layer of points to a virtual body. This virtual body is connected to the ground through a nonlinear force element following a penalty contact law, which acts as soon as the middle point of the virtual body reaches a given vertical coordinate. This is illustrated in Fig. 22.

Fig. 22
figure 22

Schematic representation of the pendulum mechanism subjected to impact

Full size image

The length of the pendulum is \(L = 0.1524\) m, height \(h = 0.0110\) m, thickness 1 mm and the length of the initial notch is \(h/2\). The mechanical properties of the pendulum are: Young modulus \(E = 2.068\) MPa; Poisson ratio \(\nu = 0.3333\); density \(\rho = 7800\)Kg/m3. The model has a \(7\times 67\) discretization with a horizon size \(\delta = 0.0048\) m. The time step of the simulation is \(\Delta t = 5\times 10^{-5}\) s, Baumgarte parameters \(\alpha = 2000\) and \(\beta = 2800\). The contact force equation is written as

$$ F_{c} = \textstyle\begin{cases} K|\varepsilon |^{1.5} & \text{if } \varepsilon > 0 \\ 0 & \text{if } \varepsilon \leq 0 \end{cases}\displaystyle , $$
(30)

where \(K\) is the stiffness of the contact and \(\varepsilon \) is the value of the penetration between the end of the pendulum and the ground. In the present case, the right end of the pendulum travels a distance \(b = 0.05\) m before contact occurs. The contact force contributes to the force vector \(\textbf{g}_{f}\) in equation (20).

The critical stretch value used in this simulation is \(s_{c} = 0.06\), while the contact stiffness \(K = 1\times 10^{8}\) N/m1.5. Figure 23 presents the deformation of the pendulum at different time instants. The flexible PD body starts from a horizontal configuration aligned with the \(x\) axis, with an initial angular velocity. At \(t = 0.12\) s the right side of the pendulum has already contacted the impact surface. From there, the crack propagates in a straight line until the body is split in two halves. When the body is separated in two, these two parts become completely independent, having separate body motions. One of the halves continues to be connected to the ground through the revolute joint, and the other half moves freely in space.

Fig. 23
figure 23

Pendulum deformation and damage at different time instants - \(K = 1\times 10^{8}\) N/m1.5, \(s_{c} = 0.06\)

Full size image

To test the influence of the value of the penalty, we now present a numerical simulation with a higher penalty value \(K = 5\times 10^{8}\) N/m1.5. This means that the contact stiffness is higher and a larger force will be applied when contact happens. Figure 24 shows the results from this simulation. Results show a different damage pattern from the previous simulation. The impact generates a much higher force, breaking almost instantly the left side of the pendulum. Yet, there is still a propagating wave that reaches the initial notch with enough intensity to propagate the crack to break the pendulum in that location. In this simulation the final damage is much more severe since three fragments can be counted separately, not counting with the free PD particles (which are points without any active bond) that also move freely.

Fig. 24
figure 24

Pendulum deformation and damage at different time instants - \(K = 5\times 10^{8}\) N/m1.5, \(s_{c} = 0.06\)

Full size image

The influence of decreasing the critical stretch to \(s_{c} = 0.015\) was also subjected to analysis. In Fig. 25 we show the results for this simulation with a higher value of critical stretch. Note that the value of penalty from the prior simulation was maintained. The results obtained in this simulation show a much more catastrophic failure. The pendulum initially breaks near the impact location, as before. However, due to a lower value of critical stretch, which implies a more brittle material, more bonds are susceptible to breakage. This leads to cracks nucleating in other locations besides the propagation of the initial notch. The pendulum is divided in five fragments following the impact, nucleation and propagation of the resulting cracks besides the countless free PD points.

Fig. 25
figure 25

Pendulum deformation and damage at different time instants - \(K = 5\times 10^{8}\) N/m1.5, \(s_{c} = 0.015\)

Full size image

6 Conclusions

This article presents a novel flexible multibody dynamics approach using peridynamics for the flexible bodies. This allows for the simulation of complex phenomena such as crack propagation and accounting for geometrical nonlinearities. This approach integrates the PD formulation into an MB framework by establishing convenient equivalences: PD point masses are interpreted as MBD rigid bodies; and PD bond forces are represented by MBD nonlinear force elements. The PD components are included in the equations of motion through lumped mass matrix terms and the bond forces contribute directly to the forces vector. The implementation of this methodology exploits the PD meshless description, thus being suitable for flexible multibody analysis. The methodology proposed is illustrated by different examples of simple mechanisms involving both flexible bodies described by the PD formulation and rigid bodies. Comparisons with results existing in the literature and FEM are presented. The results demonstrate the effect of the discretization, the horizon and the boundary implementation in the simulated response.

The current method shows potential to address relevant engineering problems such as design of mechanical systems, with focus on fatigue, considering fracture and crack propagation. This methodology also allows the design of mechanisms that involve slender structures that may exhibit large deformations and be prone to fracture. Its major drawback is the large computational effort required for the simulations on a single processor computer. Future efforts may also focus in assessing strategies to apply this framework to problems with higher computational complexity and more cost-effective numerical simulation strategies.