1 Introduction

The LuGre friction model has become very popular for the analysis of stick-slip phenomena and has recently been launched in the commercial multibody dynamics simulation software system Adams [1]. The first version of the LuGre friction model [2] published in 1995 claims that this new model is based on the average behavior of elastic bristles. A first-order bristle dynamics is proposed but not derived from a real bristle model. This first paper has already reported the dramatic loss of the break-away force with an increasing rate of the applied force. The revisited version of the LuGre model [3] focuses on the stick-slip motion and the rate dependency. A demonstration example unveils the drift problem of the LuGre model. A force significantly lower than the sticking limit applied to a body resting on a rough surface moves the body slightly forward. However, the body does not return to its original position when the applied force is set back to zero.

A non-smooth friction characteristics, including the sudden change from sticking to sliding, specifies the input to the LuGre model. However, the LuGre model dynamics transfers this non-smooth to very smooth friction characteristics, which differs in parts considerably from the specification. As reported but not further investigated in [4] this severe drawback also holds for other standard dynamic friction models.

Most of these drawbacks are not inevitable side effects but are caused in the LuGre approach by too poor a model of the bristle dynamics. As demonstrated here, the LuGre approach represents just a simplified first-step approximation of an accurate bristle model. The setup of a model with accurate first-order bristle dynamics and a consistent friction force is a straightforward task. It results in a nonlinear and implicit differential equation whose solution will not be easy because of the ambiguity of the friction characteristics. However, the implicit bristle model provides at least some insight into the physical basis of the LuGre model dynamics.

Standard examples and a more practical application demonstrate that the LuGre model is not a “what you see is what you get” approach. The standard workaround, a standard static friction model based on regularized friction characteristics, produces reliable and generally satisfactory results, but it definitely cannot maintain a stick. The paper presents a second-order dynamic friction model, which applies a more sophisticated and asymmetric regularization of general friction characteristics. It corresponds in the results to the implicit bristle-based friction model, can maintain a stick, and may serve as a practical alternative to the LuGre approach or other standard dynamic friction models.

2 Bristle-based dynamic friction modeling

2.1 General approach

As reported in [2] and [3], the LuGre friction model is supposed to be based on the average behavior of elastic bristles. Figure 1 shows two bodies, which have contact in point Q, where the broken line indicates the contact plane. Body i moves relative to body j, resulting in the velocity component \(v_{ij}\) measured in the contact plane. A fictitious bristle mounted at body i models potential shear deformations of body i and j in the contact area. The top of the bristle slides along the contact plane with the velocity

$$ v_{S} = v_{ij} - \dot{z} $$
(1)

The coordinate \(z\) represents the bristle deformation, and \(\dot{z}\) names its time derivative. The friction force \(F_{R}\) acting in the contact point Q is transferred via the bristle force

$$ F_{B} = \sigma _{0} \, z + \sigma _{1} \, \dot{z} $$
(2)

to body i, where the parameters \(\sigma _{0}\) and \(\sigma _{1}\) model the visco-elastic properties of the fictitious bristle.

Fig. 1
figure 1

Bristle-based dynamic friction model and general friction characteristics, where \(F_{Ri} = F_{R}\) and \(F_{Rj} = -F_{R}\) define the forces applied to body \(i\) and \(j\), and \(F_{R}=F_{B}\) represents the force balance at the top of the massless bristle

Full size image

Analytical friction force models have become a standard in multibody or control applications [5] and are also applied in commercial products [6]. In a more general approach, the friction force

$$ F_{R}(v_{S}) \:=\: \frac{ v_{S} }{ \lvert v_{S} \rvert } \: \mu ( \lvert v_{S} \rvert ) \: F_{N} $$
(3)

is modeled here as the product of the velocity-dependent friction coefficient \(\mu = \mu ( \lvert v_{S} \rvert )\) and the normal force \(F_{N}\). The term \(v_{S} / \lvert v_{S} \rvert \) correlates the sign of the friction force to the sign of the sliding velocity \(v_{S}\) because the model approach in Fig. 1 implies that the sliding velocity and the friction force act in the opposite direction. The friction force \(F_{R}(v_{S})\) remains undefined at vanishing sliding velocities \(v_{S} = 0\), where the inequality \(\lvert F_{R} \rvert \le \mu _{s}\, F_{N}\) just limits the ambiguity of the friction force according to Coulomb. The friction characteristics depending on the velocity

$$ \mu ( \lvert v_{S} \rvert ) \:=\: \mu _{d} + \left ( \mu _{s} - \mu _{d} \right ) e^{-\left (\lvert v_{S} \rvert / v_{A} \right )^{\alpha}} \!+ \: \nu \, \lvert v_{S} \rvert $$
(4)

combines the Coulomb friction with the Stribeck effect. The first two parts correspond to the standard LuGre model, where, similar to [7], the friction force is replaced by the friction coefficient. A parameter \(\nu > 0\) finally adds a simple viscous component. The velocity parameter \(v_{A}>0\) and the exponent \(\alpha \ge 1\) model the attenuation pattern of the static friction value \(\mu _{s}\) to the dynamic friction value \(\mu _{d}\) thus describing the Stribeck affect. The viscous component \(\nu \, \lvert v_{S} \rvert \) takes into account the hydrodynamic lubrication for larger sliding velocities \(\lvert v_{S} \rvert \gg v_{A}\). Note that, in addition, this simple model supplement will affect the attenuation pattern of the friction characteristics. In practical applications, this influence is hardly noticeable because the Stribeck effect takes place in a very low velocity range, where the viscous part is still very small. The friction characteristics defined in (4) is computed by the Matlab function uty_mu provided in Listing 8.

According to (1) and (3), the friction force \(F_{R}\) is a function of the relative velocity \(v_{ij}\) and the time derivative \(\dot{z}\) of the bristle deformation. The bristle force \(F_{B}\) as defined in (2) depends on the bristle deformation \(z\) and its time derivative. Then, the force balance at the top of the bristle \(F_{R}=F_{B}\) or \(f = F_{R} - F_{B} = 0\), respectively, results in an implicit first-order differential equation

$$ f = F_{R}(v_{ij} - \dot{z} ) - \left ( \sigma _{0} \, z + \sigma _{1} \, \dot{z} \right ) = 0 $$
(5)

which defines the dynamics of the bristle deformation. The differential equation is strongly nonlinear and, due to the Coulomb friction, also ambiguous, which makes its general solution a challenging task.

Liftoff situations, which in multibody simulations cannot be ruled out in general, are characterized by a vanishing normal force \(F_{N}=0\), which implies a vanishing friction force \(F_{R}=0\). In this special case, the differential equation (5) is simplified to

$$ - ( \sigma _{0} \, z + \sigma _{1} \, \dot{z}_{F_{R}=0} ) = 0 \quad \mbox{or}\quad \dot{z}_{F_{R}=0} = - ( \sigma _{0}/\sigma _{1}) \, z $$
(6)

Hence, the bristle eigen-dynamics or the decay of an existing bristle deformation \(z \ne 0\) during liftoff is controlled by the ratio bristle stiffness \(\sigma _{0}\) over bristle damping \(\sigma _{1}\).

The function fzero, which uses a combination of bisection, secant, and inverse quadratic interpolation methods, is applied in Matlab as a standard for solving nonlinear equations in one variable. It can solve (5), although the friction force characteristics \(F_{R}(v_{S})\), as defined by (3) and (4), exhibits a discontinuity at vanishing sliding velocities \(v_{S}=0\) where the top of the fictitious bristle sticks to the contact plane. However, the Matlab function fzero requires an appropriate initial guess \(\dot{z} = \dot{z}_{A}\), which is already sufficiently close to the expected solution. Depending on the complexity of the friction force characteristics, the force balance (5) can have several solutions. However, a nonlinear equation solver like fzero delivers just one of it, which makes the implicit friction model in this straightforward application of less practical use. That is why the implicit bristle model is just applied in Sect. 4.3 within the pulse load example as a reference for the second-order bristle model. It is represented by the Matlab functions uty_fr_impl and uty_bforce_bal as provided in the Listings 6 and 7.

Structural tire models incorporate the dynamics of bristle-like contact elements described by implicit differential equations similar to (5). The structural tire model FTire [8] uses an additional discrete state variable to distinguish between possible stick and slip solutions and applies a fully implicit formula to achieve a reliable representation of the nonlinear bristle dynamics.

2.2 Approximate solution

The Newton-Raphson algorithm provides another approach to solving nonlinear equations. Applied to (5), it yields the iteration scheme

$$ \dot{z}_{k+1} \:=\: \dot{z}_{k} - \left ( \frac{\mathrm{d}\,f}{\mathrm{d}\,\dot{z} } \right )^{\!-1} \!\! f( \dot{z}_{k}) \quad \mbox{for}\quad k=0,1,2,\dots $$
(7)

Taking (1) into account, the function derivative results in

$$ \begin{aligned} \frac{\mathrm{d}\,f}{\mathrm{d}\,\dot{z}} \:=\: & \frac{\mathrm{d}}{\mathrm{d}\,\dot{z}} \Bigl( F_{R}(v_{ij} - \dot{z} ) - \left ( \sigma _{0} \, z + \sigma _{1} \, \dot{z} \right ) \Bigr) \:=\: \frac{\mathrm{d} \, F_{R}(v_{S})}{\mathrm{d}\,v_{S}} \, \frac{\mathrm{d}\,v_{S}}{\mathrm{d}\,\dot{z}} \:-\: \sigma _{1} \\ \:=\: & \frac{\mathrm{d} \, F_{R}(v_{S})}{\mathrm{d}\,v_{S}} \left (-1 \right ) \:-\: \sigma _{1} \:=\: - \left ( \frac{\mathrm{d} \, F_{R}(v_{S})}{\mathrm{d}\,v_{S}} + \sigma _{1} \right ) \end{aligned} $$
(8)

The friction force \(F_{R}(v_{S})\) defined by (3) and (4) exhibits a sharp bend at vanishing sliding velocities \(v_{S}=0\). That is why the discontinuous derivative of the friction force with respect to the sliding velocity is approximated, similar to [9], by its global derivative

$$ \frac{\mathrm{d} \, F_{R}(v_{S})}{\mathrm{d}\,v_{S}} \:\approx \: \frac{ F_{R}(v_{S}) }{ v_{S} } \:=\: \frac{ \frac{ v_{S} }{ \lvert v_{S} \rvert } \: \mu ( \lvert v_{S} \rvert ) \, F_{N} }{ v_{S} } \:=\: \frac{ \mu ( \lvert v_{S} \rvert ) \, F_{N} }{ \lvert v_{S} \rvert } $$
(9)

Then, the iteration scheme (7) results in

$$ \begin{aligned} \dot{z}_{k+1} =~& \dot{z}_{k} - \left ( - \left ( \frac{ \mu ( \lvert v_{ij} \!-\! \dot{z}_{k} \rvert ) \, F_{N} }{ \lvert v_{ij} \!-\! \dot{z}_{k} \rvert } + \sigma _{1} \right ) \right )^{\!-1} \!\! \Bigl( F_{R}( v_{ij} \!- \! \dot{z}_{k} ) - \left ( \sigma _{0} \, z + \sigma _{1} \, \dot{z}_{k} \right ) \Bigr) \\ =~& \dot{z}_{k} + \frac{ \left ( v_{ij} \!-\! \dot{z}_{k} \right ) \, \mu ( \lvert v_{ij} \!-\! \dot{z}_{k} \rvert ) \,F_{N} \:-\: \left ( \sigma _{0} \, z + \sigma _{1} \, \dot{z}_{k} \right ) \lvert v_{ij} \!-\! \dot{z}_{k} \rvert }{ \mu ( \lvert v_{ij} \!-\! \dot{z}_{k} \rvert )\,F_{N} \:+\: \sigma _{1} \, \lvert v_{ij} \!-\! \dot{z}_{k} \rvert } \end{aligned} $$
(10)

where the definition of the friction force (3) is also taken into account. As a matter of fact, the iteration formula (10) is of little practical use because it is close to sticking situations, characterized by \(v_{ij} \!-\! \dot{z}_{k} \to 0\), and its convergence is poor. However, it can be started with the trivial guess \(\dot{z}_{k=0} = 0\) and delivered in the first step of the approximation

$$ \dot{z}_{A} \:=\: \dot{z}_{1} \:=\: \frac{ v_{ij} \, \mu ( \lvert v_{ij} \rvert )\,F_{N} \:-\: \sigma _{0} \, z \, \lvert v_{ij} \rvert }{ \mu ( \lvert v_{ij} \rvert )\,F_{N} \:+\: \sigma _{1} \, \lvert v_{ij} \rvert } $$
(11)

where the velocity-dependent friction characteristics \(\mu \) defined in (4) is evaluated for the bristle in a steady-state where \(\dot{z}=0\), and \(v_{S}=v_{ij}\) will hold. The first-step approximation (11) provides at least an initial guess \(\dot{z} \approx \dot{z}_{A}\) for the Matlab solver fzero applied to (5).

Neglecting in the denominator of (11) the dissipative term \(\sigma _{1} \lvert v_{ij} \rvert \) in comparison to the steady-state friction force \(\mu ( \lvert v_{ij} \rvert )\,F_{N}\), the first-step approximation is simplified to

$$ \dot{z}_{A} \:\approx \: \frac{ v_{ij} \, \mu ( \lvert v_{ij} \rvert )\,F_{N} \:-\: \sigma _{0} \, z \, \lvert v_{ij} \rvert }{ \mu ( \lvert v_{ij} \rvert )\,F_{N} } \:=\: v \:-\: \sigma _{0} \, \frac{ \lvert v \rvert }{ \mu ( \lvert v \rvert )\,F_{N} } \: z $$
(12)

where, in the final version, \(v\) abbreviates the symbol \(v_{ij}\). As shown in Sect. 2.3, this further simplified first-step approximation corresponds to the bristle dynamics as defined in the LuGre friction model. However, it requires \(F_{N} \ne 0\) and is therefore not valid at liftoff.

2.3 The LuGre approach

In the revisited version [3], the LuGre friction model is defined as

$$\begin{aligned} \dot{z} \:=\: & v \:-\: \sigma _{0} \, \frac{ \lvert v \rvert }{ g( v ) } \: z \end{aligned}$$
(13)
$$\begin{aligned} g(v) \:=\: & F_{d} \:+\: \left ( F_{s} - F_{d} \right ) e^{-\left ( \displaystyle v / v_{A} \right )^{\alpha}} \end{aligned}$$
(14)

where the relative velocity of body i relative to body j, measured in the contact plane, is just named \(v\) instead of \(v_{ij}\) as used here. In contrast to the notation applied in [3], the Coulomb friction force \(F_{c}\) is substituted by the dynamic friction force \(F_{d}\), and the fictitious velocity, which determines how quickly \(g(v)\) approaches the dynamic friction force \(F_{d}\), is named \(v_{A}\) instead of \(v_{s}\) to avoid a confusion with the sliding velocity \(v_{S}\) as defined in (1).

The velocity-dependent function \(g(v)\) implies \(g(v) > 0\), which is automatically granted for the often applied exponent \(\alpha =2\). The use of arbitrary exponents \(\alpha \ge 1\) requires that (14) is evaluated with \(\lvert v \rvert \) and not with the sign-dependent velocity \(v\).

The LuGre approach in [3] defines the dynamic friction force as

$$ F_{R}^{dyn} \:=\: \sigma _{0}\,z + \sigma _{1}\,\dot{z} \:+\: f(v) \:= \: F_{B} \:+\: f(v) $$
(15)

where \(F_{B}\) names the bristle force as specified in (2), and \(f(v)\) models the viscous part. According to Fig. 1, the bristle force acts as a dynamic buffer, which transfers the friction force generated in the contact point Q to the body. Hence, from a physical point of view, the viscous part of the friction force should be considered via the friction characteristics, as done in (4), and not simply added to the dynamic bristle force, as proposed in the LuGre approach (15).

The function \(g(v)\) or \(g ( \lvert v \rvert )\) represents the steady-state friction force. Similar to (3) and as done in [7], it can be separated into the product of the friction coefficients \(\mu ( \lvert v \rvert )\) and the normal force \(F_{N}\)

$$ g(v) \:\to \: g(\lvert v \rvert ) \:=\: \mu (\lvert v \rvert ) \, F_{N} \:=\: \left ( \mu _{d} \:+\: \left ( \mu _{s} - \mu _{d} \right ) e^{- \left ( \displaystyle \lvert v \rvert / v_{A} \right )^{\alpha}} \right ) F_{N} $$
(16)

Then, the LuGre bristle dynamics (13) can be written as

$$ \dot{z} \:=\: v \:-\: \sigma _{0} \, \frac{ \lvert v \rvert }{ \mu (\lvert v \rvert ) \, F_{N} } \: z $$
(17)

A comparison with the simplified first-step approximation (12) reveals that the LuGre bristle dynamics represents just a first and, in general, poor guess to the solution of the bristle dynamics defined by (5). As a consequence, the LuGre model generates dynamic friction forces, which differ in parts considerably from the pre-defined friction characteristics and cause the drawbacks reported in literature and demonstrated here.

The Matlab function in Listing 5 provides the LuGre friction model as defined by (15) and (17), where the viscous part is modeled by \(f(v) = \nu F_{N} v_{ij}\). The slightly modified LuGre approach

$$\begin{aligned} \dot{z} \:=\: & \frac{ v \, \mu ( \lvert v \rvert )\,F_{N} \:-\: \lvert v \rvert \, \sigma _{0} \, z }{ \mu ( \lvert v \rvert )\,F_{N} \:+\: \lvert v \rvert \, \sigma _{1} } \end{aligned}$$
(18)
$$\begin{aligned} \mu ( \lvert v \rvert ) \:=\: & \mu _{d} + \left ( \mu _{s} - \mu _{d} \right ) e^{ \displaystyle -\left (\lvert v \rvert / v_{A} \right )^{ \alpha}} \!+\: \nu \, \lvert v \rvert \end{aligned}$$
(19)
$$\begin{aligned} F_{R}^{dyn} \:=\: & \sigma _{0}\,z + \sigma _{1}\,\dot{z} \:=\: F_{B} \end{aligned}$$
(20)

includes liftoff situations (\(F_{N} \!=\! 0\)) and is consistent to the bristle model described in Sect. 2. But, even the modified bristle dynamics (18) represents just a rather poor first-step approximation and does not eliminate any of the reported drawbacks of the LuGre approach.

3 Regularized friction models

3.1 Standard and enhanced regularization

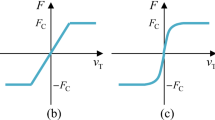
Figure 2a illustrates a standard regularization of the friction force characteristics. The ambiguous part at \(v_{S}=0\) is stretched to a finite velocity interval \(-v_{r} \le v_{S} \le +v_{r}\), where \(v_{r}>0\) is a small fictitious velocity parameter, and \(F_{R}(\pm v_{r})= \pm F_{s}\) define the friction force values which correspond to the static values \(F_{s} = \pm \mu _{s} F_{N}\). A simple straight line from \((-v_{r},-F_{s})\) to \((+v_{r},+F_{s})\) or the parabolic approach

$$ F_{R}(v_{S}) = \mu _{s} \, \frac{ v_{S} }{v_{r}} \left ( 2 - \frac{\lvert v_{S} \rvert}{v_{r}} \right ) F_{N} \quad \mbox{for} \quad \lvert v_{S} \rvert \le v_{r} $$
(21)

provides the friction force values in the regularization range \(-v_{r} \le v_{S} \le +v_{r}\). Outside the regularization range, the friction force is obtained by (3) and (4), where the friction characteristics \(\mu = \mu ( \lvert v_{S} \rvert - v_{r})\) provides a smooth transition to the regularization range. The regularized friction force characteristics is continuous and ready for use in general multibody simulations. However, it approximates stick by slow creep and cannot maintain stick.

Fig. 2
figure 2

Standard and enhanced regularization of the friction force characteristics

Full size image

Similar to the enhanced dry friction model, which is used in [10] to simulate lockable braking torques, the regularized friction characteristics is shifted in Fig. 2b horizontally such that it intersects the ordinate at the force value \(F_{0}\) required to maintain stick. The parabolic regularization (21) provides the horizontal shift of the regularized friction force characteristics \(F_{R}(v_{S})\) as

$$ \Delta v_{S} \:=\: \frac{F_{0}}{\lvert F_{0} \rvert} \, v_{r} \, w_{F} \quad \mbox{with}\quad w_{F} = \textstyle\begin{cases} 1 - \sqrt{ 1 - \lvert F_{0} \rvert / F_{s} } & \mbox{if } \lvert F_{0} \rvert \le F_{s} \\ 1 & \mbox{elsewhere} \end{cases} $$
(22)

where the term \(F_{0} / \lvert F_{0} \rvert \) adjusts the shift to the sign of the sticking force value. The regularization velocity \(v_{r}>0\) defines the shift limits \(\lvert \Delta v_{S} \rvert \le v_{r}\). The enhanced regularization is asymmetric but able to maintain stick. The Matlab function uty_fr_enh provided in Listing 4 performs the corresponding computation.

3.2 Second-order bristle model

The first-order dynamics of a massless fictitious bristle is defined by the force balance \(F_{R}=F_{B}\), which results in the nonlinear and implicit differential equation (5). Approximating the inertia force of the fictitious bristle by \(m_{b}\,\ddot{z}\), a second-order bristle dynamics is defined by

$$ m_{b}\,\ddot{z} \:=\: F_{R} - F_{B} \:=\: F_{R}(v - \dot{z} ) - \left ( \sigma _{0} \, z + \sigma _{1} \, \dot{z} \right ) $$
(23)

where \(m_{b}\) denotes the fictitious bristle mass, and (1) to (3) are used to model the friction and bristle forces \(F_{R}\) and \(F_{B}\). The parameters \(\sigma _{0}\) and \(\sigma _{1}\) defining the visco-elastic properties of the bristle are introduced in Sect. 2 and visualized in Fig. 1. At liftoff (\(F_{R}=0\)) the bristle dynamics (23) is reduced to the homogeneous second-order differential equation \(m_{b} \ddot{z} + \sigma _{1}\,\dot{z} + \sigma _{0} \, z = 0\). A fictitious bristle mass of

$$ m_{b} = \frac{\sigma _{1}^{2}}{4 \, \sigma _{0}} $$
(24)

results in two real and identical eigenvalues \(\lambda _{1} = \lambda _{2} = -\sigma _{1}/( 2 \, m_{b} ) = - 2 \, \sigma _{0} / \sigma _{1}\), which represent the aperiodic case and avoid unwanted oscillations of the fictitious bristle.

The top of the bristle slides with the velocity \(v_{S}\) along the contact area (see Fig. 1). It sticks at \(v_{S}\!=\!0\), which according to (1), is the case if \(\dot{z}\!=\!v_{ij}\) will hold. To maintain stick, the friction force \(F_{R}(v_{S}\!=\!0)\) must equal the bristle force \(F_{B}(z,\dot{z}\!=\!v)\) as defined by (2). As a consequence

$$ F_{0} = F_{B}(z,\dot{z}\!=\!v) = \sigma _{0}\,z + \sigma _{1} \,v_{ij} $$
(25)

provides the force required for the enhanced regularization of the friction characteristics, illustrated in Fig. 2b and defined by the horizontal shift (22). The computation of the second-order bristle model is straightforward and performed by the lines 22 to 26 in the Matlab function friction_models provided in Listing 3.

4 Standard demonstration models

4.1 Model setup

Figure 3 presents two standard demonstration models to study friction phenomena. Each model consists of a mass, which can move just in horizontal direction. The mass is in contact with a fixed plate or a moving belt, respectively. The weight of the mass defines the normal force \(F_{N}=m\,g\) and the friction between mass and fixed plate or mass and belt, respectively, is characterized by a friction characteristics \(\mu =\mu (\lvert v_{S} \rvert )\), which depends on the velocity as defined in (4). Newton’s law provides the dynamics of the mass as

$$ m \, \ddot{x}_{m} \:=\: F \,-\, F_{R} ~\:\mbox{where}~\: F_{R} \!=\! F_{R}(v_{S}) \!=\! F_{R}(v_{ij} \!-\! \dot{z}) ~\: \mbox{and at model}~\: \begin{aligned} 1\!:~ & F = F_{E}(t) \\ 2\!:~ & F = - k \, x_{m} \end{aligned} $$
(26)

The coordinate \(x_{m}\) describes the horizontal displacements of the mass \(m\) and \(\dot{z} \) denotes the time derivative of the bristle deformation. The external pulse load \(F_{E}(t)\), the spring stiffness \(k\), and the relative velocity \(v_{ij}\) are defined in Fig. 3. The friction and bristle parameters used within the two demonstration models are provided in Fig. 4. The weight of the mass determines in both cases the normal force, \(F_{N} \!=\! m\,g \!=\! 9.81\text{ N}\). The friction characteristics \(\mu = \mu ( \lvert v \rvert )\) and the resulting friction force \(F_{R}=F_{R}(v)\) are plotted in the velocity ranges of \(0 \le \lvert v \rvert \le 3\,v_{A}\) and \(-v_{A} \le \lvert v \rvert \le +v_{A}\), respectively. The plots on the right of Fig. 4 show the standard friction force characteristics \(F_{R} = \frac{v}{\lvert v \rvert} \, \mu ( \lvert v \rvert ) \, F_{N}\) as solid black, the simple regularized characteristics as dashed, and the asymmetric regularized ones as dotted lines. The asymmetric regularization were performed just for demonstration purpose at fixed positive and negative static force values of \(F_{0}=+4.7\text{ N}\), \(F_{0}=-3.5\text{ N}\) and \(F_{0}=+1.2\text{ N}\), \(F_{0}=-0.9\text{ N}\), respectively.

Fig. 3
figure 3

Standard models to demonstrate friction phenomena

Full size image
Fig. 4
figure 4

Friction and bristle parameters for model 1 (pulse load) and model 2 (conveyor belt) as well as the corresponding friction force characteristics \(F_{R}(v)\) in the velocity range of \(-v_{A} \le v \le +v_{A}\), including their regularizations indicated by dashed and dotted lines. (Color figure online)

Full size image

Demonstration model 1 applies the exponent \(\alpha =1\), which results in a monotonous decay of the friction characteristics \(\mu = \mu ( \lvert v \rvert )\) from \(\mu (0) \!=\! \mu _{s} \!=\! 0.6\) to \(\mu (\infty ) \!=\! \mu _{d} \!=\! 0.3\). The parameter \(\nu =0\) takes no viscous friction component into account.

Demonstration model 2 uses the exponent \(\alpha =2\), which is often applied as a standard. It results in a s-shaped transition from the static friction coefficient \(\mu (0) \!=\! \mu _{s} \!=\! 0.15\) to the dynamic friction coefficient \(\mu (\infty ) \!=\! \mu _{d} \!=\! 0.1\). A parameter \(\nu \ne 0\) takes a viscous friction component into account, which according to (4), is defined by the term \(\nu \,\lvert v \rvert \). Due to the small value of \(\nu = 0.0102\text{ s/m}\), the viscous component \(\nu \,v\) in the friction characteristics \(\mu = \mu ( \lvert v \rvert )\) is not noticeable in the plotted velocity range.

The fictitious velocity \(v_{r}\) required for the regularization of the friction characteristics, as described in Sect. 3, is simply adjusted by \(v_{r} = v_{A}/10\) to the velocity \(v_{A}\), which characterizes the attenuation of the friction characteristics or the Stribeck effect, respectively.

The friction characteristics, defined in Fig. 4 by the parameters \(\alpha \), \(\mu _{s}\), \(\mu _{d}\), \(v_{A}\), and \(\nu \), differ significantly but may approximate measured friction behaviors.

The Matlab script app_examples.m in Listing 1 provides the simulation environment for the standard examples, where the Matlab function model_dynamics in Listing 2 computes the dynamics of the mass and the different friction models.

4.2 Bristle model parameters

The parameters \(\sigma _{0}\) and \(\sigma _{1}\) describe the stiffness and damping properties of the fictitious bristle. The values defined in Fig. 4 for \(\sigma _{0}\) and \(\sigma _{1}\) indicate a connection to neither the normal force \(F_{N}\) nor the static friction value \(\mu _{s}\) or the static friction force \(F_{s}=\mu _{s}\,F_{N}\), respectively. Even the bristle eigen-dynamics, characterized by the ratio \(\sigma _{0}/\sigma _{1}\), differs from model 1 to 2.

The visco-elastic properties of a fictitious bristle, which is introduced to model the friction force in rigid body contacts, are also fictitious. Hence, an appropriate guess is required to specify the stiffness \(\sigma _{0}\) and the damping \(\sigma _{1}\) of the fictitious bristle. A bristle stiffness \(\sigma _{0}\) and a bristle damping \(\sigma _{1}\) proportional to the static friction force are proposed in [5], where a test case with three friction coupled single mass oscillators is investigated. The time constant or the ratio of stiffness to damping, which according to (6), defines the bristle eigen-dynamics, was set hereby to \(T \!=\! \sigma _{0}/\sigma _{1} \!=\! 2000\text{ s}\) without any further comment. However, relating the fictitious bristle stiffness to the static friction force means that changes in the lubrication and the environmental conditions, which strongly affect the friction, would also affect the stiffness and damping of the fictitious bristle.

The standard models applied in the literature to study friction phenomena usually consist of a single mass \(m\), which is in contact with a fixed or moving plate or belt, respectively. Then, the weight of the mass \(F_{N} \!=\! m\,g\) provides the component of the contact force normal to the contact plane. In general multibody applications, however, the normal force \(F_{N}\) is neither constant nor simply defined by the weight of one single mass. That is why, the visco-elastic properties of the fictitious bristle can hardly be related to the normal force.

For a more practical approach, one could specify a reference bristle force \(F_{Br}\) and a reference bristle deformation \(z_{r}\) caused in a steady-state by the reference bristle force. Then, the relation \(\sigma _{0} \!=\! F_{Br}/z_{r}\) provides the corresponding bristle stiffness. For simple applications, the reference bristle force and the reference bristle deformation may be related to the weight and the static friction parameter, as well as to the body dimensions. In the simplest case, the normal force is related via \(F_{N} \!=\! m\,g\) to the body mass. Similarly, the fictitious mass \(m_{r} \!=\! F_{Br}/g\) is connected to the reference bristle force. During sticking, the fictitious mass and the fictitious bristle may be considered a single mass oscillator. A bristle damping of \(\sigma _{1} \!=\! \sqrt{ \, 4 \, m_{r} \, \sigma _{0} \,}\) may serve as a first guess. It represents in analogy to (24) the aperiodic limit case for the oscillator reference mass \(m_{r}\) and fictitious bristle.

For example, a reference bristle force of \(F_{Br} \!=\! 4\text{ N} \) and a reference bristle deformation of \(z_{r} \!=\! 5.0\,\mathrm{e}{-}5\text{ m}\) will provide a bristle stiffness of \(\sigma _{0} \!=\! 4/0.00005 \!=\! 80\,000\text{ N/m}\), which is in the range of the corresponding values defined in Fig. 4. The corresponding reference mass \(m_{r} \!=\! F_{Br}/g \!=\! 4/9.81 \!=\! 0.41\text{ kg}\) delivers the bristle damping \(\sigma _{1} \!=\! 2 \, \sqrt{ \, 0.41 * 80\,000 } \!=\! 362 \text{ Ns/m}\) as a first guess, which is also close to the corresponding values defined in Fig. 4.

4.3 Pulse load

The demonstration model 1 in Fig. 3 is used in [3] to simulate a start-stop experiment. The mass \(m\) is exposed to a pulse load \(F_{I}\), which is twice switched on and off. The relative velocity between the mass and the fixed horizontal plane is defined by \(v_{ij} = v_{m}\), where \(v_{m} = \dot{x}_{m}\) describes the velocity of the mass. The experiment was simulated in Matlab with different friction models.

The results are obtained with the standard implicit solver ode15s, where similar to [4], the fault tolerances were reduced to abstol=reltol=1e-8 to produce time histories of sufficient accuracy.

The pulsating load, with \(F_{I} \!=\! 2\text{ N}\) even below the dynamic friction force of \(F_{d} \!=\! 2.943\text{ N}\), makes the mass drift at each loading cycle, when simulated with the LuGre approach and the static regularized friction force, top left plot of Fig. 5. The regularized friction force as defined and illustrated in Fig. 4 for the demonstration model 1 requires a sliding velocity of \(v_{S0} \!=\! 0.1875\text{ mm/s}\) to generate a friction force, which counteracts the load. The first impulse with the force magnitude of \(F_{E} \!=\! F_{I}\) lasts for \(\Delta t \!=\! 0.1\text{ s}\) and results in the body displacement of \(\Delta x_{m} \!=\! 0.01875\text{ mm}\). The amount of pre-sliding, and as a consequence, the drift per load cycle directly depends on the regularization velocity \(v_{r}\), which is here adjusted via \(v_{r} \!=\! v_{A}/10\) to the attenuation velocity \(v_{A}\).

Fig. 5
figure 5

Pulse load simulation results with an impulse of \(F_{I} \!=\! 2\text{ N}\) and a column by column comparison of the LuGre model (solid lines) with different friction models plotted as dashed lines. The abbreviations static, impl., and bm2 name the simple static regularized friction model, the implicit bristle model, and the second-order bristle model with asymmetric regularized friction. Small circles mark the differences in the peak values of the body velocity

Full size image

The LuGre approach, which is supposed to maintain a stick, also generates a remaining body drift at each loading cycle. The LuGre drift, here \(\Delta x_{m} \!=\! 0.02129\text{ mm}\), in a hardly predictable manner depends on the visco-elastic properties of the fictitious bristle. The implicit (impl.) and the second-order bristle model (bm2), which are entirely based on the same model parameters as the LuGre approach, exhibit no drift at all, the second and third plots in the top row of Fig. 5. The body velocities \(v_{m}(t)\), plotted in the second row of Fig. 5, reveal that the LuGre approach reacts with different sensitivities when the load is applied or released. This is the consequence of the very poor approximation of the bristle dynamics and not, as stated in [3], the consequence of the nonlinear nature of the LuGre approach.

All dynamic friction models (LuGre, impl., asym.) generate a steady-state bristle deformation of \(z_{st} \!=\! F_{E} / \sigma _{0} \!=\! 0.0513\text{ mm}\) and exhibit overshoots in the time histories of the friction forces \(F_{R}=F_{R}(t)\), the third and forth rows of Fig. 5. The implicit bristle model requires additional efforts to solve the nonlinear and ambiguous first-order differential equation. The second-order bristle model is just as easy to use as the LuGre approach and is therefore applied as reference for further studies.

If the pulse load is increased to the value of \(F_{I} \!=\! \!=\! 4.5\text{ N}\), which is larger than the dynamic friction force \(F_{d} \!=\! 2.943\text{ N,}\) but still significantly smaller than the static friction force \(F_{s} \!=\! 5.886\text{ N}\), the LuGre approach fails (see Fig. 6). The poor approximation of the bristle dynamics results in a very low break-away force, which makes the LuGre approach to slip rather than to maintain stick. As a consequence, the resulting drift of the body amounts to \(\Delta x_{m} \!\approx \! 20\text{ mm}\) after two load cycles, the right plot in top row of Fig. 6. The second-order bristle model (bm2) still produces results as expected. The time histories of the friction force \(F_{R}(t)\) and the bristle deformation \(z(t)\) look like a scaled version of the ones plotted in Fig. 5. The load increase from \(F_{I} \!=\! 3\text{ N}\) to \(F_{I} \!=\! 4.5\text{ N}\) results in increased steady-state bristle deformation of \(z_{st} \!=\! 0.1154\text{ mm}\).

Fig. 6
figure 6

Pulse load simulation results with an impulse of \(F_{I} \!=\! 4.5\text{ N}\) and comparison of LuGre versus second-order bristle model with asymmetric regularized friction (bm2)

Full size image

The influence of the bristle damping on the amount of overshoot in the dynamic friction force is illustrated in Fig. 7. The impulse load is further increased to \(F_{I} \!=\! 5.6\text{ N}\), which corresponds to 95% of the static friction force of \(F_{s} \!=\! 5.886\text{ N}\). The dashed black lines in the top plots show the time history of the corresponding external load \(F_{E}(t)\). A bristle damping of \(\sigma _{1} \!=\! 395\text{ Ns/m}\) used so far in the demonstration model 1 produces in the second-order bristle model with asymmetric regularized friction force (bm2) a dynamic overshoot in the friction force, which equals the static friction force and causes the mass to slide. In this case, the LuGre approach and the second-order bristle model generate similar results, as illustrated in the left plots of Fig. 7. The steady-state bristle deformation of \(z_{st} \!=\! 0.0755\text{ mm}\) just corresponds to the dynamic friction force, hereby.

Fig. 7
figure 7

Pulse load simulation results with an impulse of \(F_{I} \!=\! 5.6\text{ N}\) and comparison of LuGre versus second-order bristle model with asymmetric regularized friction (bm2) at bristle damping \(\sigma _{1}=395\text{ Ns/m}\) and \(\sigma _{1}=790\text{ Ns/m}\)

Full size image

An increased bristle damping reduces the dynamic overshoot. For demonstration purpose, the bristle damping was simply doubled. Now, the second-order bristle model with asymmetric regularized friction force (bm2) maintains a stick by increasing the steady-state bristle deformation to \(z_{st} \!=\! 0.1436\text{ mm}\), as shown in the right plots of Fig. 7. However, the LuGre approach still produces a too-low break-away force and fails to maintain stick regardless of the bristle damping.

4.4 Stick-slip

The demonstration model 2 in Fig. 3 is used in [4] to simulate a stick-slip experiment. At the beginning, the mass is placed at the position \(x_{m}(t\!=\!0)\!=\!0\), where the spring with the stiffness \(k\) is unloaded, and the mass moves with the belt velocity \(v_{m}(t\!=\!0)\!=\!\dot{x}_{m}(t\!=\!0)\!=\!v_{b}\) in the horizontal direction. The results, obtained with the LuGre approach, the static regularized friction model (static), and the second-order bristle dynamics with asymmetric regularized friction force characteristics (bm2), are plotted in Fig. 8. The time histories of the mass displacement \(x_{t}\), the mass velocity \(v_{m}(t) = \dot{x}_{m}(t)\), and the friction force \(F_{R}(t)\) are supplemented by the computed friction force characteristics \(F_{R}(v_{S})\). According to Fig. 3, the sliding velocity is defined for the demonstration model 2 by \(v_{S}=v_{ij}-\dot{z} = v_{m}\!-\!v_{b}-\dot{z}\), where \(v_{b}\) denotes the belt velocity, and \(\dot{z}\) is the time derivative of the bristle deformation. As long as the mass sticks to the moving belt its displacement is simply defined by \(x_{m} = v_{b}\,t\), the spring with the stiffness \(k\) generates the force \(F(t) = k\,x_{m}(t)\). At \(t=t_{ba}\), the spring force equals the static friction force, and \(k\,x_{m}(t_{ba}) = k\,v_{b}\,t_{ba} = F_{s} = \mu _{s}\,F_{N}\) provide the time \(t_{ba} = \mu _{s}\,F_{N}/(k\,v_{b})\), where the first transition from stick to slip will occur. The parameters provided in Figs. 3 and 4 for the model 2 result in a break-away time of \(t_{ba} = 7.3575\text{ s}\). As indicated by the time histories of the velocity \(v_{m}(t)\) and the friction force \(F_{R}(t)\), all friction models can reproduce this break-away event fairly well. However, a closer inspection of the zoomed part of the friction force \(F_{R}(7.0 \!\le \! t \!\le \! 8.0)\) reveals that the LuGre approach (solid black line) delivers a too-early break-away. The friction characteristics for the demonstration model 2 applies the standard attenuation exponent of \(\alpha \!=\! 2\), which makes the friction characteristics \(\mu =\mu (v)\) start with a horizontal tangent as indicated in the lower left plot of Fig. 4. As a consequence, the transition from stick to slip is slightly delayed when simulated with the second-order dynamic bristle model (solid blue line). The simple regularization applied to the static friction model (static) delays this transition even more (dotted red line).

Fig. 8
figure 8

Time histories and computed friction characteristics of a stick-slip simulation performed with the LuGre approach, a static model with a regularized friction characteristics (static), and a second-order bristle model with asymmetric regularized friction (bm2). (Color figure online)

Full size image

At \(t \!\approx \! 10\text{ s}\) the first slip to stick event takes place. The lower right plot of Fig. 8 shows the friction force \(F_{R}(t)\) in the zoomed time interval of \(16.5\text{ s} \!\le \! t \!\le \! 17.5\text{ s}\) where the mass merges the second time from slip to stick. Due to accumulated time lags, the LuGre result (solid black line) differs significantly from the results of the static friction model (dotted red line) and the second-order bristle model (solid blue line). But worse, as indicated by far too low peak in the friction force time history, the LuGre approach cannot make use of the friction force potential, which is here characterized by a static friction force of \(F_{s} \!=\! 1.47\text{ N}\). The plots in Fig. 8 encompass all successful integration time steps. Hence, even single peak events would be visible. The upper right plot in Fig. 8 shows the computed friction characteristics \(F_{R}(v_{S})\). The solid blue line represents the results of the second-order bristle model. The asymmetric regularization can fully reproduce the friction characteristics as defined for the demonstration model 2 in Fig. 4. The dotted red line holds for the static friction model. The simple regularization significantly deviates just at small sliding velocities \(v_{S} \!<\! v_{r}\) from the pre-defined one. The solid black line applies for the LuGre results. The too poor approximation of the bristle dynamics in the LuGre approach generates a rather strange and ambiguous characteristics, which deviates remarkably from the pre-defined one. It even produces sliding friction forces significantly smaller than the dynamic friction force, \(F_{R}(v_{S} \!\ne \! 0) \!<\! F_{d}\). This severe drawback of the LuGre approach has been already detected in [5]. Oddly enough, the friction force \(F_{R}\) is plotted there not versus the sliding velocity \(v_{S}\) but versus the relative velocity \(v_{ij}\) between the body and the belt, which neglects the deformation of the fictitious bristle and holds just for a steady-state sliding.

5 Festoon cable system model as a more practical application

5.1 Modeling approach

Figure 9 shows a typical festoon system, which consists of a cable, a rail, end clamps, cable trolleys, and a towing trolley. The weight of the cable festoons make the cable trolleys follow the movements of the towing trolley. Rubber buffers soften potential collisions of the cable trolleys. In a multibody approach, each festoon is modeled by a simple lumped mass system consisting of a point mass and two rope elements.

Fig. 9
figure 9

Typical crane festoon system, corresponding multibody model, and parameters

Full size image

The coordinate \(u_{TT}\) describes the horizontal motions of the towing trolley, which is simply pre-defined as a function of time \(u_{TT}=u_{TT}(t)\) in this example. The cable trolleys of mass \(m_{T}\) move along the horizontal rail. The coordinates \(x_{T1}\) and \(x_{T2}\) define their momentary positions. The positions of the lumped cable masses \(m_{C}\) are described by \(x_{C1}\), \(z_{C1}\) to \(x_{C3}\), \(z_{C3}\). The parameters \(\ell _{0}\), \(k^{+}\), \(c^{+}\) define the unloaded length as well as the stiffness and damping of each cable section. The superscript + indicates that each cable section is modeled as a rope, which just can transmit tension forces. For a continuous transition from an unstressed to a stressed rope, the dissipative part of each rope force is limited to the elastic part as described in Sect. 3.3.3 of [11] by the example of a bungee jumper.

Figure 9 also provides the parameters describing the multibody festoon system and the friction between the cable trolleys and the rail. The normal forces \(F_{N1}\!=\!F_{N2}\!=\!(m_{T}+m_{C})g \!=\! 22\text{ N}\) are applied to each cable trolley in a steady-state. A reference bristle force can be estimated by \(F_{Br} \!=\! 2\text{ N} \) because the static friction value \(\mu _{s}\) is comparatively small in this application. The roughly estimated reference bristle deformation of \(z_{r} \!=\! 5.0\,\mathrm{e-}5\text{ m}\) provides the bristle stiffness of \(\sigma _{0} \!=\! 2/0.00005 \!=\! 40\,000\text{ N/m}\). The reference mass of \(m_{r} \!=\! 2/9.81 \!=\! 0.2\text{ kg}\) derived from the reference bristle force finally delivers the aperiodic bristle damping \(\sigma _{1} \!=\! 2 \, \sqrt{ \, 0.2 * 40\,000 } \!\approx \! 180 \text{ Ns/m}\).

5.2 Simulation example

For a demonstration example, the movement of the towing trolling is defined by its velocity \(v_{TT} \!=\! \dot{u}_{TT}\). The rightmost plots of Fig. 10 provide the time histories of the towing trolley velocity \(v_{TT}(t)\) and its displacement \(u_{TT}(t)\). At the beginning (\(t=0\)), the towing trolley is placed at \(u_{TT}(t\!=\!0) \!=\! 1.5529\text{ m}\), and the festoon cable system is in a steady-state position. The horizontal distances of cable trolley T1 to the end clamp, cable trolley T2 to T1, and towing trolley TT to T2 are equally spaced, and the lumped cable masses C1, C2, and C3 are centered in between with equal sags of \(z_{C1}\!=\!z_{C2}\!=\! z_{C3} \!=\! 0.967\text{ m}\). The towing trolling movement consists of a small and slow to and fro motion (\(0\text{ s} \le t \le 14\text{ s}\)) followed by a rather fast festoon expansion maneuver (\(14\text{ s} \le t \le 24\text{ s}\)).

Fig. 10
figure 10

Trolley velocities and displacements as well as normal forces between the cable trolleys and the rail. (Color figure online)

Full size image

As done in Sect. 4.4, the friction forces between the cable trolleys and the rail are computed by three different friction models: the LuGre approach (solid black line), the static friction model (dotted red line), and the second-order bristle model (solid blue line). Some results are plotted in Fig. 10. At a first glance, the different friction models yield the same time histories of the cable trolley velocities \(v_{T1}(t)\), \(v_{T2}(t)\), the cable trolley displacements \(x_{T1}(t)\), \(x_{T2}(t)\), and the normal forces \(F_{N1}(t)\), \(F_{N2}(t)\) acting in the contacts between the cable trolleys and the rail. The motions of the trolleys \(x_{T1}(t)\), \(x_{T2}(t)\), and \(u_{TT}(t)\) cause the lumped cable masses C1, C2, and C3 to perform horizontal and vertical motions. The latter result in variations of the normal forces about the steady-state values of \(F_{N1}\!=\!F_{N2}\!=\!22\text{ N}\).

However, during the to and fro motion, the time histories of the cable trolley velocities \(v_{T1}(t)\) and \(v_{T2}(t)\), computed with LuGre approach, show some small but distinct deviations from the results obtained by the static friction and the second-order bristle model. The deviations at \(t \!\approx \! 10.3\text{ s}\) and \(t \!\approx \! 2.8\text{ s}\) as well as \(t \!\approx \! 11\text{ s}\) correlate with variations in the normal forces as indicated by their time histories \(F_{N1}(t)\) and \(F_{N2}(t)\) plotted in the lower row of Fig. 10.

According to the upper right plot in Fig. 8, the LuGre approach cannot reproduce the pre-defined friction characteristics dynamically. In the case of the festoon cable system, this drawback results in significant deviations between the pre-defined friction characteristics and the one computed via the LuGre approach (See Fig. 11). Even worse, a simple inspection of the dynamic friction characteristics \(\mu _{1}(v_{S1})\) and \(\mu _{2}(v_{S2})\) reveals differences, although the friction between the cable trolleys and the rail was modeled by the same set of parameters, as specified in Fig. 9. Hence, the LuGre friction approach is not reliable because it generates dynamic friction forces, which deviate from the pre-defined ones, and, in addition, it depends on the dynamics of the contacting bodies, in this example, the dynamic motions of the two cable trolleys are in contact with the rail and the oscillations of the lumped cable masses.

Fig. 11
figure 11

Pre-defined and computed friction characteristics during festoon cable system simulation. (Color figure online)

Full size image

The plots in the center and right column of Fig. 11 show the comparison of the pre-defined friction characteristics to the ones computed via the static and the second-order dynamic bristle model (bm2). The pre-defined friction relation \(\mu _{1} \!=\! \mu _{2}\) is reproduced by both of these friction models. The friction characteristics generated by the static friction model deviates just slightly from the pre-defined one, in particular, in the regularization ranges, \(|v_{S1}| \le \pm v_{r}\) and \(|v_{S2}| \le \pm v_{r}\). The friction characteristics computed via the second-order dynamic bristle model, which incorporates the asymmetric regularization, matches without any visible deviation the pre-defined friction characteristics.

The ratio of friction force over normal force provides the dynamic friction values as \(\mu _{1} = F_{R1}/F_{N1}\) and \(\mu _{2} = F_{R2}/F_{N2}\). The velocities of the cable trolleys \(v_{T1}\) and \(v_{T2}\) as well as the time derivatives of the bristle deformations \(\dot{z}_{1}\) and \(\dot{z}_{2}\) define the sliding velocities by \(v_{S1} = v_{T1} - \dot{z}_{1}\) and \(v_{S2} = v_{T2} - \dot{z}_{2}\), where the trivial relations \(\dot{z}_{1}=0\) and \(\dot{z}_{2}=0\) hold for the static friction model.

The plots in the lower row of Fig. 10 provide the time histories of the normal forces \(F_{N1}(t)\) and \(F_{N2}(t)\). The time histories of the friction forces \(F_{R1}(t)\) and \(F_{R2}(t)\) are plotted in Fig. 12. The second-order bristle model (bm2) and the static model generate nearly identical results, as illustrated in the plots in the top row of Fig. 12. Just minor deviations are visible at the end of the simulation interval. According to the velocity \(v_{TT}(t)\), pre-defined in the upper right plot of Fig. 10, the towing trolley comes to a sudden stop (\(v_{TT}(t) \!=\! 0\)) at \(t \!=\! 19\text{ s}\). As a consequence, the lumped cable masses as well as the cable trolleys perform oscillations, which result in a series of stick-slip events, indicated by impulse-like changes in the friction forces. The stick-slip phenomena, studied in Sect. 4.4 by the rather simple standard example of a conveyor belt, incorporates just a “single-sided” event, where the friction force \(F_{R}\), displayed in Fig. 8, exhibits sudden changes but not a change of sign. This practical and more complex example of a festoon cable system includes “two-sided” stick slip events characterized by sudden sign changes in the time histories of the friction forces \(F_{R1}(t)\) and \(F_{R2}(t)\) at the end (\(t > 19\text{ s}\)) of the expansion maneuver. The LuGre approach cannot handle these sudden sign changes properly. Throughout this paper, a friction force \(F_{R}=F_{R}(v_{S})\) is defined to act into the opposite direction of the sliding velocity \(v_{S}\). Hence, the relations \(F_{R}(v_{S}) > 0\) if \(v_{S} > 0\) and \(F_{R}(v_{S}) < 0\) if \(v_{S} < 0\) will apply for realistic friction forces. The green lines in Fig. 11 represent the pre-defined friction characteristics \(\mu _{1}(v_{S1}) = \mu _{2}(v_{S2})\). They are entirely located in the first and third quadrant of the \(\mu (v_{S})\)-diagrams. The LuGre approach produces friction values \(\mu _{1}\) and \(\mu _{2}\), which do not only differ in magnitude but are also partly located in the second and fourth quadrant, thus contradicting the dissipative nature of friction.

Fig. 12
figure 12

Friction forces between the cable trolleys and the rail computed with different friction models

Full size image

The festoon cable system approaches at \(t \!\approx \! 23\text{ s}\) a steady-state position, where the static friction model mainly operates in the regularization range by approximating stick by creep. The friction forces computed by the LuGre approach differ in parts considerably from the ones generated by the second-order bristle model (bm2), plots in the bottom row of Fig. 12. As already discussed in Sect. 4.4, the LuGre approach is not able to make use of the friction force potential, which, in particular, results in significantly lower peak values during the stick-slip events in the time interval \(19\text{ s} \!\le \! t \!\le \! 23\text{ s}\). In addition, the magnitude of the LuGre friction forces differ in the time intervals \(4\text{ s} \!\le \! t \!\le \! 11\text{ s}\) and \(12\text{ s} \!\le \! t \!\le \! 14\text{ s}\) considerably from the ones generated by the second-order bristle model. Both time intervals are related to the to and fro motion, which is studied in the following in more detail.

The Matlab implementation of the LuGre approach is double-checked by a festoon model realized in Adams, where the LuGre friction model is now available as a standard friction element. For simplicity, the cable sections were modeled in Adams by simple spring damper elements because, in this particular application, the rope feature was not activated at all. Figure 13 shows perfectly consistent time histories of the friction forces \(F_{R1}\) and \(F_{R2}\) between the cable trolley and the rail, which verifies the Matlab results by system relevant signals. The broken lines mark the friction potential, defined by the static and dynamic friction forces, which in a steady-state are given here by \(|F_{s}^{st}| = \mu _{s}\,F_{N2} = 0.08 * 22\text{ N} = 1.76\text{ N}\) and \(|F_{d}^{st}| = \mu _{d}\,F_{N2} = 0.05 * 22\text{ N} = 1.10\text{ N}\). The LuGre approach realizes just a poor approximation of the bristle dynamics and cannot make use of the full friction potential, not even during the rather slow to and fro motion in the time interval \(0\text{ s} \!\le \! t \!\le \! 14\text{ s}\).

Fig. 13
figure 13

Friction forces at cable trolley 1 and 2 computed with the LuGre friction model in Adams and Matlab as well as the steady-state friction limits. (Color figure online)

Full size image

The runtime performance of the three friction models is quite similar. It takes a small personal computer \(1.151\text{ s}\) to perform the festoon cable simulation with the LuGre friction model, \(0.901\text{ s}\) with the static friction model, and \(1.292\text{ s}\) with the second-order bushing model. As done in Sect. 4.3, the Matlab standard implicit solver ode15s with reduced fault tolerances of abstol=reltol=1e-8 was used to carry out the simulations.

5.3 To and fro motion in more detail

Figure 14 provides a zoomed view on the cable trolley displacements during the to and fro motion of the towing trolley. In the time interval \(0\text{ s} \!\le \! t \!\le \! 14\text{ s}\), the towing trolley performs a to and fro movement with an amplitude of \(\Delta u_{TT} \!=\! 0.5\text{ m}\) as defined by the corresponding plot in Fig. 10. This movement is designed such that the cable trolley 2 executes a similar but scaled motion, whereas the cable trolley 1 remains in a sticking position. The to and fro motion of the cable trolley 2 induces horizontal and vertical motions of the lumped cable mass 2. As a consequence, the cable section 3 applies a pulse load to the cable trolley 1, which in this particular case does not exceed the static friction force.

Fig. 14
figure 14

Trolley displacements during to and fro motion. (Color figure online)

Full size image

The second-order bristle model (bm2) reproduces this sticking event perfectly. The movements of the cable trolley 1 resulting from the displacement of the fictitious bristle are not visible even in the zoomed view on the left of Fig. 14. The cable trolley 2 is forced to copy the to and fro motion of the towing trolley, but the ambiguity of the Coulomb friction prevents the cable trolley 2 from returning into the initial position. The second-order bristle model (bm2) as well as the static friction model computes this remaining displacement as \(\Delta x_{T2} \!=\! 0.0179\text{ m} \!=\! 17.9\text{ mm}\). The static friction model approximates stick by a small creepage, which results here in a hardly visible displacement of the cable trolley 1 of \(\Delta x_{T1} \!=\! 0.0004\text{ m} \!=\! 0.4\text{ mm}\) at the end of the to and fro time interval.

The LuGre approach results in cable trolley displacements \(x_{T1}(t)\) and \(x_{T2}(t)\), which differ in the magnitude of centimeters from the ones obtained by the second-order bristle model (bm2). It makes the cable trolley 1 to break-away from its initial position \(x_{T1}(t\!=\!0\text{ s}) \!=\! 0.5176\text{ m}\) to \(x_{T1}(t\!=\!14\text{ s}) \!=\! 0.5384\text{ m}\). The break-away takes place at \(t \!\approx \! 10.3\text{ s}\) where, according to the lower left plot of Fig. 10, the normal force \(F_{N1}\) starts to perform some fluctuations. It is indicated in Fig. 10 by a small impulse in the time history of the velocity \(v_{T1}(t)\) but not visible in the time history of the cable trolley displacement because the overall movement \(x_{T1}(t)\) is plotted in the range from 0 to \(6\text{ m}\) and not, as done in the left plot of Fig. 14, zoomed to the interval \(0.51\text{ m} \!\le \! x_{T1} \!\le \! 0.54\text{ m}\).

The too poor first-step approximation of the bristle dynamics in the LuGre approach and no physical reason are responsible for this sudden and unexpected break-away.

The LuGre approach delivers in comparison to the second-order bristle model (bm2) a smaller amplitude and finishes the to and fro motion with a much larger offset. The larger offset of the cable trolley 2 at \(t \!=\! 14\text{ s}\) is also a consequence of the break-away event of the cable trolley 1 at \(t \!\approx \! 10.3\text{ s}\).

Figure 15 shows the influence of the friction parameters \(\mu _{s}\) and \(\mu _{d}\) on the displacements \(x_{T1}\) of the cable trolley 1. The friction parameters, defined in Fig. 9, are hereby slightly (\(\pm 10\)%) decreased or increased. The to and fro motion starts, according to Fig. 10, at \(t \!=\! 3\text{ s}\). Shortly afterward, the cable trolley 1 begins to move, when the friction level is reduced by 10%. This movement is reproduced by each of the friction models. The results for the standard friction values, plotted in Fig. 15 as solid gray lines, are already discussed and serve just as a reference. The standard friction values (\(\mu _{s} \!=\! 0.080\) and \(\mu _{d} \!=\! 0.050\)) are large enough to keep the cable trolley 1 sticking to the rail throughout the to and fro motion. The static friction model and the second-order bristle model (bm2) can approximate or reproduce this situation, as illustrated in Fig. 14 and by the solid gray lines in the center and right plots of Fig. 15. As stick means stick, a friction level increased by 10% has no visible influence on the results obtained by the static and the second-order bristle model (bm2). This fact is demonstrated by the coincidence of the dotted brown and the solid gray lines in the center and the right plot of Fig. 15.

Fig. 15
figure 15

Influence of the friction parameters \(\mu _{s}\) and \(\mu _{d}\) on the displacements \(x_{T1}\) of cable trolley 1 computed with different friction models. (Color figure online)

Full size image
Listing 1
figure 16

Matlab script: app_examples.m

Full size image

The LuGre results differ significantly. The too poor approximation of the bristle dynamics cannot reproduce the pre-defined friction characteristics, as demonstrated for the standard friction values by the plots in the left column of Fig. 11. As a consequence, the sticking situation of the cable trolley 1 is not maintained, but transferred to a break-away event, partly induced by small fluctuations of the normal force. Increasing the friction level by 10% just reduces the break-away amplitude, but does not eliminate the event. It turned out, that the break-away event becomes insignificant only if the friction level is increased by 25% in this example. Hence, the sharp stick slip decision is softened in the LuGre approach to no or insignificant break-away, break-aways with increasing amplitudes, and immediate slip. This is not in conformity to the discrete nature of the Coulomb friction.

6 Conclusion

The LuGre approach is supposed to be based on the average behavior of elastic bristles. The setup of an implicit and nonlinear bristle model with a consistent dynamic friction force demonstrates that the LuGre approach just provides a first-step approximation to the nonlinear bristle dynamics and generates a fictitious dynamic friction force that deviates in parts strongly from the pre-defined friction characteristics.

In general, the implicit bristle model requires additional effort to solve the nonlinear and mostly ambiguous force balance at the top of the fictitious bristle. That is why the implicit bristle model is applied here just in rather simple standard examples.

A regularized static friction model is used as standard in many multibody system applications. The simple regularization approximates stick by slow creep and, therefore, cannot maintain long-term sticking periods. However, apart from the small regularization range, it reproduces the pre-defined friction characteristics quite well. The second-order bristle model, presented here, maintains long-term stick because it applies a sophisticated and asymmetric regularization of the friction characteristics. It reproduces the pre-defined friction characteristics extremely well, including the stick-slip transition. Both friction models perform, regarding the quality and reliability of the results as well as the computation effort, extremely well in the standard examples, as well as in the practical application of a festoon cable system.

The LuGre approach incorporates many drawbacks that are reported in the literature and demonstrated here by the standard examples as well as the practical application of a festoon cable system. Due to the too poor first-step approximation of the bristle dynamics, the LuGre approach cannot reproduce pre-defined friction characteristics dynamically. As demonstrated by the festoon cable system example, the LuGre friction forces are even influenced by the dynamics of the multibody system, which results in different friction forces applied to separate bodies, even if only one friction characteristics is defined. A decreased friction potential, which according to Coulomb results in a discrete switch from stick to slip, is smoothened by the LuGre approach to stick, break-aways with increasing amplitudes, and finally slip.

The LuGre approach generates just a friction-like behavior, which differs in part significantly from the reliable results obtained for example by the second-order bristle model. If friction is a crucial part in a multibody system, the LuGre approach does not appear to be an Engineer’s first choice because it is not a “what you see is what you get” model.