Abstract
Flexible multibody formulations allow the dynamic analysis of mechanisms with slender or thin-walled structures that deform during their operation. However, the majority of the existing flexible multibody methodologies are formulated assuming finite element models featuring 6 nodal degrees of freedom, specifically 3 translations and 3 rotations. This work initially revises the existing flexible multibody methodology in which the modeling of the flexibility is independent of the modeling of the baseline multibody system while ensuring the coupling between the rigid and flexible components. The flexible multibody methodology includes the use of suitable reference conditions, the component mode synthesis, and the virtual bodies methodology. Commonly, solid elements found in finite element software exclusively have three nodal translation degrees of freedom, featuring no explicit angular degrees of freedom. In this work, we propose the enhancement of the existing formulation for a rigid-flexible joint to support the use of virtual bodies rigidly connected to the nodes of solid elements. The computational implementation of the methodology is demonstrated using a benchmark case. The methodology developed in this work is further applied to study the dynamics of a locomotive with a flexible bogie frame. Although not influencing the overall vehicle dynamics, the bogie flexible multibody model allows the evaluation of the PSD of the accelerations in different points of the bogie that are sensitive to structural defects. The comparison of the response of healthy and damaged bogie frames supports the development of tools to monitor the condition of bogie frames during the operation. This development will be explored in forthcoming works, thus expanding the use of flexible multibody methodologies to new applications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Multibody methodologies are valuable tools to analyze the kinematics and dynamics of mechanical systems characterized by large displacements and rotations. These systems are commonly modeled as a combination of rigid bodies interconnected by force elements and kinematic joints. However, when structural deformations are not negligible, as is the case with slender and thin-walled structures subjected to high loads, the rigid-body formulations do not describe the physics of the problem accurately. However, even if the structural deformations are not expected to affect the general dynamic response of multibody models with bulky components, the identification of their structural behavior as a function of their operation profile may be required for other types of analysis.
The floating frame of reference formulation is a common approach to describe the configuration of a flexible body. Song and Haug [1] propose one of the first implementations of the floating frame of reference formulation. In this method the position and orientation of a local reference frame attached to the flexible body are described relative to a global reference frame, whereas the body structural deformations are described relative to that local reference frame. The finite element method is commonly used to describe the flexibility of the components of multibody systems. If a complex multibody structure is modeled using the finite element method, then the total number of nodal coordinates can be excessively high, thus preventing the efficient solution of the equations of motion and the integration of the system accelerations and velocities in a reasonable time. The component mode synthesis, originally proposed in the context of multibody dynamics by Shabana and Wehage [2], allows representing the deformations of the structure using a set of modes of vibration. As a result, a smaller set of modal coordinates replaces the larger set of nodal coordinates, improving the numerical efficiency of the simulation. Yoo and Haug [3] propose complementing the modes of vibration with static correction modes to incorporate the local deformations in the regions where kinematic joints and applied forces are present. Ambrósio and Gonçalves [4] introduce a formulation for linear elastodynamics that uses a lumped mass formulation for the flexible body, using the standard system matrices output from any finite elements software while describing the deformation of the flexible body relative to a nodal fixed reference frame. It is shown that the mass matrix becomes independent of the shape functions of the finite elements used while maintaining the coupling between rigid and flexible motions. This formulation is later extended by Neto et al. [5, 6] to study flexible multibody systems with composite materials. Zwölfer and Gerstmayr [7] propose an approach that prevents the need to solve the inertia shape integrals while also avoiding the lumped mass approach, involving a nodal-based derivation of the equations of motion. There are other important formulations in the context of flexible multibody dynamics, in particular, the absolute nodal coordinate formulation proposed by Shabana et al. [8–10], which are not considered in this work as no computational advantage over the floating frame formulation is observed for the type of applications envisaged in this work, i.e., dealing with linear elastodynamics. For the same reason, the use of alternative methods for the reduction of the number of nodal degrees of freedom, such as substructuring [11] or the Craig–Bampton method [12] are also not considered.
The use of reference conditions is required to ensure the uniqueness of the flexible body displacement field, i.e., to prevent the simultaneous description of the rigid-body displacements by two sets of independent coordinates. Among the choices of reference conditions, the nodal-fixed frame conditions, the mean axis conditions [13], and the principal axis conditions [14, 15] are cited in this work. The use of nodal-fixed frame conditions involves fixing one or more nodes of the flexible element mesh to the body local reference frame, which in some cases may require the introduction of undesired constraints on the flexible body deformation. This limitation prevents the use of the nodal-fixed frame conditions in the applications foreseen in this work. Alternatively, neither the mean axis conditions nor the principal axis conditions impose any constraint, by themselves, to the body deformation field. Although possible, the use of flexible bodies in which their elastodynamics is described by the node coordinates is not efficient computationally. Instead, of an extremely large number of nodal coordinates, often tremendous when the flexible body is described by hundreds of thousands or millions of modes, the use of coordinate reduction techniques allows involving only a limited number of elastic coordinates. When using the component mode synthesis, the modes of vibration associated with the lower natural frequencies are the most common choice. However, the type and selection of deformation modes, being these modes of vibration or static modes, is not only dependent on the selection of reference conditions, but also on the existing kinematic constraints and applied forces. The use of nodal-fixed frame reference conditions would require that constrained modes, compatible with the setting of the reference conditions, are used. However, when using mean or principal axis reference conditions, the use of free–free modes of vibration is required. In any case, to limit the number of vibration modes to represent properly the deformation field of a loaded or constrained flexible body, it is necessary to complement the modes of vibration with a set of static correction modes, obtained to account for local applications of forces or kinematic constraints, as described by Yoo and Haug [3].
The efficient modeling of kinematic joints is often overlooked when modeling mechanical systems with flexible bodies. Yoo and Haug [3] derive the kinematic constraint equations for a spherical joint, a universal joint, and a revolute joint connecting flexible bodies. Shabana [16] formulates a set of kinematic joints connecting flexible bodies using auxiliary local reference frames attached to the flexible bodies. Korkealaakso et al. [17] derive three basic constraints that can be used modularly to define kinematic joints between flexible bodies. In these examples the methods already available in a multibody code involving exclusively rigid bodies cannot be used, and completely new formulations are implemented to deal with flexible bodies. In alternative, the virtual bodies methodology, originally proposed by Bae et al. [18], allows the use of kinematic joints originally formulated to connect rigid bodies. In this method, a massless body is rigidly attached to a node of the flexible body through a single rigid-flexible joint. Gonçalves and Ambrósio [19] further develop the virtual bodies methodology and apply it on the model of a road vehicle. The authors demonstrate the convenience of avoiding the derivation of new kinematic joints while mitigating the costs in terms of computational efficiency by using sparse matrix solvers to compute the solution of the system of equations of motion of a flexible multibody system. However, neither the original formulation of the virtual bodies methodology [18] nor its enhanced formulation [19] focuses on the problem of meshes with only 3 nodal DoF. This work addresses this issue and proposes a method to overcome the numerical difficulties.
The flexible multibody formulation developed in this work is applied in the context of railway dynamics, which involves the complex interaction between the vehicle and track. In the wheel–rail contact interface, normal and tangential contact forces develop and subject both subsystems to forced vibrations. The dynamics of the railway vehicle are analyzed in different frequency ranges depending on the phenomena of interest [20]. The low-frequency range, limited to approximately 20–30 Hz, mostly concerns with the rigid-body motions, which are relevant from the point of view of comfort [21, 22] and stability [23–25]. An intermediate frequency range, up to the order of magnitude of 100 Hz, is associated with vehicle and track wear and degradation [26] and may require models to represent the flexibility of the track [27], the wheelset [28], or the bogie frame [29]. Higher-frequency ranges are mostly related to noise. Therefore it is in the midrange frequencies that the formulation proposed in this work finds its major field of application.
In this paper, we propose to further develop the formulation for the linear elastodynamics proposed by Ambrósio and Gonçalves [4]. The formulation of two reference conditions, i.e., mean axis and principal axis conditions, is considered for flexible models described by finite elements with only three displacement degrees of freedom per node, which is a common feature of solid finite element meshes. In the context of the virtual bodies methodology, we propose and formulate a rigid-flexible joint taking into account the fact that the nodes of solid elements do not have angular degrees of freedom. The formulation proposed in this work is first implemented and tested in the general purpose in-house multibody software MUBODyn [30], which includes a large collection of kinematic joints, force elements, imperfect kinematic joints [31], and a library of normal and friction contact force models [32, 33]. MUBODyn is also capable to simulate the wheel–rail contact [34–37], thus enabling the study of the effect of the structural flexibility of a bogie frame of a locomotive in the context of vehicle dynamics. The dynamic analysis of structural components with damage demonstrates the need for the methodologies proposed in this work and further expands the range of applications of flexible multibody dynamics.
2 Multibody dynamics
2.1 Equations of motion of a multibody system
We use the Cartesian coordinates as the basis for the proposed multibody formulation. The position of a body \(i\) relative to the global reference frame is expressed by the vector \(\mathbf{r}_{i} = \left [ \begin{array}{c@{\quad}c@{\quad}c} x & y & z \end{array} \right ]_{i}^{T}\), whereas the vector \(\mathbf{p}_{i} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} e_{0} & e_{1} & e_{2} & e_{3} \end{array} \right ]_{i}^{T}\) describes the rigid-body orientation using Euler parameters. The equations of motion and the constraint equations are expressed using the angular velocities \(\boldsymbol{\omega} ^{\prime}_{ i}\) and accelerations \(\dot{\boldsymbol{\omega}} ^{\prime}_{ i}\) of the rigid body. This option simplifies the mathematical formulations of the various features included in the program and reduces the number of unknowns in the full system of equations of motion. However, the angular velocities \(\boldsymbol{\omega} ^{\prime}_{ i}\) in the three-dimensional space are not exact differentials and cannot be integrated. Instead, the angular velocities \(\boldsymbol{\omega} ^{\prime}_{ i}\) are first transformed into time derivatives of the Euler parameters \(\dot{\mathbf{p}}_{ i}\), which can be integrated to obtain the Euler parameters \(\mathbf{p}_{ i}\) [38].
The bodies of a multibody system can be interconnected by perfect kinematic joints, imperfect kinematic joints, and force elements. Perfect kinematic joints [38] are described by algebraic equations, expressed in terms of the coordinates of the rigid bodies by defining the Jacobian matrix \(\boldsymbol{\Phi}_{\mathbf{q}}\) and the vector of the right-hand side of the acceleration equations \(\boldsymbol{\gamma}\). The Lagrange multiplier method is used to add these constraints to the system of equations of motion through the addition of the vector of Lagrange multipliers \(\boldsymbol{\lambda}\) to the vector of unknowns. Imperfect kinematic joints impose kinematic limitations on the relative motion, which can be modeled using contact penalty force formulations, as pursued in this work, thus contributing to the general force vector \(\mathbf{g}\). Alternatively, the internal contact in imperfect joints can be described via unilateral constraint formulations, which define the Lagrange multipliers \(\boldsymbol{\lambda}\), thus defined by kinematic constraints. Similarly, the force elements contribute to the force vector \(\mathbf{g}\) by developing forces due to the relative motion between the bodies. The resulting system of the equations of motion of a multibody system is expressed by
where the vector of the system accelerations is
A multibody simulation algorithm is depicted in Fig. 1. The algorithm for the solution and integration of the equations of motion is as follows: (i) set the initial time t0, the vector \(\mathbf{q}_{0}^{\#} \) of the initial positions of the bodies, and the vector \(\dot{\mathbf{q}}\) of the initial velocities of the bodies; (ii) assemble the mass matrix \(\mathbf{M}\), the Jacobian matrix associated with the constraint equations \(\boldsymbol{\Phi}_{\mathbf{q}}\), the force vector \(\mathbf{g}\), and the vector of the right-hand side of the acceleration constraint equations \(\boldsymbol{\gamma} \); (iii) solve the equations of motion to determine the vectors of the accelerations \(\ddot{\mathbf{q}}\) and Lagrange multipliers \(\boldsymbol{\lambda} \); (iv) determine the vector of the accelerations and velocities \(\dot{\mathbf{h}}_{t} = \left [ \begin{array}{c@{\quad}c} \dot{\mathbf{q}} & \ddot{\mathbf{q}} \end{array} \right ]_{t}^{T}\); (v) integrate the vector \(\dot{\mathbf{h}}_{t}\) to obtain the vector of the positions and velocities in the next time step \(\mathbf{h}_{t + \Delta t} = \left [ \begin{array}{c@{\quad}c} \mathbf{q} & \dot{\mathbf{q}} \end{array} \right ]_{t + \Delta t}^{T}\) by using an appropriate ordinary differential equations solver; (vi) update the time variable \(t\)=\(t\)+\(\Delta t\); (vii) stop simulation if \(t\)>\(t_{\mathrm{end}}\), or else go to step (ii).
Direct integration algorithm of the multibody simulation
The time integration of vector \(\dot{\mathbf{h}}_{t}\) is performed using the Gear algorithm [39], which has variable time step and variable order. The Baumgarte stabilization method [40] controls the constraint violations.
2.2 Equations of motion of a flexible body
The formulation for flexible bodies proposed by Ambrósio and Gonçalves [4] and later revisited by Neto et al. [5, 6] in the context of flexible multibody systems with composite materials is first reviewed and, subsequently, updated to deal with finite elements with nodes with only three displacement degrees of freedom. In this formulation the position of a node \(k\) in a flexible body \(i\) is expressed in the global reference frame by
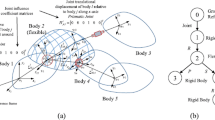
where \(\mathbf{r}_{i}\) is the position of body \(i\) in the global reference frame, as depicted in Fig. 2, and \(\mathbf{A}_{i}\) is the transformation matrix from local to global coordinates. The position of node \(k\) in the local reference frame of body \(i\) is given by
where \(\mathbf{x}^{\prime}_{k}\) is the undeformed position of node \(k\). Assuming that node \(k\) is characterized by three translational degrees of freedom and no rotational degrees of freedom, as is common in solid finite elements, the nodal displacements of node \(k\) are described by the vector \(\boldsymbol{\delta} ^{\prime}_{k}\).
Representation of the undeformed and deformed configurations of the flexible body
The differentiation of Eq. (3) renders the velocity of node \(k\) in the global reference frame, written as
where \(\tilde{\boldsymbol{\omega}} ^{\prime}_{i}\) is the skew-symmetric matrix of the vector of the angular velocities:
The properties of the skew-symmetric matrix allow rewriting Eq. (5) as
Equation (7) can be expressed using the vector \(\mathbf{q}_{i}\) of the velocities of flexible body \(i\):
where \(\mathbf{I}_{k}\) is the identity operator, which is a 3×3\(n\) matrix defined as
The vector \(\dot{\mathbf{q}}_{i}\) is defined using the absolute velocity coordinates associated with the rigid-body motion and the vector of nodal coordinates that describe the flexible body deformation velocities:
The kinetic energy of node \(k\) is
where \(m_{k}\) is the mass associated with the node, as in a finite element lumped mass formulation. Accordingly, the total kinetic energy of body \(i\) is the sum of the contributions from all the \(n\) nodes of the flexible body, given by
where \(\mathbf{M}_{i}\) is the mass matrix of the flexible body \(i\). The matrix \(\mathbf{M}_{i}\) is symmetric, and the appropriate algebraic operations result in
The structure of the matrix \(\mathbf{M}_{i}\) is independent of the formulation of the finite elements used, provided that the flexible component of the body inertia is described by a lumped mass matrix, instead of a consistent mass matrix, as shown by Ambrósio and Gonçalves [4].
The total elastic deformation energy of the flexible body is given by
where \(\mathbf{K}_{ff}\) is the global stiffness matrix of the flexible body, which can be derived from the description of the body flexibility using the finite element method.
The equations of motion are derived using the Lagrange equations
Using the definitions of the kinetic and elastic deformation energies presented in Eqs. (12) and (14) and replacing in Eq. (15) render the system of equations of motion of body \(i\):
where \(\mathbf{g}_{i}\) is the vector of external applied forces, with both rigid and flexible components, and \(\mathbf{s}_{i}\) is the vector of the quadratic velocity terms given by
The equations of motion of a constrained flexible multibody system result from using the Lagrange multipliers method to include the kinematic constraints. The system of equations of motion is
where \(\boldsymbol{\Phi}_{\mathbf{q}r}\) is the component of the Jacobian matrix associated with kinematic constraints between rigid bodies, and \(\boldsymbol{\Phi}_{\mathbf{q}f}\) is the component of the Jacobian matrix involving flexible bodies.
2.3 Reference conditions
The system of equations of motion described by Eq. (18) does not have a unique solution because the rigid-body motion is described by both the rigid and flexible displacement fields. The use of a set of reference conditions ensures the uniqueness of the flexible displacement field by defining a local reference frame used to describe the deformations of the flexible body. In turn, this reference frame is used to express the large spatial displacements and rotations of the body. In this section, we present the formulation of two different floating frame reference conditions assuming three translational nodal degrees of freedom, the principal axis conditions and mean axis conditions. In contrast to nodal fixed conditions, floating reference conditions allow the movement and rotation of the local reference frame relative to any node of the flexible body. The use of the nodal fixed conditions, despite being the most popular choice, presents notable disadvantages. First, the use of a node-fixed reference frame defines the basis to represent the deformations of the flexible body, which may not be compatible with the deformations sustained by the structure in a realistic scenario. Additionally, there are variable components of the mass matrix associated with the first moment of inertia; they are null if the center of mass of the flexible body coincides with the origin of the local reference frame, which is advantageous from a computational efficiency point of view. However, there is in general no guarantee that the center of mass of the flexible body is located in a material region of the body where finite element nodes are present, as, for example, in the case of a hollow sphere or a hollow tube. Moreover, in the presence of finite elements with only translation nodal degrees of freedom, it is not possible to fix the rotations of a single node to the reference frame of the flexible body. The use of finite elements with three degrees of freedom per node would require using three or more noncolinear nodes, implying further constraints in the deformation field of the flexible body.
The reference conditions are added to equations of motion of the flexible multibody system using the Lagrange multiplier technique, according to:
where \(\boldsymbol{\Phi}_{\mathbf{q}f}^{(rc)}\) is the Jacobian matrix associated with the selected reference conditions (\(rc\)), \(\boldsymbol{\lambda}^{(rc)}\) is the vector of the Lagrange multipliers for the reference conditions, and \(\boldsymbol{\gamma}^{(rc)}\) is the vector of the right-hand side of acceleration constraint equations of the reference conditions. Note that other strategies exist regarding the imposition of the reference conditions without using explicitly kinematic constraints, in particular, when applying fixed-node references. However, the explicit use of constraints for reference conditions is preferred in this work not only due to their generality but also because they allow us to keep the choice of elastic coordinates relatively independent from the selection of reference conditions.
2.3.1 Principal axis conditions
Under the principal axis conditions, the position of the local frame of a flexible body coincides with the instantaneous center of mass of the deformed configuration of the body. Additionally, the axes of the local reference frame are oriented parallelly to the principal axes of inertia of the flexible body in the deformed configuration [14]. The formulation of the principal axis conditions adopted in this work is analogous to that proposed by Nikravesh and Lin [15].
The three equations expressing that the position of the local reference frame is in the instantaneous center of mass of the deformed configuration of the body are
As a result, under the assumption of small and linear elastic deformations, the term associated with the first moment of inertia \(- \sum m_{k}\mathbf{A}_{i}\tilde{\mathbf{b}}^{\prime}_{k}\) in the flexible body mass matrix \(\mathbf{M}_{i}\) becomes negligible.
The axes of the reference frame are parallel to the principal axes of the flexible body if the products of inertia of the flexible body in the deformed condition are null. This condition is given by
The instantaneous inertia tensor is given by the symmetric matrix that includes the moments and products of inertia:
Assuming the use of finite elements with nodes with three translation degrees of freedom, the inertia tensor is given by
After the adequate mathematical operations, the entries of the matrix \(\mathbf{J}\) are
The products of inertia of the flexible body are identified as
The six position constraint equations associated with the principal axis conditions are combinations of Eqs. (20), (21), and (25), resulting in
The six velocity constraint equations resulting from the principal axis conditions are defined by
which is expressed in a compact form as
where the right-hand side vector of the velocity constraint equations \(\boldsymbol{\nu}^{(pa)}\) is null, and \(\boldsymbol{\Phi}_{\mathbf{q}_{f}}^{(pa)}\) is the Jacobian matrix of the principal axis conditions, which can be divided into two components. The translational component is a 3×3\(n\) matrix, which includes contributions from all the \(n\) nodes, is given by
and the angular component of the Jacobian matrix, for which the contribution from each node is
The full Jacobian matrix of the principal axis conditions is a 6×3\(n\) matrix given by
The six acceleration constraint equations result from the time differentiation of Eq. (27) and are expressed by
where \(\boldsymbol{\gamma}^{(pa)}\) is the right-hand side vector of the acceleration constraint equations given by
The use of the principal axis conditions is limited to flexible bodies with a unique set of principal axes. If at least two principal moments of inertia are equal, then there is no unique set of principal axes, and the formulation presents a singularity. Consequently, the system of equations of motion has no unique solution.
2.3.2 Mean axis conditions
Under the mean axis conditions, the local frame of a flexible body is positioned and oriented in such a way that the kinetic deformation energy is minimized relative to an observer attached to the local reference frame [13]. The mean axis conditions are defined by the stationarity of the kinetic deformation energy. Assuming the use of finite elements featuring nodes with three translational degrees of freedom, the total kinetic deformation energy of the flexible body is
The partial derivatives of the deformation kinetic energy relative to the translational and angular velocity vectors are
The stationarity of the kinetic deformation energy implies that Eq. (35) is null. Bearing in mind that the matrix \(\mathbf{A}_{i}\) is not singular, the velocity constraint equations of the mean axis conditions are defined by
which can be expressed by
The Jacobian matrix associated with the mean axis conditions in terms of the nodal translations is
The six acceleration constraint equations are determined by the time differentiation of Eq. (37) and are given by
It is worth noting that the Jacobian matrix in Eq. (38) comprises the terms of the mass matrix \(\mathbf{M}_{i}\) associated with the inertial coupling between the rigid- and flexible-body motions shown in Eq. (13). The inspection of Eq. (36) reveals that under the mean axis conditions the rigid and flexible motions of the flexible body are decoupled, allowing the simplification of the mass matrix \(\mathbf{M}_{i}\) through the elimination of the inertia coupling terms.
2.4 Virtual bodies methodology
The in-house multibody software MUBODyn used in this work features an extensive library of perfect and imperfect kinematic joints, originally formulated to connect rigid bodies in any conventional mechanical system. However, the connection between rigid and flexible bodies, as well as between flexible bodies, requires the formulation of new kinematic joints using the variables associated with the vector of nodal deformations of the flexible body \(\boldsymbol{\delta} ^{\prime}\) and its time derivates. Alternatively, the virtual bodies methodology allows the use of the original library of kinematic joints for flexible bodies with the support of a single rigid-flexible kinematic joint that rigidly connects a flexible body to a massless virtual body on a fixed location [18]. Kinematic joints connecting two flexible bodies, or a rigid and a flexible body, are defined between the respective virtual bodies and the original kinematic joints. It is clear that the use of virtual bodies increases the number of rigid-body coordinates and, consequently, the dimension of the system of equations of motion. Additionally, because virtual bodies are massless rigid bodies, they contribute to the ill-conditioning of the mass matrix \(\mathbf{M}_{i}\). However, the use of sparse matrix solvers allows mitigating the numerical difficulties and achieving computational efficiency when solving the system of equations of motion, as shown by Gonçalves and Ambrósio [19]. Therefore the virtual bodies methodology becomes a practical solution to make the most of existing libraries of kinematic joints by avoiding the laborious task of developing new kinematic joints specifically for flexible bodies while maintaining acceptable computational efficiency and algorithm robustness.
2.4.1 Formulation of a rigid–flexible joint
The virtual bodies methodology allows defining standard kinematic joints between rigid bodies instead of directly using the flexible body elastic coordinates. For this purpose, the virtual body must be connected to one or more nodes of the flexible body through a rigid–flexible joint. The formulation of the rigid–flexible joint requires the definition of six position constraint equations. In this work, we assume that the position of the local frame of the virtual body \(j\) coincides with the deformed position of a node \(k\) of the flexible body \(i\). Additionally, the relative orientation of the virtual body and the reference frame fixed to node \(k\) is invariant in time.
Translation component of the constraints
The definition of the three position constraint equations associated with the translations is equivalent to the description of a spherical joint connecting a rigid body \(j\) and a node \(k\) of the flexible body \(i\). The three position constraint equations are
The velocity constraint equations are the time derivative of Eq. (40) given by
Therefore the Jacobian matrix associated with the translation component of the rigid–flexible joint is
and the right-hand side vector of the velocities is null,
The acceleration constraint equations are the time derivative of Eq. (41) expressed by
Consequently, the right-hand side vector of the accelerations is defined by
Angular component of the constraints
The constraint equations associated with the angular coordinates depend on the number of nodal degrees of freedom. The rigid–flexible joint proposed by Gonçalves and Ambrósio [19] is formulated assuming the connection between the virtual body and a node of the flexible structure with six nodal degrees of freedom, i.e., three infinitesimal displacements and three infinitesimal rotations. The three nodal rotations define a reference frame attached to the node, and the relative orientation between the nodal reference frame and the local frame of the virtual body is invariant in time. However, when the nodal rotational degrees of freedom are not explicitly defined or do not exist, for example, using conventional solid finite elements, the angular component of the constraint must be defined differently. Assuming that the vicinity of node \(k\) is populated by other nodes, it is possible to define a reference frame using the positions of two neighboring nodes \(m\) and \(n\) and orthogonality conditions if nodes \(k\), \(m\), and \(n\) are not collinear, as depicted in Fig. 3.
Schematic representation of local coordinate systems of flexible body \(i\) and virtual body \(j\) for a rigid–flexible joint
The vector \(\mathbf{e}^{\prime}_{i1}\) is the unit vector parallel to the vector that connects nodes \(k\) and \(m\), in the local reference frame of the flexible body, according to
Likewise, the auxiliary vector \(\mathbf{a}^{\prime}_{i}\) is the unit vector parallel to the vector that connects nodes \(k\) and \(n\), in the local reference frame of the flexible body, given by
The vector \(\mathbf{e}^{\prime}_{i2}\) is the unit vector perpendicular to both \(\mathbf{e}^{\prime}_{i1}\) and \(\mathbf{a}^{\prime}_{i}\), in the local reference frame of the flexible body, expressed by the cross product between \(\mathbf{e}^{\prime}_{i1}\) and \(\mathbf{a}^{\prime}_{i}\) divided by the norm:
The vectors \(\mathbf{e}^{\prime}_{i1}\), \(\mathbf{e}^{\prime}_{i2}\), and \(\mathbf{a}^{\prime}_{i}\) define a reference system that can be used to express the position constraint equations of the rigid–flexible joint, stating that the relative orientation of the reference frame of the virtual body \(j\) and the auxiliary reference system defined in body \(i\) is invariant in time. The orientation of the local frame of the virtual body \(j\) is given by the vectors that define the columns of the respective transformation matrix given by
The invariance of the relative orientation of the reference frames is expressed by three of the nine dot products between the unit vectors that are parallel to the axes of the reference frames. The three dot products used for the position constraint equations considered are arbitrarily selected as
where \(\beta _{12}^{0}\), \(\beta _{13}^{0}\), and \(\beta _{23}^{0}\) are the cosines of the initial angles between the axes of the reference frames.
The velocity constraint equations are the time derivative of Eq. (50) expressed by
where \(\dot{\mathbf{e}}^{\prime}_{i1}\) and \(\dot{\mathbf{e}}^{\prime}_{i2}\) must be expressed using the vector of nodal velocities \(\dot{\boldsymbol{\delta}} ^{\prime}_{i}\). The vector \(\dot{\mathbf{e}}^{\prime}_{i1}\) is the time derivate of the unit vector \(\mathbf{e}^{\prime}_{i1}\) and is given by
Likewise, the vector \(\dot{\mathbf{e}}^{\prime}_{i2}\) is the time derivate of the unit vector \(\mathbf{e}^{\prime}_{i2}\):
The time derivative of vector \(\mathbf{a}^{\prime}_{i}\) is given by
Substituting Eqs. (52) and (54) into Eq. (53) renders
The velocity constraint equations can be expressed in the form
where \(\boldsymbol{\nu}^{(rf,\mathit{rot})}\) is the right-hand side vector of the velocity constraint equations, which includes the terms independent of \(\dot{\mathbf{q}}_{i}\), the vector of the velocities of body \(i\). The Jacobian matrix associated with the angular component of the rigid-flexible joint is
where the matrix \(\mathbf{D}\) is given by
The right-hand side vector of the velocity constraint equations is
The acceleration constraint equations are the time derivative of Eq. (51) and can be expressed in the form
where \(\boldsymbol{\gamma}^{(rf,\mathit{rot})}\) is the right-hand side vector of the acceleration constraint equations that collects the terms independent of the acceleration vector \(\ddot{\mathbf{q}}_{i}\). The first term of the right-hand side vector of the acceleration constraint equations is
and, similarly, the second term of the right-hand side vector of the acceleration constraint equations is
Finally, the third term of the right-hand side vector of the acceleration constraint equations is
The proposed formulation of the angular component of the rigid-flexible joint presents singularity conditions that must be avoided to guarantee the stability of the computational implementation. If the Jacobian matrix includes null rows, then the matrix of the system of equations of motion is rank-deficient, and there is no solution. For instance, this is the case if any of the following equations is true during the dynamics analysis:
Other singularity conditions exist, but it is not the aim of this section to present a comprehensive survey of all the possibilities.
2.4.2 Computational implementation of the rigid–flexible joint
The computational implementation of the rigid–flexible joint can be enhanced by a systematic methodology to define the joint data with minimum external input. The algorithm is graphically depicted in Fig. 4 and must be performed at an initialization stage prior to the simulation. Node \(k\) is the nearest node to the attachment point \(P_{i}\). The candidates to node \(m\) are iteratively evaluated, and node \(m\) is the second nearest node to point \(P_{i}\), which ensures that the singularity conditions described by Eqs. (65) and (66) are not fulfilled in the first time step. Subsequently, the candidates to node \(n\) are iteratively assessed, and node \(n\) is the third nearest node to point \(P_{i}\), which guarantees that the singularity conditions expressed by Eqs. (64) and (67) do not occur in the first time step of the analysis. The computational implementation of the algorithm requires the definition of a tolerance tol to assess the collinearity conditions described by Eqs. (64)–(67).
Algorithm for the initialization of the rigid–flexible joint
2.5 Component mode synthesis
The analysis of the flexibility of complex structures requires the solution of large systems of equations of motion and the integration of a significant number of nodal coordinates. One of the standard methodologies to reduce the number of elastic coordinates is the component mode synthesis [41]. In this approach the time-dependent variables are separated from the geometry-dependent variables. The modes used in this methodology can be the natural modes of vibration, static correction modes, or other modes of deformation. In this work, we consider the natural modes of vibration associated with the lower natural frequencies under the assumption that deformations are small and the material is linear elastic. The nodal displacements are approximated by a weighted sum of the modes of vibration associated with the natural frequencies of the structure:
where \(\mathbf{X}\) is the geometry-dependent modal matrix, and \(\mathbf{w}\) is the time-dependent vector of the contributions of the \(m\) modes of vibrations, deemed as elastic coordinated. The time-variant nodal coordinate vector \(\boldsymbol{\delta} ^{\prime}_{i}\) is thus transformed to the time-variant modal coordinate vector \(\mathbf{w}\). The time-invariant modal matrix \(\mathbf{X}\) is obtained by solving the generalized eigenvalue problem described using the finite element model of the flexible body:
The \(m\) columns of the matrix \(\mathbf{X}\) are the constant vectors \(\mathbf{x}_{m}\) of the modes of vibration related to the \(m\) natural frequencies \(\omega _{m}\) considered. Each row of the modal matrix \(\mathbf{X}\) is associated with one of the nodal coordinates of the \(n\) nodes. The matrix \(\mathbf{X}\) is time-invariant, and therefore the nodal velocities and accelerations are
If the \(m\) columns of the matrix \(\mathbf{X}\) associated with the vectors of the modes of vibration are normalized with respect to the flexible component of the diagonalized mass matrix of the flexible body \(\mathbf{M}_{ff}\), then the modal orthogonality properties apply:
where \(\boldsymbol{\Lambda} \) is a diagonal matrix containing the squares of the natural frequencies \(\omega _{m}^{2}\) associated with the modes of vibration.
The transformation from nodal to modal coordinates implies a modification of the system of equations of motion. Replacing Eqs. (68) and (71) in Eq. (18) renders
Premultiplying the second row of Eq. (74) by \(\mathbf{X}^{T}\) and using the orthogonality properties, the system of equations of motion is expressed by
The number of flexible coordinates of the system is thus reduced from 3\(n \) to \(m\). Prior to this subsection, the infinitesimal nodal translation vector \(\boldsymbol{\delta} ^{\prime}_{i}\) and its time derivatives are expressed using the nodal coordinates. Those equations can be modified to account for the transformation from nodal to modal coordinates in accordance with Eqs. (68), (70), and (71).
Generally, free–free modes, i.e., modes of vibration obtained considering a fully unconstrained finite element mesh for the flexible body, can be used with mean axis and principal axis reference conditions. However, if nodal-fixed frame conditions are used, which is not the case in this work, then the application of constrained modes of vibration compatible with the reference conditions is necessary, as fewer modes are required to represent the same displacement field. We also must reemphasize that the modes of vibration alone cannot represent very localized deformations of the flexible body, such as those due to kinematic constraints and the application of forces. The number of modes required would increase dramatically, thus reducing the computational efficiency. Instead, the set of nodes of vibration is complemented by a set of static correction modes carefully generated to account for local deformations. A methodology for the generation and use of such models is presented by Yoo and Haug [3] and is not reviewed in this work.
Figure 5 provides an overview of the data flow required to apply the flexible multibody methodology presented in Sect. 2. Using this strategy, the tasks of modeling the flexible bodies and the mechanism are performed independently. For example, different models of the flexible body can be used interchangeably without the need to modify the baseline rigid-body model.
Overview of the data flow of the flexible multibody methodology applied
3 Demonstration using a flexible slider-crank mechanism
The flexible multibody formulation presented in this work is demonstrated with a slider-crank mechanism, which is a conventional benchmark widely discussed and tested in the literature [4, 42, 43]. The mechanism includes a rigid rotating crank, a rigid slider, and a flexible connecting rod, as depicted in Fig. 6. The flexible rod has a circular cross-section. Table 1 presents the geometrical and mechanical characteristics of the mechanism. Initially, the flexible rod is oriented horizontally and is in the undeformed configuration.
Schematic representation of the flexible slider-crank mechanism
Using a 3D CAD software, the flexible connecting rod is modeled in the undeformed geometry, and the reference frame is positioned in its instantaneous center of mass. The geometrical model is exported to a finite element software, and the rod is discretized using structural 3D 10-node tetrahedral solid elements, in a total of 6283 nodes. A modal analysis of the structure in free–free conditions is performed to obtain the flexible body modeling data required by the multibody software MUBODyn: the vector of the squares of the natural frequencies \(\boldsymbol{\Lambda}\), the matrix of the modes of vibration \(\mathbf{X}\), and the diagonalized mass matrix of the flexible body \(\mathbf{M}_{ff}\). The six rigid-body modes, as well as the flexible modes of vibration associated with the eight lowest natural frequencies, corresponding to four bending modes, are all used to describe the deformations of the flexible connecting rod. The virtual bodies methodology is used to connect the flexible rod with the spherical joint in one end and the cylindrical joint in the opposite end, as illustrated in Fig. 6.
3.1 Mean axis conditions
The reference conditions considered in this simulation are the mean axis conditions. The principal axis conditions are disregarded because they are not applicable to the connecting rod, which has cylindrical symmetry. Figure 7 shows the longitudinal acceleration of the slider over time, considering both a fully rigid model and the model with a flexible connecting rod. As expected, the acceleration of the slider is unaffected by the flexibility of the rod, because the deformations are small.
Acceleration of the slider considering a rigid model and the flexible model
The quantity used to assess the computational implementation of the flexible multibody formulation, by comparison with previous results from the literature, is the deflection of the midpoint of the connecting rod. This deflection \(\delta \), shown in Fig. 8, is measured relative to the undeformed position of the rod and is normalized by the length of the rod. Figure 8 shows that the maximum normalized value of the deflection in the initial moments of the simulation is 0.0105, which is consistent with the results published in various sources in the literature [4, 42, 43]. The results suggest the formulation of the mean axis conditions, and the rigid–flexible joint considering three nodal degrees of freedom are correctly derived and implemented in the computer code.
Normalized deflection of the midpoint of the flexible connecting rod
3.2 Principal axis conditions
The principal axis conditions can be used only if the set of principal axes of the flexible body is unique, i.e., the principal inertias of the flexible body are all different. That is not the case for the flexible connecting rod with a circular cross-section. Consequently, the benchmark case is adapted to allow the verification of the implementation of the principal axis conditions. This is achieved by replacing the circular cross-section by a rectangular cross-section while ensuring that the cross-section area and the second moment of area relative to the \(y\) axis, perpendicular to the plane of motion, remain the same as in the original benchmark problem. This way the mass, inertias, and the bending stiffness in the X-Z plane of both models are preserved.
Figure 9 depicts the normalized deflection of the midpoint of the connecting rod considering the rectangular cross-section and using the principal axis conditions and the mean axis conditions. The results using the two types of reference conditions are virtually coincident and match the results shown in Fig. 8 using the circular cross-section.
Normalized deflection of the midpoint of the flexible connecting rod considering a rectangular cross-section for the mean axis conditions (MAC) and principal axis conditions (PAC)
The results obtained show that both mean axis and principal axis conditions lead to equivalent results. The computational time required to run the simulation is similar for both reference conditions. Consequently, computational efficiency is not a factor to select one of the reference conditions over the other. In any case, it must be emphasized that the principal axis conditions have the drawback of not being applicable to bodies with more than one possible set of principal axes. Still, the principal axis conditions guarantee that the origin of the local reference frame of the flexible body is always coincident with the body center of mass.
4 Dynamics of a locomotive with flexible bogie frame on a realistic track
The work presented contributes to the broader aim of defining a strategy to monitor the structural condition of the bogie frame of a locomotive. The bogie frame is the only flexible body of the multibody model of the railway vehicle, which is described using approximately 45000 structural 3D 10-node tetrahedral solid finite elements. The vehicle is simulated in realistic operation conditions to obtain the dynamic response of the locomotive with an emphasis on the bogie frame. In this section, we present the flexible multibody methodology applied, a verification of the baseline vehicle model, and a demonstration of how the flexible multibody methodologies can be used for purposes other than those traditionally associated with standard vehicle dynamics.
4.1 Multibody model of the locomotive
The vehicle is a meter-gauge diesel-electric locomotive depicted in Fig. 10. The vehicle body is supported by two bolsters through cylindrical pivots. The primary suspension of the locomotive connects the axle boxes with the bogie frame through vertical helicoidal springs and hornguides that provide lateral and longitudinal clearance between the axle boxes and bogie frame, as well as friction damping. The secondary suspension connects each bogie frame with the respective bolster with sets of rubber springs. Each bogie rests on three powered axles driven by independent electric traction motors.
Schematic representation of the locomotive and different elements [44]
Two multibody models of the locomotive are developed to run the simulations. One model is composed by rigid bodies, whereas in the other the rigid front bogie frame is replaced by a flexible bogie frame. The locomotive models used in this work are an adapted version of the rigid-body model presented by Millan et al. [44]. The adaptation consists of a simplification of the models of the primary suspension, which connects the bogie frame and the axle boxes. The relevant modifications are the replacement of the imperfect cylindrical joints, which model the clearances and friction damping phenomena by vertical linear dampers in parallel with the existing vertical linear springs. Additionally, pairs of horizontal springs are introduced connecting each axle box with the bogie frame to increase the lateral and longitudinal stiffness of the suspension. These simplifications are implemented to reduce the computational burden of combining a flexible model with the highly nonlinear impact and friction phenomena modeled by the imperfect kinematic joints, as the objective of this work is to demonstrate the realistic application of the improvements of the flexible multibody formulation presented. Nevertheless, the imperfect cylindrical joints can be included in the flexible model with the support of the rigid–flexible joint. In the locomotive, each of the three traction motors is suspended through one flexible connection with the bogie frame and a support over the respective wheelset. In the multibody models, however, each motor is simply connected to the bogie frame by a rigid kinematic joint. The virtual bodies methodology is employed to rigidly connect each motor to the bogie frame using the rigid–flexible joint presented in Sect. 2.4.1.
The bogie frame is modeled by a 3D CAD software in the undeformed geometry, and the local reference frame is initially positioned in its instantaneous center of mass. The geometry model is exported to an FE software and is discretized using solid elements. A modal analysis of the bogie frame under free–free conditions provides the vector of the squares of the natural frequencies \(\boldsymbol{\Lambda} \), the matrix of the modes of vibration \(\mathbf{X}\), and the diagonalized mass matrix of the flexible body \(\mathbf{M}_{ff}\). The flexible modes of vibration associated with the 30 lowest natural frequencies describe the deformations of the bogie frame. The lowest nonrigid natural frequency is 31.1 Hz, and the associated mode of vibration is depicted in Fig. 11. The highest natural frequency considered is 377.2 Hz. The mean axis conditions are considered in the analysis developed. No static correction mode is used in this model as the bogie frame is quite stiff, thus not experiencing notable local deformations in particular points.
Overview of the first flexible mode of vibration of the bogie frame
4.2 Wheel–rail contact methodology
The vehicle–track interaction is represented by forces developed on the wheel–rail contact surfaces, which are computed in MUBODyn according to the wheel–rail contact methodology described in Fig. 12 and further detailed in [35–37]. The inputs for the wheel–rail contact model are the kinematic quantities of the wheelsets, whereas the force vectors and respective points of application are the outputs. The contact detection problem involves the identification of the contact pairs between the wheel and rail, requiring the parameterization of the wheel and rail profiles. The calculation of the contact forces from the virtual interferences of the bodies considers the Hertz elastic contact theory [45]. The normal contact force is determined according to a modified Kelvin–Voigt model [46], which is a Hertzian model with dissipation. The elliptical contact patch is computed, as well as the longitudinal, lateral, and spin creepages, to determine the creep forces using the Polach model [47]. The final step of the algorithm is the computation and application of the force vectors on the points of contact to represent the loads transmitted between each wheel–rail contact pair. The normal component of the force vector is normal to the contacting surface, whereas the longitudinal and lateral components of the force vector are tangential to the contacting surface.
Wheel–rail contact algorithm of MUBODyn [35]
4.3 Dynamic analysis and selected results
The scenario simulated is the locomotive running with a constant speed of 70 km/h in a straight track with realistic track irregularities. There are no wagons coupled to the locomotive, and the effects of traction and braking are neglected. The maximum time step used in the simulations is 0.2 milliseconds, and the sample rate is 5000 Hz. The outputs of the dynamic simulation are the positions, velocities, and accelerations of the various bodies of the vehicle model in the time domain, which are further post-processed to obtain relevant quantities for the dynamic analysis, such as power spectral densities (PSDs) of selected accelerations. The outputs also encompass the internal and external forces, including the wheel–rail contact forces that result from the vehicle–track interaction.
Figures 13–15 feature a selection of raw results from the simulation without any type of filtering or postprocessing. Figure 13 shows the lateral and vertical wheel–rail contact forces of the left wheel of the leading wheelset. Overall, the results from the rigid and flexible models are similar, apart from some differences in the peak values of the lateral contact force. Figure 14 shows the lateral displacement and acceleration of the center of mass (CM) of the leading wheelset for the rigid and flexible models. Again, the results essentially coincide. It is clear in Fig. 14 that the wheelset undergoes a cyclic motion in the lateral direction with a frequency of approximately 1.25 Hz, which is explained by the stable hunting motion that is characteristic of a railway vehicle operating on a track with track irregularities.
Lateral and vertical contact forces on the left wheel of the leading wheelset
Kinematics of the CM of the leading wheelset: (left) lateral displacement and (right) lateral acceleration w.r.t. the local reference frame of the wheelset
Kinematics of point \(P\) of the bogie frame: (left) lateral position w.r.t global reference frame; and (right) lateral acceleration w.r.t. the local frame of the bogie frame
Figure 15 shows the lateral position and lateral acceleration of point \(P\) identified in Fig. 11. Point \(P\) is located where the front right vertical spring of the primary suspension is attached to the bogie frame. It is worth recalling that the front bogie frame is the only body where flexibility is considered in the flexible model. The impact of the structural flexibility in the lateral position of point \(P\) is limited. In contrast, there are relevant differences of the lateral acceleration of point \(P\), which are the result of the structural flexibility of the bogie frame. However, the extent of the differences in the accelerations is different throughout the frequency domain.
Figure 16 shows the PSD estimate of the lateral acceleration of point \(P\) from the two models, considering a time signal with a duration of approximately 25 s. Both responses exhibit a notable peak associated with the stable hunting motion of the bogie frame at a frequency of approximately 1.25 Hz. The two curves are similarly shaped inside the low-frequency range, commonly limited at 20 Hz, suggesting that both models represent the rigid-body motion of the vehicle with the same accuracy. Above the 20 Hz threshold, the curve associated with the flexible model exhibits peaks at approximately 27 Hz, 34 Hz, 42 Hz, 48 Hz, 62 Hz, 71 Hz, and 113 Hz, whereas the curve associated with the rigid-body model shows no significant peaks in this range. This result demonstrates that the flexible modes of vibration present a measurable contribution to the accelerations of point \(P\) if the structural deformations are of interest. On a global overview, these results show that the structural flexibility of the bogie frame has a negligible effect on the low-frequency dynamics of the vehicle. This conclusion is not surprising, since the low-frequency dynamics of the vehicle concern primarily the rigid-body modes of vibration.
PSD estimate of the lateral acceleration of point \(P\) in the local reference frame of the bogie
The analysis of Fig. 16 highlights the significant differences in the response of the bogie frame resulting from the use of rigid or flexible models. This discussion is followed by a preliminary analysis of the sensitivity of the accelerations measured in the bogie frame to the presence of structural defects. A second model of the flexible bogie frame is developed, featuring an artificial crack defined in the vertical cross-section plane of the connection between the transversal beam and the right lateral side frame identified by point Q in Fig. 11. The crack is represented by an incision that totals 40% of the cross-section area of the welded connection. Figure 17 shows the PSD estimate of the lateral acceleration of point P considering the two models. The PSD estimates reveal visible differences above a frequency of approximately 35 Hz. These results suggest that the measured accelerations measured in strategic locations of the bogie frame can be used to detect structural defects, provided that there is an algorithm that can reliably identify the deviations between the nominal and abnormal responses. The enhancements for the flexible multibody methodology presented in this work are the basis to investigate such methods in the future.
PSD estimate of the lateral acceleration of point P in the local reference frame, considering flexible models of the bogie frame in the nominal condition and damaged condition
5 Conclusions
This work presents the development and application of a flexible multibody methodology that allows separating the tasks of modeling the multibody system and developing the finite element models of the flexible bodies. This feature is enabled by the definition of various terms of the equations of motion of the flexible multibody system independently of the shape functions of the elements used. The flexible multibody methodology used is originally developed considering flexible bodies discretized by finite elements characterized by nodes with six degrees of freedom, such as beam and shell elements. To overcome this limitation, this work provides novel developments of the original formulation to allow the use of solid elements, commonly associated with nodes with three displacement degrees of freedom and without nodal rotations. Two types of floating frame reference conditions that do not explicitly use nodal rotations are derived and adopted, the principal axis conditions and the mean axis conditions. The virtual bodies methodology is applied to allow using the kinematic joints originally formulated for rigid bodies. This work also contributes with an alternative formulation of a rigid–flexible joint required to use the virtual bodies. This novel formulation allows rigid attaching rigid bodies to nodes of a flexible body using exclusively the three nodal translations of three neighboring nodes.
The revised flexible multibody methodology is implemented in the general multibody code MUBODyn and demonstrated with the analysis of a benchmark problem consisting of a slider-crank mechanism. The results from the simulation of a flexible slider-crank modeled with solid finite elements are consistent with those found in the literature, modeled with various numbers of beam elements. This is a demonstration of the validity of the formulation developed and implemented. The flexible multibody methodology is also used to study the dynamics of a locomotive with a flexible bogie frame running on a straight track with realistic track irregularities. By comparison with a rigid-body model, the results show that the structural flexibility of the bogie frame does not have a relevant influence on the dynamic behavior of the railway vehicle in the low-frequency range, as expected. However, if the response of the bogie frame above the low-frequency range is also of interest, then to analyze the structural deformations, the flexible model must be used. The results presented also include the accelerations measured on a particular location considering a bogie frame model that comprises a structural defect. The comparison with the response of the bogie frame in nominal conditions suggests that the accelerations measured on strategic locations of the structure are sensitive to the presence of a crack. The developments in this work aim to support the definition of a methodology to monitor the structural condition of the bogie frame using sensor data. The dynamic simulations using the flexible models can contribute to assess what quantities must be monitored online in different points of the structure to detect bogie frame damage. This application is the focus of further work.
References
Song, J.O., Haug, E.J.: Dynamic analysis of planar flexible mechanisms. Comput. Methods Appl. Mech. Eng. 24, 359–381 (1980)
Shabana, A.A., Wehage, R.A.: A coordinate reduction technique for dynamic analysis of spatial substructures with large angular rotations. J. Struct. Mech. 11, 401–431 (1983)
Yoo, W.S., Haug, E.J.: Dynamics of flexible mechanical systems using vibration and static correction modes. J. Mech. Transm. Autom. Des. 108, 315–322 (1986)
Ambrósio, J.A.C., Gonçalves, J.P.C.: Complex flexible multibody systems with application to vehicle dynamics. Multibody Syst. Dyn. 6, 163–182 (2001)
Neto, M.A., Ambrósio, J.A.C., Leal, R.P.: Flexible multibody systems models using composite materials components. Multibody Syst. Dyn. 12, 385–405 (2004)
Neto, M.A., Ambrósio, J.A.C., Leal, R.P.: Composite materials in flexible multibody systems. Comput. Methods Appl. Mech. Eng. 195, 6860–6873 (2006)
Zwölfer, A., Gerstmayr, J.: A concise nodal-based derivation of the floating frame of reference formulation for displacement-based solid finite elements. Multibody Syst. Dyn. 49, 291–313 (2020)
Shabana, A.A.: Finite element incremental approach and exact rigid body inertia. J. Mech. Des. 118, 171–178 (1996)
Shabana, A.A., Yakoub, R.Y.: Three dimensional absolute nodal coordinate formulation for beam elements: theory. J. Mech. Des. 123, 606–613 (2001)
Yakoub, R.Y., Shabana, A.A.: Three dimensional absolute nodal coordinate formulation for beam elements: implementation and applications. J. Mech. Des. 123, 614–621 (2001)
Wu, S.-C., Haug, E.J.: Geometric non-linear substructuring for dynamics of flexible mechanical systems. Int. J. Numer. Methods Eng. 26, 2211–2226 (1988)
Craig, R.R., Bampton, M.C.C.: Coupling of substructures for dynamic analyses. AIAA J. 6, 1313–1319 (1968)
Agrawal, O.P., Shabana, A.A.: Application of deformable-body mean axis to flexible multibody system dynamics. Comput. Methods Appl. Mech. Eng. 56, 217–245 (1986)
Canavin, J.R., Likins, P.W.: Floating reference frames for flexible spacecraft. J. Spacecr. Rockets 14, 724–732 (1977)
Nikravesh, P.E., Lin, Y.: Use of principal axes as the floating reference frame for a moving deformable body. Multibody Syst. Dyn. 13, 211–231 (2005)
Shabana, A.A.: Constrained motion of deformable bodies. Int. J. Numer. Methods Eng. 32, 1813–1831 (1991)
Korkealaakso, P., Mikkola, A., Rantalainen, T., et al.: Description of joint constraints in the floating frame of reference formulation. Proc. Inst. Mech. Eng., Part K, J. Multi-Body Dyn. 223, 133–145 (2009)
Bae, D., Han, Choi, J., An implementation method for constrained flexible multibody dynamics using a virtual body and joint. Multibody Syst. Dyn. 4, 297–315 (2000)
Gonçalves, J., Ambrósio, J.: Advanced modelling of flexible multibody systems using virtual bodies. Comput. Assist. Mech. Eng. Sci. 9, 373–390 (2002)
Bruni, S., Meijaard, J.P., Rill, G., et al.: State-of-the-art and challenges of railway and road vehicle dynamics with multibody dynamics approaches. Multibody Syst. Dyn. 49, 1–32 (2020)
Cheli, F., Corradi, R.: On rail vehicle vibrations induced by track unevenness: analysis of the excitation mechanism. J. Sound Vib. 330, 3744–3765 (2011)
Magalhães, H., Ambrósio, J., Pombo, J.: Railway vehicle modelling for the vehicle–track interaction compatibility analysis. Proc. Inst. Mech. Eng., Part K, J. Multi-Body Dyn. 230, 251–267 (2016)
Polach, O.: On non-linear methods of bogie stability assessment using computer simulations. Proc. Inst. Mech. Eng., Part F, J. Rail Rapid Transit 220, 13–27 (2006)
Kulkarni, R., Qazizadeh, A., Berg, M., et al.: Investigating the effect of the equivalent conicity function’s nonlinearity on the dynamic behaviour of a rail vehicle under typical service conditions. Veh. Syst. Dyn., 1–20 (2021)
Pagaimo, J., Magalhães, H., Costa, J.N., et al.: Derailment study of railway cargo vehicles using a response surface methodology. Veh. Syst. Dyn. 60, 309–334 (2022)
Popp, K., Kruse, H., Kaiser, I.: Vehicle-track dynamics in the mid-frequency range. Veh. Syst. Dyn. 31, 423–464 (1999)
Costa, J., Antunes, P., Magalhães, H., et al.: A novel methodology to automatically include general track flexibility in railway vehicle dynamic analyses. Proc. Inst. Mech. Eng., Part F, J. Rail Rapid Transit 235, 478–493 (2021)
Kaiser, I., Poll, G., Vinolas, J.: Modelling the impact of structural flexibility of wheelsets and rails on the wheel-rail contact and the wear. Wear, 203445 (2020)
Claus, H., Schielen, W.: Modelling and simulation of railway bogie structural vibrations. Veh. Syst. Dyn. 29, 538–552 (1998)
Pombo, J.C., Ambrósio, J.A.C.: MUltiBOdy DYnamics Analysis Program - MUBODyn: User’s Manual, Lisbon (2006)
Ambrósio, J., Pombo, J.: A unified formulation for mechanical joints with and without clearances/bushings and/or stops in the framework of multibody systems. Multibody Syst. Dyn. 42, 317–345 (2018)
Machado, M., Moreira, P., Flores, P., et al.: Compliant contact force models in multibody dynamics: evolution of the Hertz contact theory. Mech. Mach. Theory 53, 99–121 (2012)
Marques, F., Flores, P., Pimenta Claro, J.C., et al.: A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 86, 1407–1443 (2016)
Pombo, J., Ambrósio, J.: An alternative method to include track irregularities in railway vehicle dynamic analyses. Nonlinear Dyn. 68, 161–176 (2012)
Magalhães, H., Marques, F., Liu, B., et al.: Implementation of a non-Hertzian contact model for railway dynamic application. Multibody Syst. Dyn. 48, 41–78 (2020)
Marques, F., Magalhães, H., Pombo, J., et al.: A three-dimensional approach for contact detection between realistic wheel and rail surfaces for improved railway dynamic analysis. Mech. Mach. Theory 149, 103825 (2020)
Magalhaes, H., Marques, F., Antunes, P., et al.: Wheel-rail contact models in the presence of switches and crossings. Veh. Syst. Dyn., 1–33 (2022)
Nikravesh, P.: Computer-Aided Analysis of Mechanical Systems. Prentice Hall, New Jersey (1988)
Gear, C.W., Petzold, L.R.: ODE methods for the solution of differential/algebraic systems. SIAM J. Numer. Anal. 21, 716–728 (1984)
Flores, P., Machado, M., Seabra, E., et al.: A parametric study on the Baumgarte stabilization method for forward dynamics of constrained multibody systems. J. Comput. Nonlinear Dyn. 6 (2011)
Agrawal, O.P., Shabana, A.A.: Dynamic analysis of multibody systems using component modes. Comput. Struct. 21, 1303–1312 (1985)
Chu, S.-C., Pan, K.C.: Dynamic response of a high-speed slider-Crank mechanism with an elastic connecting rod. J. Eng. Ind. 97, 542–550 (1975)
Meijaard, J.P.: Validation of flexible beam elements in dynamics programs. Nonlinear Dyn. 9, 21–36 (1996)
Millan, P., Pagaimo, J., Magalhães, H., et al.: Clearance joints and friction models for the modelling of friction damped railway freight vehicles. Multibody Syst. Dyn. (2023). https://doi.org/10.1007/s11044-022-09857-6
Goldsmith, W.: Impact - the Theory and Physical Behaviour of Colliding Solids. Edward Arnold LTD, London (1960)
Flores, P., Lankarani, H.M.: Contact Force Models for Multibody Dynamics. Springer, Cham (2016)
Polach, O.: A fast wheel-rail forces calculation computer code. Veh. Syst. Dyn. 33, 728–739 (1999)
Acknowledgements
The Portuguese Foundation for Science and Technology (Fundação para a Ciência e a Tecnologia) PhD grants BD/04939/2020 and UI/BD/151204/2021 are gratefully acknowledged. Also, this work is supported by the Portuguese Foundation for Science and Technology through IDMEC, under LAETA, project UIDB/50022/2020. This work contributed to the development of the European project LOCATE, under Shift2Rail Joint Undertaking, part of the European Union’s Horizon 2020 research and innovation programme, identified by the grant agreement 881805 – LOCATE –H2020-S2RJU-OC-IP5-01-2019. The authors acknowledge the partners Evoleo (Portugal), FGC – Ferrocarrils de la Generalitat de Catalunya (Spain), HUD – University of Huddersfield (UK), UIC – Union Internationale des Chemins de fer (France), and Vibratec (France) for the contribution with data and characterization of the application case.
Funding
Open access funding provided by FCT|FCCN (b-on).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pagaimo, J., Millan, P. & Ambrósio, J. Flexible multibody formulation using finite elements with 3 DoF per node with application in railway dynamics. Multibody Syst Dyn 58, 83–112 (2023). https://doi.org/10.1007/s11044-023-09875-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-023-09875-y