1 Introduction

Biomimetic robots are robots that resemble a living organism in shape, appearance, or behavior. They are designed to use biological principles in engineered systems to behave like a natural being, allowing them to solve specific problems, impossible for standard machines [1]. A snake robot is an example of a biomimetic, hyperredundant robot with a high number of degrees of freedom. Changes in the internal shape cause the snake robot motion, which is similar to that of natural biological creatures. Each robot configuration is characterized by a series of angles in joints connecting a series of robot segments [2].

Recently, the interest in redundant modular robotic systems has increased. Robotic snakes have many shapes and sizes. Mechanical designs with contact force sensors, passive wheels, and active propulsion can be found in recent studies [3]. These systems have certain advantages in terms of low cost, robustness, and versatility. Their narrow minimum cross-section to length ratio enables them to traverse into many diverse environments and navigate through tight spaces but also uneven grounds, slopes, channels, pipes, etc. Moreover, the ability of snake robots to modify the shape of their bodies due to the extensive range of motion of their joints allows them to execute a broad spectrum of applications, such as climbing stairs, poles, or tree trunks.

The development and control of snake robots are typically quite challenging for two primary reasons. First, multiple degrees of freedom (DOF) of snake robots make them challenging to control, and therefore their mechanical design has complex interconnections of sensors, actuators, and control logic. It provides additional locomotion gaits such as side-winding, crawling, plunging, and leaping in complex and irregular surroundings that exceed the maneuverability of more conventional wheeled, tracked, and legged robots [4]. The locomotion pattern of a snake on the ground is not well described even for biological snakes, which makes the design of the locomotion pattern limited to experimentation. Second, the dependence on environment interaction is more complicated for a snake robot than for more conventional mobile robots [5, 6]. There is also the uncertainty of the friction coefficient, which significantly affects movement predictability and control.

Properties of snake robots, such as high terrain ability, redundancy, and the possibility of complete sealing of the robot body, make them usable in numerous practical applications and is an emerging research area. These robots can perform essential tasks, such as mapping, port clearing, and object identification covering large areas. They also have the capability of entering narrow spaces to investigate specific issues as critical infrastructure points, human life vital signs, or small leakage sources [7]. Other potential applications include inspection and intervention services in hazardous environments of industrial plants, manipulator tasks in tight spaces not accessible for conventional machinery, or subsea operations [8].

1.1 Snake robot visualization

The visualization tools can be divided into two types, commercial simulators and research-based simulators.

1.1.1 Commercial simulators

In [7] there was used simulation tool called Modular Snake Robot Simulator developed by KM-RoBoTa [9], a rigid-body-dynamics-based physics simulator. Simulations allow retrieving data, including angular and linear velocity for each module, torque, orientation, and position for each joint. It defines several parameters such as body dimensions, actuator control and response functions, and environment setup. During simulation, the user can build scenario, module trajectory, and contact points with the ground and reference systems.

The commercial software application developed in [10] based on Open Dynamics Engine [11] was created for the modular robot simulation and control of the actual prototypes. The studies included specific modular robot groups, particularly, pitch-pitch and pitch-yaw connections. The analysis of a modular robot with eight pitch-connecting modules moving on a plane surface allowed resolving five different gaits patterns (1D sinusoidal, rolling, rotating, turning, and side-winding). The study results showed movement, direction, stability, amplitude, step, trajectory, and pitching angle.

Furthermore, in [12] the dynamics of obstacle-aided locomotion has been simulated with the commercial software Working Model 2D [13, 14], where a spring-damper model represented the rigid-body obstacle contact. The studies analyze the motion pattern of lateral undulation with and without obstacles. Results show that the snake robot model works for the scenario with minor obstacles and compares them with the discussion made on obstacle-aided locomotion. The simulations validated the mathematical model through lateral undulation without obstacles and confirmed the necessity of projections from the ground to move forward effectively on a plane with isotropic friction. It is possible to compare well for both types of locomotion: obstacle-aided and without obstacles via experimental and simulation results. The snake robot only interacted with the ground surface through gliding and sticking.

1.1.2 Research-based simulators

Some research-based simulators, like V-Rep, ROS, SolidWorks, and Matlab, are used in various complementary configurations for these kinds of investigations.

The mathematical model of the robot implemented in [5] uses Matlab and Simulink to simulate different control strategies and gait patterns. Matlab Virtual Reality (VR) toolbox is used to construct 3D animations of the simulation to facilitate the analysis of the results. Two gait patterns, which include side-winding and lateral undulation, were considered to identify the direction of the propulsion parameters. In [15] the authors applied the multibody dynamics simulation software Autolev (now MotionGenesis [16]), where they have studied the motion of a snake robot modeled as a spring-damper system during contact with a single peg. They also do quite a few simulation studies implemented and simulated in Matlab.

1.2 Snake robot control

The task performed by a multisegment robotic system is usually defined in task space (Cartesian space), whereas control signals are described in the joint space (configuration space). The control system strategies for multisegment robotics are comprehensively reviewed in [17] with time-invariant static controllers and dynamic controllers in both task and joint spaces. The task space direct closed-loop controller is designed and experimentally tested in [18]; however, instability and slower convergence are the main issues observed. Therefore a joint space controller can offer more stability by providing independent control to the joint variables by individual tuning of joints, especially, when the joint or actuator motion is discrete.

Control in the joint space is based on the offline computation of the inverse kinematics. The disadvantage of it is that the input values specified in the task space are not included in the feedback and are adequately controlled in an open loop. So any inadequacy accuracy of mechanical structure (e.g., backlash in joints, imprecision in determining the position of the end-effector) leads to a deterioration of the control system accuracy.

To minimize the influence of these factors on the quality of control and online behavior, a multisegment system is introduced into the system control modules based on dynamical systems modeling (e.g., neural networks or state observers). Various approaches are possible:

  • Online compensation: a dynamic element can generate additional torque, which compensates for the effects related to uncertainties.

  • Offline learning and online compensation: the dynamic element can model the system and linearize couplings related to the manipulator model by changing the parameters.

The critical principle of snake robot control is the Hirose snake model [2], which is the basic building block of several control strategies. The path-following of planar snake robots has been a challenging control problem due to the complex dynamic model of snake robots with three degrees of underactuation and coupled parameters. Several control methodologies for snake robots traveling in the straight path have been developed to address the issue of controllability and stability of snake movement [19]. The popular control approach is built on the Poincaré map for the planar snake robot to follow a straight-line path [20]. This methodology is suitable for simulating snake robot movement and a given parameter choice. The author of [21] developed a controller based on the line-of-sight (LoS) guidance control law using a cascaded approach to control the movement of a snake robot traversing a straight path. The results showed that the snake robot exponentially stabilizes and follows the straight line using the look-ahead distance parameter under a given condition. In another approach, PID controller based on decoupled equations of motion is designed and tested on a snake robot, which controls the shape, yaw, and angular velocity of the snake robot [22].

In [23] a feedback control approach with virtual constraints is described for velocity tracking of snake robots on the desired reference path. Wang [24] developed and tested an adaptive path following controller with unknown friction coefficients on an 8-link snake robot, demonstrating asymptotic convergence and tracking of the desired straight path. The Lyapunov method is used to examine the closed-loop stability of the controller. The snake robot head rotation is stabilized using a control strategy based on an improved winding gait control function [25]. Moreover, the sliding-mode controller is designed and tested in simulation to control the head angle and velocity of a planar snake robot [26]. In addition, the iterative learning control strategy is designed and tested on WPI soft robotic snake to control the gait pattern [27]. However, there is a unique approach based on a central-pattern-generator controller, which is investigated for optimization, and adaptive path following of snake-like robots [28]. This strategy smooths the control signal by eliminating the serpentine function, which generates the reference trajectory of a snake robot joints.

1.3 Contributions of this work

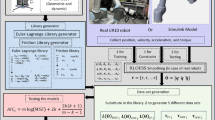
In this work, we start with a set of mathematical equations describing the movement of a snake robot in the two-dimensional space. The equations are based on the literature on the subject, mainly [20], but are modified and simplified to enable efficient implementation. Moreover, a new set of equations has been derived, which allows modeling and control of the head of the robot, rather than of its gravity center, as it is common in referenced works. Next, a Matlab simulation model is developed and tested for different robot movement scenarios. In parallel, a “mechanical” model of a snake robot, including the geometry of the joints has been developed in SOLIDWORK. This model feeds the design parameters into the dynamic Matlab model and also determines the constraints on the allowed range of movements (especially, angles) of the robot. An essential aspect of the dynamic simulation is 3-D visualization of the movement of a robot as a whole and of each joint.

A new, “resilient” control algorithm is proposed to overcome deficiencies caused by faults or lack of control command information in some joints. The algorithm, although simple, enables efficient control of the robot, even in case of two or three (out of the total of ten) joints not reacting to control commands. The algorithm has been implemented for two cases: controlling the position of the center of gravity of the robot and, more challenging, controlling the position of the robot head.

2 Model of the snake robot

The defined in the paper model is based on widely used equations of snake robot motion on the flat horizontal surface described in [20]. In these well-known models the control algorithms allow tracking the position of the robot mass center calculated as an average position of all segments. The model was redesigned to follow the desired position by using the head of the snake robot. This can be achieved by introducing position coordinates of the snake head in remodeled equations of motion.

2.1 Geometric constrains

The snake robot comprises \(N\) segments linked by \(n\) joints with one rotational degree of freedom. In this design the number of control signals is one less than the number of segments \((n=N-1)\). The joint axis of rotation is perpendicular to the ground. Each segment has identical parameters: the mass \(m\), inertia matrix \(J\), length \(2l\), and anisotropic, viscotic friction coefficients \(c_{n}\) in normal direction and \(c_{t}\) in tangential direction. The weight distribution of each segment is uniform. For simplicity, the model neglects the remaining parameters of the segment (i.e., height, width, mass center shift, and shift between motor position and the segment edge).

The configuration of the snake robot is defined in several Cartesian coordinate systems. A fixed ground defines the global coordinate system \(Oxy\), and each robot segment has a separate coordinate system \(Ox_{i}y_{i}\) defined for \(i \in (1,N)\). The origins of local systems lie in the segments centers; the \(x\)-axis lies along the length of the segments, whereas the \(y\)-axis is perpendicular to it. Figure 1 defines coordinate systems for elements of the snake robot.

Fig. 1
figure 1

Coordinate systems of the subsequent segments

Full size image

The motion of the snake robot is controlled by change of angle between subsequent segments. The joint angles are defined as \(\phi _{i}\), \(i \in (1,N-1)\), by following the convention described in [20]. The angle between the segments’ longitudinal axis \(x_{i}\) and the inertial coordinate system axis \(x\) is called the link angle \(\theta _{i}\), \(i \in (1,N)\), and is defined by the equation

$$ \phi _{i}=\theta _{i}-\theta _{i+1}. $$
(1)

Figure 2 depicts the relation between the joint angles \({\boldsymbol{\phi}}=\left [\phi _{1}, \ldots , \phi _{N-1}\right ]^{T} \in \mathbb{R}^{N-1}\) and link angles \(\boldsymbol{\theta}=\left [\theta _{1}, \ldots , \theta _{N}\right ]^{T} \in \mathbb{R}^{N}\) in the global coordinate system.

Fig. 2
figure 2

Link angle and joint angle representation

Full size image

The equations of motion, described in detail in the next section, are designated for the vector \(\overline{\boldsymbol{\phi}}\) comprising joint angles and link angle of the robot head \(\overline{\boldsymbol{\phi}}=\left [\phi _{1}, \ldots , \phi _{N-1}, \theta _{N}\right ]^{T} \in \mathbb{R}^{N}\), which is described by the equation

$$ \boldsymbol{\theta}=\mathbf{H} \overline{\boldsymbol{\phi}}, \quad \mathbf{H}= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 1 & 1 & \cdots & 1 & 1 \\ 0 & 1 & 1 & \cdots & 1 & 1 \\ \vdots & & & & & \vdots \\ 0 & 0 & 0 & \cdots & 0 & 1 \end{array}\displaystyle \right ] \in \mathbb{R}^{N \times N}. $$
(2)

The distance between axes of rotation of subsequent robot joints is equal to \(2l\), whereas the distance between mass centers of the segments \(i+1\) and \(i\) depend on the angles \(\theta _{i}\) and \(\theta _{i+1}\):

$$ \textstyle\begin{array}{l} x_{i+1}-x_{i}=l \cos \theta _{i}+l \cos \theta _{i+1}, \\ y_{i+1}-y_{i}=l \sin \theta _{i}+l \sin \theta _{i+1}. \end{array} $$
(3)

Equation (3) represents the relation between positions of two consecutive segments. The following matrix equation uniforms this dependence for the whole snake robot:

$$ \textstyle\begin{array}{l} \mathbf{D x}+l \mathbf{A} \cos \theta =\mathbf{0}, \\ \mathbf{D y}+l \mathbf{A} \sin \theta =\mathbf{0}. \end{array} $$
(4)

Equation (4) contains the concatenation of elements position vectors in distinct directions \(\boldsymbol{x}=[x_{1}, \ldots ,x_{N}]^{T}\in \mathbb{R}^{N}\) and \(\boldsymbol{y}=[y_{1}, \ldots ,y_{N}]^{T}\in \mathbb{R}^{N}\) together with auxiliary matrices \(\boldsymbol{A}\) and \(\boldsymbol{D}\), which facilitate description of the vector sum and difference:

$$ \begin{aligned} & \mathbf{D}= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} {1} & {-1} & 0 & {} & {} & 0 \\ 0 & 1 & -1 & 0 & {} & {} \\ {} & {} & {\ddots} & {\ddots} & {} & {} \\ {} & {} & 0 & 1 & -1 & 0 \\ 0 & {} & {}& 0 & {1} & {-1} \end{array}\displaystyle \right ] \in \mathbb{R}^{(N-1) \times N}, \\ & \mathbf{A}= \left [ \textstyle\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} {1} & {1} & 0 & {} & {} & 0 \\ 0 & 1 & 1 & 0 & {} & {} \\ {} & {} & {\ddots} & {\ddots} & {} & {} \\ {} & {} & 0 & 1 & 1 & 0 \\ 0 & {} & {}& 0 & {1} & {1} \end{array}\displaystyle \right ] \in \mathbb{R}^{(N-1) \times N}. \end{aligned} $$
(5)

Position of the robot head \(\boldsymbol{p}_{0}=[p_{0,x}, p_{0,y}]^{T} \in \mathbb{R}^{2}\) is described by the following equation, where \(\boldsymbol{a}^{T}=[0,0, \ldots ,1]\in \mathbb{R}^{N}\):

$$ \textstyle\begin{array}{l} p_{0,x}=a^{T}\mathbf{x}, \\ p_{0,y}=a^{T}\mathbf{y}. \end{array} $$
(6)

Combining equations (4) and (6), we get

$$ \textstyle\begin{array}{l} \mathbf{T x}= \left [ \textstyle\begin{array}{c} -l \mathbf{A} \cos \theta \\ p_{0,x} \end{array}\displaystyle \right ], \\ \mathbf{T y}= \left [ \textstyle\begin{array}{c} -l \mathbf{A} \sin \theta \\ p_{0,y} \end{array}\displaystyle \right ], \end{array} $$
(7)

where

$$ \mathbf{T}= \left [ \textstyle\begin{array}{c} \mathbf{D} \\ \mathbf{a}^{T} \end{array}\displaystyle \right ] \in \mathbb{R}^{N \times N}. $$
(8)

It can be shown that the inverse matrix of \(\boldsymbol{T}\) is

$$ \mathbf{T}^{-1}= \left [ \textstyle\begin{array}{c} \mathbf{C} ,\ \mathbf{e} \end{array}\displaystyle \right ] \in \mathbb{R}^{N \times N}, $$
(9)

where \(\boldsymbol{e}^{T}=[1,1, \ldots ,1]\in \mathbb{R}^{N}\), and

$$ \boldsymbol{C}= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 1 & {} & 1 & \ldots & 1 \\ 0 & 1 & {} & 1 & {} & \vdots \\ 0 & {} & {\ddots} & {\ddots} & {} & 1 \\ \vdots & {} & {\ddots} & {\ddots} & {} & 1 \\ 0 & \ldots & {} & {\ddots} & {} & 0 \\ \end{array}\displaystyle \right ] \in \mathbb{R}^{N \times N-1}. $$
(10)

Solution of equation (7) for position vectors \(\boldsymbol{x}\) and \(\boldsymbol{y}\) is

$$ \textstyle\begin{array}{l} \mathbf{x}= \mathbf{T}^{-1} \left [ \textstyle\begin{array}{c} -l \mathbf{A} \cos \theta \\ p_{0, x} \end{array}\displaystyle \right ]= -l \mathbf{C} \mathbf{A} \cos \theta +\boldsymbol{e} p_{0, x}, \\ \mathbf{y}= \mathbf{T}^{-1} \left [ \textstyle\begin{array}{c} -l \mathbf{A} \sin \theta \\ p_{0, y} \end{array}\displaystyle \right ]= -l \mathbf{C A} \sin \theta +\boldsymbol{e} p_{0, y}. \end{array} $$
(11)

The derivative of equation (11) defines the segments velocities expressed as

$$ \textstyle\begin{array}{l} \dot{\mathbf{x}}= l \mathbf{C A S}_{\theta} \dot{\theta} + \boldsymbol{e} \dot{p}_{0, x}, \\ \dot{\mathbf{y}}= -l \mathbf{C A C}_{\theta} \dot{\theta} + \boldsymbol{e} \dot{p}_{0, y}, \end{array} $$
(12)

where \(\mathbf{S}_{\theta}=diag(\sin (\theta )) \in \mathbb{R}^{N \times N}\) and \(\mathbf{C}_{\theta}=diag(\cos (\theta )) \in \mathbb{R}^{N \times N}\) are square matrices with trigonometric functions of link angles at the diagonal and zeros in the remaining elements.

2.2 Equations of motion

The dynamical model of the snake robot can be derived based on the torque equilibrium equation. A detailed description of the model can be found in [20] and [22]:

$$ \mathbf{M}_{\theta} \ddot{\boldsymbol{\theta}} +\mathbf{W} \dot{\boldsymbol{\theta}}^{2} -l \mathbf{S}_{\theta} \mathbf{K} \mathbf{f}_{R, x} +l \mathbf{C}_{\theta} \mathbf{K} \mathbf{f}_{R, y} = \mathbf{D}^{T} \mathbf{u}. $$
(13)

The vector \(\boldsymbol{u} \in \mathbb{R}^{N-1}\) defines the controllable parameters, actuator torques exerted on successive links. The \(\mathbf{f}_{R, x}\) and \(\mathbf{f}_{R, y}\) vectors represent components of friction force on the links in global \(x\)- and \(y\)-directions. The movement of the snake robot is possible due to the anisotropic friction force. The friction coefficient \(c_{t}\) in the longitudinal direction of each joint is much lower than the coefficient \(c_{n}\) in the lateral direction. This property allows the robot joints to slide in the forward direction. The implemented model assumes the viscosity of the friction force. Therefore \(\mathbf{f}_{R}\) is proportional to the joint velocities. The friction forces acting on all links in the global frame can be expressed as

$$ \mathbf{f}_{R}= \left [ \textstyle\begin{array}{c} \mathbf{f}_{R, x} \\ \mathbf{f}_{R, y} \end{array}\displaystyle \right ]= -\left [ \textstyle\begin{array}{c@{\quad}c} c_{t}\left (\mathbf{C}_{\theta}\right )^{2} +c_{n}\left (\mathbf{S}_{ \theta}\right )^{2} & \left (c_{t}-c_{n}\right ) \mathbf{S}_{\theta} \mathbf{C}_{\theta} \\ \left (c_{t}-c_{n}\right ) \mathbf{S}_{\theta} \mathbf{C}_{\theta} & c_{t} \left (\mathbf{S}_{\theta}\right )^{2}+c_{n}\left (\mathbf{C}_{\theta} \right )^{2} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{l} \dot{\mathbf{x}} \\ \dot{\mathbf{y}} \end{array}\displaystyle \right ] \in \mathbb{R}^{2 N}. $$
(14)

The matrices included in equation (13) are described by

$$ \begin{aligned} \mathbf{M}_{\theta} &= J \mathbf{I}_{N} +m l^{2} \mathbf{S}_{\theta} \mathbf{V} \mathbf{S}_{\theta} +m l^{2} \mathbf{C}_{\theta} \mathbf{V} \mathbf{C}_{\theta}, \\ \mathbf{W} &= m l^{2} \mathbf{S}_{\theta} \mathbf{V} \mathbf{C}_{ \theta} -m l^{2} \mathbf{C}_{\theta} \mathbf{V} \mathbf{S}_{\theta} , \\ \mathbf{V} &= \mathbf{A}^{T}\left (\mathbf{D} \mathbf{D}^{T}\right )^{-1} \mathbf{A}, \\ \mathbf{K} &= \mathbf{A}^{T}\left (\mathbf{D} \mathbf{D}^{T}\right )^{-1} \mathbf{D}. \end{aligned} $$
(15)

The dynamic model of the snake robot in the space of joint angles is derived by substitution of relation (2) into equation (13):

$$ \mathbf{M}_{\theta} \mathbf{H} \ddot{\bar{\boldsymbol{\phi}}} + \mathbf{W} \operatorname{diag}(\mathbf{H} \dot{\bar{{\boldsymbol{\phi}}}}) \mathbf{H} \dot{\bar{{\boldsymbol{\phi}}}} -l \mathbf{S}_{\theta} \mathbf{K} \mathbf{f}_{R, x} +l \mathbf{C}_{\theta} \mathbf{K} \mathbf{f}_{R, y}= \mathbf{D}^{T} \mathbf{u}. $$
(16)

An unambiguous description of the configuration of the robot snake on the flat surface requires \(N+2\) independent equations. Therefore equation (16) should be expanded by two dynamical relations. In the delivered model, those equations describe the position of the robot head. According to the laws of motion, the acceleration of each robot segment with mass \(m\) is equal to the net force acting on the system; in this case the friction force \(\mathbf{f}_{R}=[\mathbf{f}_{R, x}, \mathbf{f}_{R, y}]^{T} \in \mathbb{R}^{2 N}\) is described by equation (14) and coupling forces between segments in perpendicular directions \(\mathbf{h}_{x}=[\mathbf{h}_{x, 1}, \mathbf{h}_{x, 2},\ldots,\mathbf{h}_{x, N-1}]^{T} \in \mathbb{R}^{N-1}\) and \(\mathbf{h}_{y}=[\mathbf{h}_{y, 1}, \mathbf{h}_{y, 2},\ldots,\mathbf{h}_{y, N-1}]^{T} \in \mathbb{R}^{N-1}\):

$$ \begin{aligned} m \ddot{\mathbf{x}} &= \mathbf{f}_{R, x}+\mathbf{D}^{T} \mathbf{h}_{x}, \\ m \ddot{\mathbf{y}} &= \mathbf{f}_{R, y}+\mathbf{D}^{T} \mathbf{h}_{y}. \end{aligned} $$
(17)

The equation of motion of the robot head is described by

$$ m \ddot{\mathbf{p}}_{0}= m\left [ \textstyle\begin{array}{l} \ddot{p}_{0,x} \\ \ddot{p}_{0,y} \end{array}\displaystyle \right ]= \left [ \textstyle\begin{array}{l} \mathbf{a}^{T} \ddot{\mathbf{x}} \\ \mathbf{a}^{T} \ddot{\mathbf{y}} \end{array}\displaystyle \right ]= \left [ \textstyle\begin{array}{l} \mathbf{a}^{T}( \mathbf{f}_{R, x} +\mathbf{D}^{T}\mathbf{h}_{x}) \\ \mathbf{a}^{T} (\mathbf{f}_{R, y} +\mathbf{D}^{T}\mathbf{h}_{y})) \end{array}\displaystyle \right ]. $$
(18)

After transformations, the following equation of motion emerges:

$$ m \ddot{\mathbf{p}}_{0} -\mathbf{M}_{P} \ddot{{\theta}} -\mathbf{W}_{P} \dot{{\theta}}^{2} -\left [ \textstyle\begin{array}{l} \mathbf{G}_{P} \\ \mathbf{0}_{1 \times N} \end{array}\displaystyle \right ]\mathbf{f}_{R, x} -\left [ \textstyle\begin{array}{l} \mathbf{0}_{1 \times N} \\ \mathbf{G}_{P} \end{array}\displaystyle \right ]\mathbf{f}_{R, y} = 0, $$
(19)

where

$$ \mathbf{V}_{P}= \mathbf{a}^{T}\mathbf{D}^{T} \left (\mathbf{D D}^{T} \right )^{-1}\mathbf{A}, $$
(20)
$$ \mathbf{M}_{P}= ml \left [ \textstyle\begin{array}{l} \mathbf{V}_{P}\mathbf{S}_{\theta} \\ -\mathbf{V}_{P}\mathbf{C}_{\theta} \end{array}\displaystyle \right ], $$
(21)
$$ \mathbf{W}_{P}= ml \left [ \textstyle\begin{array}{l} \mathbf{V}_{P}\mathbf{C}_{\theta} \\ \mathbf{V}_{P}\mathbf{S}_{\theta} \end{array}\displaystyle \right ], $$
(22)
$$ \mathbf{G}_{P}= \mathbf{a}^{T}- \mathbf{a}^{T}\mathbf{D}^{T} \left ( \mathbf{D D}^{T}\right )^{-1}\mathbf{D}. $$
(23)

The final equation combining (16) and (19) has the form

$$ \overline{\mathbf{M}}(\bar{\boldsymbol{\phi}})\ddot{\boldsymbol{q}}+ \overline{\mathbf{W}}(\bar{\boldsymbol{\phi}}, \dot{\bar{\boldsymbol{\phi}}})+ \overline{\mathbf{G}}( \bar{\boldsymbol{\phi}})\mathbf{f}_{R}(\bar{\boldsymbol{\phi}}, \dot{\bar{\boldsymbol{\phi}}}, \dot{\mathbf{p}})= \overline{\mathbf{B}} \mathbf{u}, $$
(24)

where the vector \(\boldsymbol{q}\) is equal to the composition of all link angles with joint angle and position of the head:

$$ \boldsymbol{q}= \left [ \textstyle\begin{array}{c} \overline{\boldsymbol{\phi}} \\ p_{0,x} \\ p_{0,y} \end{array}\displaystyle \right ] \in \mathbb{R}^{N+2}. $$
(25)

The matrices from equation (24) are

$$ \overline{\mathbf{M}}(\overline{\boldsymbol{\phi}}) = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{H}^{T} \mathbf{M}_{\theta} (\overline{\boldsymbol{\phi}}) \mathbf{H} & \mathbf{0}_{N \times 2} \\ -\mathbf{M}_{P}\mathbf{H} & m \mathbf{I}_{2} \end{array}\displaystyle \right ], $$
(26)
$$ \overline{\mathbf{W}}(\overline{\boldsymbol{\phi}}, \dot{\overline{\boldsymbol{\phi}}}) = \left [ \textstyle\begin{array}{c} \mathbf{H}^{T} \mathbf{W}(\overline{\boldsymbol{\phi}}) \operatorname{diag}(\mathbf{H} \overline{\bar{\phi}}) \mathbf{H} \dot{\bar{\phi}} \\ -\mathbf{W}_{P}(\overline{\boldsymbol{\phi}}) \operatorname{diag}( \mathbf{H} \overline{\bar{\phi}}) \mathbf{H} \dot{\bar{\phi}} \end{array}\displaystyle \right ], $$
(27)
$$ \overline{\mathbf{G}}(\overline{\boldsymbol{\phi}})= \left [ \textstyle\begin{array}{c@{\quad}c} -l \mathbf{H}^{T} \mathbf{S}_{H \bar{\phi}} \mathbf{K} & l \mathbf{H}^{T} \mathbf{C}_{H \bar{\phi}} \mathbf{K} \\ -\mathbf{G}_{P} & \mathbf{0}_{1 \times N} \\ \mathbf{0}_{1 \times N} & -\mathbf{G}_{P} \end{array}\displaystyle \right ] , $$
(28)
$$ \overline{\mathbf{B}}= \left [ \textstyle\begin{array}{c} \mathbf{I}_{N-1} \\ \mathbf{0}_{3 \times (N-1)} \end{array}\displaystyle \right ]. $$
(29)

The dynamical model tracking the head position given by equation (24) is significantly different from the model described in [20]. The matrices \(\overline{\mathbf{M}}(\overline{\boldsymbol{\phi}})\) and \(\overline{\mathbf{W}}(\overline{\boldsymbol{\phi}}, \dot{\overline{\boldsymbol{\phi}}})\) depend on the matrices \(\mathbf{M}_{P}\) and \(\mathbf{W}_{P}\), whereas in the model in [20], those elements are filled with zeros. Also, the bottom-right submatrix of \(\overline{\mathbf{M}}(\overline{\boldsymbol{\phi}})\) is proportional to head mass instead of the weight of the whole snake. The elements of matrix \(\overline{\mathbf{G}}(\overline{\boldsymbol{\phi}})\) depend on the vector \(\mathbf{G}_{P}\) instead of \(\mathbf{e}^{T}\).

3 Control system of the snake robot

3.1 Control objective

A simple method of path-following by the snake robot is called the line-of-sight (LoS) method [29]. According to this method, the robot is tracking the straight line. This approach requires the definition of the global coordinate system \(\{x, y\}\) in which the \(x\)-axis is aligned along with the forward movement. The method adopted in this paper is called point-of-sight (PoS) method because the desired trajectory is divided into a sequence of points. The robot is following to the next point in the series, and after reaching it, the algorithm switches to tracking the consecutive point. This paper analyzes two tracking methods. The original algorithm based on [20] is tracking the position of the robot mass center, whereas the second algorithm, derived in this paper, follows the robot head.

The target position is defined in the global coordinate frame by point \(P=\{P_{x},P_{y}\}\), whereas the position of the head and center of mass of the robot is given by \(P_{\text{0}}(t)=\{p_{0,x}(t),p_{0,y}(t)\}\) and \(P_{\text{COM}}(t)=\{p_{x}(t),p_{y}(t)\}\). The values of \(p_{0,x}\) and \(p_{0,y}\) are defined by equation (6), and the position of the mass center is calculated as in [20]:

$$ \textstyle\begin{array}{l} p_{x}=e^{T}\mathbf{x}/N, \\ p_{y}=e^{T}\mathbf{y}/N. \end{array} $$
(30)

The positions of points \(P\), \(P_{\text{0}}\), and \(P_{\text{COM}}\) in the global coordinate frame is shown in Fig. 3. The distance of the robot between points along global the axes \(\{x,y\}\) is given as

$$ \left \lbrace \begin{aligned} d_{x}=P_{x}-p_{0,x}, \\ d_{y}=P_{y}-p_{0,y}, \end{aligned} \right . \qquad \mbox{or} \qquad \left \lbrace \begin{aligned} d_{x}=P_{x}-p_{x}, \\ d_{y}=P_{y}-p_{y}. \end{aligned} \right . $$
(31)
Fig. 3
figure 3

Point tracking of the robot head versus mass center

Full size image

The heading \(\bar{\theta}\) of the robot is the angle that the robot forms with the desired path, defined as the line between the selected point \(P\) and the center of mass \(P_{\text{COM}}\) or head \(P_{\text{0}}\) (see Fig. 3).

3.2 Controller design

The basic control law for each joint \(\mathbf{u}=[\mathbf{u}_{1}, \mathbf{u}_{2},\ldots\mathbf{u}_{n}]^{T} \in \mathbb{R}^{n}\), called in the paper the single joint controller (SJC), combines a component proportional to the position error and velocity damping:

$$ \mathbf{u}= k_{p}\left (\phi _{\mathrm{ref}}-\phi \right ) -k_{d} \dot{\phi}, $$
(32)

where \(k_{p}=\text{diag} \left (k_{pi}\right )\in \mathbb{R}^{n\times n}\) is the proportional matrix of position gains, \(k_{d}=\text{diag} \left (k_{di}\right ) \in \mathbb{R}^{n\times n}\) is the velocity damping matrix, and \(\phi _{\mathrm{ref}}\) is the vector of reference joints positions.

The reference joint angle of each element is defined as a sinusoidal signal with constant amplitude \(\alpha \) and frequency \(\omega \):

$$ \phi _{i, \mathrm{ref}}=\alpha \sin (\omega t+(i-1) \delta )+\phi _{o}. $$
(33)

In equation (33), \(\delta \) determines the phase shift between the joints, and \(\phi _{o}\) is a joint offset, which we assume to be identical for all joints.

The joint offset is calculated according to following equation (34), where \(k_{\theta} \in \mathbb{R}\) is the controller gain:

$$ \phi _{o}=k_{\theta}\left (\bar{\theta}-\bar{\theta}_{\text{ref }} \right ). $$
(34)

The orientation angle of the robot is calculated as an average value of all link angles:

$$ \bar{\theta}=\frac{1}{N} \sum _{i=1}^{N} \theta _{i}. $$
(35)

The reference orientation angle \(\bar{\theta}_{\text{ref}} \in R\) depends on the line connecting the tracked point \(P_{0}\) or \(P_{COM}\) of the snake and position of the target point \(P\) in reference to the global coordinate system:

$$ \bar{\theta}_{\mathrm{ref}}= -\tan ^{-1} \left (\frac{d_{y}}{d_{x}} \right ). $$
(36)

The controller structure based on the PoS guidance law is presented in Fig. 4.

Fig. 4
figure 4

Controller structure

Full size image

In the case of the controller for the snake robot, where there are no control signals in some joints (i.e., a faulty system with broken joints), the following heuristic control algorithm was chosen. The modified control signal \(\mathbf{u_{mod}}=[\mathbf{u}_{\mathrm{mod},\mathrm{1}}, \mathbf{u}_{\mathrm{mod},\mathrm{2}},\ldots \mathbf{,u}_{{\mathrm{mod}},n}]^{T} \in \mathbb{R}^{n}\) is coupled with the control signal of neighbor joint, and therefore the control law in called the coupled control (CC):

$$ \begin{aligned} u_{\mathrm{mod},\mathrm{1}}&=u_{1}, \\ u_{\mathrm{mod},\mathrm{i}}&=u_{i}+0.5(u_{i-1}), i=2,\dots ,N. \end{aligned} $$
(37)

Note that the single joint control strategy described at the beginning of this section relates control signals in individual joints to the measurements in those joints only. However, there is an interaction between the joints. Therefore a coupled control strategy that is multivariable can provide better performance. Such a strategy could be, for instance, LQR control, in which case each of the controls would depend on all measurements. A more straightforward approach, proposed above (37), is to relate the control signal to a limited number of outputs, in the simplest case, only two.

4 Simulation and visualization of the snake robot motion

The implemented framework presents a comprehensive tool to test, analyze, and tune control algorithms. It consists of two parts designed using well-known software tools. The first part, prepared in SOLIDWORKS, is a 3D model comprising the geometry of the center, the head, and the tail segments of the snake robot. A second part is MATLAB software, allowing simulation of robot dynamics. The core part of the software is a solution of equations of motion given as (24) using the Runge–Kutta fourth-order method. Hence a relationship is established between link angles and head or mass center position and the position and orientation of each robot segment. Visualization of robot movement is implemented using a MATLAB Simulink 3D Animation toolbox. The geometry of the robot segment is imported from STL file created in SOLIDWORKS.

The introduced framework allows simulating the robot motion for different geometry parameters (e.g., number of joints, weight, friction coefficients), target trajectories (position of points to follow), and control parameters (e.g., head/center tracking, controller gains, joint disturbances). The ready-to-use code with comments, helping to run the software, is available in [30] and [31]. The main LiveScript file start.mlx contains a detailed description of the model and implementation. The Simulink file VRmodel2.slx enables us to run 3D visualization of the snake motion.

4.1 Design of the snake-robot

Figures 5 and 6 show the snake robot construction details. The CAD design software allowed for checking different robot segment designs, simulation of the movement of the whole robot snake mechanism, and obtaining dynamics and kinematics parameters for the research.

Fig. 5
figure 5

Module construction: (1) Gear coupling, (2) Servomotor, (3) Flat area, (4) Cables channel is pipe, (5) Cables channel is perforation

Full size image
Fig. 6
figure 6

Robot snake construction: (A) Front view; (B) Top view; (C) Coordinate systems for each link; (D) Snake robot full view with joints, links, and centers of mass

Full size image

The robot snake is made by one single module, and it can only move on the plane surface. Because stability is an essential factor, a small flat area at the bottom has been created. The motion between the links is provided by placing a servomotor on one side of the body and a small cylinder on the opposite side. The perfect hollow set at the cylinder perfectly fits the motor gear.

Each link is intended to move in a range of 80∘, from \(-40^{\circ}\) to 40∘. For the dynamics simulation, it is assumed that the fabrication of each module is a 3D printer on ABS material. The model parameters are given in Table 1.

Table 1 Parameters of the snake robot link. Default coordinate system
Full size table

Matlab visualization of the designed snake robot is presented in Fig. 7. It also shows the position of the target point and LoS connecting robot and target. It also allows us to mark the constrains violation. When the joint angle exceeds the designed range, following the joint segment is colored red.

Fig. 7
figure 7

Robot motion visualization

Full size image

4.2 Simulation scenarios

The simulation aimed to test the quality of controlling the motion of a robotic snake. In implemented scenarios, the robot had to follow a trajectory described by a sequence of points. The crucial part of the results showed trajectory tracking performance when the robot mass center or its head reached trajectory points. Table 2 shows the position of target points for all simulations.

Table 2 Trajectory points of the followed trajectory
Full size table

The chosen point of the snake (mass center or head) has to move on a straight line, from the starting point to the first point in the table. After reaching this point, the snake rotates to follow the next point from the table. The critical issue analyzed during simulations was the following quality when simulation included some broken joints. The paper discusses the following simulations:

  • robot functioning fully (no broken joints);

  • there was one broken joint, number 3;

  • there were three broken joints, numbers 3, 5, 8;

  • there were three broken joints, where two of them are neighbors, numbers 3, 5, 6;

Furthermore, the primary control algorithm (SJC) was compared with a coupled control algorithm (CC) described in the previous sections (37). As a result, the simulations allowed us to compare the performance of four kinds of control approaches: center and head tracking with single-joint and coupled control algorithm for four motion scenarios with different disturbances.

Table 3 summarizes the controller parameters used during simulations.

Table 3 Gains of the controller
Full size table

4.3 Simulation results

Figures 8–11 show snapshots from an implemented in Simulink visualization. Figure 8 shows the robot movement when all joints are working properly, and the algorithm tracks the robot mass center. Figures 9–11 represent the robot motion with tracking of the robot head. In Figs. 8 and 9, robots do not experience any failures, whereas in Figs. 10 and 11, three joints (numbers 3, 5, and 6) are broken. In Fig. 10 the single-joint control algorithm (SJC) has been shown, whereas Fig. 11 shows the coupled control algorithm (CC). Those figures prove that the control algorithm can reach the goal defined as following a point-to-point trajectory. In the case of some joints not functioning, it would take much longer. The algorithm, which also considers the control signals sent to neighboring joints (CC algorithm), has an advantage, especially, in the case of some broken joints. This improvement exhibits in the faster movement of the robot.

Fig. 8
figure 8

3D visualization of the snake robot movement without broken joints, mass center tracking, and SJC algorithm for times 3 s, 10 s, 43 s, 100 s, 102 s, and 107 s

Full size image
Fig. 9
figure 9

3D visualization of the snake robot movement without broken joints, head tracking, and SJC algorithm for times 3 s, 10 s, 38 s, 41 s, 57 s, and 119 s

Full size image
Fig. 10
figure 10

3D visualization of the snake robot movement with three broken joints \((3,5,8)\), head tracking, and SJC algorithm for times 3 s, 78 s, 165 s, 184 s, 217 s, and 384 s

Full size image
Fig. 11
figure 11

3D visualization of the snake robot movement with thee broken joints \((3,5,8)\), head tracking, and CC algorithm for times 3 s, 33 s, 115 s, 120 s, 155 s, and 287 s

Full size image

The robot trajectories in the \(x\)–\(y\) coordinates for selected simulations, are shown in Fig. 12 for center tracking and Fig. 13 for head tracking. It is worth noting that the control design is such that it does not penalize deviations from a straight-line trajectory. The only objective is to reach a destination point. After this is achieved, the next target point is set. Therefore a control algorithm can be assessed as performing well if it reaches the destination point relatively quickly and without too much deviation/overshoot. Figures 12 and 13 show that for all sixteen simulations, all destination points have been reached. The case of coupled control algorithm seems to represent a relatively large error concerning a straight-line trajectory between the points \((1, -1)\) and \((3, -1)\), although the objective of the control is achieved. Later on, the consecutive paragraphs will compare the movement times between the joints.

Fig. 12
figure 12

Resultant trajectory tracking of the snake robot center

Full size image
Fig. 13
figure 13

Resultant trajectory tracking of the snake robot head

Full size image

The time of reaching trajectory points was used to measure the performance of the SJC and CC algorithm for the center and head tracking. Figure 14 shows this comparison for all simulation scenarios divided into four groups. The top left bar shows the performance of algorithms when all joints operate seamlessly. All five points on the trajectory were reached relatively quickly, with the robot arriving at the last point at about 250–300 seconds. The time of reaching target points is comparable for all methods. In this case, head tracking simulation is a little longer. Also a CC algorithm for center tracking took more time. However, this difference is marginal. Reaching the final point for center tracking and SJC method takes 257 s, whereas for head tracking and SJC, it took 297 s. When one or more joints are broken, we can significantly improve simulations using CC algorithm. Figure 14, top right, shows simulations for one broken joint. The difference between CC and SJC methods is equal to 38 s for center tracking and 75 s for head tracking. In this case, performance of CC algorithm for the center and head tracking is almost the same, 320 s. When there are three distanced broken joints (Fig. 14, bottom left), the difference between CC and SJC is 284 s for center tracking and 353 s for head tracking. The head-CC is faster (414 s) than center-CC (476 s). When there are three neighboring broken joints (Fig. 14, bottom right), reaching the final point to center-SJC took 1545 s, whereas reaching the same point using head tracking took 1069 s. The CC algorithms show an improvement to 853 s for center tracking and 772 s for head tracking.

Fig. 14
figure 14

Time of reaching trajectory points for different simulations

Full size image

Figures 15–18 show joints angles (nine values for the robot with ten segments) for the 16 simulation scenarios. The red lines in figures indicate the joint angle limits \(-40^{\circ}\) and \(40^{\circ}\). The comparison includes sets of results when there are no disturbances (Fig. 15), when one joint is broken (Fig. 16), when three distanced joints are broken (Fig. 17), and, finally, when three neighboring joints are broken (Fig. 18). Note that each case time limit is changing to capture the moment of reaching all target points at the trajectory. In Fig. 15, all simulations end before 300 s, and in Fig. 16, before 400 s. Simulations with SJC control for three distanced broken joints shown in Fig. 17 ends before 800 s and before 500 s for CC control. In the case of Fig. 18, when the time difference is noticeable, the center-SJC method reaches the last point in nearly 1600 s and head-SJC in 1100 s]. The CC method shows improvement to 900 s for center tracking and 800 s for head tracking.

Fig. 15
figure 15

Undisturbed joints: center tracking (top) vs. head tracking (bottom) and SJC (left) vs CC (right)

Full size image
Fig. 16
figure 16

One broken joint: center tracking (top) vs. head tracking (bottom) and SJC (left) vs. CC (right)

Full size image
Fig. 17
figure 17

Three broken joints \((3,5,8)\): center tracking (top) vs. head tracking (bottom) and SJC (left) vs. CC (right)

Full size image
Fig. 18
figure 18

Three broken joints \((3,5,6)\): center tracking (top) vs. head tracking (bottom) and SJC (left) vs. CC (right)

Full size image

As explained earlier, the movement of the robot has an oscillatory character. The angles of the joints oscillate sinusoidally according to equation (33). Due to the frequency of the oscillations, individual sinusoids are not visible, but, rather, a thick line represents the oscillatory movement. In the case of a broken joint, its angle is constant, and a straight horizontal line represents it. Noteworthy parts of Figs. 15–18 are where the joint angles exceed the limits imposed by the construction of the snake robot.

It is possible to observe that in case of no disturbances or with one broken joint, the system operates close to or slightly exceeding constraints in all eight scenarios. The turns in joints for center tracking are much sharper and lead to larger instantaneous values of joint angles. These may cause violation of the constraints, mainly observed for the center-CC method. In the case of one broken joint shown in Fig. 16, the CC algorithm performs slightly better in terms of nonviolation of constraints. For both tracking methods, the extreme values of joint angles are larger for CC methods.

It is noticeable that the CC algorithm is more aggressive than the SJC in the case of three broken joints. The results from Figs. 17 and 18 indicate more constrains violations for CC methods. However, methods with head tracking show significantly less extreme behavior.

The above analysis shows that using CC with the head tracking method gives better results than the other solutions. The improvement of the performance is seen in both time efficiency shown in Fig. 14 and frequency of constraints violation (Figs. 15–18). The improvement is significantly noticeable in case of faults such as broken joints.

5 Conclusions

This paper refers to a widely used mathematical model [20] of snake robot. This model has been modified and simplified for implementation in a simulation environment (MATLAB). For example, simulation tests have been performed for a ten-segment snake robot. Furthermore, the same robot has been modeled in SOLIDWORKS. Thus the geometric parameters have been taken into consideration, enabling sizing of each segment and determining the allowable range of movements (joint angles).

The control algorithm, based on the single joint control, proposed in [20], has been modified in a way that it allows the robot to move from a given point to the next point specified in 2D space (point-to-point tracking). Furthermore, this standard algorithm has been modified by adding (heuristically determined) contribution from the control signal from one neighboring joint. This approach can be treated as a first attempt at improving the robustness of the robot, especially, in case of faults, when some joints are not functioning or not receiving control commands. It is worth noting that the information about a fault does not have to be available to the controller. Hence the aim is improving the resilience of the controller.

Furthermore, the algorithm has been extended to a case where the robot head is controlled, i.e., it has to follow a prescribed trajectory. A suitable mathematical description of the robot dynamics has been derived for that purpose. Also, in this case, which is more difficult due to the propagation of constraints along the robot body, the robot performs well in the assigned tasks.

Several simulation scenarios have been tested with the robot moving between six points on a 2D plane. The simulations were organized with increasing the number of broken joints, hence increasing the level of difficulty for the control algorithm. The standard, single-joint controller (SJC) has been compared with coupled controller (CC) in each case. The simulations have shown, as expected, that the approach that considers the neighboring joint in control decision would have superior performance in terms of the time of reaching the destination point, compared with the single joint algorithm. However, such an approach may be more likely to approach and violate the physical constraints resulting from the robot geometry. Consequently, our plans include the implementation of constrained, multivariable control algorithms, for instance, model-based predictive control, with which it will be possible to incorporate obstacle avoidance and design the robot movement in a cluttered environment.

Another direction of future work will be the movement of the robot in 3D environment. So far, it was assumed that the robot moves on a flat plane and the movement is stipulated by a difference in friction coefficients in longitudinal and perpendicular directions for each segment. However, it may be required, e.g., for the obstacle avoidance, that a part of the robot raises from the plane or moves up or down a slope. This could be treated as an extension of the case described in the paper, where some of the joints do not function, to the case where some segments do function but are described by different equations of motion.