1 Introduction

In machine dynamics impact problems often contain large nonlinear motions and small elastic deformations, if the flexible body is relatively stiff. This is the case for steel or aluminum bodies which allows the assumption of small linear deformations. Therefore, the floating frame of reference formulation can be applied to model impacts in flexible multibody systems.

The application of the floating frame of reference formulation requires global shape functions of the flexible bodies. One way to obtain the global shape functions is to model the flexible body with isoparametric finite elements. A major drawback of isoparametric elements is the discretization of the geometry. However, an exact representation of the geometry is essential for determining the occurring contact forces and stresses in an impact problem. The discretization error can be worse in a sliding contact. The contact bodies can get entangled due to an insufficient discretization as discussed in [2]. These artificial effects from isoparametric elements might yield a model behavior, which does not necessarily represent the reality.

This motivates the use of isogeometric elements [2]. Isogeometric elements have two advantages. Firstly, the local shape functions are nonlinear basis splines (B-splines) and allow the exact representation of the geometry without any discretization errors. Secondly, it is shown in [2] that high frequency modes of flexible bodies are represented more accurate with isogeometric elements compared to isoparametric elements. However, a downside of isogeometric elements compared to isoparametric elements is the increased computational cost. The evaluation of the nonlinear shape functions of isogeometric elements is more time consuming than the evaluation of the linear shape functions of isoparametric elements.

The literature proposes a variety of different contact algorithms for isogeometric elements [10, 17, 18]. There are two main types of contact methods. The first type are the node-to-surface algorithms. They include the node-to-surface algorithm of isoparametric elements. Several node-to-surface algorithms exist for isogeometric elements. One way is to check the exterior unique knots for contact [18]. Another possibility is to define a collocation method [10, 18] which checks the collocation points for contact. The second type are integral-based descriptions of a contact, also referred to as knot-to-surface methods [10, 17]. Using the Gauss integration, the contacts of individual Gauss points can be checked. This usually results in a higher number of evaluated points compared to the node-to-surface algorithms. Therefore, a knot-to-surface method is computationally more expensive but grants a higher accuracy than the node-to-surface algorithms. Since the focus in this work is on high accuracy of the geometry by using the IGA, a knot-to-surface method is used.

The use of the floating frame of reference formulation involves the description of deformations by global shape functions. Thereby, mostly the low frequencies are considered and thus the overall flexibility of the body is included. The straightforward approach involves the modal reduction. This method captures the overall flexibility and wave propagation inside the body in case of an impact. Whereas local deformations and stresses in the contact area cannot be recovered using a moderate number of global shape functions from modal reduction [19]. Another drawback of the modal reduction is that the solution of the impact does not converge to the exact solution due to missing local deformation. This behavior is observed in [16, 20] when using the penalty method. Therefore, the Craig–Bampton method is used instead [3]. In addition to the normal modes, static shape functions are also included. Thus the deformation and stress in the contact area can be recovered very accurately. The cost of the Craig–Bampton method is the increased numerical stiffness due to the high frequency of the static shape functions and increased number of modes.

The aim of this work is to test isogeometric elements as an alternative approach to isoparametric elements in the context of the floating frame of reference approach. Therefore, it is shown how global shape functions can be determined from isogeometric finite element models, embedded in the floating frame of reference formulation and used, e.g., for impact simulations.

This work is organized in the following way. In Sect. 2 the concept of the floating frame of reference formulation is briefly summarized. The concept of the IGA is introduced in Sect. 3 and the procedure for the application with the floating frame of reference formulation is presented. Contact specific adjustments are explained in Sect. 4. In Sect. 5, Sect. 6 and Sect. 7 three application examples are presented. The findings are summarized in Sect. 8.

2 Floating frame of reference formulation

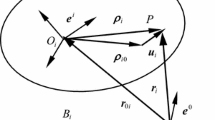
A well-known approach for simulating flexible multibody systems is the floating frame of reference formulation [12, 14]. Each flexible body of the system has a body-related moving reference frame \(\mathrm{K}_{\mathrm{R}}\). Within the inertial frame, the large nonlinear rigid body motion \({}^{\mathrm{R}}\boldsymbol{r}_{\mathrm{IR}}\) is defined, where the prescript ‘\(\mathrm{R}\)’ denotes the description in the body reference frame. In this work, a Buckens frame [12] is utilized as floating frame. The assumed small elastic deformations of the bodies are linear and are described in the corresponding body reference frame. The position of an arbitrary point \(\mathrm{P}\) on the flexible body with respect to the body reference frame is described by \({}^{\mathrm{R}}\boldsymbol{c}_{\mathrm{RP}}\). The small linear elastic deformation

$$ {}^{\mathrm{R}}\boldsymbol{u}_{\mathrm{P}}(t,\boldsymbol{c}_{\mathrm{RP}}) = \boldsymbol{\Phi }( \boldsymbol{c}_{\mathrm{RP}}) \boldsymbol{q}_{\mathrm{e}}(t) $$
(1)

can be reconstructed with the global shape functions \(\boldsymbol{\Phi }\) and the \(n_{\mathrm{q}}\) elastic coordinates \(\boldsymbol{q}_{\mathrm{e}}\). The position \({}^{\mathrm{R}}\boldsymbol{r}_{\mathrm{IP}}\) of the point \(\mathrm{P}\) within the inertial frame is expressed by

$$ {}^{\mathrm{R}}\boldsymbol{r}_{\mathrm{IP}} = {}^{\mathrm{R}}\boldsymbol{r}_{\mathrm{IR}} + {}^{\mathrm{R}}\boldsymbol{c}_{\mathrm{RP}} + {}^{\mathrm{R}}\boldsymbol{u}_{\mathrm{P}} $$
(2)

in the reference coordinate system. The description of the point \(\mathrm{P}\) in Eq. (2) can be seen in Fig. 1. The position, velocity, and acceleration of any point \(\mathrm{P}\) can be expressed in terms of the position coordinates \(\boldsymbol{z}_{\mathrm{I}}\), velocity coordinates \(\boldsymbol{z}_{\mathrm{II}}\) and accelerations \(\dot{\boldsymbol{z}}_{\mathrm{II}}\), which are defined as

$$ \boldsymbol{z}_{\mathrm{I}} = \begin{bmatrix} {}^{\mathrm{R}}\boldsymbol{r}_{\mathrm{IR}} \\ \boldsymbol{\beta}_{\mathrm{IR}} \\ \boldsymbol{q}_{\mathrm{e}}\end{bmatrix} ,~~~~\boldsymbol{z}_{\mathrm{II}} = \begin{bmatrix} {}^{\mathrm{R}}\boldsymbol{v}_{\mathrm{IR}} \\ {}^{\mathrm{R}}\boldsymbol{\omega}_{\mathrm{IR}} \\ \dot{\boldsymbol{q}}_{\mathrm{e}}\end{bmatrix} ~~~~\mathrm{and}~~~~\dot{\boldsymbol{z}}_{\mathrm{II}} = \begin{bmatrix} {}^{\mathrm{R}}\dot{\boldsymbol{v}}_{\mathrm{IR}} \\ {}^{\mathrm{R}}\dot{\boldsymbol{\omega}}_{\mathrm{IR}} \\ \ddot{\boldsymbol{q}}_{\mathrm{e}}\end{bmatrix} . $$
(3)

They consist of the rigid body deformation of the body reference frame with the translation \({}^{\mathrm{R}}\boldsymbol{r}_{\mathrm{IR}}\) and its velocity \({}^{ \mathrm{R}}\boldsymbol{v}_{\mathrm{IR}}\) from the inertial frame to the body reference frame. Rotations are represented by rotation parameters \(\boldsymbol{\beta}_{ \mathrm{IR}}\) and the angular velocity \({}^{\mathrm{R}}\boldsymbol{\omega}_{ \mathrm{IR}}\). The elastic motion is given by \(\boldsymbol{q}_{\mathrm{e}}\) and \(\dot{\boldsymbol{q}}_{\mathrm{e}}\). The equations of motion for a single flexible body are finally given by

$$\begin{aligned} \underbrace{\begin{bmatrix}m {\mathbf{E}} & m \tilde{\boldsymbol{c}}^{\intercal }& \boldsymbol{C}_{\mathrm{t}}^{\intercal }\\ m \tilde{\boldsymbol{c}} & \boldsymbol{I} & \boldsymbol{C}_{\mathrm{r}}^{\intercal }\\ \boldsymbol{C}_{\mathrm{t}} & \boldsymbol{C}_{\mathrm{r}} & \overline{\boldsymbol{M}}_{\mathrm{e}}\end{bmatrix}}_{ \boldsymbol{M}} \underbrace{\begin{bmatrix}{}^{\mathrm{R}}\dot{\boldsymbol{v}}_{\mathrm{IR}} \\ {}^{\mathrm{R}}\dot{\boldsymbol{\omega}}_{\mathrm{IR}} \\ \ddot{\boldsymbol{q}}_{\mathrm{e}}\end{bmatrix}}_{ \dot{\boldsymbol{z}}_{\mathrm{II}}} &= \underbrace{\boldsymbol{h}_{\mathrm{p}} + \boldsymbol{h}_{\mathrm{d}} + \boldsymbol{h}_{\mathrm{b}} - \boldsymbol{h}_{\mathrm{\omega }} - \boldsymbol{h}_{\mathrm{e}}}_{ \boldsymbol{h}_{\mathrm{a}}}, \end{aligned}$$
(4)

which are assembled by the standard input data (SID). The SID [12] is a well-known standard in providing elastic data in the context of the floating frame of reference formulation. In Eq. (4), the mass of the body is denoted by \(m\), the center of mass relative to \(\mathrm{K}_{\mathrm{R}}\) by \(\tilde{\boldsymbol{c}}\), the translational coordinate coupling matrix by \(\boldsymbol{C}_{\mathrm{t}}\), the rotational coordinate coupling matrix by \(\boldsymbol{C}_{\mathrm{r}}\), the mass matrix \(\overline{\boldsymbol{M}_{\mathrm{e}}}\) of the flexible body and the mass moment of inertia by \(\boldsymbol{I}\). The right-hand side vector \(\boldsymbol{h}_{\mathrm{a}}\) is composed of the vector of surface forces \(\boldsymbol{h}_{\mathrm{p}}\), the discrete forces \(\boldsymbol{h}_{\mathrm{d}}\), the body forces \(\boldsymbol{h}_{\mathrm{b}}\), the inertial forces \(\boldsymbol{h}_{\mathrm{\omega }}\) and the internal forces

$$ \boldsymbol{h}_{\mathrm{e}}= \begin{bmatrix} \boldsymbol{0} \\ \boldsymbol{0} \\ \overline{\boldsymbol{K}}_{\mathrm{e}}\boldsymbol{q}_{\mathrm{e}}+\overline{\boldsymbol{D}}_{\mathrm{e}}\dot{\boldsymbol{q}}_{\mathrm{e}}\end{bmatrix} . $$
(5)

Here \(\overline{\boldsymbol{K}}_{\mathrm{e}}\) represents the stiffness matrix and \(\overline{\boldsymbol{D}}_{\mathrm{e}}\) the damping matrix. Occurring contact forces are applied at the discrete forces \(\boldsymbol{h}_{\mathrm{d}}\).

Fig. 1
figure 1

Kinematics in the floating frame of reference formulation

Full size image

3 Global shape functions from reduced isogeometric analysis models

A major question using the floating frame of reference formulation is how to obtain the global shape functions \(\boldsymbol{\Phi }\). This section presents the key idea of the IGA and the procedure to obtain the global shape functions from an IGA model. A detailed introduction to the IGA can be found, for instance, in [2].

A general way to determine the global shape functions is to generate a finite element model of the flexible body and then to identify the global shape functions form the finite element model using model reduction techniques. The generation of a two-dimensional isogeometric finite element model is briefly explained in the following.

3.1 Basis-splines

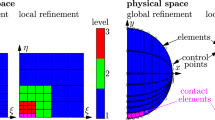
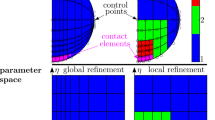
Two spaces are used in the IGA, the physical space and the parameter space. The shape functions of isogeometric elements are defined in the parameter space which can be seen on the left-hand side in Fig. 2. The parameter space is divided into elements and spanned by the knot vectors

$$ \Xi = \begin{bmatrix} \xi _{1} & \xi _{2} & \ldots & \xi _{\mathrm{n+p+1}}\end{bmatrix} ~~~\mathrm{and}~~~\mathcal{H} = \begin{bmatrix} \eta _{1} & \eta _{2} & \ldots & \eta _{\mathrm{m+q+1}}\end{bmatrix} . $$
(6)

Thereby, \(p\) and \(q\) are the polynomial orders and \(n\) and \(m\) are the numbers of the basis functions \(N_{i,\mathrm{p}}\) and \(M_{j, \mathrm{q}}\). The basis functions are based on B-splines and can be computed recursively by the Cox–de Boor algorithm. The shape functions in the \(\xi \)-direction are computed as

$$\begin{aligned} p&=0:~~~~N_{i,0}(\xi ) = \Bigg\{ \textstyle\begin{array}{l} 1~~~~\mathrm{if}~\xi _{i} < \xi < \xi _{i+1}, \\ 0~~~~\mathrm{otherwise}, \end{array}\displaystyle \end{aligned}$$
(7)
$$\begin{aligned} p&>1:~~~~N_{i,\mathrm{p}}(\xi ) = \frac{\xi - \xi _{i}}{\xi _{i+\mathrm{p}} - \xi _{i}} N_{i,\mathrm{p}-1}( \xi ) + \frac{\xi _{i+\mathrm{p}+1} - \xi }{\xi _{i+\mathrm{p}+1} - \xi _{i+1}} N_{i+1,\mathrm{p}-1}(\xi ). \end{aligned}$$
(8)

The calculation rule given by Eq. (7) and Eq. (8) is identical in \(\eta \)-direction. In practice, recursive functions are numerically inefficient. Therefore, a nonrecursive algorithm is used, which is suggested in [9].

Fig. 2
figure 2

Parameter space and physical space in the IGA

Full size image

3.2 NURBS

Besides the parameter space there is the physical space, which can be seen on the right-hand side in Fig. 2. In the physical space the control net is defined. It is formed by control points \(\boldsymbol{P}_{i,j}\) which have a corresponding weight \(w_{i,j}\). To transform the parameter space into the physical space, the NURBS basis \(R_{i,j}^{\mathrm{p,q}}\) is given by

$$ R_{i,j}^{\mathrm{p,q}}(\xi ,\eta ) = \frac{N_{i,\mathrm{p}}(\xi )M_{j,\mathrm{q}}(\eta )w_{i,j}}{\sum _{\hat{i}=1}^{\mathrm{n}} \sum _{\hat{j}=1}^{\mathrm{m}} N_{\hat{i},\mathrm{p}}(\xi ) M_{\hat{j},\mathrm{q}}(\eta ) w_{\hat{i},\hat{j}}} $$
(9)

using above B-splines \(N_{i,\mathrm{p}}\) and \(M_{j,\mathrm{q}}\). The NURBS basis and the control points then lead to the NURBS surface

$$ \boldsymbol{S} = \sum _{i=1}^{\mathrm{n}} \sum _{j=1}^{\mathrm{m}} R_{i,j}^{\mathrm{p,q}}(\xi ,\eta ) \boldsymbol{P}_{i,j}, $$
(10)

which gives the B-spline surface in the physical space.

The degrees of freedom in the IGA correspond to the displacements \(\boldsymbol{u}_{i,j}\) of the control points

$$ \boldsymbol{u}_{i,j}=\boldsymbol{P}_{i,j}-\boldsymbol{P}_{i,j}^{0}~~~~~~~~~~\text{for}~i=1...n,~j=1...m, $$
(11)

whereby \(\boldsymbol{P}_{i,j}^{0}\) represents the position of the undeformed control points and \(\boldsymbol{P}_{i,j}\) the position of the deformed ones. The deformation \(\boldsymbol{d}\) of the NURBS surface can be computed with

$$ \boldsymbol{d} = \boldsymbol{N} \boldsymbol{u} = \begin{bmatrix} R_{1,1}^{\mathrm{p,q}} & 0 & R_{1,2}^{\mathrm{p,q}} & 0 & \ldots & 0 \\ 0 & R_{1,1}^{\mathrm{p,q}} & 0 & R_{1,2}^{\mathrm{p,q}} & \ldots & R_{\mathrm{p+1,q+1}}^{\mathrm{p,q}}\end{bmatrix} \begin{bmatrix} u_{\mathrm{1,1,x}} \\ u_{\mathrm{1,1,y}} \\ u_{\mathrm{1,2,x}} \\ u_{\mathrm{1,2,y}} \\ \vdots \\ u_{\mathrm{p+1,q+1,y}}\end{bmatrix} , $$
(12)

where the basis functions of the corresponding element are summarized in \(\boldsymbol{N}\).

3.3 Equations of motion for isogeometric elements

The procedure of setting up the equations of motion for isogeometric elements is almost identical to isoparametric elements. This is because the weak Galerkin method is also applied for isogeometric elements. Like for isoparametric models, the isogeometric model requires a preprocessing [2]. This includes the determination of the local mass and stiffness matrices of each isogeometric element. For relatively stiff materials linear elasticity can be assumed. The calculation rule is identical to isoparametric elements [1]. The local mass and stiffness matrices are given by

$$\begin{aligned} \boldsymbol{K}_{\mathrm{e},j} &= \int _{\mathrm{\Omega }_{\mathrm{e},j}} \boldsymbol{B}^{\intercal }\boldsymbol{C} \boldsymbol{B} ~ \mathrm{d}\Omega _{\mathrm{e},j}~~~~~~~~~~ \text{for}~j=1...n_{\mathrm{e}}, \end{aligned}$$
(13)
$$\begin{aligned} \boldsymbol{M}_{\mathrm{e},j} &= \rho \int _{\mathrm{\Omega }_{\mathrm{e},j}} \boldsymbol{N}^{\intercal }\boldsymbol{N} ~ \mathrm{d}\Omega _{\mathrm{e},j}~~~~~~~~~~ \text{for}~j=1...n_{\mathrm{e}}, \end{aligned}$$
(14)

where \(\boldsymbol{C}\) is the material elasticity matrix and \(n_{\mathrm{e}}\) is the number of elements. The strain displacement matrix \(\boldsymbol{B}\) is assembled by differentiating the NURBS basis \(R_{i,j}^{\mathrm{p,q}}\) and using the Jacobian transformation [1]. The integration over each element \(\Omega _{\mathrm{e},j}\) is achieved by the Gauss quadrature in the parameter space. The basis functions \(\boldsymbol{N}\) and the strain displacement matrix \(\boldsymbol{B}\) are evaluated at each Gauss point. As stated in [2], the same Gauss rule for a polynomial of the order \(p\) can be applied to a \(p\)-th order NURBS function. Therefore, the Gauss order \(p+1\) is chosen in \(\xi \)-direction and order \(q+1\) in \(\eta \)-direction. The global system matrices \(\boldsymbol{K}_{\mathrm{e}}\) and \(\boldsymbol{M}_{\mathrm{e}}\) are created by assembling the corresponding element matrices. The elements are connected by shared control points. The equations of motion of the isogeometric model in a body-attached nonrotated frame are then given by

$$ \boldsymbol{M}_{\mathrm{e}} \ddot{\boldsymbol{u}} + \boldsymbol{K}_{\mathrm{e}} \boldsymbol{u} = \boldsymbol{f}_{\mathrm{e}}, $$
(15)

where the displacements of the control points are represented by \(\boldsymbol{u} \in \mathbb{R}^{n_{\mathrm{dof}}}\). The number of degrees of freedom is denoted by \(n_{\mathrm{dof}}\) and external forces by \(\boldsymbol{f}_{\mathrm{e}}\). It should be noted that Eq. (15) is only valid for a nonrotating body, otherwise a more complex inertial term would occur. Compared to isoparametric models, the system matrices \(\boldsymbol{K}_{\mathrm{e}}\) and \(\boldsymbol{M}_{\mathrm{e}}\) of isogeometric models are more dense since the number of shared control points is defined by \((p+1)\times (q+1)\). Therefore, more effort is required in the numerical solution. But since the system matrices are reduced before incorporating them into the floating frame of reference formulation, this disadvantage is not relevant in the simulation time.

3.4 Model order reduction of isogeometric elements

The most common approach for reducing the equations of motion (15) is the modal reduction. As shown in [16, 20] this leads to inaccurate results in case of impact problems, since the local deformation in the contact region is not included in the reduced basis. An alternative approach is the Craig–Bampton method [3], which is a special case of the Component-Mode-Synthesis. The idea of the Craig–Bampton method is the combination of fixed-interface normal modes and constraint modes. The normal modes are determined by an eigenvalue problem and the constraint modes by unit displacements to each predefined interface control point. These predefined control points are located on the outside of the body in the contact area where later potential forces act. A detailed description of the Craig–Bampton method for isogeometric elements can be found in [8]. The procedure results in the shape function matrix \(\boldsymbol{\Phi } \in \mathbb{R}^{n_{\mathrm{dof}} \times n_{\mathrm{q}}}\). The resulting system consists of \(n_{\mathrm{q}} \ll n_{\mathrm{dof}}\) degrees of freedom. The reduced mass and stiffness matrices are then given by

$$\begin{aligned} \overline{\boldsymbol{M}}_{\mathrm{e}} &= \boldsymbol{\Phi }^{\intercal }\boldsymbol{M}_{\mathrm{e}} \boldsymbol{\Phi } = {\mathbf{E}}, \end{aligned}$$
(16)
$$\begin{aligned} \overline{\boldsymbol{K}}_{\mathrm{e}} &= \boldsymbol{\Phi }^{\intercal }\boldsymbol{K}_{\mathrm{e}} \boldsymbol{\Phi } = \mathrm{diag}(\omega _{i}^{2}), \end{aligned}$$
(17)

where \({\mathbf{E}}\) is the identity matrix and \(\omega _{i}\) the natural frequencies.

3.5 Software implementation

The software solution used here to simulate flexible multibody systems is the Matlab toolbox DynManto [5], which is developed at the Institute of Mechanics and Ocean Engineering at the TUHH. The workflow to incorporate flexible bodies in multibody simulations is briefly summarized in the following.

The geometry is modeled in a computer-aided design tool and imported in a finite element program such as Ansys. The finite element data is then imported in the Matlab toolbox RED [5]. RED reads the elastic data, applies a model order reduction technique and determines the SID. The flexible body is then defined in DynManto using the SID to assemble the equations of motion (4).

This procedure changes only slightly for isogeometric elements. A geometry, which is based on B-splines, is designed with the in house Matlab toolbox RIGA. Currently, only simple geometries can be modeled with RIGA. Importing any geometry from a CAD program is not possible at the moment. One problem is that standard CAD programs only map the outer surface of three-dimensional bodies in a two-dimensional parameter space. This is not sufficient for a full finite element model.

To enable compatibility with the workflow described above, the data structure of the Ansys interface is adapted. Besides the global mass and stiffness matrix, the element table, the table of degrees of freedom and the coordinates of the control points are needed to enable the basic functionality. The use of the Craig–Bampton method additionally requires the specification of the identification number of the control points and the corresponding degrees of freedom of the interface control points.

4 Modeling of contacts using isogeometric elements

This section presents contact specific adjustments to the equations of motion (15) and aspects to increase the numerical efficiency. This includes the introduction of a penalty formulation for isogeometric elements.

4.1 Penalty formulation

The penalty formulation is chosen to model the contact in this work. The concept of the penalty formulation is the penalization of a penetration with a spring force. The spring constant \(c_{\mathrm{p}}\) is a tuning factor and needs to be chosen heuristically. Thereby, the penalty factor should be chosen large enough such that the results become independent of the chosen parameter [13]. Recapturing first the application of the penalty method for isoparametric elements, a set of exterior slave nodes is checked for contact. If a contact occurs, the node is loaded with the contact force

$$ \boldsymbol{f}_{\mathrm{c}} = c_{\mathrm{p}} g_{\mathrm{n}} \boldsymbol{n}, $$
(18)

where \(g_{\mathrm{n}}\) is the normal distance of the slave node to the master body, and \(\boldsymbol{n}\) the normal vector.

In each time step of the simulation the body is checked for occurring contacts. This requires the deformed NURBS surface. Initially, the displacements \(\boldsymbol{u}\) of the control points are recovered with

$$ \boldsymbol{u}=\boldsymbol{\Phi }\boldsymbol{q}_{\mathrm{e}} $$
(19)

using the global shape functions \(\boldsymbol{\Phi }\) and the elastic coordinates \(\boldsymbol{q}_{\mathrm{e}}\). With Eq. (11) and Eq. (19), the position of the deformed control points \({}^{\mathrm{R}}\boldsymbol{P}_{i,j}\) can be determined in the corresponding reference coordinate system of the flexible body. Finally, rotations of the body reference frame are considered using Tait–Bryan angles. The rotation parameters \(\boldsymbol{\beta}_{\mathrm{IR}}= \begin{bmatrix} \alpha &\beta &\gamma \end{bmatrix} ^{\intercal }\) from Eq. (3) describe rotations about the \(x\)-, \(y\)- and \(z\)-axis, respectively. The corresponding rotation matrix

$$ \boldsymbol{S}(\boldsymbol{\beta}_{\mathrm{IR}})= \begin{bmatrix} 1&0&0 \\ 0&\cos (\alpha )&-\sin (\alpha ) \\ 0&\sin (\alpha )&\cos (\alpha ) \end{bmatrix} \begin{bmatrix} \cos (\beta )&0&\sin (\beta ) \\ 0&1&0 \\ -\sin (\beta )&0&\cos (\beta ) \end{bmatrix} \begin{bmatrix} \cos (\gamma )&-\sin (\gamma )&0 \\ \sin (\gamma )&\cos (\gamma )&0 \\ 0&0&1 \end{bmatrix} $$
(20)

transforms a vector from the body reference frame to the inertial frame. To enable the check for occurring contacts, the deformed control points \({}^{\mathrm{R}}\boldsymbol{P}_{i,j}\) are transformed to the inertial frame with

$$ {}^{\mathrm{I}}\boldsymbol{P}_{i,j}=\boldsymbol{S}(\boldsymbol{\beta}_{\mathrm{IR}}){}^{\mathrm{R}} \boldsymbol{P}_{i,j}~~~~~~~~~~\text{for}~i=1...n,~j=1...m. $$
(21)

The prescript ‘\(\mathrm{I}\)’ denotes the description in the inertial frame.

In this work the contact is restricted to the contact of a body described by IGA with a rigid surface representing the master, see Fig. 3. A knot-to-surface based method using the Gauss integration [10, 17, 18] is chosen, where a set of \(n_{\mathrm{c}}\) slave elements is checked for contact. If the normal gap \(g_{\mathrm{n}}\) between the flexible body and the rigid surface is negative, the contact force

$$ {}^{\mathrm{I}}\boldsymbol{f}_{\mathrm{c},j} = \int _{\Omega _{\mathrm{e},j}} \boldsymbol{N}^{\intercal }c_{\mathrm{p}} g_{\mathrm{n}} \boldsymbol{n} ~ \mathrm{d} \Omega _{\mathrm{e},j}~~~~~~~~~~\text{for}~j=1...n_{\mathrm{c}} $$
(22)

is applied with the penalty formulation to the slave body. After all slave elements have been checked for contact and the contact forces \({}^{\mathrm{I}}\boldsymbol{f}_{\mathrm{c},j}\) have been determined, the resulting forces on the control points are assembled to the force vector

$$ {}^{\mathrm{I}}\boldsymbol{f}_{i,j}= \begin{bmatrix} f_{i,j,\mathrm{x}} \\ f_{i,j,\mathrm{y}} \\ 0\end{bmatrix} ~~~~~~~~~~\text{for}~i=1...n,~j=1...m. $$
(23)

The forces \(f_{i,j,\mathrm{x}}\) and \(f_{i,j,\mathrm{y}}\) act on each individual control point in \(x\)- and \(y\)-direction, respectively. The forces \({}^{\mathrm{I}}\boldsymbol{f}_{i,j}\) are described in the inertial frame, since the contact check is performed within the inertial frame. In order to determine the contact forces with respect to the flexible body, the forces \({}^{\mathrm{I}}\boldsymbol{f}_{i,j}\) are transformed to the body reference frame with

$$ {}^{\mathrm{R}}\boldsymbol{f}_{i,j}=\boldsymbol{S}^{\intercal }(\boldsymbol{\beta}_{\mathrm{IR}}){}^{\mathrm{I}}\boldsymbol{f}_{i,j}~~~~~~~~~~\text{for}~i=1...n,~j=1...m. $$
(24)

As mentioned before, the contact forces are assigned at the discrete forces \(\boldsymbol{h}_{\mathrm{d}}\) in Eq. (4). The discrete forces \(\boldsymbol{h}_{\mathrm{d}}\) consist of three components, including the components of translation \(\boldsymbol{h}_{\mathrm{dt}}\) and rotation \(\boldsymbol{h}_{\mathrm{dr}}\) of the rigid body, as well as the discrete forces \(\boldsymbol{h}_{\mathrm{de}}\) affecting the elastic deformation. The discrete forces \(\boldsymbol{h}_{\mathrm{d}}\) are then summarized in

$$ \boldsymbol{h}_{\mathrm{d}}= \begin{bmatrix} \boldsymbol{h}_{\mathrm{dt}} \\ \boldsymbol{h}_{\mathrm{dr}} \\ \boldsymbol{h}_{\mathrm{de}}\end{bmatrix} =\sum _{i=1}^{\mathrm{n}}\sum _{j=1}^{\mathrm{m}} \begin{bmatrix} {\mathbf{E}} \\ {}^{\mathrm{R}}\tilde{\boldsymbol{P}}_{i,j} \\ \boldsymbol{\Phi }^{\intercal }({}^{\mathrm{R}}\boldsymbol{P}_{i,j})\end{bmatrix} {}^{\mathrm{R}}\boldsymbol{f}_{i,j}. $$
(25)

The contact resolution of isoparametric elements depends on the number of nodes in the contact area. In contrast to isogeometric elements the resolution depends primarily on the number of knots in the contact region. When the Gauss integration is used, the contact resolution additionally depends on the order of the B-splines. The resolution can be further increased by choosing a higher Gauss order. However, here the Gauss order \(p+1\) and \(q+1\) as defined in Sect. 3.3 is used. Thereby, \(p+1\) or \(q+1\) Gauss points are checked in each of the previously selected contact elements.

Fig. 3
figure 3

Penalty method based on the Gauss integration

Full size image

4.2 Increasing the numerical efficiency

One major drawback of the Craig–Bampton method is the numerical stiffness of the resulting equations of motion [11]. The frequencies of the normal modes are relatively low and the frequencies of the constraint modes relatively high. The high frequency Craig–Bampton modes are important to capture the local deformation of the contact region, however have no influence on the wave propagation. The wave propagation is determined by the normal modes. One simple approach to increase the numerical performance is presented in [15] to efficiently damp the high frequency modes. This procedure has also been applied to reduced isoparametric element models [19] and is also used here for the reduced IGA model. By defining the Rayleigh damping coefficients

$$\begin{aligned} \alpha _{1} &= 4 \pi ^{2} f_{1} f_{2} \alpha _{2}, \end{aligned}$$
(26)
$$\begin{aligned} \alpha _{2} &= \frac{\kappa }{\pi (f_{1} + f_{2})}, \end{aligned}$$
(27)

the damping matrix

$$ \overline{\boldsymbol{D}}_{\mathrm{e}} = \alpha _{1} \overline{\boldsymbol{M}}_{\mathrm{e}} + \alpha _{2} \overline{\boldsymbol{K}}_{\mathrm{e}} $$
(28)

can be determined. The frequencies \(f_{1}\) and \(f_{2}\) represent the frequency band of the normal modes. Thereby, frequencies between \(f_{1}\) and \(f_{2}\) are only minimally damped, which is necessary for capturing the wave propagation, where frequencies above \(f_{2}\) are critically damped. The damping parameter \(\kappa \) is a tuning factor. Heuristic testing showed that the value \(\kappa =0.001\) does improve the numerical performance and has only a small influence on the elastic dynamic effects. The resulting damping matrix \(\overline{\boldsymbol{D}}_{\mathrm{e}}\) is then updated in the inner forces \(\boldsymbol{h}_{\mathrm{e}}\) in Eq. (5).

5 Application Example I: impact of a sphere

As a first application example, the impact of two identical spheres is considered. The constellation is shown in Fig. 4. Both spheres have a radius of \(r=10~\mbox{mm}\). The chosen material is aluminum, therefore the Young’s modulus is chosen as \(E= 7.28\times 10^{10}~\mbox{Pa}\), the density as \(\rho = 2789~{\frac{\text{kg}}{\text{m}^{3}}}\) and the Poisson’s ratio as \(\nu =0.33\). Both spheres have an initial velocity of \(v_{0} = 0.1~{\frac{\text{m}}{\text{s}}}\) and gravity is ignored.

Fig. 4
figure 4

Impact of two identical spheres

Full size image

In this section the proposed reduced isogeometric element model is compared to the analytical solution by Hertz [6]. Additionally, a comparison to a full nonlinear isoparametric model simulated in Ansys is done.

5.1 Hertz impact

As a reference, the analytical solution for the impact of two spheres by Hertz is used [6]. For the impact of two spheres, they are modeled as mass points. During contact the contact force

$$ f_{\mathrm{Hertz}} = \frac{4}{3} E^{*} \sqrt{r^{*}} \delta ^{3/2} $$
(29)

acts between the spheres, where \(\delta \) denotes the displacement between the center of mass of the spheres. This corresponds to the overlap of the undeformed spheres, see Fig. 4. The equivalent Young’s modulus \(E^{*}\) and the equivalent radius \(r^{*}\) are determined by

$$\begin{aligned} \frac{1}{E^{*}} &= \frac{1-\nu _{1}^{2}}{E_{1}} + \frac{1-\nu _{2}^{2}}{E_{2}}, \end{aligned}$$
(30)
$$\begin{aligned} \frac{1}{r^{*}} &= \frac{1}{r_{1}} + \frac{1}{r_{2}}. \end{aligned}$$
(31)

The Young’s modulus of the two spheres is denoted by \(E_{1}\) and \(E_{2}\), the Poisson’s ratio by \(\nu _{1}\) and \(\nu _{2}\), the radius by \(r_{1}\) and \(r_{2}\). Due to the symmetry of two identical spheres, the lower sphere, as shown is Fig. 4, is modeled by a rigid surface. An equivalent assumption can be found in [21] where the Hertz contact between two identical cylinders is modeled.

The contact width \(a\) and the maximum pressure \(p_{0}\) are given by

$$\begin{aligned} a &= \sqrt{r \delta }, \end{aligned}$$
(32)
$$\begin{aligned} p_{0} &= \frac{3 f_{\mathrm{Hertz}}}{2 \pi a^{2}}. \end{aligned}$$
(33)

Thus the Mise stress along the symmetry axis can be calculated as

$$ \sigma _{\mathrm{Mise}}(y) = p_{0} \Bigg|\frac{3}{2} \frac{a^{2}}{a^{2} + y^{2}} - (1 + \nu ) \Bigg(1 - \frac{y}{a} \arctan {\Big(\frac{a}{y}\Big)}\Bigg)\Bigg|. $$
(34)

5.2 Isogeometric model

To reduce the computational cost of the IGA impact simulation, the sphere is substituted by an axisymmetric semicircle. Thus a rotational symmetry model is used. This means that fewer interface control points are needed, the number of elastic coordinates \(n_{\mathrm{q}}\) is reduced and the number of points at which the contact is evaluated is reduced. However, the flexible body cannot perform a rigid body rotation, but only a rigid body translation along the symmetry axis. Due to symmetry, the lower sphere, as shown is Fig. 4, is modeled by a rigid surface. The order of the B-splines is given by \(p=2\) and \(q=1\). The knot vectors for a semicircle are

$$ \Xi = \begin{bmatrix} 0 & 0 & 0 & 1 & 1 & 1\end{bmatrix} ~~~~\mathrm{and}~~~~\mathcal{H} = \begin{bmatrix} 0 & 0 & 1 & 1\end{bmatrix} . $$
(35)

The corresponding control points and weights are

$$ \boldsymbol{P}^{0}_{i,j,1}= \begin{bmatrix} 0&0 \\ r&r \\ r&r\end{bmatrix} ,~~~~\boldsymbol{P}^{0}_{i,j,2}= \begin{bmatrix} -r&r \\ -r&r \\ 0&0\end{bmatrix} ~~~~\mathrm{and}~~~~\boldsymbol{W}_{i,j}= \begin{bmatrix} 1 & 1 \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 1 & 1 \end{bmatrix} . $$
(36)

However, the definition of the order, knots and control points is only sufficient for the exact visualization of the geometry. To obtain an exact solution of the impact problem, the model must be refined, especially in the contact area [22]. Two common methods for refinement are the order elevation [7] and the insertion of knots [2]. The final model is depicted in Fig. 5a. The order is elevated to \(p=4\) and \(q=3\). The minimum edge length of an element in the contact zone is \(50~\upmu \mbox{m}\). This results in 1 evaluation point per \(10~\upmu \mbox{m}\), since the Gaussian order \(p+1\) is selected in the \(\xi \)-direction.

Fig. 5
figure 5

Finite element models of a rotationally symmetric sphere

Full size image

The isogeometric model is reduced with the Craig–Bampton method. The number of normal modes is chosen as 6, and 10 interface control points on the lower side are used to determine the constraint modes. Therefore, the resulting number of elastic coordinates is \(n_{\mathrm{q}}=26\).

For comparison, the full IGA model is used. In order to include it in the same framework, the full IGA model is modally transformed using all modes. With \(n_{\mathrm{dof}}=614\) degrees of freedom this leads to \(n_{\mathrm{q}}=614\) elastic coordinates.

5.3 Isoparametric model

Beside the analytical solution and the proposed reduced isogeometric model, an isoparametric finite element model is used for comparison. Four-noded plane elements are utilized. The axisymmetric model is generated in Ansys and visualized in Fig. 5b. The minimum edge length in the contact zone is \(10~\upmu \mbox{m}\). As with the isogeometric model in Sect. 5.2, this results in 1 evaluation point per \(10~\upmu \mbox{m}\). This isoparametric finite element model has \(n_{\mathrm{dof}}=3588\) degrees of freedom and due to the contact elements a full nonlinear analysis has to be performed.

5.4 Simulation results and analysis

Simulations of \(0.1~\mbox{ms}\) are performed for analysis and comparison. The isoparametric model is solved with a fixed step size of \(0.1~\upmu \mbox{s}\) in Ansys. Thereby, both the penalty formulation and normal Lagrange formulation are applied. Since the results of the two formulations are nearly identical in this simulation setup, only the penalty solution is presented for the isoparametric model. The isogeometric model is solved in the Matlab toolbox DynManto. As stated in Sect. 4.1, the penalty factor \(c_{\mathrm{p}}\) is an independent tuning factor. Heuristic testing showed, that the numerical solution converged for the penalty factor \(c_{\mathrm{p}}= 5\times10^{18}~\mbox{N}/\mbox{m}\). This means that higher penalty factors yield the same results. An overview of both models can be found in Table 1. The simulations differ mainly in the short calculation time of the isogeometric model reduced with CMS compared to the isoparametric model. The isogeometric model which is modally transformed takes much longer than the isogeometric CMS model. The reason for this is the lower number of elastic coordinates in the CMS model. The differences in the results are discussed in the following. The solution by Hertz in Sect. 5.1 is used as a reference.

Table 1 Finite element models of an axisymmetric sphere
Full size table

In Fig. 6 the occurring contact force is displayed. The maximum absolute error of the isogeometric model is \(1~\mbox{N}\). The maximum absolute error of the isoparametric model is slightly lower, it is \(0.7~\mbox{N}\). There is no discernible difference between the CMS model and the full IGA model. The low frequency normal modes already map the overall elastic behavior, and the selected constraint modes are sufficient to describe the deformation in the contact area in this application example. However, the computation time of the CMS model is significantly lower compared to the full IGA model.

Fig. 6
figure 6

Time course of the contact force

Full size image

The relationship between contact force \(f_{\mathrm{c}}\) and displacement \(\delta \) is shown in Fig. 7. The nonlinear relationship is well represented by all finite element models. Again, no difference can be seen between the IGA CMS model and the full IGA model.

Fig. 7
figure 7

Displacement \(\delta \) with respect to the force \(f_{\mathrm{c}}\)

Full size image

The von Mises stress along the symmetry axis is given in Eq. (34) and visualized in Fig. 8. For the comparison, the time step was chosen at which the occurring stresses are maximum in the respective simulation. The maximum stress occurring in the flexible body is slightly better represented by the isoparametric model than by the isogeometric model. However, the overall stress is better represented by the isogeometric model. Overall, the differences are very small and are of minor practical importance. The distribution of the von Mises stress in the contact area is shown in Fig. 9. It shows that the reduced IGA model reproduces the stresses predicted by the nonlinear isoparametric model very accurately.

Fig. 8
figure 8

Maximum von Mises stress

Full size image
Fig. 9
figure 9

Von Mises stress in the contact area

Full size image

6 Application Example II: impact of a long rod

Whilst the first application example exhibits quasistatic behavior, the second application example shows significant elastodynamic effects. For this second test case a long cylindrical aluminum rod with length of \(\ell = 1~\mbox{m}\) and radius of \(r = 10~\mbox{mm}\) is used. At one end, the rod has a spherical end which impacts on a rigid surface. The wave speed in the rod can be computed, following, e.g., [4], with

$$\begin{aligned} c_{\mathrm{rod}} = \sqrt{\frac{E}{\rho }} = {5109}~{\frac{\text{m}}{\text{s}}}. \end{aligned}$$
(37)

In the following it is investigated whether a reduced isogeometric model can represent the wave propagation, and this model is again composed to a full nonlinear isoparametric model in Ansys.

The initial velocity of the rod is \(v_{0}=0.3~\text{m} /\text{s}\). The axisymmetric isogeometric finite element model is depicted in Fig. 10a and the isoparametric model in Ansys in Fig. 10b. As with the isogeometric sphere model in Sect. 5.2, the order is given by \(p=2\) and \(q=1\). The knot vectors can be taken from Eq. (35). The corresponding control points and weights are

$$ \boldsymbol{P}^{0}_{i,j,1}= \begin{bmatrix} 0&0 \\ r&r \\ r&r\end{bmatrix} ,~~~~\boldsymbol{P}^{0}_{i,j,2}= \begin{bmatrix} 0& \ell \\ 0& \ell \\ r& \ell \end{bmatrix} ~~~~ \mathrm{and}~~~~\boldsymbol{W}_{i,j}= \begin{bmatrix} 1 & 1 \\ \frac{1}{\sqrt{2}} & 1 \\ 1 & 1 \end{bmatrix} . $$
(38)

Due to the spherical end of the rod, the contact area is rounded in a circle. The order is elevated to \(p=6\) and \(q=5\). The minimum edge length of an element in the contact zone is \(35~\upmu \mbox{m}\). This results in 1 evaluation point per \(5~\upmu \mbox{m}\), since the Gaussian order \(p+1\) is selected in the \(\xi \)-direction. The number of normal modes is chosen as 100, and 25 interface control points on the lower side are used to determine the constraint modes.

Fig. 10
figure 10

Section of the finite element models of an axisymmetric rod

Full size image

The isoparametric finite element model has a minimum edge length in the contact area of \(5~\upmu \mbox{m}\). As with the isogeometric model, this results in 1 evaluation point per \(5~\upmu \mbox{m}\). The isoparametric model is solved with a fixed step size of \(0.1~\upmu \text{s}\) in Ansys.

Testing showed again that the numerical solution of the reduced IGA model converged for the penalty factor of \(c_{\mathrm{p}}= 1\times10^{18}~\mbox{N}/\mbox{m}\) and greater. An overview of the models is given in Table 2. As already observed in Sect. 5.4, the reduced isogeometric model again requires less computing time.

Table 2 Finite element models of an axisymmetric rod
Full size table

To monitor the wave propagation, the velocity in \(y\)-direction of a control point or a node is visualized in Fig. 11. For the sake of simplicity, no distinction will be made in the following between the terms “control point” and “node”. Instead, the designation “point” is chosen. Both points are located on the symmetry axis at the top of the one meter long rod. The corresponding contact force of the impact is depicted in Fig. 12. The \(x\)-axis in Fig. 11 and Fig. 12 represents the integer multiples of the time it takes for the wave to travel one meter. The impact starts at the time stamp \(t_{0}=0~\mbox{s}\). In the beginning, both points at the top end of the rod keep the initial velocity of the rod. The impact of the rod induces a wave, which reaches the monitored points at the time \(t=t_{1}\). As the wave has reached the end of the rod, the wave is reflected and moves back to the contact area. Between the times \(t=t_{1}\) and \(t=t_{2}\) the contact force remains almost constant. This shows that the rod, in contrast to the sphere, is not able to push itself off the rigid surface by decompressing the local deformation. Only the re-entry of the wave in the contact area at the time \(t=t_{2}\) allows an end of the impact and the contact force decreases. At the time \(t=t_{3}\) the wave arrives again at the monitored point and a periodic oscillation behavior of the velocity is established.

Fig. 11
figure 11

Velocity of the control point and the node in the rod

Full size image
Fig. 12
figure 12

Contact force of the impact of the rod

Full size image

The temporal course of the velocity in Fig. 11 shows that both the isogeometric and isoparametric finite element models represent the wave propagation accurately. The wave speed from Eq. (37) is well mapped, which shows that the IGA is also capable of predicting elastodynamic behavior in a long rod well.

7 Application Example III: impact of a rotating body

In a third application example an impact problem with a large rotation is considered. As described in [14], the floating frame of reference formulation can model large rotations of flexible bodies. This application example is intended to show that this is also feasible with an IGA model. In the course of this, a rotating cylinder impacts on a rigid surface as depicted in Fig. 13.

Fig. 13
figure 13

Impact of a rotating cylinder

Full size image

The initial rotational velocity is \(\omega _{0}=2\pi\ /\mbox{s}\) and the initial translational velocity in vertical direction is \(v_{0}= 0.1~\mbox{m}/\mbox{s}\). Due to the rotation, sliding friction is induced with the coefficient \(\mu =0.3\). The frictional force acts in negative \(x\)-direction and thus will change the rotational velocity.

The cylinder is modeled by a two-dimensional circle with radius of \(r= 0.1~\mbox{m}\) and plane strain material behavior. The material is steel, therefore the Young’s modulus is chosen as \(E=2.1\times10^{11}~\mbox{Pa}\), the density as \(\rho = 7850~{\frac{\text{kg}}{\text{m}^{3}}}\) and the Poisson’s ratio as \(\nu =0.3\). The knot vectors for a circle are

$$ \Xi = \begin{bmatrix} 0 & 0 & 0 & 1 & 1 & 1\end{bmatrix} ~~~~\mathrm{and}~~~~\mathcal{H} = \begin{bmatrix} 0 & 0 & 0 & 1 & 1 & 1\end{bmatrix} , $$
(39)

and the order of the B-splines is given by \(p=q=2\). The corresponding control points are

$$ \boldsymbol{P}^{0}_{i,j,1}= \begin{bmatrix} -r\frac{1}{\sqrt{2}}&0&r\frac{1}{\sqrt{2}} \\ -r\frac{2}{\sqrt{2}}&0&r\frac{2}{\sqrt{2}} \\ -r\frac{1}{\sqrt{2}}&0&r\frac{1}{\sqrt{2}}\end{bmatrix} ~~~~\mathrm{and}~~~~\boldsymbol{P}^{0}_{i,j,2}= \begin{bmatrix} r\frac{1}{\sqrt{2}}&r\frac{2}{\sqrt{2}}&r\frac{1}{\sqrt{2}} \\ 0&0&0 \\ -r\frac{1}{\sqrt{2}}&-r\frac{2}{\sqrt{2}}&-r\frac{1}{\sqrt{2}}\end{bmatrix} , $$
(40)

and the weights are

$$ \boldsymbol{W}_{i,j}= \begin{bmatrix} 1&\frac{1}{\sqrt{2}}&1 \\ \frac{1}{\sqrt{2}}&1&\frac{1}{\sqrt{2}} \\ 1&\frac{1}{\sqrt{2}}&1\end{bmatrix} . $$
(41)

The order is elevated to \(p=q=4\) and the model is refined by inserting additional knots. Then, a model reduction is performed using the Craig–Bampton method. The number of normal modes is chosen as 10, and 26 interface control points on the lower side are used to determine the constraint modes. An overview of the final model is given in Table 3. The penalty factor \(c_{\mathrm{p}}=1\times10^{17}~\mbox{N}/\mbox{m}\) is determined in a series of simulation as described in Sect. 4.1.

Table 3 IGA model of a cylinder represented by a circle with plane strain material behavior
Full size table

As a reference the translational and rotational velocities after the impact can be determined with the principle of conservation of linear and angular momentum. An elastic impact is assumed and the moment of inertia of the cylinder about the \(z\)-axis is \(I=\frac{1}{2}mr^{2}\). With the defined initial velocities

$$\begin{aligned} \boldsymbol{v}_{0}&= \begin{bmatrix} v_{\mathrm{x0}} \\ v_{\mathrm{y0}} \end{bmatrix}= \begin{bmatrix} 0 \\ -v_{0} \end{bmatrix}= \begin{bmatrix} 0 \\ -0.1~\mbox{m}/\mbox{s} \end{bmatrix}, \end{aligned}$$
(42)
$$\begin{aligned} \omega _{0}&=2\pi\ /\mbox{s}, \end{aligned}$$
(43)

the velocities after the impact are determined by

$$\begin{aligned} \boldsymbol{v}_{1}&= \begin{bmatrix} v_{\mathrm{x1}} \\ v_{\mathrm{y1}} \end{bmatrix}= \begin{bmatrix} 2\mu v_{\mathrm{y0}} \\ -v_{\mathrm{y0}} \end{bmatrix}= \begin{bmatrix} -0.06~\mbox{m}/\mbox{s} \\ 0.1~\mbox{m}/\mbox{s} \end{bmatrix}, \end{aligned}$$
(44)
$$\begin{aligned} \omega _{1}&=\frac{m r v_{\mathrm{x1}} + I \omega _{0}}{I}\approx 1.618\pi\ /\mbox{s}. \end{aligned}$$
(45)

The calculated velocities can be used for validating an impact simulation. Figure 14 shows good agreement with the analytical solution in Eq. (44). The rotational velocity around the \(z\)-axis is visualized in Fig. 15. The excitation of the impact in tangential direction causes small vibrations in the cylinder. Nevertheless, the rotational velocity oscillates around the previously calculated value \(\omega _{1}\) in Eq. (45). Finally the position of the cylinder center of mass can be seen in Fig. 16. Due to the friction component of the contact force, the cylinder moves to the left after the impact.

Fig. 14
figure 14

Translational velocity of the cylinder

Full size image
Fig. 15
figure 15

Rotational velocity of the cylinder around the \(z\)-axis

Full size image
Fig. 16
figure 16

Position of the cylinder center of mass

Full size image

8 Summary

Overall, it can be concluded that it is feasible to obtain the global shape functions for flexible multibody systems from isogeometric finite element models. By choosing the appropriate data interface, the global shape functions of the IGA can be smoothly included into a pre-existing flexible multibody simulation toolbox. Due to the use of a model reduction of the IGA model a significant reduction of computation time is achieved compared to the nonreduced fully nonlinear isoparametric finite element model.

The application of isogeometric elements for an impact simulation leads to accurate results in a quasistatic setup as presented for the sphere impact. The results of the isogeometric models agree very well with the isoparametric models and the analytical solution by Hertz. This can also be observed in the occurring contact forces and stresses in the flexible body. One reason for minimal differences in the results can be the reduction by the Craig–Bampton method. Additionally, the second application example of the impact of a long rod shows a good representation of an elastodynamic behavior when compared to an isoparametric reference model. A key feature of the floating frame of reference formulation, the handling of large rotations, is demonstrated in the third application example.