Hierarchical refinement in isogeometric analysis for flexible multibody impact simulations

Abstract

Detailed impact simulations in flexible multibody systems can be simulated based on reduced isogeometric analysis (IGA) models. However, a precise simulation of an impact requires a high element resolution in the contact area. Usually in IGA, global refinement methods are used, which are easy to implement. However, in the literature, also the use of hierarchical local refinement is proposed. The local refinement generates fewer countable degrees of freedom compared to an equivalent global refinement. Numerous application areas can be found in the literature, such as contact simulations, where the computational effort is reduced by local refinement. In this work, we introduce the inclusion of hierarchically refined IGA models within the floating frame of reference formulation. Thereby, the hierarchically refined IGA model is reduced and applied in impact simulations. In two application examples, we simulate the impact of two- and three-dimensional spheres and compare with an analytical solution. The focus here is on the comparison of calculation times and accuracy of globally and locally refined reference models. The third application example consists of two flexible double pendulums and is devoted to systems in which the bodies undergo both arbitrary rigid body motions and small elastic deformations.

1 Introduction

In impact problems within flexible multibody systems, the rigid body motions before and after impact are often large whereas only small elastic deformations occur during impact. This is the case for relatively stiff materials. Flexible bodies made of steel or aluminum are considered stiff, which allows the application of the floating frame of reference formulation [15] in this work. The use of the floating frame of reference formulation requires global shape functions $\boldsymbol{\varPhi}$ of the flexible bodies to model the body flexibility. The global shape functions can be obtained by the finite element method [1] and a reduction method, such as the Craig–Bampton method [3]. When simulating flexible multibody systems and impacts, the bodies are usually meshed with isoparametric elements. A major drawback of isoparametric elements is the discretization of the geometry. Since the calculation of the contact force is based on the geometry of the finite element model, errors can occur. An alternative to isoparametric elements is the isogeometric analysis (IGA) [2], whose use is motivated by two advantages. First, the use of nonuniform rational basis splines (NURBSs) as local shape functions of the elements allows an exact representation of the body geometry. Second, high modes of flexible bodies are represented more accurately compared to isoparametric elements [2]. The latter advantage is useful in impact simulations based on the floating frame of reference formulation introduced in the later course of this work. These advantages are bought by increased computational costs in the evaluation of the spline-based nonlinear local shape functions compared to linear shape functions of isoparametric elements.

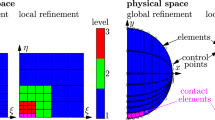
An accurate impact simulation, which captures the local deformation, requires a high element resolution in the contact area, as this is where the largest elastic deformations and stresses occur. However, the refinement methods usually used in IGA only allow global refinement. The refinement of a semicircle representing an axisymmetric sphere is exemplified in Fig. 1. The left-hand side is refined globally, and the right-hand side uses hierarchical refinement. In addition to the physical space, the parameter space is also shown, which we will introduce in a later chapter. When the number of elements is increased in the contact area, additional elements and control points are created over the entire body. The control points represent the degrees of freedom in the IGA, and thus the global refinement greatly increases the number of equations in the finite element model. One method for local refinement is a hierarchical approach, where subordinate levels are introduced, as displayed in Fig. 1. The hierarchical refinement is widely used in the literature. It is applied in elementary fluid and structural analysis [14], heat conduction problems [4], topology optimization [10], and contact simulations [20]. The aforementioned literature summarizes that the computational effort can be reduced due to the smaller number of degrees of freedom compared to global refinement. These examples are mostly from statics. In this work, we apply the hierarchical refinement in a dynamic problem. The aim of this work is to include hierarchically refined models within the floating frame of reference formulation, which involves model reduction, e.g., using the Craig–Bampton method. In application examples, we evaluate whether the computational effort of hierarchically refined models is reduced compared to globally refined models. Therefore we evaluate two- and three-dimensional impact simulations. This paper is partially based on [12].

Fig. 1

Example of a semicircle representing an axisymmetric sphere that should be refined in the contact area

The remainder of this paper is organized as follows: Initially, the concept of the floating frame of reference formulation is briefly summarized in Sect. 2. Section 3 introduces the concepts of the IGA, the hierarchical refinement, and the extraction of the global shape functions. The contact algorithm is briefly explained in Sect. 4. Sections 5–7 cover detailed discussions of three application examples, and the results are summarized in Sect. 8.

2 Floating frame of reference formulation

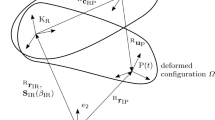
When simulating flexible multibody systems, the floating frame of reference formulation is a well-established approach [15]. A large nonlinear rigid body motion of the body frame $\mathrm{K}_{ \mathrm{R}}$ can be described within the inertial frame $\mathrm{K}_{ \mathrm{I}}$. In this work, we use Buckens frames and tangent frames [15] as floating frames. Provided that the body deformations remain small and linear elastic, they can be described conveniently in the body frame $\mathrm{K}_{\mathrm{R}}$. Using the global shape functions $\boldsymbol{\varPhi}$ and the $n_{\mathrm{q}}$ elastic coordinates $\boldsymbol{q}_{\mathrm{e}}$, the elastic deformation can be approximated. The equations of motion of a single flexible body are given by

$$ \underbrace{\begin{bmatrix}m \mathbf{E}&m\tilde{\boldsymbol{c}}^{\intercal}&\boldsymbol{C}_{\mathrm{t}}^{\intercal}\\m\tilde{\boldsymbol{c}}&\boldsymbol{I}&\boldsymbol{C}_{\mathrm{r}}^{\intercal}\\\boldsymbol{C}_{\mathrm{t}}&\boldsymbol{C}_{\mathrm{r}}&\overline{\boldsymbol{M}}_{\mathrm{e}}\end{bmatrix}}_{ \boldsymbol{M}} \underbrace{\begin{bmatrix}{}^{\mathrm{R}}\dot{\boldsymbol{v}}_{\mathrm{IR}}\\{}^{\mathrm{R}}\dot{\boldsymbol{\omega}}_{\mathrm{IR}}\\\ddot{\boldsymbol{q}}_{\mathrm{e}}\end{bmatrix}}_{ \dot{\boldsymbol{z}}_{\mathrm{II}}}= \underbrace{\boldsymbol{h}_{\mathrm{p}}+\boldsymbol{h}_{\mathrm{d}}+\boldsymbol{h}_{\mathrm{b}}-\boldsymbol{h}_{\mathrm{\omega}}-\boldsymbol{h}_{\mathrm{e}}}_{ \boldsymbol{h}_{\mathrm{a}}}, $$

(1)

where ${}^{\mathrm{R}}\boldsymbol{v}_{\mathrm{IR}}$ is the velocity of the rigid body motion from the inertial frame to the reference frame, and ${}^{ \mathrm{R}}\boldsymbol{\omega}_{\mathrm{IR}}$ is the angular velocity. In Eq. (1) the mass of the body is denoted by $m$, the center of mass relative to the body frame by $\tilde{\boldsymbol{c}}$, the translational coupling matrix by $\boldsymbol{C}_{\mathrm{t}}$, the rotational coupling matrix by $\boldsymbol{C}_{ \mathrm{r}}$, and the mass moment of inertia by $\boldsymbol{I}$. The right-hand side vector $\boldsymbol{h}_{\mathrm{a}}$ is composed of the vector of surface forces $\boldsymbol{h}_{\mathrm{p}}$, the discrete forces $\boldsymbol{h}_{\mathrm{d}}$, the body forces $\boldsymbol{h}_{\mathrm{b}}$, and the inertial forces $\boldsymbol{h}_{\mathrm{\omega}}$. The mass matrix $\overline{\boldsymbol{M}}_{ \mathrm{e}}$ of a linear elastic body, as well as the stiffness $\overline{\boldsymbol{K}}_{\mathrm{e}}$ and damping matrix $\overline{\boldsymbol{D}}_{ \mathrm{e}}$ needed to compute the inner forces $\boldsymbol{h}_{\mathrm{e}}$, are introduced in a later section. Contact forces are considered in the discrete forces $\boldsymbol{h}_{\mathrm{d}}$. The standard input data (SID), a well-known standard in providing elastic data in the context of the floating frame of reference formulation [15], is used to assemble the equations of motion (1). For the formulation of the equations of motion and the transient analysis, the Matlab toolbox DynManto [5] is used. The resulting equations of motion are solved by the ode15s Matlab solver with numerical differentiation formulas (NDF).

3 Global shape functions from IGA

Determining the global shape functions $\boldsymbol{\varPhi}$ is a key issue in using the floating frame of reference formulation. A general way to determine the global shape functions is to generate a finite element model of the flexible body and then identify the global shape functions from the finite element model using model reduction techniques. In this section, we briefly present the idea of the IGA and the procedure to obtain the global shape functions from an IGA model. A more detailed introduction to the IGA can be found in [2]. Additionally, the concept of hierarchical refinement and a methodology to locally refine isogeometric models are introduced based on [14].

3.1 Basis splines

The IGA consists of three spaces: the physical space, the parameter space, and the index space. The first two spaces are essential for understanding the IGA. The shape functions of isogeometric elements are defined in the parameter space, which can be seen for a two-dimensional example on the lower part of Fig. 1. The parameter space is divided into elements and spanned by the knot vectors $\boldsymbol{\varXi}= \begin{bmatrix} \xi _{1} & \xi _{2} & \ldots & \xi _{\mathrm{n+p+1}}\end{bmatrix}$ and . Thereby, $p$ and $q$ are the orders of the basis functions, and $n$ and $m$ are the numbers of the basis functions $N_{i,\mathrm{p}}$ and $M_{j, \mathrm{q}}$. The orders of the basis functions can be subsequently increased with the algorithm in [7]. In IGA the local shape functions are based on B-splines, which can be computed recursively with the Cox–de Boor algorithm [2]. In $\xi$-direction the B-splines are computed as

$$\begin{aligned} p&=0:~~~~N_{i,0}(\xi ) = \Bigg\{ \textstyle\begin{array}{l} 1~~~~\mathrm{if}~\xi _{i} \leq \xi < \xi _{i+1}, \\ 0~~~~\mathrm{otherwise}; \end{array}\displaystyle \end{aligned}$$

(2)

$$\begin{aligned} p&>1:~~~~N_{i,\mathrm{p}}(\xi )= \frac{\xi -\xi _{i}}{\xi _{i+\mathrm{p}}-\xi _{i}}N_{i,\mathrm{p}-1}( \xi )+ \frac{\xi _{i+\mathrm{p}+1}-\xi}{\xi _{i+\mathrm{p}+1}-\xi _{i+1}}N_{i+1, \mathrm{p}-1}(\xi ). \end{aligned}$$

(3)

The calculation rule given by Eqs. (2) and (3) is identical in the $\eta$-direction. In practice, recursive functions are numerically inefficient. Therefore the nonrecursive algorithm suggested in [7] is used.

3.2 Nonuniform rational basis splines

Besides the parameter space, there is the physical space, which can be seen on the upper part of Fig. 1. In the physical space the control points $\boldsymbol{P}_{i,j}$ are defined, which are arranged by the control net. The task of the control points is to span the geometry in the physical space. The dimension of the control points corresponds to the numbers of B-splines $n$ and $m$ in the parameter space. In addition to the physical position, each control point has a weight $w_{i,j}$. The transformation from the parameter space into the physical space requires the NURBS basis $R_{i,j}^{\mathrm{p,q}}$ given by

$$ R_{i,j}^{\mathrm{p,q}}(\xi ,\eta ) = \frac{N_{i,\mathrm{p}}(\xi )M_{j,\mathrm{q}}(\eta )w_{i,j}}{\sum _{\hat{i}=1}^{\mathrm{n}} \sum _{\hat{j}=1}^{\mathrm{m}} N_{\hat{i},\mathrm{p}}(\xi ) M_{\hat{j},\mathrm{q}}(\eta ) w_{\hat{i},\hat{j}}}. $$

(4)

The NURBS basis $R_{i,j}^{\mathrm{p,q}}$ and the control points $\boldsymbol{P}_{i,j}$ then lead to the NURBS surface

$$ \boldsymbol{S} = \sum _{i=1}^{\mathrm{n}} \sum _{j=1}^{\mathrm{m}} R_{i,j}^{ \mathrm{p,q}}(\xi ,\eta ) \boldsymbol{P}_{i,j} $$

(5)

in the physical space. The degrees of freedom in the IGA correspond to the displacements of the control points

$$ \boldsymbol{u}_{i,j}=\boldsymbol{P}_{i,j}-\boldsymbol{P}_{i,j}^{0}, $$

(6)

where $\boldsymbol{P}_{i,j}^{0}$ represents the position of the control points in the undeformed and $\boldsymbol{P}_{i,j}$ in the deformed configuration. The deformation $\boldsymbol{d}$ of the NURBS surface can be written in matrix–vector notation as

$$ \boldsymbol{d} = \underbrace{\begin{bmatrix}R_{1,1}^{\mathrm{p,q}} & 0 & R_{1,2}^{\mathrm{p,q}} & 0 & \ldots & 0 \\ 0 & R_{1,1}^{\mathrm{p,q}} & 0 & R_{1,2}^{\mathrm{p,q}} & \ldots & R_{\mathrm{p+1,q+1}}^{\mathrm{p,q}}\end{bmatrix}}_{ \boldsymbol{N}} \underbrace{\begin{bmatrix}u_{\mathrm{1,1,x}} \\ u_{\mathrm{1,1,y}} \\ u_{\mathrm{1,2,x}} \\ u_{\mathrm{1,2,y}} \\ \vdots \\ u_{\mathrm{p+1,q+1,y}}\end{bmatrix}}_{ \boldsymbol{u}}, $$

(7)

where the basis functions of the corresponding element are summarized in matrix $\boldsymbol{N}$.

3.3 Hierarchical refinement

The concept of the hierarchical refinement relies on the property of B-splines to be represented by a linear combination of finer B-splines defined on smaller knot intervals. With the calculation rule

$$ a_{j} = 2^{-p} \begin{pmatrix} p + 1 \\ j\end{pmatrix} = 2^{-p} \frac{(p+1)!}{j!\,(p+1-j)!}, $$

(8)

we can determine the linear coefficients to represent a B-spline in a higher level with B-splines of lower level. Note that Eq. (8) is only valid for uniform knot vectors. As an example, a quadratic B-spline with the high-level knot vector

$$ \boldsymbol{\varXi}_{1} = \begin{bmatrix} 0 & 1 & 2 & 3\end{bmatrix} $$

(9)

should be represented by a number of lower-level B-splines with the corresponding low-level knot vector

$$ \boldsymbol{\varXi}_{2} = \begin{bmatrix} 0 & \underline{0.5} & 1 & \underline{1.5} & 2 & \underline{2.5} & 3\end{bmatrix} . $$

(10)

The inserted knots in Eq. (10) are underlined. By applying Eq. (8) the concept of the hierarchical refinement can be visualized in Fig. 2. The procedure, which is implemented and used in this work, is briefly summarized in the following. For a detailed introduction to the hierarchical refinement, see [14].

Fig. 2

Concept of the hierarchical refinement in the IGA

Initially, the parameter space is divided into different hierarchy levels. Recapturing the motivation example in Fig. 1, the corresponding parameter space is displayed on the right-hand side. This division is made up by intervals in knot coordinates. The concept of hierarchical refinement is that a finer mesh resolution can be defined section by section. Therefore the levels are initialized using the global knot insertion algorithm described in [2]. With this algorithm, the position of the control points and their weights can be determined for the finer mesh. The number of hierarchy levels is denoted as $n_{ \mathrm{lvl}}$.

In hierarchical refinement, B-splines of higher level are based on B-splines of lower level. For the construction of higher-level B-splines, the linear combination coefficient matrix $\boldsymbol{A}$ is determined by solving

$$ N_{i,\mathrm{p}}^{\ell} = \boldsymbol{A}^{\ell}_{i,j} N_{j,\mathrm{p}}^{\ell + 1},\quad \ell =1,\dots ,n_{\mathrm{lvl}}-1, $$

(11)

between all $n_{\mathrm{lvl}}$ hierarchy levels. A detailed description of this procedure can be found in [8].

In the next step, we define the elements with the knot vectors of different levels and intervals, which define the hierarchy level with respect to the knot coordinates. The previous step allows certain B-splines to be identified as inactive. Thus the associated control points of each element can be determined. Thereby, the control points can be located in different hierarchy levels. The control points that are not part of an element are identified as inactive.

The hierarchical B-splines of the example introduced at the beginning in Fig. 1 are depicted in Fig. 3. We can see that B-splines of different hierarchy levels can be active, e.g., at the knot coordinate $\xi = 0.2$ in Fig. 1. This overlap becomes relevant when calculating the NURBS basis from Eq. (4). The B-splines of different dimensions of the parameter space need to be multiplied out. These intersections of the B-splines lead to the fact that for the computation of the NURBS, any level can interact with any level of the other dimensions in the parameter space. The more hierarchical levels are created, the more combinations of possible intersections of the B-splines can occur. This may increase the calculation time of the hierarchical NURBS basis compared to a globally refined model. In addition to the more complex calculation of the NURBS, the B-splines from the different hierarchy levels must be constructed, which takes additional computation time.

Fig. 3

Concept of the hierarchical refinement in the IGA

3.4 Model order reduction

As with the floating frame of reference formulation, we assume that only small elastic deformations occur in a relatively stiff material. Therefore we assume linear elasticity and apply the weak Galerkin method as for isoparametric elements [1]. From this the equations of motion of the complete finite element model are then given by

$$ \boldsymbol{M}_{\mathrm{e}}\ddot{\boldsymbol{u}}_{\mathrm{e}}+\boldsymbol{K}_{\mathrm{e}} \boldsymbol{u}_{\mathrm{e}}=\boldsymbol{f}_{\mathrm{e}}. $$

(12)

For the incorporation of the isogeometric model into the flexible multibody simulation, the global shape functions $\boldsymbol{\varPhi}$ are required. The global shape functions $\boldsymbol{\varPhi}$ necessary for establishing Eq. (1) can be determined from the linear system equations (12) with a model order reduction method. The straightforward approach for reducing the equations of motion (12) is modal reduction. However, as shown in [17], modal reduction leads to inaccurate results in case of impact problems, since the local deformation in the contact region is not included in the reduced model. Alternatively, the Craig–Bampton method [3] is used, which has already been successfully applied to impact problems with isoparametric elements [17]. The key idea of the Craig–Bampton method is combining fixed-interface normal modes and constraint modes. The normal modes represent the overall flexibility, and the constraint modes allow a relatively accurate representation of the deformation in a specific area of the flexible body, e.g., the contact area. For the constraint modes, predefined interface control points on the exterior surface can be selected. The procedure results in the global shape functions $\boldsymbol{\varPhi}$, which are orthogonalized and normalized to the mass matrix. The reduced mass and stiffness matrix are then given by

$$\begin{aligned} \overline{\boldsymbol{M}}_{\mathrm{e}}=\boldsymbol{\varPhi}^{\intercal}\boldsymbol{M}_{ \mathrm{e}}\boldsymbol{\varPhi}=\mathbf{E}\quad \mbox{and}\quad \overline{\boldsymbol{K}}_{\mathrm{e}}=\boldsymbol{\varPhi}^{\intercal}\boldsymbol{K}_{ \mathrm{e}}\boldsymbol{\varPhi}=\mathrm{diag}(\omega _{i}^{2}), \end{aligned}$$

(13)

respectively, where $\mathbf{E}$ is the identity matrix, and $\omega _{i}$ are the natural frequencies. Since the normal modes tend to be low and the constrained modes of high frequency, the equations of motion (1) become numerically stiff. Therefore the higher frequency modes are strongly damped, whereas the lower modes remain undamped. In this work, we use modal damping to increase the numerical performance. This method is already applied in impact simulations with isoparametric elements [17–19].

4 Contact handling in IGA

There are several methods for discretizing the contact of two isogeometric bodies. Two frequently used types of methods are the integral description of the contact and the node-to-segment methods. In the integral description of the contact, Gauss points of preselected elements are checked [13]. The number of evaluation points depends on the number of elements in the contact area and on the order of the B-splines due to the Gauss integral. For node-to-segment methods, the number of evaluation points depends only on the number of elements in the contact area. Since node-to-segment methods require fewer points to be checked for contact and the accuracy is still comparable to that of an integral description [9], a node-to-segment method is chosen for this work.

For node-to-segment methods, different collocation methods, e.g., Botella points, can be used [9]. The following section briefly summarizes the contact algorithm described in [13]. This collocation method is combined with the penalty method for contact treatment. An optimal choice of the penalty factor $c_{\mathrm{p}}$ for static contact is described in [11]. For dynamical contact treatment, the corresponding penalty factor is chosen heuristically. Thereby, the penalty factor should be chosen large enough such that the results become independent of the chosen parameter [16]. When the penalty factor is increased beyond its converging value, the differential equation (1) becomes stiffer, and the simulation time is unnecessarily increased, or the simulation might even terminate unsuccessfully. Although the penalty method allows penetration of the bodies, the penetration is negligibly small when using the above procedure to determine the penalty factor. If no penetration is desired, then the Lagrange method can be used [8].

At each time step, the individual bodies must be checked for contact. To this end, the position of the deformed control points $\boldsymbol{P}_{i,j}$ is determined. First, the control points displacements are recovered from

$$ \boldsymbol{u}_{\mathrm{e}}=\boldsymbol{\varPhi}\boldsymbol{q}_{\mathrm{e}} $$

(14)

with the global shape functions $\boldsymbol{\varPhi}$ and the elastic coordinates $\boldsymbol{q}_{\mathrm{e}}$. After that, the position of the control points is computed from Eq. (6). In case of contact between two bodies, one body is defined as the contact body, and the other as the target body, as depicted in Fig. 4. The Botella points, which are located on the outer surface of the contact body and in the contact area, are tested for contact with the exterior surface of the target body. The contact check is achieved by solving

$$ \left (\frac{\partial \boldsymbol{x}_{\mathrm{T}}(\xi )}{\partial \xi}\right )^{ \intercal}\left (\boldsymbol{x}_{\mathrm{C}}-\boldsymbol{x}_{\mathrm{T}}(\xi )\right )=0 $$

(15)

with the Newton–Raphson method for the respective knot coordinate $\xi$. This knot coordinate $\xi$ corresponds to the target point $\boldsymbol{x}_{\mathrm{T}}(\xi )$, which is closest to the current Botella point $\boldsymbol{x}_{\mathrm{C}}$ of the contact body.

Fig. 4

Contact detection between two bodies

As a side note, the contact evaluation of isoparametric elements requires checking every contact element individually with each target element resulting in a high number of element combinations, whereas in the IGA, an evaluation point is checked with an interval on the exterior surface of the target body, which is more convenient.

The distance $g_{\mathrm{n}}$ between the contact and target points is determined by

$$ g_{\mathrm{n}}=\boldsymbol{n}^{\intercal}(\boldsymbol{x}_{\mathrm{C}}-\boldsymbol{x}_{ \mathrm{T}}(\xi )), $$

(16)

where the normal vector $\boldsymbol{n}$ is orthogonal to the surface of the target body. If the normal gap $g_{n}$ is greater than zero, then there is no contact. Otherwise, the contact force for the current sampling point is determined by

$$ \boldsymbol{f}_{\mathrm{c}} = c_{\mathrm{p}}g_{\mathrm{n}}\boldsymbol{N}^{\intercal} \boldsymbol{n}\hat{\omega}_{i}, $$

(17)

where $c_{\mathrm{p}}$ is the penalty factor, $\boldsymbol{N}$ is the local shape functions, and $\hat{\omega}_{i}$ is the collocation weight of the current collocation point. See [9] for the derivation of the collocation weight. To eliminate the distinction between contact and target body, they are switched, and the contact force is averaged. After the contact search, the discrete forces can be calculated with

$$ \boldsymbol{h}_{\mathrm{d}} = \sum _{i=1}^{\mathrm{n}}\sum _{j=1}^{\mathrm{m}} \begin{bmatrix} \mathbf{E} \\ \tilde{\boldsymbol{P}}_{i,j} \\ \boldsymbol{\varPhi}^{\intercal}_{i,j}\end{bmatrix} \boldsymbol{f}_{\mathrm{c},i,j} $$

(18)

and inserted into Eq. (1). The contact algorithm described above is implemented in Matlab. However, for computational efficiency, the algorithm is compiled into a MATLAB executable (MEX) file. The contact search can be parallelized with respect to the contact evaluation points.

5 Application Example I: impact of two axisymmetric spheres

The aim of this application example is to compare globally and locally refined isogeometric models in the context of an impact simulation in a flexible multibody system. We investigate whether a locally refined model has the same accuracy as an equivalent globally refined model and how locally and globally refined models differ in computation time.

In this application example, we simulate the impact of two spheres. This simple example is a well-suited benchmark, since Hertzian contact theory provides an analytical solution [6]. For simplicity, the spheres are identical. Thus the problem is symmetric. Despite the symmetry, we model both spheres. However, we exploit the axisymmetric property of a sphere. The simulation setup is visualized in Fig. 5. The radii of the spheres are $r=1~\mbox{cm}$, and the selected material is steel. Therefore Young’s modulus is chosen as $E= 2.11\mbox{e}11~\text{Pa}$, the density as $\rho = 7850~\mbox{kg}/\mbox{m}^{3}$, and Poisson’s ratio as $\nu =0.3$. Both spheres have an initial velocity of $v_{0}= 0.1~\mbox{m}/\mbox{s}$, and the gravity is ignored. For the initialization of the geometry, the knot vectors of the semicircle are defined as $\boldsymbol{\varXi}= \begin{bmatrix} 0&0&0&1&1&1\end{bmatrix}$ and . The initial order of the B-splines is given by $p=2$ and $q=1$. The control points and weights in the physical space are

$$ \boldsymbol{P}_{i,j,\mathrm{x}}^{0}= \begin{bmatrix} 0&0 \\ r&r \\ r&r\end{bmatrix} ,\qquad \boldsymbol{P}_{i,j,\mathrm{y}}^{0}= \begin{bmatrix} -r&r \\ -r&r \\ 0&0\end{bmatrix} ,\quad \mbox{and}\quad \boldsymbol{w}_{i,j}= \begin{bmatrix} 1&1 \\ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}} \\ 1&1\end{bmatrix} . $$

(19)

After defining the geometry, the model is globally refined to better represent the overall elastic deformation. In the course of this, the order of the B-splines is increased by two resulting in $p=2+2=4$ and $q=1+2=3$. Adding 15 knots in the $\xi$-direction and 24 knots in the $\eta$-direction increases the number of elements from one to 400. This refined model serves as a starting point for various benchmark models. It is worth noting that all tested models have an element edge length of 10 μm in the contact area. All models are reduced with the Craig–Bampton method using ten normal modes, and the exterior control points in the contact area are used for the constrained modes.

Fig. 5

Impact of two spheres

Four locally refined models are compared in the following studies, in which the number of hierarchy levels $n_{\mathrm{lvl}}$ is varied between three and six. Each of these four locally refined models has an equivalent globally refined reference model. The equivalence is that the knot vectors of the globally refined models are identical to the knot vectors in the lowest level of the locally refined models. The investigated models are listed in Table 1 and visualized in Fig. 6.

Fig. 6

Detailed plot of the contact area of the hierarchically refined axisymmetric models

Table 1 Globally and locally refined models of an axisymmetric sphere

The number of interface control points is nearly identical for all models. Accordingly, the number of elastic coordinates $n_{\mathrm{q}}$ after the model reduction is almost identical regardless of whether the model is globally or locally refined. In addition, the number of degrees of freedom $n_{ \mathrm{dof}}$ decreases as the number of hierarchy levels $n_{ \mathrm{lvl}}$ increases. In terms of preprocessing, the locally refined models are slightly faster because they have fewer degrees of freedom than the globally refined models. The dimensions on the left side of the four IGA models in Figs. 6a–6d represent the height of the lowest hierarchy level, which becomes relevant in the further course of the analysis. The model with $n_{\mathrm{lvl}}=5$ hierarchy levels in Fig. 6c represents the most uniform distribution of elements. Since the goal in this application example is creating an element length of 10 μm in the contact area, models with more than six hierarchy levels are not necessary, as shown in Fig. 6d.

In addition to the isogeometric models, an isoparametric model is tested for validation. Similarly to the IGA models, the isoparametric model uses an element length of 10 μm. The full model is simulated in Ansys without reduction.

The impacts in this work are simulated for $0.1~\mbox{ms}$ using a penalty approach. As mentioned before, the penalty factor $c_{ \mathrm{p}}$ is increased until the results become independent of the penalty factor. As a first guess for the penalty factor, the optimal penalty factor for static contact can be determined according to [11]. The procedure yields penalty factors around $c_{\mathrm{p}}= 1\mbox{e}19~\mbox{N}/\mbox{m}$. With this initial information, the penalty factor for the dynamical contact can be determined heuristically. Therefore the maximum contact forces of the reduced IGA models and of the analytic solution by Hertz [6] are visualized in Fig. 7. Two observations can be made from Fig. 7. First, it is observed in Fig. 7a that the penalty factor is independent of the number of hierarchy levels. Second, globally and locally refined models behave almost identically here, as seen in Fig. 7b. Figure 7 shows that for the penalty factors $c_{\mathrm{p}}$ greater than $\mbox{5e18}~\mbox{N}/\mbox{m}$, the maximum contact force remains constant. Therefore this factor is used for the following simulations. As mentioned before, the penalty method allows penetration. However, the ratio between the maximum normal gap $g_{\mathrm{n}}$ and the maximum deformation in the contact area is only ${2}\%$. Note that the calculation time also increases with increasing penalty factor, since the equations of motion become stiffer. For the penalty factor $c_{\mathrm{p}}= {5\mbox{e}18}~\mbox{N}/\mbox{m}$, the maximum relative error of the contact force with respect to the analytical solution [6] can be evaluated. As mentioned in Sect. 3.4, modal damping is used in this work, resulting in a maximum relative error of ${1}\%$ for all models. In the previous work [12], Rayleigh damping is used, and the error is slightly higher at ${2}\%$. The reason for this is that modal damping only dampens the high-frequency modes, leaving the low-frequency modes undamped.

Fig. 7

Contact force error compared to analytic solution by Hertz [6]

The same procedure to determine the penalty factor is used for the isoparametric model in Ansys as for the IGA models. This results in the penalty factor $c_{\mathrm{p}}=5\mbox{e}17~\mbox{N}/\mbox{m}$. In Fig. 8 the analytical solution by Hertz, a hierarchically refined model, its globally refined reference model, and the isoparametric model are visualized. Both the IGA models and the isoparametric model well represent the analytical solution of the impact. Although all models use the same element resolution in the contact area, the Ansys model performs worst in this setup.

Fig. 8

Contact forces of axisymmetric sphere models

Next, we discuss the influence of the number of hierarchy levels $n_{ \mathrm{lvl}}$ on the computation time of the impact simulation shown in Fig. 9. The computation time does not include the preprocessing, only the time integration. It is worth mentioning that the hierarchical refinement algorithm used in [12] has been improved here in performance. Previous suboptimal implementations have been revised, and overlapping hierarchy levels whose NURBS are zero are not multiplied out. Additionally, the usage of modal damping increases the performance of the locally and globally refined models. Although the contact search can be parallelized with respect to the evaluation points, sequentially executed simulations are more independent of the architecture of the computer, the MEX implementation of parallel for-loops, and the used operating system Windows. Therefore the sequential computation allows a better relative comparison of the individual models. The processor used is the Intel W-2295 model with 18 cores. Note that the following qualitative observations may depend on the particular application example.

Fig. 9

Comparison of computation times

Observing the computation time of the sequential simulation in Fig. 9a, we can see that the computation time increases with the number of hierarchy levels. In contrast, the computation time of the globally refined reference models decreases. The latter observation can be attributed to the fact that the number of degrees of freedom $n_{\mathrm{dof}}$ decreases; see Table 1. Since the globally refined models have only one level in the parameter space, it is likely that the number of degrees of freedom $n_{\mathrm{dof}}$ directly influences the computation time. If the number of degrees of freedom $n_{\mathrm{dof}}$ is smaller, then the matrix of global shape functions $\boldsymbol{\varPhi}\in \mathbb{R}^{n_{ \mathrm{dof}}\times n_{\mathrm{q}}}$ is also smaller. Thereby, the matrix multiplications in the course of the contact algorithm, e.g., Eqs. (14) and (18), are computed faster for models with fewer degrees of freedom $n_{\mathrm{dof}}$. However, this effect is rather small, as can be seen in the computation time of the globally refined models in Fig. 9a. This can be explained by the fact that matrix multiplications are relatively inexpensive to calculate, in contrast to, for example, matrix inversions.

Although the degrees of freedom of the locally refined models decrease as the number of hierarchy levels increases, the aforementioned effect does not seem to be dominant here. In the literature [4, 10, 14, 20] the degrees of freedom $n_{\mathrm{dof}}$ saved by local refinement are listed as an advantage. This advantage does not apply in this example since the models are reduced with the Craig–Bampton method. The reduced mass and stiffness matrix are then used in the evaluation of the equations of motion in the context of the floating frame of reference formulation. However, the number of degrees of freedom $n_{\mathrm{dof}}$ of hierarchically refined models is lower compared to globally refined models, but the number of elastic coordinates $n_{\mathrm{q}}$ is almost identical regardless of the type of refinement; see Table 1. After model reduction, the number of degrees of freedom $n_{\mathrm{dof}}$ only has an influence on the global shape functions $\boldsymbol{\varPhi}$. As described before, the influence of the size of the global shape functions is rather small. Since the number and position of contact evaluation points are also identical for the respective globally and locally refined models, the evaluation of the NURBS in the course of the contact evaluation remains the last possible reason for the difference in computation time. In fact, additional computational effort in computing hierarchical NURBS described in Sect. 3.3 is responsible for the higher computational time in Fig. 9a.

In the parallel computation shown in Fig. 9b, the globally refined models are likewise faster. However, the difference between the globally and locally refined models is much smaller compared to the sequential computation in Fig. 9a. In this case the locally refined models seem to benefit more from the parallel computation than the globally refined models, whereby the MEX implementation could be responsible for this. The Ansys solution is simulated with a step size of $100~\mbox{ns}$ and requires $200~\mbox{s}$ of computation time. Therefore the computation time is slightly higher than that for the IGA models in Fig. 9b.

In the last analysis of this application example, the von Mises stresses are observed to occur at maximum impact force. The von Mises stresses are maximal when the impact force is the highest [6]. With the analytical solution by Hertz [6], the von Mises stresses along the symmetry axis of the sphere are displayed in Fig. 10. Initially, we can observe that all locally refined models can well represent the stresses. However, it is noticeable that we can see a small oscillation at the $y$-position, where a switch of the hierarchy level takes place. The height of the lowest hierarchical level from Fig. 6 is indicated by the circles in the stress analysis in Fig. 10. For comparison, we tested an unreduced hierarchical IGA model. To include it in the same framework, the unreduced IGA model is modally transformed. The oscillations still occur and thus are independent of the model reduction. Further analysis reveals that this effect does not influence the overall behavior and is only a minor local phenomenon. Using a hierarchically refined model with no order elevation or a coarser element resolution in hierarchy level above, the contact area increases the local effects in the von Mises stresses. However, the overall contact force is still well mapped compared to the analytic solution. In the globally refined models, which are not shown here, these small oscillations do not occur.

Fig. 10

Maximum von Mises stresses along the symmetry axis of the locally refined models

6 Application Example II: impact of two three-dimensional spheres

In the second application example, the previous application example from Sect. 5 is extended and simulated with full three-dimensional models instead of two-dimensional axisymmetric half circles. The motivation of this extension is monitoring the behavior of the computation time when three-dimensional, hierarchically refined models are used, as shown in Fig. 11. The question arises whether the gap in the computation time between globally and locally refined model increases due to more linear combinations of B-splines in three dimensions instead of two or other effects dominate. In the course of this analysis, three hierarchically refined models with three to five levels and their corresponding globally refined reference models are compared. Additionally, a full isoparametric model is simulated in Ansys to validate the impact results of the IGA models. The penalty factor is again determined to be $c_{\mathrm{p}}= {5\mbox{e}18}~\mbox{N}/\mbox{m}$ for the IGA models and $c_{\mathrm{p}}= {5\mbox{e}17}~\mbox{N}/\mbox{m}$ for the isoparametric model following the procedure as in Sect. 5. The number of degrees of freedom before and after the model reduction are summarized in Table 2. The number and size of predefined contact elements are identical for all six models. Here the lowest level of the locally refined models is defined as the contact region.

Fig. 11

Setup of the spheres with $n_{\mathrm{lvl}}=5$ levels

Table 2 Globally and locally refined models of a sphere

The differences in the number of degrees of freedom and the preprocessing time are now significantly larger compared to the first application example. As in the first application example, the number of degrees of freedom $n_{ \mathrm{dof}}$ decreases as the number of levels increases. However, the number of elastic coordinates $n_{\mathrm{q}}$ varies for the locally refined models and is only constant for the globally refined models. Additionally, it is noticeable that all locally refined models have less elastic coordinates than the globally refined ones. The reason for this difference can be monitored in Fig. 12.

Fig. 12

Contact areas of spheres for various refinement levels

The number of elastic coordinates corresponds to the number of interface control points, of which the model in Fig. 12a has the fewest. Considering Fig. 12, we can see that the respective levels adjacent to the contact areas have different element resolutions. The element resolution is lowest for the model in Fig. 12a. Therefore the number of interface control points at the edges of the hierarchical model with $n_{\mathrm{lvl}}=3$ levels is the lowest compared to the other models. The effect of the differences is visualized in Fig. 13 representing the computation times. In contrast to the previous application example, the simulations are only evaluated with parallelized computing. Figure 13a shows that the hierarchical model with $n_{\mathrm{lvl}}=3$ levels takes the least computation time. The same observation was made in the first application example in Fig. 9 and was reasoned on the number of intersecting levels. In this three-dimensional simulation the effect is further enhanced by the small number of elastic coordinates. However, all hierarchical models take less computation time than the globally refined reference models. The Ansys solution is simulated with a step size of $10~\mbox{ns}$ and requires $6~\mbox{h}$ $33~\mbox{min}$ of computation time. Therefore the computation time is slightly higher than for the hierarchical IGA models and lower than for the globally refined IGA models in Fig. 13.

Fig. 13

Comparison of computation times

The small number of elastic coordinates of the hierarchically refined models compared to the globally refined models raises the question whether the reduced computation time is bought by a reduced accuracy. The contact forces of the six IGA models and the isoparametric model simulated in Ansys are shown in Fig. 14 and compared to the analytical solution by Hertz [6]. All models well reproduce the contact force curve. In the detailed view in Fig. 14, we can see that the globally refined models and the Ansys model represent the maximum occurring force minimally better than the locally refined models. However, the advantage of reducing the computation time by a factor of about three outweighs the insignificantly worse accuracy. Comparing the hierarchical model in Fig. 12c with its global reference model in Fig. 12d, the hierarchical model has less interface control points in the outer contact area. In this area, elastic deformation and penetration are lower than in the center of the contact area. Thus no significant differences in the contact force occur.

Fig. 14

Contact forces of three-dimensional spheres

Since the outer contact area is less important, the number of interface control points of the globally refined model could be further reduced. By handpicking the interface control points in the outer contact area a simulation time equivalent to that in a hierarchically refined model may be achieved. However, the hierarchical refinement achieves a reduced number of elastic coordinates fully automatically. This is beneficial when implementing an adaptive online refinement within a flexible multibody impact simulation in future works.

7 Application Example III: multibody simulation of two flexible double pendulums

The third application example demonstrates the usage of the hierarchical refinement in impact simulations with more than two flexible bodies and large rigid body rotations. Therefore the impact of two flexible double pendulums is investigated; see Fig. 15. Hierarchically refined models are used to handle the flexible bodies in contact. In this setup the flexible multibody system consists of two double pendulums where the connection between the suspension and the sphere is modeled by a flexible rod. The rods are modeled by globally refined isogeometric models, which are modally reduced with $n_{\mathrm{q}}=20$ elastic coordinates. The pendulum on the left-hand side in Fig. 15 is initially deflected by $\alpha _{0}=19{^{\circ}}$ and $\beta _{0}= 20.079{^{\circ}}$. The two angles are chosen such that at the time of impact, we have $\alpha =\beta =0{^{\circ}}$. Both double pendulums have no initial velocity. Since gravity is under consideration with the gravitational constant $g=9.81~\mbox{m}/\mbox{s}^{2}$, the initial values of the elastic coordinates of the four flexible bodies need to be determined. A straightforward approach is to solve the equations of motion for the elastic coordinates $\boldsymbol{q}_{\mathrm{e}}$ so that the accelerations $\ddot{\boldsymbol{q}}_{\mathrm{e}}$ vanish. Subsequently, the flexible multibody system is simulated for $175~\mbox{ms}$. The simulation consists of three phases listed in Table 3.

Fig. 15

Simulation setup of two flexible double pendulums

Table 3 Computation time of two flexible double pendulums

The first phase has the longest simulation time and shortest computation time. Although large rigid-body motions occur, the computation time is small since the high-frequency elastic modes are not yet excited. Due to the contact in the second phase, the high modes are induced, and small step sizes are required for the second and third phases. The impact excites oscillations in the spheres and in the two rods. The maximum elastic deflections of the rod of the right pendulum are shown in Fig. 16. For better visibility, only the elastic deflection and position of the center line of the rod without the rigid body motion are displayed. Finally, the simulation is validated by a rigid body simulation with Hertzian contact [6]. The contact forces of the flexible and rigid body simulation are visualized in Fig. 17. The preimpact phase is highlighted in white, the impact phase in gray, and the postimpact phase in light gray. In particular, the long preimpact phase to the contact area can be seen in Fig. 17a. The impact phase is relatively short and is shown in Fig. 17b. The area in gray before the impact belongs to the impact phase, since a subsequent time step of the preimpact phase would already lead to an impact. Both the impact time and the course of the contact force are well represented by the flexible multibody simulation.

Fig. 16

Maximum elastic deflections of the oscillating rod

Fig. 17

Validation of the contact force with Hertz in a rigid body simulation

8 Conclusions

Overall, we can conclude that it is feasible to obtain global shape functions for flexible multibody systems from hierarchically refined isogeometric finite element models. A model reduction with the Craig–Bampton method can be performed, and the global shape functions of the IGA can be smoothly included in the floating frame of reference formulation. Subsequently, an impact simulation can be performed using the penalty formulation. The penalty factor converges for hierarchically refined models, and the differences in the accuracy between the locally and globally refined models are minor. In the two-dimensional application example, the locally and globally refined models are approximated with the same number of elastic coordinates. However, since the hierarchical NURBS in the contact routine are more complex, the overall computation time using the locally refined models is higher than using the globally refined models. In the three-dimensional application example, the locally refined models require less interface control points than the globally refined models, which significantly reduces the effort to solve the equations of motion. Similarly to hierarchical refined models in statics, computational savings can also be achieved in flexible multibody simulations.