1 Introduction

In the field of multibody dynamics, the system of equations of motion is highly complex due to the mixed set of differential and algebraic equations. This kind of systems present particular characteristics complicating their numerical treatment. This paper discusses on two mathematical aspects in order to solve also highly complex multibody problems arising in practice. One aspect concentrates on the rotational parametrization in order to get a simplified structure of the equations of motion and the second aspect focuses on the numerical time integration procedure in order to solve the system of equations in reasonable time also for industrial applications.

Euler parameters as a special choice of quaternions are frequently used to define the orientation of the rigid bodies of a multibody system since the rotation matrix becomes quite simple in this case and the equations of motion are simplified. Compared to other parametrizations of SO(3), Euler parameters are singularity-free and avoid the introduction of trigonometric functions. These preferences contribute to reduce the computational time in a multibody simulation program, although an inner constraint has to be observed as four parameters \(e_{0}, e_{1}, e_{2}, e_{3}\) are used for describing the three rotational degrees of freedom of a rigid rotation. The equations of motion for rigid bodies in terms of the unit quaternions can be found, e.g., in pioneering work by Nikravesh [19], and as well for flexible bodies, e.g., in the work by Yoo and Haug [27] and in the references cited therein. Another advantage of Euler parameters is that the Jacobian matrices of these nonlinear equations are only moderately complicated compared to other parametrizations and can be implemented in a multibody simulation code by analytical formulas [22]. This property is essential for obtaining the adjoint equations of a multibody system which are introduced for solving optimization and inverse problems efficiently; see e.g. [15].

As one possibility for the time discretization of the governing differential algebraic system of equations in index-3 formulation, the well-known Newmark integration formulas can be chosen [18]. Since numerical damping cannot be introduced with the Newmark family integrators unless the order of accuracy is decreased, Hilber, Hughes and Taylor [13] proposed the so-called HHT \(\alpha \)-method which can still maintain second order accuracy and stability. A variable damping depending on the value of the parameter \(\alpha \) in the interval \([-\frac{1}{3}, 0]\) is involved. The smaller the value of \(\alpha \) the larger the artificial damping can be chosen in order to damp out high frequency oscillations that are of no interest. When choosing \(\alpha =0\), there is no damping. However, if Euler parameters are used for the description of the generalized coordinates regarding the rotation, the Newmark formulas also influence the numerical behavior of the Euler parameters and therefore may introduce spurious damping with a high amount also in simple examples in which the system is conservative. An investigation on how the numerical energy dissipation changes with the step size is relevant.

Several authors have discussed on the problem of the artificial numerical damping of the HHT time integration procedure, see e.g. [9, 12, 17, 20], but to the best knowledge of the authors, not in the case when Euler parameters are utilized.

One of the fundamental discussions on energy–momentum conserving algorithms has been introduced by Simo et al. [25]. Therein, various implicit time stepping algorithms are presented which preserves exactly the total angular momentum and the total energy. Various authors in the field of multibody dynamics used the Newmark formulas within the HHT \(\alpha \)-method in order to get rid of high frequency oscillations that often occur in multibody applications due to involved constraints and flexible bodies. An approach proposed by Bauchau [4] deals with high frequencies in the multibody system with a self-stabilization algorithm which enforces the constraints in a multibody system in an index-2 formulation similar to the GGL method [11], but avoiding the introduction of additional Lagrange multipliers. Another approach concerning the stabilization of constrained mechanical systems has been presented by García Orden [10], in which the artificial energy introduced in the system can be controlled from various points of view. The group around Arnold, Cardona and Brüls [2, 3] suggests a Lie group time integration of constrained systems and presents a stabilized index-2 formulation in terms of Euler parameters; see e.g. [1]. Terze et al. [26] propose a Lie group integration method for an index-1 formulation for constrained multibody systems by a reformulated Munthe–Kaas algorithm based on the work by Müller et al. [14] in which the importance of constraint satisfaction in the Lie group configuration is pointed out. Moreover, the group around Betsch and Steinmann discusses on the constrained integration of rigid body dynamics in [7], in which the main idea is to enforce the Euler parameter constraint on velocity level without resorting to a particular rotational parameterization, while in [6] especially a conserving numerical time integration in terms of quaternions is presented also following the ideas of rigid body dynamics in terms of directors, as e.g. in [5].

The present paper discusses the numerical damping effect of the HHT algorithm on the rotational motion of a rigid body if Euler parameters are used. Therefore, we consider the simple case of a rotation about a single axis under the influence of a constant moment which should lead to a linearly increasing angular velocity. We first derive an explicit formula for the numerical damping resulting from one time integration step, which shows the influence of the time step size and of the process parameter \(\alpha \). We will see that the dissipative effect exists even if \(\alpha \) is set to zero.

However, the dissipation for a simple rotational motion is a severe problem of the HHT method in combination with Euler parameters which does not occur for other parametrizations of SO(3). The reason is that a constant rotation is described by oscillations of the Euler parameters which are numerically damped like “physical” oscillations of flexible structures. Whereas numerical damping is welcome in the latter case, in particular for high frequency oscillations, it is very unfavorable in the first case, e.g. for analyzing applications in rotordynamics. But since both, the HHT method and Euler parameters, have also significant advantages in multibody dynamics a solution of the outlined incompatibility would be preferable.

Hence, in the second part of this paper, we develop a modified HHT time integration scheme for the use of Euler parameters. This method is a compromise between the pure Newmark method and its canonical extension to SO(3), which was first presented in [24] and applies the Newmark formulas completely on the Lie algebra of SO(3). Since the latter approach requires the computation of the exponential map to update the rotation during each time increment, the original computational efficiency of Euler parameters is lost. Moreover, the determination of Jacobian matrices is cumbersome in this case. The key idea of the new method proposed below is to use the modified Newmark formula on velocity level only and to add the velocity constraint for Euler parameters. We show that the numerical damping effect is significantly improved and vanishes if \(\alpha =0\) with this approach.

2 Euler parameters

We start with a brief review of the Euler parameter description for rotational motions, which are e.g. derived in Nikravesh [19] or Shabana [21]. The Euler parameters \(\mathbf{e}= (e_{0},e_{1},e_{2},e_{3})^{ \mathsf{T}}\) are defined by an axis of rotation \(\mathbf{v}=(v_{x},v _{y},v_{z})^{\mathsf{T}}\) and by the corresponding rotation angle \(\varphi \) in the following way:

$$ e_{0} = \cos \frac{\varphi }{2}, \qquad e_{1} = v_{x} \sin \frac{ \varphi }{2}, \qquad e_{2} = v_{y} \sin \frac{\varphi }{2}, \qquad e _{3} = v_{z} \sin \frac{\varphi }{2} . $$
(1)

A rotation matrix \(\mathbf{A}\in \) SO(3), which defines the orientation of a body fixed reference frame in space, can be written in the form

$$ \mathbf{A}= \left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c} e_{0}^{2} + e_{1}^{2} - e_{2}^{2} - e_{3}^{2} & 2 e_{1} e_{2} - 2 e _{0} e_{3} & 2 e_{1} e_{3} + 2 e_{0} e_{2} \\ 2 e_{1} e_{2} + 2 e_{0} e_{3} & e_{0}^{2} + e_{2}^{2} - e_{3}^{2} - e _{1}^{2} & 2 e_{2} e_{3} - 2 e_{0} e_{1} \\ 2 e_{1} e_{3} - 2 e_{0} e_{2} & 2 e_{2} e_{3} + 2 e_{0} e_{1} & e_{0} ^{2} + e_{3}^{2} - e_{1}^{2} - e_{2}^{2} \end{array}\displaystyle \right ) . $$
(2)

It contains only quadratic expressions in \(e_{i}\). The body fixed angular velocity vector and the angular acceleration vector are given by

$$ \boldsymbol{\omega }= 2\mathbf{L}\dot{\mathbf{e}} \quad \text{and} \quad \dot{\boldsymbol{\omega }}= 2\mathbf{L}\ddot{\mathbf{e}} $$
(3)

where

$$ \mathbf{L}= \begin{pmatrix} -e_{1} & e_{0} & e_{3} & -e_{2} \\ -e_{2} & -e_{3} & e_{0} & e_{1} \\ -e_{3} & e_{2} & -e_{1} & e_{0} \end{pmatrix} . $$
(4)

Since the rotation vector \(\mathbf{v}\) in Eq. (1) is a unit vector, Euler parameters must satisfy the constraint equation

$$ C(\mathbf{e})= e_{0}^{2} + e_{1}^{2} + e_{2}^{2} + e_{3}^{2} - 1 = \mathbf{e}^{\mathsf{T}} \mathbf{e}- 1 = 0. $$
(5)

The respective constraint condition on velocity level reads

$$ 2e_{0} \dot{e}_{0} + 2e_{1}\dot{e}_{1} + 2e_{2} \dot{e}_{2} + 2e_{3} \dot{e}_{3} = 2 \mathbf{e}^{\mathsf{T}} \dot{\mathbf{e}} = 0. $$
(6)

For the subsequent computations the following properties of \(\mathbf{L}\) and \(\mathbf{e}\), which can easily be verified, are needed:

$$ \mathbf{L}\mathbf{e}=\textbf{0}, \qquad \dot{\mathbf{L}} \dot{ \mathbf{e}}=\textbf{0}, \qquad \mathbf{L}\mathbf{L}^{\mathsf{T}}= \mathbf{I}_{3}, \qquad \mathbf{L}^{\mathsf{T}}\mathbf{L}=\mathbf{I} _{4}-\mathbf{e}\mathbf{e}^{\mathsf{T}} $$
(7)

where \(\mathbf{I}_{3}\) and \(\mathbf{I}_{4}\) denote the three and four dimensional unity matrices.

The rotational equations of motion for an unconstrained rigid body parameterized in the three dimensional space, e.g. by using Euler angles, can be written as

$$\begin{aligned} \mathbf{J}\dot{\boldsymbol{\omega }} + \tilde{\boldsymbol{ \omega }} \mathbf{J}\boldsymbol{\omega }= \mathbf{m} \end{aligned}$$
(8)

in which \(\mathbf{J}= \text{diag}(I_{x},I_{y},I_{z})\) represents the inertia tensor in the principal axes frame for the sake of simplicity. The vector \(\mathbf{m}\) denotes the sum of all external moments acting on the body. The matrix \(\tilde{\boldsymbol{\omega }}\) describes a skew-symmetric matrix associated with the angular velocity vector \(\boldsymbol{\omega }\). In terms of Euler parameters \(\boldsymbol{\omega }\) and \(\dot{\boldsymbol{\omega }}\) can be expressed by Eq. (3). Moreover, it can be shown that \(\tilde{\boldsymbol{\omega }}=2\mathbf{L}\dot{\mathbf{L}}^{\mathsf{T}}\). If Eq. (8) is premultiplied with \(2 \mathbf{L}^{\mathsf{T}}\) and enhanced by the constraint force \(\frac{1}{2}\mathbf{C}_{\mathbf{e}}^{\mathsf{T}}\lambda = \mathbf{e} \lambda \) resulting from Eq. (5), the equations of rotational motion in terms of Euler parameters are obtained:

$$\begin{aligned} 4\mathbf{L}^{\mathsf{T}} \mathbf{J}\mathbf{L}\ddot{\mathbf{e}} + 8 \mathbf{L}^{\mathsf{T}}\mathbf{L}\dot{\mathbf{L}}^{\mathsf{T}} \mathbf{J} \mathbf{L}\dot{\mathbf{e}} + \mathbf{e}\lambda = 2 \mathbf{L}^{\mathsf{T}} \mathbf{m}. \end{aligned}$$
(9)

A detailed derivation of Eq. (9) is presented in [23]. Together with the constraint equations Eq. (5) it forms a set of differential algebraic equations for \(\mathbf{e}(t)\) and the Lagrange multiplier \(\lambda (t)\) if the external moment \(\mathbf{m}\) is known. The Lagrange multiplier \(\lambda (t)\) turns out to be zero, which can be seen after a premultiplication of Eq. (9) with \(\mathbf{e}^{ \mathsf{T}}\). Since \(\mathbf{L}\mathbf{e}=\textbf{0}\), this results in \(\mathbf{e}^{\mathsf{T}}\mathbf{e}\lambda = 0\) or \(\lambda =0\). But note that this holds only for the description of the rotational motion given by Eq. (9). If the constraint equation is used to modify Eq. (9), the Lagrange multiplier can also attain non-zero values, see [23] for details.

3 The dynamics of Euler parameters for a rotation about a single axis

To analyze the impact of the HHT method on the dynamics of Euler parameters we consider the special case where a body rotates only about the first principal axis and is driven by a constant moment \(\mathbf{m}=(M_{x},0,0)^{\mathsf{T}}\). The rotation vector is then given by \(\mathbf{v}=(1,0,0)^{\mathsf{T}}\) and the Euler parameters defined by Eq. (1) reduce to

$$ e_{0} = \cos \frac{\varphi }{2}, \qquad e_{1} = \sin \frac{\varphi }{2}, \qquad e_{2} = 0, \qquad e_{3} = 0 . $$
(10)

The \(\mathbf{L}\)-matrix from Eq. (4) becomes

$$ \mathbf{L}= \begin{pmatrix} -e_{1} & e_{0} & 0 & 0 \\ 0 & 0 & e_{0} & e_{1} \\ 0 & 0 & -e_{1} & e_{0} \end{pmatrix} . $$
(11)

The angular velocity and the angular acceleration according to Eq. (3) are given by

$$\begin{aligned} \omega _{x} = \omega &= 2 (-e_{1}\dot{e}_{0} + e_{0}\dot{e}_{1}) = \dot{\varphi } , \end{aligned}$$
(12)
$$\begin{aligned} \dot{\omega }_{x} = \dot{\omega } &= 2 (-e_{1} \ddot{e}_{0} + e_{0} \ddot{e}_{1}) = \ddot{ \varphi }, \end{aligned}$$
(13)

and \(\omega _{y}=\omega _{z}=0\). Equation (9) for the general three dimensional case simplifies to

$$\begin{aligned} 4 I_{x} e_{1} (e_{1} \ddot{e}_{0} - e_{0} \ddot{e} _{1} ) + 8 I_{x} e_{1} (e_{1} \dot{e}_{0} - e_{0} \dot{e}_{1}) (e _{0} \dot{e}_{0} + e_{1} \dot{e}_{1}) + e_{0} \lambda &= -2 e_{1} M _{x} , \end{aligned}$$
(14)
$$\begin{aligned} - 4 I_{x} e_{0} (e_{1} \ddot{e}_{0} - e_{0} \ddot{e}_{1} ) - 8 I_{x} e_{0} (e_{1} \dot{e}_{0} - e_{0} \dot{e}_{1}) (e_{0} \dot{e}_{0} + e_{1} \dot{e}_{1}) + e_{1} \lambda &= 2 e_{0} M_{x} . \end{aligned}$$
(15)

From Eq. (6) one could readily conclude that the second terms on the left sides vanish for the exact solution. Moreover, since also \(\lambda =0\) as shown above, both Eqs. (14) and (15) are equivalent to

$$ e_{0} \ddot{e}_{1} - e_{1} \ddot{e}_{0} = \frac{1}{2} \frac{M_{x}}{I _{x}}. $$
(16)

Using Eq. (13), we see that \(\ddot{\varphi } = M_{x}/I _{x}\) and, for zero initial conditions, \(\varphi = (M_{x} t^{2})/(2 I _{x})\). Inserting in Eq. (10) we finally arrive at the expected result

$$ e_{0}(t) = \cos \biggl(\frac{M_{x}}{I_{x}}\frac{t^{2}}{4} \biggr), \qquad e_{1}(t) = \sin \biggl(\frac{M_{x}}{I_{x}} \frac{t^{2}}{4} \biggr). $$

However, the properties \(\lambda =0\) and \(e_{0} \dot{e}_{0} + e_{1} \dot{e}_{1}=0\) which we have used for the derivation of Eq. (16), are eventually not satisfied exactly, if we apply a numerical solution procedure. Hence, we do not further simplify Eqs. (14) and (15) at this point and discuss what happens if the HHT method is employed for solving these equations numerically.

4 The classical HHT \(\alpha \)-method

As one possibility for the time discretization of second order differential equations, the classical Newmark integration formulas [18] are widely employed. They relate positions, velocities and accelerations at the time step \(t_{n}\) with the respective quantities at a later time step \(t_{n+1}=t_{n}+h\). For Euler parameters, these formulas read

$$\begin{aligned} \mathbf{e}_{n+1} =& \mathbf{e}_{n} + h\dot{ \mathbf{e}}_{n}+\frac{h ^{2}}{2}(1-2\beta )\ddot{ \mathbf{e}}_{n} + h^{2}\beta \ddot{\mathbf{e}}_{n+1} , \end{aligned}$$
(17)
$$\begin{aligned} \dot{\mathbf{e}}_{n+1} =& \dot{\mathbf{e}}_{n} + h(1- \gamma ) \ddot{\mathbf{e}}_{n} + h\gamma \ddot{\mathbf{e}}_{n+1} . \end{aligned}$$
(18)

If \(\mathbf{e}_{n}\), \(\dot{\mathbf{e}}_{n}\) and \(\ddot{\mathbf{e}} _{n}\) are already known, \(\mathbf{e}_{n+1}\) and \(\dot{\mathbf{e}}_{n+1}\) are expressed in terms of \(\ddot{\mathbf{e}}_{n+1}\). In the original Newmark method, the lacking equation for \(\ddot{\mathbf{e}}_{n+1}\) is simply the equation of motion at \(t_{n+1}\). However, the Hilber, Hughes and Taylor (HHT) \(\alpha \)-method [13] uses a weighting of the force terms in the equations of motion at the time instances \(t_{n}\) and \(t_{n+1}\). The weighting factor \(\alpha \), usually defined in the interval \([-\frac{1}{3}, 0]\), introduces numerical damping into the integration scheme. It is also used to compute the parameters \(\beta \) in Eq. (17) and \(\gamma \) in Eq. (18) as

$$ \beta = \frac{1}{4}(1-\alpha )^{2} \quad \text{and}\quad \gamma = \frac{1}{2}(1-2\alpha ) . $$
(19)

When applied to Eq. (9), the HHT method claims

$$\begin{aligned} &4\mathbf{L}^{\mathsf{T}}_{n+1} \mathbf{J} \mathbf{L}_{n+1} \ddot{\mathbf{e}}_{n+1} + (1+\alpha )8 \mathbf{L}_{n+1}^{\mathsf{T}} \mathbf{L}_{n+1}\dot{ \mathbf{L}}_{n+1}^{\mathsf{T}}\mathbf{J} \mathbf{L}_{n+1} \dot{\mathbf{e}}_{n+1} -\alpha 8\mathbf{L}_{n}^{ \mathsf{T}} \mathbf{L}_{n}\dot{\mathbf{L}}_{n}^{\mathsf{T}} \mathbf{J} \mathbf{L}_{n}\dot{\mathbf{e}}_{n} \\ &\quad{} + (1+\alpha )\mathbf{e}_{n+1}\lambda _{n+1} - \alpha \mathbf{e}_{n} \lambda _{n} = (1+\alpha )2 \mathbf{L}_{n+1}^{\mathsf{T}}\mathbf{m}_{n+1} - \alpha 2 \mathbf{L}_{n}^{\mathsf{T}}\mathbf{m}_{n}. \end{aligned}$$
(20)

Equations (17), (18), (20) and the constraint \(\mathbf{e}_{n+1}^{\mathsf{T}} \mathbf{e}_{n+1} - 1 = 0\) is a set of nonlinear equations determining \(\mathbf{e}_{n+1}\), \(\dot{\mathbf{e}}_{n+1}\), \(\ddot{\mathbf{e}}_{n+1}\) and \(\lambda _{n+1}\) which, in general, must be solved numerically by using Newton’s method.

5 The effect of the HHT method and the Euler parametrization on a simple rotation

To study the effect of the HHT method when it is used in combination with Euler parameters we consider again a single rotation about the x-axis and compute one time integration step explicitly. In this case, we can solve Eqs. (14) and (15) and set \(e_{2}=e_{3}=0\). The Newmark formulas for \(e_{0}\) and \(e_{1}\) read

$$ \begin{aligned} e_{0} &= e_{0}' + h \dot{e}_{0}' + \frac{1}{2}h^{2}(1-2\beta ) \ddot{e}_{0}' + h^{2}\beta \ddot{e}_{0}, \\ e_{1} &= e_{1}' + h \dot{e}_{1}' + \frac{1}{2}h^{2}(1-2 \beta ) \ddot{e}_{1}' + h^{2}\beta \ddot{e}_{1}, \\ \dot{e}_{0} &= \dot{e}_{0}' + h(1- \gamma ) \ddot{e}_{0}' + h\gamma \ddot{e}_{0} , \\ \dot{e}_{1} &= \dot{e}_{1}' + h(1- \gamma ) \ddot{e}_{1}' + h\gamma \ddot{e}_{1} . \end{aligned} $$
(21)

For simplicity, we characterize here the state variables at time step \(t_{n}\) (denoted as old state) with a prime whereas the respective variables at \(t_{n+1}\) (denoted as new state) are not specifically marked. For the old state, we assume \(\varphi =0\) as the rotation angle and \(\dot{\varphi }=\omega '\) as the angular velocity. Then, from Eq. (10), we obtain

$$ e_{0}' = 1, \qquad e_{1}' = 0, \qquad \dot{e}_{0}' = 0, \qquad \dot{e} _{1}' = \frac{\omega '}{2}, \qquad \ddot{e}_{0}' = -\frac{\omega ' {}^{2}}{4} . $$
(22)

As Eqs. (14) and (15) should be satisfied at \(t_{n}\), we may conclude that

$$ \lambda ' = 0, \qquad \ddot{e}_{1}' = \frac{1}{2}\frac{M_{x}}{I_{x}} . $$
(23)

After inserting Eqs. (22) and (23) in Eq. (21) we obtain the following equations for the new state:

$$ \begin{aligned} e_{0} &= 1 - \frac{h^{2}}{8}(1-2\beta )\omega '{}^{2} + h^{2}\beta \ddot{e}_{0} , \\ e_{1} &= \frac{h}{2} \omega ' + \frac{h^{2}}{4}(1-2\beta )\frac{M _{x}}{I_{x}} + h^{2}\beta \ddot{e}_{1} , \\ \dot{e}_{0} &= -\frac{h}{4}(1-\gamma )\omega '{}^{2} + h\gamma \ddot{e}_{0} , \\ \dot{e}_{1} &= \frac{1}{2}\omega ' + \frac{h}{2}(1-\gamma ) \frac{M _{x}}{I_{x}} + h\gamma \ddot{e}_{1} . \end{aligned} $$
(24)

The remaining equations for the new state are obtained from specializing Eq. (20) for the rotation about the x-axis. By using also Eqs. (22) and (23) for the old state, we get

$$\begin{aligned} &4 I_{x} e_{1} (e_{1} \ddot{e}_{0} - e_{0} \ddot{e} _{1} ) + (1+ \alpha ) 8 I_{x} e_{1} (e_{1} \dot{e}_{0} - e_{0} \dot{e}_{1}) (e_{0} \dot{e}_{0} + e_{1} \dot{e}_{1}) + (1+\alpha ) e _{0} \lambda \\ &\quad = -2 (1+\alpha ) e_{1} M_{x} , \end{aligned}$$
(25)
$$\begin{aligned} & - 4 I_{x} e_{0} (e_{1} \ddot{e}_{0} - e_{0} \ddot{e}_{1} ) - (1+\alpha ) 8 I_{x} e_{0} (e_{1} \dot{e}_{0} - e_{0} \dot{e}_{1}) (e _{0} \dot{e}_{0} + e_{1} \dot{e}_{1}) + (1+\alpha ) e_{1} \lambda \\ &\quad = 2 (1+\alpha ) e_{0} M_{x} - 2 \alpha M_{x}. \end{aligned}$$
(26)

Equations (24), (25), (26) and the constraint equation \(e_{0}^{2}+e_{1}^{2}=1\) determine the new state variables \(e_{0}\), \(e_{1}\), \(\dot{e}_{0}\), \(\dot{e}_{1}\), \(\ddot{e}_{0}\), \(\ddot{e}_{1}\) and \(\lambda \). The Lagrange multiplier \(\lambda \) can be readily eliminated. For that, we multiply Eq. (25) with \(e_{1}\), Eq. (26) with \(-e_{0}\) and add both equations. By using also \(e_{0}^{2}+e_{1} ^{2}=1\) and dividing by \(4 I_{x}\), we obtain

$$ e_{1} \ddot{e}_{0} - e_{0} \ddot{e}_{1} + 2(1+\alpha ) (e_{1} \dot{e} _{0} - e_{0} \dot{e}_{1}) (e_{0} \dot{e}_{0} + e_{1} \dot{e}_{1}) = -\frac{M _{x}}{2I_{x}} (1 + \alpha - \alpha e_{0} ) . $$
(27)

After insertion of the Newmark formulas given in Eq. (24), this equation contains only the unknowns \(\ddot{e}_{0}\) and \(\ddot{e}_{1}\). Moreover, after inserting Eq. (24) also in the constraint equation \(e_{0}^{2}+e_{1}^{2}=1\) another equation for \(\ddot{e}_{0}\) and \(\ddot{e}_{1}\) is obtained. The latter one is a quadratic equation from which \(\ddot{e}_{0}\) can be expressed by \(\ddot{e}_{1}\) and also inserted in Eq. (27). Finally, we end up with a single fourth order polynomial equation for \(\ddot{e}_{1}\), which is hard to solve analytically. However, if we introduce a series expansion of the equation up to third order terms in the time step size \(h\), the quartic equation reduces to a quadratic equation in \(\ddot{e}_{1}\). From its solution the remaining state variables \(e_{0}\), \(e_{1}\), \(\dot{e}_{0}\), \(\dot{e}_{1}\), \(\ddot{e}_{0}\) can be computed just by insertion. We are especially interested in the angular velocity associated to the new state which is defined by Eq. (12). After a further series expansion in terms of \(h\) the new angular velocity reads

$$ \omega = \omega ' + \frac{M_{x}}{I_{x}} h + \frac{1}{4} \alpha \omega '{}^{3} h^{2} + \frac{M_{x}}{I_{x}} \frac{10 \alpha ^{4} + 3 \alpha ^{3} - 12 \alpha ^{2} + 11 \alpha - 4}{16 (\alpha -1)^{2}} \omega ' {}^{2} h^{3} + O\bigl(h^{4}\bigr) $$
(28)

where Eqs. (19) have also been taken into account. We can now see that the terms up to first order in \(h\) accelerate the rotation correctly according to the physical law \(I_{x} \dot{\omega }=M_{x}\). However, the succeeding terms cause numerical damping if \(\alpha \in [-\frac{1}{3},0]\). The damping in the leading term is proportional to \(\omega '{}^{3}\). Hence, the effect increases significantly with increasing angular velocity, but it can be eliminated by setting \(\alpha =0\). However, numerical damping is still present even for \(\alpha =0\), since the third order term in \(h\) is \(-M_{x}/I_{x} \omega '{}^{2} h^{3}/4\) if \(\alpha \) is zero. We conclude that the application of the HHT method is no good choice for simulating systems with spinning bodies if the rotations are described with Euler parameters.

6 A modified HHT-scheme for Euler parameters

To overcome the problem of spinning bodies outlined in the previous section, we suggest a modification of the Newmark formulas for the simulation of rotational motions which are described in Euler parameters. Modified Newmark formulas for rotational motions were already presented by Simo and Vu-Quoc in 1988 [24]. They basically introduced the rotation vector \(\boldsymbol{\theta }_{n}\) transforming the rotation matrix \(\mathbf{A}_{n}\) at time \(t_{n}\) into the rotation matrix \(\mathbf{A} _{n+1}\) at time \(t_{n+1}\). With the skew-symmetric tensor \(\tilde{\boldsymbol{\theta }}_{n}\) associated to \(\boldsymbol{\theta } _{n}\) and with the exponential map for SO(3), the relation between \(\mathbf{A}_{n}\) and \(\mathbf{A}_{n+1}\) can be written in the following form:

$$ \mathbf{A}_{n+1} = \exp (\tilde{\boldsymbol{\theta }}_{n}) \mathbf{A} _{n} . $$
(29)

Herein, \(\tilde{\boldsymbol{\theta }}_{n}\) is interpreted as an element of the Lie algebra of SO(3). Physically speaking, the vector\(\boldsymbol{\theta }_{n}\) is a rotation vector in the inertial frame which is represented in the body fixed frame by the vector \(\mathbf{A}_{n}^{\mathsf{T}}\boldsymbol{\theta }_{n}\). Since the time derivatives of the body fixed rotation vector are equivalent to the body fixed angular velocity vector \(\boldsymbol{\omega }\) and the angular acceleration vector \(\dot{\boldsymbol{\omega }}\), Simo and Vu-Quoc applied the Newmark formulas to discretize the relation between \(\boldsymbol{\theta }\), \(\boldsymbol{\omega }\) and \(\dot{\boldsymbol{\omega }}\) at the time instances \(t_{n}\) and \(t_{n+1}\) in the following form:

$$\begin{aligned} \mathbf{A}_{n}^{\mathsf{T}}\boldsymbol{\theta }_{n} =& h \boldsymbol{\omega }_{n}+\frac{h^{2}}{2}(1-2\beta ) \dot{ \boldsymbol{\omega }}_{n} + h^{2}\beta \dot{\boldsymbol{ \omega }}_{n+1} , \end{aligned}$$
(30)
$$\begin{aligned} \boldsymbol{\omega }_{n+1} =& \boldsymbol{\omega }_{n} + h(1-\gamma )\dot{\boldsymbol{\omega }}_{n} + h\gamma \dot{ \boldsymbol{\omega }} _{n+1} . \end{aligned}$$
(31)

Equations (30), (31) and (29) can be interpreted as a canonical extension of the classical Newmark formulas to the structure of the rotation group SO(3). In principle, they are applicable to any parametrization of the rotation matrix. However, the practical use of the modified Newmark formulas requires the computation of the exponential map and, for solving the nonlinear equation for the new state at \(t_{n+1}\), its linearization with respect to the rotation parameters.

As an alternative, which is simpler to implement, we propose to replace in the classical Newmark formulas only Eq. (18) with Eq. (31) and to still use Eq. (17) instead of Eq. (30). By inserting the relations \(\omega =2\mathbf{L}\dot{e}\) and \(\dot{\omega }=2\mathbf{L}\ddot{e}\) in Eq. (31), we obtain (after dividing by 2)

$$ \mathbf{L}_{n+1}\dot{\mathbf{e}}_{n+1} = \mathbf{L}_{n} \dot{\mathbf{e}}_{n} + h(1-\gamma ) \mathbf{L}_{n}\ddot{\mathbf{e}} _{n} + h\gamma \mathbf{L}_{n+1}\ddot{\mathbf{e}}_{n+1} . $$

Since these are only three equations whereas Eq. (18) contains four equations for the four Euler parameters, we add Eq. (6) at \(t_{n+1}\), i.e. \(\mathbf{e}_{n+1}^{ \mathsf{T}}\dot{\mathbf{e}}_{n+1}=0\), as the fourth equation. Hence, the modified Newmark formula replacing Eq. (18) reads

$$ \left ( \textstyle\begin{array}{c} \mathbf{L}_{n+1} \\ \mathbf{e}_{n+1}^{\mathsf{T}} \end{array}\displaystyle \right ) \dot{ \mathbf{e}}_{n+1} = \left ( \textstyle\begin{array}{c} \mathbf{L}_{n}\dot{\mathbf{e}}_{n} + h(1-\gamma )\mathbf{L}_{n} \ddot{\mathbf{e}}_{n} + h\gamma \mathbf{L}_{n+1}\ddot{\mathbf{e}}_{n+1} \\ 0 \end{array}\displaystyle \right ). $$

The \(4\times 4\)-matrix on the left side is orthogonal and can be inverted easily by transposing. Hence, the latter equation can be resolved for \(\dot{\mathbf{e}}_{n+1}\), yielding

$$\begin{aligned} \dot{\mathbf{e}}_{n+1} =& \left ( \textstyle\begin{array}{c} \mathbf{L}_{n+1} \\ \mathbf{e}_{n+1}^{\mathsf{T}} \end{array}\displaystyle \right )^{\mathsf{T}} \left ( \textstyle\begin{array}{c} \mathbf{L}_{n}\dot{\mathbf{e}}_{n} + h(1-\gamma )\mathbf{L}_{n} \ddot{\mathbf{e}}_{n} + h\gamma \mathbf{L}_{n+1}\ddot{\mathbf{e}}_{n+1} \\ 0 \end{array}\displaystyle \right ) \\ =& \mathbf{L}_{n+1}^{\mathsf{T}} \bigl(\mathbf{L}_{n} \dot{\mathbf{e}}_{n} + h(1-\gamma )\mathbf{L}_{n}\ddot{ \mathbf{e}} _{n} \bigr) + h\gamma \mathbf{L}_{n+1}^{\mathsf{T}} \mathbf{L}_{n+1} \ddot{\mathbf{e}}_{n+1}. \end{aligned}$$
(32)

Using the general relation \(\mathbf{L}^{\mathsf{T}}\mathbf{L}= \mathbf{I}_{4} - \mathbf{e}\mathbf{e}^{\mathsf{T}}\) and adding Eq. (17), our modified Newmark formulas for the Euler parameters are summarized as follows:

$$\begin{aligned} \mathbf{e}_{n+1} =& \mathbf{e}_{n} + h\dot{ \mathbf{e}}_{n}+\frac{h ^{2}}{2}(1-2\beta )\ddot{ \mathbf{e}}_{n} + h^{2}\beta \ddot{\mathbf{e}}_{n+1}, \end{aligned}$$
(33)
$$\begin{aligned} \dot{\mathbf{e}}_{n+1} =& \mathbf{L}_{n+1}^{\mathsf{T}} \bigl(\mathbf{L} _{n}\dot{\mathbf{e}}_{n} + h(1-\gamma )\mathbf{L}_{n} \ddot{\mathbf{e}}_{n} \bigr) + h\gamma \bigl(\mathbf{I}_{4} - \mathbf{e}_{n+1} \mathbf{e}_{n+1}^{\mathsf{T}} \bigr) \ddot{\mathbf{e}}_{n+1} . \end{aligned}$$
(34)

These formulas replace Eqs. (17) and (18) and guarantee that the angular velocity vector stays in the Lie algebra of SO(3). Equations (20), (33), (34) and the constraint \(\mathbf{e}_{n+1}^{ \mathsf{T}} \mathbf{e}_{n+1} = 1\) form a set of nonlinear equations determining \(\mathbf{e}_{n+1}\), \(\dot{\mathbf{e}}_{n+1}\), \(\ddot{\mathbf{e}}_{n+1}\) and \(\lambda _{n+1}\). Note that, unlike Eq. (18), Eq. (34) is now nonlinear in the Euler parameters \(\mathbf{e}_{n+1}\). But like in the classical Newmark method, \(\mathbf{e}_{n+1}\) can be expressed by \(\ddot{\mathbf{e}}_{n+1}\) from Eq. (33) and after inserting in Eq. (34), \(\dot{\mathbf{e}}_{n+1}\) becomes a function of \(\ddot{\mathbf{e}}_{n+1}\), too. Hence, Eq. (20) and the constraint equation \(\mathbf{e}_{n+1}^{\mathsf{T}} \mathbf{e}_{n+1} = 1\) finally contain only \(\ddot{\mathbf{e}}_{n+1}\) and \(\lambda _{n+1}\) as unknowns. Like in the classical HHT method, the solution of these equations must be computed with Newton’s method. In Appendix B it is shown, how the Jacobian matrix changes when the modified Newmark formulas are applied to the rotational part of the equations of motion.

7 The simple rotation with the modified HHT method

We now show that the HHT method with the modified Newmark formulas preserves the angular momentum of a spinning body if \(\alpha =0\). Like in Sect. 5, we consider a rotation about the x-axis, where \(e_{2}=e_{3}=0\). The old state at time \(t_{n}\) is again defined by Eqs. (22) and (23), i.e. by

$$ \mathbf{e}_{n} = \left ( \textstyle\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array}\displaystyle \right ) , \qquad \dot{\mathbf{e}}_{n} = \left ( \textstyle\begin{array}{c} 0 \\ \omega /2 \\ 0 \\ 0 \end{array}\displaystyle \right ) , \qquad \ddot{ \mathbf{e}}_{n} = \left ( \textstyle\begin{array}{c} -\omega ^{2}/4 \\ M_{x}/2I_{x} \\ 0 \\ 0 \end{array}\displaystyle \right ) , \qquad \mathbf{L}_{n} = \left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\displaystyle \right ). $$

The new state at \(t_{n+1}\) is described by

$$\begin{aligned} \mathbf{e}_{n+1} &= \left ( \textstyle\begin{array}{c} e_{0} \\ e_{1} \\ 0 \\ 0 \end{array}\displaystyle \right ) , \qquad \dot{\mathbf{e}}_{n+1} = \left ( \textstyle\begin{array}{c} \dot{e}_{0} \\ \dot{e}_{1} \\ 0 \\ 0 \end{array}\displaystyle \right ) , \qquad \ddot{ \mathbf{e}}_{n+1} = \left ( \textstyle\begin{array}{c} \ddot{e}_{0} \\ \ddot{e}_{1} \\ 0 \\ 0 \end{array}\displaystyle \right ) , \\ \mathbf{L}_{n+1} &= \left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -e_{1} & e_{0} & 0 & 0 \\ 0 & 0 & e_{0} & e_{1} \\ 0 & 0 & -e_{1} & e_{0} \end{array}\displaystyle \right ). \end{aligned}$$

Inserting in Eqs. (33) and (34) yields the relations

$$\begin{aligned} e_{0} &= 1 - \frac{h^{2}}{8}(1-2\beta )\omega '{}^{2} + h^{2}\beta \ddot{e}_{0} , \end{aligned}$$
(35)
$$\begin{aligned} e_{1} &= \frac{h}{2} \omega ' + \frac{h^{2}}{4}(1-2\beta )\frac{M _{x}}{I_{x}} + h^{2}\beta \ddot{e}_{1} , \end{aligned}$$
(36)
$$\begin{aligned} \dot{e}_{0} &= -\frac{1}{2} \biggl(\omega ' + \frac{M_{x}}{I_{x}} h (1 - \gamma ) \biggr) e_{1} + h\gamma \bigl(1-e_{0}^{2} \bigr)\ddot{e} _{0} - h \gamma e_{0} e_{1} \ddot{e}_{1} , \end{aligned}$$
(37)
$$\begin{aligned} \dot{e}_{1} &= \frac{1}{2} \biggl(\omega ' + \frac{M_{x}}{I_{x}} h (1 - \gamma ) \biggr) e_{0} + h\gamma \bigl(1-e_{1}^{2} \bigr)\ddot{e}_{1} - h \gamma e _{0} e_{1} \ddot{e}_{0}, \end{aligned}$$
(38)

which replace Eq. (24). They can be solved with Eq. (27) for the new state. Since the modified Newmark formulas satisfy the constraint equation on velocity level \(\mathbf{e}_{n+1}^{\mathsf{T}}\dot{\mathbf{e}}_{n+1}=e_{0}\dot{e}_{0}+e _{1}\dot{e}_{1}=0\), the quadratic velocity term in Eq. (27) is zero and the equation now reduces to the much simpler form

$$ e_{1} \ddot{e}_{0} - e_{0} \ddot{e}_{1} = -\frac{M_{x}}{2I_{x}} (1 + \alpha - \alpha e_{0} ) . $$
(39)

We first multiply Eq. (35) with \(e_{1}\), Eq. (36) with \(-e_{0}\) and add both equations. This yields

$$\begin{aligned} & \biggl(1 - \frac{h^{2}}{8}(1-2\beta )\omega '{}^{2} \biggr) e_{1} - \biggl( \frac{h}{2} \omega ' + \frac{h^{2}}{4}(1-2\beta ) \frac{M_{x}}{I _{x}} \biggr) e_{0} \\ &\quad = - h^{2}\beta (e_{1} \ddot{e}_{0} - e_{0} \ddot{e}_{1} ) = h^{2}\beta \frac{M_{x}}{2I_{x}} (1 + \alpha - \alpha e_{0} ) \end{aligned}$$
(40)

where we have already used Eq. (39). Equation (40) and the constraint equation \(e_{0}^{2}+e_{1}^{2}=1\) can be solved for \(e_{0}\) and \(e_{1}\). The series expansion of \(e_{0}\) in terms of \(h\) up to third order is given by

$$ e_{0} = 1 - \frac{1}{8}\omega '{}^{2} h^{2} - \frac{1}{8} \frac{M_{x}}{I _{x}} \omega ' h^{3} + O \bigl(h^{4}\bigr) . $$
(41)

(The second solution for \(e_{0}\) has the constant part −1 and can be excluded, because \(e_{0}\) must tend to \(+1\) for \(h\to 0\) as we had \(e_{0}'=1\) for the old state.)

Finally, we are again interested in the angular velocity, given by Eq. (12), which is associated to the new state. By using Eqs. (37) and (38) we obtain

$$\begin{aligned} \omega =& 2 (-e_{1}\dot{e}_{0} + e_{0}\dot{e}_{1}) \\ =&-2e_{1} \biggl[-\frac{1}{2} \biggl(\omega ' + \frac{M_{x}}{I_{x}} h (1 - \gamma ) \biggr) e_{1} + h\gamma \bigl(1-e_{0}^{2} \bigr) \ddot{e}_{0} - h\gamma e_{0} e_{1} \ddot{e}_{1} \biggr] \\ &{}+2e_{0} \biggl[\frac{1}{2} \biggl(\omega ' + \frac{M_{x}}{I_{x}} h (1 - \gamma ) \biggr) e_{0} + h\gamma \bigl(1-e_{1}^{2} \bigr)\ddot{e} _{1} - h\gamma e_{0} e_{1} \ddot{e}_{0} \biggr]. \end{aligned}$$

With \(e_{0}^{2}+e_{1}^{2}=1\) this simplifies to

$$ \omega = \omega ' + \frac{M_{x}}{I_{x}} h (1-\gamma ) - h\gamma 2(e _{1} \ddot{e}_{0} - e_{0} \ddot{e}_{1}) $$

since some terms cancel, and by using Eq. (39) we end up with

$$ \omega = \omega ' + \frac{M_{x}}{I_{x}} h + \frac{M_{x}}{I_{x}} h \gamma \alpha (1-e_{0}) . $$
(42)

It can now be seen that our modified HHT method yields the physically exact solution \(\omega = \omega ' + h M_{x}/I_{x}\) if the damping parameter \(\alpha \) is zero. In this case, the numerical integrator conserves the angular momentum. Moreover, if the damping parameter \(\alpha \) is negative, the term

$$ \frac{M_{x}}{I_{x}} h \gamma \alpha (1-e_{0}) = \frac{M_{x}}{I_{x}} h \gamma \alpha \biggl( \frac{1}{8}\omega '{}^{2} h^{2} + \frac{1}{8}\frac{M _{x}}{I_{x}} \omega ' h^{3} + O\bigl(h^{4}\bigr) \biggr) $$

where Eq. (41) has been inserted for \(e_{0}\), introduces a small numerical damping, which is of the order \(h^{3}\) and proportional to \(\omega '{}^{2}\). Recall that the numerical damping of the classical HHT method which we have discussed in Sect. 5 is of the order \(h^{2}\) and the leading term is proportional to \(\omega '{}^{3}\). Hence, the numerical properties of the proposed new integrator are significantly better than the properties of the classical HHT method.

8 The local integration error of the modified HHT method

The objective of the present subsection is to make a general statement on the local integration error of the proposed integration method. In particular, we want to demonstrate that the error at the end of one integration step with respect to the time step size \(h\) has order 3 for the positions and order 2 for the velocities, as shown in [16] for the classical HHT method. To obtain a series expansion of the local integration error we compute the differences of the positions \(\mathbf{e}_{n+1}\) and the velocities \(\dot{\mathbf{e}} _{n+1}\) after an integration step and the Taylor series expansion

$$\begin{aligned} \tilde{\mathbf{e}}_{n+1} =& \mathbf{e}_{n} + h\dot{ \mathbf{e}}_{n}+\frac{h ^{2}}{2}\ddot{\mathbf{e}}_{n} + \frac{h^{3}}{6}\dddot{\mathbf{e}}_{n} + O \bigl(h^{4}\bigr) , \end{aligned}$$
(43)
$$\begin{aligned} \dot{\tilde{\mathbf{e}}}_{n+1} =& \dot{\mathbf{e}}_{n} + h \ddot{\mathbf{e}}_{n}+ \frac{h^{2}}{2}\dddot{ \mathbf{e}}_{n} + O\bigl(h ^{3}\bigr) . \end{aligned}$$
(44)

Therefore, the Newmark integration formula of Eq. (33) is rewritten in the equivalent form

$$\begin{aligned} \mathbf{e}_{n+1} =& \mathbf{e}_{n} + h\dot{ \mathbf{e}}_{n}+\frac{h ^{2}}{2}\ddot{\mathbf{e}}_{n} + h^{2}\beta \mathbf{x} , \end{aligned}$$
(45)
$$\begin{aligned} \ddot{\mathbf{e}}_{n+1} =& \ddot{\mathbf{e}}_{n} + \mathbf{x} , \end{aligned}$$
(46)

where the unknown \(\mathbf{x}\) represents the change in the acceleration from time \(t_{n}\) to \(t_{n+1}\). In a next step, also Eq. (34) is rewritten in terms of \(\mathbf{x}\) which is now much more complicated since \(\mathbf{x}\) enters also \(\mathbf{e}_{n+1}\) and the matrix \(\mathbf{L}_{n+1}\) via \(\mathbf{e} _{n+1}\) which has to be substituted from Eq. (45). However, since \(\mathbf{L}\) is a linear function of the Euler parameter vector \(\mathbf{e}\) due to Eq. (4), the matrix \(\mathbf{L}_{n+1}\) can be computed by simply inserting Eq. (45) in Eq. (4). For our purposes, it is sufficient to consider only the linear terms in \(h\) given by

$$ \mathbf{L}_{n+1} = \mathbf{L}_{n} + h \dot{ \mathbf{L}}_{n} + O\bigl(h^{2}\bigr). $$

After inserting in Eq. (32) we obtain the modified Newmark formula for \(\dot{\mathbf{e}}_{n+1}\) up to first order terms in \(h\) as

$$ \begin{aligned} \dot{\mathbf{e}}_{n+1} &= ( \mathbf{L}_{n} + h \dot{\mathbf{L}} _{n} )^{\mathsf{T}}\mathbf{L}_{n}\dot{\mathbf{e}}_{n} + h(1- \gamma ) \mathbf{L}_{n}^{\mathsf{T}}\mathbf{L}_{n} \ddot{\mathbf{e}} _{n} + h\gamma \mathbf{L}_{n}^{\mathsf{T}} \mathbf{L}_{n} (\ddot{\mathbf{e}} _{n}+\mathbf{x} ) + O \bigl(h^{2}\bigr) \\ &= \mathbf{L}_{n}^{\mathsf{T}}\mathbf{L}_{n} \dot{ \mathbf{e}}_{n} + h \bigl[\dot{\mathbf{L}}_{n}^{\mathsf{T}} \mathbf{L}_{n} \dot{\mathbf{e}}_{n} + \mathbf{L}_{n}^{\mathsf{T}}\mathbf{L}_{n} \ddot{ \mathbf{e}}_{n} + \gamma \mathbf{L}_{n}^{\mathsf{T}} \mathbf{L} _{n} \mathbf{x} \bigr] + O\bigl(h^{2}\bigr). \end{aligned} $$

By using the Euler parameter identities Eqs. (6) and (7) and assuming a perfectly consistent state at time \(t_{n}\), it can be shown (see Appendix A) that

$$ \mathbf{L}_{n}^{\mathsf{T}}\mathbf{L}_{n} \dot{ \mathbf{e}}_{n} = \dot{\mathbf{e}}_{n} \quad \text{and} \quad \dot{\mathbf{L}}_{n}^{ \mathsf{T}}\mathbf{L}_{n} \dot{\mathbf{e}}_{n} + \mathbf{L}_{n}^{ \mathsf{T}} \mathbf{L}_{n}\ddot{\mathbf{e}}_{n} = \ddot{\mathbf{e}} _{n}. $$

Hence, we end up with the simpler expression

$$ \dot{\mathbf{e}}_{n+1} = \dot{\mathbf{e}}_{n} + h \bigl[\ddot{\mathbf{e}} _{n} + \gamma \mathbf{L}_{n}^{\mathsf{T}} \mathbf{L}_{n} \mathbf{x} \bigr] + O\bigl(h^{2}\bigr) . $$
(47)

If we expand the acceleration increment in the form

$$ \mathbf{x}=\mathbf{x}_{0} + h\mathbf{x}_{1} + h^{2}\mathbf{x}_{2} + h ^{3} \mathbf{x}_{3} + \cdots $$
(48)

we can see that it is sufficient to determine only the term \(\mathbf{x}_{0}\) to obtain \(\mathbf{e}_{n+1}\) from Eq. (45) up to second order and \(\dot{\mathbf{e}} _{n+1}\) from Eq. (47) up to first order in \(h\) and, hence, to show that the position and velocity errors are of order \(h^{3}\) and \(h^{2}\), respectively.

The acceleration increment \(\mathbf{x}\) is obtained from inserting Eqs. (45), (46) and (47) in Eq. (20), where the Lagrange multiplier \(\lambda _{n+1} = \lambda _{n}+y\) is an additional unknown. The resulting equation for \(\mathbf{x}\) and \(y\) has the general form \(\mathbf{F}(\mathbf{x},y,h)=\textbf{0}\) if we consider the external moments \(\mathbf{m}_{n}\) and \(\mathbf{m}_{n+1}\) as known. Inserting Eq. (48) and a similar series expansion for the Lagrange multiplier increment

$$ y=y_{0} + h y_{1} + h^{2} y_{2} + h^{3} y_{3} + \cdots $$
(49)

yields

$$ \mathbf{F}\bigl(\mathbf{x}_{0} + h \mathbf{x}_{1} + h^{2}\mathbf{x}_{2} + h ^{3}\mathbf{x}_{3} + \cdots , y_{0} + h y_{1} + h^{2} y_{2} + h^{3} y _{3} + \cdots , h\bigr) = \textbf{0}. $$
(50)

Since this equation must also hold for \(h \to 0\), we may conclude that

$$ \mathbf{F}(\mathbf{x}_{0}, y_{0}, 0) = \textbf{0} $$
(51)

as one condition for the zero order terms \(\mathbf{x}_{0}\) and \(y_{0}\). This expression is obtained by setting \(h=0\) everywhere in Eq. (20), yielding

$$ \begin{aligned} \textbf{0} ={}& \mathbf{F}(\mathbf{x}_{0}, y_{0}, 0) \\ ={}& 4\mathbf{L}^{\mathsf{T}}_{n} \mathbf{J}\mathbf{L}_{n}( \ddot{\mathbf{e}}_{n}+\mathbf{x}_{0}) + (1+\alpha )8 \mathbf{L}_{n} ^{\mathsf{T}}\mathbf{L}_{n}\dot{ \mathbf{L}}_{n}^{\mathsf{T}} \mathbf{J}\mathbf{L}_{n} \dot{\mathbf{e}}_{n} -\alpha 8\mathbf{L}_{n} ^{\mathsf{T}}\mathbf{L}_{n}\dot{\mathbf{L}}_{n}^{\mathsf{T}} \mathbf{J}\mathbf{L}_{n}\dot{\mathbf{e}}_{n} \\ & + (1+\alpha )\mathbf{e}_{n}(\lambda _{n}+y_{0}) - \alpha \mathbf{e} _{n}\lambda _{n} - (1+\alpha )2 \mathbf{L}_{n}^{\mathsf{T}}\mathbf{m} _{n+1} + \alpha 2 \mathbf{L}_{n}^{\mathsf{T}}\mathbf{m}_{n} \\ ={}& 4\mathbf{L}^{\mathsf{T}}_{n} \mathbf{J}\mathbf{L}_{n} \mathbf{x} _{0} + (1+\alpha )\mathbf{e}_{n} y_{0} \\ & + 4\mathbf{L}^{\mathsf{T}}_{n} \mathbf{J}\mathbf{L}_{n} \ddot{\mathbf{e}} + 8\mathbf{L}_{n}^{\mathsf{T}} \mathbf{L}_{n} \dot{\mathbf{L}}_{n}^{\mathsf{T}} \mathbf{J}\mathbf{L}_{n} \dot{\mathbf{e}}_{n} + \mathbf{e}_{n} \lambda _{n} - (1+\alpha )2 \mathbf{L}_{n}^{\mathsf{T}}\mathbf{m}_{n+1} + \alpha 2 \mathbf{L}_{n} ^{\mathsf{T}}\mathbf{m}_{n} . \end{aligned} $$

Assuming that the old state at \(t_{n}\) satisfies the exact equations of motion given by Eq. (9) and that the external moment is continuous in time, i.e. \(\mathbf{m}_{n+1} = \mathbf{m}_{n} + O(h)\) the last line vanishes and we end up with

$$ 4\mathbf{L}^{\mathsf{T}}_{n} \mathbf{J} \mathbf{L}_{n} \mathbf{x}_{0} + (1+\alpha ) \mathbf{e}_{n} y_{0} = \textbf{0} $$
(52)

for \(\mathbf{x}_{0}\) and \(y_{0}\). The second equations which implicitly defines \(y_{0}\) results from the constraint equation \(C(\mathbf{e} _{n+1}) = \mathbf{e}_{n+1}^{\mathsf{T}} \mathbf{e}_{n+1} - 1 = 0\). Inserting Eq. (45) we obtain

$$ \begin{aligned} \mathbf{e}_{n+1}^{\mathsf{T}} \mathbf{e}_{n+1} - 1 ={}& \mathbf{e}_{n} ^{\mathsf{T}} \mathbf{e}_{n} + h^{2} \dot{\mathbf{e}}_{n}^{\mathsf{T}} \dot{\mathbf{e}}_{n} +\frac{1}{4}h^{4} \ddot{ \mathbf{e}}_{n}^{ \mathsf{T}}\ddot{\mathbf{e}}_{n} + h^{4}\beta ^{2} \mathbf{x}^{ \mathsf{T}}\mathbf{x} \\ & + 2 h \mathbf{e}_{n}^{\mathsf{T}} \dot{\mathbf{e}}_{n} + h^{2} \mathbf{e}_{n}^{\mathsf{T}}\ddot{ \mathbf{e}}_{n} + 2 h^{2}\beta \mathbf{e}_{n}^{\mathsf{T}} \mathbf{x} \\ & + h^{3} \dot{\mathbf{e}}_{n}^{\mathsf{T}} \ddot{ \mathbf{e}}_{n} + h ^{3} \beta \dot{\mathbf{e}}_{n}^{\mathsf{T}} \mathbf{x} \\ & + h^{4} \beta \ddot{\mathbf{e}}_{n}^{\mathsf{T}} \mathbf{x}- 1 = 0. \end{aligned} $$

Assuming also here that the old state at \(t_{n}\) satisfies the constraint equation and its derivatives

$$ \mathbf{e}_{n}^{\mathsf{T}} \mathbf{e}_{n} - 1 =0, \qquad \mathbf{e} _{n}^{\mathsf{T}} \dot{\mathbf{e}}_{n} = 0, \qquad \dot{\mathbf{e}} _{n}^{\mathsf{T}} \dot{ \mathbf{e}}_{n} + \mathbf{e}_{n}^{\mathsf{T}} \ddot{ \mathbf{e}}_{n} = 0, $$

exactly, the constraint equations reduces to

$$ h^{2} \bigl(2\beta \mathbf{e}_{n}^{\mathsf{T}} \mathbf{x} \bigr) + h ^{3} \bigl(\dot{\mathbf{e}}_{n}^{\mathsf{T}} \ddot{\mathbf{e}}_{n} + \beta \dot{\mathbf{e}}_{n}^{\mathsf{T}} \bigr) + h^{4} \biggl(\frac{1}{4} \ddot{ \mathbf{e}}_{n}^{\mathsf{T}}\ddot{\mathbf{e}}_{n} + \beta ^{2} \mathbf{x}^{\mathsf{T}}\mathbf{x}+ \beta \ddot{ \mathbf{e}}_{n}^{ \mathsf{T}} \mathbf{x} \biggr) = 0. $$

Using our series expansion Eq. (48), we obtain

$$ h^{2} \bigl(2\beta \mathbf{e}_{n}^{\mathsf{T}} \mathbf{x}_{0} \bigr) + O\bigl(h^{3}\bigr) = 0, $$

from which the additional equation

$$ 2\beta \mathbf{e}_{n}^{\mathsf{T}} \mathbf{x}_{0} = 0 $$
(53)

can be derived for \(\mathbf{x}_{0}\). Collecting Eqs. (52) and (53) in matrix notation yields

$$ \left ( \textstyle\begin{array}{c@{\quad }c} 4\mathbf{L}^{\mathsf{T}}_{n} \mathbf{J}\mathbf{L}_{n} & (1+\alpha ) \mathbf{e}_{n} \\ 2\beta \mathbf{e}_{n}^{\mathsf{T}} & 0 \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{c} \mathbf{x}_{0} \\ y_{0} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{c} 0 \\ 0 \end{array}\displaystyle \right ) $$
(54)

for the zero order terms \(\mathbf{x}_{0}\) and \(y_{0}\). Since the matrix on the left side is nonsingular, the solution is \(\mathbf{x}_{0}= \textbf{0}\) and \(y_{0} = 0\). Hence, the acceleration increment has the order \(\mathbf{x}= O(h)\) and from Eqs. (45) and (47) we see that

$$\begin{aligned} \mathbf{e}_{n+1} =& \mathbf{e}_{n} + h\dot{ \mathbf{e}}_{n}+\frac{h ^{2}}{2}\ddot{\mathbf{e}}_{n} + O\bigl(h^{3}\bigr) , \end{aligned}$$
(55)
$$\begin{aligned} \dot{\mathbf{e}}_{n+1} =& \dot{\mathbf{e}}_{n} + h \ddot{\mathbf{e}} _{n} + O\bigl(h^{2}\bigr) . \end{aligned}$$
(56)

Finally, the differences between one time step of the modified HHT method in Eqs. (43) and (44), and the Taylor series given by Eqs. (55) and (56) is described by

$$ \mathbf{e}_{n+1} - \tilde{\mathbf{e}}_{n+1} = O \bigl(h^{3}\bigr) \quad \text{and}\quad \dot{\mathbf{e}}_{n+1} - \dot{\tilde{\mathbf{e}}}_{n+1} = O\bigl(h^{2}\bigr). $$

We note that it has been shown for general Lie group integrators that the order of convergence can even be three for positions and two for velocities [2]. However, in our context, we aim for an easy to implement integrator which has at least equal convergence properties as the classical HHT method but avoids the artificial damping effect which occurs when Euler parameters are used. As the analysis of a simple rotation in Sect. 7 demonstrates, the order of the integration error may even be higher if the damping parameter \(\alpha \) is zero. Nevertheless, in practice, the introduction of numerical damping is unavoidable in complex industrial examples because otherwise the integrator usually fails to converge.

9 The use of the modified HHT method in complex multibody systems

In multibody systems, Eq. (9) is embedded in the differential algebraic equations of motion with the general form

$$\begin{aligned} \mathbf{M}(\mathbf{q})\ddot{\mathbf{q}} + \mathbf{C}_{\mathbf{q}}^{ \mathsf{T}}( \mathbf{q})\lambda =& \mathbf{Q}(\dot{\mathbf{q}}, \mathbf{q},t), \end{aligned}$$
(57)
$$\begin{aligned} \mathbf{C}(\mathbf{q},t) =&0 , \end{aligned}$$
(58)

where \(\mathbf{M}(\mathbf{q})\) is the mass matrix, \(\mathbf{C}( \mathbf{q},t)\) the vector of constraint equations and \(\mathbf{C}_{ \mathbf{q}}^{\mathsf{T}}(\mathbf{q})\) its Jacobian with \(\lambda \) as the vector of Lagrange multipliers. \(\mathbf{Q}(\dot{\mathbf{q}}, \mathbf{q},t)\) denotes the vector of gyroscopic and generalized forces. In the globally redundant description, the vector \(\mathbf{q}\in \mathbb{R}^{N}\) contains translational, rotational and flexible components for every body of the system. The Euler parameters \(\mathbf{e}_{i}\) of body \(i\) are components of \(\mathbf{q}\) representing its rotational degrees of freedom.

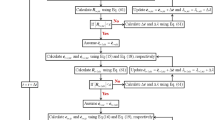
In the classical HHT method, the equations of motions are discretized by the formulas

$$\begin{aligned} \mathbf{q}_{n+1} =&\mathbf{q}_{n}+h \dot{\mathbf{q}}_{n}+ \frac{h^{2}}{2}\bigl[(1-2\beta )\ddot{ \mathbf{q}}_{n}+2\beta \ddot{\mathbf{q}}_{n+1}\bigr] , \end{aligned}$$
(59)
$$\begin{aligned} \dot{\mathbf{q}}_{n+1} =&\dot{\mathbf{q}}_{n}+h \bigl[(1-\gamma ) \ddot{\mathbf{q}}_{n}+\gamma \ddot{ \mathbf{q}}_{n+1}\bigr] . \end{aligned}$$
(60)

When using the modified HHT method, the components of \(\mathbf{q}\) with the Euler parameters have to be replaced by Eqs. (33) and (34) whereas the remaining components of \(\mathbf{q}\) can still be discretized with Eqs. (59) and (60). Moreover, in the HHT algorithm, the acceleration terms in the equations of motion are evaluated at \(t_{n+1}\) and all other terms are weighted in the interval \([t_{n},t _{n+1}]\) by setting

$$ (\mathbf{M}\ddot{\mathbf{q}})_{n+1} + (1 + \alpha ) \bigl( \mathbf{C}_{ \mathbf{q}}^{\mathsf{T}}\lambda -\mathbf{Q} \bigr)_{n+1} - \alpha \bigl( \mathbf{C}_{\mathbf{q}}^{\mathsf{T}} \lambda -\mathbf{Q}\bigr)_{n} = \mathbf{0} $$
(61)

with \(\alpha \in [-\frac{1}{3},0]\). Here, all terms with subscript \((\dots )_{n+1}\) are evaluated at time \(t_{n+1}\) and terms with subscript \((\dots )_{n}\) are evaluated at time \(t_{n}\). After expressing \(\mathbf{q}_{n+1}\) and \(\dot{\mathbf{q}}_{n+1}\) by Eqs. (59) and (60), and by Eqs. (33) and (34) for Euler parameters, respectively, the following equations have to be solved for \(\ddot{\mathbf{q}}_{n+1}\) and \(\lambda \):

$$\begin{aligned} \frac{1}{1+\alpha }(\mathbf{M}\ddot{\mathbf{q}})_{n+1} + \bigl( \mathbf{C} _{\mathbf{q}}^{\mathsf{T}}\lambda -\mathbf{Q} \bigr)_{n+1} - \frac{\alpha }{1+ \alpha }\bigl(\mathbf{C}_{\mathbf{q}}^{\mathsf{T}} \lambda -\mathbf{Q}\bigr)_{n} =: \mathbf{R}_{n+1}, \end{aligned}$$
(62)
$$\begin{aligned} \mathbf{C}(\mathbf{q}_{n+1},t_{n+1}) =: \mathbf{C}_{n+1} . \end{aligned}$$
(63)

For that purpose, a Newton–Raphson scheme is commonly applied. The increments \(\Delta \ddot{\mathbf{q}}^{(k)}\) and \(\Delta \lambda ^{(k)}\) for an update step \(\ddot{\mathbf{q}}_{n+1}^{(k+1)} = \ddot{\mathbf{q}}_{n+1}^{(k)} + \Delta \ddot{\mathbf{q}}^{(k)}\), \(\lambda ^{(k+1)} = \lambda ^{(k)} + \Delta \lambda ^{(k)}\) are obtained from the linearization of the residua \(\mathbf{R}_{n+1}\) and \(\mathbf{C}_{n+1}\) with respect to \(\ddot{\mathbf{q}}_{n+1}\) and \(\lambda \) given by

$$ \mathbf{J}_{n+1}^{(k)} \left ( \textstyle\begin{array}{c} \Delta \ddot{\mathbf{q}}^{(k)} \\ \Delta \lambda ^{(k)} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{c} -\mathbf{R}_{n+1}^{(k)} \\ -\mathbf{C}_{n+1}^{(k)} \end{array}\displaystyle \right ) . $$
(64)

The Jacobian matrix \(\mathbf{J}_{n+1}^{(k)}\) computes as

$$ \mathbf{J}_{n+1}^{(k)} = \left ( \textstyle\begin{array}{c@{\quad }c} \frac{1}{1+\alpha } \mathbf{M}+ ( \frac{1}{1+\alpha } ( \mathbf{M}\ddot{\mathbf{q}})_{\mathbf{q}}+ (\mathbf{C}_{\mathbf{q}} ^{\mathsf{T}}\lambda )_{\mathbf{q}}- \mathbf{Q}_{\mathbf{q}} ) \mathbf{J}_{0} - \mathbf{Q}_{\dot{\mathbf{q}}}\mathbf{J}_{1} & \mathbf{C}_{\mathbf{q}}^{\mathsf{T}} \\ \mathbf{C}_{\mathbf{q}}\mathbf{J}_{0} & \mathbf{0} \end{array}\displaystyle \right )_{n+1}^{(k)} $$
(65)

where \((\,\,)_{\mathbf{q}}= \partial /\partial \mathbf{q}\) and \((\,\,)_{\dot{\mathbf{q}}} = \partial /\partial \dot{\mathbf{q}}\). The two matrices \(\mathbf{J}_{0,n+1}\) and \(\mathbf{J}_{1,n+1}\) contain the derivatives of \(\mathbf{q}_{n+1}\) and \(\dot{\mathbf{q}}_{n+1}\) with respect to \(\ddot{\mathbf{q}}_{n+1}\) according to Eqs. (59) and (60), and to Eqs. (33) and (34) for Euler parameters. Since Eqs. (59) and (33) are equivalent, we obtain the generally valid formula

$$ \mathbf{J}_{0,n+1} = \frac{\partial \mathbf{q}_{n+1}}{\partial \ddot{\mathbf{q}}_{n+1}} = h^{2} \beta \mathbf{I}_{N} $$
(66)

where \(\mathbf{I}_{N}\) is the \(N \times N\) unity matrix. However, the computation of the Jacobian matrix

$$ \mathbf{J}_{1,n+1} = \frac{\partial \dot{\mathbf{q}}_{n+1}}{\partial \ddot{\mathbf{q}}_{n+1}} $$
(67)

is more sophisticated now. Let the vector of generalized coordinates be defined by

$$ \mathbf{q}^{\mathsf{T}} = \bigl(\mathbf{r}_{1}^{\mathsf{T}}, \mathbf{e} _{1}^{\mathsf{T}}, \mathbf{f}_{1}^{\mathsf{T}}, \mathbf{r}_{2}^{ \mathsf{T}}, \mathbf{e}_{2}^{\mathsf{T}}, \mathbf{f}_{2}^{\mathsf{T}}, \dots \bigr) $$

where \(\mathbf{r}_{i} \in \mathbb{R}^{3}\) denote the translational degrees of freedom, e.g. the reference point coordinates of body \(i\), \(\mathbf{e}_{i}\) its Euler parameters describing the axis orientation of the floating reference frame and \(\mathbf{f}_{i}\in \mathbb{R}^{N _{f,i}}\) its flexible degrees of freedom. For integrating \(\mathbf{r} _{i}\) and \(\mathbf{f}_{i}\) Eq. (60) can be applied, whereas for \(\mathbf{e}_{i}\) Eq. (34) is used. Hence, \(\mathbf{J}_{1,n+1}\) is a block diagonal matrix of the form

$$ \mathbf{J}_{1,n+1} = \text{diag} \biggl( h\gamma \mathbf{I}_{3}, \frac{\partial \dot{\mathbf{e}}_{n+1}}{\partial \ddot{\mathbf{e}}_{n+1}}\bigg\vert _{1}, h\gamma \mathbf{I}_{N_{f,1}}, h\gamma \mathbf{I}_{3}, \frac{\partial \dot{\mathbf{e}} _{n+1}}{\partial \ddot{\mathbf{e}}_{n+1}}\bigg\vert _{2}, h\gamma \mathbf{I}_{N_{f,2}}, \dots \biggr) $$
(68)

where \(\mathbf{I}_{k}\) always denotes the \(k\)-dimensional unity matrix. For computing the derivatives \(\partial \dot{\mathbf{e}}_{n+1}/\partial \ddot{\mathbf{e}}_{n+1}\), Eq. (33) has to be first inserted in Eq. (34). The resulting formula reads

$$ \frac{\partial \dot{\mathbf{e}}_{n+1}}{\partial \ddot{\mathbf{e}}_{n+1}}= h^{2}\beta \hat{\mathbf{w}} + h\gamma \bigl(\mathbf{I}_{4}- \mathbf{e}_{n+1} \mathbf{e}_{n+1}^{\mathsf{T}} \bigr)- h^{3}\gamma \beta \bigl(\mathbf{e}_{n+1}\ddot{\mathbf{e}}_{n+1}^{\mathsf{T}}+ \bigl(\mathbf{e}_{n+1}^{\mathsf{T}}\ddot{\mathbf{e}}_{n+1} \bigr) \mathbf{I}_{4} \bigr) $$
(69)

where the skew-symmetric matrix

$$ \hat{\mathbf{w}} = \left ( \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 & -w_{x} & -w_{y} & -w_{z} \\ w_{x} & 0 & w_{z} & -w_{y} \\ w_{y} & -w_{z} & 0 & w_{x} \\ w_{z} & w_{y} & -w_{x} & 0 \end{array}\displaystyle \right ) $$
(70)

is generated from the components of the vector \(\mathbf{w}=\mathbf{L} _{n}\dot{\mathbf{e}}_{n} + h(1-\gamma )\mathbf{L}_{n} \ddot{\mathbf{e}}_{n}\) which is given by the old state at \(t_{n}\) and fixed during the Newton–Raphson iteration. The derivation of Eq. (69) is included in Appendix B. Note that if the classical Newmark formula Eq. (60) is applied also to the Euler parameters, the Jacobian matrix from Eq. (67) is simply given by \(\mathbf{J}_{1,n+1}=h\gamma \mathbf{I}_{N}\). However, the additional computational effort for the assembly of \(\mathbf{J} _{1,n+1}\) does not lead to an increase of the overall computational time. In all our numerical examples we even observed rather lower computational times as with the classical Newmark formula which can be explained by the faster convergence of the Newton–Raphson process.

10 Numerical example

The software uses Euler parameters for the description of the rotational motions and can utilize the HHT method both in the classical and modified form presented in this paper.

10.1 Heavy top

As a first numerical example we consider the heavy top (cf. Brüls and Cardona [8]), which has found much interest in mechanics and serves as a benchmark problem for our modified HHT method. Figure 1 shows the schematics of the heavy top in the three dimensional space. The mass is \(m=15.0\), the inertia tensor is \(\mathbf{J}=\text{diag}(0.234375,0.46875,0.234275)\) and the location of the center of mass defined in the body coordinate system is \(\vec{x}_{cm}=(0,1,0)^{\mathsf{T}}\). The gravitational field with fixed acceleration vector is given by \(\vec{g}=(0,0,-9.81)^{\mathsf{T}}\). The initial angular velocity at \(t=0\) is set to \(\vec{\omega }=(0,150,-4.61538)^{ \mathsf{T}}\) and all other initial conditions are supposed to be consistent with the initial angular velocities. For the heavy top, the convergence behavior of the HHT method with the modified Newmark formulas is studied numerically. For this study the damping parameter \(\alpha =-0.2\). In Fig. 2 the asymptotic behavior of the global error in the three local angular velocity components for \(h\rightarrow 0\) is visualized in terms of the integrated error

$$ e_{\omega } := \sum_{i=1}^{3} \int _{0}^{1}\text{abs}\bigl(\omega _{i}(t) - \omega _{i,\text{ref}}(t)\bigr)\,dt. $$

In that case the numerical solution for \(h = 1.0 \times 10^{-3}\), \(h = 5.0 \times 10^{-4}\), \(h = 1.0 \times 10^{-4}\), \(h = 5.0 \times 10^{-5}\) and \(h = 1.0 \times 10^{-5}\) are compared to the reference solution, which is computed numerically with the very small time step size \(h = 1.0 \times 10^{-6}\) and a damping parameter \(\alpha =-0.1\). In double logarithmic scale, the plot of the global error in all three components of the angular velocity are straight lines of the slope \(+1\). This numerical test indicates second order convergence for the angular velocity. Figure 3 shows the velocity coordinates of the center of mass defined in the global coordinate system over the time, while in Fig. 4 the angular velocity about the x-axis in the body fixed coordinate system is visualized. In order to proof the accuracy of the modified HHT method, the energy of the heavy top example is plotted over the time; see Fig. 5. It shows the influence of the damping parameter \(\alpha \) on the total energy dissipation.

Fig. 1
figure 1

Benchmark problem Heavy top

Full size image
Fig. 2
figure 2

Global error of HHT over the step size \(h\) for \(t\in [0,1]\)

Full size image
Fig. 3
figure 3

Velocity coordinates of the center of mass

Full size image
Fig. 4
figure 4

Body fixed angular velocity about x-axis

Full size image
Fig. 5
figure 5

Energy conservation with the step size \(h=10^{-5}\) for \(t\in [0,10]\)

Full size image

10.2 V8—crank drive

As a second numerical example we consider a V8 crank drive which was modeled in our multibody simulation software FreeDyn. The system is composed of 17 rigid bodies, the crank shaft, 8 conrods and 8 pistons. Each rigid body has three translational degrees of freedom for the description of the position in space and for the description of the orientation Euler parameter have been used. The bodies are connected by algebraic constraint equations such that we end up with a set of differential algebraic equations with 119 differential equations and 118 constraint equations. The mechanical system is shown in Fig. 6. The crank drive is accelerated about the x-axis by a torque on the crank shaft depicted in Fig. 7.

Fig. 6
figure 6

V8 crank drive

Full size image
Fig. 7
figure 7

Torque on the crank shaft about the x-axis

Full size image

Figure 8 shows the angular velocity of the crank shaft computed with both methods. The damping parameter has been set to \(\alpha =-0.3\) and \(h = 1.0 \times 10^{-4}\) has been chosen for the time step size. It can be seen clearly that the classical integrator does not yield a reasonable result for this example since the angular velocity does not increase after some time due to the numerical damping, which is not in accordance with the physical laws of motion. However, the modified HHT method accelerates the crank shaft nearly correct.

Fig. 8
figure 8

Angular velocity about x-axis with step size \(h = 1.0 \times 10^{-4}\)

Full size image

For the present example, the convergence behavior of the HHT method with the modified Newmark formulas is studied numerically. For this study the damping parameter \(\alpha =-0.3\). In Fig. 9 the asymptotic behavior of the global error in the angular velocity of the crankshaft for \(h\rightarrow 0\) is visualized in terms of the integrated error

$$ e_{\omega } := \int _{0}^{9}\text{abs}\bigl(\omega (t) - \omega _{\text{ref}}(t)\bigr) \,dt. $$

Here the numerical solution for \(h = 1.0 \times 10^{-3}\), \(h = 5.0 \times 10^{-4}\), \(h = 1.0 \times 10^{-4}\) and \(h = 5.0 \times 10^{-5}\) are compared to the reference solution. The reference solution has been computed numerically with a very small time step size \(h = 1.0 \times 10^{-5}\) and a damping parameter \(\alpha =-0.1\). In double logarithmic scale, the plot of the global error in the angular velocity are straight lines of the slope \(+1\). These numerical test results indicate second order convergence for the angular velocity.

Fig. 9
figure 9

Global error of HHT over the step size \(h\) for \(t\in [0,9]\)

Full size image

Moreover, the influence of the damping parameter \(\alpha \) on the solution has been analyzed. Therefore, the present example has been solved with the HHT method with the modified Newmark formulas and a time step size \(h = 1.0 \times 10^{-4}\). In Fig. 10 the asymptotic behavior of the global error in the angular velocity of the crankshaft for \(\alpha \rightarrow 0\) is visualized. It can be seen that the error is a function of the damping parameter \(\alpha \) to the power of 2.

Fig. 10
figure 10

Global error of HHT over the damping parameter \(\alpha \) for \(t\in [0,15]\) and \(h = 1.0 \times 10^{-4}\)

Full size image