Three-dimensional, one-point collision with friction

Abstract

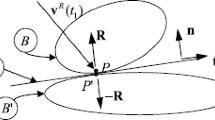
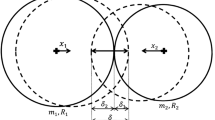
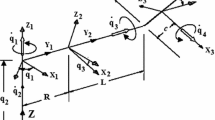
This paper deals with one-point collision with friction in three-dimensional, simple non-holonomic multibody systems. With Keller’s idea regarding the normal impulse as an independent variable during collision, and with Coulomb’s friction law, the system equations of motion reduce to five, coupled, nonlinear, first order differential equations. These equations have a singular point if sticking is reached, and their solution is ‘navigated’ through this singularity in a way leading to either sticking or sliding renewal in a uniquely defined direction. Here, two solutions are presented in connection with Newton’s, Poisson’s and Stronge’s classical collision hypotheses. One is based on numerical integration of the five equations. The other, significantly faster, replaces the integration by a recursive summation. In connection with a two-sled collision problem, close agreement between the two solutions is obtained with a few summation steps.

Appendices

Appendix A

The kinetic energy of a system S of ν particles described in Sect. 2 is given by $E = 1/2\sum_{i = 1}^{\nu} m_{i}(\mathbf {v}^{P_{i}} )^{2}$, a positive quantity which can be cast into the form

$$ E = - 1/2\sum_{r = 1}^{p} \sum_{s = 1}^{p} m_{rs}u_{r}u_{s} = 1/2\mathbf {u}( -\mathbf {M})\mathbf {u}^{T} > 0;\quad \mathbf {u}\hat{ = }|u_{1},\ldots,u_{p}|$$

(63)

where $m_{rs}\hat{ =} - \sum_{i = 1}^{\nu} m_{i} \mathbf {v}_{r}^{P_{i}} \cdot \mathbf {v}_{s}^{P_{i}}$, if $\mathbf {v}_{t}^{P_{i}} = 0$, i=1,…,ν (see (2)), rendering the mass matrix −M symmetric and positive definite. Now, the coefficient matrix $\mathfrak{M}$ of (23)–(25) is also positive definite. To show this, note that $\mathfrak{M}$ can be written

$$ \mathfrak{M} = \mathbf {V}\bigl( - \mathbf {M}^{ - 1}\bigr)\mathbf {V}^{T}$$

(64)

where V is 3×p matrix appearing in (14). Because −M hence −M ⁻¹ are positive definite matrices, one can write ([32], p. 109)

$$ - \mathbf {M}^{ - 1} = \mathbf {A}\mathbf {A}^{T} = \mathbf {A}^{T}\mathbf {A}.$$

(65)

Thus,

$$ \mathfrak{M} = \mathbf {V}\mathbf {A}\mathbf {A}^{T}\mathbf {V}^{T} = \mathbf {B}\mathbf {B}^{T};\quad \mathbf {B}= \mathbf {V}\mathbf {A}$$

(66)

and, since det(BB ^T)=detBdetB ^T=(detB)²>0, then $\det\mathfrak{M}= \det(\mathbf {B}\mathbf {B}^{T}) > 0$, where

$$ \det\mathfrak{M} = m_{nn}m_{ss}m_{tt} -\bigl(m_{nn}m_{ts}^{2} +m_{tt}m_{ns}^{2} + m_{ss}m_{nt}^{2}\bigr) + 2m_{nt}m_{ns}m_{ts} > 0.$$

(67)

By the same token, the removal of the first, second or third row of V reduces V(−M ⁻¹)V ^T to 2×2 diagonal submatrices of $\mathfrak{M}$, obtained by the removal of the first, second or third row-and-column of $\mathfrak{M}$, respectively. As with the 3×3 case, these submatrices have positive determinants, namely

$$ m_{nn}m_{tt} - m_{nt}^{2} > 0,\quad m_{nn}m_{ss} - m_{ns}^{2} > 0,\quad m_{tt}m_{ss} - m_{ts}^{2} > 0.$$

(68)

The removal of any two of the rows of V reduces V(−M ⁻¹)V ^T to one of the diagonal elements of $\mathfrak{M}$, positive numbers defined in the first, third and last of (15). Thus, the principal submatrices of $\mathfrak{M}$ are all positive, hence $\mathfrak{M}$ is positive definite ([32], p. 250).

Appendix B

If g(μ,ϕ)=0 and h(μ,ϕ)=0 (see (44)), then also μg(μ,ϕ)=0 and μh(μ,ϕ)=0; and these equations become, if the substitutions u=μcϕ and v=μsϕ are used,

$$ \mu g\mathop{ =} \limits_{(32)} - m_{tt}u^{2} - 2m_{ts}uv - m_{ss}v^{2}+ m_{nt}u + m_{ns}v = 0,$$

(69)

$$ \mu h\mathop{ =} \limits_{(33)} = m_{ts}u^{2} - 2\bigl[(m_{tt} - m_{ss})/2\bigr]uv- m_{ts}v^{2} - m_{ns}u + m_{nt}v = 0,$$

(70)

even and odd functions, respectively of v,m _ns and m _ts (μg(v,m _ns ,m _ts )=μg(−v,−m _ns ,−m _ts )=0 and μh(v,m _ns ,m _ts )=−μh(−v,−m _ns ,−m _ts )=0). The coordinate transformation |u′v′|=|uv|T, where the columns of T are the eigenvectors of the coefficient matrix g=|m _tt m _ts ; m _ts m _ss |, brings (69) into the form λ ₁ u′²+λ ₂ v′²+( )u′+( )v′=0, where λ ₁ and λ ₂ are the eigenvalues of g ([32], p. 255) given by

$$ \lambda_{1,2} = \bigl\{ (m_{tt} + m_{ss}) \pm \bigl[(m_{tt} + m_{ss})^{2} -4(m_{tt}m_{ss} - m_{ts}^{2})\bigr]^{1/2}\bigr\} /2.$$

(71)

Here λ ₁>0 and λ ₂>0 (the expression under the root is always positive and smaller than m _tt +m _ss ), therefore (69) represents an ellipse passing through the origin, as illustrated in Fig. 4 for the example of Sect. 5. Similarly for (70), the eigenvalues of the coefficient matrix h=|m _ts −(m _tt −m _ss )/2; −(m _tt −m _ss )/2−m _ts | are

$$ \lambda_{1,2} = \pm\bigl\{ m_{ts}^{2} +\bigl[(m_{tt} - m_{ss})/2\bigr]^{2}\bigr\} ^{1/2},$$

(72)

and, since λ ₁>0 and λ ₂=−λ ₁, (70) represents a hyperbola with orthogonal asymptotes parallel to the lines u′=±v′. Its branches are called ‘remote’ and ‘near’, the latter passing through the origin (Fig. 4). The normalized (unit) eigenvectors of g and h are Sines and Cosines of ϕ _e and ϕ _h , uniquely determined angles describing the orientation of the major axes of the ellipse and the hyperbola with respect to the u−v axes. ϕ _e and ϕ _h satisfy the relations

$$ t(2\phi_{e}) = 2m_{ts}/(m_{tt} - m_{ss}),\quad t(2\phi_{h}) = - 1/2(m_{tt} -m_{ss})/m_{ts},$$

(73)

so that the angle between the major axes of the ellipse and the hyperbola is π/4 (see Fig 4). Moreover, the ellipse and the hyperbola intersect at the origin u=v(=μ)=0, where they are perpendicular, i.e.,

$$ g(\mu,\phi)|_{\mu= 0} = 0 \quad\Rightarrow\quad t\phi= -m_{nt}/m_{ns}; h(\mu,\phi)|_{\mu= 0} = 0\quad \Rightarrow\quad t\phi = m_{ns}/m_{nt};$$

(74)

and at point (μ _c ,ϕ _c ) described by (43) as a unique solution of (44) (or (69) and (70)), hence lie on the near branch of the hyperbola (so that the remote branch does not intersect the ellipse). Note that point (0,0) is not a solution of (44), for g(0,0)=m _nt ≠h(0,0)=m _ns (see (32) and (33)). Now g(μ,ϕ) can be written

$$ g(\mu,\phi) = m_{nt}c\phi+ m_{ns}s\phi+ \mu \bigl[ - |c\phi s\phi \|m_{tt} m_{ts};m_{ts} m_{ss}\|c\phi s\phi|^{T}\bigr].$$

(75)

The expression multiplying μ comprises a negative number (Appendix A, (68)). Consequently, if l is a line passing through the origin and point (μ _e ,ϕ _e ) on the ellipse (g(μ _e ,ϕ _e )=0), then the (cylindrical) coordinates μ and ϕ _e of points of l satisfy either g(μ,ϕ _e )>0 or g(μ,ϕ _e )<0, depending on whether the indicated point is inside (μ<μ _e ) or outside (μ>μ _e ) the ellipse. If a circle of radius μ is drawn with its center at the origin, then the orientation angles of lines passing through the origin and each of the intersection points of the circle with the hyperbola (two or four), are solutions of h(μ,ϕ)=0. If outside the ellipse, these points satisfy g(μ,ϕ)<0 (e.g., Points A and B in Fig. 4). However, if μ<μ _c , then one, and only one of these points, namely $(\mu,\hat{\phi} )$, lies within the ellipse (e.g., Points C in Fig. 4); and, because $g(\mu,\hat{\phi} ) > 0$, it accommodates sliding renewal in direction $\hat{\phi}$ (Sect. 3.3). Points B accommodate angle $\bar{\phi}$ (Sect. 3.2) and Point D accommodates μ _c and ϕ _c ((43)).

Fig. 4

The ellipse and the hyperbola for the example of Sect. 5, with circular segments designating μ=0.6, 1.1, 1.6 and μ _c =1.21

Appendix C

In 2D systems

• 1. m _ns =m _ts =m _ss =0, hence c _n =c _t =c _s =0 (see (41a)–(41c)); and μ _c and ϕ _c (43) become undefined. With ϕ≡0 and dϕ/dI _n =0 (34a)–(34e) remain intact.

• 2. Equations (25)–(27) reduce to dv _n =Δ/m _tt dI _n , dI _t =−m _nt /Δ, dI _s =0 where $\Delta\hat{ =} m_{nn}m_{tt} -m_{nt}^{2}$, hence (45a)–(45e) become dϕ/dI _n =0, ds/dI _n =0, dv _n /dI _n =Δ/m _tt , dI _t /dI _n =−m _nt /m _tt , dI _s /dI _n =0.

• 3. The solution of h(μ,ϕ)=0, g(μ,ϕ)>0 is $\hat{\phi} =\pi$, leaving (46a)–(46e) intact.

The procedure of Sect. 4 can be applied to 2D systems if modified accordingly.