1 Introduction

Functionally graded materials (FGMs) are multiphase inhomogeneous materials whose mechanical properties vary gradually and continuously with location within the material. In recent years, FGMs have been widely used in many engineering and technological systems, such as tribology, biomechanics, automotive engineering, and thermal barriers. They are usually used as coatings or interfacial zones and thus improve the surface properties, suppress the localized high stresses, and provide prevention against unfavorable thermal and chemical effects.

A great many efforts have been devoted to investigating the contact problems of FGMs. The two-dimensional contact problems of an FG isotropic half plane are investigated by Giannakopoulos and Pallot (2000), Vasu and Bhandakkar (2018) and Peng et al. (2019) using Fourier integral transform technique. Frictional and frictionless plane strain contact problems of an FG coated isotropic half plane are studied by Guler and Erdogan (2007), Ke and Wang (2007), Choi and Paulino (2008) and Attia and El-Shafei (2019). Sliding plane strain contact problem of a laterally graded FG orthotropic half plane (Arslan 2017), an FG orthotropic coated half plane (Alinia et al. 2018) and an FG orthotropic coated isotropic layer (Yilmaz et al. 2019) are examined using Fourier integral transform technique when the system is pressed by the rigid flat or cylindrical punches. Axisymmetric contact problems of an FG half plane or FG coated half plane are investigated by Giannakopoulos and Suresh (1997), Aizikovich et al. (2002), Vasiliev et al. (2014) and Volkov et al. (2019) using Hankel transform technique. Yaylacı et al. (2022) and Yaylacı et al. (2023) studied the contact problem of an FG layer using both analytical and Finite Element Method. Vibration and buckling of FG beams using analytical, finite element, and artificial neural network methods is examined by Turan et al. (2023) and Yaylacı et al. (2023).

Among contact problems, the moving contact problem, in which the motion of the punch at constant velocity is analyzed, has an important place. If the relative velocity of one of the contacting surfaces with respect to the other is small enough, the dynamic character of the phenomenon can be neglected. However, in practice, there are cases where the velocity of one body relative to the other is so large that the dynamic character of the problem must be taken into account (Galin 2008). Frictional moving contact problem of an isotropic FGM coated half plane (Balci and Dag 2019) and orthotropic FG coated isotropic layer (Çömez 2022) are examined analytically, using Fourier integral transform technique. Çömez (2015), Balci and Dag (2018) and Balci and Dag (2018) examined the moving contact problem in the framework of linear elasticity theory. The rigid punch slides over the coating with a constant subsonic velocity.

If a layer whose body force is neglected is pressed against another layer or half-plane to which it is not bonded, the contact zone remains in a finite area and this kind of contact is referred as a receding contact. El-Borgi et al. (2014), El-Borgi et al. (2021), Cao et al. (2021) and Öner et al. (2022) examined the two-dimensional receding contact problems of an FG layer resting on a homogeneous half plane using integral transform technique. Öner (2021) studied the frictionless receding contact problem of an orthotropic coating/isotropic substrate system.

Since inertia effect has been neglected in the studies mentioned above so far, they are static contact problems except for moving contact. On the other hand, in moving contact problems, the external loads are constant, that is, they do not depend on time. In mechanical engineering, geomechanics and earthquake engineering the coated systems are often subjected to the dynamic forces that may lead to contact damage (Keawsawasvong and Senjuntichai 2019). Therefore, many researchers have focused on studying the dynamic responses of contacting systems. Karasudhi et al. (1968) examined the vibration of a rigid rectangular plate on the surface of an unloaded half plane. Forced oscillation of a rigid rectangular footing welded to the half plane is studied by Luco and Westmann (1972) and Luco et al. (1974) using the theory of the singular integral equation and finite element method, respectively. Vertical, horizontal, rocking and coupled compliances were examined for small frequency parameter. This study is extended to the large range of the frequency parameter without making an a priori assumption concerning the contact stresses by Hryniewicz (1981). Two-dimensional dynamic contact problem between a half plane and a rigid wedge-shaped or parabolic punch is investigated by Aboudi (1977). The dynamic response of a rigid rectangular footings lying on a layered anisotropic soil is presented by Gazetas (1981), Lin et al. (2013) and Han et al. (2015). Dynamic response of a rigid strip footing on the surface of viscoelastic soils under vertical loading is examined by Israil and Ahmad (1989) using boundary element method. Rajapakse and Senjuntichai (1995) and Senjuntichai et al. (2018) investigated the dynamic response of a multi-layered poroelastic medium under time-harmonic loads and fluid sources using Fourier transform and stiffness matrix method. Naghieh et al. (1997) investigated the contact mechanics of a viscoelastic layer bonded to a rigid substrate and indented by a frictionless rigid punch.

Dynamic contact problem on vertical motions of an absolutely rigid body on an elastic half-space is examined by Argatov (2007) and Argatov (2009). Copetti and Fernández (2014) studied the one-dimensional dynamic contact problem of a thermoviscoelastic nonlinear rod. Fernández and Santamarina (2015) investigated a dynamic contact problem between a viscoelastic body and a deformable obstacle. Sofonea (1997) investigated a problem of unilateral contact between an elastic viscoplastic body and a rigid frictionless foundation.

The dynamic response of a transversely isotropic layered half-space under surface loads is considered by Eskandari-Ghadi et al. (2008) using Fourier expansions and Hankel transforms. The dynamic response of a rigid circular and rectangular footing resting on saturated soil are investigated by Kassir et al. (1989) and Ma et al. (2009), respectively. Using boundary element method, vertical and rocking compliances were calculated for rigid foundations of arbitrary shape lying on a half plane (Shahi and Noorzad 2011). Ai et al. (2017) and Ai and Ye (2022) investigated the vertical and rocking vibration of a flexible or rigid footing on the surface of layered transversely isotropic half-space using analytical layer element method. Dynamic response of a homogeneous elastic or viscoelastic coated half-plane indented by harmonic Hertz load or rigid flat punch that transmits harmonic vertical load is studied by Wang et al. (2020) and Wang et al. (2023) using Helmholtz functions and Fourier transform. Vertical and horizontal vibrations of a rigid rectangular footing resting on the surface of a viscoelastic half-plane are investigated by Zheng et al. (2020) and Zheng et al. (2021) using the Fourier transform, respectively. Lyu et al. (2022) studied the dynamic response of FG coated half plane indented by a rigid cylindrical punch when the materials are elastic. Recently, Çömez (2022) studied the dynamic response of a viscoelastic orthotropic coated half plane indented by a rigid flat punch, analytically.

Although the dynamic contact analysis of homogeneous elastic materials has been investigated by many researchers, the studies on the dynamic response of viscoelastic materials are quite limited. Also, as a result of the literature search, only one study on FGM was found (Lyu et al. 2022) in the open literature. However, this study is limited for the elastic FGMs. To the best knowledge of the author, dynamic response of FG viscoelastic material has not been investigated, yet. To fill this gap in the literature, the author investigates analytically in this paper the dynamic stress analysis of an FG viscoelastic coated homogeneous viscoelastic half plane. A vertical harmonic load acts on the coated half plane via flat punch. Using Helmholtz functions and Fourier transform general stress and displacement expressions are obtained. Performing the boundary conditions, the contact problem is converted to the Cauchy-type singular integral equation, and it is solved numerically using the Gauss-Chebyshev integration formulas.

2 Formulation of the problem

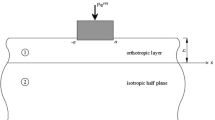
Consider the plane strain dynamic contact problem as shown in Fig. 1. A homogeneous viscoelastic half plane is coated with an FG viscoelastic layer with the height of \(h\). The coating is pressed on its surface by a rigid flat punch with the half length \(a\). The flat punch transmits a time harmonic concentrated normal load \(Pe^{i\omega t}\), where \(P\) is the amplitude of the load, \(\omega \) is the circular frequency of the load.

Fig. 1
figure 1

Geometry of the dynamic contact problem

Full size image

The plane elastodynamic equation of motion, in the absence of body forces, can be written as follows (Ugural and Fenster 2011)

$$\begin{aligned} \frac{\partial \sigma _{xj}}{\partial x} + \frac{\partial \tau _{xzj}}{\partial z} &= \rho _{j}(z)\frac{\partial ^{2}u_{j}}{\partial t^{2}}\qquad j = 1,2 \end{aligned}$$
(1a)
$$\begin{aligned} \frac{\partial \tau _{xzj}}{\partial x} + \frac{\partial \sigma _{zj}}{\partial z} &= \rho _{j}(z)\frac{\partial ^{2}w_{j}}{\partial t^{2}} \end{aligned}$$
(1b)

where \(u\), \(w\) are the \(x \)- and \(z \)-components of the displacement vector, \(\rho \) is the mass density and \(t\) denotes the time variable. Note that, \(j = 1\) and \(j = 2\) denote the FG coating and homogeneous half plane, respectively.

The constitutive relations of the isotropic and viscoelastic material can be written as follows (Timoshenko and Goodier 1951)

$$\begin{aligned} \sigma _{xj} &= \left ( \lambda _{j}(z) + 2\mu _{j}(z) \right )\frac{\partial u_{j}}{\partial x} + \lambda _{j}(z)\frac{\partial w_{j}}{\partial z} \end{aligned}$$
(2a)
$$\begin{aligned} \sigma _{zj} &= \lambda _{j}(z)\frac{\partial u_{j}}{\partial x} + \left ( \lambda _{j}(z) + 2\mu _{j}(z) \right )\frac{\partial w_{j}}{\partial z} \end{aligned}$$
(2b)
$$\begin{aligned} \tau _{xzj} &= \mu _{j}(z)(\frac{\partial u_{j}}{\partial z} + \frac{\partial w_{j}}{\partial x}) \end{aligned}$$
(2c)

where \(\lambda _{j}\) and \(\mu _{j}\) are the Lame constants. The material properties of the FGM coating and homogeneous half plane can be written as follows (Wang et al. 2023)

$$\begin{aligned} \lambda _{1}(z) &= \frac{\nu _{1}E_{10}^{*}e^{\gamma z}}{(1 + \nu _{1})(1 - 2\nu _{1})}(1 + i \eta _{1}), \\ \mu _{1}(z) &= \frac{E_{10}^{*}e^{\gamma z}}{2(1 + \nu _{1})}(1 + i \eta _{1}),\qquad \rho _{1}(z) = \rho _{10}e^{\gamma z} \end{aligned}$$
(3a)
$$\begin{aligned} \lambda _{2}(z) &= \lambda _{2} = \frac{\nu _{2}E_{2}^{*}}{(1 + \nu _{2})(1 - 2\nu _{2})}(1 + i \eta _{2}), \\ \mu _{2}(z) &= \mu _{2} = \frac{E_{2}^{*}}{2(1 + \nu _{2})}(1 + i \eta _{2}),\qquad \rho _{2}(z) = \rho _{2} \end{aligned}$$
(3b)

where \(\nu \), \(\eta \) and \(\gamma \) are the Poisson’s ratio, loss factor and inhomogeneity parameter, respectively. In a steady time-harmonic motion, the complex modulus can be expressed as \(E_{j} = E_{j}^{*}(1 + i\eta _{j})\), where \(E^{*}\) is the storage modulus. Note that, \(E_{10}^{*}\) and \(\rho _{10}\) are the storage modulus and mass density on the top surface of the coating. The viscoelastic properties of the coating and half-plane are simply modeled by the linear hysteretic damping. It is assumed that hysteretic damping exists in the covering and half-plane, which can be described by the complex module. The damping of this material not only conforms to the actual condition of the material, but also provides mathematical convenience (Wang et al. 2023). Note that loss factor, \(\eta \), is taken constant to enable the solution of the problem (Lyu et al. 2022).

Substituting Eqs. (2a)–(2c) into Eqs. (1a)–(1b) following partial differential equation system (PDEs) for the displacements of the FGM coating can be obtained

$$\begin{aligned} &(\lambda _{10} + 2\mu _{10})\frac{\partial ^{2}u_{1}}{\partial x^{2}} + \mu _{10}\frac{\partial ^{2}u_{1}}{\partial z^{2}} + (\lambda _{10} + \mu _{10})\frac{\partial ^{2}w_{1}}{\partial x\partial z} + \gamma \mu _{10}\left ( \frac{\partial u_{1}}{\partial z} + \frac{\partial w_{1}}{\partial x} \right ) \\ &\quad = \rho _{10}\frac{\partial ^{2}u_{1}}{\partial t^{2}} \end{aligned}$$
(4a)
$$\begin{aligned} &(\lambda _{10} + 2\mu _{10})\frac{\partial ^{2}w_{1}}{\partial z^{2}} + \mu _{10}\frac{\partial ^{2}w_{1}}{\partial x^{2}} + (\lambda _{10} + \mu _{10})\frac{\partial ^{2}u_{1}}{\partial x\partial z} + \gamma \left ( (\lambda _{10} + 2\mu _{10})\frac{\partial w_{1}}{\partial z} + \lambda _{10}\frac{\partial u_{1}}{\partial x} \right ) \\ &\quad = \rho _{10}\frac{\partial ^{2}w_{1}}{\partial t^{2}} \end{aligned}$$
(4b)

where \(\lambda _{10}\) and \(\mu _{1 0}\) Lamé constant and can be written as follows

$$ \lambda _{10} = \frac{\nu _{1}E_{10}^{*}}{(1 + \nu _{1})(1 - 2\nu _{1})}(1 + i \eta _{1}),\qquad \mu _{1 0} = \frac{E_{10}^{*}}{2(1 + \nu _{1})}(1 + i \eta _{1}). $$
(5)

With the help of Helmholtz functions and integral transformation techniques, dynamic stresses and displacements for the FG layer and homogeneous half-plane are obtained as complex integrals. To solve Eqs. (4a)–(4b) following Helmholtz functions can be presented:

$$ u_{j} = \frac{\partial \phi _{j}}{\partial x} - \frac{\partial \psi _{j}}{\partial z},\qquad w_{j} = \frac{\partial \phi _{j}}{\partial z} + \frac{\partial \psi _{j}}{\partial x} $$
(6)

In a steady time-harmonic motion, the potential Helmholtz functions can be expresses in the harmonic form as follows

$$ \phi _{j}(x,z,t) = \phi _{j}^{(0)}(x,z)e^{i\omega t},\qquad \psi _{j}(x,z,t) = \psi _{j}^{(0)}(x,z)e^{i\omega t} $$
(7)

where \(\phi _{j}^{(0)}(x,z)\) and \(\psi _{j}^{(0)}(x,z)\) are the complex amplitudes of potential functions.

Substituting (7) and (6) into the (4a)–(4b) following PDEs can be obtained for the FGM coating

$$\begin{aligned} & - \rho _{10}\omega ^{2}\frac{\partial \psi _{1}^{(0)}}{\partial z} - \mu _{10}\frac{\partial ^{3}\psi _{1}^{(0)}}{\partial z^{3}} - \mu _{10}\frac{\partial ^{3}\psi _{1}^{(0)}}{\partial x^{2}\partial z} + \rho _{10}\omega ^{2}\frac{\partial \phi _{1}^{(0)}}{\partial x} + (\lambda _{10} + 2\mu _{10})\frac{\partial ^{3}\phi _{1}^{(0)}}{\partial x\partial z^{2}} \\ & \quad {} + (\lambda _{10}+ 2\mu _{10})\frac{\partial ^{3}\phi _{1}^{(0)}}{\partial x^{3}} +\gamma \left [ - \mu _{10}\frac{\partial ^{2}\psi _{1}^{(0)}}{\partial z^{2}} + \mu _{10}\frac{\partial ^{2}\psi _{1}^{(0)}}{\partial x^{2}} + 2\mu _{10}\frac{\partial ^{2}\phi _{1}^{(0)}}{\partial x\partial z} \right ] = 0 \end{aligned}$$
(8a)
$$\begin{aligned} & \rho _{10}\omega ^{2}\frac{\partial \psi _{1}^{(0)}}{\partial x} + \mu _{10}\frac{\partial ^{3}\psi _{1}^{(0)}}{\partial x^{3}} + \mu _{10}\frac{\partial ^{3}\psi _{1}^{(0)}}{\partial x\partial z^{2}} + \rho _{10}\omega ^{2}\frac{\partial \phi _{1}^{(0)}}{\partial z}+ (\lambda _{10} + 2\mu _{10})\frac{\partial ^{3}\phi _{1}^{(0)}}{\partial x^{2}\partial z} \\ & \quad {} + (\lambda _{10} + 2\mu _{10})\frac{\partial ^{3}\phi _{1}^{(0)}}{\partial z^{3}} + \gamma \left [ 2\mu _{10}\frac{\partial ^{2}\psi _{1}^{(0)}}{\partial x\partial z} + (\lambda _{10} + 2\mu _{10})\frac{\partial ^{2}\phi _{1}^{(0)}}{\partial z^{2}} + \lambda _{10}\frac{\partial ^{2}\phi _{1}^{(0)}}{\partial x^{2}} \right ] = 0 \end{aligned}$$
(8b)

By applying the inverse Fourier transforms (Sneddon 1972) regarding \(x\), the following expressions may be written

$$\begin{aligned} \phi _{j}^{(0)}(x,z) &= \frac{1}{2\pi} \int _{ - \infty}^{\infty} \tilde{\phi}_{j}^{(0)}(k,z) e^{ - ikx}dk \end{aligned}$$
(9a)
$$\begin{aligned} \psi _{j}^{(0)}(x,z) &= \frac{1}{2\pi} \int _{ - \infty}^{\infty} \tilde{\psi}_{j}^{(0)}(k,z) e^{ - ikx}dk \end{aligned}$$
(9b)

where \(k\) is the Fourier transform parameter and \(\tilde{\phi}_{j}^{(0)}(k,z)\) and \(\tilde{\psi}_{j}^{(0)}(k,z)\) are the Fourier transforms of \(\phi _{j}^{(0)}(x,z)\) and \(\psi _{j}^{(0)}(x,z)\), respectively.

Substituting (9a)–(9b) into (8a)–(8b) following ordinary differential equation system (ODEs) is obtained

$$\begin{aligned} &\left ( k^{3}\left ( \lambda _{10} + 2\mu _{10} \right ) - k\rho _{10}\omega ^{2} \right )\tilde{\phi}_{1}^{(0)} - i\left ( k^{2}\mu _{10} - \rho _{10}\omega ^{2} \right )\frac{d\tilde{\psi}_{1}^{(0)}}{dz} - k\left ( \lambda _{10} + 2\mu _{10} \right )\frac{d^{2}\tilde{\phi}_{1}^{(0)}}{dz^{2}} \\ &\quad {} + i\mu _{10}\frac{d^{3}\tilde{\psi}_{1}^{(0)}}{dz^{3}} + i\gamma \mu _{10}\left ( k^{2}\frac{d\tilde{\psi}_{1}^{(0)}}{dz} + 2ik\frac{d\tilde{\phi}_{1}^{(0)}}{dz} + \frac{d^{2}\tilde{\psi}_{1}^{(0)}}{dz^{2}} \right ) = 0 \end{aligned}$$
(10a)
$$\begin{aligned} &i\left ( k^{3}\mu _{10} - k\rho _{10}\omega ^{2} \right )\tilde{\psi}_{1}^{(0)} + \left ( - k^{2}\left ( \lambda _{10} + 2\mu _{10} \right ) + \rho _{10}\omega ^{2} \right )\frac{d\tilde{\phi}_{j}^{(0)}}{dz} - ik\mu _{10}\frac{d^{2}\tilde{\psi}_{1}^{(0)}}{dz^{2}} \\ &\quad {} + \left ( \lambda _{10} + 2\mu _{10} \right )\frac{d^{3}\tilde{\phi}_{1}^{(0)}}{dz^{3}} + \gamma \left ( - 2ik\mu _{10}\frac{d\tilde{\psi}_{1}^{(0)}}{dz} - k^{2}\lambda _{10}\frac{d\tilde{\phi}_{1}^{(0)}}{dz} + (\lambda _{10} + 2\mu _{10})\frac{d^{2}\tilde{\phi}_{1}^{(0)}}{dz^{2}} \right ) = 0 \end{aligned}$$
(10b)

Upon solving ODEs (10a)–(10b), \(\tilde{\phi}_{1}^{(0)}\) and \(\tilde{\psi}_{1}^{(0)}\) can be obtained as follows

$$\begin{aligned} \tilde{\phi}_{1}^{(0)} &= \sum _{s = 1}^{4} A_{1s}e^{n_{1s}z} \end{aligned}$$
(11a)
$$\begin{aligned} \tilde{\psi}_{1}^{(0)} &= \sum _{s = 1}^{4} A_{1s}m_{1s}e^{n_{1s}z} \end{aligned}$$
(11b)

where \(A_{1s}\) (\(s = 1,\ldots4\))are the unknowns that will be determined from the boundary conditions of the problem and

$$\begin{aligned} n_{11} &= - \frac{\gamma}{2} + \Biggl(k^{2} + (\frac{\gamma}{2})^{2} - \frac{\lambda _{10} + 3\mu _{10}}{2\mu _{10}(\lambda _{10} + 2\mu _{10})}\rho _{10}\omega ^{2} \\ &\quad {}- \sqrt{ - k^{2}\gamma ^{2}\frac{\lambda _{10}}{(\lambda _{10} + 2\mu _{10})} + \frac{(\lambda _{10} + \mu _{10})^{2}}{4\mu _{10}^{2}(\lambda _{10} + 2\mu _{10})^{2}}\rho _{10}^{2}\omega ^{4}}\Biggr)^{1/2} \end{aligned}$$
(12a)
$$\begin{aligned} n_{12} &= - \frac{\gamma}{2} - \Biggl(k^{2} + (\frac{\gamma}{2})^{2} - \frac{\lambda _{10} + 3\mu _{10}}{2\mu _{10}(\lambda _{10} + 2\mu _{10})}\rho _{10}\omega ^{2} \\ &\quad {}- \sqrt{ - k^{2}\gamma ^{2}\frac{\lambda _{10}}{(\lambda _{10} + 2\mu _{10})} + \frac{(\lambda _{10} + \mu _{10})^{2}}{4\mu _{10}^{2}(\lambda _{10} + 2\mu _{10})^{2}}\rho _{10}^{2}\omega ^{4}}\Biggr)^{1/2} \end{aligned}$$
(12b)
$$\begin{aligned} n_{13} &= - \frac{\gamma}{2} + \Biggl(k^{2} + (\frac{\gamma}{2})^{2} - \frac{\lambda _{10} + 3\mu _{10}}{2\mu _{10}(\lambda _{10} + 2\mu _{10})}\rho _{10}\omega ^{2} \\ &\quad {}+ \sqrt{ - k^{2}\gamma ^{2}\frac{\lambda _{10}}{(\lambda _{10} + 2\mu _{10})} + \frac{(\lambda _{10} + \mu _{10})^{2}}{4\mu _{10}^{2}(\lambda _{10} + 2\mu _{10})^{2}}\rho _{10}^{2}\omega ^{4}}\Biggr)^{1/2} \end{aligned}$$
(12c)
$$\begin{aligned} n_{14} &= - \frac{\gamma}{2} - \Biggl(k^{2} + (\frac{\gamma}{2})^{2} - \frac{\lambda _{10} + 3\mu _{10}}{2\mu _{10}(\lambda _{10} + 2\mu _{10})}\rho _{10}\omega ^{2} \\ &\quad {}+ \sqrt{ - k^{2}\gamma ^{2}\frac{\lambda _{10}}{(\lambda _{10} + 2\mu _{10})} + \frac{(\lambda _{10} + \mu _{10})^{2}}{4\mu _{10}^{2}(\lambda _{10} + 2\mu _{10})^{2}}\rho _{10}^{2}\omega ^{4}}\Biggr)^{1/2} \end{aligned}$$
(12d)
$$ m_{1s} = - \frac{i\left ( k^{2}\left ( \left ( n_{1s} + \gamma \right )\lambda _{10} + 2n_{1s}\mu _{10} \right ) + n_{1s}\left ( - n_{1s}(n_{1s} + \gamma )(\lambda _{10} + 2\mu _{10}) - \rho _{10}\omega ^{2} \right ) \right )}{k^{3}\mu _{10} - k\left ( n_{1s}(n_{1s} + 2\gamma )\mu _{10} + \rho _{10}\omega ^{2} \right )} $$
(13)

Substituting (11a)–(11b) and (7) into the (6) the displacement expressions for the FGM coating can be obtained as follows

$$\begin{aligned} u_{1}(x,z,t) &= \frac{1}{2\pi} \int _{ - \infty}^{\infty} - ie^{ i\omega t}\sum _{s = 1}^{4} A_{1s} e^{ n_{1s} z}\left ( k - i m_{1s}n_{1s} \right ) e^{ - i k x}dk \end{aligned}$$
(14a)
$$\begin{aligned} w_{1}(x,z,t) &= \frac{1}{2\pi} \int _{ - \infty}^{\infty} - ie^{ i\omega t}\sum _{s = 1}^{4} A_{1s} e^{ n_{1s} z}\left ( k m_{1s} + i n_{1s} \right ) e^{ - i k x}dk \end{aligned}$$
(14b)

Inserting displacement expressions (14a)–(14b) into the (2a)–(2c) the stress components for the viscoelastic FG layer can be obtained as follows

$$\begin{aligned} &\sigma _{x1}(x,z,t) \\ &= \frac{1}{2\pi} \int _{ - \infty}^{\infty} e^{i\omega t}e^{\gamma z}\left [ \sum _{i = 1}^{s} A_{1s}e^{n_{1s}z}\left ( n_{1s}^{2}\lambda _{10} + 2i k m_{1s}n_{1s}\mu _{10} - k^{2}(\lambda _{10} + 2\mu _{10}) \right ) \right ]e^{ - i k x}dk \end{aligned}$$
(15a)
$$\begin{aligned} &\sigma _{z1}(x,z,t) \\ &= \frac{1}{2\pi} \int _{ - \infty}^{\infty} e^{i\omega t}e^{\gamma z}\left [ \sum _{i = 1}^{s} A_{1s}e^{n_{1s}z}\left ( - k^{2}\lambda _{10} - 2i k m_{1s}n_{1s}\mu _{10} + n_{1s}^{2}(\lambda _{10} + 2\mu _{10}) \right ) \right ]e^{ - i k x}dk \end{aligned}$$
(15b)
$$\begin{aligned} &\tau _{xz1}(x,z,t) \\ &= - \frac{1}{2\pi} \int _{ - \infty}^{\infty} e^{i\omega t}\mu _{10}e^{\gamma z}\left [ \sum _{i = 1}^{s} A_{1s}e^{n_{1s}z}\left ( k^{2}m_{1s} + 2i k n_{1s} + m_{1s}n_{1s}^{2} \right ) \right ]e^{ - i k x}dk \end{aligned}$$
(15c)

In Eqs. (10a)–(10b), taking \(\gamma = 0\) and replacing the subscript \(j = 1\) with \(j = 2\) the governing equations for the homogeneous viscoelastic half plane can be obtained as follows

$$\begin{aligned} & \left ( k^{3}\left ( \lambda _{2} + 2\mu _{2} \right ) - k\rho _{2}\omega ^{2} \right )\tilde{\phi}_{2}^{(0)} - i\left ( k^{2}\mu _{2} - \rho _{2}\omega ^{2} \right )\frac{d\tilde{\psi}_{2}^{(0)}}{dz} \\ &\quad {}- k\left ( \lambda _{2} + 2\mu _{2} \right )\frac{d^{2}\tilde{\phi}_{2}^{(0)}}{dz^{2}} + i\mu _{2}\frac{d^{3}\tilde{\psi}_{2}^{(0)}}{dz^{3}} = 0 \end{aligned}$$
(16a)
$$\begin{aligned} &i\left ( k^{3}\mu _{2} - k\rho _{2}\omega ^{2} \right )\tilde{\psi}_{2}^{(0)} + \left ( - k^{2}\left ( \lambda _{2} + 2\mu _{2} \right ) + \rho _{2}\omega ^{2} \right )\frac{d\tilde{\phi}_{2}^{(0)}}{dz} \\ &\quad {}- ik\mu _{2}\frac{d^{2}\tilde{\psi}_{2}^{(0)}}{dz^{2}} + \left ( \lambda _{2} + 2\mu _{2} \right )\frac{d^{3}\tilde{\phi}_{2}^{(0)}}{dz^{3}} = 0 \end{aligned}$$
(16b)

When the same steps in FG layer are followed, the displacement and stress expressions for the homogeneous viscoelastic half plane can be obtained as follows:

$$\begin{aligned} &u_{2}(x,z,t) = \frac{1}{2\pi} \int _{ - \infty}^{\infty} - ie^{ i\omega t}\left ( A_{21}ke^{ n_{21} z} - iB_{21}m_{21}e^{ m_{21} z} \right ) e^{ - i k x}dk \end{aligned}$$
(17a)
$$\begin{aligned} &w_{2}(x,z,t) = \frac{1}{2\pi} \int _{ - \infty}^{\infty} - ie^{ i\omega t}\left ( iA_{21}n_{21}e^{ n_{21} z} + B_{21}k e^{ m_{21} z} \right ) e^{ - i k x}dk \end{aligned}$$
(17b)
$$\begin{aligned} &\sigma _{x2}(x,z,t) \\ & = \frac{1}{2\pi} \int _{ - \infty}^{\infty} e^{i\omega t}\left [ A_{21}\left ( n_{21}^{2}\lambda _{2} - k^{2}\left ( \lambda _{2} + 2\mu _{2} \right ) \right )e^{ n_{21} z} + 2i k m_{21} \mu _{2}B_{21}e^{ m_{21} z} \right ]e^{ - i k x}dk \end{aligned}$$
(17c)
$$\begin{aligned} &\sigma _{z2}(x,z,t) \\ &= \frac{1}{2\pi} \int _{ - \infty}^{\infty} e^{i\omega t}\left [ A_{21}\left ( - k^{2}\lambda _{2} + n_{21}^{2}\left ( \lambda _{2} + 2\mu _{2} \right ) \right )e^{ n_{21} z} - 2i k m_{21} \mu _{2}B_{21}e^{ m_{21} z} \right ]e^{ - i k x}dk \end{aligned}$$
(17d)
$$\begin{aligned} &\tau _{xz2}(x,z,t) = \frac{1}{2\pi} \int _{ - \infty}^{\infty} - e^{i\omega t}\mu _{2}\left [ 2i k n_{21}A_{21}e^{ n_{21} z} + \left ( k^{2} + m_{21}^{2} \right )B_{21}e^{ m_{21} z} \right ]e^{ - i k x}dk \end{aligned}$$
(17e)

where

$$ n_{21} = \sqrt{\frac{k^{2}\left ( \lambda _{2} + 2\mu _{2} \right ) - \rho _{2}\omega ^{2}}{\left ( \lambda _{2} + 2\mu _{2} \right )}},\qquad m_{21} = \sqrt{\frac{k^{2}\mu _{2} - \rho _{2}\omega ^{2}}{\mu _{2}}}, $$
(18a,b)

3 The boundary and continuity conditions and the singular integral equation

The boundary conditions for the dynamic contact problem described in Fig. 1 can be written as follows (Wang et al. 2023)

$$\begin{aligned} \sigma _{z1}(x,h,t) &= - p(x)e^{i\omega t}\qquad - a \le x \le a \end{aligned}$$
(19a)
$$\begin{aligned} \tau _{xz1}(x,h,t)& = 0\qquad - \infty < x < \infty \end{aligned}$$
(19b)
$$\begin{aligned} \sigma _{z1}(x,0,t) &= \sigma _{z2}(x,0,t)\qquad - \infty < x < \infty \end{aligned}$$
(19c)
$$\begin{aligned} \tau _{xz1}(x,0,t) &= \tau _{xz2}(x,0,t)\qquad - \infty < x < \infty \end{aligned}$$
(19d)
$$\begin{aligned} u_{1}(x,0,t) &= u_{2}(x,0,t)\qquad - \infty < x < \infty \end{aligned}$$
(19e)
$$\begin{aligned} w_{1}(x,0,t) &= w_{2}(x,0,t)\qquad - \infty < x < \infty \end{aligned}$$
(19f)

where \(p(x)\) is the unknown contact stress between the rigid flat punch and the FG coating on the contact zone \(( - a,a)\). Since friction is neglected, no shear stress occurs between the punch and the layer (19b). On the other hand, since the layer and half plane are fully bonded to each other, the traction and displacements are equal for both parts at the interface, i.e. the interface continuity condition is provided (18c-18f).

Using boundary conditions given by (19a)–(19f), six algebraic equations can be obtained to determine the six unknowns which are \(A_{1s}\) (\(s = 1,..4\)), \(A_{21}\) and \(B_{21}\). Taking the Fourier transform to boundary conditions the unknowns can be obtained in terms of the unknown contact stress \(p(x)\) as follows

$$ \begin{aligned}[b] A_{1s} &= A_{1s}^{p}\int _{ - a}^{a} p(\xi ) e^{ik\xi} d\xi ,\qquad A_{21} = A_{21}^{p}\int _{ - a}^{a} p(\xi ) e^{ik\xi} d\xi ,\\ B_{21} &= B_{21}^{p}\int _{ - a}^{a} p(\xi ) e^{ik\xi} d\xi \end{aligned} $$
(20)

Since the expressions of \(A_{1s}^{p}\), \(B_{1s}^{p}\) and \(B_{21}^{p}\) are too long they are not given here. Substituting (20) into the mixed boundary conditions for the flat punch

$$ \frac{dw_{1}(x,h,t)}{dx} = 0\qquad - a < x < a $$
(21)

following integral equation may be obtained

$$ \frac{1}{2\pi} \int _{ - a}^{a} p(\xi )d\xi \left [ \int _{ - \infty}^{\infty} M_{1}(k)e^{ik(\xi - x)}dk \right ] = 0 $$
(22)

where

$$ M_{1}(k) = - k\left \{ i\sum _{s = 1}^{4} A_{1s}^{p}\left ( k - im_{1s}n_{1s} \right )e^{ n_{1s} h} \right \} $$
(23)

When Eq. (23) is arranged following integral equation is obtained:

$$ \frac{1}{\pi} \int _{ - a}^{a} p(\xi )d\xi \int _{0}^{\infty} \left [ i\operatorname{Re} [M_{1}(k)] - \operatorname{Im} [M_{1}(k)] \right ]\sin [k(\xi - x)]dk = 0 $$
(24)

Note that, following singular terms arise in the kernels of integral equation (24)

$$ \beta _{1} = \lim _{k \to \infty} \operatorname{Re} [M_{1}(k)],\qquad \beta _{2} = \lim _{k \to \infty} \operatorname{Im} [M_{1}(k)] $$
(25)

Unlike non-viscoelastic material, both real and imaginary parts of the singular term are formed here. The kernel \(M_{1}(k)\) at the Eqs. (24) diverges to a constant number, that is, the singular term, after a certain value of the integral constant. In order to calculate this non-closed integral, the singular term is removed from the kernel of the integral, and on the other hand, the closed integral is taken with the help of integral transform tables and added to expression (24) again, following Cauchy-type singular integral equation can be obtained

$$ \frac{1}{\pi} \int _{ - a}^{a} p(\xi )d\xi \left [ \frac{\beta}{\xi - x} + K_{1}(x,\xi ) \right ] = 0 \qquad (- a < x < a) $$
(26)

where

$$\begin{aligned} \beta &= i\beta _{1} - \beta _{2} \end{aligned}$$
(27a)
$$\begin{aligned} K_{1}(x,\xi ) &= \int _{0}^{\infty} \left [ i\left \{ \operatorname{Re} [M_{1}(k)] - \beta _{1} \right \} - \left \{ \operatorname{Im} [M_{1}(k)] - \beta _{2} \right \} \right ] \sin [k(\xi - x)]dk \end{aligned}$$
(27b)

The solution of the singular integral equation must satisfy the following equilibrium condition

$$ \int _{ - \infty}^{\infty} \sigma _{z1}(x,h)dx = - \int _{ - a}^{a} p(\xi )d\xi = - P $$
(28)

4 On the solution of the singular integral equation

If the contact stress converges to zero at the ends of the contact, the index of the integral equation is “−1” due to smooth contact. On the other hand, if the punch has sharp corners, the stress at these points where the contact ends goes to infinity, that is, singularity occurs and the index of the integral equation is “0”. In the third case, if one corner of the punch is sharp and the other smooth, the index of the integral equation is “1” (Erdogan 1978).

In this problem, since the contact stress is singular at the ends of the contact, the index of the integral equation takes the value “0” as explained in the foregoing paragraph (Erdogan 1978). By introducing the following normalizations:

$$ \xi = a r,\qquad x = a s $$
(29)

the singular integral equation (26) and equilibrium condition (28) become

$$\begin{aligned} \frac{1}{\pi} \int _{ - 1}^{1} p(\xi )d\xi \left [ \frac{\beta}{r - s} + a K_{1}(s,r) \right ] &= 0 \end{aligned}$$
(30a)
$$\begin{aligned} a\int _{ - 1}^{1} p(r)dr &= P \end{aligned}$$
(30b)

The obtained singular integral equation (30a) can be solved through many numerical methods. Among the methods, Gauss-Chebyshev integration technique which is a special case of Gauss-Jacobi quadrature has remarkable advantages on solving singular integral equations such as convergence and ease of application. Since there is no friction, a singular integral equation of the first kind is obtained and therefore the Gauss-Chebyshev integration formulation is used instead of the general Gauss-Jacobi integration formulation (Erdogan 1978). Hence, the solution of the singular integral equation Eq. (30a) can be assumed as

$$ p(r) = \frac{g(r)}{\sqrt{1 - r^{2}}} $$
(31)

Thus, Eqs. (30a)–(30b) can be converted into following algebraic equations using Gauss-Chebyshev integration formula

$$\begin{aligned} \frac{1}{N}\sum _{m = 1}^{N} g(r_{m})\left [ \frac{\beta}{r_{m} - s_{\varsigma}} + a K_{1}(s_{\varsigma},r_{m}) \right ] &= 0\qquad \varsigma = 1,2...N - 1 \end{aligned}$$
(32a)
$$\begin{aligned} a\frac{1}{N}\sum _{m = 1}^{N} g(r_{m}) &= \frac{P}{\pi}, \end{aligned}$$
(32b)

where

$$\begin{aligned} r_{m} &= cos(\frac{2m - 1}{2N}\pi )\qquad m = 1,2...N \end{aligned}$$
(33a)
$$\begin{aligned} s_{\varsigma} &= cos(\frac{\varsigma}{N}\pi )\qquad \varsigma = 1,2...N - 1 \end{aligned}$$
(33b)

Equations (32a)–(32b) gives \(N\) equations to determine the \(N\) unknowns \(g(r_{m})\).

After determining the contact stress, dynamic vertical impedance can be determined as follows (Luco and Westmann 1972)

$$ K_{v} = \frac{P}{\pi \mu _{2}^{*}\delta _{f}} = \operatorname{Re} (K_{v}) + i\omega _{0}\operatorname{Im} (K_{v}/\omega _{0}) $$
(34)

where \(\omega _{0}\) is the dimensionless external excitation frequency and is expressed as \(\omega _{0} = \omega h\sqrt{\rho _{2}/\mu _{2}^{*}}\). \(\delta _{f}\) is the maximum displacement under the punch. Real part of \(K_{v}\) represents the real elastic stiffness of the FG coated half plane and imaginary part of \(K_{v}\) represents the energy dissipation. Namely, the FG coated half plane can be modeled as a “spring” with stiffness coefficient \(\operatorname{Re} (K_{v})\) and a “dashpot” with damping coefficient \(\operatorname{Im} (K_{v}/\omega _{0})\) in an oscillating system (Wang et al. 2023).

5 Numerical results

In this section the effect of the external excitation frequency \(\omega _{0} = \omega h\sqrt{\rho _{2}/\mu _{2}^{*}}\), loss factor ratio \(\Gamma _{1} = \eta _{1}/\eta _{2}\), Young’s modulus ratio \(\Gamma _{2} = E_{1}/E_{2}\), density ratio \(\Gamma _{3} = \rho _{1}/\rho _{2}\), ratio of Poisson’s ratio \(\Gamma _{4} = \nu _{1}/\nu _{2}\), normalized load factor \(P/(\mu _{2}^{*}h)\) and punch radius \(R/h\) on the contact width \(a/h\), normalized dynamic contact stress \(p(x)h/P\) and dynamic in-plane stress \(\sigma _{x}(x,h)h/P\) are analyzed. In the analysis, the material of the half plane is aluminum with the parameters: \(E_{2}^{*} = 70\text{ GPa}\), \(\rho _{2} = 2780\text{ kg} /\text{m}^{3}\), \(\nu _{2} = 0.33\). Since the number of collocation points \(N=30\) was considered sufficient, \(N=30\) was chosen in the following analyses.

Firstly, in order to verify this solution a comparison study is performed. For this purpose, numerical results of a special case obtained from the presented solution, that is \(\gamma \to 0\), are compared by Wang et al. (2023) where homogeneous layer is considered (Fig. 2 and Fig. 3). It is shown a great accordance between the present results and Wang et al. (2023).

Fig. 2
figure 2

Validation of the dynamic contact stress for a homogeneous viscoelastic layer bonded to a viscoelastic half plane; comparison with Wang et al. (2023) (\(\gamma h = 0\), \(\Gamma _{1} = 5\), \(\Gamma _{2} = 2\), \(\Gamma _{3} = 1\), \(\Gamma _{4} = 1\))

Full size image
Fig. 3
figure 3

Comparison of the dynamic vertical impedance \(K_{v}\) between the present results and Wang et al.’s results (\(\gamma h = 0\), \(\Gamma _{1} = 5\), \(\Gamma _{2} = 2\), \(\Gamma _{3} = 1\), \(\Gamma _{4} = 1\))

Full size image

Figure 4 shows the effect of inhomogeneity parameter \(\gamma \) on the dynamic vertical impedance. \(\gamma = 0\) corresponds to the homogeneous state. At negative values of \(\gamma \), the layer is stiff, while at positive values of \(\gamma \), the layer is soft. At lower excitation frequency \(\omega _{0} \le 1\) the effect of inhomogeneity parameter \(\gamma \) very slight on the real part. However, imaginary part very sensitive to the change of all the values of excitation frequency. The real part takes both positive and negative values while the imaginary part takes only positive values. For \(\omega _{0} \to 0\) the real part takes the same value for all values of inhomogeneity parameter \(\gamma \). In the homogeneous case, both the real and the imaginary part are more oscillatory.

Fig. 4
figure 4

The effect of the inhomogeneity parameter \(\gamma h\) on the dynamic vertical impedance \(K_{v}\) (\(\omega _{0} = 3\), \(\Gamma _{1} = 5\), \(\Gamma _{2} = 2\), \(\Gamma _{3} = 1\), \(\Gamma _{4} = 1\), \(P/(\mu _{2}h) = 10^{ - 3}\), \(a/h = 1\))

Full size image

The effect of the excitation frequency on the absolute value of dynamic contact stress is illustrated in Fig. 5. Because the rigid flat the punch, the contact stress goes to infinity at the corner of punch. The distribution of the contact stress is almost smooth at lower excitation frequency \(\omega _{0} \le 2\). However, the dynamic behavior of the contact stress becomes increasingly oscillatory as the external excitation frequency increases after \(\omega _{0} > 2\). The dynamic contact stress at the center of the punch is smallest in the static case and maximum at higher excitation frequency.

Fig. 5
figure 5

The effect of the excitation frequency \(\omega _{0}\) on the dynamic contact stress. (\(\gamma h = - 1.5\), \(\Gamma _{1} = 5\), \(\Gamma _{2} = 2\), \(\Gamma _{3} = 1\), \(\Gamma _{4} = 1\), \(P/(\mu _{2}h) = 10^{ - 3}\), \(a/h = 1\))

Full size image

Figure 6 shows the effect of the inhomogeneity parameter \(\gamma h\) on the absolute value of dynamic contact stress. Since \(\omega _{0} = 4\) is chosen constant, the contact stress is oscillatory at all \(\gamma h\) values. On the other hand, oscillatory behavior becomes clear when \(\gamma h\) increases positively, i.e., as the layer softens. At \(\gamma h = 1.5\) and \(\gamma h = 2\), the stress behavior is almost the same. The dynamic contact stress at the center of the punch decreases as the layer becomes stiffer.

Fig. 6
figure 6

The effect of the inhomogeneity parameter \(\gamma h\) on the dynamic contact stress. (\(\omega _{0} = 4\), \(\Gamma _{1} = 5\), \(\Gamma _{2} = 2\), \(\Gamma _{3} = 1\), \(\Gamma _{4} = 1\), \(P/(\mu _{2}h) = 10^{ - 3}\), \(a/h = 1\))

Full size image

Figure 7 illustrates the effect of the loss factor ratio \(\Gamma _{1}\) on the dynamic contact stress. At the lower values of loss factor \(\Gamma _{1} \le 4\) the contact stress almost insensitive to the change of loss factor. However, the contact stress at the center of punch decreases as \(\Gamma _{1} > 4\). Unlike the loss factor, the influence of Young’s modulus ratio \(\Gamma _{2}\) on the dynamic contact stress behavior is obvious (Fig. 8). When \(\Gamma _{2} = 0.25\), the contact stress is highly oscillating. The maximum contact stress at the center of punch occurs when \(\Gamma _{2} = 0.5\).

Fig. 7
figure 7

The effect of the loss factor ratio \(\Gamma _{1}\) on the dynamic contact stress. (\(\omega _{0} = 3\), \(\gamma h = - 1.5\), \(\Gamma _{2} = 2\), \(\Gamma _{3} = 1\), \(\Gamma _{4} = 1\), \(P/(\mu _{2}h) = 10^{ - 3}\), \(a/h = 1\))

Full size image
Fig. 8
figure 8

The effect of the Young’s modulus ratio \(\Gamma _{2}\) on the dynamic contact stress. (\(\omega _{0} = 3\), \(\gamma h = - 1.5\), \(\Gamma _{1} = 5\), \(\Gamma _{3} = 1\), \(\Gamma _{4} = 1\), \(P/(\mu _{2}h) = 10^{ - 3}\), \(a/h = 1\))

Full size image

The effect of the density ratio \(\Gamma _{3}\) on the dynamic contact stress is presented in Fig. 9. Although the omega is large, i.e., \(\omega _{0} = 3\), the contact stress is smooth in the case of \(\Gamma _{3} \le 0.5\). As \(\Gamma _{3}\) increases, the contact stress under the punch also increases. Figure 10 shows the effect of the ratio of Poisson’s ratio \(\Gamma _{4}\) on the contact stress. Contact stress is oscillatory all the values of Poisson’s ratio. The contact stress almost insensitive to the change of Poisson’s ratio when \(\Gamma _{4} \le 1.2\).

Fig. 9
figure 9

The effect of the density ratio \(\Gamma _{3}\) on the dynamic contact stress. (\(\omega _{0} = 3\), \(\gamma h = - 1.5\), \(\Gamma _{1} = 5\), \(\Gamma _{2} = 2\), \(\Gamma _{4} = 1\), \(P/(\mu _{2}h) = 10^{ - 3}\), \(a/h = 1\))

Full size image
Fig. 10
figure 10

The effect of the ratio of Poisson’s ratio \(\Gamma _{4}\) on the dynamic contact stress. (\(\omega _{0} = 3\), \(\gamma h = - 1.5\), \(\Gamma _{1} = 5\), \(\Gamma _{2} = 2\), \(\Gamma _{3} = 1\), \(P/(\mu _{2}h) = 10^{ - 3}\), \(a/h = 1\))

Full size image

The effect of the indentation load \(P\) and punch length \(a\) on the dynamic contact stress are shown in Fig. 11 and Fig. 12, respectively. At the lowest values of indentation load the contact stress is almost smooth. The same relation occurs for the punch length \(a\). As expected, dynamic contact stress increases as the indentation load increases. Since the contact stress is distributed over a larger area, the stress decreases as the punch length increases. Increased indentation load may cause crack formation and propagation and contact damage. Such undesirable damage can be avoided by selecting a smaller load.

Fig. 11
figure 11

The effect of the indentation load \(P\) on the dynamic contact stress. (\(\omega _{0} = 3\), \(\gamma h = 0.75\), \(\Gamma _{1} = 5\), \(\Gamma _{2} = 2\), \(\Gamma _{3} = 1\), \(\Gamma _{4} = 1\), \(a/h = 1\))

Full size image
Fig. 12
figure 12

The effect of the punch length \(a/h\) on the dynamic contact stress. (\(\omega _{0} = 3\), \(\gamma h = 0.75\), \(\Gamma _{1} = 5\), \(\Gamma _{2} = 2\), \(\Gamma _{3} = 1\), \(\Gamma _{4} = 1\), \(P/(\mu _{2}h) = 10^{ - 3}\))

Full size image

6 Conclusion

In this study, contact response of an FG viscoelastic isotropic layer indented by a harmonic vertical load is investigated. The FG layer is indented by a rigid flat punch and fully bonded to the homogeneous viscoelastic half plane. Using Fourier integral transform, Helmholtz potential functions and the boundary condition of the contact problem a first kind singular integral equation is obtained and utilized numerically with Gauss-Chebyshev integration formula. The effects of some parameters on the dynamic contact stress are discussed. The results show that:

  • As the external excitation frequency increases, the contact stress becomes more oscillatory.

  • At a lower excitation frequency, the effect of the homogeneity parameter on the actual part is very small. However, the imaginary part is very sensitive to the change of all values of the excitation frequency.

  • The dynamic contact stress at the center of the punch decreases as the layer becomes stiffer.

  • At the lowest values of indentation load the contact stress is almost smooth. The same relation occurs for the punch length.

  • At the lower values of loss factor the contact stress almost insensitive to the change of loss factor. Unlike the loss factor, the influence of Young’s modulus ratio on the dynamic contact stress behavior is obvious.

  • This study can be extended to the case where the punch is circular or parabolic. It can also be considered as a receding contact problem where the layer and the half-plane are not bonded to each other.