Frictional contact problem of a coated half plane pressed by a rigid punch with coupled stress elasticity

Abstract

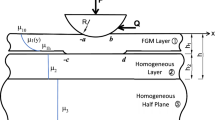
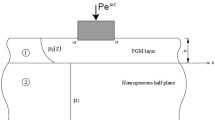
This paper considers the size-dependent plane frictional contact problem of a homogeneous coated half-plane indented by a rigid punch based on the couple stress elasticity. Using the Fourier integral transform technique in addition to the boundary and compatibility conditions, the mixed-boundary value problem is converted into a singular integral equation of the second kind. The integral equation is further derived and normalized for the cylindrical and flat punch case profiles. Applying the Gauss–Jacobi integration formula, the resulting singular integral equation is reduced to a system of algebraic equations. The obtained results are first validated based on those published for the case of a frictionless contact problem of a half-plane indented by rigid cylindrical and flat punches and solved based on the couple stress theory. A detailed parametric study is then performed to investigate the effect of the characteristic material length, the friction coefficient, the layer height, the shear modulus, the indentation load and Poisson’s ratio on the contact and in-plane stresses.

Appendices

Appendix A

1.1 Expressions of the displacements in terms of $A_j$, $B_j$, and $C_j$ $(j=1, \ldots ,4)$

$$\begin{aligned} u_1 (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\frac{1}{{2\mu _1 }}\xi \left( {IA_1 \hbox {e}^{ - \xi y} + \frac{1}{\xi }IA_2 \hbox {e}^{ - \xi y} \left( { - 2 + 2\nu _1 + \xi y} \right) + IA_3 \hbox {e}^{\xi y} + \frac{1}{\xi }IA_4 \hbox {e}^{\xi y} \left( {2 - 2\nu _1 + \xi y} \right) } \right. } \nonumber \\&\quad \left. + {B_1 \hbox {e}^{ - \xi y} - B_2 \hbox {e}^{\xi y} - \frac{1}{\xi }\gamma B_3 \hbox {e}^{\gamma y} + \frac{1}{\xi }\gamma B_4 \hbox {e}^{ - \gamma y} } \right) \hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.1a)

$$\begin{aligned} v_1 (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\frac{1}{{2\mu _1 }}\xi \left( {A_1 \hbox {e}^{ - \xi y} + \frac{1}{\xi }A_2 \hbox {e}^{ - \xi y} \left( {1 - 2\nu _1 + \xi y} \right) - A_3 \hbox {e}^{\xi y} - \frac{1}{\xi }A_4 \hbox {e}^{\xi y} \left( { - 1 + 2\nu _1 + \xi y} \right) } \right. } \nonumber \\&\quad \left. { - I\left( {B_1 \hbox {e}^{ - \xi y} + B_2 \hbox {e}^{\xi y} + B_3 \hbox {e}^{\gamma y} + B_4 \hbox {e}^{ - \gamma y} } \right) } \right) \hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.1b)

$$\begin{aligned} \omega _1 (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\frac{1}{{2\mu _1 }}\left( {2I\xi ( - 1 + \nu _1 )A_2 \hbox {e}^{ - \xi y} + 2I\xi ( - 1 + \nu _1 )A_4 \hbox {e}^{\xi y} + \frac{1}{2}B_3 \left( {\gamma ^2 - \xi ^2 } \right) \hbox {e}^{\gamma y} } \right. } \nonumber \\&\quad \left. + {\frac{1}{2}B_4 \left( {\gamma ^2 - \xi ^2 } \right) \hbox {e}^{ - \gamma y} } \right) \hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.1c)

$$\begin{aligned} u_2 (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\frac{1}{{2\mu _2 }}\xi \left( {IC_1 \hbox {e}^{\xi y} + \frac{1}{\xi }IC_2 \hbox {e}^{\xi y} \left( {2 - 2\nu _2 + \xi y} \right) - \frac{\gamma }{\xi }C_3 \hbox {e}^{\gamma y} - C_4 \hbox {e}^{\xi y} } \right) \hbox {e}^{ - I\xi x} \hbox {d}\xi } \end{aligned}$$

(A.1d)

$$\begin{aligned} v_2 (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\frac{1}{{2\mu _2 }}\xi \left( { - C_1 \hbox {e}^{\xi y} - \frac{1}{\xi }C_2 \hbox {e}^{\xi y} \left( { - 1 + 2\nu _2 + \xi y} \right) - IC_3 \hbox {e}^{\gamma y} - IC_4 \hbox {e}^{\xi y} } \right) } \,\hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.1e)

$$\begin{aligned} \omega _2 (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\frac{1}{{2\mu _2 }}\left( {2I\xi ( - 1 + \nu _2 )C_2 \hbox {e}^{\xi y} + \frac{1}{2}C_3 \left( {\gamma ^2 - \xi ^2 } \right) \hbox {e}^{\gamma y} } \right) } \,\hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.1f)

1.2 Expressions of the stresses in terms of $A_j$, $B_j$, and $C_j$ $(j=1, \ldots ,4)$

$$\begin{aligned} \sigma _{xx1} (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\xi ^2 \left( {A_1 \hbox {e}^{ - \xi y} + \frac{1}{\xi }A_2 \hbox {e}^{ - \xi y} \left( { - 2 + \xi y} \right) + A_3 \hbox {e}^{\xi y} + \frac{1}{\xi }A_4 \hbox {e}^{\xi y} \left( {2 + \xi y} \right) } \right. } \nonumber \\&\quad \left. - {IB_1 \hbox {e}^{ - \xi y} + IB_2 \hbox {e}^{\xi y} + \frac{1}{\xi }I\gamma B_3 \hbox {e}^{\gamma y} - \frac{1}{\xi }I\gamma B_4 \hbox {e}^{ - \gamma y} } \right) \hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.2a)

$$\begin{aligned} \sigma _{yy1} (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\xi ^2 \left( { - A_1 \hbox {e}^{ - \xi y} - A_2 y\hbox {e}^{ - \xi y} - A_3 \hbox {e}^{\xi y} - A_4 y\hbox {e}^{ - \xi y} + IB_1 \hbox {e}^{ - \xi y} - IB_2 \hbox {e}^{\xi y} } \right. } \nonumber \\&\quad \left. - {I\frac{\gamma }{\xi }B_3 \hbox {e}^{\gamma y} + I\frac{\gamma }{\xi }B_4 \hbox {e}^{ - \gamma y} } \right) \,\hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.2b)

$$\begin{aligned} \sigma _{xy1} (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\xi ^2 \left( { - IA_1 \hbox {e}^{ - \xi y} - \frac{1}{\xi }IA_2 \hbox {e}^{ - \xi y} \left( { - 1 + \xi y} \right) + IA_3 \hbox {e}^{\xi y} + \frac{1}{\xi }IA_4 \hbox {e}^{\xi y} \left( {1 + \xi y} \right) } \right. } \nonumber \\&\quad \left. - {B_1 \hbox {e}^{ - \xi y} - B_2 \hbox {e}^{\xi y} - \frac{{\gamma ^2 }}{{\xi ^2 }}B_3 \hbox {e}^{\gamma y} - \frac{{\gamma ^2 }}{{\xi ^2 }}B_4 \hbox {e}^{ - \gamma y} } \right) \hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.2c)

$$\begin{aligned} \sigma _{yx1} (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\xi ^2 \left( { - IA_1 \hbox {e}^{ - \xi y} - \frac{1}{\xi }IA_2 \hbox {e}^{ - \xi y} \left( { - 1 + \xi y} \right) + IA_3 \hbox {e}^{\xi y} + \frac{1}{\xi }IA_4 \hbox {e}^{\xi y} \left( {1 + \xi y} \right) } \right. } \nonumber \\&\quad \left. - {B_1 \hbox {e}^{ - \xi y} - B_2 \hbox {e}^{\xi y} - B_3 \hbox {e}^{\gamma y} - B_4 \hbox {e}^{ - \gamma y} } \right) \hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.2d)

$$\begin{aligned} \sigma _{xx2} (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\xi ^2 \left( {C_1 \hbox {e}^{\xi y} + \frac{1}{\xi }C_2 \hbox {e}^{\xi y} \left( {2 + \xi y} \right) + \frac{1}{\xi }I\gamma C_3 \hbox {e}^{\gamma y} + IC_4 \hbox {e}^{\xi y} } \right) } \,\hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.2e)

$$\begin{aligned} \sigma _{yy2} (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\xi ^2 \left( { - C_1 \hbox {e}^{\xi y} - C_2 y\hbox {e}^{\xi y} - \frac{1}{\xi }I\gamma C_3 \hbox {e}^{\gamma y} - IC_4 \hbox {e}^{\xi y} } \right) } \,\hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.2f)

$$\begin{aligned} \sigma _{xy2} (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\xi ^2 \left( {IC_1 \hbox {e}^{\xi y} + \frac{1}{\xi }IC_2 \hbox {e}^{\xi y} \left( {1 + \xi y} \right) - \frac{{\gamma ^2 }}{{\xi ^2 }}C_3 \hbox {e}^{\gamma y} - C_4 \hbox {e}^{\xi y} } \right) } \,\hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.2g)

$$\begin{aligned} \sigma _{yx2} (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\xi ^2 \left( {IC_1 \hbox {e}^{\xi y} + \frac{1}{\xi }IC_2 \hbox {e}^{\xi y} \left( {1 + \xi y} \right) - C_3 \hbox {e}^{\gamma y} - C_4 \hbox {e}^{\xi y} } \right) } \,\hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.2h)

1.3 Expressions of the couple stresses in terms of $A_j$, $B_j$, and $C_j$ $(j=1, \ldots ,4)$

$$\begin{aligned} m_{yz1} (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\xi \left( { - B_1 \hbox {e}^{ - \xi y} + B_2 \hbox {e}^{\xi y} + \frac{\gamma }{\xi }B_3 \hbox {e}^{\gamma y} - \frac{\gamma }{\xi }B_4 \hbox {e}^{ - \gamma y} } \right) } \,\hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.3a)

$$\begin{aligned} m_{yz2} (x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\left( {\gamma C_3 \hbox {e}^{\gamma y} + C_4 \xi \hbox {e}^{\xi y} } \right) } \,\hbox {e}^{ - I\xi x} \hbox {d}\xi \end{aligned}$$

(A.3b)

$$\begin{aligned} {m_{xz1}}(x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty { - I\xi \left( {{B_1}{\hbox {e}^{ - \xi y}} + {B_2}{\hbox {e}^{\xi y}} + {B_3}{\hbox {e}^{\gamma y}} + {B_4}{\hbox {e}^{ - \gamma y}}} \right) } \,{\hbox {e}^{ - I\xi x}}\hbox {d}\xi \end{aligned}$$

(A.3c)

$$\begin{aligned} {m_{xz2}}(x,y)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty { - I\xi \left( {{C_3}{\hbox {e}^{\gamma y}} + {C_4}{\hbox {e}^{\xi y}}} \right) } \,{\hbox {e}^{ - I\xi x}}\hbox {d}\xi \end{aligned}$$

(A.3d)

Appendix B

1.1 Classical solution of the considered contact problem

For the classical solution, the displacement and stress components in the layer can be written as follows [31]:

$$\begin{aligned} u_1\left( {x,y} \right)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\;\left[ {\left( {D_1 + D_2 y} \right) \,\hbox {e}^{ - \xi y} + \left( {D_3 + D_4 y} \right) \,\hbox {e}^{\xi y} } \right] } \,\,\hbox {e}^{ - i\xi x} \hbox {d}\xi \end{aligned}$$

(B.1a)

$$\begin{aligned} v_1\left( {x,y} \right)&= - \frac{1}{{2\pi }}I\int \limits _{ - \infty }^\infty {\,\left[ {\left[ {D_1 + \left( {\frac{\kappa _1 }{\xi } + y} \right) D_2 } \right] \,\hbox {e}^{ - \xi y} + \left[ { - D_3 + \left( {\frac{\kappa _1 }{\xi } - y} \right) D_4 } \right] \,\hbox {e}^{\xi y} } \right] } \;\hbox {e}^{ - i\xi x} \hbox {d}\xi \end{aligned}$$

(B.1b)

$$\begin{aligned} \frac{{\sigma _{xx1} \left( {x,y} \right) }}{{2\mu _1 }}&= - \frac{1}{{2\pi }}I\int \limits _{ - \infty }^\infty {\xi \left[ {D_1 \hbox {e}^{ - \xi y} + \left( {\frac{{\kappa _1 - 3}}{{2\xi }} + y} \right) D_2 \hbox {e}^{ - \xi y} + D_3 \hbox {e}^{\xi y} + \left( {y - \frac{{\kappa _1 - 1}}{{2\xi }}} \right) D_4 \hbox {e}^{\xi y} } \right] } \hbox {e}^{ - i\xi x} \hbox {d}\xi \end{aligned}$$

(B.1c)

$$\begin{aligned} \frac{{\sigma _{yy1} \left( {x,y} \right) }}{{2\mu _1 }}&= \frac{1}{{2\pi }}I\int \limits _{ - \infty }^\infty {\,\xi \left[ {D_1 \hbox {e}^{ - \xi y} + \left( {\frac{{\kappa _1 + 1}}{{2\xi }} + y} \right) D_2 \hbox {e}^{ - \xi y} + D_3 \hbox {e}^{\xi y} + \left( {y - \frac{{\kappa _1 + 1}}{{2\xi }}} \right) D_4 \hbox {e}^{\xi y} } \right] } \hbox {e}^{ - i\xi x} \hbox {d}\xi \end{aligned}$$

(B.1d)

$$\begin{aligned} \frac{{\sigma _{yx1} \left( {x,y} \right) }}{{2\mu _1 }}&= - \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\xi \,\left[ {D_1 \hbox {e}^{ - \xi y} + \left( {\frac{{\kappa _1 - 1}}{{2\xi }} + y} \right) D_2 \hbox {e}^{ - \xi y} - D_3 \hbox {e}^{\xi y} - \left( {y - \frac{{\kappa _1 - 1}}{{2\xi }}} \right) D_4 \hbox {e}^{\xi y} } \right] } \hbox {e}^{ - i\xi x} \hbox {d}\xi \end{aligned}$$

(B.1e)

For the half-plane, the expressions of the displacements and stresses become [31]

$$\begin{aligned} u_2\left( {x,y} \right)&= \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {\;\left[ {\left( {E_1 + E_2 y} \right) \,\hbox {e}^{|\xi | y} } \right] } \,\,\hbox {e}^{ - i\xi x} \hbox {d}\xi \end{aligned}$$

(B.2a)

$$\begin{aligned} v_2\left( {x,y} \right)&= - \frac{1}{{2\pi }}I\int \limits _{ - \infty }^\infty {\,\left[ \frac{|\xi |}{\xi } {\left[ {-E_1 + \left( {\frac{\kappa _2 }{|\xi | } - y} \right) E_2 } \right] \,\hbox {e}^{|\xi | y} } \right] } \;\hbox {e}^{ - i\xi x} \hbox {d}\xi \end{aligned}$$

(B.2b)

$$\begin{aligned} \frac{{\sigma _{xx2} \left( {x,y} \right) }}{{2\mu _2 }}&= - \frac{1}{{2\pi }}I\int \limits _{ - \infty }^\infty {\xi \left[ {E_1 \hbox {e}^{ |\xi | y} + \left( {y-\frac{{\kappa _2 - 3}}{{2|\xi | }} } \right) E_2 \hbox {e}^{|\xi | y} } \right] } \hbox {e}^{ - i\xi x} \hbox {d}\xi \end{aligned}$$

(B.2c)

$$\begin{aligned} \frac{{\sigma _{yy2} \left( {x,y} \right) }}{{2\mu _2 }}&= \frac{1}{{2\pi }}I\int \limits _{ - \infty }^\infty {\,\xi \left[ {E_1 \hbox {e}^{ |\xi | y} + \left( {y-\frac{{\kappa _2 + 1}}{{2|\xi | }} } \right) E_2 \hbox {e}^{|\xi | y} } \right] } \hbox {e}^{ - i\xi x} \hbox {d}\xi \end{aligned}$$

(B.2d)

$$\begin{aligned} \frac{{\sigma _{yx2} \left( {x,y} \right) }}{{2\mu _2 }}&= - \frac{1}{{2\pi }}\int \limits _{ - \infty }^\infty {|\xi | \,\left[ {E_1 \hbox {e}^{ |\xi | y} + \left( {y-\frac{{\kappa _2 - 1}}{{2|\xi | }} } \right) E_2 \hbox {e}^{|\xi | y} } \right] } \hbox {e}^{ - i\xi x} \hbox {d}\xi \end{aligned}$$

(B.2e)

Applying the boundary conditions (17)(a–d) and (20) yields the following singular integral equation:

$$\begin{aligned} \eta \beta _4 \,p\left( x \right) + \frac{1}{\pi }\int \limits _{ - a}^b {p\left( t \right) \hbox {d}t} \left[ {\frac{{\beta _3 }}{{t - x}} + K_3 \left( {x,t} \right) + \eta \,K_4 \left( {x,t} \right) } \right] = \mu _1 \frac{x}{R} \quad \left( { - a< x < b} \right) \end{aligned}$$

(B.3)

where

$$\begin{aligned} {K_3}\left( {x,t} \right)&= \int \limits _0^\infty {\frac{1}{\Delta }\left[ {\left( { - 2\left( {1 + {\kappa _1}m} \right) \left( {1 + \frac{{{\kappa _2}}}{m}} \right) - 2\left( {{\kappa _2} - {\kappa _1}m} \right) \left( {1 - \frac{1}{m}} \right) {\hbox {e}^{ - 4\xi h}}} \right) + 1} \right] \sin \xi \left( {t - x} \right) \hbox {d}\xi } + \nonumber \\&\quad \int \limits _0^\infty {\frac{1}{\Delta }\left[ {\left( {8\xi h\left( {m - 1} \right) \left( {\frac{{{\kappa _2}}}{m} + 1} \right) {\hbox {e}^{ - 2\xi h}}} \right) + 1} \right] \sin \xi \left( {t - x} \right) \hbox {d}\xi } \end{aligned}$$

(B.4a)

$$\begin{aligned} {K_4}\left( {x,t} \right)&= \int \limits _0^\infty {\frac{1}{\Delta }} \left[ {\left( {2\left( {1 + {\kappa _1}m} \right) \left( {1 + \frac{{{\kappa _2}}}{m}} \right) - 2\left( {{\kappa _2} - {\kappa _1}m} \right) \left( {1 - \frac{1}{m}} \right) {\hbox {e}^{ - 4\xi h}}} \right) - 1} \right] \cos \xi \left( {t - x} \right) \hbox {d}\xi + \nonumber \\&\quad \int \limits _0^\infty {\frac{1}{\Delta }} \left[ {\left( { - 4\left( {\left( {{\kappa _1}m + \frac{{{\kappa _2}}}{m}} \right) + 2{\kappa _1}\frac{{1 - {\kappa _2}}}{{{\kappa _1} - 1}} + 4{\xi ^2}{h^2}\left( {\frac{{m - 1}}{{{\kappa _1} - 1}}} \right) \left( {\frac{{{\kappa _2}}}{m} + 1} \right) } \right) {\hbox {e}^{ - 2\xi h}}} \right) - 1} \right] \nonumber \\&\quad \cos \xi \left( {t - x} \right) \hbox {d}\xi \end{aligned}$$

(B.4b)

$$\begin{aligned} \beta _3&= - \frac{{1 + \kappa _1 }}{4}, \quad \beta _4 = \frac{{ - 1 + \kappa _1 }}{4}, \quad \kappa _1 = 3 - 4\nu _1 \end{aligned}$$

(B.4c)