1 Introduction

The use of timber as a construction material is on the rise due to its high strength-to-weight ratio and positive environmental impact, which constitutes an essential contribution to a sustainable future. Since timber products have a good load-bearing capacity under both compressive and tensile loading, they can be used for a multitude of structural components. Timber is a fully renewable resource with a low carbon footprint and high carbon storage capacity. Compared to other structural materials like concrete or steel, it can be more easily reused or recycled at the end of its life cycle (Ozyhar et al. 2013; Bengtsson et al. 2022). Due to their major benefits concerning sustainability, timber structures have developed rapidly during the last decades, not least as the result of the EU move toward more environmentally sustainable building practices (Vidal-Sallé and Chassagne 2007).

Timber, being a heterogeneous and orthotropic material, shows various constitutive relationships under tensile and compressive loading. Timber has unique and independent mechanical properties in three perpendicular axes defined by the grain direction: longitudinal (parallel to the grain), radial, and tangential (across the grain) (Fortino et al. 2009). Furthermore, the mechanical properties of timber including strength, the modulus of elasticity, shear modulus, and Poisson ratio are dependent on the grain direction. It should also be distinguished if the timber is loaded by compression or tension (Huč and Svensson 2018).

The viscoelastic material properties are required for a numerical simulation of the time-dependent behavior of wood. Numerous research considering the time-dependent characteristics of wood and wood composites has been carried out (Ranta-Maunus 1975; Bažant 1985; Hunt and Shelton 1987; Holzer et al. 1989; Toratti 1992; Liu 1994; Hanhijärvi and Hunt 1998). Whereas basic information about viscoelasticity is given in Nowacki (1965) and Lockett (1974) for example, bending creep tests can be found in Zhou et al. (1999) and Bengtsson and Kliger (2003). Tests under tensile and compressive loading can be found in Toratti and Svensson (2000). Theoretical investigations concerning constitutive laws and models were described by Kaliske (2000), Svensson and Toratti (2002), Hanhijärvi and Mackenzie-Helnwein (2003), Fortino et al. (2009).

2 Methods

2.1 Viscoelastic model based on Kelvin chain

2.1.1 Integral (Volterra) formulation

Volterra, by utilizing the theory of integral equations, was a major contributor to the theory of viscoelasticity. The Riesz representation theorem for a linear functional may be used to obtain the basic constitutive equations for linear materials with memory. They are given by

$$ \sigma = G * d\varepsilon = \int _{0}^{t} G \left ( t - \tau \right ) d\varepsilon \left ( \tau \right ), $$
(1)
$$ \varepsilon = J * d\sigma = \int _{0}^{t} J \left ( t - \tau \right ) d\sigma ( \tau ), $$
(2)

where the Stieltjes convolution integral is denoted by *, \(G\) and \(J\) denote the relaxation modulus and creep compliance, respectively, \(\sigma \) is the stress, \(\varepsilon \) is the strain, \(J\) is the Stieltjes inverse of \(G\), and, conversely, \(G\) is the Stieltjes inverse of \(J\).

The Stieltjes convolution theorem states that if \(f(t) \) and \(g(t)\) are equal to zero in the region \(t\in (-\infty ,0)\) and \(f\) and \(g^{(1)}\) are continuous in the interval \(t\in [0,-\infty )\), then

$$ f * dg = g \left ( 0 \right ) f + f * g^{\left ( 1 \right )}. $$
(3)

Thus we have

$$ \sigma \left ( t \right ) = G \left ( t \right ) \varepsilon \left ( 0 \right ) + \int _{0}^{t} G \left ( t - \tau \right ) \frac{d\varepsilon}{d\tau} d\tau $$
(4)

and

$$ \varepsilon \left ( t \right ) = J \left ( t \right ) \sigma \left ( 0 \right ) + \int _{0}^{t} J \left ( t - \tau \right ) \frac{d\varepsilon}{d\tau} d\tau . $$
(5)

Unfortunately, the kernel \(J(t-\tau )\) in the Volterra integral equation leads to a primitive integral-type formulation for creep analysis, in which the entire variable history must be stored and then used for the next step. This approach is only applicable for small-scale 1D or 2D analysis under simple loading, as its computational cost is affordable. However, for the structural analysis of the long-term behaviors of large creep-sensitive structures such as large-span shells, the computational cost will be extremely high if the entire variable history must be stored and available at every time step.

Furthermore, for large-scale structures, creep will strongly interact with other physical and mechanical phenomena, e.g., relaxation, damage, and environment variations, to name a few. These influencing phenomena are usually memory independent and thus not compatible with the integral-type formulation. Therefore, for large-scale creep structural analysis, it is necessary to convert the integral-type formulation to the rate-type algorithm for creep analysis.

2.1.2 Differential (rate-type) formulation

The realistic stress–strain relation based on the linear viscoelasticity can be approximated by the rheological models that are usually presented as systems of the Kelvin and Maxwell elements or their hybrids. For creep, a Kelvin chain is more convenient because a Maxwell chain requires converting the compliance function to a relaxation function, which adds numerical cost. After all, the compliance function (creep curve) is easier to obtain than the relaxation curve.

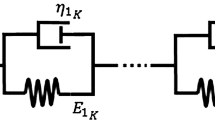
The specific (retardation) time \(\tau \) is a quantity that helps to distinguish between slow and fast creep using the generalized Kelvin chain. Creep shorter than \(0.05\tau \) is considered to be instantaneous, whereas almost no viscous effect is observed for creep longer than \(3\tau \). There are many phenomenological processes with various specific times in the real material. It is therefore necessary to use several segments with different specific times for the proper numerical description of creep development. Each segment contains a damper for the viscous response representation and a spring to represent the elastic response.

The Kelvin chain consists of these elements connected in series. To capture the instantaneous elastic strain, the first segment contains a solitary spring without a damper; see Fig. 1.

Fig. 1
figure 1

Generalized Kelvin chain schematic.

Full size image

The constitutive forms for the \(j\)th spring and \(j\)th damper with time-dependent properties, \(E_{j} (t)\) and \(\eta _{j} \left ( t \right )\), are

$$ \frac{d \sigma _{j}^{e}}{dt} = E_{j} \left ( t \right ) \frac{d \varepsilon _{j}}{dt}, $$
(6)
$$ \sigma _{j}^{v} = \eta _{j} \left ( t \right ) \frac{d \varepsilon _{j}}{dt}. $$
(7)

If the spring and damper in the element are connected in parallel, then the stresses add up and the strains are equal to

$$ \sigma _{j} = \sigma _{j}^{e} + \sigma _{j}^{v}, $$
(8)
$$ \varepsilon _{j} = \varepsilon _{j}^{e} = \varepsilon _{j}^{v}. $$
(9)

To obtain the constitutive formula for one element of the Kelvin chain, it is necessary to derive the stress and substitute the result into the previous relations for the spring and the damper:

$$ \frac{d \sigma _{j}}{dt} = \frac{d \sigma _{j}^{e}}{dt} + \frac{d \sigma _{j}^{v}}{dt} = E_{j} \left ( t \right ) \frac{d \varepsilon _{j}}{dt} + \frac{d \eta _{j}}{dt} \frac{d \varepsilon _{j}}{dt} + \eta _{j} \left ( t \right ) \frac{d^{2} \varepsilon _{j}}{d t^{2}}, $$
(10)
$$ \frac{d \sigma _{j}}{dt} = \left ( E_{j} \left ( t \right ) + \frac{d \eta _{j}}{dt} \right ) \frac{d \varepsilon _{j}}{dt} + \eta _{j} \left ( t \right ) \frac{d^{2} \varepsilon _{j}}{d t^{2}}. $$
(11)

Due to the serial connection of individual Kelvin elements, the form for the result stress is

$$ \sigma \left ( t \right ) = \sigma _{j} \left ( t \right ) = E_{0} \varepsilon _{0} \left ( t \right ), $$
(12)

and the form for the resulting strain of the Kelvin chain is

$$ \varepsilon \left ( t \right ) = \sum _{j =0}^{M} \varepsilon _{j} ( t ). $$
(13)

The differential equation for obtaining a single \(j\)th Kelvin element is

$$ \frac{d \varepsilon _{j}}{dt} + \frac{\eta _{j} \left ( t \right )}{D_{j} \left ( t \right )} \frac{d^{2} \varepsilon _{j}}{d t^{2}} = \frac{1}{D_{j} \left ( t \right )} \frac{d\sigma}{dt}, $$
(14)

where

$$ D_{j} \left ( t \right ) = E_{j} \left ( t \right ) + \frac{d \eta _{j}}{dt}. $$
(15)

\(M\) differential equations are derived with unknown variables \(\varepsilon _{j}\). The assumption is that the stress increment in the interval of \(\left \langle t_{i-1}, t_{i} \right \rangle \) is known. The initial conditions are the strain \(\varepsilon _{j} ( t_{i-1} )\) and the strain velocity \(\frac{d \varepsilon _{j}}{dt} ( t_{i-1} )\) at the end of the previous increment. The conditions for \(t_{0}\) are

$$ \varepsilon _{j} \left ( t_{0} \right ) =0, $$
(16)
$$ \frac{d \varepsilon _{j}}{dt} \left ( t_{0} \right ) = \frac{\sigma \left ( t_{0} \right )}{\eta _{j} \left ( t_{0} \right )}. $$
(17)

In case of constant stress \(\sigma \left ( t \right ) = \sigma _{0}\), due to the derived differential equation (17), the equation transforms into the following forms:

$$ \frac{d \varepsilon _{j}}{dt} + \tau _{j} \left ( t_{i - {1} / {2}} \right ) \frac{d^{2} \varepsilon _{j}}{d t^{2}} =0 $$
(18)

and

$$ \varepsilon _{j} \left ( t \right ) = J \left ( t, t_{0} \right ) \sigma _{0} $$
(19)

with the following analytical solution:

$$ \varepsilon _{j} \left ( t \right ) = \mathrm{C}_{1} + \mathrm{C}_{2} \exp \left ( - \frac{t}{\tau} \right ) $$
(20)

The integration constants \(C_{1}\) and \(C_{2}\) are

$$ \mathrm{C}_{1} = \frac{\sigma _{0} \tau}{\eta \left ( t_{0} \right )}, $$
(21)
$$ \mathrm{C}_{2} = \frac{\sigma _{0} \tau}{\eta \left ( t_{0} \right )} \exp \left ( \frac{t_{0}}{\tau} \right ). $$
(22)

The relation between the constant stress and strain is

$$ \varepsilon _{j} \left ( t \right ) = J ( t, t_{0} ) \sigma _{0}, $$
(23)

where

$$ J \left ( t, \mathrm{t}_{0} \right ) = \frac{1- \exp \left ( \frac{-t- t_{0}}{\tau} \right )}{D \left ( \mathrm{t}_{0} \right )} H \left ( t - \mathrm{t}_{0} \right ). $$
(24)

In the case of tasks with time-dependent stress, the assumption of constant stress during one time step is too restrictive, and it is more suitable to assume a linear change of stress over the time interval. This leads to a more stable calculation and more accurate results in every time step. Additionally, the time step can be larger. It is possible to solve the differential equation accurately for the time interval \(\left \langle t_{i-1}, t_{i} \right \rangle \) of the size \(\Delta t= t_{i} - t_{i-1}\). This is valid under the following assumptions:

$$ \frac{1}{D_{j} \left ( t \right )} \frac{d\sigma}{dt} = const, $$
(25)
$$ \tau _{j} \left ( t \right ) = \frac{\eta _{j} ( t )}{D_{j} ( t )} = const. $$
(26)

Thus the differential equation (14) simplifies to

$$ \frac{d \varepsilon _{j}}{dt} + \tau _{j} \left ( t_{i - {1} / {2}} \right ) \frac{d^{2} \varepsilon _{j}}{d t^{2}} = \frac{1}{D_{j} \left ( t_{i - {1} / {2}} \right )} \frac{\Delta \sigma}{\Delta t}, $$
(27)

where

$$ \Delta \sigma = \sigma \left ( t_{i} \right ) = \sigma \left ( t_{i -1} \right ). $$
(28)

The analytical solution of the simplified equation (27) is

$$ \varepsilon _{j} \left ( t \right ) = C_{1} + C_{2} \exp \left ( - \frac{t - t_{i -1}}{\tau _{j}} \right ) + \frac{\Delta \sigma}{\Delta t D_{j}^{( i - {1} / {2)}}} \left ( t - t_{i -1} \right ). $$
(29)

By differentiating this equation we obtain

$$ \dot{\varepsilon _{j}} \left ( t \right ) =- \frac{C_{2}}{\tau _{j}} \exp \left ( - \frac{t - t_{i -1}}{\tau _{j}} \right ) + \frac{\Delta \sigma}{\Delta t D_{j}^{( i - {1} / {2)}}}, $$
(30)

and by substituting \(t = t_{i -1}\), knowing the state variable of strain velocity of the \(j\)th element \(\varepsilon _{j}^{(i-1)}\) at the time of \(t_{i -1}\), we obtain a single equation containing one unknown constant of integration \(C_{2}\):

$$ - \frac{C_{2}}{\tau _{j}} + \frac{\Delta \sigma}{\Delta t D_{j}^{( i - {1} / {2)}}} = \dot{\varepsilon}_{j}^{\left ( i -1 \right )} \Rightarrow C_{2} = \frac{\tau _{j} \Delta \sigma}{\Delta t D_{j}^{( i - {1} / {2)}}} - \tau _{j} \dot{\varepsilon}_{j}^{\left ( i -1 \right )}. $$
(31)

The constant \(C_{1}\) is obtained by the substitution of \(C_{2}\) and state variables of the \(j\)th element, \(\varepsilon _{j}^{\left ( i-1 \right )}\) and \(\dot{\varepsilon}_{j}^{(i-1)}\), into the first nonderivative equation (29):

$$ C_{1} = \varepsilon _{j}^{\left ( i -1 \right )} + \tau _{j} \dot{\varepsilon}_{j}^{\left ( i -1 \right )} - \frac{\tau _{j} \Delta \sigma}{\Delta t D_{j}^{( i - {1} / {2)}}}. $$
(32)

By introducing the notation

$$ \beta _{j}^{\left ( i \right )} = \exp \left ( - \frac{\Delta t_{i}}{\tau _{j}} \right ), \lambda _{j}^{\left ( i \right )} = \frac{\tau _{j}}{\Delta t} \left ( 1- \beta _{j}^{\left ( i \right )} \right ) $$
(33)

we obtain the forms for strain and strain velocity of the \(j\)th element at time \(t_{i}\):

$$ \dot{\varepsilon}_{j}^{\left ( i \right )} = \beta _{j}^{\left ( i \right )} \dot{\varepsilon}_{j}^{\left ( i -1 \right )} + \frac{1- \beta _{j}^{\left ( i \right )}}{\Delta t D_{j}^{( i - {1} / {2)}}} \Delta \sigma , $$
(34)
$$ \varepsilon _{j}^{\left ( i \right )} = \varepsilon _{j}^{\left ( i -1 \right )} + \Delta t \lambda _{j}^{\left ( i \right )} \dot{\varepsilon}_{j}^{\left ( i -1 \right )} + \frac{1- \lambda _{j}^{\left ( i \right )}}{D_{j}^{i - {1} / {2}}} \Delta \sigma . $$
(35)

After substituting relations for a single Kelvin element derived above into the formula of Kelvin chain form, the relation becomes

$$ \varepsilon ^{( i )} = \sum _{j =0}^{M} \varepsilon _{j}^{\left ( i \right )} = \sum _{j =0}^{M} \varepsilon _{j}^{\left ( i -1 \right )} = \Delta t \sum _{j =1}^{M} = \lambda _{j}^{\left ( i \right )} \dot{\varepsilon}_{j}^{\left ( i -1 \right )} + \left ( \frac{1}{D_{0}^{( i - {1} / {2)}}} + \sum _{j =1}^{M} \frac{1- \lambda _{j}^{\left ( i \right )}}{D_{j}^{( i - {1} / {2)}}} \right ) \Delta \sigma $$
(36)

or, in the abbreviated form,

$$ \varepsilon ^{\left ( i \right )} = \varepsilon ^{\left ( i -1 \right )} +\Delta \varepsilon ^{v} + \frac{\Delta \sigma}{E^{ve}}, $$
(37)

where

$$ \Delta \varepsilon ^{v} =\Delta t \sum _{j =1}^{M} \lambda _{j}^{\left ( i \right )} \dot{\varepsilon}_{j}^{\left ( i -1 \right )} $$
(38)

and

$$ E^{ve} = \left ( \frac{1}{D_{0}^{( i - {1} / {2)}}} + \sum _{j =1}^{M} \frac{1- \lambda _{j}^{\left ( i \right )}}{D_{j}^{( i - {1} / {2)}}} \right )^{-1}. $$
(39)

The resulting formula for the stress increment calculation follows Jirásek and Zeman (2006):

$$ \Delta \sigma = E^{ve} \left ( \Delta \varepsilon -\Delta \varepsilon ^{v} \right ). $$
(40)

The advantages of the presented viscoelastic model consist of

  1. 1.

    the differential formulation using a generalized Kelvin chain and

  2. 2.

    the exact analytical integration of this differential formulation in a single time increment due to the assumption of a linear stress change in this time increment.

The assumption of linear stress change in a single time increment should be remembered while choosing the time-step size, for example, in the case of stress relaxation, when the stress development is nonlinear, it is necessary to divide the whole time interval into smaller time steps with nearly linear stress development.

From the mathematical point of view, the evolution equations are systems of second-order ODEs. An efficient and robust numerical scheme to generate solutions for both of these systems is the explicit fifth-order Runge–Kutta scheme with extended region of stability due to Ghosh and Lopez-Pamies (2021). For our purposes of practical creep calculations, it is possible to assume that the stress course in one time step is linear and thus there is no need to implement the explicit fifth-order Runge–Kutta scheme introduced by Lawson (1966) and Ghosh and Lopez-Pamies (2021). However, for highly nonlinear tasks, it would be better to use a robust scheme introduced to solve the governing initial-boundary value problem based on a conforming Crouzeix–Raviart finite-element discretization of space and a high-order accurate explicit Runge–Kutta discretization of time, which are particularly well suited to deal with the challenges posed by finite deformations and the incompressibility constraint of the rubber (Ghosh et al. 2021). Extreme care must be exercised in the choice of time-integration scheme based on a wide range of numerical experiments and comparisons with alternative implicit schemes, together with its proven success in integrating a variety of other types of nonlinear systems of first-order ODEs. The authors use the explicit fifth-order Runge–Kutta scheme introduced by Lawson (1966). A key advantage of this scheme is that it allows solving the problem explicitly. The governing equations of initial-boundary value problem are discretized into the system of coupled nonlinear algebraic equations.

All the forms above are stated for the description of uniaxial loading. For the purposes of the two- or three-dimensional theory, the relations for the realistic multiaxial loading need to be derived. It is necessary to take into account the orthotropic material characteristics of wood. The relations for the orthotropic plane are stated below. We use the following notation for the tree ring directions: \(x\) (\(L\)) for longitudinal, \(y\) (\(R\)) for radial, and \(z\) (\(T\)) for tangential directions.

The stress tensor components for 3D are written as the vector

$$ \boldsymbol{\sigma}^{( i )} = \boldsymbol{\sigma} \left ( t_{i} \right ) = \left ( \textstyle\begin{array}{l} \textstyle\begin{array}{c} \sigma _{x} \left ( t_{i} \right )\\ \sigma _{y} \left ( t_{i} \right )\\ \sigma _{xy} \left ( t_{i} \right ) \end{array}\displaystyle \\ \tau _{yz} ( t_{i} )\\ \tau _{xz} ( t_{i} )\\ \tau _{xy} ( t_{i} ) \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{l} \textstyle\begin{array}{c} \sigma _{L} \left ( t_{i} \right )\\ \sigma _{R} \left ( t_{i} \right )\\ \sigma _{LR} \left ( t_{i} \right ) \end{array}\displaystyle \\ \tau _{RT} ( t_{i} )\\ \tau _{LT} ( t_{i} )\\ \tau _{LR} ( t_{i} ) \end{array}\displaystyle \right ). $$
(41)

The stress \(\boldsymbol{\sigma}^{( i )}\) at the time step \(t_{i}\) is calculated from the known stress \(\boldsymbol{\sigma}^{( i-1 )}\) at the time step \(t_{i-1}\) and the stress increment \(\Delta \boldsymbol{\sigma}\):

$$ \boldsymbol{\sigma}^{( i )} = \boldsymbol{\sigma}^{( i-1 )} + \Delta \boldsymbol{\sigma} . $$
(42)

The stress increment is calculated as

$$ \Delta \boldsymbol{\sigma} = \mathbf{C}^{ve ( i )}:( \Delta \boldsymbol{\varepsilon} - \Delta \boldsymbol{\varepsilon}^{v} ), $$
(43)

where the stiffness matrix \(\mathbf{C}^{ve ( i )}\) is obtained by inverting the compliance matrix \(\mathbf{D}^{ve ( i )}\), which is stated using the effective viscoelastic modulus calculated from the 1D form (39).

The effective viscoelastic compliance matrix is defined as

$$ \mathbf{D}^{ve \left ( i \right )} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \frac{1}{E_{x}^{ve}} & \frac{- \nu _{yx}}{E_{y}^{ve}} & \frac{- \nu _{zx}}{E_{z}^{ve}} & 0 & 0 & 0\\ \frac{- \nu _{xy}}{E_{x}^{ve}} & \frac{1}{E_{y}^{ve}} & \frac{- \nu _{zy}}{E_{z}^{ve}} & 0 & 0 & 0\\ \frac{- \nu _{xz}}{E_{x}^{ve}} & \frac{- \nu _{yz}}{E_{y}^{ve}} & \frac{1}{E_{z}^{ve}} & 0 & 0 & 0\\ 0 & 0 & 0 & \frac{1}{2G_{yz}^{ve}} & 0 & 0\\ 0 & 0 & 0 & 0 & \frac{1}{2G_{xz}^{ve}} & 0\\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2G_{xy}^{ve}} \end{array}\displaystyle \right ], $$
(44)

and the effective viscoelastic stiffness matrix is its inversion:

$$ \mathbf{C}^{ve \left ( i \right )} = \left ( \mathbf{D}^{ve \left ( i \right )} \right )^{-1} = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \frac{1- \nu _{yz} \nu _{zy}}{E_{y} E_{z} \Delta} & \frac{\nu _{yx} + \nu _{zx} \nu _{yz}}{E_{y} E_{z} \Delta} & \frac{\nu _{zx} + \nu _{yx} \nu _{zy}}{E_{y} E_{z} \Delta} & 0 & 0 & 0\\ \frac{\nu _{xy} + \nu _{xz} \nu _{zy}}{E_{z} E_{x} \Delta} & \frac{1- \nu _{zx} \nu _{xz}}{E_{z} E_{x} \Delta} & \frac{\nu _{zy} + \nu _{zx} \nu _{xy}}{E_{z} E_{x} \Delta} & 0 & 0 & 0\\ \frac{\nu _{xz} + \nu _{xy} \nu _{yz}}{E_{x} E_{y} \Delta} & \frac{\nu _{yz} + \nu _{xz} \nu _{yx}}{E_{x} E_{y} \Delta} & \frac{1- \nu _{xy} \nu _{yx}}{E_{x} E_{y} \Delta} & 0 & 0 & 0\\ 0 & 0 & 0 & 2 G_{yz} & 0 & 0\\ 0 & 0 & 0 & 0 & 2 G_{zx} & 0\\ 0 & 0 & 0 & 0 & 0 & 2 G_{xy} \end{array}\displaystyle \right ), $$
(45)

where \(\Delta = \frac{1- \nu _{xy} \nu _{yx} - \nu _{yz} \nu _{zy} - \nu _{zx} \nu _{xz} - 2\nu _{xy} \nu _{yz} \nu _{zx}}{E_{x} E_{y} E_{z}}\).

The viscoelastic increment matrix \(D^{ve}\) contains the effective viscoelastic modules (see (49)). For \(k,l=x,y,z\), we have \(E_{kk}^{ve} = E_{k}^{ve}\) and \(E_{kl}^{ve} = G_{kl}^{ve}\), where

$$ E_{kl}^{ve} = \left ( \frac{1}{D_{kl,0}} + \sum _{j=1}^{M} \frac{1- \lambda _{kl,0}}{D_{kl,j}} \right )^{-1}. $$
(46)

The auxiliary variables are defined as \(\tau _{kl,j} = \frac{\eta _{kl,j}}{E_{kl,j}}\), \(\beta _{kl,j} = \exp \left ( \frac{- \Delta t}{\tau _{kl,j}} \right )\), and \(\lambda _{kl,j} = \frac{\tau _{kl,j}}{\Delta t} \left ( 1- \beta _{kl,j} \right )\).

The viscoelastic strain increment is then calculated as

$$ \Delta \varepsilon _{kl}^{v} = \Delta t \sum _{j=1}^{M} \lambda _{kl,j} \frac{d\varepsilon _{kl,j}^{(i-1)}}{dt}, $$
(47)

where the state variables from the previous time step \(t_{i-1}: \frac{d\varepsilon _{kl,j}^{(i-1)}}{dt}\) are used. These state variables from the previous time step are used for the actualization of the variables using

$$ \frac{d\varepsilon _{kl,j}^{(i)}}{dt} = \beta _{kl,j} \frac{d\varepsilon _{kl,j}^{(i-1)}}{dt} + \frac{1- \beta _{kl,j}}{\Delta t D_{kl,j}} \Delta \sigma _{kl}. $$
(48)

The retardation time of the \(j\)th Kelvin chain element in a specific material direction of wood is a fraction of the given viscosity and the elasticity modulus of the \(j\)th element in the specific material direction. These viscosity parameters and the modulus of elasticity are defined by fitting from the creep curves depending on time (Ozyhar et al. 2013; Bengtsson et al. 2022). For the purposes of this study, we use the particle swarm optimization method.

If the method of differential formulation were not used, it would be necessary to evaluate the compliance function \(i\) times to get the strain values at the \(i\)th time step. For \(n\) time steps, the compliance function would need to be evaluated \(1+2+\dots +n=\ n(n+1)/2\) times. The number of operations therefore increases with the square of the number of time steps, and the calculation time increases accordingly.

In the practical use of this numerical model, the stress and strain developments are not evaluated at a single point of the structure, but rather at many points distributed throughout the structure. In the case of simulation using the finite element method, these are the Gaussian integration points of all the elements into which the structure is divided. In addition, it is necessary to store the stress values in memory at all selected time steps for each integration point, because when computing \(\varepsilon _{tn}\), the values of \(\sigma _{ti}\) for every \(i\) from 0 to \(n\) must be known. This also increases the space complexity in proportion to the number of the time steps. As a result, direct numerical integration is only suitable for tasks with a low number of time steps and integration points.

For the large-scale computations, it is therefore necessary to have a more efficient method that removes the disadvantages of a numerical solution based on direct integration. The chosen approach is based on the differential formulation, i.e., on the description of the rheological model using a differential equation. In the case of a generalized Kelvin chain, the viscoelastic material behavior is described as a spring and damper system.

Denote by \(\varepsilon _{i}\) the numerical approximation of the strain \(\varepsilon _{ti} \) at the time step \(t_{i}\), \(i=0,\ 1,\ 2,\dots ,n\). If the value \(\varepsilon _{i-1}\) for the discrete time \(t_{i-1}\) is known from the previous time step, then the value of \(\varepsilon _{i}\) can be calculated by the approximate solution of the differential equation in the interval of [\(t_{i-1}, t_{i} \)]. Using common methods, the derivative \(\dot{\varepsilon} \) is approximated by the differential substitution \(\frac{\varepsilon _{i} - \varepsilon _{i-1}}{\Delta t} \), and the equation is written, for example, for the discrete time \(t_{i-1}\) (then it would be Euler’s backward method). The strain value \(\varepsilon _{i}\) can easily be calculated from the resulting linear equation, and the whole procedure can be repeated for the next time interval. The suggested process would be sufficient to highly varying stress, which leads to need to compute very short time steps to capture the stress development correctly. However, it often happens that the stress development is smooth even within a long period of time, and it is therefore possible to use longer time steps. The error evolved from the differential compensation then increases, and Euler’s forward method may eventually lose numerical stability as the time step exceeds a certain critical value, which yields unusable results.

The stated reasons led to the development of an alternative numerical method, which is based on the fact that for a constant right-hand side of the equation and constant coefficients, under the given assumptions, we are able to solve the differential equation analytically by the above-described exponential algorithm.

2.2 Identification of Kelvin chain parameters by particle swarm optimization

The Kelvin chain material model is a rheological scheme where the Kelvin–Voight models form a series. The compliance function for a single Kelvin–Voight model can be formulated by the equation

$$ J_{0} \left ( t \right ) = \frac{1}{E} \left ( 1- e^{- \frac{E}{\eta} t} \right ) H \left ( t \right ), $$
(49)

where \(H \left ( t \right ) =1\) for \(t>0\) and \(H \left ( 0 \right ) =0\).

The Kelvin chain model is able to approximate creep behavior in a better way due to higher number of parameters, which transform the compliance function to the so-called Dirichlet or Prony series:

$$ J_{0} \left ( t \right ) = \left [ \frac{1}{E_{0}} + \sum _{j =1}^{M} \frac{1}{E_{j}} \left ( 1- e^{- \frac{t}{\tau _{j}}} \right ) \right ] H \left ( t \right ), $$
(50)

where \(\tau _{j} = \frac{\eta _{j}}{E_{j}}\) is the retardation time. Utilization of the Kelvin chain material model for the practical analysis of the viscous response of structures is based on the measured or standardized relations between the creep coefficient and time. Therefore it is necessary to use the creep function as an input of the model instead of \(M\) unknown pairs of \(E_{j}\) and \(\tau _{j}\). The implemented algorithm identifying Kelvin chain parameters is designed to work with the creep function that is inverse to the above-mentioned compliance function. The approximation of the creep function via Dirichlet series was modified for the purpose of the algorithm into the following form:

$$ \varphi \left ( t \right ) = E_{0} + \sum _{j =1}^{M} E_{j} \left ( 1- e^{- \frac{t}{\tau _{j}}} \right ). $$
(51)

The problem of identifying unknown coefficients of experimental data series is described by Bažant and Wu (1973) with a proven use of the least squares method (LSM) for the determination of \(E_{j}\), where the values of retardation times \(\tau _{j}\) had been chosen empirically to ensure that coverage of the time axis in the logarithmic scale. Complete identification of all the parameters is possible by finding the roots of a polynomial whose coefficients are the determinants of matrices obtained from the approximated creep function and its derivatives (Bažant and Jirásek 2018). The identification of parameters can also be formulated as an optimization task. This approach is described by Distéfano (1970) and Pister (1972). These authors solved the identification problem using the nonlinear optimization method. It is possible to use more demanding modern optimization algorithms based on the imitation of natural processes with respect to actual computing power. This idea is used within the designed algorithm, where the optimization is solved using the particle swarm strategy (Kennedy and Eberhart 1995; Shi and Eberhart 1998).

The implemented identification algorithm is the combination of Bažant’s (1973) proposed LSM with the empirically determined values of \(\tau _{j}\) and the optimization with refined values, which is used to get an approximation of the user-defined creep curve as accurate as possible. The objective function was defined as an \(RMSE\) error,

$$ \mathrm{RMSE} = \sqrt{\frac{\sum _{i =1}^{n} \left ( y_{i}^{*} - y_{i} \right )^{2}}{n}}, $$
(52)

where \(y_{i}^{*}\) is the creep coefficient value obtained using the Dirichlet series, \(y_{i}\) is the user-defined creep coefficient value, and \(n\) is the number of points. Optimization constraints are defined by the inequalities

$$ 0.9 \tau _{j} \leq \tau _{j}^{*} \leq 1.1 \tau _{j}, $$
(53)

where \(\tau _{j}\) is the value of the empirically estimated retardation time, and \(\tau _{j}^{*}\) is the value of retardation time obtained using the particle swarm method.

2.3 Input material characteristics

For the purposes of this paper, the time-independent material properties are meant those that are stated immediately after the load application, and the time-dependent material properties are meant those that are stated after a certain time from the load application. These are the “secant” properties, which describe the constant stress to the strain value increased by the value of the viscoelastic creep strain. These time-dependent properties show the viscous behavior of material.

Two sets of the orthotropic material properties are presented to get the comparison of two approaches. In the first case the orthotropic empirical creep curve properties for beech wood are listed, which are used for Kelvin chain parameter identification. The second approach stemming from the Eurocode 5 (2004) standard uses the reduced values of the elasticity modulus for the time step \(t=365\) days (Table 1). The reduction is done using the creep coefficient

$$ \varphi = \frac{\varepsilon ^{c}}{\varepsilon ^{e}}, $$
(54)
$$ \varepsilon = \varepsilon ^{e} + \varepsilon ^{c} =(1+ \varphi ) \varepsilon ^{e}, $$
(55)
$$ \frac{\sigma}{E_{L,\mathrm{t}=365}} = \frac{\sigma}{E_{L,\mathrm{t}=0}} \left ( 1+ \varphi _{t=365} \right ), $$
(56)
$$ E_{L,\mathrm{t}=365} = \frac{E_{L,\mathrm{t}=0}}{(1+ \varphi _{t=365} )}. $$
(57)
Table 1 Engineering material properties of wood
Full size table

Longitudinal and radial experimental creep curves as model inputs are inspired by Ozyhar et al. (2013) and Bengtsson et al. (2022). The data were measured for shorter time periods, so extrapolation is used for the description of input creep coefficients (Fig. 2). The shape of the extrapolated curves is inspired by Endo and de Carvalho Pereir (2017), where the experimental data for glass fiber composite material are shown. Creep curves shown below in Fig. 2 were used for fitting the parameters of the Kelvin chain model.

Fig. 2
figure 2

Input creep curves of the creep coefficients at longitudinal and transversal directions inspired by Ozyhar et al. (2013) and Bengtsson et al. (2022).

Full size image

The experimental loading stresses for obtaining the creep curves in the Fig. 2 were 26.2 MPa in the longitudinal and 11.9 MPa in the radial direction, according to Ozyhar et al. (2013) and Bengtsson et al. (2022). The initial value of the shear modulus \(G_{LR, t =0}\) is taken from Milch et al. (2016). The shear time-dependent creep data were not available, which led to the application of the transversal creep curve for the description of shear creep, because the transversal creep is more intense than the longitudinal one.

2.4 Kelvin chain model validation

2.4.1 Numerical implementation of the initial boundary value problem

The orthotropic generalized Kelvin chain was algorithmized, programmed, and implemented into the FEM solver for shell (wall and plate) elements. Two major numerical approximations are necessary in the finite element solution of the generic initial boundary value problems:

  1. 1.

    A numerical integration scheme is introduced to solve the initial value problem defined by the constitutive equations of the model that relate stresses to the history of deformations. The original time-continuous constitutive equations are transformed into incremental (or time-discrete) counterparts.

  2. 2.

    A finite element discretization: this comprises a standard finite element approximation of the virtual work statement, where the domain of the body and the associated functional sets are replaced with finite-dimensional counterparts generated by finite element interpolation functions.

With the introduction of the above approximations, the original initial boundary value problem is reduced to a set of incremental (generally nonlinear) algebraic finite element equations to be solved at each time increment of the considered time interval. The solution of the associated algebraic system, with particular emphasis on the quadratically convergent Newton–Raphson algorithm.

2.4.2 Benchmark tests

Nine benchmark tests of the model were done, and the results were compared to standardized approach (Eurocode 5 2004). All the physical quantities are represented in the local (planar) coordinate system \(x\), \(y\), \(z\). The displacement in the \(x\)-direction is marked as \(u\), \(y\)-direction as \(v\), and \(z\)-direction as \(w\).

The benchmark tests geometries, loads, and boundary conditions are specified in Fig. 3. Geometries A1, A2, B1, B2, C, D1, D2, G1, and G2 are represented as a simple wall of \(1\times1\times1\) meters. Geometry E is 2 meters long and 0.4 meters high beam, and F is a composite wall made of a steel core and wooden walls.

Fig. 3
figure 3

Benchmark tasks specification.

Full size image

The tasks A1 and A2 are examples of 1D compression tests of pure creep with one boundary fixed. Load is applied in the longitudinal (A1) and radial (A2) directions. The tasks B1 and B2 are pure relaxation examples with a prescribed displacement and one fixed edge. Again, B1 is loaded parallelly to the wood grain and B2 across the grain. The benchmark task C shows the combination of creep and relaxation on a plane example with one edge constantly loaded and three fixed edges. The tests D1 and D2 show a deformation (deflection) of a bending plate with a surface load in the z-direction. The plate D1 is supported on two opposite edges, and D2 has supports on all the edges. The task E presents a maximal creep deflection of the beam in the middle of its length. The behavior of the wood–steel composite material (steel core covered by wooden walls) is presented in the task F. The last tasks G1 and G2 show a creep behavior of the wooden plate with time-dependent force development to present the influence of loading history via state variables. The task G1 compares the displacement caused by \(3F\) applied during whole time interval to the two-step load of \(F+2F\) and 2\(F+F\). The task G2 compares the displacement caused by \(2F\) applied during the entire time interval to the three-step load of \(2F-F+F\) and \(F-F+2F\).

3 Results and discussions

3.1 Identification of Kelvin chain parameters by particle swarm optimization results

This part of the study is focused on the influence of the number of the Kelvin chain elements on the form of the resulting approximation. The effect of the number of elements is described on two (longitudinal and radial) creep curves of wood loaded by tension. Every identification task with optimization performed for 50 particles and 1000 iterations of the algorithm was repeated 100 times.

The results showed that it is not possible to approximate the input curve with only three Kelvin chain elements. This conclusion is clearly demonstrated in Fig. 4 (upper left), where a fairly large deviation of the result from the input curve is visible. A value of the average RMSE error stated in Table 2 is orders of magnitude higher than in other examples.

Fig. 4
figure 4

The comparison of identified parameters and input creep curves.

Full size image
Table 2 Averaged RMSE errors
Full size table

The most accurate results are achieved when using five Kelvin–Voight elements in series. The averaged RMSE errors reached the values of \(0.001266289 \pm 1.27\cdot 10^{-4}\) for longitudinal creep tension and \(0.002733644 \pm 2.84\cdot 10^{-4}\) for radial creep tension. These results are graphically indistinguishable from the input curves. In the cases of seven and nine elements, the results are also accurate enough, but the averaged calculating time consumption of the single identification is 1.7 times higher for seven elements and 2.6 higher for nine elements; see Table 2. Visible differences can always be noted at the end of the curve, as shown in Fig. 4 (bottom left and right). These reasons led to the decision to use five Kelvin chain elements for the numerical model, because the time consumption in case of seven elements was lower, but the accuracy of the identification is almost the same.

3.2 Numerical simulation validation results

The orthotropic viscoelastic material model based on the generalized Kelvin chain is validated on the numerical benchmark tasks below. When taking account of creep according to Eurocode 5 (2004), stresses are assumed constant during the period of load application. The stress reduction without a change in strain (relaxation) is only taken into account to a limited degree in this standardized approach. If we assume a linear elastic behavior, then a proportionality could be presumed, and the structure response would also reflect the relaxation at the ratio of (\(1+\varphi \)). This correlation, however, is lost for the nonlinear stress–strain relationship. Thus it becomes clear that this procedure must be understood as an approximation. Therefore a reduction of the stresses due to relaxation and nonlinear creep cannot or can only be approximately represented by the standardized approach given by Eurocode 5 (2004). This is demonstrated in the following examples, where the dependence of the results on the size of the time step is shown for the individual load cases.

For the purposes of this study, the standardized approach was slightly modified (stiffness reducing), which allowed us to compare the results of Kelvin chain in various time-steps and, finally, in the case of stress redistribution.

3.2.1 A1 and A2: validation of the orthotropic generalized Kelvin chain on the pure creep example

Figure 5 shows the displacement during constant loading of walls in the longitudinal and radial directions. It is obvious that the Kelvin chain model shows identical results regardless of the time-step size (1, 10, and 100 increments). In both longitudinal and radial directions, these results also agree with the standardized approach, which uses the elasticity modulus reduction. This correlation was predicted in case of correct fitting of Kelvin chain parameters because of pure creep tasks. The correctness of Kelvin chain parameters fitting and the accuracy of model results for constant loading in the longitudinal and radial direction were confirmed by these tasks.

Fig. 5
figure 5

Tasks A1 and A2: displacement (deformation) in longitudinal (left side) and radial (right side) directions.

Full size image

3.2.2 B1 and B2: validation of the orthotropic generalized Kelvin chain on the pure relaxation example

Figure 6 shows stress development computed for the longitudinal and radial directions during holding the constant strain, the so-called relaxation. The Kelvin chain model shows different behavior at different time-step sizes. The results are dependent on the time-step number. In case of higher numbers of time steps, the results correspond to the standardized approach of elasticity modulus reduction in both directions. It can be observed that there is a difference between the final values of the stress for 1-, 10-, and 100-time increments. This slight difference was expected, and it is explained by a nonlinear time-dependent stress development in the pure relaxation task. It is clear from the above theory and assumptions of the Kelvin chain that this model is only accurate for a linear stress development. Therefore, with pure creep, one time increment is sufficient, because the stress is even constant, but in case of relaxation (nonlinear stress development), it is necessary to use more time steps (in the tasks B1 and B2, at least 10). This study presents advanced time integration of Kelvin chain, which assumes the linear change of the stress during the time-step. It would also be possible to use the direct integration method assuming constant stress during the entire time-step, but that would require many more time-steps – on the order of up to 1000 times more. This could significantly increase the total time of computation, and for a smaller number of time-steps, there would even be convergence problems (unstable computation, divergence, or oscillation), and, finally, the accuracy of the results would be very poor.

Fig. 6
figure 6

Stress development in longitudinal (left side) and radial (right side) directions.

Full size image

3.2.3 C: validation of the orthotropic generalized Kelvin chain on the example of the creep and relaxation combination

Task C presents the example of a board, which is loaded on its surface by a constant force operating in the longitudinal (\(x\)) direction and fixed in the radial (\(y\)) direction. The displacement in the longitudinal direction and the stress development in the radial direction were evaluated in Fig. 7. It can be observed that the Kelvin chain model gives identical results for any time-step size in the case of longitudinal displacement (creep), but in the radial direction, the stress development differs compared to the standardized approach. The relaxation results are now also dependent on the number of time-steps and, besides, significantly do not correlate with the standardized method of the elastic modulus reduction. The difference between these relaxation computation approaches is given by the orthotropy of the Kelvin chain model, which causes different behavior in the case of the multiaxial stress than in the case of the linear standardized method. This difference was also expected to occur because of the different nature of these approaches under multiaxial stress.

Fig. 7
figure 7

Displacement in longitudinal direction (left) and stress development in radial direction (right).

Full size image

3.2.4 D1 and D2: validation of the orthotropic generalized Kelvin chain on the bending plate test

Figure 8 shows two variants of the plate deflection development. The left side presents a plane supported on two opposite edges; the right side presents a plane supported on all the edges as shown in the Fig. 3. The stress dominates in the longitudinal (\(x\)) direction, and radial stress can be neglected in the task D1, which causes a good accordance of Kelvin chain model results to the standardized approach. In task D2, there are stresses in both longitudinal and radial directions, which causes the discordance between the model and standardized methods. These results were expected due to the different nature of the used methods applied on multiaxial stress. The orthotropic Kelvin chain model behaves differently than the standardized method of elastic modulus reduction. The results are independent of the number of time-steps, because the bending is almost the pure creep example without significant relaxation.

Fig. 8
figure 8

The displacement perpendicular to the plane of the plate (deflection). Task D1 (left side): plane supported on two opposite edges. Task D2 (right side): supports on all the edges.

Full size image

3.2.5 E: validation of the orthotropic generalized Kelvin chain on the bending wall test

The deformation of a plane model of the beam is shown in the Fig. 9. The results are independent of the number of time-steps, because of almost pure creep in this example. The stress occurs predominantly in the longitudinal (\(x\)) direction, which is the reason why the results of the Kelvin chain model correspond to the standardized approach.

Fig. 9
figure 9

Plane displacement of the wall in the \(y\)-direction.

Full size image

3.2.6 F: validation of the orthotropic generalized Kelvin chain on the compression hybrid wall test

The benchmark task F is focused on the relaxation of the composite material (wooden wall with steel core). The left side of Fig. 10 shows the stress development, which proves that the compressive stress decreases (relaxation) because of the steel core, which does not allow deformation (creep). On the other hand, the stress in the steel core increases (see Fig. 10, right side) because of the embracement of the relaxed stress from the wooden walls. A time-dependent stress development occurs in the steel core despite the assigned linear time-independent properties. It is a consequence of the time-dependent viscous behavior of wooden walls, which are connected to the steel core. The results are dependent on the number of time increments because the relaxation occurs. As the number of time increments increases, the results of Kelvin chain model converge more and more with the standardized method results. It is caused by the dominating uniaxial stress and the minimal perpendicular stress.

Fig. 10
figure 10

Stress development in wooden walls (left side) and in the steel core (right side).

Full size image

3.2.7 G: validation of the generalized Kelvin chain model on the example of varying load and its advantages

The tested viscoelastic model with the differential formulation based on the generalized Kelvin chain is finally tested on the task with varying load. Figure 11 shows that the Kelvin chain model is able to operate reliably even in the case of varying loading history without saving the state variables from all the time-steps. The state variables from the previous time-step are sufficient, which is the most significant advantage of this approach. It is obvious that the final values of displacement are highly dependent on the loading history in case of viscous models, as opposed to linear nonviscous models.

Fig. 11
figure 11

The benchmark test with varying load. Displacement in longitudinal direction on two-step (left side) and three-step (right side) loading examples.

Full size image

4 Conclusions

The time-dependent viscoelastic material model based on the orthotropic generalized Kelvin for wall and plate (shell) elements was algorithmized, programmed, and implemented into the FEM solver. This material model was validated, and it was confirmed that it is well applicable to creep calculations and, with an appropriate choice of the time step size, also for stress relaxation calculations, as shown in the validation tasks. Furthermore, it is shown how the model can consider the loading history without the need to store the state variables at all solved time-steps, which is a consequence of the differential formulation. The time step size influence on the results accuracy was analyzed. Since this model is suitable primarily for creep calculations, it has been proven that with a linear change of stress, only one time-step is sufficient to achieve an accurate result thanks to the exact exponential integration. If the stress develops nonlinearly, then it is necessary to solve the task in several time-steps, the size of which is determined by the degree of the nonlinearity of the stress development.

In conclusion, it can be stated that the analyzed viscoelastic material model can be used for all types of tasks if the time-step setting is suitably chosen, which is shown by the results of the performed benchmark tasks.