Experimental evaluation and uncertainty quantification for a fractional viscoelastic model of salt concrete

Abstract

This study evaluates and analyzes creep testing results on salt concrete of type M2. The concrete is a candidate material for long-lasting structures for sealing underground radioactive waste repository sites. Predicting operational lifetime and security aspects for these structures requires specific constitutive equations to describe the material behavior. Thus, we analyze whether a fractional viscoelastic constitutive law is capable of representing the long-term creep and relaxation processes for M2 concrete. We conduct a creep test to identify the parameters of the fractional model. Moreover, we use the Bayesian inversion method to evaluate the identifiability of the model parameters and the suitability of the experimental setup to yield a reliable prediction of the concrete behavior. Particularly, this Bayesian analysis allows to incorporate expert knowledge as prior information, to account for limited experimental precision and finally to rigorously quantify the post-calibration uncertainty.

1 Introduction

The disposal of radioactive waste in deep geological repository sites is accompanied by the problem of long-lasting and safe backfilling of deposits and drifts, such that containment is guaranteed and a contamination of the environment becomes extremely unlikely. The sealing of repositories in salt rock is performed by salt concrete and the concrete of type M2 (DBE 2004) is a candidate material for this objective in German disposal sites. The safety aspect and the extremely long operational lifetime of corresponding concrete structures require a profound knowledge of the material behavior including the mechanical properties. Particular phenomena of concrete, which have to be considered especially on long time scales, are creep and relaxation processes, which are generalized as viscoelastic material behavior (Christensen 2013; Lakes 1999; Creus 1986). The quantification of these phenomena is problematic and subject to large uncertainties.

Our study aims to model and predict the viscoelastic behavior of concrete M2. Therefore, accurate experiments, an appropriate model, experimental evaluation and model calibration with uncertainty analysis are required. Accordingly, we analyze creep tests with M2 specimens that run for about two years. To model the measured creep behavior, a fractional viscoelastic constitutive law (Bagley and Torvik 1985; Schmidt and Gaul 2002b; Mainardi 2010) was assessed, i.e. the material is modelled using fractional differential and integral operators (Samko et al. 1993; Oldham and Spanier 1974; Podlubny 1999; Diethelm 2010) in order to account for long-term creep over decades. Fractional calculus was used by several authors in the thirties and forties of the last century as an empirical method for describing viscoelastic material behavior, see the references in Mainardi (2010, Chap. 3.5). Particularly, Scott Blair (1947) used a fractional derivative of strain to model an intermediate material behavior interpolating between Hooke’s and Newton’s laws. Later, Koeller (1984) introduced the springpot¹ as a new rheological element that can be used in mechanical network models besides spring and dashpot, leading to a valid description of viscoelastic materials. A well-known model of this type is the fractional Zener model, see Mainardi (2010, Chap. 3.2), which is used in this article. The associated model parameters for concrete M2 are determined from the experimental data by a least-squares calibration and the identifiability of these parameters from the chosen experiments is evaluated by an informed Bayesian inversion (Congdon 2003; Besag et al. 1995).

The main question in this paper is whether a parameter identification for the considered model is possible from the given experimental data, particularly in view of the experimental duration which is short compared to the characteristic time scales of creep. More specifically, we examine the identifiability of the model parameters in terms of probability distributions. Thereby, we formulate a sufficient amount of constraints and reasonable soft information on the parameters in order to see how this influences or improves the parameter inference and whether it leads to plausible combinations of parameters with acceptable uncertainty intervals. Moreover, the differences between the results of least-squares calibration and Bayesian inversion are studied.

Well-known results on fractional calculus and the considered viscoelastic model are introduced in Sect. 2. The experimental setup, the data and their correspondence to the model parameters are illustrated in Sect. 3. After an introduction to Bayesian analysis and an explanation of the choice of prior parameter distributions in Sect. 4, the results of calibration and inference are discussed in Sect. 5 and the paper is concluded in Sect. 6.

2 Fractional calculus in viscoelastic constitutive equations

2.1 Introduction to linear viscoelasticity

The mechanical behavior of a deformable body, aside from the general principles of mechanics (i.e. equilibrium and compatibility equations), is determined by a characteristic material behavior specified by constitutive equations, which relate forces and deformations. Assuming only small displacements of the body, forces and deformations can be described by the Cauchy stress tensor $\boldsymbol{\sigma }$ and the infinitesimal strain tensor $\boldsymbol{\varepsilon }$ as defined in any textbook on continuum mechanics (Gurtin 1981). The characteristic property of a viscoelastic constitutive equation is that the stress at a certain time instant depends on the entire history of the strain and vice versa. Besides this memory hypothesis, three other assumptions lead to a quite general viscoelastic constitutive equation. These assumptions are

• causality (no future stress (resp. strain) state can affect the current strain (resp. stress) state),

• linearity (the principle of superposition holds),

• non-ageing (the material behavior is independent of shifts on the time scale).

The resulting viscoelastic constitutive equation is given by

$$ \varepsilon _{ij}(t)=\int _{-\infty }^{t} J_{ijkl}(t-\tau )\sigma _{kl}'( \tau )\mathrm{d}\tau , $$

(1)

see Christensen (2013), Creus (1986), Lakes (1999). Here, the functions $J_{ijkl}$ are known as creep functions and describe the strain increase of a material under a unit step stress (given by the Heaviside function $\Theta (t)$). Particularly, it follows from (1) by integrating the Dirac delta function

$$ \sigma _{kl}(t)=\sigma _{kl}^{0}\Theta (t)\quad \Rightarrow \quad \varepsilon _{ij}(t)=\sigma _{kl}^{0} J_{ijkl}(t). $$

(2)

An alternative representation of the constitutive law in terms of stress relaxation can be obtained by reversing the roles of stress and strain in (1). This so-called relaxation representation, see e.g. Christensen (2013, Chap. 1.2), is not considered here, as we are interested in modelling creep.

The general tensorial constitutive equations (1) can be simplified by using intrinsic symmetries of the stress and strain tensors as well as material symmetries. For the applications in this article, we consider the most simple case of isotropic material behavior. This leads to a description by only two remaining creep functions $J_{\mathrm{h}}$, $J_{\mathrm{d}}$, such that

$$\begin{aligned} \varepsilon _{\mathrm{h}}(t)&=\int _{-\infty }^{t} J_{\mathrm{h}}(t- \tau )\sigma _{\mathrm{h}}'(\tau )\mathrm{d}\tau , \end{aligned}$$

(3)

$$\begin{aligned} \boldsymbol{\varepsilon }_{\mathrm{d}}(t)&=\int _{-\infty }^{t} J_{\mathrm{d}}(t- \tau )\boldsymbol{\sigma }_{\mathrm{d}}'(\tau )\mathrm{d}\tau , \end{aligned}$$

(4)

where

$$ \begin{aligned} \varepsilon _{\mathrm{h}}&=\frac{1}{3}\varepsilon _{ii},\quad \sigma _{ \mathrm{h}}=\frac{1}{3}\sigma _{ii}, \\ \boldsymbol{\varepsilon }_{\mathrm{d}}&=\boldsymbol{\varepsilon }-\varepsilon _{ \mathrm{h}}\mathbf{I},\quad \boldsymbol{\sigma }_{\mathrm{d}}=\boldsymbol{\sigma }- \sigma _{\mathrm{h}}\mathbf{I} \end{aligned} $$

(5)

are the hydrostatic (subscript $\mathrm{h}$) and deviatoric (subscript $\mathrm{d}$) components of the strain tensor $\boldsymbol{\varepsilon }$ and the stress tensor $\boldsymbol{\sigma }$, see Gurtin and Sternberg (1962) for a detailed derivation. Hence, (3) and (4) are two one-dimensional independent functional equations that fully represent the constitutive law. Subsequently, we will omit the subscripts $\mathrm{h}$ and $\mathrm{d}$ of the creep functions as long as their general properties are discussed.

From energy considerations and using the principle of fading memory (Christensen 2013, Chap. 3), one can obtain monotonicity conditions for creep functions and their first and second derivatives, i.e.

$$ J(t)\geq 0,\quad \dot{J}(t)\geq 0,\quad \ddot{J}(t)\leq 0,\quad t \geq 0. $$

(6)

Moreover, as we are interested in describing viscoelastic solids, we assume an initial elastic material response and finite asymptotic creep, such that

$$ J(0)=J_{0}>0,\quad \lim _{t\to \infty }J(t)=J_{\infty }< \infty . $$

(7)

The most simple creep function that satisfies (6) and (7) is given by Christensen (2013, Chap. 1.5)

$$ J(t)=J_{0}+(J_{\infty }-J_{0})\left (1-\mathrm{e}^{- \frac{t}{\tau _{\varepsilon }}}\right ),\quad 0< J_{0}< J_{\infty }< \infty ,\ \tau _{\varepsilon }>0, $$

(8)

where $\tau _{\varepsilon }$ is a characteristic time quantity called retardation time. It determines the time scale in which creep takes place, see Fig. 1.

Fig. 1

Creep modeled by a single exponential function (Zener model)

As a mechanistic idea, the creep function (8) is associated with a mechanical network model consisting of two springs (modulus $E_{1},\ E_{2}$) and a dashpot (viscosity $\eta$), named Zener model (Zener 1948), see Fig. 2. Connecting Hooke’s law for a spring $\sigma =E\varepsilon$ and Newton’s law for a dashpot $\sigma =\eta \dot{\varepsilon }$, the Zener model is represented by an ordinary differential equation (Mainardi 2010)

$$ (E_{1}+E_{2})\sigma (t)+\eta \dot{\sigma }(t)=E_{1}E_{2}\varepsilon (t)+E_{1} \eta \dot{\varepsilon }(t), $$

(9)

which leads, under the assumption of a unit stress step at $t=0$ and the initial condition $J(0)=\frac{1}{E_{1}}$, to the creep function representation

$$ J(t)=\frac{1}{E_{1}}+\frac{1}{E_{2}}\left (1-\mathrm{e}^{- \frac{E_{2}}{\eta }t}\right ), $$

(10)

which is equivalent to (8) when defining the respective parameters by comparing the coefficients.

Fig. 2

Zener model

The applicability of the Zener model to fit real material data is limited as the creep process usually proceeds over a large time range. A possible improvement is given by the Prony series approach, considering several retardation times $\tau _{i},\ i=1,\dots ,n$, leading to a creep function

$$ J(t)=J_{0}+\sum _{i=1}^{n}J_{i}\left (1-\mathrm{e}^{- \frac{t}{\tau _{i}}}\right ),\quad \sum _{i=1}^{n}J_{i}=J_{\infty }-J_{0}. $$

(11)

However, a creep function of the form (11) fits the experimental creep data only in the measured time ranges and predicts a fast decay of creep outside the measured time span, which results in a bad extrapolation (Bagley and Torvik 1985; Schmidt and Gaul 2002a). A different approach, related to fractional calculus, leads to a solution of this problem, see Sect. 2.3.

2.2 Introduction to fractional calculus

The following terms and properties are well-known results from fractional calculus, see e.g. Diethelm (2010), Oldham and Spanier (1974), Podlubny (1999), Samko et al. (1993). Let $T>0$ and $f\in L_{1}(-\infty ,T]$ be an integrable function. The Liouville-Weyl fractional integral of $f$ of order $\alpha \in (0,1)$ is introduced as (Mainardi 2010)

$$ \mathrm{I}^{\alpha }f(t)=\int _{-\infty }^{t} \frac{(t-\tau )^{\alpha -1}}{\Gamma (\alpha )}f(\tau )\mathrm{d}\tau , \quad t\in [0,T], $$

(12)

where $\Gamma$ represents the Euler Gamma function

$$ \Gamma (\alpha )=\int _{0}^{\infty }u^{\alpha -1}\mathrm{e}^{-u} \mathrm{d}u, \quad \alpha >0. $$

(13)

It can easily be checked that (12) simplifies to a plain primitive of $f$ at the limit $\alpha \to 1$. To examine the limit for $\alpha \to 0$, consider the following. If, additionally, the function $f$ is absolutely continuous (in the sense of Samko et al. (1993, Chap. 2, Def. 6.1)) and $f$ and $f'$ vanish in an appropriate manner in the negative time limit, we obtain by partial integration of (12)

$$ \mathrm{I}^{\alpha }f(t)=\int _{-\infty }^{t} \frac{(t-\tau )^{\alpha }}{\Gamma (1+\alpha )}f'(\tau )\mathrm{d}\tau . $$

(14)

The representation (14) shows, that (12) is a plain identity for $\alpha \to 0$. Together, this provides the intuition that the fractional integral for $\alpha \in (0,1)$ is something between the identity and the first-order primitive.

Furthermore, the Liouville-Weyl fractional derivative of Caputo type of order $\alpha \in (0,1)$ of an absolutely continuous function $f$ is given as (Mainardi 2010)

$$ {^{\mathrm{C}}\mathrm{D}^{\alpha }}f(t)=\mathrm{I}^{1-\alpha } \dot{f}(t)=\int _{-\infty }^{t} \frac{(t-\tau )^{-\alpha }}{\Gamma (1-\alpha )}f'(\tau )\mathrm{d} \tau ,\quad t\in [0,T], $$

(15)

which is (one possible definition for) a left inverse of the operator $\mathrm{I}^{\alpha }$, i.e.

$$ {^{\mathrm{C}}\mathrm{D}^{\alpha }}\mathrm{I}^{\alpha }f=f,\quad f \in L_{1}(-\infty ,T], $$

(16)

see Samko et al. (1993, Chap. 2, § 6.2). Similar to the fractional integral, the fractional derivative interpolates between the identity and the first-order derivative. To see this, consider the fractional derivatives of the function $x(t)=t\,\chi _{(0,\infty )}(t)$ in Fig. 3, where $\chi _{(0,\infty )}$ is the unit function vanishing on $(-\infty ,0]$. Further details regarding fractional integrals and derivatives are given, e.g., in Oldham and Spanier (1974), Podlubny (1999), Diethelm (2010) and especially for functions with unbounded domains in Samko et al. (1993).

Fig. 3

Fractional Caputo derivative of the linear function $f(t)=t\,\chi _{(0,\infty )}(t)$ for various values of $\alpha \in [0,1]$

Before we explain the role of fractional calculus in viscoelasticity, we want to emphasize one more theoretical aspect, which is important for the further reasoning, i.e. we want to investigate the problem

$$ \begin{aligned} {^{\mathrm{C}}\mathrm{D}^{\alpha }}f(t)&=\gamma f(t)+\delta , \quad t\geq 0, \\ f(t)&=0,\quad t\leq 0, \end{aligned} $$

(17)

which represents a linear functional equation with a given initial function. (17) is equivalent to the fractional initial value problem

$$ \begin{aligned} {^{\mathrm{C}}\mathrm{D}_{0}^{\alpha }}f(t)&=\gamma f(t)+\delta , \quad t\geq 0, \\ f(0)&=0, \end{aligned} $$

(18)

where

$$ {^{\mathrm{C}}\mathrm{D}_{0}^{\alpha }}f(t)=\int _{0}^{t} \frac{(t-\tau )^{-\alpha }}{\Gamma (1-\alpha )}f'(\tau )\mathrm{d} \tau ,\quad t\in [0,T] $$

(19)

is the fractional Caputo derivative with zero initialization time. The difference from (15) is merely the lower integration bound. The solution of (18) contains the so-called one-parameter Mittag-Leffler function

$$ \mathrm{E}_{\alpha }(t)=\sum _{k=0}^{\infty }\frac{t^{k}}{\Gamma (\alpha k+1)}, $$

(20)

see Gorenflo et al. (2014) and is through Diethelm (2010, Thm. 7.2) given by

$$ f(t)=\frac{1}{\gamma }\int _{0}^{t} \delta \frac{\mathrm{d}}{\mathrm{d}\tau }\mathrm{E}_{\alpha }\left (\gamma \tau ^{\alpha }\right )\mathrm{d}\tau =\frac{\delta }{\gamma }\left [ \mathrm{E}_{\alpha }\left (\gamma \tau ^{\alpha }\right )\right ]_{0}^{t}=- \frac{\delta }{\gamma }\left (1-\mathrm{E}_{\alpha }\left (\gamma t^{\alpha }\right )\right ). $$

(21)

2.3 Fractional Zener model

Comparing (1) and (14), one can see, as in Mainardi (2010, Chap. 3), that a slowly increasing creep function of the form

$$ J(t)=\frac{1}{p}\frac{t^{\alpha }}{\Gamma (1+\alpha )},\quad p>0,\ \alpha \in (0,1) $$

(22)

leads to a (one-dimensional) constitutive law

$$ \varepsilon (t)=\frac{1}{p}\mathrm{I}^{\alpha }\sigma (t),\quad p>0,\ \alpha \in (0,1), $$

(23)

which is in view of (16) equivalent to

$$ \sigma (t)=p{^{\mathrm{C}}\mathrm{D}^{\alpha }}\varepsilon (t), \quad p>0,\ \alpha \in (0,1). $$

(24)

The constitutive law (24) defines another rheological element besides spring and dashpot, called springpot (Koeller 1984), which is depicted as a rhombus, see Fig. 4a. However, a springpot is not sufficient to describe a viscoelastic solid, because (22) satisfies (6) but not (7).

Fig. 4

Fractional viscoelastic models

In view of the classical Zener model, one can consider a spring (modulus $E_{1}$) in series with a springpot (parameters $p,\ \alpha$) with another spring (modulus $E_{2}$) in parallel, which is known as fractional Zener model (Mainardi 2010), see Fig. 4b. For the first spring one can obtain the creep function

$$ J_{1}(t)=\frac{1}{E_{1}}, $$

(25)

whereas the second spring parallel to the springpot leads to the problem

$$ \begin{aligned} {^{\mathrm{C}}\mathrm{D}^{\alpha }}J_{2}(t)&=-\frac{E_{2}}{p}J_{2}(t)+ \frac{1}{p},\quad t\geq 0, \\ J_{2}(t)&=0,\quad t\leq 0 \end{aligned} $$

(26)

of the form (17). Finally, using (21) leads to the overall creep function

$$ J(t)=J_{1}(t)+J_{2}(t)=\frac{1}{E_{1}}+\frac{1}{E_{2}}\left (1- \mathrm{E}_{\alpha }\left (-\frac{E_{2}}{p}t^{\alpha }\right )\right ). $$

(27)

The creep behavior according to (27) is shown in Fig. 5. The limit case $\alpha \to 1$ results in the classical Zener model (10), which shows creep in a small time range, whereas smaller values of $\alpha \in (0,1)$ lead to an extended time window of creep.

Fig. 5

Creep function of a fractional Zener model for $E_{1}=E_{2}=1~\text{GPa}$, $p=1~\text{GPa}\,\mathrm{d}^{\alpha }$ and various values of $\alpha \in (0,1)$

Comparing (8) with (27), one obtains a generalized retardation time

$$ \tau _{\varepsilon }=\left (\frac{p}{E_{2}}\right )^{\frac{1}{\alpha }}, $$

(28)

which again determines the characteristic time scale in which creep occurs. Finally, to obtain a full model for the three-dimensional material behavior, one can consider a long-term creep function of the form (27) for hydrostatic (3) and deviatoric (4) strain and stress components (Schmidt and Gaul 2002a), i.e. one can choose

$$\begin{aligned} J_{\mathrm{h}}(t)&=\frac{1}{E_{1,\mathrm{h}}}+ \frac{1}{E_{2,\mathrm{h}}}\left (1-\mathrm{E}_{\alpha _{\mathrm{h}}} \left (-\frac{E_{2,\mathrm{h}}}{p_{\mathrm{h}}}t^{\alpha _{\mathrm{h}}} \right )\right ), \end{aligned}$$

(29)

$$\begin{aligned} J_{\mathrm{d}}(t)&=\frac{1}{E_{1,\mathrm{d}}}+ \frac{1}{E_{2,\mathrm{d}}}\left (1-\mathrm{E}_{\alpha _{\mathrm{d}}} \left (-\frac{E_{2,\mathrm{d}}}{p_{\mathrm{d}}}t^{\alpha _{\mathrm{d}}} \right )\right ) \end{aligned}$$

(30)

in (3) and (4).

The model in (29) and (30) has eight parameters $E_{1,\mathrm{h}}>0$, $E_{2,\mathrm{h}}>0$, $p_{\mathrm{h}}>0$, $\alpha _{\mathrm{h}}\in (0,1)$, $E_{1,\mathrm{d}}>0$, $E_{2,\mathrm{d}}>0$, $p_{\mathrm{d}}>0$ and $\alpha _{\mathrm{d}}\in (0,1)$. All these parameters have to be chosen or calibrated to obtain a predictive model, and classical literature values from simpler models cannot easily be transferred. Therefore, experimental data and a calibration procedure (possibly taking into account uncertainties and soft information) must be used.

3 Experimental design and parameter fitting

For calibrating the parameters in (29) and (30), we use data from an experiment described in Sect. 3.1, followed by a discussion on parameter identification in Sect. 3.2 and a reparametrization for Bayesian inversion in Sect. 3.3.

3.1 Test record and data

We ran a series of tests at the Materials Testing Institute (MPA) of the University of Stuttgart from January 2019 to January 2021. These experiments consist of creep and shrinkage tests for three specimens made of concrete M2. The cylinder-shaped concrete bodies were produced at the Materials Testing Institute in Brunswick and the tests at the MPA Stuttgart started when the specimens were 56 days old.

Just before starting the tests, we determined the compressive strength of M2 as $25\text{ MPa}$ on average. The creep tests are driven at a constant compressive axial load of $8.3\text{ MPa}$, which is about $\frac{1}{3}$ of the compressive strength and hence small enough that no cracks occur during the tests.

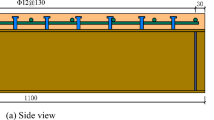
The shortening of the specimens in the axial direction is measured with the help of three dial gauges, while the lateral strain is determined using two strain gauges, see Fig. 6. The deformation is measured in the central part of the specimens, where the boundary effects have decayed and homogeneous stress and strain states can be assumed.

Fig. 6

Experimental setup of creep tests

In parallel with the creep tests, we measure the autogenic shrinkage of the unloaded specimens with dial gauges, as shrinkage is not covered by the constitutive model and has to be subtracted from the measured data to obtain the elastic and creep strains. The deformation data are recorded in logarithmic time steps, which is important for parameter identification. All details regarding the test series are summarized in Table 1. The results of the measurements are depicted in Fig. 7.

Fig. 7

Measured absolute values of axial and lateral strains for all specimens, mean strains and shrinkage with error bars representing empirical standard deviation

Table 1 Details of test series with concrete M2

For each of the three specimens, the strains measured by the multiple dial and strain gauges were averaged and shown together with error bars that represent an uncertainty of one empirical standard deviation. The bottom right graph shows the averages of the axial and lateral strain of the three specimens as well as the mean shrinkage.

3.2 Parametrization and parameter identification

In the given creep tests, we consider an approximately constant load that is applied (almost) instantaneously at the beginning of the test. This results in the stress history

$$ \boldsymbol{\sigma }(t)=\boldsymbol{\sigma }_{0}\Theta (t), $$

(31)

where $\boldsymbol{\sigma }_{0}$ is the initial stress with hydrostatic part $\sigma _{0,\mathrm{h}}$ and deviatoric part $\boldsymbol{\sigma }_{0,\mathrm{d}}$, and $\Theta (t)$ is still the Heaviside function. For this case, in view of (2) and using the constitutive laws (29) and (30), we obtain the strain components

$$ \begin{aligned} \varepsilon _{\mathrm{h}}(t)&=\sigma _{0,\mathrm{h}}\left ( \frac{1}{E_{1,\mathrm{h}}}+\frac{1}{E_{2,\mathrm{h}}}\left (1- \mathrm{E}_{\alpha _{\mathrm{h}}}\left (- \frac{E_{2,\mathrm{h}}}{p_{\mathrm{h}}}t^{\alpha _{\mathrm{h}}} \right )\right )\right ), \\ \boldsymbol{\varepsilon }_{\mathrm{d}}(t)&=\boldsymbol{\sigma }_{0,\mathrm{d}}\left ( \frac{1}{E_{1,\mathrm{d}}}+\frac{1}{E_{2,\mathrm{d}}}\left (1- \mathrm{E}_{\alpha _{\mathrm{d}}}\left (- \frac{E_{2,\mathrm{d}}}{p_{\mathrm{d}}}t^{\alpha _{\mathrm{d}}} \right )\right )\right ) \end{aligned} $$

(32)

for $t\geq 0$. For the specific compression test performed at the MPA, we consider stress and strain tensors that can be expressed in the principal coordinate system $I$ of the test cylinders (Fig. 8) as

$$ _{I}\boldsymbol{\sigma }= \begin{pmatrix} 0&0&0 \\ 0&0&0 \\ 0&0&\sigma _{zz} \end{pmatrix} ,\quad _{I} \boldsymbol{\varepsilon }= \begin{pmatrix} \varepsilon _{xx}&0&0 \\ 0&\varepsilon _{yy}&0 \\ 0&0&\varepsilon _{zz} \end{pmatrix} , $$

(33)

where $\sigma _{zz},\varepsilon _{zz}<0$ and $\varepsilon _{xx}=\varepsilon _{yy}>0$. The assumptions in (33) are justified by the uniaxial loading in $\mathbf{e}_{z}^{I}$-direction, the axisymmetry and the purely axial stretch in the principal directions of the specimens observed in the experiments, at least in the central area of the concrete bodies, where the measurements are performed. All quantities $\sigma _{zz},\varepsilon _{xx}=\varepsilon _{yy}, \varepsilon _{zz}$ that occur in (33) are measured within the experiments. A connection between (32) and (33) may be derived using (5) as

$$ \begin{aligned} _{I}\sigma _{\mathrm{h}}&=\frac{1}{3}\sigma _{zz},\quad _{I} \boldsymbol{\sigma }_{\mathrm{d}}=-\frac{1}{3}\sigma _{zz} \begin{pmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&-2 \end{pmatrix} , \\ _{I}\varepsilon _{\mathrm{h}}&=\frac{1}{3}(2\varepsilon _{xx}+ \varepsilon _{zz}),\quad _{I}\boldsymbol{\varepsilon }_{\mathrm{d}}= \frac{1}{3}(\varepsilon _{xx}-\varepsilon _{zz}) \begin{pmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&-2 \end{pmatrix} . \end{aligned} $$

(34)

Particularly, using (34), the constitutive law for the deviatoric components reduces to a scalar equation with

$$ _{I}\sigma _{\mathrm{d}}=-\frac{1}{3}\sigma _{zz},\quad _{I} \varepsilon _{\mathrm{d}}=\frac{1}{3}(\varepsilon _{xx}-\varepsilon _{zz}). $$

(35)

Fig. 8

Model of a concrete specimen with stress and strain state expressed in the inertial coordinate system

Finally, using (32) and (34) together with the measured data, we are able to identify the parameters in (29) and (30).

To illustrate the influence of its parameters, we show the creep function (27) of the fractional Zener model in a log-log plot (Fig. 5, Fig. 9) and study the resulting S-shaped graphs. Clearly, the initial value of the creep function corresponding to the purely elastic component of the material response is given by $E_{1}$ as

$$ J(0)=\frac{1}{E_{1}}. $$

(36)

The slope of the central part of the graph, i.e. the velocity of the creep, is determined by the parameter $\alpha$ (Fig. 5). A change in the springpot coefficient $p$ results in a shift of the graph along the time axis (Fig. 9a), whereas the parameter $E_{2}$ determines the asymptotic behavior as

$$ \lim _{t\to \infty }J(t)=\frac{1}{E_{1}}+\frac{1}{E_{2}}, $$

(37)

see Fig. 9b.

Fig. 9

Creep function of a fractional Zener model for $E_{1}=1~\text{GPa}$, $\alpha =0.5$

The parameter identification is performed in two qualitatively different steps. First, a best-fit calibration is obtained from a nonlinear least-squares optimization. Second, the parameters are considered as random variables and their (joint) probability distributions are determined depending on prior assumptions and the experimental results using Bayesian inversion. The results of the first method can be found in Sect. 5.1. The second method is introduced in Sect. 4 and evaluated and compared with the first method in the rest of Sect. 5.

3.3 Reparametrization for Bayesian inversion

For the Bayesian inversion, we consider a slightly different, reorganized parameter set than in (29) and (30). The reorganization does not change the model equations, but makes the problem more easily accessible to expert knowledge to obtain more informed prior probability distributions. Particularly, the elastic material response can be described by Young’s modulus $E$ and the Poisson’s ratio $\nu$, which are related to the original elastic parameters $E_{1,\mathrm{h}}$ and $E_{1,\mathrm{d}}$ as (Gurtin 1973, Sect. 22)

$$ E_{1,\mathrm{h}}=\frac{E}{1-2\nu },\quad E_{1,\mathrm{d}}= \frac{E}{1+\nu }. $$

(38)

Moreover, instead of using the parameters $p_{\mathrm{h}}$, $p_{\mathrm{d}}$ to identify the time range in which creep occurs, we consider characteristic retardation times $\tau _{\mathrm{h}}$, $\tau _{\mathrm{d}}$ as in (28), viz.

$$ \tau _{\mathrm{h}}=\left (\frac{p_{\mathrm{h}}}{E_{2,\mathrm{h}}} \right )^{\frac{1}{\alpha _{\mathrm{h}}}},\quad \tau _{\mathrm{d}}= \left (\frac{p_{\mathrm{d}}}{E_{2,\mathrm{d}}}\right )^{\frac{1}{\alpha _{\mathrm{d}}}}, $$

(39)

such that (32) can be reformulated as

$$ \begin{aligned} \varepsilon _{\mathrm{h}}(t)&=\sigma _{0,\mathrm{h}}\left ( \frac{1-2\nu }{E}+\frac{1}{E_{2,\mathrm{h}}}\left (1-\mathrm{E}_{ \alpha _{\mathrm{h}}}\left (-\left (\frac{t}{\tau _{\mathrm{h}}} \right )^{\alpha _{\mathrm{h}}}\right )\right )\right ), \\ \varepsilon _{\mathrm{d}}(t)&=\sigma _{0,\mathrm{d}}\left ( \frac{1+\nu }{E}+\frac{1}{E_{2,\mathrm{d}}}\left (1-\mathrm{E}_{ \alpha _{\mathrm{d}}}\left (-\left (\frac{t}{\tau _{\mathrm{d}}} \right )^{\alpha _{\mathrm{d}}}\right )\right )\right ) \end{aligned} $$

(40)

with new parameters $E>0$, $\nu \in (0,0.5)$, $E_{2,\mathrm{h}}>0$, $\alpha _{\mathrm{h}}\in (0,1)$, $\tau _{\mathrm{h}}>0$, $E_{2,\mathrm{d}}>0$, $\alpha _{\mathrm{d}}\in (0,1)$ and $\tau _{\mathrm{d}}>0$.

4 Bayesian analysis

4.1 Introduction to Bayesian inversion

Suppose we have the following forward model:

$$ \boldsymbol{d}= M(\boldsymbol{\theta }) + \boldsymbol{e}, $$

(41)

where $M$ is the deterministic model (40) together with (34), $\boldsymbol{\theta }$ denotes the vector of uncertain parameters $E$, $\nu$, $E_{2,\mathrm{h}}$, $\alpha _{\mathrm{h}}$, $\tau _{\mathrm{h}}$, $E_{2,\mathrm{d}}$, $\alpha _{\mathrm{d}}$, $\tau _{\mathrm{d}}$ for the model $M$, $\boldsymbol{d}$ represents the measurement data $(\varepsilon _{xx}(t_{i}),\varepsilon _{zz}(t_{i}))_{i=1,\dots , n}$, and $\boldsymbol{e}$ represents unavoidable measurement errors. The purpose of Bayesian inversion is to infer the posterior distribution of the uncertain model parameters $\boldsymbol{\theta }$ given prior knowledge about $\boldsymbol{\theta }$ and the measurement data $\boldsymbol{d}$.

The posterior distribution of the uncertain parameters $\boldsymbol{\theta }$ can be obtained through Bayes’ rule as (Congdon 2003)

$$ p(\boldsymbol{\theta }\mid \boldsymbol{d}) = \frac{p(\boldsymbol{\theta }) p(\boldsymbol{d}\mid \boldsymbol{\theta })}{p(\boldsymbol{d})} \propto p(\boldsymbol{\theta }) p(\boldsymbol{d}\mid \boldsymbol{\theta }), $$

(42)

where $p(\boldsymbol{\theta })$ is the prior distribution of the unknown parameters, which describes the prior knowledge (expert knowledge) about $\boldsymbol{\theta }$ independent of the data $\boldsymbol{d}$; $p(\boldsymbol{d}\mid \boldsymbol{\theta })$ is the likelihood function, which quantifies how probable are the measured data $\boldsymbol{d}$ for a given realization of uncertain parameters $\boldsymbol{\theta }$; and $p(\boldsymbol{d})$ is the so-called marginal likelihood.

The marginal likelihood $p(\boldsymbol{d})$ is a normalization factor for the posterior distribution. Since $p(\boldsymbol{d})$ is not a function of the parameters $\boldsymbol{\theta }$, it is often ignored when making inference of parameters. This allows the posterior distribution to be written as proportional to the product of prior and likelihood, as reflected in the last part of the equation (42) (Cary and Chapman 1988).

When representing experimental errors and imprecisions via a multivariate Gaussian distribution for $\boldsymbol{e}$ in (41), the likelihood function can be expressed as

$$ p(\boldsymbol{d}\mid \boldsymbol{\theta }) = \frac{\exp \left (-\frac{1}{2} (\boldsymbol{d}-M(\boldsymbol{\theta }))^{\mathrm{T}} \boldsymbol{\Sigma }^{-1}_{\boldsymbol{e}}(\boldsymbol{d}-M(\boldsymbol{\theta })) \right )}{\sqrt{ (2\pi )^{n_{d}} \det (\boldsymbol{\Sigma _{e}}) }} , $$

(43)

where $\boldsymbol{\Sigma _{e}}$ is the covariance matrix of the error term $\boldsymbol{e}$ and $n_{d}$ is the number of measurements. In this work, the number of measurements is $n_{d} = 2n$, where $n$ is the number of time steps in which we obtain strain data from the experiments. The variance² of the error term $\boldsymbol{e}$ is set as $s_{\boldsymbol{e},x}^{2} = \left (0.1\mathrm{\frac{mm}{m}}\right )^{2}$ for $(\varepsilon _{xx}(t_{i}))_{i=1,\dots , n}$ and $s_{\boldsymbol{e},z}^{2} = \left (0.5\mathrm{\frac{mm}{m}}\right )^{2}$ for $(\varepsilon _{zz}(t_{i}))_{i=1,\dots , n}$ according to the maximal empirical variances in the experiments (see Fig. 7). The covariance matrix $\boldsymbol{\Sigma _{e}}$ is a diagonal matrix with the diagonal elements $s_{\boldsymbol{e},x}^{2}$ (first element to $n$th element) and $s_{\boldsymbol{e},z}^{2}$ ($(n+1)$th element to the last element), which assumes the independence of the measurement errors.

A powerful tool for solving Bayesian inversion problems is the Markov chain Monte Carlo (MCMC) method (Besag et al. 1995; Worden and Hensman 2012). In this work, we will use the popular Metropolis-Hastings algorithm (Hastings 1970) to solve our problem.

4.2 Choice of prior distributions of model parameters

Choosing proper prior distributions for the model parameters is important for Bayesian inversion. In this work, we choose the prior distributions as follows. Associated samplings and plots are given in Sect. 5 in Figs. 11 and 13.

Young’s modulus $E$ : log-normal distribution

Young’s modulus $E$ is purely positive and can vary by orders of magnitude (i.e., it makes sense to look at $\ln {E}$). We have expectations (mean value) of $E$ from external data (see below), and these data show roughly symmetric scattering (standard deviation). To accommodate these pieces of information, we need a purely positive 2-parameter distribution on the log-scale that can be roughly symmetric. On the log-scale with a given mean and variance, the log-normal distribution is the max-entropic distribution (least information), and it is relatively symmetric after the back-transformation if the standard deviation is small compared to the mean.

From the literature (DBE 2004, Sect. 6.2), we get the mean and variance of $E$ as $\mu _{E} = 13.5$ GPa and $s_{E}^{2} = \left (1.5~\text{GPa}\right )^{2}$.³ Then, we can calculate the corresponding parameters for the log-normal distribution as (Krishnamoorthy 2015)

$$ \mu = \ln \left ( \frac{\mu _{E}^{2}}{\sqrt{\mu _{E}^{2}+s_{E}^{2}}} \right ) \approx 2.6\,, \qquad s^{2} = \ln \left ( 1 + \frac{s_{E}^{2}}{\mu _{E}^{2}} \right ) \approx 0.012\,. $$

(44)

Poisson’s ratio $\nu$: beta distribution

Poisson’s ratio $\nu$ is bounded between 0 and 0.5, and we expect it to be mostly below 0.4, and typically around 0.3 (DBE 2004, Sect. 6.3). Therefore, we need a two-side-bounded distribution with two parameters (to tune the mean and the standard deviation). We see no specific reason for a symmetric distribution of $\nu$. As the beta distribution (Krishnamoorthy 2015) is a bounded 2-parameter distribution with flexible shape, it is a good choice. Since the original beta distribution is defined on the interval $[0,1]$, we will use a scaled beta distribution for $\nu$ as $2\nu \sim \mathrm{Beta}(\alpha ,\beta )$ with $\alpha = 8$ and $\beta = 4$, which leads to a desired maximum probability density at about 0.3.

$E_{2,\mathrm{h}}$ and $E_{2,\mathrm{d}}$ : improper distribution

All we know about $E_{2,\mathrm{h}}$ and $E_{2,\mathrm{d}}$ is that they are positive. We have made the observation that over geological time scales and geological pressures rocks can act like fluids. And as design engineers, we fear that concrete may do the same. Hence, we choose the prior PDF $p(\theta ) \sim 1/\theta$ for both $E_{2,\mathrm{h}}$ and $E_{2,\mathrm{d}}$, because it puts a lot of the probability mass close to zero (which is the limiting case of asymptotically viscous behavior). This distribution is often suggested for variables where no other information than positivity exists (Robert et al. 2009), and it is the limiting case of the log-normal distribution for $s_{E_{2}}\to \infty$. Although this is a so-called improper distribution (without normalization), it is enough for MCMC simulation.

$\alpha _{\mathrm{h}}$ and $\alpha _{\mathrm{d}}$ : uniform distribution

In the given model, the admissible intervals for $\alpha _{\mathrm{h}}$ and $\alpha _{\mathrm{d}}$ are $[0,1]$. We know nothing more than the interval over $\alpha _{\mathrm{h}}$ and $\alpha _{\mathrm{d}}$. Because the uniform distribution is the max-entropic (least information) distribution under these conditions (Robert et al. 2009), we choose the prior distribution $U(0,1)$ for both $\alpha _{\mathrm{h}}$ and $\alpha _{\mathrm{d}}$.

$\tau _{\mathrm{h}}$ and $\tau _{\mathrm{d}}$ : tailored improper distribution

For the retardation time $\tau$, we know that it is positive, and we believe that all orders of magnitude are equally probable. Hence, we start from a uniform prior on the real axis for $\log {\tau }$ (which is similar to the assumptions for $E_{2,\mathrm{h}}$ and $E_{2,\mathrm{d}}$), but then softly exclude the cases that would be implausibly fast. This leads to a soft lower bound expressed by the CDF of the standard normal distribution. Thus, our PDF of the chosen prior distribution for both $\log {\tau _{\mathrm{h}}}$ and $\log {\tau _{\mathrm{d}}}$ can be expressed as

$$ p(\log (\tau )) = \Phi \left ( \frac{\log (\tau ) - \log (\tau _{0})}{s_{\log (\tau )}} \right ), $$

(45)

where $\Phi$ is the CDF of the standard normal distribution, $\tau _{0} = 1000$ d, and $s_{\log (\tau )} = 1$.

Besides the univariate choice of parameters described above, there are some further constraints relating several of the model parameters. These joint constraints result from the assumption that the lateral strain of the specimens is positive and monotonically increasing. An opposite behavior is only known from materials with a special micro-structure and cannot be supposed to occur for concrete without phase transition (which is implausible in our experiments). Necessary conditions for increasing lateral strain can be derived by considering the relations

$$ \begin{aligned} \varepsilon _{xx}= _{I}\!\varepsilon _{\mathrm{h}}+ _{I}\! \varepsilon _{\mathrm{d}}&=\sigma _{0,\mathrm{h}}J_{\mathrm{h}}+ \sigma _{0,\mathrm{d}}J_{\mathrm{d}},\quad \dot{\varepsilon }_{xx}= \sigma _{0,\mathrm{h}}\dot{J}_{\mathrm{h}}+\sigma _{0,\mathrm{d}} \dot{J}_{\mathrm{d}}, \\ \sigma _{0,\mathrm{h}}&=\frac{1}{3}\sigma _{zz}< 0,\ \sigma _{0, \mathrm{d}}=-\frac{1}{3}\sigma _{zz}>0 \end{aligned} $$

(46)

according to (34) using (29) and (30). For $\varepsilon _{xx}$ to be positive, the limits $t\to 0$ and $t\to \infty$ in (29) and (30), using (46), result in the conditions

$$ \frac{1}{E_{1,\mathrm{h}}}< \frac{1}{E_{1,\mathrm{d}}} $$

(47)

and

$$ \frac{1}{E_{1,\mathrm{h}}}+\frac{1}{E_{2,\mathrm{h}}}< \frac{1}{E_{1,\mathrm{d}}}+\frac{1}{E_{2,\mathrm{d}}}, $$

(48)

respectively. The first condition (47) is, in view of (38), equivalent to $\nu >0$ and hence automatically fulfilled by the chosen univariate prior distribution for $\nu$. The second condition (48) provides an additional constraint. To obtain conditions for $\dot{\varepsilon }_{xx}$ to be positive, we consider the approximation of the Mittag-Leffler function for $t\to 0$ and $t\to \infty$, viz.

$$ \mathrm{E}_{\alpha }\left (-\left (\frac{t}{\tau }\right )^{\alpha }\right )\sim 1-\frac{1}{\Gamma (1+\alpha )}\left (\frac{t}{\tau } \right )^{\alpha }+\mathcal{O}(t^{2\alpha }),\quad t\rightarrow 0+ $$

(49)

and

$$ \mathrm{E}_{\alpha }\left (-\left (\frac{t}{\tau }\right )^{\alpha }\right )\sim \frac{1}{\Gamma (1-\alpha )}\left (\frac{t}{\tau }\right )^{- \alpha }+\mathcal{O}(t^{-2\alpha }),\quad t\rightarrow \infty , $$

(50)

see Erdélyi (1953, p. 210, (21)). Using these properties in (29) and (30) (omitting subscripts) leads to the expansions

$$ J(t)\sim \left \lbrace \textstyle\begin{array}{l @{\quad }l} \frac{1}{E_{1}}+\frac{1}{E_{2}\Gamma (1+\alpha )}\left ( \frac{t}{\tau }\right )^{\alpha }+\mathcal{O}(t^{2\alpha }) & t \rightarrow 0+, \\ \frac{1}{E_{1}}+\frac{1}{E_{2}}\left (1-\frac{1}{\Gamma (1-\alpha )} \left (\frac{t}{\tau }\right )^{-\alpha }\right )+\mathcal{O}(t^{-2 \alpha }) & t\rightarrow \infty \end{array}\displaystyle \right . $$

(51)

and

$$ \tau \dot{J}(t)\sim \left \lbrace \textstyle\begin{array}{l @{\quad }l} \frac{\alpha }{E_{2}\Gamma (1+\alpha )}\left (\frac{t}{\tau }\right )^{ \alpha -1}+\mathcal{O}(t^{2\alpha -1}) & t\rightarrow 0+, \\ \frac{\alpha }{E_{2}\Gamma (1-\alpha )}\left (\frac{t}{\tau }\right )^{- \alpha -1}+\mathcal{O}(t^{-2\alpha -1}) & t\rightarrow \infty , \end{array}\displaystyle \right . $$

(52)

where (52) together with (46) finally reveals the necessary condition

$$ \alpha _{\mathrm{h}}>\alpha _{\mathrm{d}}$$

(53)

for $\dot{\varepsilon }_{xx}>0$. The conditions (48) and (53) are used as additional constraints on Bayesian inversion, leading to joint prior distributions. A summary of the chosen prior distributions is given in Table 2.

Table 2 Summary of the chosen prior distributions

5 Results and discussion

5.1 Quality of fit

A parameter fitting was obtained for the mean experimental data using a weighted nonlinear least squares method (squared residuals weighted by $\frac{1}{s_{\boldsymbol{e}}^{2}}$, where $s_{\boldsymbol{e},x}^{2} = \left (0.1~\frac{\text{mm}}{\text{m}}\right )^{2}$ for $(\varepsilon _{xx}(t_{i}))_{i=1,\dots , n}$ and $s_{\boldsymbol{e},z}^{2} = \left (0.5~\frac{\text{mm}}{\text{m}}\right )^{2}$ for $(\varepsilon _{zz}(t_{i}))_{i=1,\dots , n}$). As implementation we choose MATLAB’s lsqnonlin.m. The corresponding optimal parameters are

$$ \begin{aligned} E&=9.38~\text{GPa},\quad \nu =0.17,\quad E_{2,\mathrm{h}}=3.32~\text{GPa},\quad E_{2,\mathrm{d}}=2.04~\text{GPa}, \\ \alpha _{\mathrm{h}}&=0.62,\quad \alpha _{\mathrm{d}}=0.42,\quad \tau _{\mathrm{h}}=14.79\,\mathrm{d},\quad \tau _{\mathrm{d}}=5.11\, \mathrm{d}\end{aligned} $$

(54)

and the resulting predicted curves for hydrostatic and deviatoric components together with experimental data are shown in Fig. 10. The fitted curves provide a good representation of the experimental results and it is shown that the slow creep process of concrete M2 is (at least over the experimental duration) well described by the fractional Zener model. Small deviations, plausibly due to measurement errors just after loading the specimens, are visible. The fit of the deviatoric strain component is slightly better than for the hydrostatic part. For the visibly deviant data points we included $\pm 2s_{\boldsymbol{e}}$ error bars ($\sim 95\%$ confidence level) into the figure to demonstrate the likely explanation by measurement inaccuracies. We omitted the other intervals to avoid cluttering the figures.

Fig. 10

Results of parameter identification using the method of weighted nonlinear least squares with selected error bars showing a $\sim 95$% confidence level

5.2 Identified parameter distributions

A Bayesian inversion was performed in view of the experimental data and assumed prior information of Sect. 4.2 using an MCMC with $N=5\cdot 10^{7}$ samples. The resulting marginal histograms of the posterior distributions for the eight model parameters are shown in Fig. 11 together with the sampled prior distributions. Furthermore, the parameters (54) from the least-squares calibration (best fit) as well as the samples with the maximal likelihood value (ML) and with the maximal posterior probability (MAP) are visualized in the histograms. The histograms show comparably smooth unimodal distributions. The best fit and the ML sample are close, which indicates a good mixing in the MCMC. To understand this argument, note that the (weighted) least squares calibration and the maximum likelihood fit are, under the condition of a Gaussian likelihood, analytically identical.

Fig. 11

Posterior and prior marginal histograms together with best fit, ML and MAP

Marginal posterior distributions are in some cases widespread (Fig. 11g, Fig. 11h) and partly similar to the prior distributions (Fig. 11a, Fig. 11b). This indicates weakly informative data, i.e. the prior information influences the posterior distributions more than the knowledge from the experimental results. This assertion is supported by the location of the ML and MAP samples. The distance between ML and MAP is quite large and the MAP is typically located in regions of high prior probability. Possible reasons for the weak inference of the parameters are given by the relatively large empirical variation of the experimental results⁴ (Fig. 7) and a remaining compensation among the parameters. The latter statement becomes visible in the scatter plots in Fig. 12, showing two-dimensional projections of parameter correlations. Particularly, the triples $(E_{2,\mathrm{h}},\alpha _{\mathrm{h}},\log (\tau _{\mathrm{h}}))$ and $(E_{2,\mathrm{d}},\alpha _{\mathrm{d}},\log (\tau _{\mathrm{d}}))$ show strong correlations. This indicates that a plain least squares optimization is inappropriate because it fails to quantify the remaining uncertainties that are substantial and nonlinear in this case.

Fig. 12

Scatter plots of identified parameters

5.3 Comparing constrained and unconstrained priors

The univariate prior distributions given in Sect. 4.2 are additionally constrained by the conditions (48) and (53), leading to joint priors for $E_{2,\mathrm{h}}$, $E_{2,\mathrm{d}}$, $\alpha _{\mathrm{h}}$ and $\alpha _{\mathrm{d}}$. The constrained and unconstrained prior distributions as well as the associated posterior distributions are shown in Fig. 13. As (48) suggests, the univariate prior distribution of $E_{2,\mathrm{h}}$ is shifted to larger values, whereas lower values of $E_{2,\mathrm{d}}$ show a higher probability. Similarly, (53) renders larger values of $\alpha _{\mathrm{h}}$ and smaller values of $\alpha _{\mathrm{d}}$ more likely. Particularly, the uniform marginal priors of $\alpha _{\mathrm{h}}$ and $\alpha _{\mathrm{d}}$ become linear distributions due to the constraint (53). The posterior distributions of $E_{2,\mathrm{h}}$ and $E_{2,\mathrm{d}}$ substantially change under the influence of the additional constraints, whereas $\alpha _{\mathrm{h}}$ and $\alpha _{\mathrm{d}}$ are only slightly affected.

Fig. 13

Comparison of joint and unconstrained prior distributions

5.4 Comparison to calibration optimization

The graphs in Fig. 11 show a relatively wide gap between the parameter set (54) obtained from the least squares calibration and the MAP

$$ \begin{aligned} E&=13.48~\text{GPa},\quad \nu =0.31,\quad E_{2,\mathrm{h}}=0.20~\text{GPa}, \quad E_{2,\mathrm{d}}=0.16~\text{GPa}, \\ \alpha _{\mathrm{h}}&=0.16,\quad \alpha _{\mathrm{d}}=0.12,\quad \tau _{\mathrm{h}}=1.346\cdot 10^{10}\,\mathrm{d},\quad \tau _{ \mathrm{d}}=4.461\cdot 10^{11}\,\mathrm{d}\end{aligned} $$

(55)

resulting from the MCMC. As already mentioned in Sect. 5.2, this indicates weakly informative experimental data. This reconfirms the importance of a Bayesian analysis, already stated in Sect. 5.2. However, the argument this time is that the expert knowledge, literature values and plausibility constraints that can be used in Bayesian analysis significantly influence the result, which can once again be decision relevant.

5.5 Overall assessment

Another remarkable result of the MCMC is the gap between the global maximum of the multivariate posterior distribution (i.e. of MAP) and the maxima in the marginal histograms of $E_{2,\mathrm{h}}$ (Fig. 11c), $\log (\tau _{\mathrm{h}})$ (Fig. 11g) and $\log (\tau _{\mathrm{d}})$ (Fig. 11h). This indicates a highly nonlinear interrelation of the parameters in the joint posterior distribution. In order to check the plausibility of the location of the MAP, we consider bar plots in Fig. 14 that show the maximal posterior density within the classes of the posterior histogram. The bar plots maximize, where the MAP lies (as expected). Particularly, the plots for $\log (\tau _{\mathrm{h}})$ (Fig. 14g) and $\log (\tau _{\mathrm{d}})$ (Fig. 14h) are relatively flat, which shows that the associated parameter values with maximal probability are weakly identifiable.

Fig. 14

MAP and ML per bin

For a plausibility check of the location of the ML, additional similar bar plots showing the maximal likelihood found within the histogram classes are shown in Fig. 14. Analogously, these bar plots should maximize near the ML, which is fulfilled in all graphs of Fig. 14. The bar plots for $E$ (Fig. 14a) and $\nu$ (Fig. 14b) show a relatively large variation.

The plots in Fig. 14 emphasize that the nonlinear parameter interactions (and the discussed offsets of global to univariate maxima) are not merely an artefact of our chosen implementation, but facts of poor identifiability.

Finally, we demonstrate the consequences of parameter interactions and measurement uncertainties for the prediction of the future material behavior in Fig. 15. The graphs show simulations of the lateral and axial strains of our concrete specimens for $10^{9}$ days under the same constant loading conditions as in the experiment, but for different parameter sets. Particularly, we plotted the simulated strains for 250 realizations of the prior and posterior distributions (satisfying $\varepsilon _{xx}(t)>0$ and $\dot{\varepsilon }_{xx}(t)>0$ for all $t>0$). The results for all posterior realizations, least squares and MAP parameter sets remain quite close to the experimental data and to each other during the experimental time range. However, they become more widespread afterwards due to parameter compensation effects and uncertainties. Specifically, it can be seen that the least squares and MAP parameter sets do not satisfy the monotonicity condition for $\varepsilon _{xx}$. This confirms that (53) is necessary but not sufficient.

Fig. 15

Long-term prediction of strains within the creep tests for different parameter sets. The prediction for the ML parameter set is omitted as the graphs of ML and the best fit realization are really close

Note that the forward uncertainty quantification shown here does not account for all possible sources of uncertainty. While we capture parametric uncertainties and measurement uncertainties within the fractional Zener model, our study does not include uncertainties pertaining to the choice of model equations (such as alternatives to the Zener model), possible long-term ageing effects of concrete, or uncertainties in boundary conditions. This means that the posterior realizations of the parameters visualize a lower bound on the evolution of the uncertainties. Still, the identified spreading of the predicted strains on large time scales shows that the uncertainty quantification is really necessary. However, a comparison with the prior realizations (which fill the graphs almost completely) illustrates that the considered experiments yield a lot of information and that a longer experimental time could improve the prediction.

6 Conclusion

This article provides and analyzes experimental data from long-term creep tests on a salt concrete of type M2 and extensively discusses whether the material behavior can be modelled by a fractional viscoelastic constitutive law. It is shown that a fractional Zener model for hydrostatic and deviatoric stress and strain components yields a beautiful description of the experimental results over the full trial period of two years (Fig. 10). Furthermore, the applied Bayesian inversion yields a probability distribution with plausible combinations of model parameters (Fig. 11). However, the uncertainty quantification reveals that the parameters of the fractional model are only weakly identifiable from the current experimental setup, i.e. the (posterior) probability distributions of the parameters are comparably widespread and their shapes are mainly influenced by prior information (instead of experimental data). As a consequence, the parameter set obtained from the least squares calibration is quite different to the set with maximal posterior probability. Particularly, this effect occurs more severely for the parameters related to the hydrostatic stress and volumetric strain components and for both generalized retardation times. Possible reasons for the weak identifiability are given by large variances of the experimental results (which are not unusual in concrete creep tests, though), the strongly nonlinear interrelation of the model parameters within the model behavior and the experimental setup, which does not allow separate measurement of volumetric and deviatoric effects, which should be considered in prospective measurements.

The computational cost and scientific effort for a Bayesian analysis are admittedly much higher than for a least-squares calibration. However, we are convinced that the benefits of such a Bayesian analysis outweigh these costs, as it measures the parameter identifiability and provides a quantification of the post-calibration uncertainty, which represents the foundation for the computation of predictive uncertainties and the optimal design of experiments. Moreover, the Bayesian analysis reveals nonlinear parameter interactions and allows information from expert elicitation.

The results of this paper can be used in a next step to obtain a forward uncertainty quantification, i.e. an estimation of the transfer of parameter uncertainty to the uncertainty of deformation of concrete structures for long time spans. For an even more complete uncertainty quantification, uncertainties from the choice between competing models, ageing effects and uncertain boundary conditions can be included. Additionally, future experiments can be designed, that are optimal with respect to a certain criterion, e.g. a failure limit of a concrete structure. These tasks will be considered in our future work.