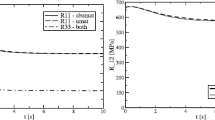Abstract
A constitutive material law for linear viscoelasticity in the time domain is presented. It does not only allow for anisotropic elastic behavior but also for anisotropic (i.e. direction dependent) relaxation response. Under the assumption of thermo–rheological simple material behavior, the model is capable to account for direction dependent time–temperature-shift functions.
The application is demonstrated for a linear viscoelastic matrix material reinforced by linear viscoelastic continuous fibers. The effective orthotropic linear viscoelastic response of the composite is computed by means of a periodic unit cell approach. These data, evaluated at different temperatures, are used to calibrate the input for the developed material law. Predictions from the latter are compared to the results from the unit cell simulations.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
The apparent effects of viscoelasticity manifest itself in a time dependent response to loading and accompanying energy dissipation. Relaxation or creep occurs when a material is exposed to quasi-static loads and load changes. Viscoelastic effects are widespread in natural and in engineering materials. Among them are almost all biological tissues and most polymers, in particular thermoplastic materials. As fiber reinforced plastics, they have gained importance in lightweight design and for industrial applications. Such composites often have elongated reinforcements with preferred orientation. Consequently, their properties are direction depended and the consideration of anisotropy becomes inevitable. In engineering composites, composition and spatial arrangement allow for the tailoring of the properties to meet certain demands arising from service loads of composites parts.
For the design process, computational tools are desired which are capable to predict the response of composite materials. There are two groups of models which serve for this purpose. First, micromechanical approaches which are based on a detailed representation of the geometry of the composite’s constituents, and second, constitutive material laws which describe the homogenized behavior of the composite. The latter are well suited for structural analyses of large scale components and parts made from composites, because they can handle general multi-axial time varying loading scenarios.
A general introduction into viscoelasticity can be found, e.g. in (Lakes 2009; Gurtin and Sternberg 1962; Schapery 2000) which focus predominantly on isotropic behavior. Transversely isotropic (and orthotropic) viscoelastic models have been presented, e.g. in (Holzapfel 2000; Bergström and Boyce 2001), based on invariants of the strain representation, which are commonly used for biological soft tissues. Typically, they combine nonlinear orthotropic elasticity with linear isotropic viscosity. Anisotropic formulations are presented in (Li et al. 2016; Pettermann and DeSimone 2018; Endo and de Carvalho Pereira 2017) which treat the direction dependence not only of the elasticity but also of the relaxation contribution. A linear viscoelastic constitutive law in the time domain for cubic material symmetry is presented in (Pettermann and Hüsing 2012) and applied to highly porous structures. Linear and nonlinear orthotropic viscoelasticity adopting not the full set of orthotropic viscous effects is presented in (Melo and Radford 2004; Kaliske 2000) and applied to composites and foam materials, respectively. An anisotropic nonlinear viscoelastic constitutive law has been introduced in (Schapery 1969) which found widespread application to study composite materials.
Micromechanical approaches based on numerical schemes are presented in (Brinson and Lin 1998; Liu and Brinson 2006; Brinson and Knauss 1991) to study composites. However, such approaches pertain to material characterization rather than formulating an anisotropic viscoelastic constitutive law. Micromechanical approaches based on (semi) analytical schemes are presented in (Hashin 1966; Friebel et al. 2006). Typically, Laplace transforms are utilized and the back transformation is facilitated by numerical means.
For the treatment of temperature dependent relaxation response in the context of linear viscoelasticity, the common approach is to introduce a time–temperature-shift function (TTS), based on the assumption that relaxation processes take place faster at higher temperatures; see e.g. (Lakes 2009; Tschoegl et al. 2002). This way, a functional relation between temperature and the so called reduced time can be established. Materials obeying the above assumption are called thermo–rheological simple. However, not all materials are thermo–rheological simple, as has been shown for polymer blends, block co-polymers, multi-phase system, and the like in, e.g. (Fesko and Tschoegl 1971; Caruthers and Cohen 1980; Tao et al. 2018). Micromechanical modeling to predict thermo–rheological complex response has been applied for some composite material in (Brinson and Knauss 1991) based on unit cell approaches, and e.g. in (Kaplan and Tschoegl 1974; Gibson et al. 1982; Nakano 2013) based on stress and strain coupling considerations. The concept of thermo–rheological simplicity, also, establishes a relation between temperature and frequency for considerations in the frequency domain. It is not only used in simulations but is also widely utilized in experimental material characterization.
The present paper somewhat extends the concept of thermo–rheological simplicity by introducing direction dependent TTS functions. An orthotropic material model is set up to allow for independent TTS functions with respect to the principal material directions, in each of which thermo–rheological simple response is assumed. The developments are based on the constitutive material law for linear thermo–viscoelasticity in the time domain with orthotropic material symmetry under plane stress assumption as presented in (Pettermann and DeSimone 2018, 2016). The formulation of the constitutive material law allows not only for elastic orthotropy but also for orthotropic relaxation behavior, i.e. the viscous part of the response is direction dependent. The formulation of the TTS functions is orthotropic as well. The constitutive law is implemented into the commercial FEM package ABAQUS/Standard (R2018) (Dassault Systémes Simulia Corp., Providence, RI, USA) using the interface “user supplied material routine” (UMAT).
The developments are exemplified on a continuous fiber reinforced composite with dissimilar generic material data of the constituents. Both the fiber and the matrix material is linear viscoelastic and possess different TTS functions. A periodic unit cell approach is employed to compute a set of homogenized composite responses. These are used to calibrate the input parameters for the developed constitutive law. The predicted behavior by the latter is compared to the unit cell simulations with respect to the quality of the orthotropic material fit including the TTS. The concept of direction dependent TTS functions is discussed, and the predictive capabilities for the present example is assessed.
In addition, linear elastic fibers as well as fibers with the same TTS function as the matrix are employed to study its effect on the composite’s temperature dependent relaxation.
2 Constitutive model
The constitutive model as presented in (Pettermann and DeSimone 2018, 2016) is briefly reviewed. It is formulated for linear viscoelasticity under plane stress conditions and orthotropic material symmetry. The equations, however, are of general character and can be extended to tri-axial settings in a straightforward manner.
The hereditary integral in tensorial form reads
adopting plane stress and Voigt notation, stress and strain are given as
The time dependent material tensor for orthotropic materials under plane stress,
is composed of individual relaxation functions,
which are given by Prony series expansions with \(R_{ij \; 0}\) being the instantaneous values, i.e. the elasticity tensor elements giving the short term behavior. The sum over \(k\) Prony terms contains the relative relaxation elements, \(r_{ij \; k}\), and the corresponding characteristic times, \(\tau ^{r_{ij \; k}}\).
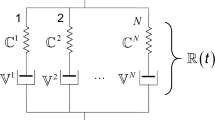
This formulation requires extended treatment in contrast to the isotropic (or uni-axial) case which can be formulated by uncoupled scalar equations. In the present formulation of the relaxation tensor, Eq. (3), each terms can exhibit its own independent relaxation behavior. Also, each term can exhibit its own independent TTS function which will be exploited next.
The temperature dependence of viscoelastic material response is widely treated by introducing a reduced time; see e.g. (Lakes 2009; Tschoegl et al. 2002). This way, it is accounted for the fact that the internal deformation mechanisms can act faster at higher temperatures. The reduced time,
modifies the “real” time, \(t\), by the shift function, \(A_{ij}(T)\), which depends on the temperature, \(T\). Note that the formulation of Eqs. (3) and (4) offers the opportunity to treat each relaxation function \(R_{ij}(t_{{\mathrm{red}} \; ij})\) in dependence of its own individual reduced time. This is enabled by direction dependent TTS functions, \(A_{ij}(T)\), and applying Eq. (5).
For polymers the empirical Williams–Landel–Ferry (WLF) shift function is often used which reads,
with \(T_{{\mathrm{ref}} \; ij} \) being the reference temperature and \(C_{1 \; ij}\) and \(C_{2 \; ij}\) are constants pertaining to the particular material under consideration.
The implementation of the viscoelastic model is carried out by means of the UMAT option for ABAQUS/Standard (R2018) (Dassault Systémes Simulia Corp., Providence, RI, USA). For details of the numerical solution strategy see (Pettermann and DeSimone 2018). Arrhenius shift functions are implemented, too, and not only the parameters but even the type of shift function can be selected individually for each element \(R_{ij}(t_{{\mathrm{red}} \; ij})\) within one analysis run. These features, however, are not used in the present study. Here, only a set of individual WLF functions, \(A_{ij}(T)\), is used.
3 Example — composite
To apply the developments a composite material with continuous fiber reinforcement of 40%vol is studied. In the following, for the relaxation tensor elements Voigt notation is used as given in Eqs. (3) and (4). In contrast, stress and strain components are printed in their two index tensor representations.
Both fiber and matrix material are taken to be isotropic, linear viscoelastic, and thermo–rheological simple. Generic material behavior is assumed; see Tables 1 and 2. The instantaneous Young’s modulus of the fibers is ten times the one for the matrix, the instantaneous Poisson’s ratio is assumed to be identical. The bulk response is linear elastic (i.e. no bulk relaxation occurs, \(k=0\)) for matrix as well as fiber material. Each relaxation function for the shear responses is given by one Prony term only, whereby the matrix shows more pronounced but slower relaxation. The WLF shift function parameters for the matrix follows some common values, whereas the WLF function of the fibers reflect a more pronounced temperature dependence. The ABAQUS/Standard built in material model is employed to model the matrix and fiber behavior. Graphs of the shear relaxation functions for the matrix and the fiber material as functions of the temperature are shown in Fig. 1.
3.1 Unit cell homogenization
Now the effective behavior of the composite material is predicted by computational homogenization based on periodic unit cell simulations. For the case of linear viscoelastic composites, the entire constitutive behavior can be extracted by computational homogenization of unit cells in a consistent way. The response is solely and comprehensively determined by the relaxation tensor elements as given in Eqs. (3) and (4). They can be computed by a set of three independent load cased for plane stress situations as in the present study, or by six independent load cases for full anisotropy in tri-axial cases. Particularly suited for that purpose are uni-axial strain Heaviside steps. Once the \(R_{ij}(t)\) are predicted, proper terms for the Prony series have to be calibrated to achieve a suitable fit. The latter is the only approximation to get from the unit cell results to the homogenized representation by the constitutive material law. Note that the above described procedure is not possible for other dissipative material responses and anisotropic nonlinear (visco)elasticity. In such cases, free/dissipation energy potentials have to be given which cannot be gained in a direct and consistent way from unit cell homogenization.
The employed FEM unit cell (Pettermann and Suresh 2000) represents a periodic hexagonal arrangement of aligned fibers in three-dimensional space; see Fig. 2. Eight-noded isoparametric continuum elements with linear interpolation functions and full integration are used. The unit cell is equipped with fully periodic displacement boundary conditions to allow for arbitrary loading scenarios. Note that the periodicity in 3-direction is shifted by half of the unit cell width to reduce its size. To apply the loads and to read the responses, the concept of the macroscopic degrees of freedom, see e.g. (Böhm 2004), is utilized. Thereby, the four master nodes which sit at the corners of the unit cell at the coordinate axes are used to control the homogeneous (far field) stresses and strains. To achieve the required plane stress conditions, i.e. \(\sigma _{3i}=0\), the corresponding master node on the 3-axis show force free boundary conditions. The boundary conditions of the remaining master nodes are displacement controlled to realize the set of required Heaviside step loading conditions for evaluation of \(R_{ij}(t)\) in Eqs. (3) and (4). For example, a Heaviside step displacement at \(t=0\) is applied to represent \(\varepsilon _{11}(t>0)=1\), and \(\varepsilon _{22}=\gamma _{12}=0\) at any time. From the reaction forces at the master nodes, the stress responses follow which correspond to \(R_{11}(t)\) and \(R_{12}(t)\), respectively. For the remaining elements of \(R_{ij}(t)\), Heaviside step strains of \(\varepsilon _{22}(t>0)=1\) and \(\gamma _{12}(t>0)=1\) are applied and evaluated accordingly (see also (Pettermann and DeSimone 2018)).
The simulations are carried out for four constant temperatures each of which is assumed to be in stress free state, i.e. no thermal expansion effects are considered. The predicted temperature dependent effective relaxation behavior of the composite is shown in Fig. 3 (thick lines). Note that even if the constituents of the composite are thermo–rheologically simple, the homogenized response of the composite does not need to be.
Temperature dependent relaxation functions \(R_{ij}\) of the composite for 8, 4, 0, and −4 °C, unit cell predictions (thick lines), corresponding homogenized responses of the constitutive law with direction dependent shift functions (Table 3, thin solid lines) and selected results with isotropic shift functions from fiber (thin dashed) and matrix (thin dotted) data, respectively
3.2 Constitutive law calibration and predictions
Next, the material parameter for the UMAT input can be calibrated, including direction dependent TTS functions. The short and long term values, i.e. \(R_{ij \; 0}\) and \(R_{ij}(t \rightarrow \infty )\) as well as \(\sum _{k} r_{ij \; k}\), can be computed directly from the short and long term responses of the unit cell and are not influenced by the TTS. It remains the fitting of the relative relaxation elements, \(r_{ij \; k}\), (if \(k>1\)) and the corresponding characteristic times, \(\tau ^{r_{ij \; k}}\). This is done for \(T=T_{\mathrm{ref}}=0\) °C, which is taken as the reference temperature for the WLF data in all cases throughout this example. The complete data set is listed in Table 3. Note that a proper fit for the coupling term \(R_{12}(t)\) requires (at least) two Prony terms since it does show a change of curvature when displayed in linear time (corresponding effects have been discussed in (Pettermann and DeSimone 2018)). The response of \(R_{11}(t)\), \(R_{22}(t)\), and \(R_{33}(t)\) can be fitted properly by one term each. For the sake of completeness, the values \(r_{ij}=0\) are added to Table 3. The WLF shift parameters are fitted based on the unit cell responses, too, also accounting for direction dependence.
Single element simulations are carried out and the predictions by the constitutive law are added to Fig. 3 (thin solid lines), including direction dependent time–temperature shifts. For selected cases, results computed by means of the isotropic shift functions of the fiber (thin dashed lines) and the matrix (thin dotted lines) material, respectively, are added.
3.3 Discussion of direction dependent TTS
The most straightforward interpretation can be given for the shear response, i.e. \(R_{33}\). The calibration of the relaxation response with one Prony term is sufficient. For the pertinent shear loading scenario the matrix properties dominate the effective relaxation behavior. The characteristic time is the same as for the matrix and the relative relaxation element is slightly lower owing to the presence of the fibers. The WLF shift parameters are essentially identical to that of the matrix material and fit the temperature dependence very well. Moreover, thermo–rheological simple behavior for this relaxation element applies, and the TTS shift function of the matrix material is inherited to the composite. Application of the shift function of the fiber material (thin dashed lines) does not give rise to satisfactory predictions. Equivalent interpretations hold true for \(R_{22}\), i.e. loading perpendicular to the fibers. At high temperature the fit shows some minor deviations.
The response in fiber direction, \(R_{11}\), is widely dominated by the presence of the continuous fibers (and their material properties). The temperature dependence of the relaxation is more pronounced, i.e. the curves are more spread out, owing to the TTS function of the fibers. At high and low temperatures, moreover, thermo–rheological simplicity seems to be violated to some extent. Note that the unit cell predictions give the “correct” response (within the framework of computational homogenization), while the UMAT results resemble thermo–rheological simple behavior. The UMAT predictions (in combination with direction dependent shift functions) may be considered acceptable in a certain temperature range for which a particular fit can be found. Neither the application of the shift function of the fiber material nor the one of the matrix material give rise to satisfactory predictions. In fact the developed direction dependent shift functions contribute to a much better approximation of the temperature dependent behavior of the studied orthotropic composite.
The relaxation element which implicitly carries the Poisson effect, \(R_{12}\), shows the most complicated behavior. The fit for the reference temperature (\(T_{\mathrm{ref}}=0\) °C) is facilitated by two Prony terms and shows some minor deviation at short times. For the other temperatures the deviation increases. In comparison to the thermo–rheological simple assumption by the UMAT, the unit cell predictions show a variation of the maximum slope in the graphs. At the highest temperature the fit does not well resemble the response, in particular for short times. However, the approximation is much better than applying the isotropic shift functions from fiber or matrix material. Alternatively, the fit could be made with respect to another reference temperature to better represent a certain temperature range, of course, compromising the predictions at deviating temperatures. Note that the predicted response by the unit cell at the highest temperature shows a non-monotonic behavior in time, a behavior which has been addressed in (Pettermann and DeSimone 2018), too.
For the present example with generic material data, the effective direction dependent TTS functions which imply thermo–rheological simple behavior can be applied with a sufficient degree of accuracy for the most important properties. The highest deviations arise for the coupling element which may be considered as being of “secondary” importance. In any case, the approximated individual direction dependent TTS functions work much better than some unique one would do. Considering the capability of an analytical constitutive law, such a compromise is considered viable, even more, as it enables the simulation of large components.
Moreover, the present formulation of the constitutive law allows for a (straightforward) extension of the implementation with more intricate shifting functions. Doing so, the full capability of different shifting functions for the different \(R_{ij}\) would be maintained, including a possible mixture of shifting types.
3.4 Variation of the fiber material
In addition, linear elastic fibers as well as fibers with the same TTS function than the matrix are employed. Matrix material (Table 1), fiber arrangement, and fiber volume fraction are kept the same throughout these investigations. Homogenization by the periodic unit cell approach is carried out to study the effect on the composite’s temperature dependent relaxation.
First, linear elastic, isotropic glass fibers are used as reinforcement with an Young’s modulus of \(E=70000\) MPa and a Poisson’s ratio of \(\nu =0.2\) The relaxation tensor, \(R_{ij}(t)\), of course, exhibits the expected orthotropic behavior with direction dependent elasticity and relaxation. Predictions for various temperatures, however, revealed that the TTS function of the matrix material applies to all elements of the relaxation tensor (no graphs shown) and thermo–rheological simplicity holds true.
Second, a linear viscoelastic, isotropic fiber material is chosen which is dissimilar from the matrix but has the same TTS function as the matrix. In fact, the instantaneous elasticities and the Prony term are taken from Table 2 and the WLF data from Table 1 to prescribe the fiber properties. Again, the relaxation tensor, \(R_{ij}(t)\), exhibits the expected orthotropic behavior with direction dependent elasticity and relaxation. Predictions for various temperatures show that the identical TTS functions of matrix and fiber now apply to all elements of the relaxation tensor (no graphs shown) and thermo–rheological simple material behavior is resembled.
4 Summary
A constitutive material law for linear viscoelasticity in the time domain with orthotropic material symmetry under plane stress assumption is presented, and it is extended to allow for direction dependent time–temperature-shift functions. The concept of thermo–rheological simple materials is widened in the sense that different directions can have their individual shift functions. The developments are implemented into the commercial FEM package ABAQUS/Standard using the interface “user supplied material routine”.
As an example a model composite is studied with orthotropic material symmetry in a plane stress setting. It is composed of two distinct isotropic linear viscoelastic constituents with different time–temperature-shift functions. The effective response is predicted by computational homogenization employing unit cell simulations. From those the material parameters for the developed constitutive law are calibrated, including direction dependent shift functions. The responses are compared and discussed in terms of thermo–rheological simplicity and the direction dependent effective shift functions.
For some directions the effective shift functions work well, for some other directions they are of approximate character. However, a significant improvement compared to some direction independent time–temperature-shift functions is demonstrated.
Moreover, the present formulation of the constitutive law allows for an extension of the implementation with more intricate shifting functions, while maintaining the capability of different shifting functions for the different \(R_{ij}\), including a possible mixture of shifting types.
For composites with linear elastic fibers embedded in a linear viscoelastic matrix, the composite exhibits the shift function of the matrix, independent of the direction.
Finally, the constitutive material law enables the simulation of large structures which is far beyond the feasibility of numerical micromechanics based approaches. This way, the developed constitutive law provides a tool for structural analyses of components made from orthotropic linear viscoelastic materials.
References
Bergström, J., Boyce, M.: Constitutive modeling of the time-dependent and cyclic loading of elastomers and application to soft biological tissues. Mech. Mater. 33(9), 523–530 (2001)
Böhm, H.J.: A short introduction to continuum micromechanics. In: Mechanics of Microstructured Materials, pp. 1–40. Springer, Berlin (2004)
Brinson, L., Knauss, W.: Thermorheologically complex behavior of multi-phase viscoelastic materials. J. Mech. Phys. Solids 39(7), 859–880 (1991)
Brinson, L., Lin, W.: Comparison of micromechanics methods for effective properties of multiphase viscoelastic composites. Compos. Struct. 41(3), 353–367 (1998)
Caruthers, J., Cohen, R.: Consequences of thermorheological complexity in viscoelastic materials. Rheol. Acta 19(5), 606–613 (1980)
Endo, V.T., de Carvalho Pereira, J.C.: Linear orthotropic viscoelasticity model for fiber reinforced thermoplastic material based on Prony series. Mechanics of Time-Dependent Materials 21(2), 199–221 (2017)
Fesko, D., Tschoegl, N.: Time–temperature superposition in thermorheologically complex materials. J. Polym. Sci., C Polym. Symp. 35(1), 51–69 (1971)
Friebel, C., Doghri, I., Legat, V.: General mean-field homogenization schemes for viscoelastic composites containing multiple phases of coated inclusions. Int. J. Solids Struct. 43(9), 2513–2541 (2006)
Gibson, A., Jawad, S., Davies, G., Ward, I.: Shear and tensile relaxation behaviour in oriented linear polyethylene. Polymer 23(3), 349–358 (1982)
Gurtin, M.E., Sternberg, E.: On the linear theory of viscoelasticity. Arch. Ration. Mech. Anal. 11(1), 291–356 (1962)
Hashin, Z.: Viscoelastic fiber reinforced materials. AIAA J. 4(8), 1411–1417 (1966)
Holzapfel, G.A.: Nonlinear Solid Mechanics, vol. 24. Wiley, Chichester (2000)
Kaliske, M.: A formulation of elasticity and viscoelasticity for fibre reinforced material at small and finite strains. Comput. Methods Appl. Mech. Eng. 185(2), 225–243 (2000)
Kaplan, D., Tschoegl, N.: Time–temperature superposition in two-phase polyblends. In: Recent Advances in Polymer Blends, Grafts, and Blocks, pp. 415–430. Springer, Berlin (1974)
Lakes, R.S.: Viscoelastic Materials. Cambridge University Press, Cambridge (2009)
Li, J., Kwok, K., Pellegrino, S.: Thermoviscoelastic models for polyethylene thin films. Mech. Time-Depend. Mater. 20(1), 13–43 (2016)
Liu, H., Brinson, L.C.: A hybrid numerical-analytical method for modeling the viscoelastic properties of polymer nanocomposites. J. Appl. Mech. 73(5), 758–768 (2006)
Melo, J.D.D., Radford, D.W.: Time and temperature dependence of the viscoelastic properties of peek/im7. J. Compos. Mater. 38(20), 1815–1830 (2004)
Nakano, T.: Applicability condition of time–temperature superposition principle (ttsp) to a multi-phase system. Mech. Time-Depend. Mater. 17(3), 439–447 (2013)
Pettermann, H.E., DeSimone, A.: A linear thermo-viscoelastic orthotropic constitutive law — application to composites. In: Drechsler, K. (ed.) Proceedings of the 17th European Conference on Composite Materials, Paper Nr. TUE1-BUD-3.051. European Society for Composite Materials, Munich (2016)
Pettermann, H.E., DeSimone, A.: An anisotropic linear thermo-viscoelastic constitutive law. Mech. Time-Depend. Mater. 22(4), 421–433 (2018)
Pettermann, H., Hüsing, J.: Modeling and simulation of relaxation in viscoelastic open cell materials and structures. Int. J. Solids Struct. 49(19), 2848–2853 (2012)
Pettermann, H.E., Suresh, S.: A comprehensive unit cell model: a study of coupled effects in piezoelectric 1–3 composites. Int. J. Solids Struct. 37(39), 5447–5464 (2000)
Schapery, R.A.: On the characterization of nonlinear viscoelastic materials. Polym. Eng. Sci. 9(4), 295–310 (1969)
Schapery, R.: Nonlinear viscoelastic solids. Int. J. Solids Struct. 37(1), 359–366 (2000)
Tao, W., Shen, J., Chen, Y., Liu, J., Gao, Y., Wu, Y., Zhang, L., Tsige, M.: Strain rate and temperature dependence of the mechanical properties of polymers: a universal time–temperature superposition principle. J. Chem. Phys. 149(4), 044105 (2018)
Tschoegl, N.W., Knauss, W.G., Emri, I.: The effect of temperature and pressure on the mechanical properties of thermo-and/or piezorheologically simple polymeric materials in thermodynamic equilibrium–a critical review. Mech. Time-Depend. Mater. 6(1), 53–99 (2002)
Acknowledgements
Part of the work of HEP has been done during a sabbatical stay at SISSA in summer 2018.
Funding
Open access funding provided by TU Wien (TUW).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pettermann, H.E., Cheyrou, C. & DeSimone, A. Modeling and simulation of anisotropic linear viscoelasticity. Mech Time-Depend Mater 25, 679–689 (2021). https://doi.org/10.1007/s11043-020-09468-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11043-020-09468-8